随着我国核电发电量的不断提升，到2030年累计产生的乏燃料预计超过4×10⁴ t^[1-2]。为了满足日益增长的乏燃料后处理需求，急需适用于核辐射环境的各类操作机器人，代替人类完成诸如取样、检测、搬运和检修等相关作业。目前，机器人已逐渐应用于核工业领域，在一定程度上解决了处理效率低下、人员操作困难等问题^[3]。涉核作业机器人安装于乏燃料后处理热室内，电机集中安装于机器人顶端并放置于热室外，以避免电子设备受到核辐射等干扰^[4-5]。机器人一般通过齿轮传动链将动力传递给各个关节，实现热室内的相关操作，使操作人员免受核辐射影响^[6]。机器人的齿轮传动链较长，且关节均采用齿轮嵌套结构，机器人自重又较大，同时其末端夹钳会受到操作负载的作用，因此机器人关节以及连杆会产生相应的受力变形，进而影响到末端的操作精度。因此，研究涉核作业机器人的刚度与末端变形具有十分重要的意义。

对于一般的机械结构，常见的刚度建模方法主要有结构矩阵分析法（matrix analysis of structure，MSA）^[7-8]、有限元分析法（finite element analysis，FEA）^[9]和虚拟关节法（virtual joint method，VJM）^[10-11]等3种。采用MSA时，为了减少求解计算量，需要将复杂结构进行简化，再结合线性叠加原理等对机器人刚度进行建模，相较于FEA，效率有较大提升，但会降低刚度模型的精度；FEA可以对复杂结构进行三维建模，但针对机器人的不同位姿，需要重新建模并求解，处理效率较低，其一般用于对刚度建模理论的佐证；VJM则将机器人连杆视为刚体件、关节视为柔性件，不仅可以减少求解工程量，还可以满足较高的精度要求，因此其应用较多。

关于机器人刚度与末端变形，国内外已有了一些研究。如：Abele等^[12]基于连杆刚性假设，计算了关节柔度引起的机器人末端变形，并对机器人的铣削轨迹进行了补偿；Chen等^[13]在Abele研究的基础上，考虑了末端载荷对机器人姿态的微小影响，提出了保守同余变换（conservative congruence transformation，CCT），提高了机器人刚度建模的准确性；Alicia等^[14]通过在机器人末端执行器上施加外力模拟实际工况，来提高关节刚度的辨识精度，进而提高机器人末端刚度计算的精确性；Kim等^[15]为了处理机器人应用中由应用扳手引起的结构偏转的顺应性误差，提出了一种基于机器人身体框架计算每个关节精确补偿量的关节柔顺误差补偿方法；郭英杰等^[16]研究了机器人末端变形与力之间的耦合关系，建立了机器人刚度模型，并基于该模型提出了变形预测与补偿方法；王一等^[17]为了降低机器人机械臂自重和末端负载对机器人定位精度的影响，提出了一种定位误差补偿方法；孙龙飞等^[18]基于能量法计算了机器人末端变形，建立了全域刚度预估模型；张永贵等^[19]将机器人的关节、连杆作为柔性件处理，推导出机械臂柔度矩阵，提出了一种包含力-角位移、力-位移、力矩-角位移、力矩-位移等数据的刚度椭球模型，来分析机器人的刚度特性。上述研究主要集中于普通工业机器人，涉及涉核作业机器人的研究文献较少。

本文首先分析了涉核作业机器人的结构及全齿轮耦合传动原理，建立了运动学模型；其次，求解了机器人关节力矩与连杆广义力，建立了关节刚度模型和连杆刚度模型，综合得到了机器人末端变形模型；最后，通过有限元方法分析求解了机器人末端变形，并进行了现场测试，来验证所建模型的准确性。

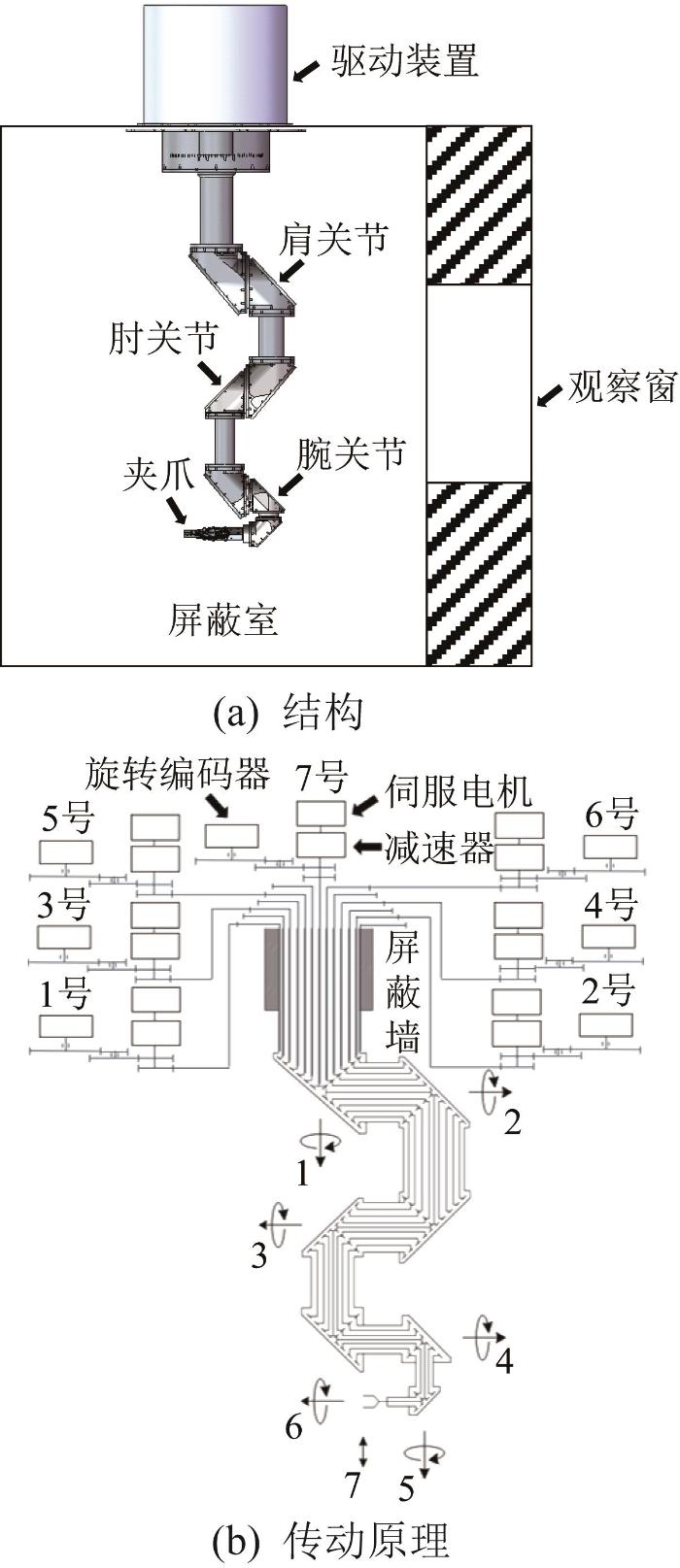
考虑到在涉核环境中不允许使用电机、传感器等电子元件，机器人采用全齿轮耦合传动，外壳采用不锈钢材料，且采取全密封设计。机器人结构及传动原理如图1所示。伺服电机等电子元件均放置于机器人顶端，以保证机器人能正常、可靠地运行。

采用七轴设计方案。机器人主要由伺服电机、行星减速器、直齿圆柱齿轮、锥齿轮、同心轴和夹爪等组成，形成了7条齿轮传动链。传动链i（i=1, 2, …, 7）分别用来控制机器人肩关节转动、肩关节摆动、肘关节摆动、腕关节摆动、腕关节转动、夹爪转动和夹爪张合等。

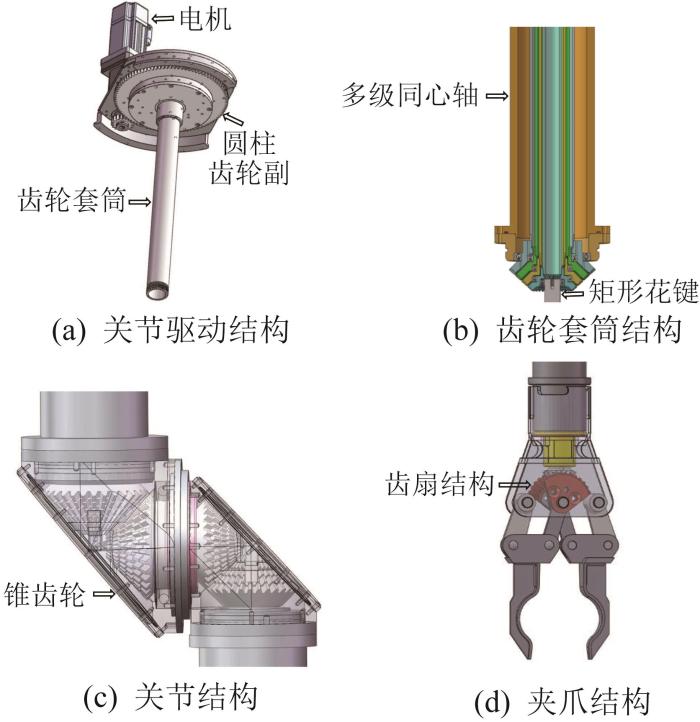
机器人传动系统的结构如图2所示。图2(a)为机器人关节驱动结构，电机通过减速器减速后驱动圆柱齿轮副，从而带动齿轮套筒旋转。图2(b)为齿轮套筒结构，其以多级同心轴结构的形式组合而成，套筒与齿轮之间采用矩形花键连接来传递扭矩。图2(c)为关节结构，其采用全密封设计，通过锥齿轮带动关节转动或摆动。图2(d)为夹爪结构，其为齿扇结构，将齿轮的旋转运动转换为夹爪的张合运动。不同夹爪采用相同的安装接口，可以满足不同操作对象或作业任务的使用要求。

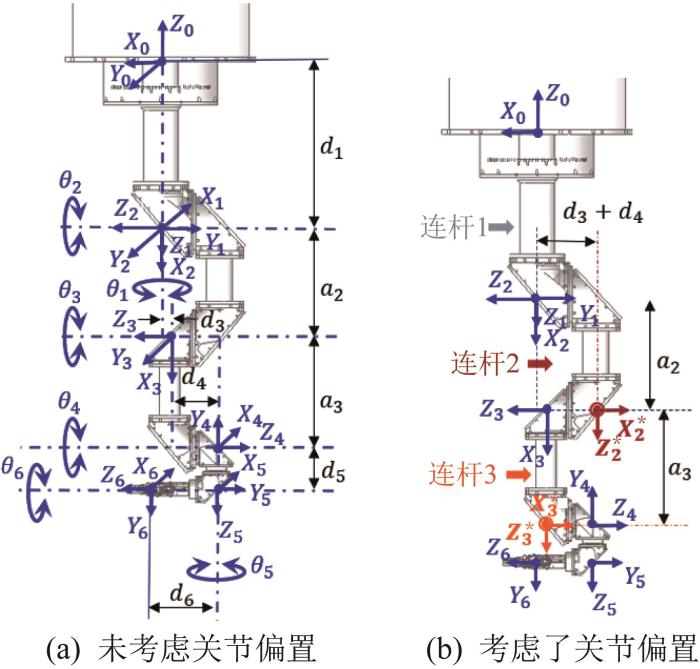
由于机器人结构的不对称性，其运动学建模过程比较复杂。根据机器人运动学建模理论，采用D-H（Denavit-Hartenberg）法建立机器人连杆坐标系，如图3所示，相应的D-H参数如表1所示。表中：ai-1为连杆长度，αi-1为连杆扭角，di为连杆偏置距离，θi为关节转角。

考虑到机器人存在关节偏置，且连杆2、连杆3的长度较长，产生的柔性变形较为显著，为精确求解机器人连杆末端广义力及末端变形，在连杆2和连杆3的末端新增了2个坐标系{2*}和{3*}，如图3(b)所示。考虑到坐标系较多，为了突出2个新增坐标系，图3(b)中略去了部分原坐标轴的标注。

根据机器人运动学理论，采用运动学参数降维的方法^[20]简化运动学计算，得到坐标系{i}相对于坐标系{i-1}的坐标变换矩阵：

式中：s表示sin，c表示cos。

根据式(1)，可依次求出10T、21T、32T、43T、54T、65T，则可得机器人坐标系{6}相对于坐标系{0}的齐次变换矩阵：

由于在原有坐标系的基础上新增了坐标系{2*}和{3*}，则原坐标系下的齐次变换矩阵32T等价于新坐标系下的2*2TT32*，原坐标系下的齐次变换矩阵43T等价于新坐标系下的3*3TT43*，其中：

因此，新坐标系下齐次变换矩阵60T为：

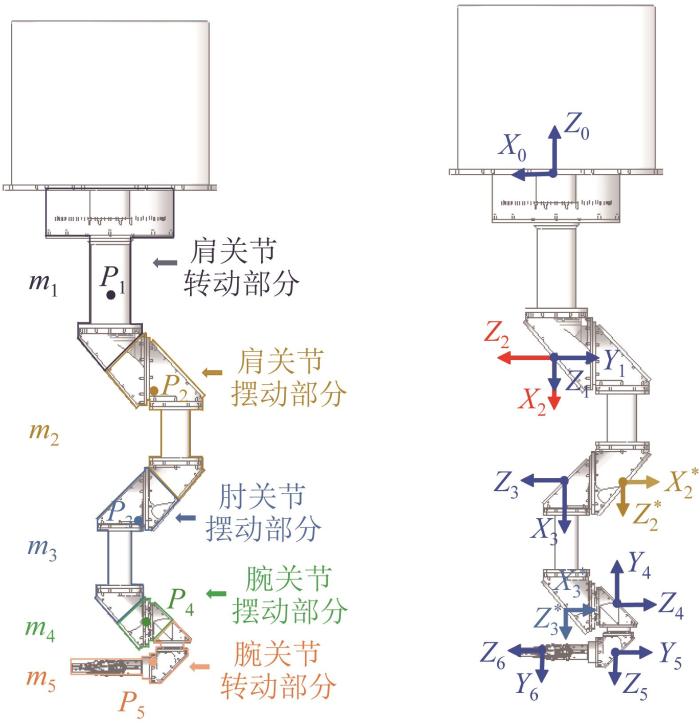
涉核作业机器人的自重相对其载荷较大，因此在肩关节摆动、肘关节摆动、腕关节摆动和腕关节转动时，各个关节会在自重的影响下受到力矩的作用，各连杆末端也会因广义力的作用产生柔性变形。机器人各部分质量与质心如图4所示，各质心坐标如表2所示。

1）各部分质量相对各坐标系的等效广义力。

由于腕转部分的质量对各个关节和连杆末端均有影响，下面以腕转部分质量为例，求解其相对各坐标系的等效广义力。

步骤1：求解腕转部分质量m5在坐标系{5}下的重力矢量。

由于坐标系{0}与机器人基座相连，在坐标系{0}下的重力矢量为00m5gT。通过左乘旋转矩阵05R，求出m5在坐标系{5}下的重力矢量55为：

步骤2：求解重力矢量55在坐标系{5}下的等效广义力5f5m5m5T。

根据力矩求解公式，可求得重力矢量55在坐标系{5}下的广义力为5f5m5m5T。其中:

步骤3：求解重力矢量55在坐标系{4}下的等效广义力4f5m4m5T。

式中：4p5表示坐标系{5}的坐标原点在坐标系{4}中的位置，4p5表示4p5的反对称矩阵。以下同理。

步骤4：求解重力矢量55在坐标系{3*}下的等效广义力3*f5m3*m5T。

根据式(8)，先求出重力矢量55相对坐标系{3}的广义力3f5m3m5T，再根据式(9)求出 3*f5m3*m5T。

步骤5：同理，根据步骤3和步骤4，分别求解重力矢量55在坐标系{2*}下的等效广义力2*f5m2*m5T、在坐标系{1}下的等效广义力1f5m1m5T及在坐标系{6}下的等效广义力6f5m6m5T。

机器人其他部分质量相对各坐标系的等效广义力可按照上述步骤同理求得。

2）自重作用下的关节等效广义力与力矩。

肩转动关节和摆动关节受机器人自重产生的等效广义力Fj1G、Fj2G分别为：

肘摆动关节受机器人自重产生的等效广义力Fj3G为：

腕摆动关节和转动关节受机器人自重产生的等效广义力Fj4G、Fj5G分别为：

求解出各关节的等效广义力后，可求出各关节的力矩TjiG：

3）自重作用下的连杆广义力。

关节1、关节2、关节3末端的坐标系分别为{1}、{2*}、{3*}。同理，在机器人自重作用下，连杆1、连杆2、连杆3末端受到的等效广义力Fl1G、Fl2G、Fl3G分别为：

设JT为机器人的力雅克比矩阵，则机器人末端受到的外力Fe=[fxfyfzmxmymz]T与其对应的关节力矩TjFe=diag[Tj1FeTj2FeTj3FeTj4FeTj5FeTj6Fe]的关系为：

在机器人末端负载Fe作用下，连杆1、连杆2和连杆3末端的等效广义力分别为：

综上，在自重和负载作用下，机器人关节受到的总扭矩矩阵Tj为：

在机器人自重和负载作用下，连杆1、连杆2、连杆3末端受到的等效广义总力Fli为：

机器人的驱动装置安装在机器人顶端，传动链较长，且齿轮套筒结构包含多根同心轴，机器人绕关节轴线的扭转刚度相对较小，并且机器人关节处的支撑轴承采用高刚度交叉滚子轴承，因此，对机器人关节刚度进行建模时，仅需考虑绕关节轴线的扭转刚度。

机器人的传动链由伺服电机、行星减速器、直齿圆柱齿轮、锥齿轮、传动轴和输出轴等零部件组成。

1）轴类零件的扭转刚度。

机器人各关节的传动链中，齿轮间的旋转运动通过花键空心轴来传递，则其扭转刚度k_z为：

式中：G为材料剪切模量，D为轴的外径，d为轴的内径，L为轴的长度。

2）直齿圆柱齿轮副啮合刚度。

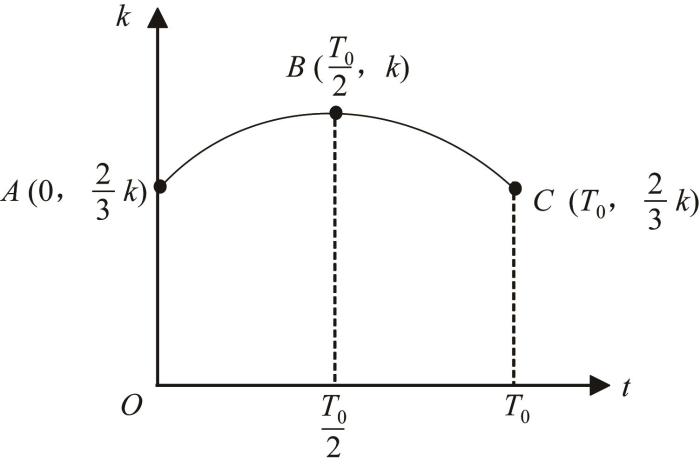
一个啮合周期T₀内单对轮齿啮合的刚度曲线如图6所示^[21]。其中，A、B、C分别为啮入点、节点和啮出点，啮入点和啮出点的刚度只占节点刚度k的2/3。

单对轮齿节点B处的啮合刚度kB为：

式中：q为节点柔度的最小值，mm⋅μm/N。

重合度为ε的轮齿平均啮合刚度kε为：

将圆柱齿轮副啮合刚度转化为圆柱齿轮扭转啮合刚度k_T：

式中：b为齿宽，r_c为从动轮的节圆半径。

3）锥齿轮副啮合刚度。

可用锥齿轮齿宽中点处的当量圆柱齿轮来等效替代锥齿轮。根据锥齿轮的分锥角δ和齿数z，计算当量圆柱齿轮齿数z_v, zv=z/cosδ。根据锥齿轮的大端模数m和齿宽系数ψ，计算当量圆柱齿轮模数m_v，mv=m(1-0.5ψ)。将锥齿轮副的啮合刚度转化为锥齿轮的扭转啮合刚度k′_T，可得：

式中：r′_c为锥齿轮的分度圆半径，kvε为当量圆柱齿轮副平均啮合刚度。

关节等效刚度是指将传动链中各零部件的刚度折算到关节输出轴，再根据机器人各关节之间的串联关系计算出机器人关节扭转刚度。

机器人关节的等效刚度由各零部件的刚度串联而成。根据机器人刚度计算方法，单个关节等效刚度kji为：

式中：kr为零部件绕自身轴线的扭转刚度，n为减速器的减速比。

计算得到肩转动关节的等效扭转刚度kθ1、肩摆动关节的等效扭转刚度kθ2、肘摆动关节的等效扭转刚度kθ3、腕摆动关节的等效扭转刚度kθ4、腕转动关节的等效扭转刚度kθ5、夹爪转动关节的等效扭转刚度kθ6，最后得到机器人关节扭转刚度矩阵 k_θ 为：

根据上述建立的关节扭转刚度矩阵，通过式(32)可以求出各关节的弹性变形矩阵dj：

机器人在自重和末端负载作用下，根据式(19)和式(32)可以求得末端变形Δδθ为：

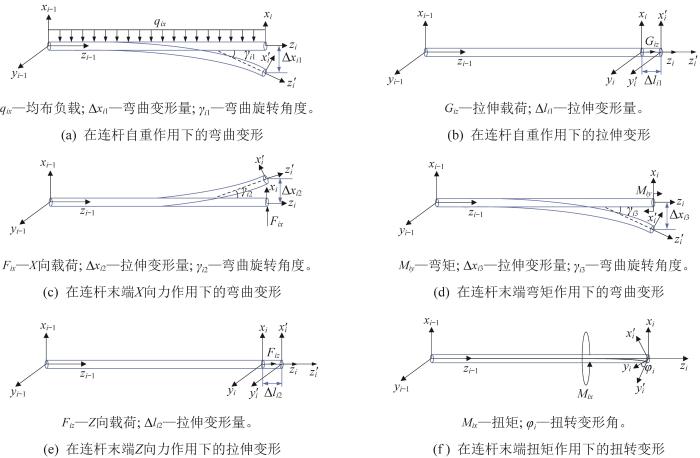
机器人在自重和末端负载作用下，其关节之间连杆的细长结构会产生相应的挠度变形。考虑到连杆均为结构相对简单的套筒结构，将各连杆简化后结合连杆自重及末端受到的力和力矩，来计算连杆在受力后产生的变形以及相应的机器人末端变形。

本文基于伯努利-欧拉梁假设理论，计算连杆在力和力矩作用下的弯曲变形。柔性杆变形包括拉伸变形、弯曲变形以及扭转变形。连杆变形如图6所示。

机器人末端受到载荷的作用，叠加自重的影响，则各连杆末端受到的广义力Fli=[Fli,xFli,yFli,zMli,xMli,yTli]T，在连杆坐标系下连杆自重Gli=[GixGiyGiz000]T。机器人连杆的末端变形量δli（i=1, 2, 3）为：

式中：CF、CG为柔度矩阵。

式中：li为连杆长度，EIiz为连杆的抗弯强度，GIip为连杆的抗扭强度，E为弹性模量，G为剪切模量，Ai为连杆的截面面积。

上述连杆末端变形分析是建立在刚体假设的基础上，即不考虑机器人结构微变形。但是在机器人自重和末端负载的作用下，机器人连杆会发生变形，因此求解坐标变换矩阵时，应当引入连杆的变形量。那么，考虑连杆变形的各连杆坐标系之间的转换矩阵ii-1'为：

考虑连杆柔性变形的基坐标系相对末端坐标系的变换矩阵为：

连杆柔性变形的坐标变换矩阵60'可以看作是基于连杆刚体假设的坐标变换矩阵60T经过坐标变换ΔT得到，即：

两边同时左乘06T，可得：

式中：Δn、Δo、Δa为旋转矩阵，描述了60'的X向、Y向、Z向的单位向量相对于60T的方向余弦；Δp为位置向量。

由机器人学理论可知，微分运动矢量d=[dxdydz]T和微分转动矢量δ=[δxδyδz]T对应的微分算子∇为：

则微分运动矢量和微分转动矢量可表示为：

由此，可以得到考虑连杆变形的机器人末端变形量为：

根据线性叠加原理，结合式(33)和式(42)，可得机器人末端变形模型ΔδS为：

采用SolidWorks软件构建涉核作业机器人模型。设置其结构自重为1 960 N，最大末端载荷为10 kg。将所建的机器人结构模型导入ANSYS Workbench软件进行静力学有限元分析。

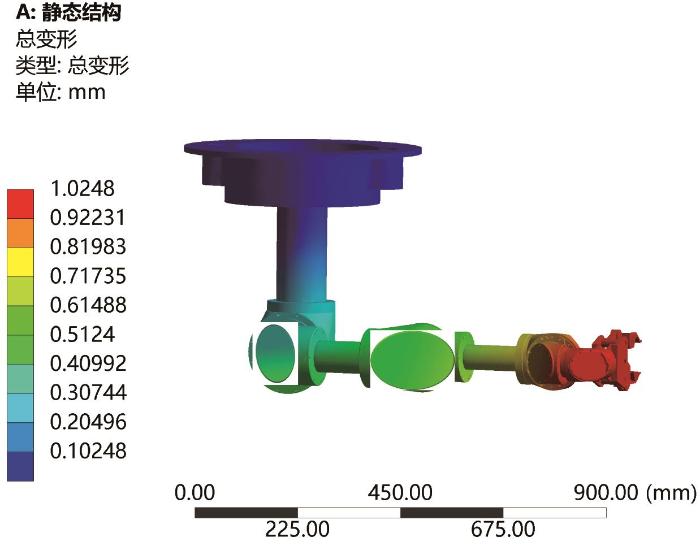
在不同机器人姿态及不同负载作用下，机器人末端变形量会有相应的变化。例如，当机器人肩关节摆动90°，即机器人呈肩关节L形位姿时，负载离关节轴的距离最大，同时机器人自重对关节的重力矩也最大，机器人末端变形量最大。在该位姿下机器人仅受自重作用时，其末端变形云图如图7所示。

由图7可知，当机器人仅受自重作用，末端夹爪上未施加负载时，其末端的最大变形量为1.025 mm。

当机器人呈肩关节L形、肘关节L形两种姿态时，可分别仿真得到其在不同负载下的末端变形量。

为了进一步验证机器人末端变形模型的准确性，通过实验来测量机器人在不同位姿及不同负载下的末端变形量。选择的2种机器人位姿如图8所示。第1种位姿是将机器人肩关节逆时针旋转90°，即呈肩关节L形位姿；第2种位姿是将机器人肘关节逆时针旋转90°，即呈肘关节呈L形位姿。

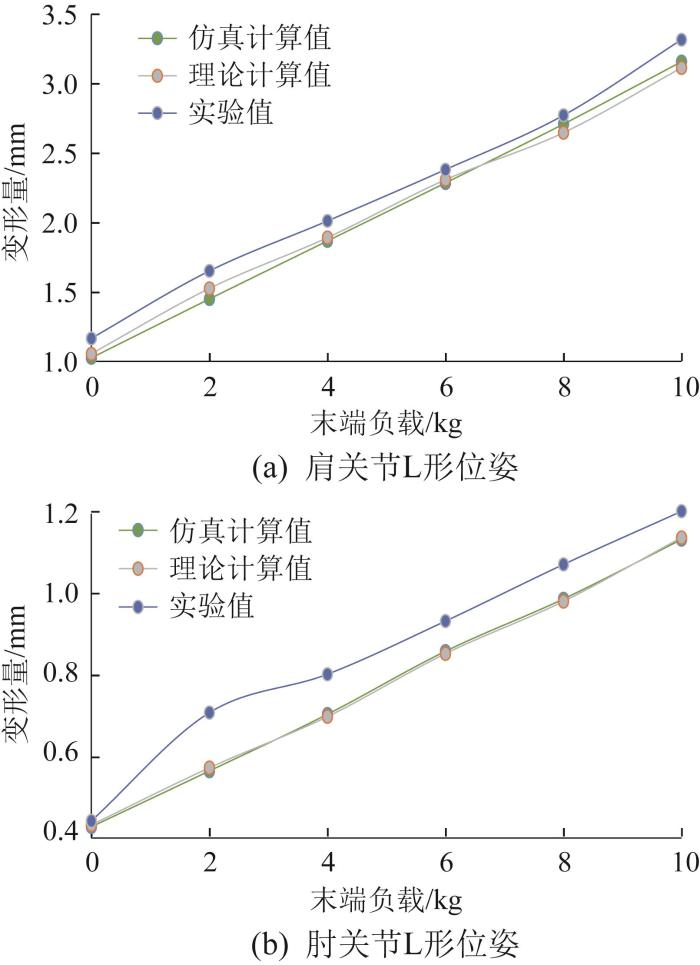
当机器人呈肩关节L形和肘关节L形位姿时，分别在其末端悬挂不同质量的砝码，在每种负载工况下进行10次实验，记录机器人末端测量点的坐标并取平均值。机器人末端最大负载可达10 kg，因此分别在机器人末端悬挂0、2、4、6、8、10 kg砝码进行实验。机器人末端变形量如图9所示。

由图9可知，当机器人呈肩关节L形或肘关节L形位姿时，其末端变形的理论计算值、仿真计算值与实验值基本吻合。其中，理论计算值与仿真计算值很接近，而实验值比理论计算值平均大0.12 mm。造成这种偏差的原因可能是理论计算时只考虑了关节的扭转刚度，未考虑所有连杆的变形等。机器人呈肩关节L形位姿时末端变形量较大。

在上述实验中，机器人均在工作空间的右半区域运行，因此齿侧间隙对机器人末端变形的影响可以忽略不计。综上所述，涉核作业机器人末端刚度模型具有较高的准确度。

1）本文以涉核作业机器人为研究对象，分析了机器人结构及全齿轮耦合传动原理，设立了2个考虑关节偏置的机器人连杆末端坐标系{2*}和{3*}，建立了新的机器人运动学模型。

2）针对机器人因自重和负载作用产生的关节力矩和末端变形问题，提出了一种将机器人传动关节视为柔性部件来求解关节扭转刚度、基于伯努利-欧拉梁假设理论求解机器人连杆刚度的求解方法，并根据线性叠加原理得到了机器人末端变形模型。

3）通过机器人末端变形有限元仿真分析及机器人在不同位姿下的末端变形测试实验，验证了末端变形模型的正确性。本文所提出的机器人末端变形建模方法对机器人的设计优化和末端变形补偿具有一定的借鉴价值。

本文链接：https：//www.zjujournals.com/gcsjxb/CN/10.3785/j.issn.1006-754X.2025.05.124