驱动副共面平行的3-P(2-SS)型并联机器人运动特性及动力学分析

doi:10.3785/j.issn.1006-754X.2025.05.177

驱动副共面平行的3-P(2-SS)型并联机器人运动特性及动力学分析

李瑾^,^,

山西工程技术学院机械工程系，山西阳泉 045000

Kinematic characteristics and dynamics analysis of 3-P(2-SS) robot with coplanar parallel driving pairs

LI Jin^,^,

Department of Mechanical Engineering, Shanxi Institute of Technology, Yangquan 045000

收稿日期: 2025-03-20 修回日期: 2025-06-29

基金资助:

山西省阳泉市基础研究项目. 2022JH054

Received: 2025-03-20 Revised: 2025-06-29

作者简介 About authors

李　瑾（1989—），男，讲师，硕士，从事机器人技术研究，E-mail：342040973@163.com,https://orcid.org/0009-0007-7221-7435 , E-mail：342040973@163.com

摘要

由3个平行且共面的移动副驱动的3-P(2-SS)型并联机器人相对传统构型更适合在狭长区域作业。针对该机器人，构建了其运动学方程和雅可比矩阵，并分析了其运动学方程的多解性。利用其运动学方程和螺旋理论，证实了在正常工况下机器人动平台始终只有3个平移自由度，并简化了机器人的运动学方程和雅可比矩阵。利用雅可比矩阵条件数分析了机器人的灵巧性，当2侧的滑块位于动平台同侧时，机器人的灵巧性较好；机器人在奇异点和运动范围边界附近时灵巧性较差。基于拉格朗日方程构建了机器人动力学模型，利用最小角速度假设解决了连杆的局部自由度带来的动力学不确定问题，通过动坐标系变换解决了连杆惯性张量相对静坐标系的不恒定问题，得到了机器人动力学方程。通过动力学计算结果与运动仿真结果的对比，证实了动力学方程的正确性，最小角速度假设导致的驱动力计算结果误差在可控范围内。研究结果表明，驱动副共面平行的3-P(2-SS)并联机器人具有良好的操作性，提出的动力学建模方法为该型机器人力控制系统的构建提供了理论基础。

关键词： 3-P(2-SS) ; 并联机器人 ; 自由度 ; 灵巧性 ; 动力学

Abstract

The 3-P(2-SS) parallel robot driven by three parallel and coplanar prismatic pairs is more suitable for operation in narrow and long areas compared to the traditional configurations. For this robot, its kinematic equations and Jacobian matrix were established, and the multi-solution nature of the kinematic equations was analyzed. By using the kinematic equations and the screw theory, it was confirmed that under normal working conditions, the robot's moving platform always had only three translational degrees of freedom, thereby simplifying the robot's kinematic equations and Jacobian matrix. The dexterity of the robot was analyzed using the condition number of the Jacobian matrix. The robot exhibited better dexterity when the sliders on both sides were located on the same side of the moving platform; the robot's dexterity deteriorated when it was near the singular points and the boundaries of the motion range. A robot dynamic model was established based on the Lagrange equation. The issue of dynamic uncertainty caused by the local degrees of freedom of the link was resolved using the minimum angular velocity assumption, the problem of the non-constant inertia tensor of the ink relative to the static coordinate system was addressed through transformation of the moving coordinate system, and the robot dynamic equation was obtained. By comparing the results of the dynamics calculation and motion simulation, the correctness of the dynamic equation was confirmed, with the error in the driving force calculation results caused by the minimum angular velocity assumption being within an acceptable range. The research results indicate that the 3-P(2-SS) parallel robot with coplanar parallel driving pairs has excellent operability, and the proposed dynamics modeling method provides a theoretical foundation for the construction of control systems for this type of robot.

Keywords： 3-P(2-SS) ; parallel robot ; degree of freedom ; dexterity ; dynamics

PDF (1979KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

李瑾. 驱动副共面平行的3-P(2-SS)型并联机器人运动特性及动力学分析[J]. 工程设计学报, 2025, 32(5): 646-654 doi:10.3785/j.issn.1006-754X.2025.05.177

LI Jin. Kinematic characteristics and dynamics analysis of 3-P(2-SS) robot with coplanar parallel driving pairs[J]. Chinese Journal of Engineering Design, 2025, 32(5): 646-654 doi:10.3785/j.issn.1006-754X.2025.05.177

并联机器人在机构刚度、运动精度、负载能力、力矩分布、稳定性和速度等方面具有显著优势^[1]。3-P(2-SS)机构由3个并联的移动副（P）驱动，每个移动副与动平台之间通过2条并联的运动链连接，每条运动链由2个球铰（S）及其之间的连杆构成。该机构常用于3D打印机、Delta机器人等。国内外学者对3-P(2-SS)机器人的研究多集中于其传统构形，即机构的3个移动副竖直均布于动平台工作空间的外侧，动平台横向工作空间有限。本文以驱动副共面平行的3-P(2-SS)型并联机器人为研究对象，分析其运动特性及动力学性能。该机器人由于3个移动副共面且位于动平台上部，动平台沿移动副方向的运动范围可随着移动副滑轨的伸长而增大，因此其更适合在狭长区域进行物品分拣、包装、搬运等工作。

国内外学者对机器人进行自由度分析时，对于简单机构，常采用Grubler-Kutzbach公式进行计算^[2-3]；对于复杂的多支链或过约束机构，常采用李群与李代数及螺旋理论进行分析^[4-7]；对于特定形位的自由度，常采用雅可比矩阵法分析其奇异性^[3,8]。本文利用机器人运动学方程和螺旋理论，对机器人的自由度进行分析，以简化其运动学方程与雅可比矩阵。

对机器人灵巧性进行分析时，学者们常采用可达工作空间、全姿态工作空间、灵活度等指标评价机器人的工作空间^[9-12]，采用雅可比矩阵条件数、可操作度、最小奇异值等指标评价机器人的运动性能^[11,13-14]，采用力传递效率等指标评价机器人的动力学性能^[7]。本文采用分析并联机器人时常用的雅可比矩阵条件数指标，根据简化后的雅可比矩阵，通过机器人移动副取不同运动学逆解时的灵巧性分析，来确定机器人动平台最佳运动范围和移动副最佳运动学逆解位置。

针对并联机器人的动力学研究，主要集中在高效高精度动力学建模^[6,15]、刚柔耦合动力学分析^[16]、高精度控制驱动系统分析^[17]等方面，而对于机器人机构中局部自由度的处理鲜有讨论。本文针对2-SS双球铰运动链中局部自由度导致的运动不确定性问题，利用最小角速度假设，采用机构近似替代法，求解机器人动力学方程，并进行运动仿真验证。

1 驱动副共面平行3-P(2-SS)机器人运动机构设计

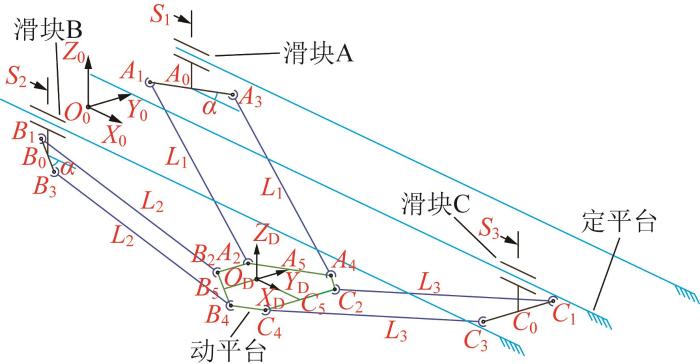
驱动副共面平行3-P(2-SS)机器人的运动机构如图1所示。在机器人定平台上设置静坐标系 ${O_{0}}$ ，在动平台上设置的动坐标系 ${O_{D}}$ 为工具坐标系。机器人的结构参数如表1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 驱动副共面平行3-P(2-SS)机器人运动机构简图

Fig.1 Motion mechanism schematic of 3-P(2-SS) robot with coplanar parallel driving pairs

表1 驱动副共面平行3-P(2-SS)机器人结构参数

Table 1 Structural parameters of 3-P(2-SS) robot with coplanar parallel driving pairs

参数	含义
$L_{1}$	连杆 $A_{1} A_{2}$ 、 $A_{3} A_{4}$ 的长度
$L_{2}$	连杆 $B_{1} B_{2}$ 、 $B_{3} B_{4}$ 的长度
$L_{3}$	连杆 $C_{1} C_{2}$ 、 $C_{3} C_{4}$ 的长度
$M$	$B_{5} O_{D}$ 、 $A_{5} O_{D}$ 的长度
$N$	$C_{5} O_{D}$ 的长度
$E$	相邻移动副滑轨的间距
$α$	$A_{1} A_{3}$ 、 $B_{1} B_{3}$ 与X₀轴之间的夹角 $A_{2} A_{4}$ 、 $B_{2} B_{4}$ 与X_D轴之间的夹角
$T$	$A_{0} A_{1}$ 、 $A_{0} A_{3}$ 、 $A_{5} A_{2}$ 、 $A_{5} A_{4}$ 、 $B_{0} B_{1}$ 、 $B_{0} B_{3}$ 、 $B_{5} B_{2}$ 、 $B_{5} B_{4}$ 、 $C_{0} C_{1}$ 、 $C_{0} C_{3}$ 、 $C_{5} C_{2}$ 、 $C_{5} C_{4}$ 的长度

新窗口打开| 下载CSV

2 驱动副共面平行3-P(2-SS)机器人运动学方程

设动坐标系 ${O_{D}}$ 的原点 $O_{D}$ 在静坐标系 ${O_{0}}$ 下的位置矢量为:

{}^{0} D = [\begin{matrix} x_{D} & y_{D} & z_{D} \end{matrix}]

设3个滑块上 $A_{0}$ 、 $B_{0}$ 、 $C_{0}$ 点沿X₀向的位移分别为 $S_{1}$ 、 $S_{2}$ 、 $S_{3}$ ，3个滑块上球铰铰点沿X₀向的位移分别为 $S_{A 1}$ 、 $S_{A 3}$ 、 $S_{B 1}$ 、 $S_{B 3}$ 、 $S_{C 1}$ 、 $S_{C 3}$ ，则各滑块上球铰铰点在静坐标系 ${O_{0}}$ 下的位置矢量为：

\{\begin{matrix} \begin{array}{l} {}^{0} A_{1} = {[\begin{matrix} S_{A 1} & E - T s α & 0 \end{matrix}]}^{T} \\ {}^{0} A_{3} = {[\begin{matrix} S_{A 3} & E + T s α & 0 \end{matrix}]}^{T} \\ {}^{0} B_{1} = {[\begin{matrix} S_{B 1} & - E + T s α & 0 \end{matrix}]}^{T} \\ {}^{0} B_{3} = {[\begin{matrix} S_{B 3} & - E - T s α & 0 \end{matrix}]}^{T} \\ {}^{0} C_{1} = {[\begin{matrix} S_{C 1} & T & 0 \end{matrix}]}^{T} \\ {}^{0} C_{3} = {[\begin{matrix} S_{C 3} & - T & 0 \end{matrix}]}^{T} \end{array} \end{matrix}

式中：s表示sin。下文同。

动平台上各球铰铰点在动坐标系 ${O_{D}}$ 下的位置矢量为：

\{\begin{array}{l} {}^{D} A_{2} = {[\begin{matrix} - T c α & M - T s α & 0 \end{matrix}]}^{T} \\ {}^{D} A_{4} = {[\begin{matrix} T c α & M + T s α & 0 \end{matrix}]}^{T} \\ {}^{D} B_{2} = {[\begin{matrix} - T c α & - M + T s α & 0 \end{matrix}]}^{T} \\ {}^{D} B_{4} = {[\begin{matrix} T c α & - M - T s α & 0 \end{matrix}]}^{T} \\ {}^{D} C_{2} = {[\begin{matrix} N & T & 0 \end{matrix}]}^{T} \\ {}^{D} C_{4} = {[\begin{matrix} N & - T & 0 \end{matrix}]}^{T} \end{array}

式中：c表示cos。下文同。

设动坐标系 ${O_{D}}$ 由静坐标系 ${O_{0}}$ 先绕X₀轴旋转 $ψ$ 角，再绕Y₀轴旋转 $θ$ 角，最后绕Z₀轴旋转 $ϕ$ 角而成，则动坐标系 ${O_{D}}$ 相对静坐标系 ${O_{0}}$ 的旋转矩阵 ${}_{D}^{0} R$ 为:

{}_{D}^{0} R = R o t (z, ϕ) R o t (y, θ) R o t (x, ψ) = [\begin{matrix} c ϕ c θ & c ϕ s θ s ψ - s ϕ c ψ & c ϕ s θ c ψ + s ϕ s ψ \\ s ϕ c θ & s ϕ s θ s ψ + c ϕ c ψ & s ϕ s θ c ψ - c ϕ s ψ \\ - s θ & c θ s ψ & c θ c ψ \end{matrix}]

则动平台上球铰铰点在静坐标系 ${O_{0}}$ 下的位置矢量为：

\{\begin{array}{l} {}^{0} A_{2} = {}_{D}^{0}R {}^{D}A A_{2} + {}^{0}D \\ {}^{0} A_{4} = {}_{D}^{0}R {}^{D}A A_{4} + {}^{0}D \\ {}^{0} B_{2} = {}_{D}^{0}R {}^{D}B B_{2} + {}^{0}D \\ {}^{0} B_{4} = {}_{D}^{0}R {}^{D}B B_{4} + {}^{0}D \\ {}^{0} C_{2} = {}_{D}^{0}R {}^{D}C C_{2} + {}^{0}D \\ {}^{0} C_{4} = {}_{D}^{0}R {}^{D}C C_{4} + {}^{0}D \end{array}

根据各连杆长度，可得：

\{\begin{array}{l} |A_{1} A_{2}| = |A_{3} A_{4}| = L_{1} \\ |B_{1} B_{2}| = |B_{3} B_{4}| = L_{2} \\ |C_{1} C_{2}| = |C_{3} C_{4}| = L_{3} \end{array}

由式(1)至式(6)可得机器人的运动学方程组 $f$ ：

\{\begin{array}{l} f (1) = [{}^{0}A A_{1} - {}^{0}A A_{2}]^{T} [{}^{0}A A_{1} - {}^{0}A A_{2}] - {L_{1}}^{2} = 0 \\ f (2) = [{}^{0}B B_{1} - {}^{0}B B_{2}]^{T} [{}^{0}B B_{1} - {}^{0}B B_{2}] - {L_{2}}^{2} = 0 \\ f (3) = [{}^{0}C C_{1} - {}^{0}C C_{2}]^{T} [{}^{0}C C_{1} - {}^{0}C C_{2}] - {L_{3}}^{2} = 0 \\ f (4) = [{}^{0}A A_{3} - {}^{0}A A_{4}]^{T} [{}^{0}A A_{3} - {}^{0}A A_{4}] - {L_{1}}^{2} = 0 \\ f (5) = [{}^{0}B B_{3} - {}^{0}B B_{4}]^{T} [{}^{0}B B_{3} - {}^{0}B B_{4}] - {L_{2}}^{2} = 0 \\ f (6) = [{}^{0}C C_{3} - {}^{0}C C_{4}]^{T} [{}^{0}C C_{3} - {}^{0}C C_{4}] - {L_{3}}^{2} = 0 \end{array}

式(1)至式(4)代入式(7)得到的运动学方程组展开式中，L₁、L₂、L₃、 $M$ 、 $N$ 、 $E$ 、 $α$ 、 $T$ 均为与机器人结构相关的常量。滑块上球铰的位移为运动输入量，可用矢量 $q$ 表示，即：

q = {[\begin{matrix} S_{A 1} & S_{A 3} & S_{B 1} & S_{B 3} & S_{C 1} & S_{C 3} \end{matrix}]}^{T}

$x_{D}$ 、 $y_{D}$ 、 $z_{D}$ 、 $ψ$ 、 $θ$ 、 $ϕ$ 为动平台的运动输出量，可用矢量 $x$ 表示，即：

x = {[\begin{matrix} \begin{matrix} x_{D} & y_{D} & z_{D} \end{matrix} & ψ & θ & ϕ \end{matrix}]}^{T}

则机器人运动学方程组可以简化为：

f (x, q) = 0_{6 \times 1}

求解机器人运动学正解为已知 $q$ ，求解 $x$ ，反之为求解机器人运动学逆解。求解运动学逆解时，同一滑块上2个球铰的位置还需满足：

\begin{matrix} \{\begin{array}{l} S_{A 1} - S_{A 3} = - 2 T c α \\ S_{B 1} - S_{B 3} = - 2 T c α \\ S_{C 1} - S_{C 3} = 0 \end{array} \end{matrix}

将式(8)对时间求导，得到：

\frac{\partial f}{\partial x} \dot{x} + \frac{\partial f}{\partial q} \dot{q} = 0_{6 \times 1}

设 $J_{x}$ 和 $J_{q}$ 分别为：

J_{x} = \frac{\partial f}{\partial x} = [\begin{matrix} \frac{\partial f (1)}{\partial x_{D}} & \frac{\partial f (1)}{\partial y_{D}} & \dots & \frac{\partial f (1)}{\partial ϕ} \\ \frac{\partial f (2)}{\partial x_{D}} & \frac{\partial f (2)}{\partial y_{D}} & \dots & \frac{\partial f (2)}{\partial ϕ} \\ ⋮ & ⋮ & ⋮ \\ \frac{\partial f (6)}{\partial x_{D}} & \frac{\partial f (6)}{\partial y_{D}} & \dots & \frac{\partial f (6)}{\partial ϕ} \end{matrix}]

J_{q} = - \frac{\partial f}{\partial q} = - [\begin{matrix} \frac{\partial f (1)}{\partial S_{A 1}} & \frac{\partial f (1)}{\partial S_{A 3}} & \dots & \frac{\partial f (1)}{\partial S_{C 3}} \\ \frac{\partial f (2)}{\partial S_{A 1}} & \frac{\partial f (2)}{\partial S_{A 3}} & \dots & \frac{\partial f (2)}{\partial S_{C 3}} \\ ⋮ & ⋮ & ⋮ \\ \frac{\partial f (6)}{\partial S_{A 1}} & \frac{\partial f (6)}{\partial S_{A 3}} & \dots & \frac{\partial f (6)}{\partial S_{C 3}} \end{matrix}]

可得：

J_{x} \dot{x} = J_{q} \dot{q}

当 $J_{q}$ 的逆矩阵存在时，式(10)为：

\begin{matrix} \{\begin{array}{l} \dot{q} = J \dot{x} \\ J = J_{q}^{- 1} J_{x} \end{array} \end{matrix}

式(11)中， $J$ 即为机器人的运动学雅可比矩阵。

3 驱动副共面平行3-P(2-SS)机器人自由度分析

3.1　基于运动学方程的自由度分析

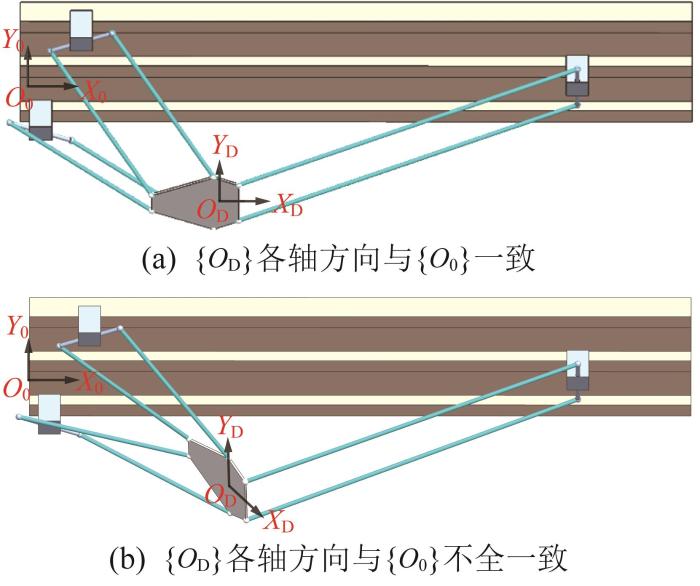
求解机器人运动学正解时，3个滑块位置确定，此时机器人的运动学模型类似于Gough-Stewart机器人。根据相关研究可知，理论上动平台的位姿最多可以有40个正解^[18-20]。因此，在初始安装动平台时，动坐标系 ${O_{D}}$ 的各轴方向可以与静坐标系 ${O_{0}}$ 一致（如图2(a)所示），也可以不全一致（如图2(b)所示）。在这2种情况下机器人的运动性能不同。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 动平台不同安装姿态

Fig.2 Different installation poses of moving platform

求解动平台逆解 $q$ 时，由于同一滑块上的2个球铰速度相同，可得：

\{\begin{matrix} {\dot{S}}_{A 1} = {\dot{S}}_{A 3} \\ {\dot{S}}_{B 1} = {\dot{S}}_{B 3} \\ {\dot{S}}_{C 1} = {\dot{S}}_{C 3} \end{matrix}

(12)

在动平台运动过程中，其转动速度不全为0时动平台会产生转动。利用式(8)至式(12)进行计算，求得在 $ψ = θ = ϕ = 0$ 的条件下，机器人在非奇异形位移动时，始终有：

\dot{ψ} = \dot{θ} = \dot{ϕ} = 0

因此，当动平台的初始安装位置为 ${O_{D}}$ 的各轴方向与 ${O_{0}}$ 一致时，机器人在非奇异形位范围内移动，动平台姿态会保持不变，只具有3个移动自由度。

3.2　基于螺旋理论的自由度分析

可利用旋量法进一步分析动平台的运动自由度。当动平台初始安装位置为 ${O_{D}}$ 各轴方向与 ${O_{0}}$ 一致时，由于 $ψ = θ = ϕ = 0$ ，机器人的运动学方程可简化为：

f (x_{D 0}, q_{0}) = 0_{3 \times 1}

运动输入量为：

q_{0} = {[\begin{matrix} S_{1} & S_{2} & S_{3} \end{matrix}]}^{T}

运动输出量为：

x_{D 0} = {[\begin{matrix} x_{D 0} & y_{D 0} & z_{D 0} \end{matrix}]}^{T}

求得此时动平台的位姿为：

\{\begin{array}{l} x_{D 0} = \frac{{S_{1}}^{2} + {S_{2}}^{2} - 2 {(N - S_{3})}^{2} + 2 {(M - E)}^{2} - {L_{1}}^{2} - {L_{2}}^{2} + 2 {L_{3}}^{2}}{2 (S_{1} + S_{2}) + 4 (N - S_{3})} \\ y_{D 0} = \frac{{L_{1}}^{2} - {L_{2}}^{2} - {S_{1}}^{2} + {S_{2}}^{2} - 2 x_{D 0} (S_{2} - S_{1})}{4 (M - E)} \\ z_{D 0} = \pm \sqrt[]{{L_{3}}^{2} - {y_{D 0}}^{2} - {(x_{D 0} + N - S_{3})}^{2}} \end{array}

滑块运动位置的逆解为：

\{\begin{array}{l} S_{1} = \pm \sqrt[]{{L_{1}}^{2} - {z_{D 0}}^{2} - {(y_{D 0} + M - E)}^{2}} + x_{D 0} \\ S_{2} = \pm \sqrt[]{{L_{2}}^{2} - {z_{D 0}}^{2} - {(y_{D 0} - M + E)}^{2}} + x_{D 0} \\ S_{3} = \pm \sqrt[]{{L_{3}}^{2} - {z_{D 0}}^{2} - {y_{D 0}}^{2}} + x_{D 0} + N \end{array}

(13)

由式(13)可知机器人的运动与结构参数 $T$ 、 $α$ 无关，但为避免机器人奇异，需 $α$ <90°。

设坐标系 ${O_{0}}$ 中3个坐标轴的单位向量分别为 $s_{x}$ 、 $s_{y}$ 与 $s_{z}$ 。机器人的3个滑动副各可以看作一条运动链，以滑块A所在的运动链为例进行分析。设：

\begin{array}{l} s_{x}^{A} = s_{x} = {[\begin{matrix} 1 & 0 & 0 \end{matrix}]}^{T} \\ s_{y}^{A} = s_{y} = {[\begin{matrix} 0 & 1 & 0 \end{matrix}]}^{T} \\ s_{z}^{A} = s_{z} = {[\begin{matrix} 0 & 0 & 1 \end{matrix}]}^{T} \end{array}

滑块A相对定平台移动副的单位螺旋为：

{\hat{ξ}}_{S 1}^{A} = [\begin{matrix} 0_{3 \times 1} \\ s_{x}^{A} \end{matrix}]

运动链上每个球铰用3个相互垂直相交的转动副等效替代，因此运动链A上4个球铰的单位运动螺旋为：

\begin{matrix} {\hat{ξ}}_{A i x}^{A} = [\begin{matrix} s_{x}^{A} \\ O A_{i} \times s_{x}^{A} \end{matrix}] \\ {\hat{ξ}}_{A i y}^{A} = [\begin{matrix} s_{y}^{A} \\ O A_{i} \times s_{y}^{A} \end{matrix}] \\ {\hat{ξ}}_{A i z}^{A} = [\begin{matrix} s_{z}^{A} \\ O A_{i} \times s_{z}^{A} \end{matrix}] \end{matrix} (i = 1, 2, 3, 4)

各相关向量为：

O A_{1} = [\begin{matrix} S_{1} - T c α \\ E - T s α \\ 0 \end{matrix}]

，

O A_{2} = [\begin{matrix} x_{D 0} - T c α \\ y_{D 0} - T s α + M \\ z_{D 0} \end{matrix}]

O A_{3} = [\begin{matrix} S_{1} + T c α \\ E + T s α \\ 0 \end{matrix}]

，

O A_{4} = [\begin{matrix} x_{D 0} + T c α \\ y_{D 0} + T s α + M \\ z_{D 0} \end{matrix}]

由于运动链A的P(2-SS)机构属于串并联型，因此先求2-SS机构的约束螺旋。将支链A₁A₂中的全部运动单位螺旋组成其运动空间螺旋组，即：

S_{A 12}^{A} = [\begin{matrix} \begin{matrix} {\hat{ξ}}_{A 1 x}^{A} & {\hat{ξ}}_{A 1 y}^{A} & {\hat{ξ}}_{A 1 z}^{A} & {\hat{ξ}}_{A 2 x}^{A} & {\hat{ξ}}_{A 2 y}^{A} \end{matrix} & {\hat{ξ}}_{A 2 z}^{A} \end{matrix}]

设：

Δ = [\begin{matrix} 0_{3 \times 3} & E_{3 \times 3} \\ E_{3 \times 3} & 0_{3 \times 3} \end{matrix}]

构造方程组为：

{(Δ S_{A 12}^{A})}^{T} x = 0_{6 \times 1}

(14)

通过求解方程组，得到其所有j个线性无关的解:

ζ_{A 12}^{A} = [\begin{matrix} ζ_{A 121}^{A} & ζ_{A 122}^{A} & \dots & ζ_{A 12 j}^{A} \end{matrix}]

$ζ_{A 12}^{A}$ 为支链A₁A₂中j个反螺旋即支链A₁A₂的约束螺旋组。同理可求得支链A₃A₄的约束螺旋组 $ζ_{A 34}^{A}$ 。

构造运动链A中2-SS机构的约束螺旋矩阵：

ζ_{A 1234}^{A} = [\begin{matrix} ζ_{A 12}^{A} & ζ_{A 34}^{A} \end{matrix}]

构造方程组为：

{(Δ ζ_{A 1234}^{A})}^{T} x = 0_{6 \times 1}

(15)

求解方程组(15)，得到其所有线性无关解 $S_{Α 1234}^{A}$ ，即为运动链A中2-SS机构的运动空间螺旋。

构造运动链A中P(2-SS)机构整体的运动空间螺旋组，即：

S^{A} = [\begin{matrix} {\hat{ξ}}_{S 1}^{A} & S_{A 1234}^{A} \end{matrix}]

利用式(14)可求得支链A的总约束螺旋 $ζ^{A}$ 。

同理，求出其他2个并联支链B与C的约束螺旋 $ζ^{B}$ 和 $ζ^{C}$ ，组成整个运动系统的约束螺旋：

C^{p b} = [\begin{matrix} ζ^{A} & ζ^{B} & ζ^{C} \end{matrix}]

利用式(15)可求得动平台的运动空间螺旋组：

C^{p b} = {[\begin{matrix} 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \end{matrix}]}^{T}

则可求得动平台自由度数 $r^{p b}$ ，即：

r^{p b} = d i m (C^{p b}) = 3

综上，可得动平台仅具有沿着3个轴方向运动的移动自由度。下文默认 ${O_{D}}$ 各轴方向与 ${O_{0}}$ 方向一致且每条运动链上两连杆平行。由于动平台姿态始终保持不变，式(13)亦适用于动平台运动过程中，求解可得：

[\begin{matrix} {\dot{S}}_{1} \\ {\dot{S}}_{2} \\ {\dot{S}}_{3} \end{matrix}] = [\begin{matrix} 1 & \frac{y_{D} + M - E}{x_{D} - S_{1}} & \frac{z_{D}}{x_{D} - S_{1}} \\ 1 & \frac{y_{D} - M + E}{x_{D} - S_{2}} & \frac{z_{D}}{x_{D} - S_{2}} \\ 1 & \frac{y_{D}}{x_{D} + N - S_{3}} & \frac{z_{D}}{x_{D} + N - S_{3}} \end{matrix}] [\begin{matrix} {\dot{x}}_{D} \\ {\dot{y}}_{D} \\ {\dot{z}}_{D} \end{matrix}]

即机器人雅可比矩阵为：

{\dot{q}}_{0} = J_{0} {\dot{x}}_{0}

J_{0} = [\begin{matrix} 1 & \frac{y_{D} + M - E}{x_{D} - S_{1}} & \frac{z_{D}}{x_{D} - S_{1}} \\ 1 & \frac{y_{D} - M + E}{x_{D} - S_{2}} & \frac{z_{D}}{x_{D} - S_{2}} \\ 1 & \frac{y_{D}}{x_{D} + N - S_{3}} & \frac{z_{D}}{x_{D} + N - S_{3}} \end{matrix}]

4 驱动副共面平行3-P(2-SS)机器人灵巧性分析

灵巧性是指机械系统在任意方向轻松移动和施加力和扭矩的能力。雅可比矩阵条件数可用作机器人灵巧性的性能指标函数，即：

c o n d (J_{0}) = ‖J_{0}‖ \cdot ‖J_{0}^{- 1}‖

对于并联机器人，可用雅可比矩阵条件数表征机器人远离奇异点的程度。当条件数无穷大时，机器人处于奇异位形，此时机器人末端执行器的自由度减小，其处于失控状态。条件数越小，雅可比矩阵越接近于正交矩阵，机器人距离奇异点越远，在各个方向的运动能力越均匀，则操作性能越好。

利用式(13)求解运动学逆解，可得到机器人的运动范围。由于动平台沿X₀向的移动范围随3个移动副运动范围的变化而变化，且条件数不随动平台沿X₀向的移动变而化，因此不予探讨。

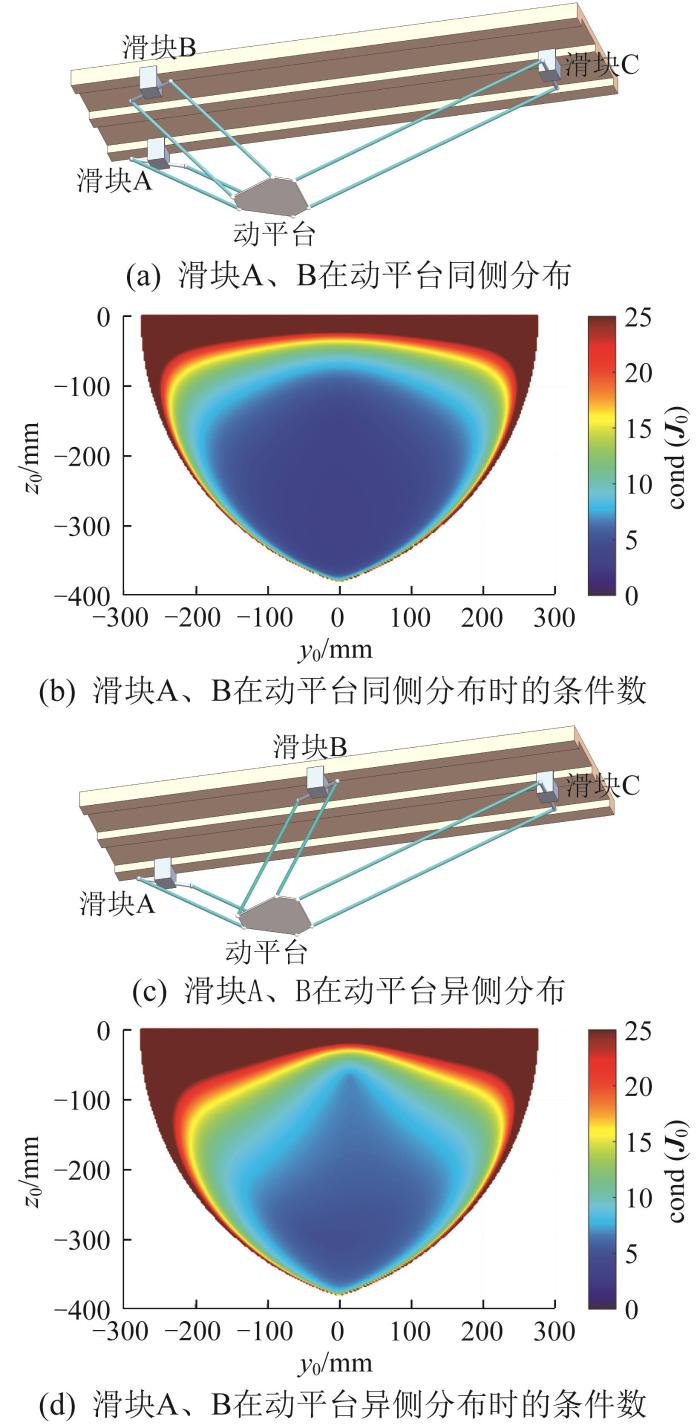
可计算得到动平台在Y₀向和Z₀向的条件数分布。由于机器人的运动学逆解有多个，当取不同逆解时，机器人的条件数不同。取不同运动学逆解时雅可比矩阵条件数如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 取不同运动学逆解时雅可比矩阵条件数

Fig.3 Condition number of Jacobi matrix with different kinematic inverse solutions

如图3(a)所示，滑块A、B位于动平台X₀向一侧，滑块C位于另一侧时，由图3(b)可知：条件数呈Y₀向对称分布，且接近 $y_{0} = 0$ 时条件数变小；沿Z₀向远离0时，条件数减小。通过计算 $|J_{0}|$ 值可知， $z_{0} = 0$ 时， $|J_{0}| = 0$ ，为机器人奇异点；机器人的最佳运动范围为图中蓝色区域，总体上为机器人远离奇异点和运动边界的位置。

如图3(c)所示，滑块A位于动平台X₀向一侧，滑块B、C位于另一侧时，由图3(d)可知：条件数呈Y₀向不对称分布；相比图3(b)，条件数总体变大，可控性变差，最佳运动范围变小。

5 驱动副共面平行3-P(2-SS)机器人动力学分析

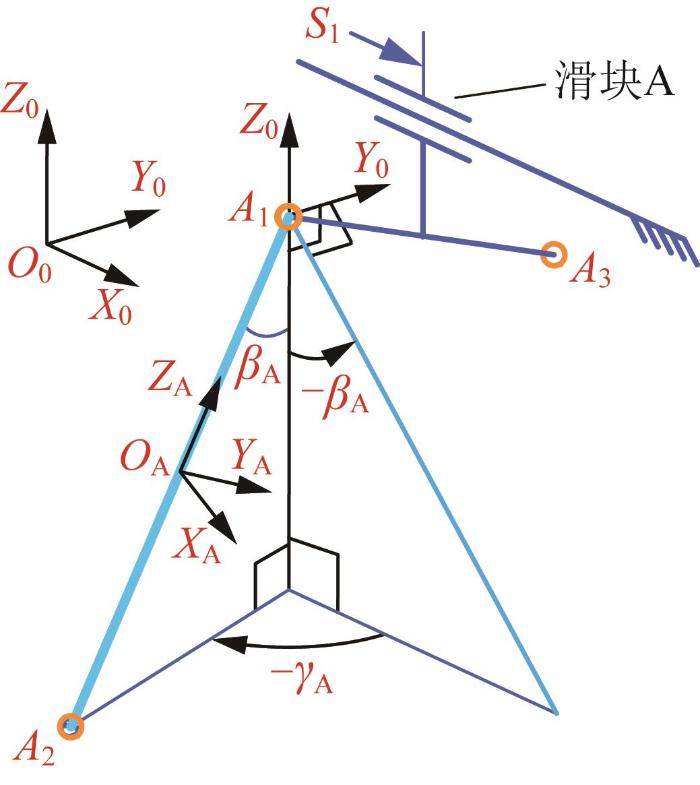
可以用拉格朗日方程求解机器人动力学问题。由机器人结构可知，每条运动链上一对连杆的动力学参数及运动状态一致，设置机器人动力学参数如表2所示。连杆的转动角速度和惯性张量都相对于其自身动坐标系，以保证连杆运动时惯性张量始终为定值。如连杆 $A_{1} A_{2}$ 的动坐标系如图4所示。为简化计算，忽略了关节摩擦力的影响^[17]。

表2 驱动副共面平行3-P(2-SS)机器人动力学参数

Table 2 Dynamics parameters for 3-P(2-SS) robot with coplanar parallel driving pairs

参数	含义
$g$	重力加速度
$m_{D}$	动平台质量
$m_{S 1}$	滑块A质量
$m_{S 2}$	滑块B质量
$m_{S 3}$	滑块C质量
$m_{l 1}$	连杆 $A_{1} A_{2}$ 、 $A_{3} A_{4}$ 的质量
$m_{l 2}$	连杆 $B_{1} B_{2}$ 、 $B_{3} B_{4}$ 的质量
$m_{l 3}$	连杆 $C_{1} C_{2}$ 、 $C_{3} C_{4}$ 的质量
$v_{l 1}$	连杆 $A_{1} A_{2}$ 、 $A_{3} A_{4}$ 沿 $\{O_{0}\}$ 各轴向的平动速度
$v_{l 2}$	连杆 $B_{1} B_{2}$ 、 $B_{3} B_{4}$ 沿 $\{O_{0}\}$ 各轴向的平动速度
$v_{l 3}$	连杆 $C_{1} C_{2}$ 、 $C_{3} C_{4}$ 沿 $\{O_{0}\}$ 各轴向的平动速度
${}^{A}_{l 1}$	连杆 $A_{1} A_{2}$ 、 $A_{3} A_{4}$ 相对 $\{O_{A}\}$ 的惯性张量
${}^{B}_{l 2}$	连杆 $B_{1} B_{2}$ 、 $B_{3} B_{4}$ 相对 $\{O_{B}\}$ 的惯性张量
${}^{C}_{l 3}$	连杆 $C_{1} C_{2}$ 、 $C_{3} C_{4}$ 相对 $\{O_{C}\}$ 的惯性张量
${}^{A}_{l 1}$	连杆 $A_{1} A_{2}$ 、 $A_{3} A_{4}$ 相对 $\{O_{A}\}$ 的转动角速度
${}^{B}_{l 2}$	连杆 $B_{1} B_{2}$ 、 $B_{3} B_{4}$ 相对 $\{O_{B}\}$ 的转动角速度
${}^{C}_{l 3}$	连杆 $C_{1} C_{2}$ 、 $C_{3} C_{4}$ 相对 $\{O_{C}\}$ 的转动角速度

新窗口打开| 下载CSV

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 连杆 $A_{1} A_{2}$ 的动坐标系 ${O_{A}}$

Fig.4 Coordinate system ${O_{A}}$ attached to link $A_{1} A_{2}$

机器人系统的拉格朗日算子L为：

L = K - P

机器人的总势能 $P$ 包含动平台和6根连杆的重力势能，即：

P = P_{D} + 2 P_{l 1} + 2 P_{l 2} + 2 P_{l 3}

\begin{array}{l} P_{D} = m_{D} g z_{D} \\ P_{l 1} = m_{l 1} g z_{D} / 2 \\ P_{l 2} = m_{l 2} g z_{D} / 2 \\ P_{l 3} = m_{l 3} g z_{D} / 2 \end{array}

机器人的总动能 $K$ 包括动平台和3个滑块的移动动能、6根连杆的平动动能和转动动能，即：

K = K_{D} + K_{S 1} + K_{S 2} + K_{S 3} + 2 K_{l 1} + 2 K_{l 2} + 2 K_{l 3}

K_{D} = m_{D} {\dot{z}}_{D}^{2} / 2

K_{S 1} = m_{S 1} {\dot{S}}_{1}^{2} / 2

K_{S 2} = m_{S 2} {\dot{S}}_{2}^{2} / 2

K_{S 3} = m_{S 3} {\dot{S}}_{3}^{2} / 2

K_{l 1} = m_{l 1} |{v_{l 1}}^{2}| / 2 + |{}^{A} {ω_{l 1}}^{T} {}^{A}I I_{l 1} {}^{A}ω ω_{l 1}| / 2

K_{l 2} = m_{l 2} |{v_{l 2}}^{2}| / 2 + |{}^{B} {ω_{l 2}}^{T} {}^{B}I I_{l 2} {}^{B}ω ω_{l 2}| / 2

K_{l 3} = m_{l 3} |{v_{l 3}}^{2}| / 2 + |{}^{C} {ω_{l 3}}^{T} {}^{C}I I_{l 3} {}^{C}ω ω_{l 3}| / 2

v_{l 1} = {[\begin{matrix} ({\dot{S}}_{1} + {\dot{x}}_{D}) / 2 & {\dot{y}}_{D} / 2 & {\dot{z}}_{D} / 2 \end{matrix}]}^{T}

v_{l 2} = {[\begin{matrix} ({\dot{S}}_{2} + {\dot{x}}_{D}) / 2 & {\dot{y}}_{D} / 2 & {\dot{z}}_{D} / 2 \end{matrix}]}^{T}

v_{l 3} = {[\begin{matrix} ({\dot{S}}_{3} + {\dot{x}}_{D}) / 2 & {\dot{y}}_{D} / 2 & {\dot{z}}_{D} / 2 \end{matrix}]}^{T}

以连杆 $A_{1} A_{2}$ 为例，求解连杆转动角速度。设 ${}^{0}_{l 1}$ 为连杆 $A_{1} A_{2}$ 相对 ${O_{0}}$ 的转动角速度，通过向量关系：

O_{0} O_{D} = O_{0} A_{1} + A_{1} A_{2} + A_{2} O_{D}

可得 $A_{1} A_{2}$ 的解为：

A_{1} A_{2} = {[\begin{matrix} x_{D} - S_{1} & y_{D} + M - E & z_{D} \end{matrix}]}^{T}

得到连杆 $A_{1} A_{2}$ 的速度方程为:

{[\begin{matrix} {\dot{x}}_{D} & {\dot{y}}_{D} & {\dot{z}}_{D} \end{matrix}]}^{T} = {[\begin{matrix} {\dot{S}}_{1} & 0 & 0 \end{matrix}]}^{T} + {{}^{0}ω}_{l 1} \times A_{1} A_{2}

由于连杆 $A_{1} A_{2}$ 两端都通过球铰连接，连杆 $A_{1} A_{2}$ 存在绕自身轴线转动的局部自由度，即式(16)中 ${}^{0}_{l 1}$ 有无数解。考虑到连杆实际转动时会沿转动阻尼最小的方向转动， ${}^{0}_{l 1}$ 与 $A_{1} A_{2}$ 垂直时其模最小，取此时 ${}^{0}_{l 1}$ 解，即：

{}^{0}_{l 1} = A_{1} A_{2} \times \frac{{[\begin{matrix} {\dot{x}}_{D} - {\dot{S}}_{1} & {\dot{y}}_{D} & {\dot{z}}_{D} \end{matrix}]}^{T}}{{L_{1}}^{2}}

滑块位置对机器人动力学方程有显著影响，根据前文灵巧性分析结果，本文主要求解滑块处于图3(a)所示分布位置时机器人的动力学方程。可将A₁处的球铰用2个分别绕Y₀向和Z₀向转动的转动副进行替代，设定 $\{O_{A}\}$ 为连杆 $A_{1} A_{2}$ 上的动坐标系，其原点 $O_{A}$ 位于 $A_{1} A_{2}$ 的质心处，Z $_{A}$ 轴的方向为 $A_{2} A_{1}$ 方向，Y $_{A}$ 轴平行于X₀O₀Y₀平面，如图4所示。坐标系 $\{O_{A}\}$ 可看作 $\{O_{0}\}$ 先绕Y₀轴逆转 $- β_{A}$ 角，再绕Z₀轴逆转 $- γ_{A}$ 角，则可求得2次转动的角度值为：

\{\begin{array}{l} c o s (- β_{A}) = - \frac{z_{D}}{L_{1}} \\ s i n γ_{A} = \frac{y_{D} + M - E}{- L_{1} s i n β_{A}} \end{array}

可求得 ${}^{0}_{l 1}$ 与 ${}^{A}_{l 1}$ 的关系方程为:

\begin{array}{l} {}^{A}_{l 1} = R o t (y, - β_{A}) R o t (z, - γ_{A}) {{}^{0}ω}_{l 1} = \\ [\begin{matrix} c β_{A} & 0 & - s β_{A} \\ 0 & 1 & 0 \\ s β_{A} & 0 & c β_{A} \end{matrix}] [\begin{matrix} c γ_{A} & s γ_{A} & 0 \\ - s γ_{A} & c γ_{A} & 0 \\ 0 & 0 & 1 \end{matrix}] [\begin{matrix} {}^{0} ω_{l 1 x} \\ {}^{0} ω_{l 1 y} \\ {}^{0} ω_{l 1 z} \end{matrix}] \end{array}

由式(17)至(19)可解得 ${}^{A}_{l 1}$ 。同理，设定 ${O_{B}}$ 及 ${O_{C}}$ 后可解得 ${}^{B}_{l 2}$ 及 ${}^{C}_{l 3}$ 。

根据拉格朗日算子方程计算，得到3个移动副的驱动力为：

F_{S 1} = \frac{d}{d t} \frac{\partial L}{\partial {\dot{S}}_{1}} - \frac{\partial L}{\partial S_{1}} = {\dot{S}}_{1} \frac{\partial}{\partial S_{1}} \frac{\partial L}{\partial {\dot{S}}_{1}} + {\ddot{S}}_{1} \frac{\partial}{\partial {\dot{S}}_{1}} \frac{\partial L}{\partial {\dot{S}}_{1}} + {\dot{S}}_{2} \frac{\partial}{\partial S_{2}} \frac{\partial L}{\partial {\dot{S}}_{1}} + {\ddot{S}}_{2} \frac{\partial}{\partial {\dot{S}}_{2}} \frac{\partial L}{\partial {\dot{S}}_{1}} + {\dot{S}}_{3} \frac{\partial}{\partial S_{3}} \frac{\partial L}{\partial {\dot{S}}_{1}} + {\ddot{S}}_{3} \frac{\partial}{\partial {\dot{S}}_{3}} \frac{\partial L}{\partial {\dot{S}}_{1}} - \frac{\partial L}{\partial S_{1}}

F_{S 2} = \frac{d}{d t} \frac{\partial L}{\partial {\dot{S}}_{2}} - \frac{\partial L}{\partial S_{2}} = {\dot{S}}_{1} \frac{\partial}{\partial S_{1}} \frac{\partial L}{\partial {\dot{S}}_{2}} + {\ddot{S}}_{1} \frac{\partial}{\partial {\dot{S}}_{1}} \frac{\partial L}{\partial {\dot{S}}_{2}} + {\dot{S}}_{2} \frac{\partial}{\partial S_{2}} \frac{\partial L}{\partial {\dot{S}}_{2}} + {\ddot{S}}_{2} \frac{\partial}{\partial {\dot{S}}_{2}} \frac{\partial L}{\partial {\dot{S}}_{2}} + {\dot{S}}_{3} \frac{\partial}{\partial S_{3}} \frac{\partial L}{\partial {\dot{S}}_{2}} + {\ddot{S}}_{3} \frac{\partial}{\partial {\dot{S}}_{3}} \frac{\partial L}{\partial {\dot{S}}_{2}} - \frac{\partial L}{\partial S_{2}}

F_{S 3} = \frac{d}{d t} \frac{\partial L}{\partial {\dot{S}}_{3}} - \frac{\partial L}{\partial S_{3}} = {\dot{S}}_{1} \frac{\partial}{\partial S_{1}} \frac{\partial L}{\partial {\dot{S}}_{3}} + {\ddot{S}}_{1} \frac{\partial}{\partial {\dot{S}}_{1}} \frac{\partial L}{\partial {\dot{S}}_{3}} + {\dot{S}}_{2} \frac{\partial}{\partial S_{2}} \frac{\partial L}{\partial {\dot{S}}_{3}} + {\ddot{S}}_{2} \frac{\partial}{\partial {\dot{S}}_{2}} \frac{\partial L}{\partial {\dot{S}}_{3}} + {\dot{S}}_{3} \frac{\partial}{\partial S_{3}} \frac{\partial L}{\partial {\dot{S}}_{3}} + {\ddot{S}}_{3} \frac{\partial}{\partial {\dot{S}}_{3}} \frac{\partial L}{\partial {\dot{S}}_{3}} - \frac{\partial L}{\partial S_{3}}

6 驱动副共面平行3-P(2-SS)机器人运动仿真验证

在NX软件中构建机器人三维模型，并利用其运动仿真模块的NX_motion求解器求解，得到机器人运动时各移动副的驱动力。将仿真结果与动力学计算结果进行对比，如图5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

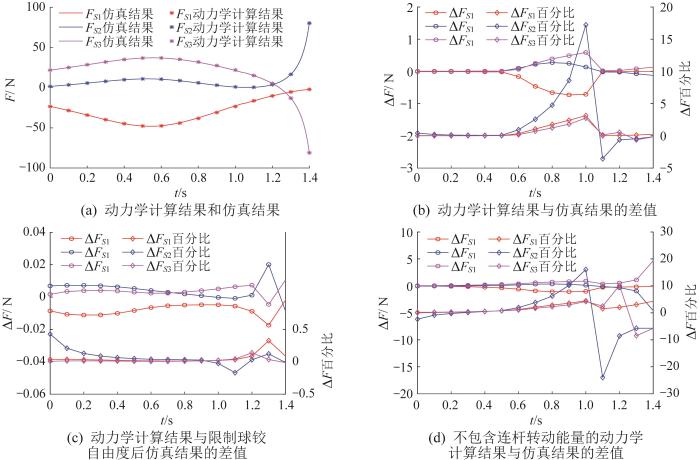
图5 驱动副共面平行3-P(2-SS)机器人移动副驱动力动力学计算结果与仿真结果的对比

Fig.5 Comparison of dynamics calculation results with simulation results of mobile auxiliary drive force of 3-P(2-SS) robot with coplanar parallel driving pairs

由图5(a)可知，移动副驱动力仿真结果与动力学计算结果具有良好的一致性。

由图5(b)可知，移动副驱动力仿真结果与动力学计算结果的差值ΔF在1 N之内，当驱动力较小时，ΔF百分比较大。产生偏差的原因主要是动力学计算时连杆的角速度矢量是按照垂直于连杆轴线的最小量计算的，而在实际系统中连杆具有绕自身轴线的局部自由度，其运动仿真过程中的转速与动力学计算时有一定偏差。

若在运动仿真过程中限制球铰的1个自由度，则运动仿真结果与动力学计算结果的最大偏差可减小到0.02 N及0.5%之内，如图5(c)所示，由此验证了动力学方程建模的可靠性。

工程上构建类似结构的动力学方程时常采用简化方程，忽略了连杆的转动能量。不包含6条连杆转动能量的情况下动力学计算结果与仿真结果的差值如图5(d)所示，两者的最大差值接近5 N，远大于图5(b)所示，因此动力学计算时忽略连杆转动能量会造成较大的误差。相比直接忽略连杆转动能量的方法，采用本文提出的连杆转动近似替代法可有效提升动力学计算的准确度。

综合来说，采用本文提出的动力学方法可以满足机器人机构设计、选型及动力学分析的需求，在进行精确力控制时需要引入运动阻尼等变量进行修正。

7 结论

1）针对由3个平行且共面的移动副驱动的3-P(2-SS)型并联机器人，建立了其运动学方程和雅可比矩阵，分析了其运动学方程的多解性。

2）通过运动学方程并结合螺旋理论分析了机器人的自由度，证实了在非奇异位形下，当动坐标系各轴方向与静坐标系一致时，该并联机器人仅具备3个平移自由度，转动自由度被完全约束，简化了机器人的运动学方程和雅可比矩阵。

3）利用雅可比矩阵条件数分析了机器人的灵巧性，分析了滑块分布模式对机器人灵巧性的影响。当2侧滑块位于动平台同侧时，机器人的灵巧性较好；机器人远离奇异点和运动范围边界附近时，其灵巧性较好。

4）基于拉格朗日方程构建了机器人动力学模型，利用最小角速度假设解决了连杆的局部自由度带来的动力学不确定问题，通过动坐标系变换解决了连杆惯性张量相对静坐标系的不恒定问题，得到了机器人的动力学方程。通过动力学计算结果与仿真结果的对比，验证了动力学建模的正确性，最小角速度假设导致的驱动力计算结果误差在可控范围内。

综上，驱动副共面平行的3-P(2-SS)并联机器人具有良好的操作性，本文提出的动力学建模方法为该型机器人力控制系统的构建提供了理论基础。

本文链接：https：//www.zjujournals.com/gcsjxb/CN/10.3785/j.issn.1006-754X.2025.05.177

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

田波，娄军强，沈家旭，等.

可用于微创手术的毫米级微小并联机器人的设计、制造及实现

［J］. 机械工程学报， 2024， 60（17）： 147-155.