随着机器人技术的快速发展，其在救援^[1-2]、巡检^[3-4]、星际勘探^[5-6]等复杂任务场景中的应用需求持续增长。在高危环境中，通常存在结构复杂和难以触及的区域，移动机器人能够代替人类进入这些高危环境执行高风险任务。然而，传统轮式、腿式和履带式移动机器人的移动模式单一^[7-10]，无法适应多种复杂环境。因此，具有多种运动模式的移动机器人应运而生。

刘超等^[11]提出了一种新型的空间单闭链6R机构，可实现蠕动、转向和内翻三种运动模式。Ping等^[12]设计了一种可携带数据采集器等设备的多模式移动运载机构，可实现多种运动模式的自由切换。Zhang等^[13]提出了一种新型的管道蠕动并联机构，可完成管道内的多种复杂任务。Michaud等^[14]研发了轮-履-腿多模式移动机器人AZIMUT，该机器人能在轮式、履带式及腿式三种移动模式之间灵活切换，可适应多种地形。陈致等^[15]提出了一种可重构的空间开/闭链6R移动并联机构，通过调节单环6R机构的开合状态，该移动并联机构能够实现3种不同的运动模式。Li等^[16]提出的4-RSR并联滚动机构可实现多种运动模式的切换。张春燕等^[17]提出了一种可变向多地形移动全R副并联机器人，有效地提高了移动机器人对多重复杂地形环境的适应能力。近年来，轮-腿式复合机器人作为一种新型的多模式移动机器人，受到了广泛关注。这类机器人结合了轮式和腿式移动的优点，能够在复杂地形中实现运动模式的灵活切换。He等^[18]研制的四轮腿式机器人TAWL的腿部和轮部可协同工作，采用多种复杂的减速器和传动机制，提高了其在复杂地形中的适应能力。Wang等^[19]设计的双轮腿式机器人Ollie采用五连杆结构，结合了轮式和腿式机器人的优势，能够适应不平坦的地形并实现越障。

然而，上述移动机器人大多通过自身变形或可重构设计来实现多模式切换等功能，普遍存在折展能力不足、占用空间较大及携带不便等局限性。针对这些问题，本文结合多模式理论和折展设计思想，提出了一种基于可变径平台的多模式移动并联机器人。结合轮-腿式机器人的设计思路，通过可变径平台的伸缩性来提升机器人在复杂地形中的适应能力和灵活性，以解决传统多模式移动机器人无法适应多样化环境的问题，旨在为多功能移动机器人的发展和应用提供理论支持与实践经验。

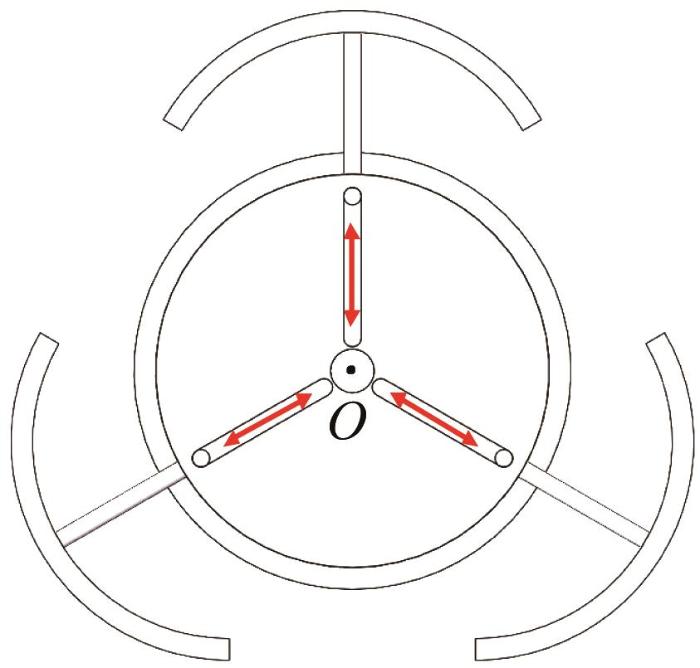
为了提升移动机器人在复杂环境下的变形能力与适应性，设计了图1所示的可变径平台作为机器人的伸缩平台。该平台能够沿径向伸展和收缩，从而实现灵活的结构与形态变化。

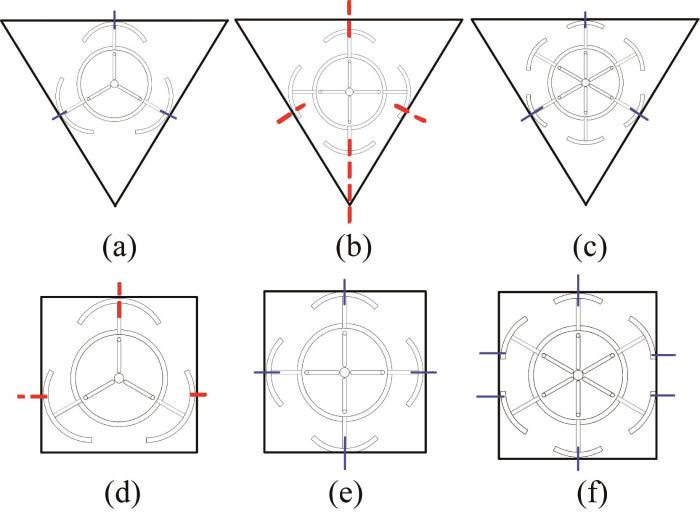
考虑到机器人的运动稳定性和整体质量，伸缩杆的数量宜控制在3~6根。如图2(a)所示，3根伸缩杆在三角形空间内受力均匀，而4根伸缩杆在该空间内受力不均匀，如图2(b)所示。在矩形空间内，3根伸缩杆受力不均匀，见图2(d)，而4根伸缩杆在该空间内受力均匀，见图2(e)。如图2(c)和图2(f)所示，6根伸缩杆在2种空间内均受力平衡，适应性较强（根据对称性原则，不考虑5根伸缩杆）。综合考虑，本文设计的可变径平台由6根伸缩杆沿径向均匀分布形成。

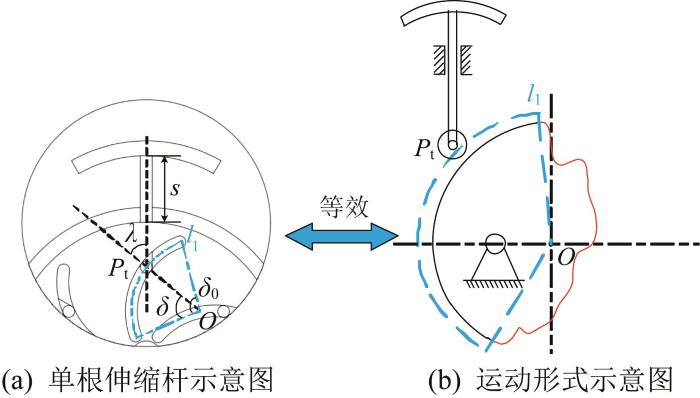
在平台变径过程中，6根伸缩杆分别沿图1所示的槽形轮廓作往复运动。为减少驱动元件数量并保证平台运动的流畅性，在圆心处采用图3所示的滚子推杆盘形凸轮机构作为驱动机构，以实现伸缩运动。为使伸缩运动平滑无卡顿，采用偏心圆形凸轮

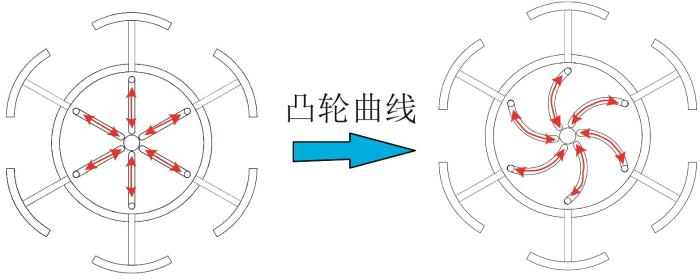
机构，其推程段轮廓用于实现驱动力传递；伸缩杆在力封闭作用下作为凸轮机构的从动件。如图4所示，随着伸缩杆在偏心圆形凸轮机构外轮廓处的位移变化，其运动轨迹由直线变为凸轮曲线，以适应不同地形下的外力变化。

根据机械原理，在中低速、中等载荷工况下，凸轮机构需具备优良的综合性能，以适应工作转速及特定载荷的需求。鉴于采用余弦加速度运动规律（即简谐运动规律）时，从动件的速度与加速度相对较小，本文选用该运动规律作为伸缩杆的运动规律。余弦加速度运动规律的位移方程可表示为：

式中：s为伸缩杆位移，δ0为推程运动角，δ为凸轮转角，h为伸缩杆沿推程移动的距离。

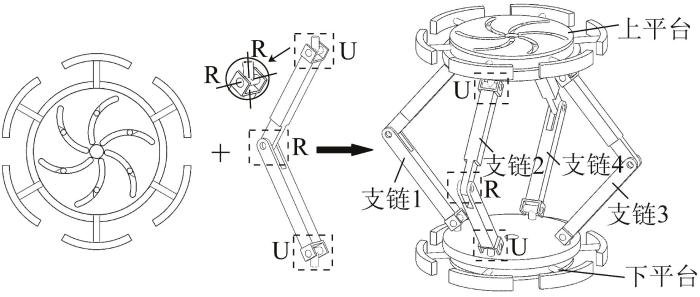
相较于采用P副驱动的移动机器人，以R副驱动的移动机器人的优势在于：R副不仅能作为机器人的驱动结构，还能用于接地支撑，扩展了机器人支撑区域的多样性。此外，R副有助于支链的弯曲与折叠，可提升机器人的折展性能。基于此，根据上述可变径平台，遵循对称性原则，设计了以4-URU并联机构为主体的可变径多模式移动并联机器人，如图5所示。该机器人的上下平台为对称的2个可变径平台，4条URU支链环绕平台圆形轮廓均匀分布，两两对称。对于单条URU支链，其上下U副对称连接上下平台，2个U副之间连接R副。其中，U副的一条轴线与上下平台的公法线平行，另一条轴线与中间R副的轴线平行，且U副可等效为2个轴线垂直相交的R副。

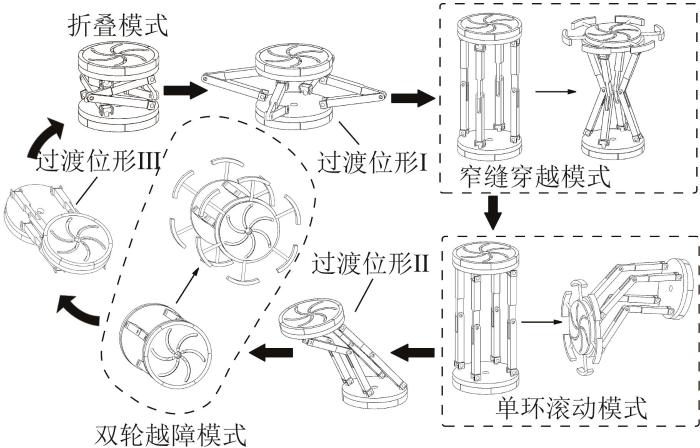
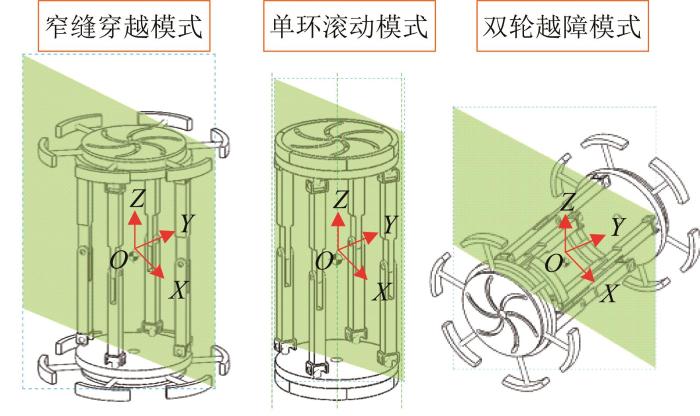
当各URU支链中的运动副轴线方向发生变化时，其旋量与约束轴线都将发生变化，进而导致机器人自由度发生变化，最终实现机器人的模式切换。如图6所示，本文所设计的机器人包括便于携带的折叠模式、适用于在狭窄空间内移动的窄缝穿越模式、适用于台阶攀爬的单环滚动模式以及适用于跨越障碍物的双轮越障模式。折叠模式通过过渡位形Ⅰ切换为窄缝穿越模式；窄缝穿越模式在初始位形下通过U副轴线变化切换为单环滚动模式；单环滚动模式通过过渡位形Ⅱ切换为双轮越障模式；双轮越障模式通过过渡位形Ⅲ切换回折叠模式。

单个可变径平台仅需1个驱动电机即可带动6根伸缩杆运动，故其自由度固定，不受机器人模式切换的影响。因此，下文将对可变径多模式移动并联机器人的主体——4-URU并联机构进行自由度分析。

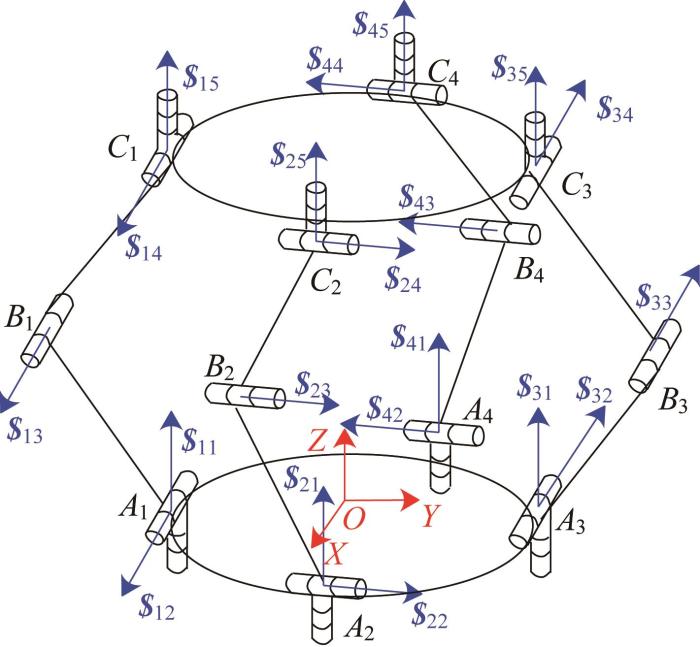
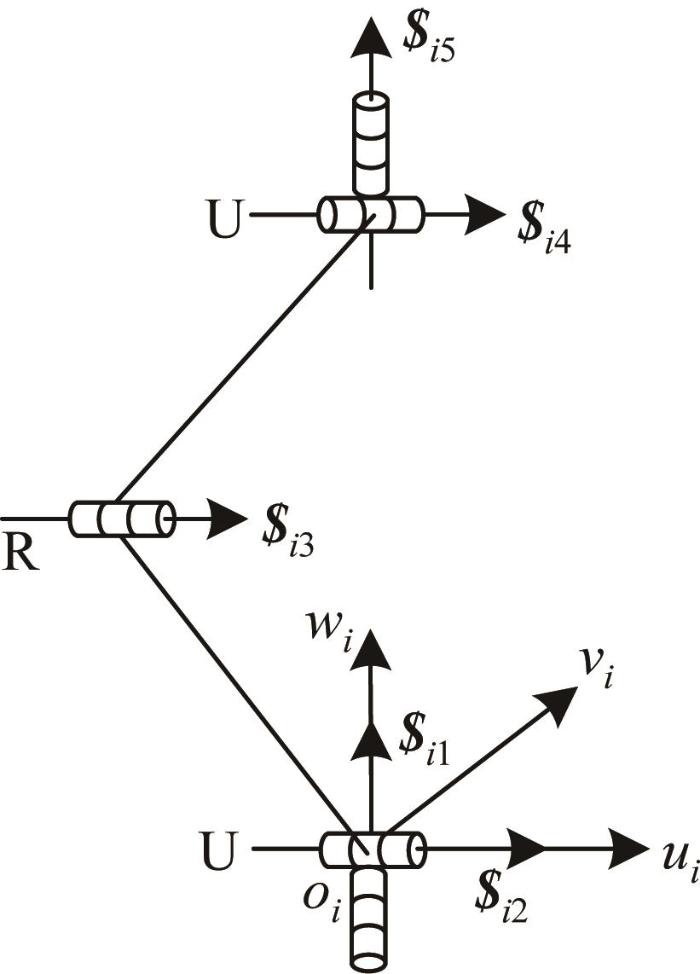
如图7所示，4-URU并联机构中所有U副沿轴线方向分布2个垂直相交的螺旋，R副沿轴线方向分布单个螺旋。选取其中一条URU支链进行分析，如图8所示。以螺旋$i1和$i2的交点o_i 为坐标原点，建立支链局部坐标系oi-uiviwi。

根据图8，单条URU支链（以支链1为例）中各运动副的运动螺旋为：

式中：d、e、f为并联机构几何位形的相关参数。

基于螺旋互易积为零的原理^[20]，采用代数方法进行求解，得到该支链的反螺旋：

通过对反螺旋的分析可知，该支链的反螺旋节距趋于无穷大，从而形成一个作用于Y方向的约束力偶，其方向与上方U副平面的法线方向一致。同理，另外3条支链也具有相同性质。4个力偶同时作用于上平台，每个力偶均垂直于对应的U副平面，且与上平台保持平行。由于这些力偶位于同一平面，且其中仅有2个力偶是线性无关的，可以推断出4-URU并联机构存在2个冗余约束。4条支链施加的约束条件共同限制了上平台绕X轴和Y轴的转动，故该并联机构能够沿X、Y、Z轴方向自由移动，且可绕Z轴旋转。根据螺旋理论，窄缝穿越、单环滚动、双轮越障等不同模式下4-URU并联机构的自由度如表1所示（运动螺旋以支链1为例，其余支链同理可得）。由于折叠模式为静态模式，不对其自由度进行分析。

折展比（机器人在展开状态和折叠状态下的尺寸比值）作为一个关键参数，能够有效衡量机器人的变形能力，并表征其适应物理环境的灵活性。按照空间形态，折展比可分为线折展比、面折展比和体折展比三类。鉴于U副可看作2个轴线相交且能够相对独立旋转的R副，当每条URU支链的U副绕Z轴的转动自由度被锁定时，支链会转变为平行的RRR支链结构。此时，移动并联机器人能够沿可变径平台法线方向进行折叠，显著提高了整体结构的折展性能，增强了机器人在复杂环境中的变形能力和适应性。

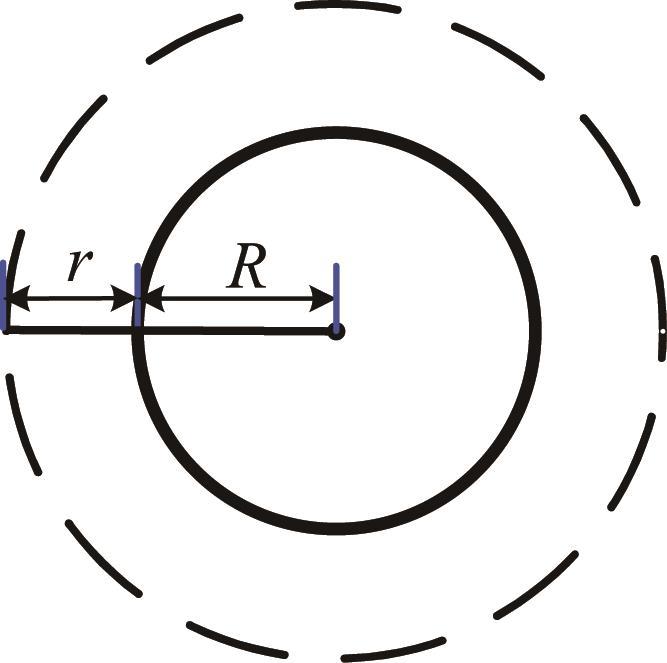
在折叠模式下，整个机器人的折展有2个面维度：一个是平台的横向折展，另一个是支链的纵向折展。可变径平台的折展原理如图9所示。在收拢状态下，圆形平台的半径为R；在展开状态下，伸缩杆的伸出长度为r，则平台的横向面折展比η_a为：

式中：S₁为平台收拢时的覆盖面积，S₂为平台展开后的覆盖面积。

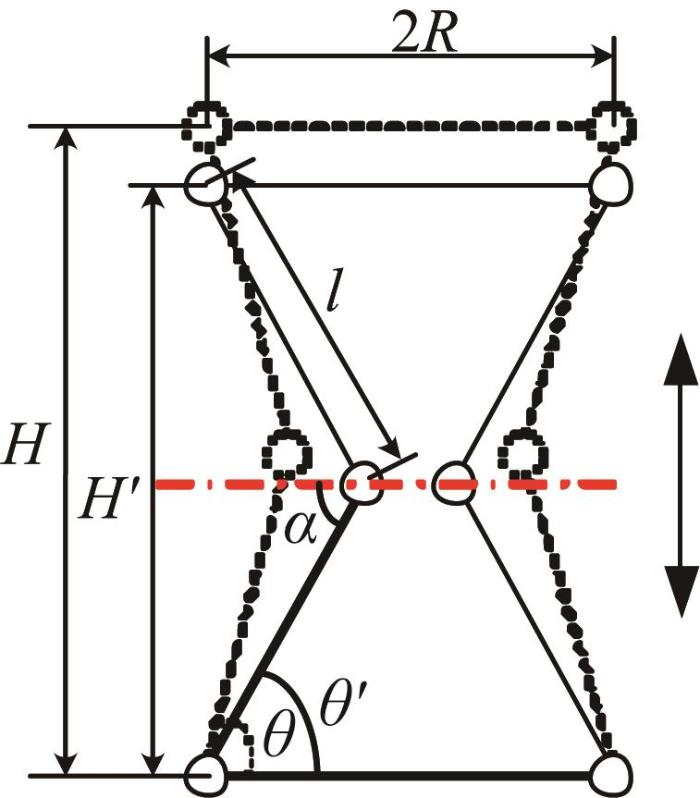
机器人的纵向面折展比需要从支链角度入手。URU支链的折展原理如图10所示。假设上平台相较于下平台的初始高度为H，折叠后的高度为H'，连杆长度为l，连杆与下平台的初始夹角为θ，折叠后的角度为θ'，纵向折叠角度为α，且α=θ'。通过分析可知：

根据面折展比的定义，该机器人的纵向面折展比ηb可表示为折叠后高度H'与初始高度H的比值：

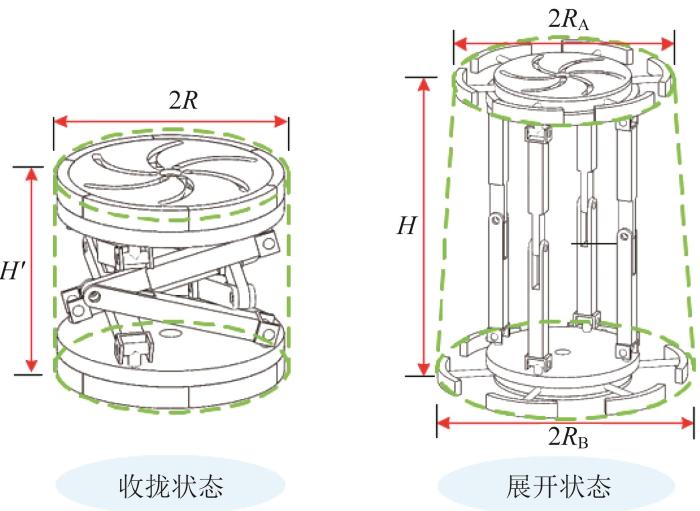
机器人的体折展比是反映其整体折展能力的重要指标。所设计的机器人在收拢与展开状态下的体积包络示意如图11所示。基于上文对面折展比的分析，根据图11综合得到该机器人的体折展比。在展开状态下，假设上、下平台的外接圆半径分别为RA和RB，则有：

式中：r_A为上平台伸缩杆的伸出长度，r_B为下平台伸缩杆的伸出长度。

根据式(4)至(6)，得到整个机器人的体折展比η：

式中：V_f为机器人收拢时的包络体积，V_d为机器人展开时的包络体积。

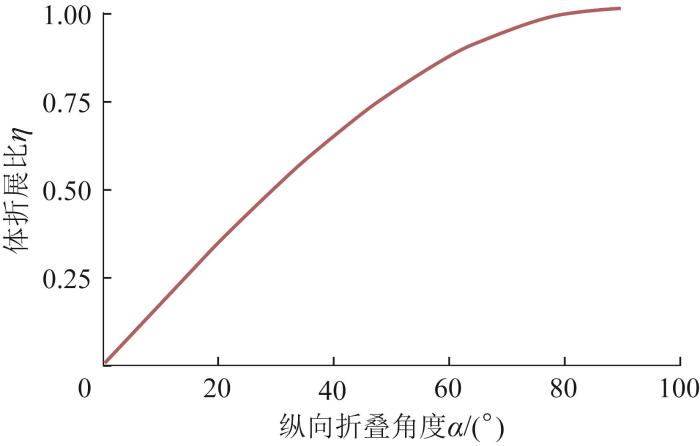
当上下平台均完全展开时，展开状态下的包络体积达到最大，此时RA=RB。若初始夹角θ=90°，根据折叠过程中存在的等量关系，当纵向折叠角度α∈[0°, 90°]时，机器人的体折展比变化曲线如图12所示。

当机器人切换为窄缝穿越模式时，为了适应不同的狭窄缝隙，机器人的4条支链两两垂直，从侧面观察，可看作2个平面6R机构沿支链A2C2对称分布。

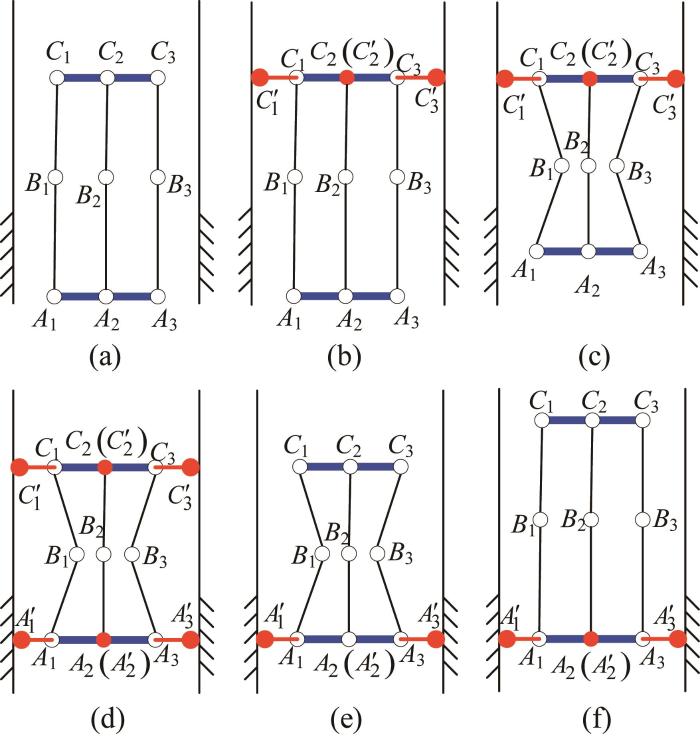
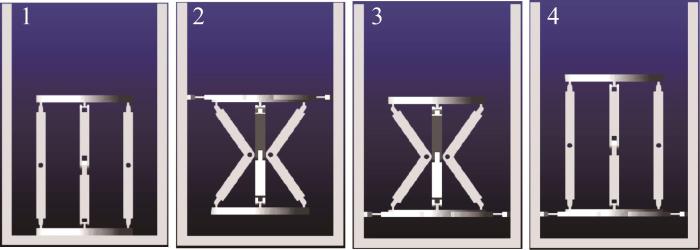
机器人的窄缝穿越步态如图13所示。其中：图13(a)所示为窄缝穿越过程的初始位置，此时支链AiCi呈向内竖直状态；图13(b)所示为平台C1C3向外展开伸缩杆，当C1'和C3'接触窄缝内壁时停止；图13(c)所示为支链AiCi呈向内收拢状态，此时平台A1A3向上升高；图13(d)所示为平台A1A3向外展开伸缩杆，当A1'和A3'接触窄缝内壁时停止；图13(e)所示为平台C1C3的伸缩杆向内收拢；图13(f)所示为支链AiCi呈直线状态，平台C1C3再次升高。重复图13(a)至图13(f)所示的步态，机器人可实现在窄缝内的向上穿越。

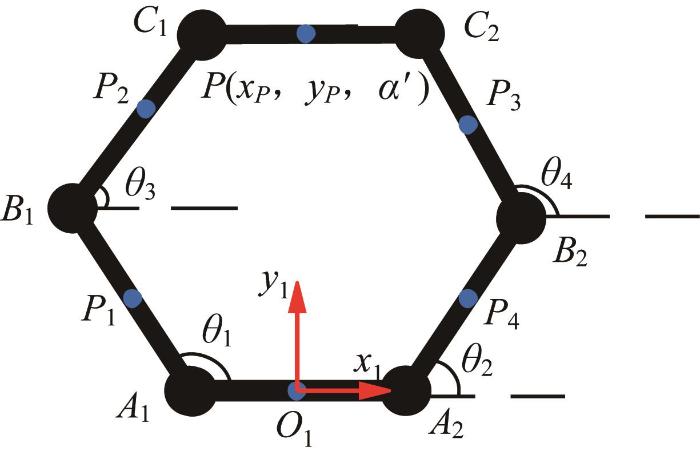
当机器人切换为单环滚动模式时，其4条支链两两平行，其中支链A1C1与支链A3C3的动作相同，支链A2C2与支链A4C4的动作相同，从侧面观察，整个机器人可等效为平面6R连杆机构。单环滚动模式下机器人的运动学模型如图14所示。在A₁A₂中点O₁处建立直角坐标系O₁-x₁y₁z₁，以A1和A₂的连线为x₁轴，指向A2方向为正，垂直地面向上为y₁轴正方向，P点为C1和C2的中点；P_k (k=1, 2, …, 4)为杆A1B1、B1C1、B2C2和A2B2的中点。杆A1B1、A2B2、B2C2、B1C1与x₁轴的夹角分别为θ1、θ2、θ3、θ4，取逆时针方向为正方向。

采用矢量方程法对平面6R连杆机构的各关节进行位置分析，P点的位置可表示为：

由式(9)和式(10)可得单环滚动模式下机器人在x₁轴、y₁轴方向上的位置，当给定θ1、θ2和θ3时，θ1、θ2、θ3和θ4的关系可由式(11)通过矢量法求得：

式中： l_C1C2为C₁指向C₂的方向向量。

通过对位置方程进行微分运算，可推导该机器人的速度方程：

式中：A、B、C为与速度相关的几何参数。

对式(12)进行进一步求导，可得该机器人的加速度方程，从而为后文分析提供理论基础。

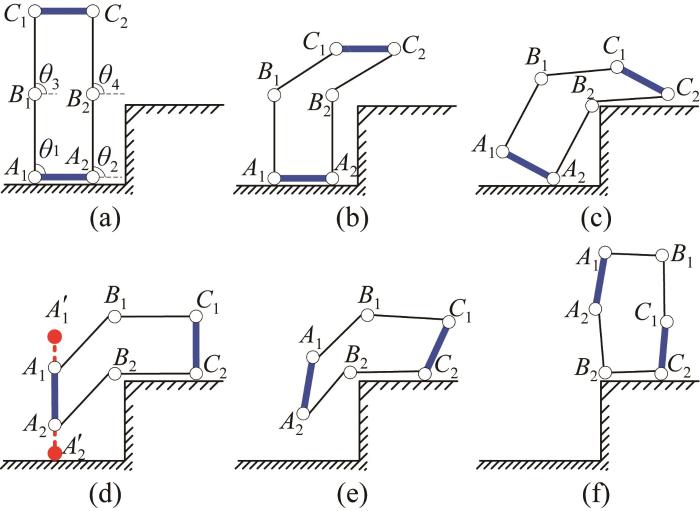
机器人在执行单环滚动步态时的瞬时状态如图15所示。其中：图15(a)所示为机器人在单环滚动模式下的初始位置，此时A1B1与B1C1共线，A2B2与B2C2共线，A1A2平行并贴紧下台阶面，C1C2与A1A2平行，该步态下机器人整体侧视图呈矩形；图15(b)所示为C1C2接近上台阶面状态，此时θ1和θ2保持不变，θ3和θ4变小；图15(c)所示为C2接触上台阶面，A1离开下台阶面，机器人整体向前滚动；图15(d)所示为平台C1C2垂直于上台阶面，平台A1A2展开伸缩杆，并以A2'为支点提高整体质心位置；图15(e)所示为平台A1A2到达一定高度并收拢伸缩杆，为完成台阶攀爬做准备。图15(f)所示为A2B2垂直于上台阶面，机器人整体侧视图再次呈矩形，至此机器人完成台阶攀爬，机器人质心到达最高点。

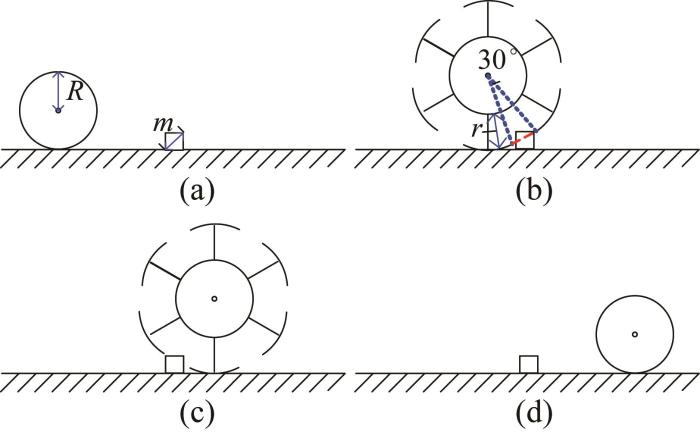
当机器人在非结构化路面上遇到障碍物（最大长度为m）时，其切换为双轮越障模式，对应的越障步态如图16所示。其中：图16(a)所示为机器人在双轮越障模式下的初始位置，此时各伸缩杆处于原始状态；图16(b)所示为机器人在接近障碍物之前所处的展开状态，此时6根伸缩杆均匀伸出（伸出长度为r），从而为跨越障碍物做好准备。图16(c)所示为机器人成功跨越障碍物的瞬时状态；图16(d)所示为机器人在离开障碍物后恢复为初始状态的过程。

根据图16(b)，在伸展状态下，可变径平台均匀伸出6根伸缩杆，伸缩杆末端将初始圆形平台划分为相同的六部分，相邻伸缩杆间的夹角为60°。当伸缩杆沿运动轨迹伸出r，相邻伸缩杆间有一段可跨越障碍物的间隙n，根据余弦定理，可得：

化简式(13)可得：

根据图16，若要确保机器人能够顺利跨越障碍物，相邻伸缩杆间隙n必须大于或等于障碍物的最大长度m，即：

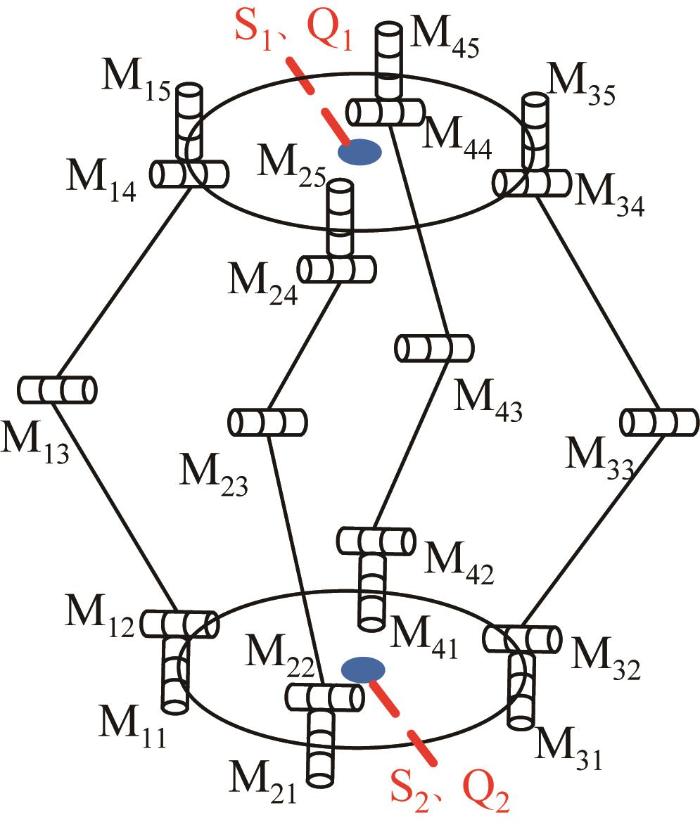
为实现移动并联机器人在多种模式下的运动，每个驱动关节沿转动轴线安装1台伺服舵机，如图17所示，每个$ij(i=1, 2, …, 4，j=1, 2, …, 5)处对应一台伺服舵机Mij。为实现上、下平台的折展，各需1台电机驱动6根伸缩杆运动，故在上、下平台法向轴线处分别安装减速电机S₁和S₂。此外，在双轮越障模式下，需用2台相同的电机驱动机器人滚动，故在上、下平台法向轴线处分别安装减速电机Q₁和Q₂。通过对驱动电机实施分时控制，可实现多种运动模式的切换，从而灵活调节机器人的运动状态。

根据文献[21]，将各伺服舵机与减速电机的工作状态分为驱动（●）、锁定（○）、失效（⊗）三种类型。通过改变伺服舵机与减速电机的工作状态，使机器人的自由度发生变化，从而实现不同运动模式的切换。对于分布在各支链上的伺服舵机Mij，当Mij处于驱动状态时，与主动副相连的连杆之间的角度可根据要求改变；当Mij处于锁定状态时，与主动副相连的连杆之间的角度无法改变；当Mij处于失效状态时，与主动副相连的连杆之间的角度可随意改变。对于分布在平台上的减速电机S₁、S₂、Q₁和Q₂，仅有驱动（●）、锁定（○）两种状态。不同模式下驱动电机的状态如表2所示，其中虚线框内S、Q独立表示。

机器人运动的动态稳定性通常由ZMP（zero moment point，零力矩点）轨迹来评估。为此，本文探讨了不同运动模式下移动并联机器人质心轨迹的变化，并基于质心轨迹分析各运动模式的稳定性与适用性。ZMP坐标可由重力和惯性力的合力推导得到，采用达朗贝尔原理进行推导。假设机器人各个连杆的质量为m_a，连杆的质心坐标为(x_a, y_a, z_a )，其受力状态由重力与惯性力的合力决定，该合力F可表示为：

式中： x¨a、y¨a、z¨a分别为第a根连杆沿X、Y、Z方向的加速度，g为重力加速度。

根据ZMP的定义，机器人所受合力绕ZMP的力矩都为0，则可得ZMP的X、Y方向坐标（由于Z方向坐标恒定不变，故不作分析）：

机器人的运动速度较小，故惯性力对位置的影响较小，相较于重力的影响，惯性力的影响可忽略不计。在这种情况下，ZMP坐标的计算可简化为对质心位置的分析。如图18所示，以机器人结构中心为原点构建坐标系O-XYZ，X轴方向为运动方向，Z轴方向垂直于地面向上，Y轴由右手定则确定。由于机器人结构及其运动的特殊性，其质心只在YOZ平面内发生变化，故只需判断质心投影是否在支撑范围内即可。

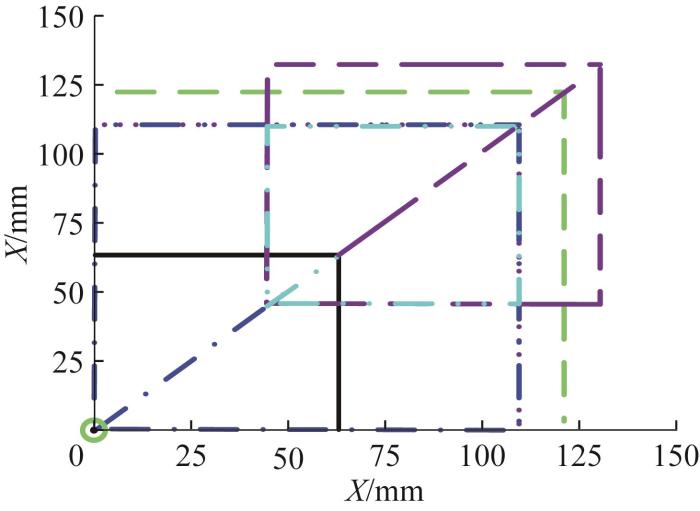
经分析，窄缝穿越模式下机器人的支撑多边形为窄缝两侧与支撑杆接触所覆盖的矩形，质心一直处于中间位置，故该模式下质心一直保持在支撑多边形内部；双轮越障模式下的支撑多边形为机器人下方与地面接触点所围的区域且一直保持在中间位置，即质心位置始终保持在该区域内；单环滚动模式下机器人质心位置的判断相对复杂，需根据式(17)计算质心位置的动态变化。单环滚动模式下机器人质心的变化曲线如图19所示，各矩形线框代表质心的稳定区域。若机器人的质心始终保持在该区域内，则说明机器人一直保持稳定。综上所述，在3种运动模式下，机器人质心始终未越过支撑面的边界，表明机器人在不同运动模式下能够维持动态平衡。

为评估所设计的移动并联机器人的稳定性及其越障性能，借助ADAMS软件对机器人在非结构化地形中的多种运动模式进行仿真分析。

在机器人仿真模型中，上、下平台的外接圆直径设为200 mm，连杆长度设为170 mm，其余环境相关参数如表3所示。基于所构建的机器人仿真模型，对其在不同运动模式下的性能进行分析。

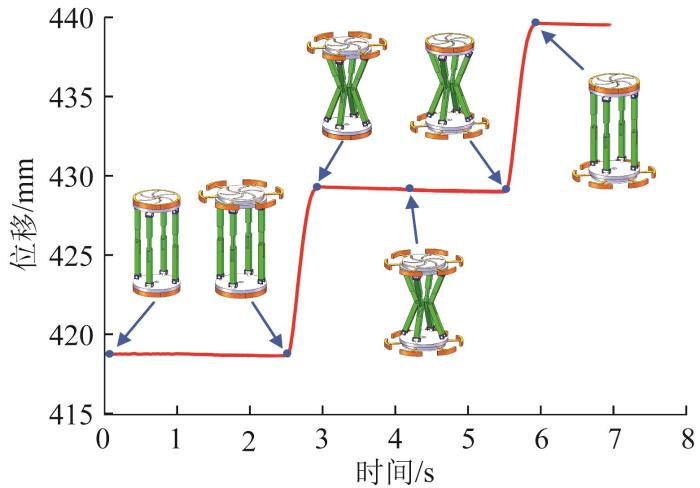
在窄缝穿越模式下，仿真时间设为7 s，步数设置为1 000，设置两面对称墙壁形成窄缝。该模式下机器人的整个运动步态如图20所示。为了更直观地展示机器人的运动特性，选取机器人上平台的质心为测点，该质心的位移仿真结果如图21所示。结果表明，该机器人在7 s内成功地在窄缝内完成了一段向上攀爬；从上平台质心的位移曲线可以看出，上平台质心基本呈阶梯状上升，但在1—2.5 s、3—5.5 s和6—7 s内有轻微下降趋势。由此可以推测，在理想条件下，由于摩擦力不足，窄缝穿越模式下的机器人在重力作用下会出现整体轻微下滑的趋势，但不影响整体运动稳定性。

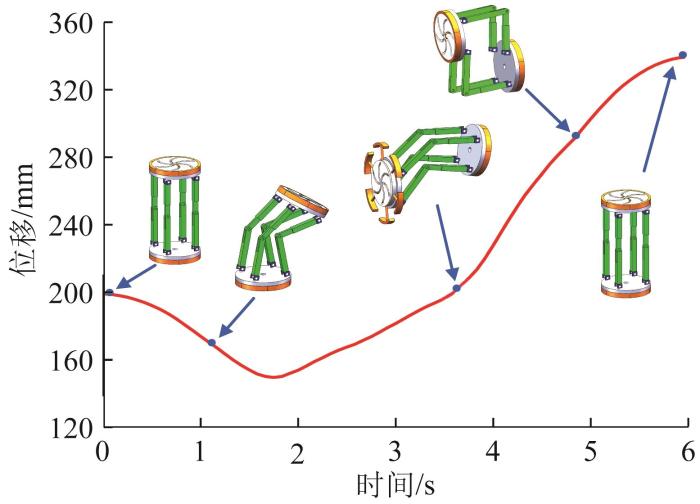
在单环滚动模式下，仿真时间设为6 s，步数设置为800，设置单个平面台阶。该模式下机器人的整个运动步态如图22所示。选取整个机器人的质心为测点，该质心的位移仿真结果如图23所示。结果表明，机器人在6 s内可以成功完成攀爬动作；从机器人质心位移曲线可以看出，单环滚动模式下质心先降低再缓慢升高，整个运动过程相对流畅。

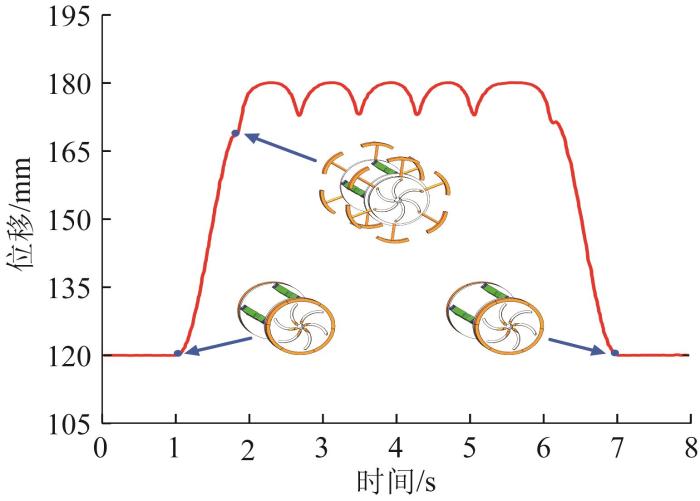
在双轮越障模式下，仿真时间设为8 s，步数设置为1 000，并设置截面为矩形的长条障碍物。该模式下机器人的整个运动步态如图24所示。选取整个机器人的质心为测点，该质心的位移仿真结果如图25所示。结果表明，机器人在8 s内成功地完成了越障动作；从机器人质心位移曲线可以看出，整个越障过程相对稳定，当伸缩杆完全展开后，机器人质心有一定的波动，但不影响整个运动过程的稳定性。

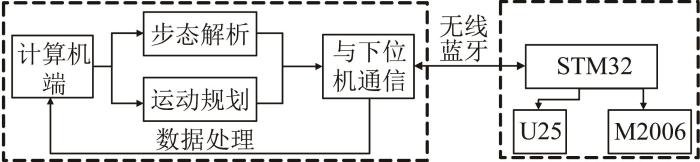
为了验证上文理论分析与仿真结果的准确性，开展机器人样机实验。搭建的机器人样机如图26所示。其中：伺服舵机选用Fashion Star品牌的U25舵机，减速电机选用RoboMaster M2006直流无刷减速电机。机器人样机的基本参数如表4所示。选用STM32控制板，机器人的整体控制逻辑如图27所示。

利用搭建的机器人样机开展窄缝穿越模式、单环滚动模式和双轮越障模式下的运动实验。

如图28所示，机器人可顺利完成窄缝穿越模式下的所有步态，在单个运动周期内可向上攀爬60 mm。

如图29所示，机器人在单环滚动模式下成功地攀爬上了高度为170 mm的台阶。

如图30所示，当伸缩杆完全展开时，机器人可顺利越过障碍物，完成双轮越障滚动。

1）本文提出了一种可变径多模式移动并联机器人设计方案。该机器人具备多环境适应能力和多模式运动特性。通过可变径平台与4-URU并联机构的结合，该机器人不仅能适应多种非结构化复杂环境，还弥补了传统轮式、腿式及履带式机器人在越障能力、灵活性和承载能力上的不足。结合轮-腿式复合机器人的设计思路，有效地提升了机器人在实际应用中的操作灵活性和任务完成效率。

2）基于螺旋理论和ZMP理论的分析结果表明，所设计的机器人在不同模式下的自由度可灵活切换，且能保持较高的动态稳定性。通过对机器人在折叠模式、窄缝穿越模式、单环滚动模式以及双轮越障模式下的运动学分析，得到了其在不同模式下的运动特性。

3）仿真结果与样机实验结果一致，验证了本文所提出的设计方案与分析方法的可行性。ADAMS仿真结果显示，机器人在不同模式下的质心轨迹连续平稳，其越障和攀爬过程流畅；样机实验进一步验证了机器人在实际环境中的有效性。综上，所设计的可变径多模式移动并联机器人对复杂环境下多功能移动机器人的研究具有重要的参考价值，为其在救援、巡检及勘探等领域的进一步推广应用奠定了基础。

本文链接：https：//www.zjujournals.com/gcsjxb/CN/10.3785/j.issn.1006-754X.2025.05.107