随着人类活动范围与探索边界的扩展，地面移动机构被广泛应用于太空探索、除险排爆、地震救援和深海采集等极端复杂作业环境^[1-4]。传统地面移动机构按移动形式可分为轮式^[5]、腿式^[6]和履带式^[7]等。其中：轮式移动机构在平整的结构化路面上具有平稳性高和移动快速的优势^[8]；腿式移动机构在崎岖山路等凹凸地形上具有良好的越障性能^[9]；履带式移动机构在起伏多变的非结构化路面上具有优越的稳定性和通过性^[10]。

鉴于履带式移动机构具有接地比压小、适应环境能力强等特点^[11]，国内外学者针对其越障能力和环境适应性的进一步提升开展了深入研究。所设计的履带式移动机构可分为摆臂式履带移动机构^[12]、复合式履带移动机构^[13]、可变形履带移动机构^[14]和自适应差动履带移动机构^[15]等。美国iRobot公司设计的摆臂式履带移动机器人PackBot ^[16]在传统前端带轮的侧方增加了2组履带式摆臂，当机器人需要跨越障碍物时，控制电机驱动摆臂转动，使得摆臂与地面形成一定角度，以辅助机器人通过障碍物。Michaud等^[17]研制的腿-履带-轮式机器人AZIMUT由4个三角形履带模块和车体组成，每个履带模块包含3个电机，当机器人需要通过复杂地形时，通过控制电机使履带模块实现轮式、履带式和腿式移动功能的转换，以适应不同地形。赵希庆等^[18]设计的四连杆可变形履带式机器人基于平行四杆机构原理，将履带配置在连杆机构一侧，在履带总长一定的条件下，该机器人通过连杆与履带的协同变形实现越障功能。姚燕安等^[15]研制的自适应差动履带机器人采用欠驱动方式，将行星式履带移动机构^[19]作为行走装置，并通过行星轮转动来实现机器人的快速越障功能。综上所述，可通过增加履带摆臂^[16,20]、轮-履-腿切换^[17]、履带变形^[18,21]等方式来提高履带式移动机构的越障能力和环境适应能力；同时，可通过采用欠驱动方式来提高越障速度^[22-23]，且无需复杂的传感器和控制程序。

为克服现有履带移动机构在快速越障和适应复杂地形环境方面的局限性，基于行星式履带移动机构提出了一种行星式欠驱动可变形履带移动机构，通过控制变形驱动电机来实现履带移动机构运动模式（直臂模式、正交模式和过渡模式）的切换，从而实现快速越障和适应复杂地形的功能。相较于现有的可变形履带移动机构，行星式欠驱动可变形履带移动机构在越障的快速响应能力方面展现出显著优势^[24]。由于采用了可变形的结构设计，该履带移动机构在面对路面起伏剧烈、沟槽坑洼等复杂恶劣的地形环境时能够迅速调整履带姿态，以应对各种路面环境。此外，行星式欠驱动可变形履带结构简单且可靠，减少了潜在的故障风险，可提升整个履带移动机构的稳定性。本文研究内容如下：首先，对履带移动机构进行运动学分析，得到其质心高度和接地面积，并分析其适用环境；然后，对履带移动机构进行越障分析，计算其最大越障宽度/高度以及所需的最大驱动扭矩，并开展动力学仿真验证；最后，制作履带移动机构的原理样机，通过实验来验证其越障的可行性。

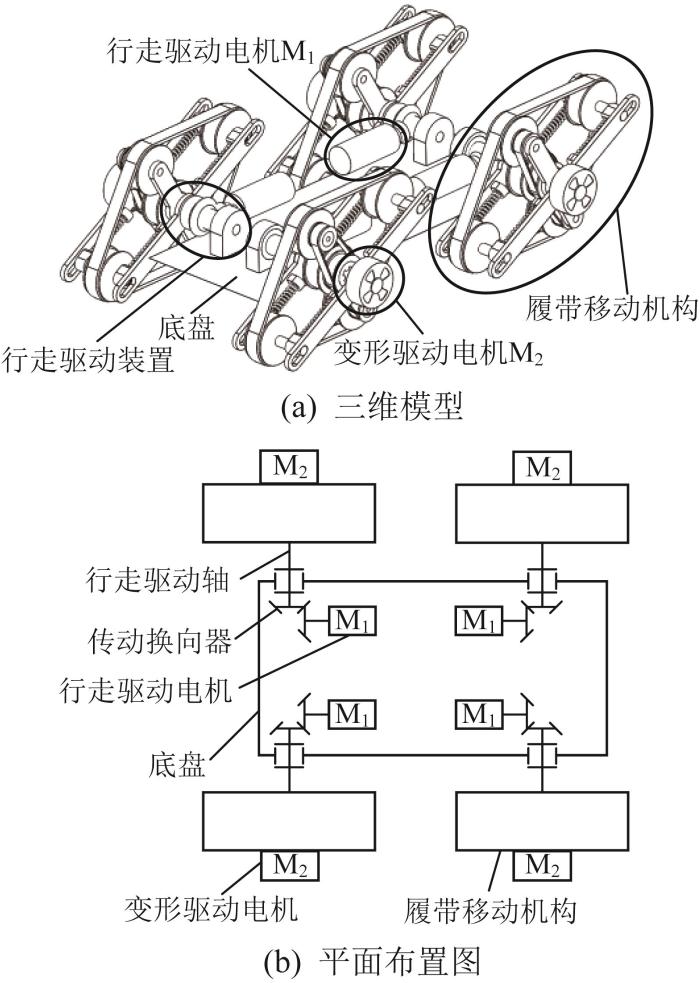
行星履带式整车模型如图1所示。整车呈对称式布局，主要由底盘、行走驱动装置、行星式欠驱动可变形履带移动机构、行走驱动电机M₁和变形驱动电机M₂构成。其中：行走驱动装置包括传动换向器和行走驱动轴；履带移动机构可绕行走驱动轴的轴线旋转，其一侧连接控制履带变形的电机M₂；履带移动机构由电机M₁驱动，以完成整车的行走、转弯与越障等功能。

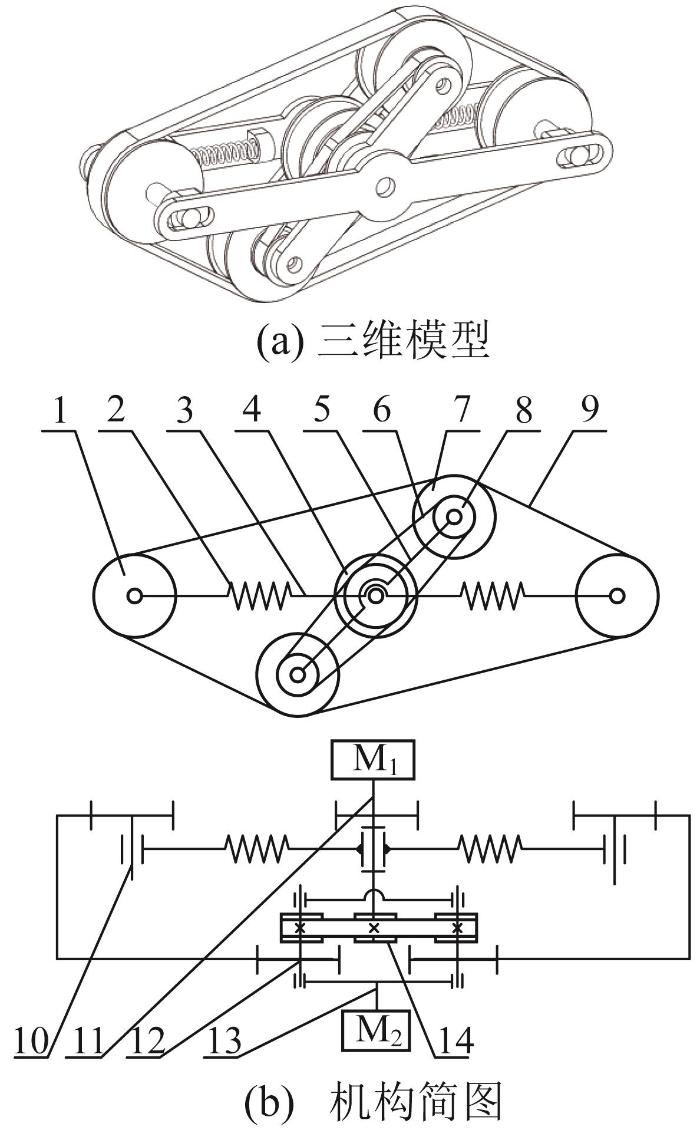
行星式欠驱动可变形履带移动机构的构型如图2所示，主要由履带驱动轮系（包括从动轮、弹簧、侧板、主动轮、履带和从动轴）和行星轮系（包括行星杆、同步带、行星轮、行星从动轮、行星轴、变形驱动轴和行星主动轮）构成。其中，变形驱动轴未在图2(a)中标注。

行走驱动电机M₁通过行走驱动轴驱动主动轮和行星主动轮同步转动，以带动同步带、行星轮和行星从动轮转动，进而带动从动轮和履带转动，实现履带移动机构的移动功能。变形驱动电机M₂通过变形驱动轴带动行星杆转动，使得行星杆与侧板的夹角（即行星杆转角）发生变化；在履带长度为固定值的约束下，行星杆带动履带发生变形，使得从动轮和从动轴沿侧板两端的滑槽移动，且从动轴与弹簧连接，保证了履带具有一定的张紧力，从而实现履带移动机构的变形功能。

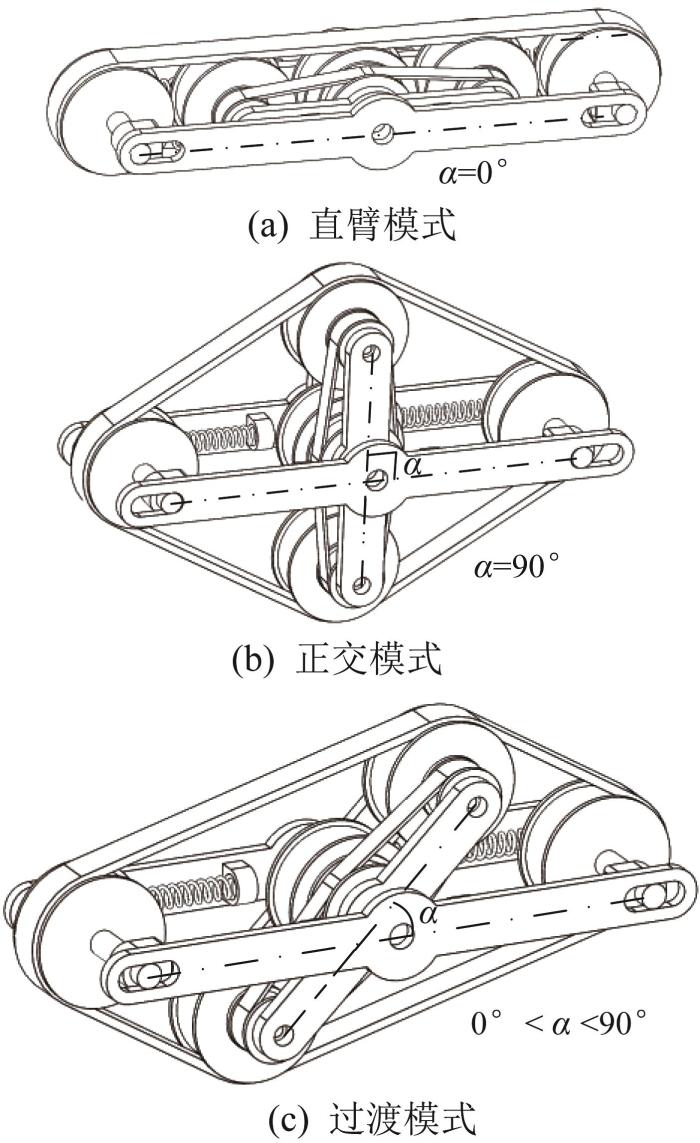
履带移动机构通过控制变形驱动电机M₂驱动行星杆转动来实现自身质心高度和接地面积的调整。根据行星杆转角α的变化，履带移动机构可实现3种运动模式（直臂模式、正交模式和过渡模式）的切换，如图3所示。直臂模式履带移动机构的行星杆转角α=0°，如图3(a)所示；正交模式履带移动机构的行星杆转角α=90°，如图3(b)所示；过渡模式履带移动机构的行星杆转角α=0°~90°，如图3(c)所示。

在行星式欠驱动可变形履带移动机构的运动过程中，行走驱动电机M₁带动主动轮和履带的转动为1个自由度，变形驱动电机M₂带动行星杆的转动为1个自由度，整个履带移动机构绕行走驱动轴轴线的转动为1个自由度，即该履带移动机构具有3个自由度。由于履带移动机构绕行走驱动轴轴线转动的自由度未被限制，因此其属于欠驱动装置。

该履带移动机构的主要特点为可自适应复杂地形，并能够以最小耗能的状态进行移动。地球上所有系统均倾向于耗能最小的状态。根据最小耗能原理，在任何耗能过程的每一瞬间，系统将在相应的约束条件下以最小耗能的方式完成能量转化与状态变化^[25]。履带移动机构在平整路面上会以低耗能状态进行移动；当遇到较高障碍物而不能以原始低耗能状态进行移动时，履带移动机构不需要传感器等识别设备，可瞬时将牵引力转化为绕主动轮轴线方向转动的扭矩，以实现绕行走驱动轴的旋转，从而减少越障响应时间，实现快速翻滚越障。

综上，所设计的履带移动机构基于欠驱动方式和最小耗能原理，采用较少驱动电机和传感器，使得控制程序较为简单可靠，进而减小了整体重量，实现了快速越障并降低了成本。

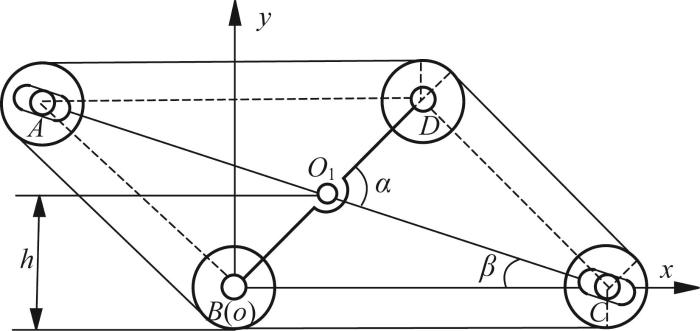
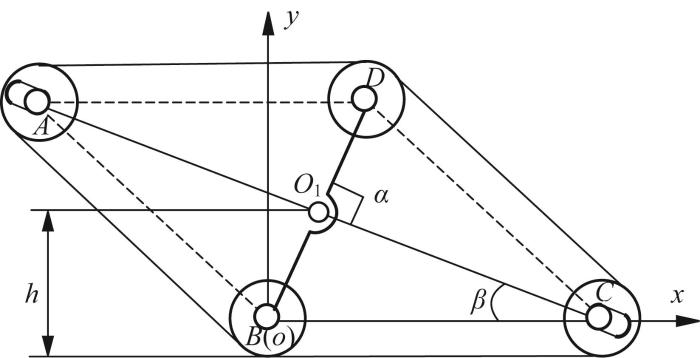
在变形驱动电机M₂的控制下，行星式欠驱动可变形履带移动机构的质心高度h和接地面积S随行星杆转角α的变化而变化。当α=0°时，履带移动机构切换为直臂模式；当α=90°时，履带移动机构切换为正交模式；当0°<α<90°时，履带移动机构切换为过渡模式。为分析履带移动机构的质心高度h、接地面积S与行星杆转角α的关系，选择具有一般意义的过渡模式进行具体分析。过渡模式履带移动机构的结构简图如图4所示。图中：A、B、C、D表示履带轮，其中A、C为从动轮，B、D为行星轮；行星轮中心连线BD表示行星杆，其长度为l_BD；外轮廓线表示履带，假定履带不发生变形时的定长为l（平行四边形ABCD周长与单个履带轮周长之和）。当行星杆BD转动时，连线AC与BD的夹角α（行星杆转角）发生改变，同时履带发生变形，在定长l的约束下，从动轮A、C沿侧板滑槽移动，进而使履带轮B、C与地面接触。

根据履带定长和履带轮A、B、C、D中心组成的平行四边形ABCD，建立几何模型并构建坐标系o-xy。其中，坐标系原点位于行星轮B的中心，x轴与履带轮B、C的中心连线重合，y轴过行星轮B中心并垂直于x轴。履带移动机构的质心高度h为质心O₁到地面的距离，接地面积S为履带宽度w与履带接地长度的乘积。履带移动机构的尺寸参数及算例值如表1所示。

为推导履带移动机构的质心高度h、接地面积S与行星杆转角α的关系，将分析过程分为两部分：1）以α为自变量，推导l_BC 、l_AC 与夹角β的表达式；2）根据l_BC 和l_AC，计算h和S。

1）根据平行四边形ABCD对角线和周长的关系以及三角形余弦定理，当行星杆转角α满足0°<α<90°时，可得：

联立式(1)中方程进行计算，可得：

其中：

2）根据△BCO₁面积的几何关系，可得：

联立式(2)和式(3)，计算得到过渡模式履带移动机构的质心高度h和接地面积S：

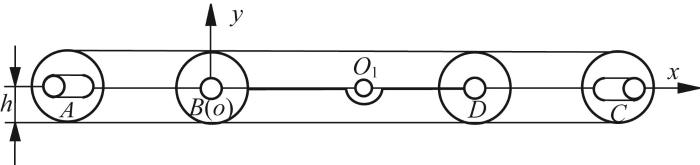
当α=0°时，履带移动机构切换为直臂模式，其结构简图如图5所示，行星杆BD与连线AC平行，从动轮A、C分别移动到侧板滑槽最外侧，进而与地面接触，此时履带接地长度为l_AC。

根据履带周长l等于履带接地长度l_AC 的2倍与单个履带轮周长之和，履带移动机构质心高度h（记为h₀）等于履带轮直径的一半，接地面积S（记为S₀）等于履带宽度w与履带接地长度l_AC 的乘积，可得：

联立式(5)中方程进行计算，可得：

当α=90°时，履带移动机构切换为正交模式，其结构简图如图6所示。此时平行四边形ABCD切换为菱形，即4条边均相等，履带接地长度为l_BC。根据式(4)，计算得到正交模式履带移动机构的质心高度h（记为h₁）和接地面积S（记为S₁）：

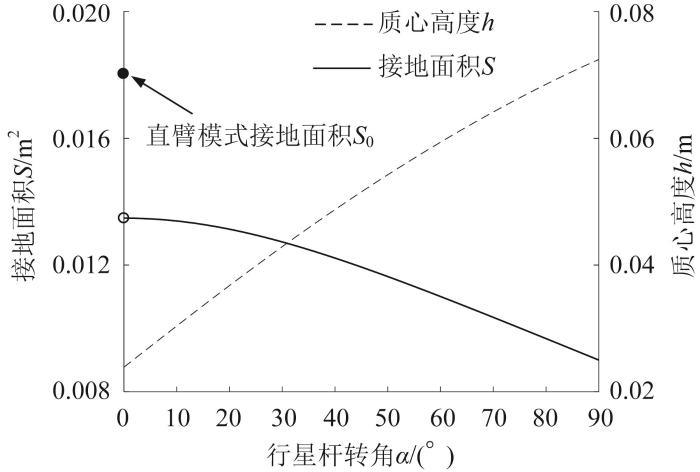
履带移动机构的质心高度h、接地面积S与行星杆转角α的关系如图7所示。由图7可知，直臂模式履带移动机构的质心高度h₀=0.024 m，由于履带接地长度为l_AC，接地面积S₀=0.018 m²，见图7中实心点位置；正交模式履带移动机构的质心高度h₁=0.072 m，接地面积S₁=0.009 m²；过渡模式履带移动机构的质心高度h随行星杆转角α的增大而增大，接地面积S随行星杆转角α的增大而减小。

综上，直臂模式履带移动机构的质心最低且接地面积最大；正交模式履带移动机构的质心最高且接地面积最小；过渡模式履带移动机构的质心高度和接地面积均介于直臂模式与正交模式之间。

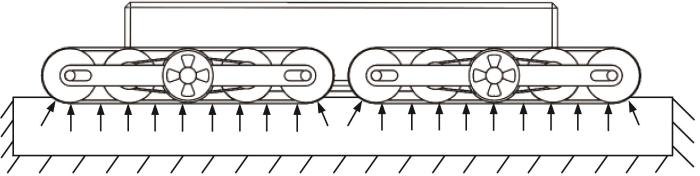
轮式移动机构通过松软路面时会出现下陷现象，而履带移动机构因接地面积大，通常不会出现明显的下陷现象。对于本文所设计的履带移动机构，其在直臂模式下具有接地面积大和质心低的特点，因此该模式履带移动机构的接地比压小且运行状态较稳定，可将车体重量均匀分散到地面上，进而减小履带移动机构的下陷深度，减小车体克服侧向挤压力所做的功，以保证履带移动机构具有足够的牵引力进行移动。直臂模式履带移动机构受力示意如图8所示。

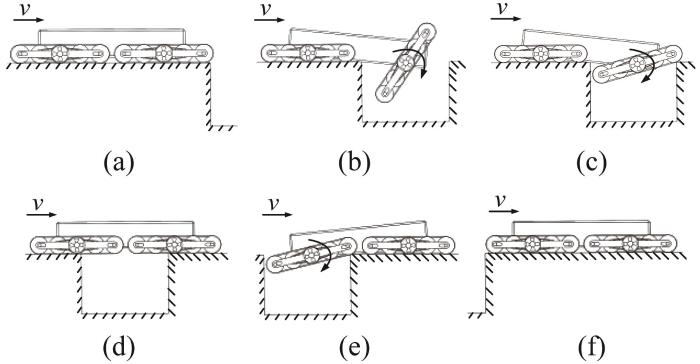
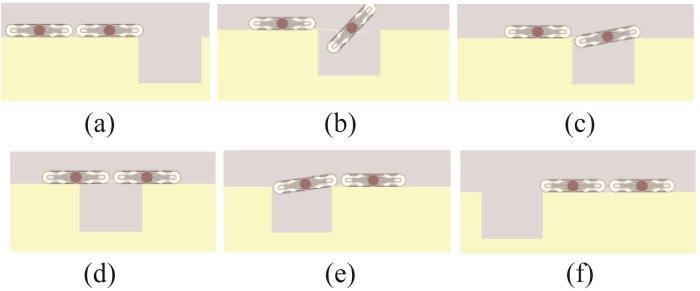
直臂模式履带移动机构的接地面积最大，故可跨越较宽的沟槽，其跨越沟槽的过程如图9所示。当车体中心靠近沟槽左侧断面时，前端履带移动机构接触沟槽右侧断面并支撑车体，通过前、后端履带移动机构提供“前扒后蹬”的牵引力，推动前端履带移动机构跨越沟槽，如图9(a)至图9(d)所示。随后，后端履带移动机构以相同的方式跨越至沟槽右侧，并恢复为越障前状态，如图9(e)至图9(f)所示。至此，直臂模式履带移动机构完成沟槽跨越^[20]。通过分析可知，直臂模式履带移动机构适合在松软路面和沟槽较宽的路面上移动。

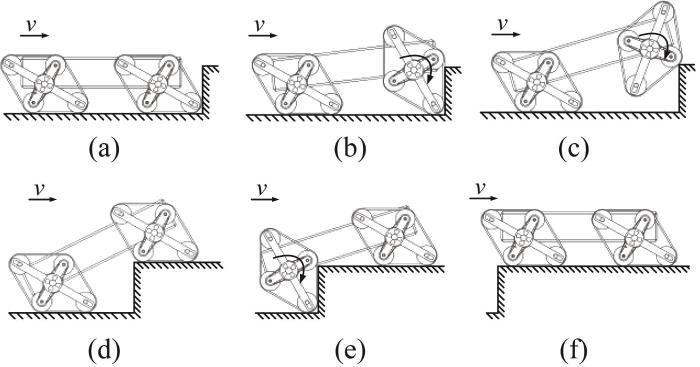
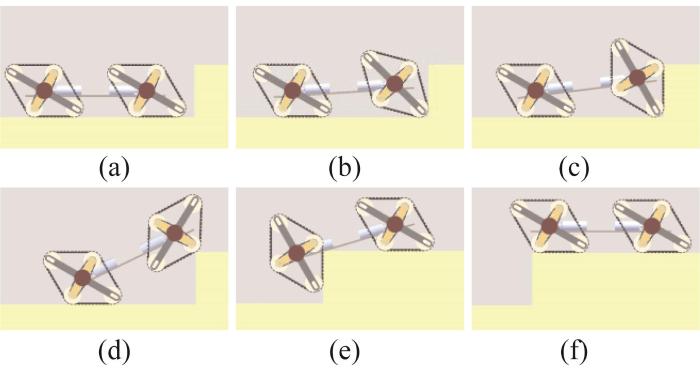
正交模式履带移动机构具有质心高的特点，故可翻越较高的凸台，其翻越凸台的过程如图10所示。当前端履带移动机构因接触凸台而无法向前移动时，其瞬时将牵引力转化为绕行走驱动轴轴线转动的扭矩，以实现顺时针旋转并翻越至凸台上方，如图10(a)至图10(d)所示。随后，后端履带移动机构以相同的方式翻越至凸台上方，并恢复为越障前状态，如图10(e)至图10(f)所示。至此，正交模式履带移动机构完成凸台翻越。通过分析可知，由于正交模式履带移动机构可抬高车体质心，且可绕行走驱动轴轴线转动，因此该模式履带移动机构适合在含有高障碍物的路面上移动。

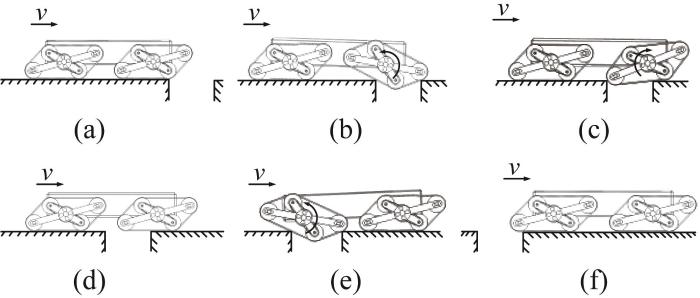
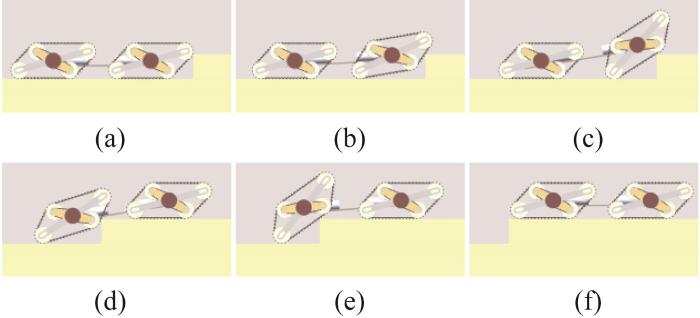
过渡模式履带移动机构的质心高度和接地面积介于直臂模式与正交模式之间，故该模式履带移动机构既具有一定的沟槽跨越能力又具有一定的凸台翻越能力。过渡模式履带移动机构跨越沟槽的过程如图11所示（以行星杆转角α=45°为例）。当前端履带移动机构接触沟槽左侧断面时，其顺时针转动并前倾，直至其从动轮与沟槽右侧断面接触，通过前、后端履带移动机构的牵引力推动前端履带移动机构跨越沟槽，如图11(a)至图11(d)所示。随后，后端履带移动机构以相同的方式跨越沟槽，并恢复为越障前状态，如图11(e)至图11(f)所示。至此，过渡模式履带移动机构完成沟槽跨越。

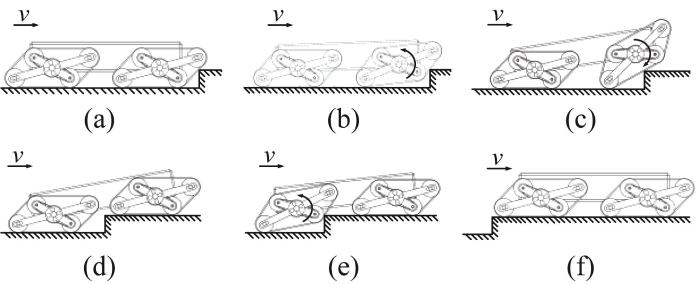
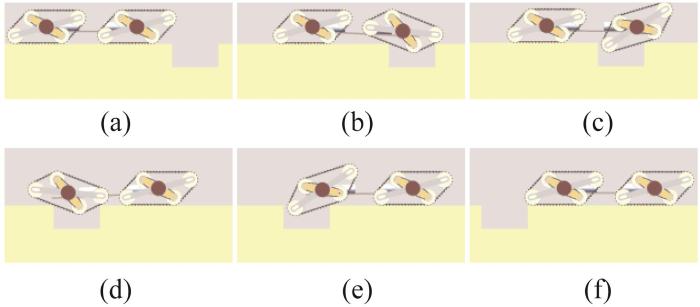
过渡模式履带移动机构翻越凸台的过程如图12所示（行星杆转角α=45°）。当前端履带移动机构接触凸台时，通过前、后端履带移动机构的牵引力推动前端履带移动机构翻越凸台，如图12(a)至图12(d)所示。随后，后端履带移动机构以相同的方式翻越凸台，并恢复为越障前状态，如图12(e)至图12(f)所示。至此，过渡模式履带移动机构完成凸台翻越。

由于过渡模式履带移动机构既能抬高车体质心又能增大接地面积，且具有一定的迎面角（履带与地面的夹角），可通过斜坡和碎石地形，因此该模式履带移动机构适合在同时含有沟槽和凸台等复合型障碍物的凹凸路面上移动。

为分析行星式欠驱动可变形履带移动机构的越障能力，基于3种运动模式（直臂模式、正交模式和过渡模式）下履带移动机构的越障过程，计算其可跨越的最大沟槽宽度、可翻越的最大凸台高度以及越障所需的驱动扭矩。其中，履带移动机构的运动参数及算例值如表2所示。

由于行星履带式整车为对称式布局，前、后端履带移动机构的越障方式完全相同，当前端履带移动机构越障时，后端履带移动机构及车体为前端履带移动机构提供推力及重力；当后端履带移动机构越障时，前端履带移动机构及车体为后端履带移动机构提供拉力及重力。因此，只需对前端履带移动机构的越障过程进行受力分析。

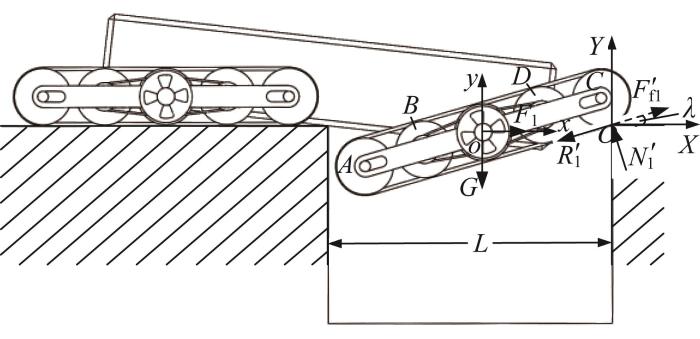
鉴于直臂模式履带移动机构的接地面积最大，本文主要分析其可跨越的最大沟槽宽度以及所需的驱动扭矩。在直臂模式下，从动轮两侧的弹簧未发生弹性形变且在运动过程中由振动引起的弹簧形变可忽略不计，故在驱动扭矩计算中不考虑弹簧弹性势能对电机扭矩的影响。直臂模式履带移动机构跨越沟槽时的受力分析如图13所示，主要分为2个阶段：第一阶段为车体重心到达沟槽左侧断面时，前端履带移动机构的从动轮C与沟槽右侧断面接触以支撑住车体，履带移动机构以从动轮C为转动中心顺时针旋转，直至侧板与地面平行，即λ=0°；第二阶段为前端履带移动机构与水平面平行后，通过前、后端履带移动机构提供的牵引力推动车体向前移动，进而完成沟槽跨越。由于第二阶段不需要电机提供翻转扭矩，即所需的驱动扭矩较小，因此本文主要针对第一阶段进行分析。为方便分析计算，建立以主动轮中心为原点的履带移动机构坐标系o-xy和以沟槽右侧断面与履带移动机构交点为原点的世界坐标系O-XY。

根据图13所示的几何关系，可得直臂模式履带移动机构可跨越的沟槽宽度L：

将表1和表2中的相关数据代入式(8)，计算得到直臂模式履带移动机构可跨越的最大沟槽宽度为258 mm。

对履带移动机构进行独立分析，设其重心在坐标系o-xy中的坐标为(x₀, y₀)，则重心在坐标系O-XY中的坐标(x_G, y_G)可表示为：

求式(9)的二阶导数，可得履带移动机构沿Ｘ轴与Y轴方向的加速度，对应的表达式为：

根据矢量动力学原理，得到履带移动机构的力平衡方程^[22]：

式中：m为履带移动机构的质量。

则履带移动机构跨越沟槽所需满足的条件为：

直臂模式履带移动机构跨越沟槽的临界状态为Ff1'=R1'，且Jλ¨=0始终成立。经计算可得，电机输出扭矩M（即驱动扭矩）为：

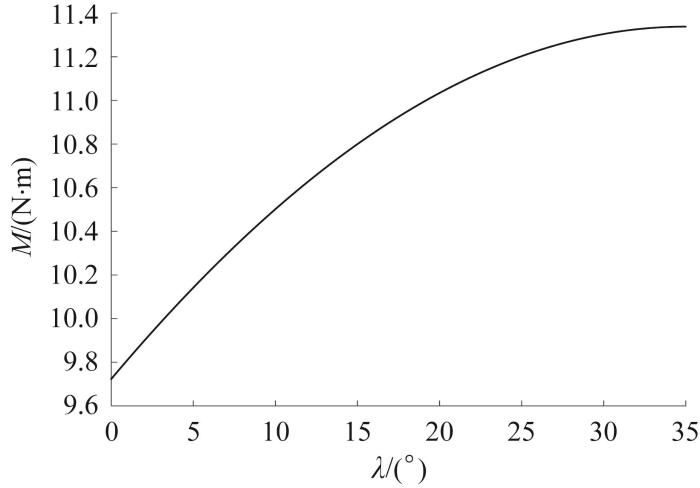
根据式(13)，直臂模式履带移动机构跨越沟槽第一阶段所需的驱动扭矩M与侧板夹角λ的关系如图14所示，其中λ∈[arctan μ₁, 0°]，利用式(11)计算得到λ∈[35°, 0°]。由图14可以看出，直臂模式履带移动机构在跨越沟槽过程中所需的驱动扭矩M随侧板夹角λ的减小而减小，当λ=35°时，即履带移动机构处于跨越沟槽第一阶段的初始位置时，其所需的驱动扭矩最大，为11.30 N·m。

鉴于正交模式履带移动机构的质心最高，本文主要分析该模式履带移动机构可翻越的最大凸台高度及所需的驱动扭矩。正交模式履带移动机构翻越凸台的过程（由行走驱动电机提供动力）可分为2个阶段：第一阶段为履带移动机构以从动轮C为转动中心顺时针旋转，直到履带CD段接触凸台；第二阶段为履带移动机构以行星轮D为转动中心顺时针旋转，进而翻转至凸台上方，直到履带AD段接触凸台。

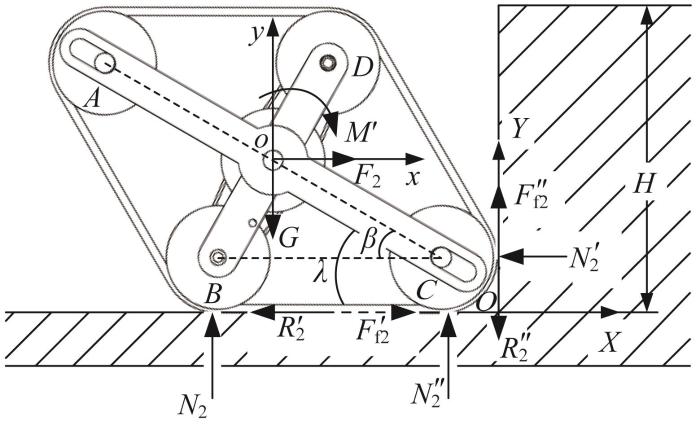
1）正交模式履带移动机构翻越凸台第一阶段的受力分析如图15所示。为方便分析计算，建立以主动轮中心为原点的履带移动机构坐标系o-xy和以凸台与地面的交点为原点的世界坐标系O-XY。

根据图15所示的几何关系，可得正交模式履带移动机构可翻越的凸台高度H：

将式(3)和α=90°代入式(14)，可得：

将表1中的相关数据代入式(15)，计算得到正交模式履带移动机构可翻越的最大凸台高度为136 mm。由式(15)可知，当越障高度远大于行星杆长度时，前端履带移动机构不能越过障碍物平面，无法有效越障。

在履带移动机构以从动轮C为转动中心顺时针旋转的过程中，侧板夹角λ∈[β, 90°-β]，利用式(2)和表1数据计算得到λ∈[29.85°, 60.15°]。根据矢量动力学原理，可得到履带移动机构的力和力矩平衡方程^[23]：

则履带移动机构翻越凸台所需满足的条件为：

在正交模式履带移动机构翻越凸台第一阶段的临界状态下，地面对行星轮的支持力为0 N。假设履带与地面、障碍物之间无相对位移，则临界条件下N₂=0 N，Ff2'=R2'，Ff2″=R2″，且Jλ¨=0始终成立。经计算可得，电机输出扭矩M为：

根据式(18)，正交模式履带移动机构翻越凸台第一阶段所需的驱动扭矩M与侧板夹角λ的关系如图16所示。由图16可以看出，正交模式履带移动机构在翻越凸台第一阶段所需的驱动扭矩M随侧板夹角λ的增大而减小，当λ=29.85°时，即履带移动机构处于翻越凸台第一阶段的初始位置时，其所需的驱动扭矩最大，为7.15 N·m。

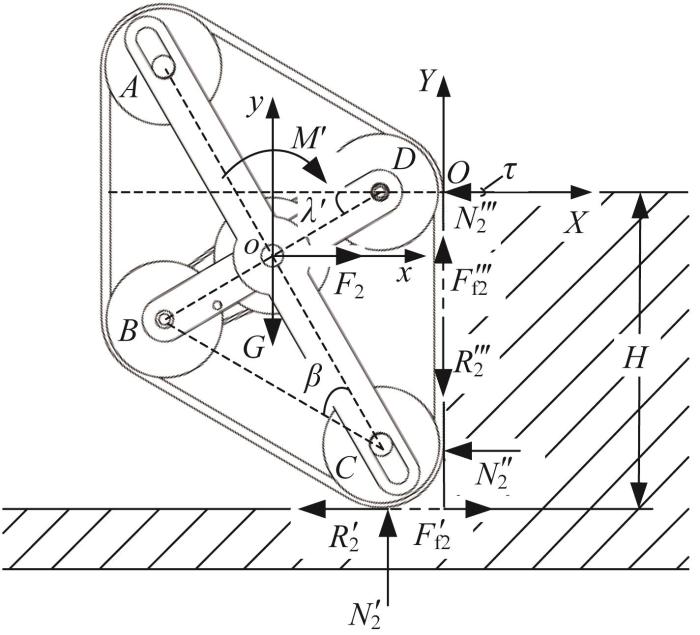
2）正交模式履带移动机构翻越凸台第二阶段的受力分析如图17所示。为方便分析计算，建立以主动轮中心为原点的履带移动机构坐标系o-xy和以凸台与行星轮D的交点为原点的世界坐标系O-XY。

在履带移动机构以行星轮D为转动中心顺时针旋转的过程中，行星杆夹角λ'∈[-β, 90°+β]。①当λ'∈[-β, 0°]时，车体对履带移动机构的推力F₂和单个履带移动机构承受的重力G均阻碍履带移动机构翻转；②当λ'∈[0°, 90°]时，车体对履带移动机构的推力F₂助力履带移动机构翻转，而单个履带移动机构承受的重力G阻碍翻转；③当λ'∈[90°, 90°+β]时，车体对履带移动机构的推力F₂和单个履带移动机构承受的重力G均助力履带移动机构翻转。因此，当λ'∈[-β, 0°]时，履带移动机构所需的驱动扭矩最大，本文主要分析该过程的驱动扭矩。利用式(2)和表1数据，计算得到λ'∈[-29.85°, 0°]。

根据矢量动力学原理，可得履带移动机构的力和力矩平衡方程：

则履带移动机构翻越凸台所需满足的条件为：

在正交模式履带移动机构翻越凸台第二阶段的临界状态下，地面对从动轮C的支持力为0 N。假设履带与地面、障碍物之间无相对位移，则临界条件下N2'=N2″=0 N，Ff2'=R2'，Ff2‴=R2‴，且Jλ¨'=0始终成立。经计算可得，电机输出扭矩M为：

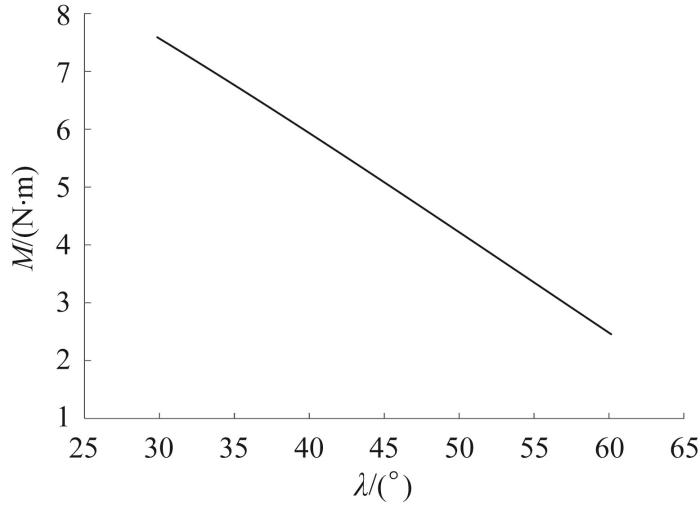
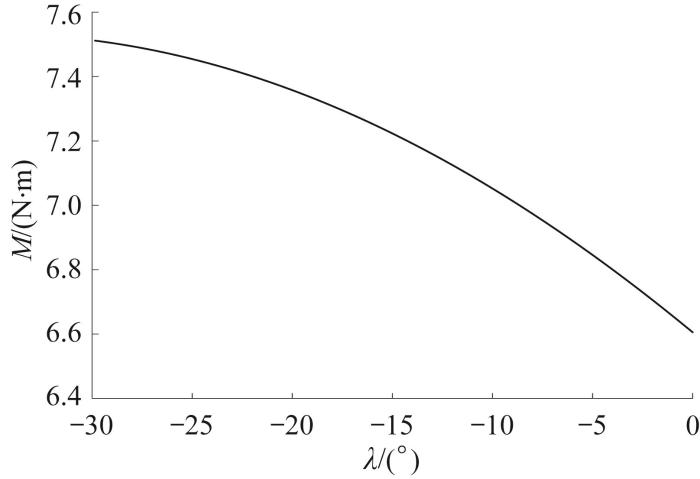
根据式(21)，正交模式履带移动机构翻越凸台第二阶段所需的驱动扭矩M与行星杆夹角λ'的关系如图18所示。由图18可知，正交模式履带移动机构在翻越凸台第二阶段所需的驱动扭矩M随行星杆夹角λ'的增大而减小，当λ'=-29.85°时，即履带移动机构处于翻越凸台第二阶段的初始位置时，其所需的驱动扭矩最大，为7.50 N·m。

通过对比正交模式履带移动机构翻越凸台第一阶段和第二阶段所需的驱动扭矩，发现第二阶段所需的驱动扭矩较大。为确保正交模式履带移动机构能实现凸台翻越，其最大驱动扭矩应取7.50 N·m

直臂模式和正交模式履带移动机构均需电机提供翻转扭矩来实现越障功能，而过渡模式履带移动机构越障时不需要电机提供翻转扭矩，该模式下越障所需的驱动扭矩小于直臂模式和正交模式。因此，本文只对过渡模式履带移动机构可跨越的沟槽宽度和可翻越的凸台高度进行分析。

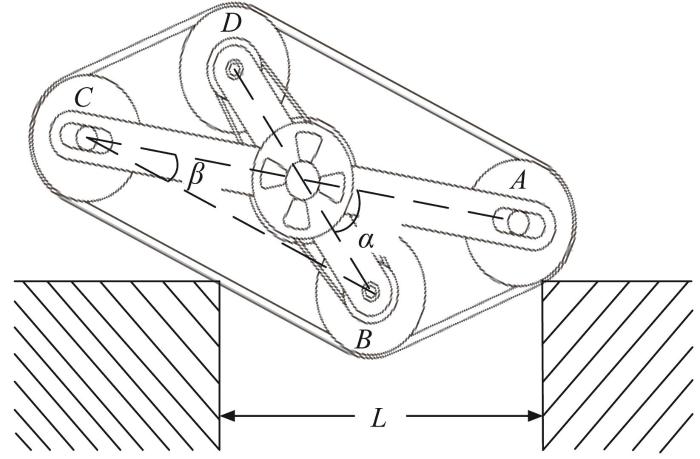
过渡模式履带移动机构跨越沟槽的分析简图如图19所示。根据图19所示的几何关系，计算得到其可跨越的沟槽宽度L：

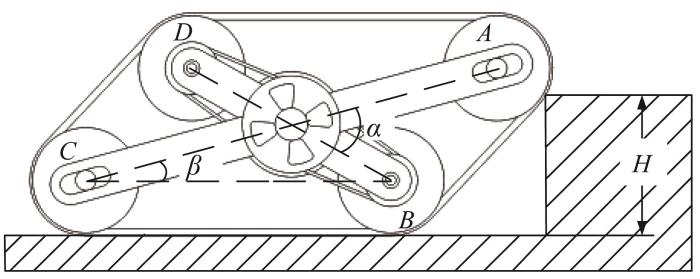
过渡模式履带移动机构翻越凸台的分析简图如图20所示。根据图20所示的几何关系，计算得到其可翻越的凸台高度H：

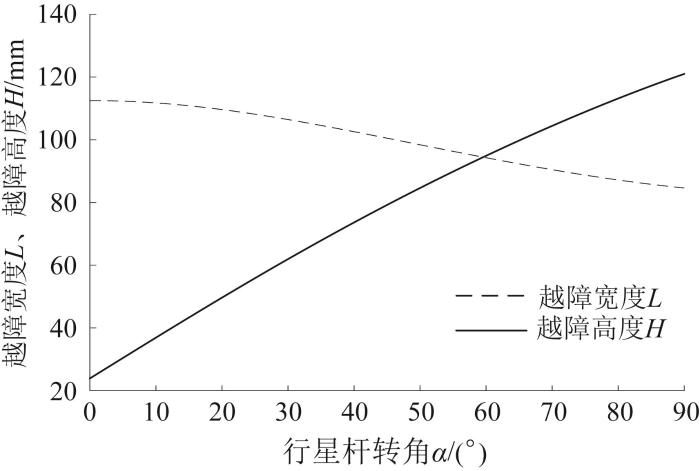
过渡模式履带移动机构可跨越的沟槽宽度L和可翻越的凸台高度H与行星杆转角α的关系如图21所示。由图20可知，履带移动机构可翻越的凸台高度H对行星杆转角α的变化更为敏感；当α=59.6°时，履带移动机构同时实现沟槽跨越和凸台翻越的越障高度/宽度达到极大值，越障高度和越障宽度均为94.5 mm。

综上所述，直臂模式履带移动机构可跨越的沟槽最宽，最大宽度为258 mm；正交模式履带移动机构可翻越的凸台最高，最大高度为136 mm；过渡模式履带移动机构可跨越的沟槽宽度和可翻越的凸台高度介于直臂模式和正交模式之间，当α=59.6°时，其可跨越的沟槽宽度和可翻越的凸台高度均为94.5 mm。在越障过程中，直臂模式履带移动机构所需的驱动扭矩最大，为11.30 N·m。

为验证所设计的行星式欠驱动可变形履带移动机构越障的可行性，在ADAMS软件中建立履带移动机构的三维模型及越障仿真环境（具体参数见表1和表2），对其在3种运动模式（直臂模式、正交模式和过渡模式）下的越障能力进行仿真分析。

设置沟槽的宽度、深度分别为258 mm和240 mm，对直臂模式履带移动机构跨越沟槽的过程进行仿真分析，结果如图22所示。通过对比发现，直臂模式履带移动机构跨越沟槽的仿真过程与理论分析一致，验证了该模式履带移动机构跨越沟槽的可行性。

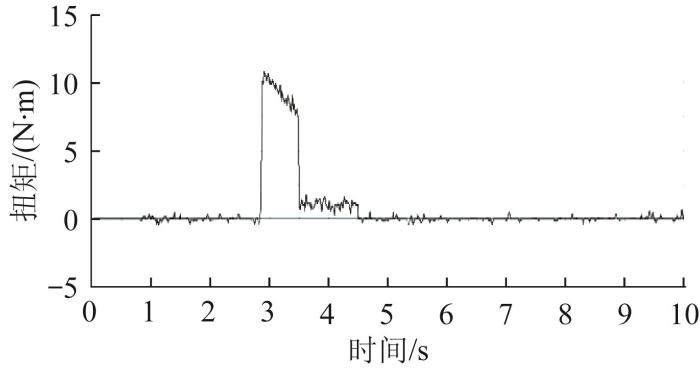
提取直臂模式履带移动机构跨越沟槽仿真过程中前端行走驱动电机的输出扭矩，结果如图23所示。从图23中可以看出，履带移动机构在越障初始位置处所需的驱动扭矩最大，为10.95 N·m，仿真结果与理论计算值11.30 N·m接近。由于扭矩计算方式的不同，两者的相对误差为3.20%，误差较小，说明理论计算得到的直臂模式履带移动机构跨越沟槽时所需的驱动扭矩准确。

设置凸台高度为136 mm，对正交模式履带移动机构翻越凸台的过程进行仿真分析，结果如图24所示。通过对比发现，正交模式履带移动机构翻越凸台的仿真过程与理论分析一致，验证了该模式履带移动机构翻越凸台的可行性。

同理，提取正交模式履带移动机构翻越凸台仿真过程中前端行走驱动电机的输出扭矩，结果如图25所示。从图25中可以看出，正交模式履带移动机构翻越凸台所需的最大驱动扭矩为7.38 N·m，仿真值与理论计算值7.50 N·m接近。由于扭矩计算方式的不同，两者的相对误差为1.63%，误差较小，说明理论计算得到的正交模式履带移动机构翻越凸台时所需的驱动扭矩准确。

设置沟槽的宽度、深度分别为94.5 mm和50 mm，对过渡模式履带移动机构跨越沟槽的过程进行仿真分析，结果如图26所示。通过对比发现，过渡模式履带移动机构跨越沟槽的仿真过程与理论分析一致，验证了该模式履带移动机构跨越沟槽的可行性。

设置凸台高度为94.5 mm，对过渡模式履带移动机构翻越凸台的过程进行仿真分析，结果如图27所示。通过对比发现，过渡模式履带移动机构翻越凸台的仿真过程与理论分析一致，验证了该模式履带移动机构翻越凸台的可行性。

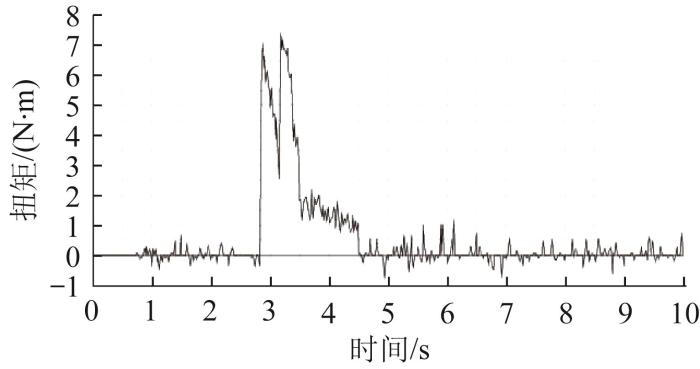
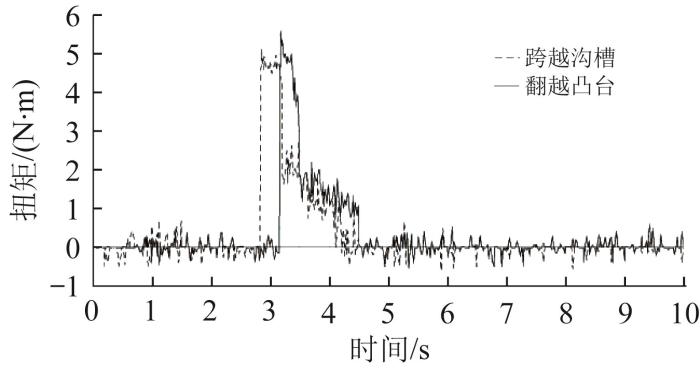
提取过渡模式履带移动机构跨越沟槽和翻越凸台仿真过程中前端行走驱动电机的输出扭矩，结果如图28所示。从图28中可以看出，履带移动机构跨越沟槽所需的最大驱动扭矩为5.1 N·m，翻越凸台所需的最大驱动扭矩为5.6 N·m。通过对比发现，过渡模式履带移动机构越障过程中所需的驱动扭矩小于直臂模式与正交模式，与理论计算结果一致。

通过越障仿真发现，所设计的履带移动机构能够顺利越过沟槽和凸台等障碍物，并得出直臂模式履带移动机构跨越沟槽时所需的驱动扭矩最大，验证了理论分析的准确性，这可为履带移动机构实物设计过程中驱动电机的选型提供指导。

为进一步验证所设计的行星式欠驱动可变形履带移动机构的越障性能，制作了行星履带式整车样机并开展越障实验，分别选取直臂模式下的沟槽跨越、正交模式下的凸台翻越和过渡模式下的凸台翻越这3种情况进行分析（3种工况均为3种模式下的极限工况）。

直臂模式履带移动机构跨越沟槽实验如图29所示。实验结果表明，该履带移动机构在直臂模式下可跨越宽度为256 mm的沟槽。

正交模式履带移动机构翻越凸台实验如图30所示。实验结果表明，该履带移动机构在正交模式下可翻越高度为135 mm的凸台。

过渡模式履带移动机构翻越凸台实验如图31所示。实验结果表明，该履带移动机构在过渡模式下可翻越高度为94 mm的凸台。

通过实验验证了所设计的履带移动机构可通过改变履带形状来提升整体的越障性能，其在各种复杂地面上均具有较好的通过性，越障过程与理论分析和仿真分析一致。

1）本文设计了一种新型的行星式欠驱动可变形履带移动机构，并对其构型、原理与运动模式进行了详细介绍；同时，构建了履带移动机构的动力学理论模型，并通过仿真验证了其越障性能。

2）行星式欠驱动可变形履带移动机构通过控制变形驱动电机来实现3种运动模式（直臂模式、正交模式和过渡模式）的切换。其中：直臂模式适用于松软平坦或含较宽沟槽的路面；正交模式适用于含较高凸台的路面；过渡模式适用于同时含沟槽和凸台的凹凸路面。

3）行星式欠驱动可变形履带移动机构通过控制自身形状来改变其质心高度和接地面积，不需要复杂的控制程序和传感器，可依靠自身的自适应性实现快速越障，缩短了越障响应时间，显著提高了越障能力和环境适应能力，并降低了成本。