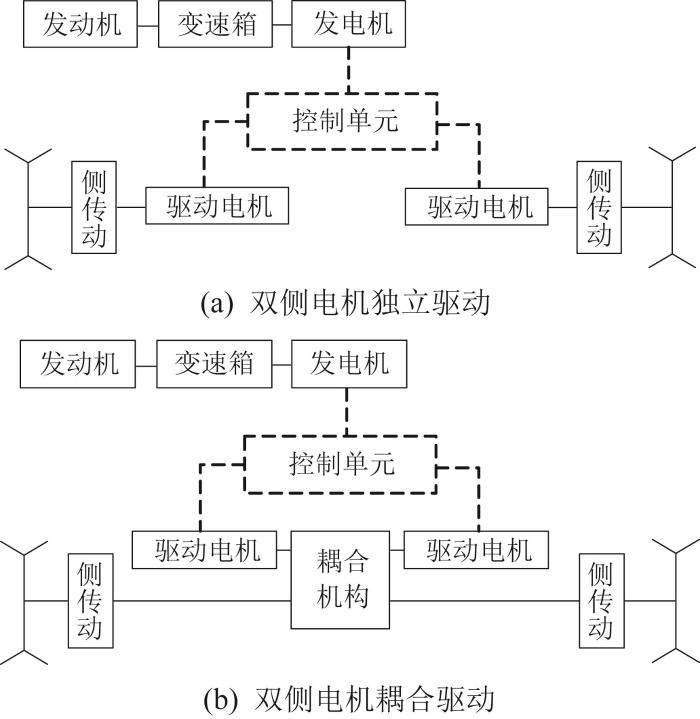
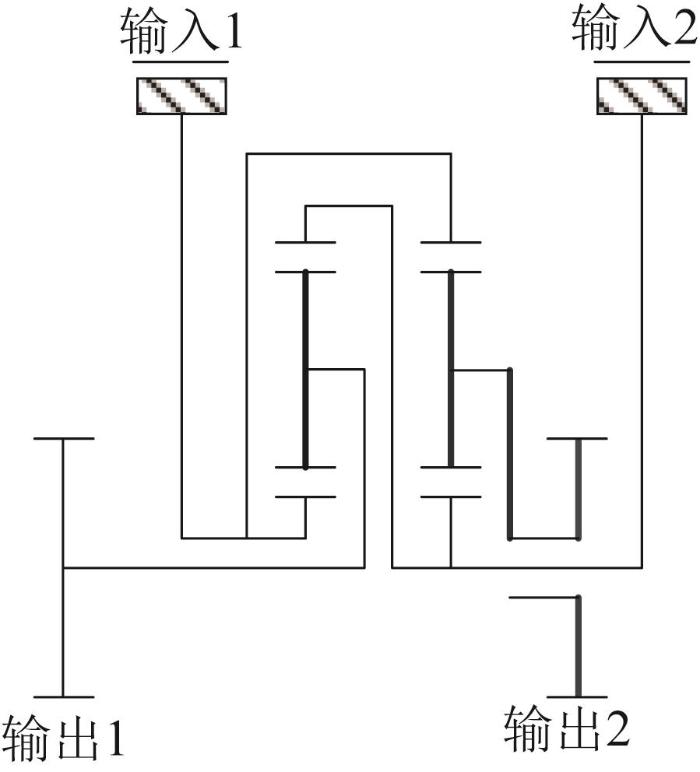
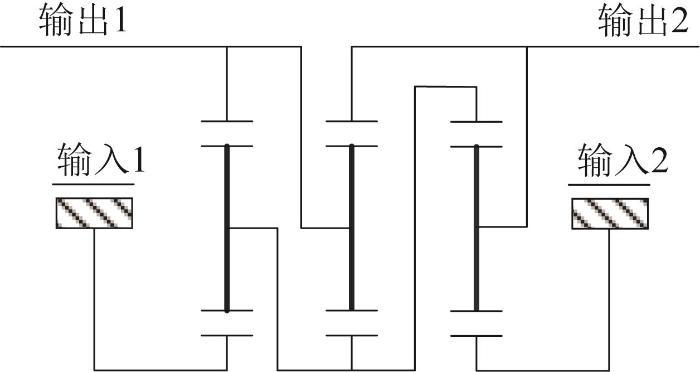
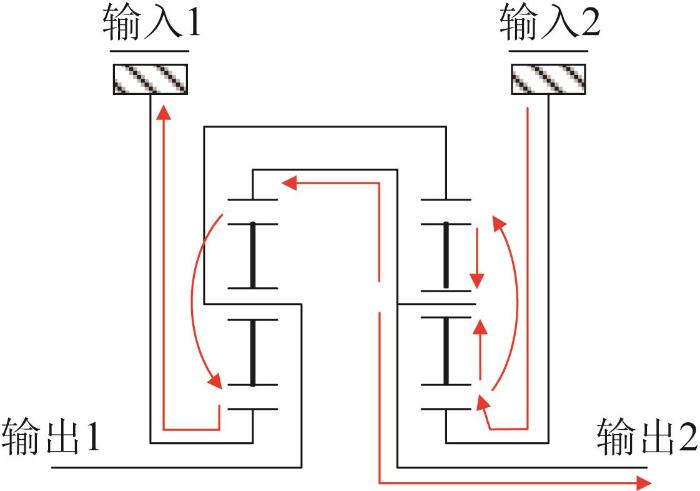
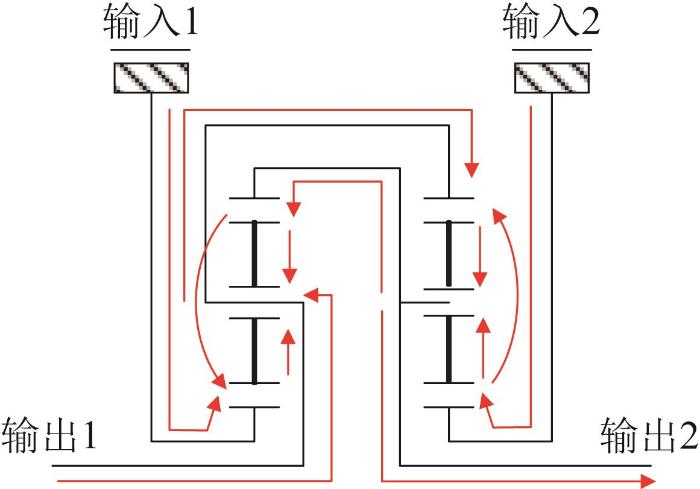
传统的履带车辆传动系统仅具备机械输出的能力,无法满足新一代履带车辆大功率电能传输和更高的机动性要求。而大功率机电复合传动系统兼具机械功率输出和电功率输出的能力,使履带车辆具有更高的速度及更好的平顺性和机动性。此外,机械结构的减少能降低履带车辆运行时的噪声。最初的机电复合传动为双侧电机独立驱动[1 -2 ] ,转向再生功率以电功率的形式回流至高速侧,这对高速侧电机的过载能力要求很高。为了解决电机过载问题,在双侧电机中间增加一个功率耦合机构来改变功率回流路径[3 -4 ] ,使得回流功率以机械功率的形式通过功率耦合机构回流至高速侧,从而降低了电机的功率需求。机电复合传动如图1 所示。
图1
图1
机电复合传动示意图
Fig.1
Schematic diagram of electromechanical compound transmission
目前最常用的机电复合传动构型设计方法包括图论、杠杆法和D矩阵法等。如:Arnaudov等[5 ] 提出了一种新的基于杠杆模型的三端口图论模型,该模型可以分析行星齿轮机构的速度、扭矩和效率等,但计算较为复杂,效率较低;Chen等[6 ] 提出了一种基于几何结构的多级行星自动变速器设计方法,通过“效率”这一重要指标来筛选构型;Deng等[7 ] 针对单行星排的构型设计,提出了一种基于等效树图的模型,降低了构型的筛选难度,但是模型的表示方法较复杂,不能进一步拓展到多行星排的构型设计;Geng等[8 ] 提出了一种新的拓扑图,用于功率分流系统的构型设计,该方法能有效解决设计过程中机械结构的干涉问题;Gao等[9 -10 ] 提出了一种新型行星齿轮拓扑图表示方法,揭示了传动比与拓扑结构的关联关系,显著提升了传动系统的构型设计效率。拓扑图论法能清晰表达复杂行星排的连接关系,但现有拓扑模型侧重于几何连接,未与系统的运动学-动力学特征直接关联,并缺乏系统性的参数筛选准则,需结合人工经验剔除冗余构型。Yang等[11 ] 提出了一种改进的杠杆法,来设计具有高速比的最优构型,以满足高功率密度轮毂电机的需求;Kim等[12 -13 ] 提出了一种复合杠杆法,它是一种适用于寻找单行星排或两行星排混合动力系统最优构型方案的构型搜索方法;Song等[14 -15 ] 改进了复合杠杆法,在寻求最优的多模式构型中,从设计层面最大限度消除了冗余构型,减少了与优化相关的计算工作。杠杆法及其衍生方法适用于单行星排或两行星排混合动力系统,通过杠杆模型分析系统的转速、扭矩和效率特性,可直观反映行星排的力学关系,便于快速评估基础构型的运动学性能,但难以量化再生功率传递条件,无法在拓扑设计阶段筛选出无效构型。为了进一步降低电机功率,通过添加一组行星排,将发动机和发电机连入参考构型,生成了三行星排的基础拓扑结构方案[16 ] 。而针对混合动力履带车辆三行星排构型方案的优化设计,秦兆博等[17 -18 ] 改进了Peng等[19 ] 提出的矩阵建模方法,分析了基于3排行星传动的多模式拓扑构型,结果表明,3排行星传动的多模式拓扑构型能更好地保证发动机工作点的配置,维持发动机工作在高效率区。D矩阵法适用于计算机快速筛选,具有一定的盲目性,且计算量较大。综上所述,现有方法在单一功能(如几何连接、效率评估)上具有一定优势,但均存在一定的局限:其一,无法在构型设计阶段有效剔除冗余方案;其二,模型复杂度较高,导致工程应用受限。
本文通过运动拓扑图论模型,将构型设计与性能分析深度融合,兼容了两行星排与三行星排构型,采用白点-灰点拓扑规则统一表示多级传动元件,突破了传统方法对行星排数量的限制,可为高功率混合动力履带车辆传动系统的优化提供高效的方法。
1 行星排图论模型
行星排用1个白点和3个灰点表示,其中白点表示行星排,灰点表示行星排的太阳轮、行星轮和齿圈。从运动学的角度看,白点可以看成是转速汇集器,3个灰点的转速乘以一个比例因子后传递给白点,汇集到白点的转速之和为0。对于每个灰点,比例因子为所对应元件的特征参数。对于行星排,太阳轮、齿圈、行星轮所对应的特征参数分别为1、k 、-1-k 。行星排元件基于拓扑关系的图论表示如表1 所示。其中,s表示太阳轮,c表示行星轮,r表示齿圈,z 为齿数。
2 耦合机构的数学特征分析
2.1 实现直驶和转向功能的数学特征
履带车辆直驶时,两侧的输入转速相同;转向时,一侧的输入转速升高,另一侧的输入转速降低。为了满足上述要求,耦合机构转速和转矩的自由度均为2。存在实数a 1 ,使得输入与输出的转速和转矩存在如下线性关系[20 ] :
ω i n 1 ω i n 2 = a 1 1 - a 1 1 - a 1 a 1 ω o u t 1 ω o u t 2 (1)
T i n 1 T i n 2 = a 1 2 a 1 - 1 a 1 - 1 2 a 1 - 1 a 1 - 1 2 a 1 - 1 a 1 2 a 1 - 1 T o u t 1 T o u t 2 (2)
式中:ω i n 1 、 ω i n 2 ω o u t 1 、 ω o u t 2 T i n 1 、 T i n 2 T o u t 1 、 T o u t 2
2.2 实现转向再生功率传递的构型研究
变速机构并不会影响再生功率的传递,因此本文主要针对耦合机构进行分析。若不考虑功率损失,输出功率P out 与输入功率P in 满足如下关系:
P i n 1 + P i n 2 = P o u t 1 + P o u t 2 (3)
如果转向再生功率能从低速侧履带传递到高速侧履带,有助于降低电机的功率设计参数,则有:
P i n 1 - P i n 2 < P o u t 1 - P o u t 2 (4)
根据式(1)和式(2),分析为实现转向的再生功率的传递。直驶时,两侧输出端的转速相同,设为ω 0 ,输出端的转矩为T 0 ;转向时,低速侧输出转速降低Δω ,高速侧输出转速增加Δω ,低速侧输出转矩降低ΔT ,高速侧输出转矩增加ΔT ,则可计算出履带两侧输出功率和电机功率的变化。
Δ P o u t 1 = - T 0 ⋅ Δ ω - ω 0 ⋅ Δ T + Δ ω ⋅ Δ T (5)
Δ P o u t 2 = T 0 ⋅ Δ ω + ω 0 ⋅ Δ T + Δ ω ⋅ Δ T (6)
Δ P i n 1 = - α ⋅ T 0 ⋅ Δ ω - ω 0 α ⋅ Δ T + Δ ω ⋅ Δ T (7)
Δ P i n 2 = α ⋅ T 0 ⋅ Δ ω + ω 0 α ⋅ Δ T + Δ ω ⋅ Δ T (8)
则履带车辆两侧输出功率差Δ P out 和输入电机功率差Δ P in 分别为:
Δ P o u t = 2 ⋅ T 0 ⋅ Δ ω + ω 0 ⋅ Δ T (9)
Δ P i n = 2 ⋅ α ⋅ T 0 ⋅ Δ ω + 1 α ⋅ ω 0 ⋅ Δ T (10)
根据转向再生功率传递条件,应当满足式(3),将式(5)至式(8)代入(3),化简后可得[10 ] :
f α = α ⋅ Δ ω ω 0 + 1 α ⋅ Δ T T 0 - Δ ω ω 0 - Δ T T 0 (11)
f α > 0 (12)
通过分析可知,为了实现转向再生功率的传递,应当有:
α > 1 (13)
耦合机构设计时,满足式(1)、式(2)和式(3),便可实现履带车辆直驶和转向功能,同时再生功率可通过耦合机构以机械功率的形式传递至履带高速侧。
3 行星排构型拓扑综合方法
3.1 两行星排构型拓扑
对于双输入双输出耦合机构,为了保证两侧独立转向,两侧输出必须保持独立,因此构型的自由度为2。如果要获得转速自由度f w = 2 图2 (a)所示。
图2
图2
两行星排拓扑构型
Fig.2
Dual-planetary gear topological configuration
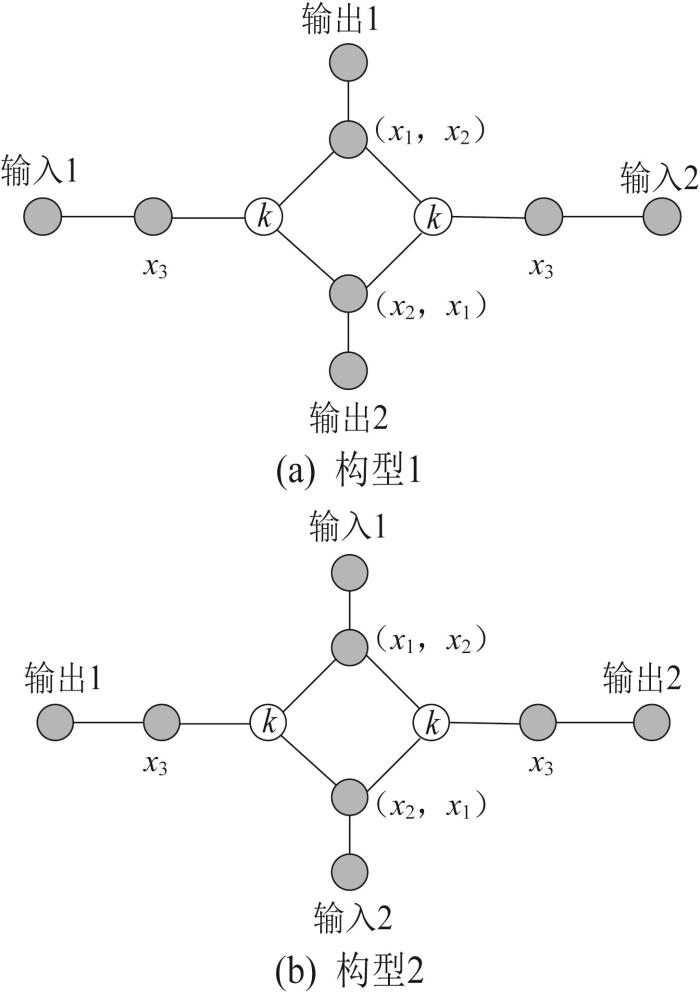
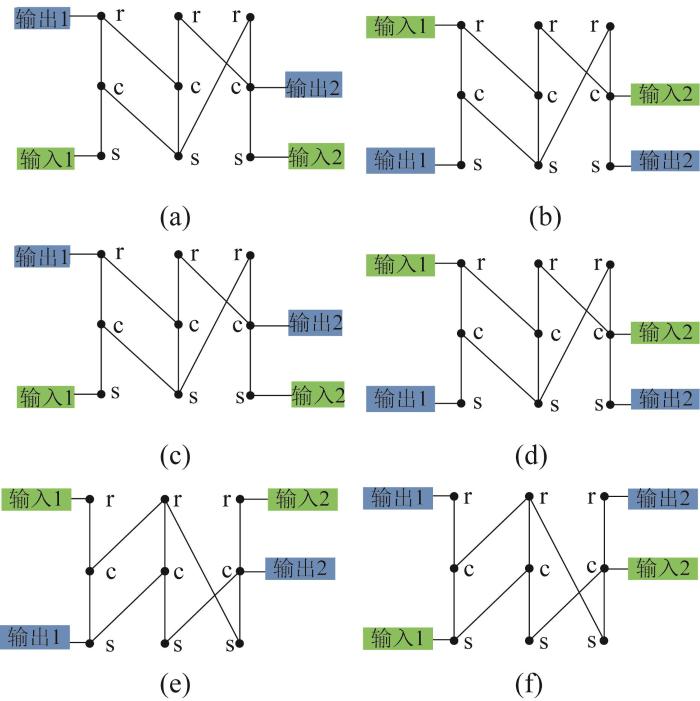
在基本拓扑构型的基础上,需要选择输出位置。行星排数目为2、转速自由度为2的构型,基本构件数目为4。对于履带车辆,理论上有C 4 2 图3 所示。其中,行星排3个元件的特征参数分别用x 1 、 x 2 、 x 3
图3
图3
两行星排拓扑方案
Fig.3
Dual-planetary gear topological scheme
从对称性的角度看,假设两行星排的特征参数k 1 、k 2 相同,即k 1 = k 2 = k
图3 (a)为第1类构型的拓扑结构。根据行星排转速和转矩约束方程,可以得到输入转速与输出转速的关系为:
ω i n 1 ω i n 2 = - x 1 x 3 - x 2 x 3 - x 2 x 3 - x 1 x 3 ⋅ ω o u t 1 ω o u t 2 (14)
T i n 1 T i n 2 = x 1 ⋅ x 3 x 1 2 - x 2 2 - x 2 ⋅ x 3 x 1 2 - x 2 2 - x 2 ⋅ x 3 x 1 2 - x 2 2 x 1 ⋅ x 3 x 1 2 - x 2 2 ⋅ T o u t 1 T o u t 2 (15)
通过式(5)至式(8)进行计算,可得α = x 1 - x 2 x 3
x 1 + x 2 + x 3 = 0 (16)
x 1 + x 2 = x 3 (17)
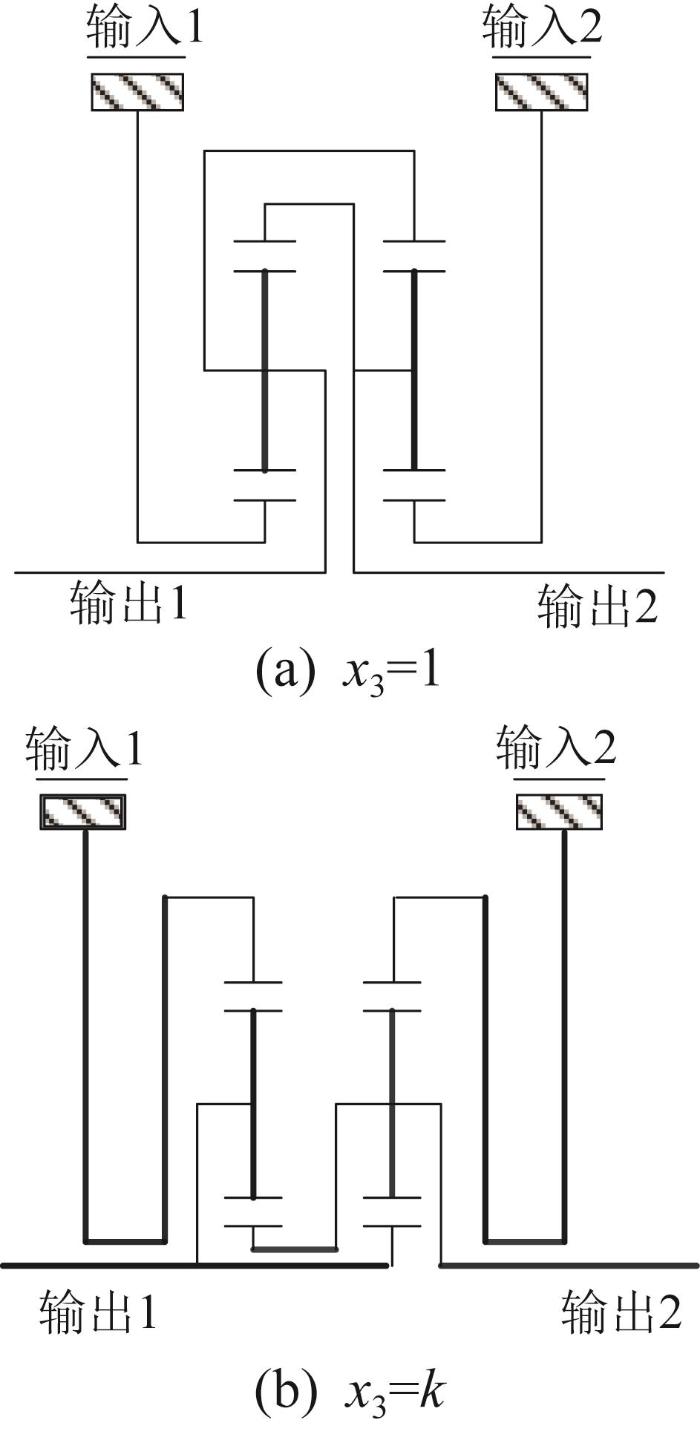
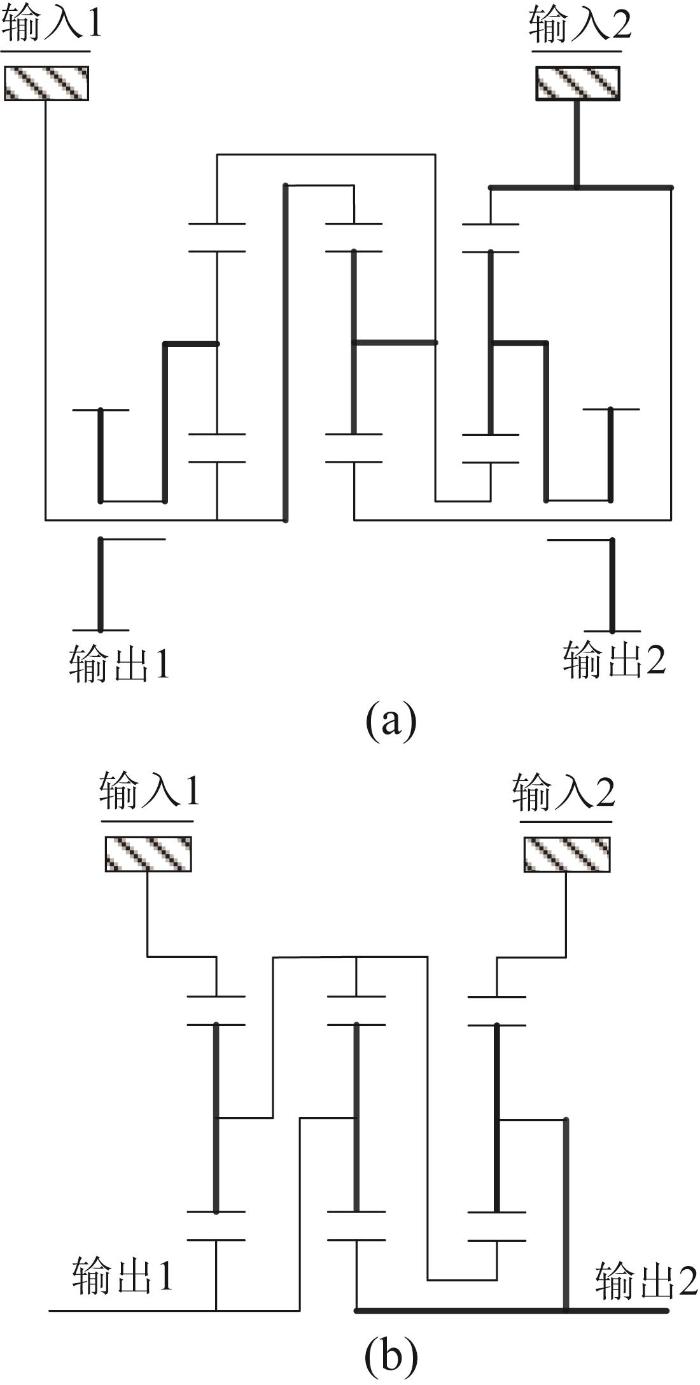
因此,当x 1 ⋅ x 2 < 0 α > 1 x 3 x 3 = 1 x 3 = k 图4 所示。
图4
图4
两行星排构型1 下的传动方案
Fig.4
Transmission scheme for dual-planetary gear configuration 1
图3 (b)为第2类构型的拓扑结构。根据行星排转速和转矩约束方程,可以得到输入转速与输出转速的关系为:
ω i n 1 ω i n 2 = - x 1 ⋅ x 3 x 1 2 - x 2 2 x 2 ⋅ x 3 x 1 2 - x 2 2 x 2 ⋅ x 3 x 1 2 - x 2 2 - x 1 ⋅ x 3 x 1 2 - x 2 2 ⋅ ω o u t 1 ω o u t 2 (18)
T i n 1 T i n 2 = x 1 ⋅ x 3 x 1 2 - x 2 2 - x 2 ⋅ x 3 x 1 2 - x 2 2 - x 2 ⋅ x 3 x 1 2 - x 2 2 x 1 ⋅ x 3 x 1 2 - x 2 2 ⋅ T o u t 1 T o u t 2 (19)
由式(5)至式(8)的计算,可得α = x 3 x 1 - x 2 式(16)和式(17)可知,当x 1 ⋅ x 2 > 0 α > 1 x 1 x 2 x 3 x 3 = - 1 - k 图5 所示。
图5
图5
两行星排构型2 下的传动方案
Fig.5
Transmission scheme for dual-planetary gear configuration 2
3.2 三行星排构型拓扑
图6
图6
三行星排拓扑构型
Fig.6
Triple-planetary gear topological configuration
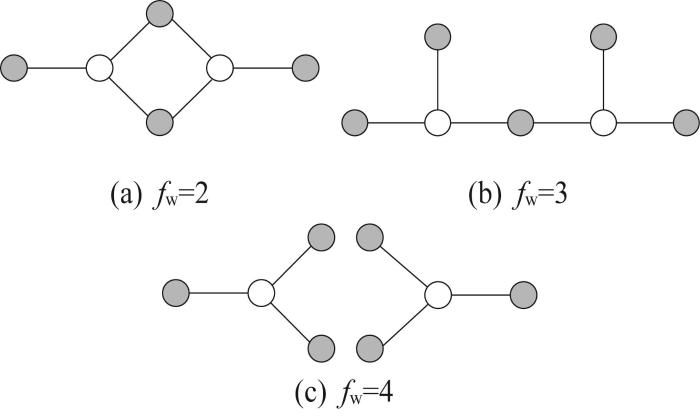
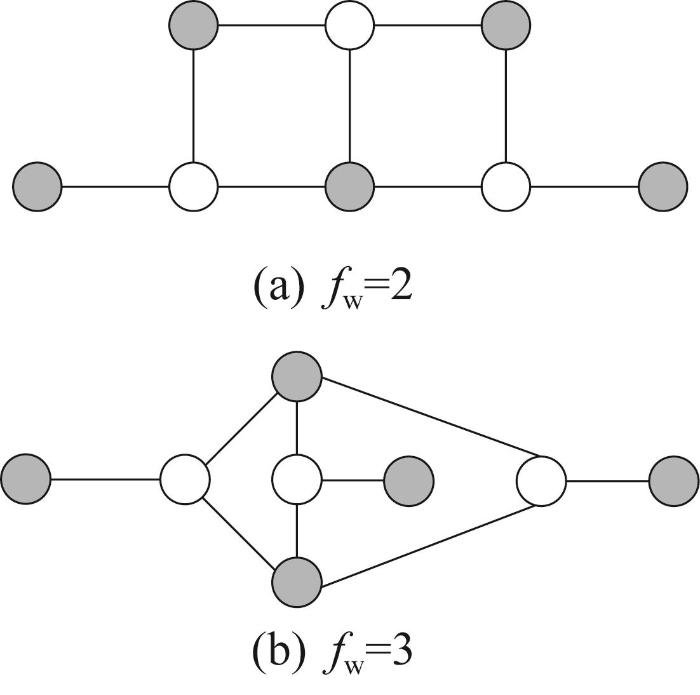
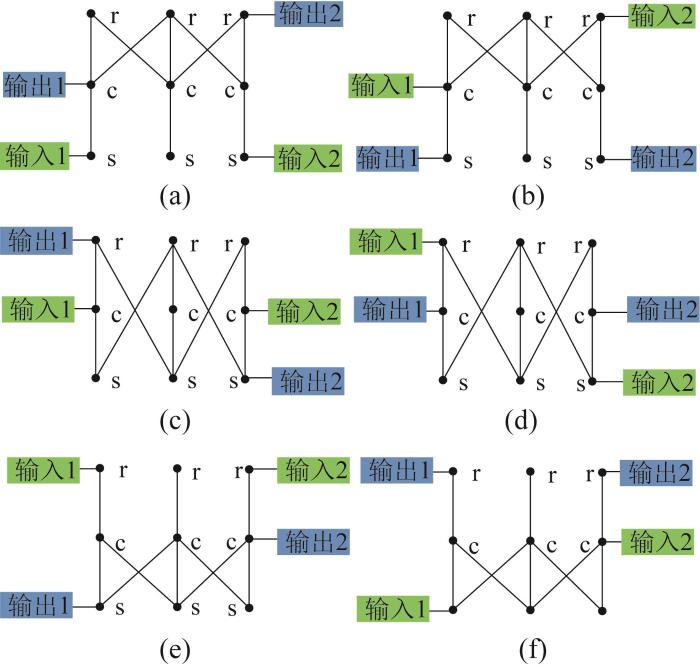
对于三行星排的构型,如果要获得转速自由度为2的构型,行星排之间的固连数目为4,如图6 (a)所示。因此,理论上有C 4 2 k 1 = k 2 = k 3 = k 图7 所示。
图7
图7
f w =2
Fig.7
Triple-planetary gear topological scheme with f w =2
对于图6 (b)所示构型,可以获得的可行方案也有2种,如图8 所示。
图8
图8
f w =3
Fig.8
Triple-planetary gear topological scheme with f w =3
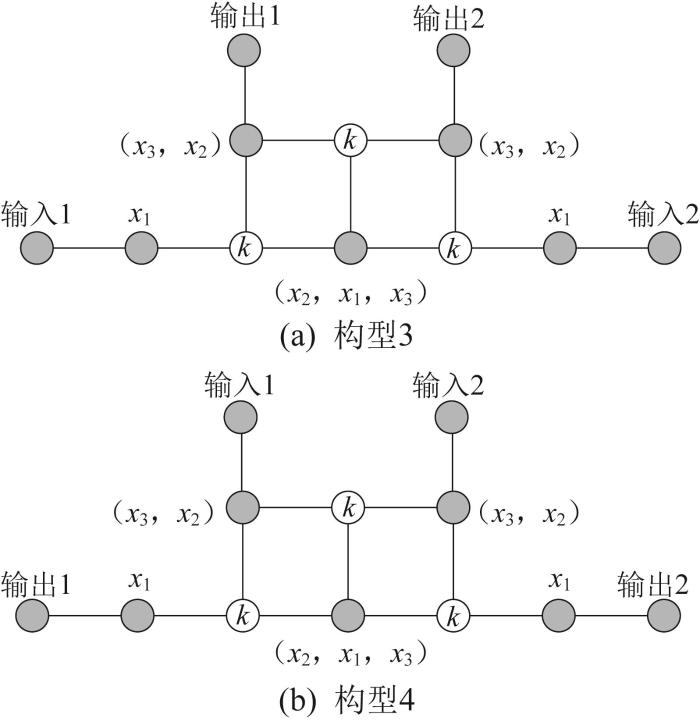
对于图7 (a)所示的输出方案,x 1 图9 所示。
图9
图9
f w =2
Fig.9
Connection methods for triple-planetary gear with f w =2
对于图9 (a)所示的构型,根据行星排转速和转矩约束方程,可以得到输入转速与输出转速、输入转矩与输出转矩的关系为:
ω i n 1 ω i n 2 = 1 + k + k 2 - k + k 2 - k + k 2 1 + k + k 2 ω o u t 1 ω o u t 2 (20)
T i n 1 T i n 2 = 1 + k + k 2 1 + 2 k + 2 k 2 k + k 2 1 + 2 k + 2 k 2 k + k 2 1 + 2 k + 2 k 2 1 + k + k 2 1 + 2 k + 2 k 2 T o u t 1 T o u t 2 (21)
式(20)和式(21)的系数矩阵满足式(1)和式(2)的形式,且a 1 = 1 + k + k 2 图9 (a)所示的构型能实现直驶和转向。α = 1 + 2 k + 2 k 2 > 1 式(13),则该构型能实现功率回流。该传动方案如图10 所示。
图10
图10
图9(a) 对应的传动方案
Fig.10
Transmission scheme corresponding to figure 9 (a)
对于图9 (b)所示的构型,根据行星排转速和转矩约束方程,可以得到输入转速与输出转速、输入转矩与输出转矩的关系为:
ω i n 1 ω i n 2 = 1 + k + k 2 1 + 2 k + 2 k 2 k + k 2 1 + 2 k + 2 k 2 k + k 2 1 + 2 k + 2 k 2 1 + k + k 2 1 + 2 k + 2 k 2 ω o u t 1 ω o u t 2 (22)
T i n 1 T i n 2 = 1 + k + k 2 - k + k 2 - k + k 2 1 + k + k 2 T o u t 1 T o u t 2 (23)
式(22)和式(23)的系数矩阵满足式(1)和式(2)的形式,且a 1 = 1 + k + k 2 图9 (b)所示的构型能实现直驶和转向。计算可得α < 1 式(13),则该构型不能实现功率回流。
同理,通过分析x 1 图9 (d)、图9 (e)所示。其传动方案如图11 所示。
图11
图11
图9(d) 、图9(e) 对应的传动方案
Fig.11
Transmission scheme corresponding to figure 9 (d) and (e)
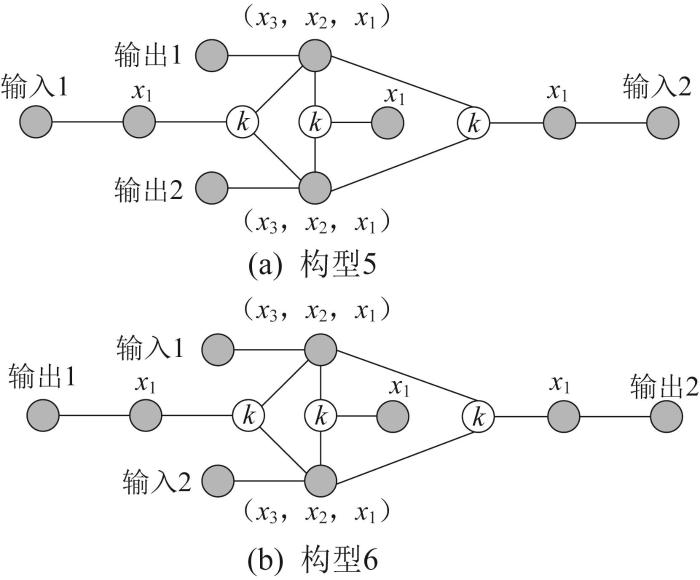
对于图8 所示的输出方案,x 1 图12 所示。
图12
图12
f w =3
Fig.12
Connection methods for triple-planetary gear with f w =3
对于图12 (a)所示的构型,根据行星排转速和转矩约束方程,可以得到输入转速与输出转速的关系为:
ω i n 1 ω i n 2 = 1 + k - k 1 + k - k ω o u t 1 ω o u t 2 (24)
式(24)不满足式(1)的数学特征,故不能实现履带车辆的转向,该方案不可行。同理,通过对剩下的构型进行分析可知,图8 所示的输出方案不能实现转向,故三行星排拓扑能得到3种可行的传动方案。
4 功能验证
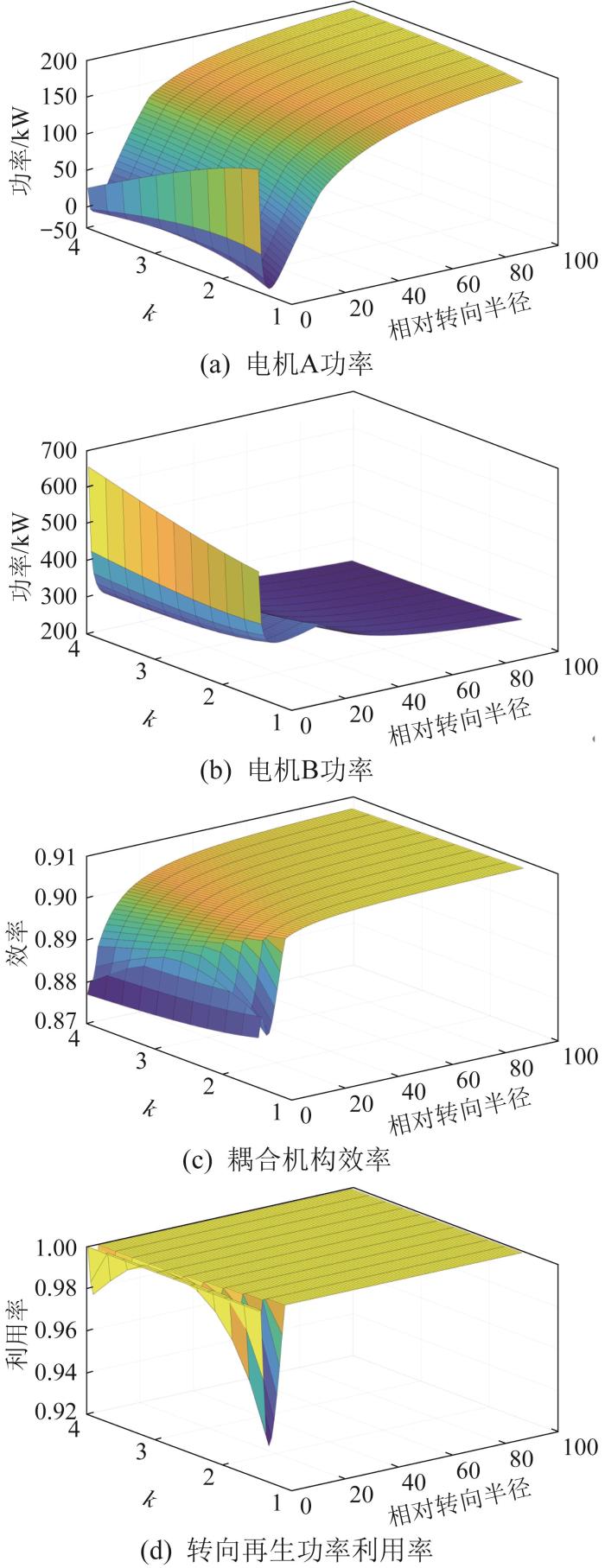
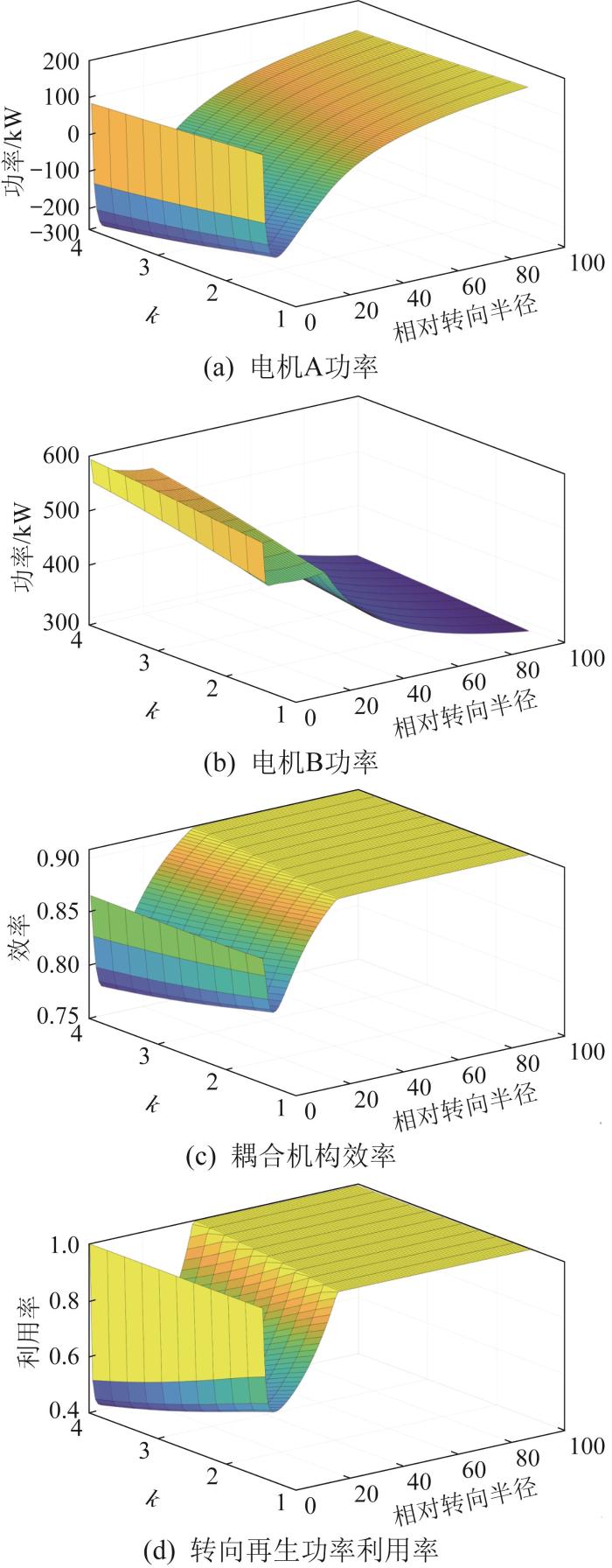
履带车辆转向时,其外侧的功率需求远大于直驶时。为了避免在车辆转向过程中产生双电机过大的功率冗余,使双电机的功率在直驶和转向过程均得到充分利用,本文以电机功率、耦合机构效率、转向再生功率利用率为分析依据,开展优选构型的分析和评价。以图4 (a)所示的两行星排传动方案和图11 (a)所示的三行星排传动方案为例,对其进行仿真分析。仿真中,取k =1.5~4,履带车辆模型的参数如表2 所示。两行星排、三行星排特征参数对传动性能的影响分别如图13 和图14 所示。
图13
图13
两行星排特征参数对传动性能的影响
Fig.13
Impact of dual-planetary gear characteristic parameter on transmission performance
图14
图14
三行星排特征参数对传动性能的影响
Fig.14
Impact of triple-planetary gear characteristic parameter on transmission performance
由图13 可知:当车辆相对转向半径较大时,两侧电机的功率差较小,特征参数对耦合机构效率的影响较小;当相对转向半径较小时,特征参数对两 侧电机功率的影响较大;当特征参数较小时,耦合机构效率和转向再生功率利用率较高。
由图14 可知:当车辆相对转向半径较大时,两侧电机的功率差较小,特征参数对耦合机构效率的影响较小;当相对转向半径较小时,电机A的功率为负,其处于发电状态,表明转向再生功率一部分以电功率的形式回流,导致转向再生功率利用率较低。
同理,对其余构型进行仿真分析。通过对比6种方案的仿真结果可知,图4 (a)所示方案的效率和转向再生功率利用率最高,其峰值分别为89.3%和78.5%,且合理的特征参数的范围最大,故图4 (a)所示的方案最优。
对图4 (a)所示的方案进行功率流向分析。履带车辆有直线行驶、中心转向和单边转向等3种常用工况和电机驱动转向工况。本节给出各工况对应的传动系统的功率流向。
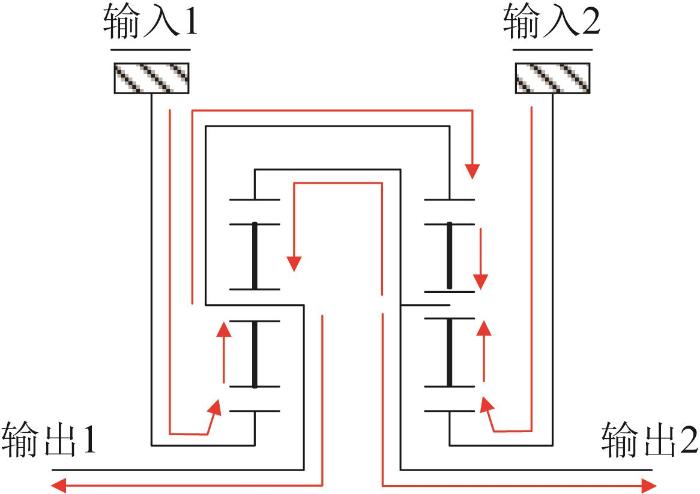
1)直线行驶。该工况下传动系统的功率流向如图15 所示,可知左右两侧的功率完全一致。
图15
图15
直线行驶时传动系统的功率流向
Fig.15
Power flow in transmission system during straight-line driving
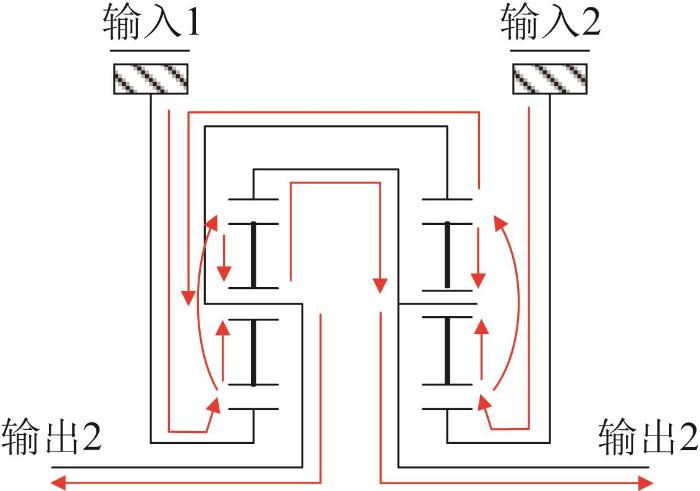
2)中心转向。该工况下传动系统的功率流向如图16 所示,可知两侧履带与电机反向运动。
图16
图16
中心转向时传动系统的功率流向
Fig.16
Power flow in transmission system during pivot steering
3)单边转向。该工况下传动系统的功率流向如图17 所示,可知内侧履带抱死,无功率传递。
图17
图17
单边转向时传动系统的功率流向
unilateral steering
Fig.17
Power flow in transmission system during unilateral steering
4)电机驱动转向。该工况下传动系统的功率流向如图18 所示,可知双侧电机都对外输出功率,同时内侧履带功率回流。
图18
图18
电机驱动转向时传动系统的功率流向
Fig.18
Power flow in transmission system during motor diving steering
5 履带车辆性能仿真分析
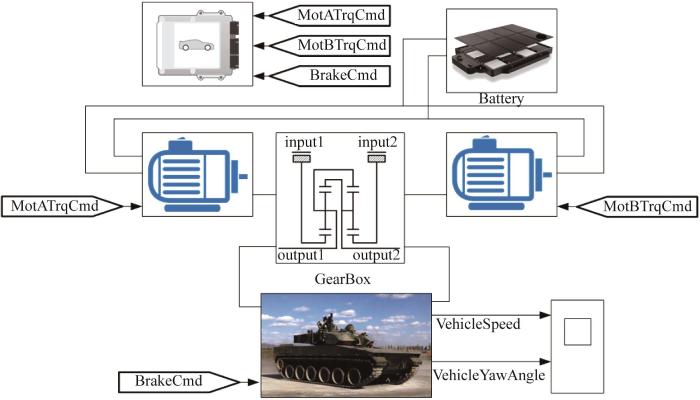
本文基于MATLAB/Simulink软件,搭建了履带车辆动力学仿真模型,如图19 所示。其包含驾驶模块、控制策略以及动力学模块。建模中车辆参数如表3 所示。其中,ISG(integrated starter generator)为集成式启动发电机,K 1 至K 7 为变速箱内行星排和轮边减速器的特征参数,i 1 、i 2 为变速箱内普通齿轮的传动比。
图19
图19
履带车辆动力学仿真模型
Fig.19
Dynamics simulation model of tracked vehicle
为了对所提出的多流复合传动构型下履带车辆的直驶动力性和转向能力进行仿真测试,设定了直驶循环和直驶与转向复合两种测试工况。
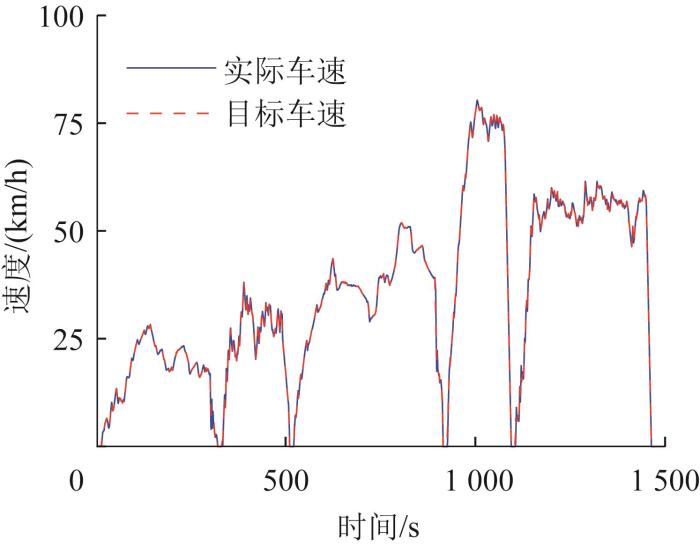
直驶循环测试工况下车辆速度和驱动电机的输出扭矩分别如图20 和图21 所示。由图20 可知,在不同的加速需求及匀速行驶工况下,车辆速度均能较好地跟踪目标速度。由图21 可知,直驶状态下两侧驱动电机的输出扭矩相同,满足了车辆直驶的动力需求。
图20
图20
直驶循环测试工况下车辆速度
Fig.20
Speed of vehicle under straight-line circular test condition
图21
图21
直驶循环测试工况下驱动电机输出扭矩
Fig.21
Output torque of drive motor under straight-line circular test condition
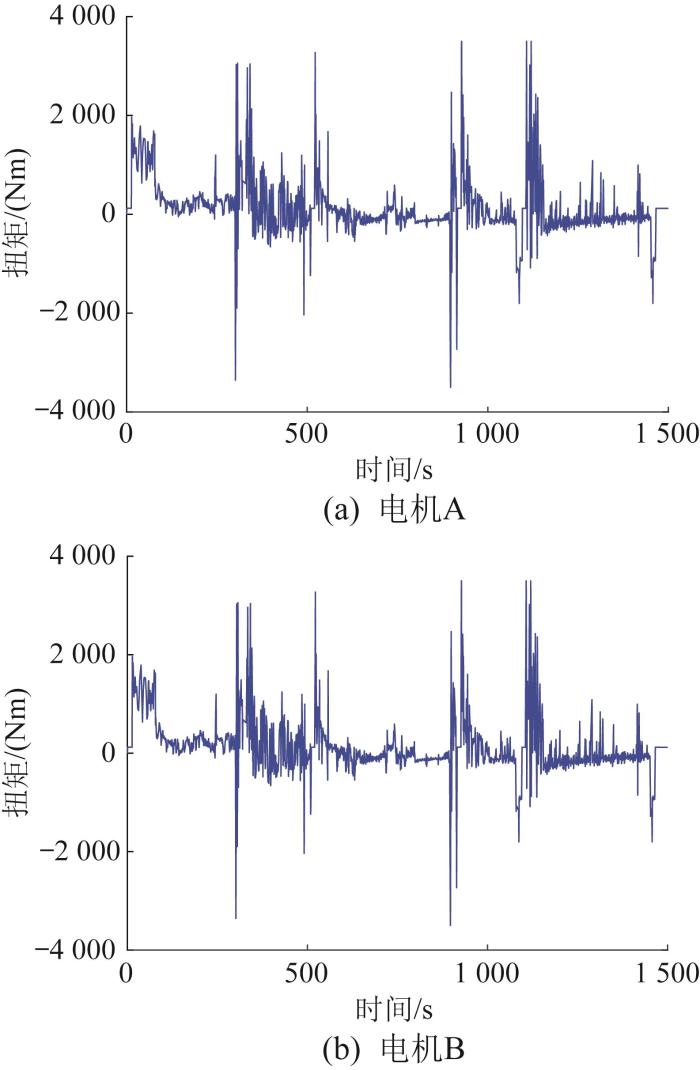
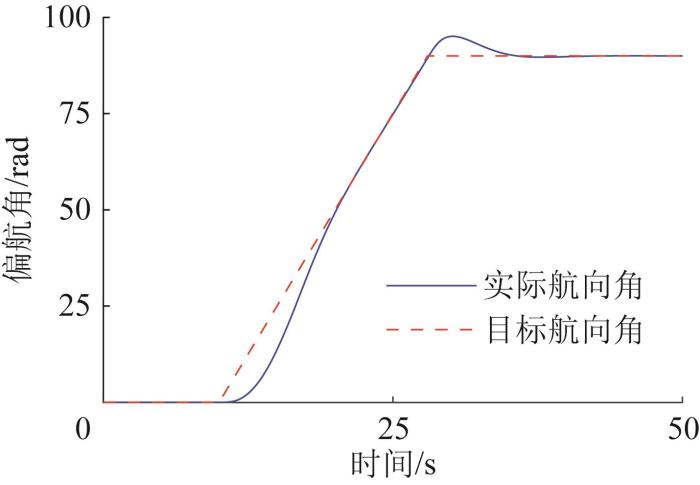
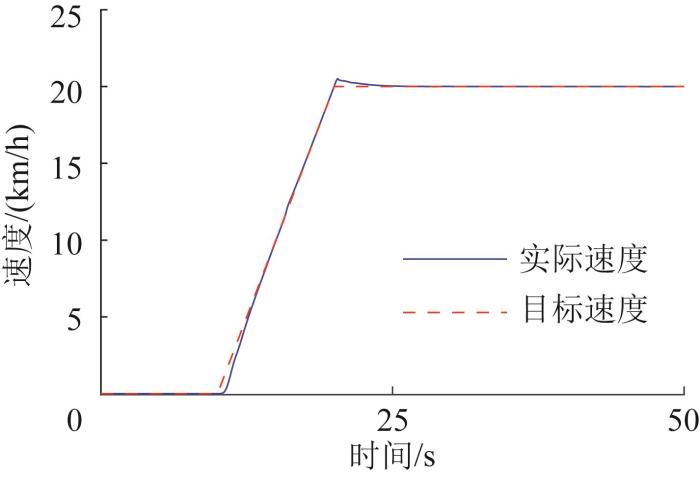
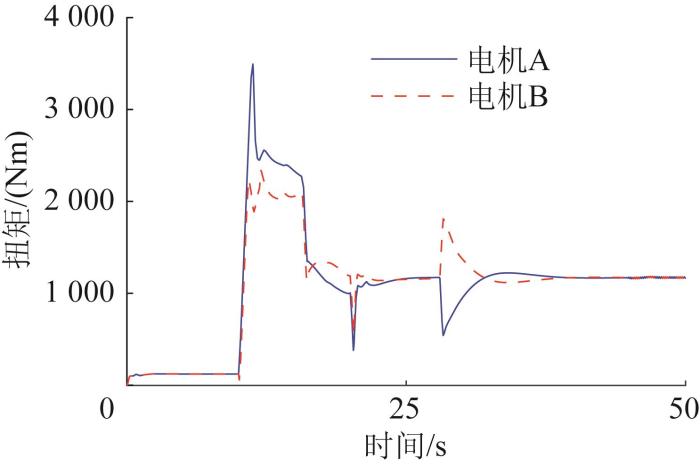
直驶与转向复合仿真时,车辆首先进行匀加速直线行驶,之后在匀加速行驶过程中转向。在该测试工况下车辆偏航角和纵向速度分别如图22 和图23 所示,驱动电机的输出扭矩如图24 所示。由图22 和图23 可知,车辆偏航角和纵向速度都基本与目标值一致,车辆偏航角的跟踪精度大于94%,纵向速度的跟踪误差小于2.1%。由图24 可知,两侧驱动电机产生了扭矩差,驱动两侧履带产生速差,车辆进行转向。
图22
图22
直驶与转向复合测试工况下车辆偏航角
Fig.22
Yaw angle of vehicle under combined test condition of straight-line driving and turning
图23
图23
直驶与转向复合测试工况下车辆纵向速度
Fig.23
Longitudinal velocity of vehicle under combined test condition of straight-line driving and turning
图24
图24
直驶与转向复合测试工况下驱动电机输出扭矩
Fig.24
Output torque of drive motor under combined test condition of straight-line driving and turning
6 结 论
1)根据行星排的3个主要元件,作者提出了一种运动拓扑图论模型来表示传动机构。与现有的图论模型相比,本文提出的图论模型能够较好地反映传动机构各个构件(元件)之间的运动学关系。
2)基于履带车辆的行驶力学特性,分析了实现直驶和转向再生功率传递的参数特征,给出了耦合构型的设计判定特征。
3)针对两行星排和三行星排构型,通过电机功率、耦合机构效率、转向再生功率利用率的分析,得出了最优传动方案,并进行其直驶和转向工况下的功率流分析。车辆性能仿真测试表明,车辆速度、偏航角都与目标值基本一致。
参考文献
View Option
[1]
陈兵 , 马凯璇 , 刘洋 , 等 双电机驱动履带车辆直驶稳定性分层控制策略
[J]. 吉林大学学报(工学版) , 2023 , 53 (10 ): 2752 -2760 .
[本文引用: 1]
CHEN B MA K X LIU Y et al Straight driving stability hierarchical control for dual-motor driving electric tracked vehicle
[J]. Journal of Jilin University (Engineering and Technology Edition) , 2023 , 53 (10 ): 2752 -2760 .
[本文引用: 1]
[2]
张杰 , 袁东 , 张朋 , 等 双侧电传动履带车辆模糊前馈-反馈转向控制
[J]. 兵工学报 , 2020 , 41 (8 ): 1688 -1696 .
[本文引用: 1]
ZHANG J YUAN D ZHANG P et al Steering control based on fuzzy feedforward and feedback for dual-motor electric drive tracked vehicle
[J]. Acta Armamentarii , 2020 , 41 (8 ): 1688 -1696 .
[本文引用: 1]
[3]
魏巍 , 闫清东 , 刘城 , 等 装甲车辆设计 [M]. 2版 . 北京 : 北京理工大学出版社 , 2022 .
[本文引用: 1]
WEI W YAN Q D LIU C et al Design of armored vehicles [M]. 2th ed . Beijing : Beijing Institute of Technology Press , 2022 .
[本文引用: 1]
[4]
生辉 , 项昌乐 , 盖江涛 , 等 双侧电机耦合驱动履带车辆单侧电机故障模式下车辆安全控制
[J]. 兵工学报 , 2023 , 44 (11 ): 3498 -3507 .
[本文引用: 1]
SHENG H XIANG C L GAI J T et al Vehicle safety control of tracked vehicle driven by two-sided motor coupling under the failure mode of one-sided motor
[J]. Acta Armamentarii , 2023 , 44 (11 ): 3498 -3507 .
[本文引用: 1]
[5]
ARNAUDOV K KARAIVANOV D Alternative method for analysis of complex compound planetary gear trains: essence and possibilities
[C]//Power Transmissions: Proceedings of the 4th International Conference . Sinaia, Romania , June 20-23 , 2012 .
[本文引用: 1]
[6]
CHEN H CHEN X A A new methodology for multistage multispeed planetary transmission design based on geometry
[J]. Journal of Mechanical Design , 2021 , 143 (11 ): 113401 .
[本文引用: 1]
[7]
DENG T TANG P SU Z H et al Systematic design and optimization method of multimode hybrid electric vehicles based on equivalent tree graph
[J]. IEEE Transactions on Power Electronics , 2020 , 35 (12 ): 13465 -13474 .
[本文引用: 1]
[8]
GENG M J DING H F KE T et al Topological graph representation and configuration synthesis for power-split hybrid transmissions of multi-planetary gear trains
[J]. Journal of Mechanical Design , 2023 , 145 (12 ): 123401 .
[本文引用: 1]
[9]
GAO M F HU J B Kinematic analysis of planetary gear trains based on topology
[J]. Journal of Mechanical Design , 2018 , 140 (1 ): 012302 .
[本文引用: 1]
[10]
[本文引用: 2]
GAO M F HU J B LI X L et al Study on the characteristics of configuration for the transmission of tracked vehicles to achieve the transfer of steering regenerative power
[J]. Journal of Mechanical Engineering , 2019 , 55 (24 ): 137 -144 .
DOI:10.3901/jme.2019.24.137
[本文引用: 2]
[11]
YANG X D SHAO Y M WANG L M et al Configuration design of dual-input compound power-split mechanism for in-wheel motor-driven electrical vehicles based on an improved lever analogy method
[J]. Journal of Mechanical Design , 2021 , 143 (10 ): 104501 .
[本文引用: 1]
[12]
KIM H KUM D Comprehensive design methodology of input- and output-split hybrid electric vehicles: in search of optimal configuration
[J]. IEEE/ASME Transactions on Mechatronics , 2016 , 21 (6 ): 2912 -2923 .
[本文引用: 1]
[13]
BARHOUMI T KIM H KUM D Automatic generation of design space conversion maps and its application for the design of compound split hybrid powertrains
[J]. Journal of Mechanical Design , 2018 , 140 (6 ): 063401 .
[本文引用: 1]
[14]
SONG C HWANG J KUM D Efficient design space exploration of multi-mode, two-planetary-gear, power-split hybrid electric powertrains via virtual levers
[J]. IEEE Transactions on Intelligent Transportation Systems , 2020 , 23 (4 ): 3498 -3509 .
[本文引用: 1]
[15]
BARHOUMI T KUM D Designing a super-fast prius: systematic design of multispeed eCVT via virtual design space
[J]. IEEE Transactions on Transportation Electrification , 2024 , 10 (1 ): 263 -276 .
[本文引用: 1]
[16]
胡建军 , 薛首志 , 刘子睿 一种履带车辆三行星排混合动力系统构型优化设计方案
[J]. 中国公路学报 , 2024 , 37 (7 ): 317 -328 .
[本文引用: 1]
HU J J XUE S Z LIU Z R Optimization design for a hybrid electric powertrain system with three-planetary gear sets of tracked vehicles
[J]. China Journal of Highway and Transport , 2024 , 37 (7 ): 317 -328 .
[本文引用: 1]
[17]
[本文引用: 1]
QIN Z B Optimal design methodology of the electro-mechanical transmission system for hybrid tracked vehicles
[D]. Beijing : Tsinghua University , 2018 : 46 -47 ,
DOI:10.1115/1.4039687
[本文引用: 1]
[18]
LI R FAN J J HAN Z D et al Configuration design and control of hybrid tracked vehicle with three planetary gear sets
[J]. Journal of Central South University , 2021 , 28 (7 ): 2105 -2119 .
[本文引用: 1]
[19]
PENG H QIN D T HU J J et al Synthesis and analysis method for powertrain configuration of single motor hybrid electric vehicle
[J]. Mechanism and Machine Theory , 2020 , 146 : 103731 .
[本文引用: 1]
[20]
韩政达 , 毛明 , 马晓枫 , 等 履带车辆机电复合传动耦合机构数学特征的研究
[J]. 车辆与动力技术 , 2012 (1 ): 1 -2 , 12 .
[本文引用: 1]
HAN Z D MAO M MA X F et al Research on mathematical characteristics of coupling mechanism for electro-mechanical transmission tracked vehicle
[J]. Vehicle & Power Technology , 2012 (1 ): 1 -2 , 12 .
[本文引用: 1]
双电机驱动履带车辆直驶稳定性分层控制策略
1
2023
... 传统的履带车辆传动系统仅具备机械输出的能力,无法满足新一代履带车辆大功率电能传输和更高的机动性要求.而大功率机电复合传动系统兼具机械功率输出和电功率输出的能力,使履带车辆具有更高的速度及更好的平顺性和机动性.此外,机械结构的减少能降低履带车辆运行时的噪声.最初的机电复合传动为双侧电机独立驱动[1 -2 ] ,转向再生功率以电功率的形式回流至高速侧,这对高速侧电机的过载能力要求很高.为了解决电机过载问题,在双侧电机中间增加一个功率耦合机构来改变功率回流路径[3 -4 ] ,使得回流功率以机械功率的形式通过功率耦合机构回流至高速侧,从而降低了电机的功率需求.机电复合传动如图1 所示. ...
双电机驱动履带车辆直驶稳定性分层控制策略
1
2023
... 传统的履带车辆传动系统仅具备机械输出的能力,无法满足新一代履带车辆大功率电能传输和更高的机动性要求.而大功率机电复合传动系统兼具机械功率输出和电功率输出的能力,使履带车辆具有更高的速度及更好的平顺性和机动性.此外,机械结构的减少能降低履带车辆运行时的噪声.最初的机电复合传动为双侧电机独立驱动[1 -2 ] ,转向再生功率以电功率的形式回流至高速侧,这对高速侧电机的过载能力要求很高.为了解决电机过载问题,在双侧电机中间增加一个功率耦合机构来改变功率回流路径[3 -4 ] ,使得回流功率以机械功率的形式通过功率耦合机构回流至高速侧,从而降低了电机的功率需求.机电复合传动如图1 所示. ...
双侧电传动履带车辆模糊前馈-反馈转向控制
1
2020
... 传统的履带车辆传动系统仅具备机械输出的能力,无法满足新一代履带车辆大功率电能传输和更高的机动性要求.而大功率机电复合传动系统兼具机械功率输出和电功率输出的能力,使履带车辆具有更高的速度及更好的平顺性和机动性.此外,机械结构的减少能降低履带车辆运行时的噪声.最初的机电复合传动为双侧电机独立驱动[1 -2 ] ,转向再生功率以电功率的形式回流至高速侧,这对高速侧电机的过载能力要求很高.为了解决电机过载问题,在双侧电机中间增加一个功率耦合机构来改变功率回流路径[3 -4 ] ,使得回流功率以机械功率的形式通过功率耦合机构回流至高速侧,从而降低了电机的功率需求.机电复合传动如图1 所示. ...
双侧电传动履带车辆模糊前馈-反馈转向控制
1
2020
... 传统的履带车辆传动系统仅具备机械输出的能力,无法满足新一代履带车辆大功率电能传输和更高的机动性要求.而大功率机电复合传动系统兼具机械功率输出和电功率输出的能力,使履带车辆具有更高的速度及更好的平顺性和机动性.此外,机械结构的减少能降低履带车辆运行时的噪声.最初的机电复合传动为双侧电机独立驱动[1 -2 ] ,转向再生功率以电功率的形式回流至高速侧,这对高速侧电机的过载能力要求很高.为了解决电机过载问题,在双侧电机中间增加一个功率耦合机构来改变功率回流路径[3 -4 ] ,使得回流功率以机械功率的形式通过功率耦合机构回流至高速侧,从而降低了电机的功率需求.机电复合传动如图1 所示. ...
1
2022
... 传统的履带车辆传动系统仅具备机械输出的能力,无法满足新一代履带车辆大功率电能传输和更高的机动性要求.而大功率机电复合传动系统兼具机械功率输出和电功率输出的能力,使履带车辆具有更高的速度及更好的平顺性和机动性.此外,机械结构的减少能降低履带车辆运行时的噪声.最初的机电复合传动为双侧电机独立驱动[1 -2 ] ,转向再生功率以电功率的形式回流至高速侧,这对高速侧电机的过载能力要求很高.为了解决电机过载问题,在双侧电机中间增加一个功率耦合机构来改变功率回流路径[3 -4 ] ,使得回流功率以机械功率的形式通过功率耦合机构回流至高速侧,从而降低了电机的功率需求.机电复合传动如图1 所示. ...
1
2022
... 传统的履带车辆传动系统仅具备机械输出的能力,无法满足新一代履带车辆大功率电能传输和更高的机动性要求.而大功率机电复合传动系统兼具机械功率输出和电功率输出的能力,使履带车辆具有更高的速度及更好的平顺性和机动性.此外,机械结构的减少能降低履带车辆运行时的噪声.最初的机电复合传动为双侧电机独立驱动[1 -2 ] ,转向再生功率以电功率的形式回流至高速侧,这对高速侧电机的过载能力要求很高.为了解决电机过载问题,在双侧电机中间增加一个功率耦合机构来改变功率回流路径[3 -4 ] ,使得回流功率以机械功率的形式通过功率耦合机构回流至高速侧,从而降低了电机的功率需求.机电复合传动如图1 所示. ...
双侧电机耦合驱动履带车辆单侧电机故障模式下车辆安全控制
1
2023
... 传统的履带车辆传动系统仅具备机械输出的能力,无法满足新一代履带车辆大功率电能传输和更高的机动性要求.而大功率机电复合传动系统兼具机械功率输出和电功率输出的能力,使履带车辆具有更高的速度及更好的平顺性和机动性.此外,机械结构的减少能降低履带车辆运行时的噪声.最初的机电复合传动为双侧电机独立驱动[1 -2 ] ,转向再生功率以电功率的形式回流至高速侧,这对高速侧电机的过载能力要求很高.为了解决电机过载问题,在双侧电机中间增加一个功率耦合机构来改变功率回流路径[3 -4 ] ,使得回流功率以机械功率的形式通过功率耦合机构回流至高速侧,从而降低了电机的功率需求.机电复合传动如图1 所示. ...
双侧电机耦合驱动履带车辆单侧电机故障模式下车辆安全控制
1
2023
... 传统的履带车辆传动系统仅具备机械输出的能力,无法满足新一代履带车辆大功率电能传输和更高的机动性要求.而大功率机电复合传动系统兼具机械功率输出和电功率输出的能力,使履带车辆具有更高的速度及更好的平顺性和机动性.此外,机械结构的减少能降低履带车辆运行时的噪声.最初的机电复合传动为双侧电机独立驱动[1 -2 ] ,转向再生功率以电功率的形式回流至高速侧,这对高速侧电机的过载能力要求很高.为了解决电机过载问题,在双侧电机中间增加一个功率耦合机构来改变功率回流路径[3 -4 ] ,使得回流功率以机械功率的形式通过功率耦合机构回流至高速侧,从而降低了电机的功率需求.机电复合传动如图1 所示. ...
Alternative method for analysis of complex compound planetary gear trains: essence and possibilities
1
2012
... 目前最常用的机电复合传动构型设计方法包括图论、杠杆法和D矩阵法等.如:Arnaudov等[5 ] 提出了一种新的基于杠杆模型的三端口图论模型,该模型可以分析行星齿轮机构的速度、扭矩和效率等,但计算较为复杂,效率较低;Chen等[6 ] 提出了一种基于几何结构的多级行星自动变速器设计方法,通过“效率”这一重要指标来筛选构型;Deng等[7 ] 针对单行星排的构型设计,提出了一种基于等效树图的模型,降低了构型的筛选难度,但是模型的表示方法较复杂,不能进一步拓展到多行星排的构型设计;Geng等[8 ] 提出了一种新的拓扑图,用于功率分流系统的构型设计,该方法能有效解决设计过程中机械结构的干涉问题;Gao等[9 -10 ] 提出了一种新型行星齿轮拓扑图表示方法,揭示了传动比与拓扑结构的关联关系,显著提升了传动系统的构型设计效率.拓扑图论法能清晰表达复杂行星排的连接关系,但现有拓扑模型侧重于几何连接,未与系统的运动学-动力学特征直接关联,并缺乏系统性的参数筛选准则,需结合人工经验剔除冗余构型.Yang等[11 ] 提出了一种改进的杠杆法,来设计具有高速比的最优构型,以满足高功率密度轮毂电机的需求;Kim等[12 -13 ] 提出了一种复合杠杆法,它是一种适用于寻找单行星排或两行星排混合动力系统最优构型方案的构型搜索方法;Song等[14 -15 ] 改进了复合杠杆法,在寻求最优的多模式构型中,从设计层面最大限度消除了冗余构型,减少了与优化相关的计算工作.杠杆法及其衍生方法适用于单行星排或两行星排混合动力系统,通过杠杆模型分析系统的转速、扭矩和效率特性,可直观反映行星排的力学关系,便于快速评估基础构型的运动学性能,但难以量化再生功率传递条件,无法在拓扑设计阶段筛选出无效构型.为了进一步降低电机功率,通过添加一组行星排,将发动机和发电机连入参考构型,生成了三行星排的基础拓扑结构方案[16 ] .而针对混合动力履带车辆三行星排构型方案的优化设计,秦兆博等[17 -18 ] 改进了Peng等[19 ] 提出的矩阵建模方法,分析了基于3排行星传动的多模式拓扑构型,结果表明,3排行星传动的多模式拓扑构型能更好地保证发动机工作点的配置,维持发动机工作在高效率区.D矩阵法适用于计算机快速筛选,具有一定的盲目性,且计算量较大.综上所述,现有方法在单一功能(如几何连接、效率评估)上具有一定优势,但均存在一定的局限:其一,无法在构型设计阶段有效剔除冗余方案;其二,模型复杂度较高,导致工程应用受限. ...
A new methodology for multistage multispeed planetary transmission design based on geometry
1
2021
... 目前最常用的机电复合传动构型设计方法包括图论、杠杆法和D矩阵法等.如:Arnaudov等[5 ] 提出了一种新的基于杠杆模型的三端口图论模型,该模型可以分析行星齿轮机构的速度、扭矩和效率等,但计算较为复杂,效率较低;Chen等[6 ] 提出了一种基于几何结构的多级行星自动变速器设计方法,通过“效率”这一重要指标来筛选构型;Deng等[7 ] 针对单行星排的构型设计,提出了一种基于等效树图的模型,降低了构型的筛选难度,但是模型的表示方法较复杂,不能进一步拓展到多行星排的构型设计;Geng等[8 ] 提出了一种新的拓扑图,用于功率分流系统的构型设计,该方法能有效解决设计过程中机械结构的干涉问题;Gao等[9 -10 ] 提出了一种新型行星齿轮拓扑图表示方法,揭示了传动比与拓扑结构的关联关系,显著提升了传动系统的构型设计效率.拓扑图论法能清晰表达复杂行星排的连接关系,但现有拓扑模型侧重于几何连接,未与系统的运动学-动力学特征直接关联,并缺乏系统性的参数筛选准则,需结合人工经验剔除冗余构型.Yang等[11 ] 提出了一种改进的杠杆法,来设计具有高速比的最优构型,以满足高功率密度轮毂电机的需求;Kim等[12 -13 ] 提出了一种复合杠杆法,它是一种适用于寻找单行星排或两行星排混合动力系统最优构型方案的构型搜索方法;Song等[14 -15 ] 改进了复合杠杆法,在寻求最优的多模式构型中,从设计层面最大限度消除了冗余构型,减少了与优化相关的计算工作.杠杆法及其衍生方法适用于单行星排或两行星排混合动力系统,通过杠杆模型分析系统的转速、扭矩和效率特性,可直观反映行星排的力学关系,便于快速评估基础构型的运动学性能,但难以量化再生功率传递条件,无法在拓扑设计阶段筛选出无效构型.为了进一步降低电机功率,通过添加一组行星排,将发动机和发电机连入参考构型,生成了三行星排的基础拓扑结构方案[16 ] .而针对混合动力履带车辆三行星排构型方案的优化设计,秦兆博等[17 -18 ] 改进了Peng等[19 ] 提出的矩阵建模方法,分析了基于3排行星传动的多模式拓扑构型,结果表明,3排行星传动的多模式拓扑构型能更好地保证发动机工作点的配置,维持发动机工作在高效率区.D矩阵法适用于计算机快速筛选,具有一定的盲目性,且计算量较大.综上所述,现有方法在单一功能(如几何连接、效率评估)上具有一定优势,但均存在一定的局限:其一,无法在构型设计阶段有效剔除冗余方案;其二,模型复杂度较高,导致工程应用受限. ...
Systematic design and optimization method of multimode hybrid electric vehicles based on equivalent tree graph
1
2020
... 目前最常用的机电复合传动构型设计方法包括图论、杠杆法和D矩阵法等.如:Arnaudov等[5 ] 提出了一种新的基于杠杆模型的三端口图论模型,该模型可以分析行星齿轮机构的速度、扭矩和效率等,但计算较为复杂,效率较低;Chen等[6 ] 提出了一种基于几何结构的多级行星自动变速器设计方法,通过“效率”这一重要指标来筛选构型;Deng等[7 ] 针对单行星排的构型设计,提出了一种基于等效树图的模型,降低了构型的筛选难度,但是模型的表示方法较复杂,不能进一步拓展到多行星排的构型设计;Geng等[8 ] 提出了一种新的拓扑图,用于功率分流系统的构型设计,该方法能有效解决设计过程中机械结构的干涉问题;Gao等[9 -10 ] 提出了一种新型行星齿轮拓扑图表示方法,揭示了传动比与拓扑结构的关联关系,显著提升了传动系统的构型设计效率.拓扑图论法能清晰表达复杂行星排的连接关系,但现有拓扑模型侧重于几何连接,未与系统的运动学-动力学特征直接关联,并缺乏系统性的参数筛选准则,需结合人工经验剔除冗余构型.Yang等[11 ] 提出了一种改进的杠杆法,来设计具有高速比的最优构型,以满足高功率密度轮毂电机的需求;Kim等[12 -13 ] 提出了一种复合杠杆法,它是一种适用于寻找单行星排或两行星排混合动力系统最优构型方案的构型搜索方法;Song等[14 -15 ] 改进了复合杠杆法,在寻求最优的多模式构型中,从设计层面最大限度消除了冗余构型,减少了与优化相关的计算工作.杠杆法及其衍生方法适用于单行星排或两行星排混合动力系统,通过杠杆模型分析系统的转速、扭矩和效率特性,可直观反映行星排的力学关系,便于快速评估基础构型的运动学性能,但难以量化再生功率传递条件,无法在拓扑设计阶段筛选出无效构型.为了进一步降低电机功率,通过添加一组行星排,将发动机和发电机连入参考构型,生成了三行星排的基础拓扑结构方案[16 ] .而针对混合动力履带车辆三行星排构型方案的优化设计,秦兆博等[17 -18 ] 改进了Peng等[19 ] 提出的矩阵建模方法,分析了基于3排行星传动的多模式拓扑构型,结果表明,3排行星传动的多模式拓扑构型能更好地保证发动机工作点的配置,维持发动机工作在高效率区.D矩阵法适用于计算机快速筛选,具有一定的盲目性,且计算量较大.综上所述,现有方法在单一功能(如几何连接、效率评估)上具有一定优势,但均存在一定的局限:其一,无法在构型设计阶段有效剔除冗余方案;其二,模型复杂度较高,导致工程应用受限. ...
Topological graph representation and configuration synthesis for power-split hybrid transmissions of multi-planetary gear trains
1
2023
... 目前最常用的机电复合传动构型设计方法包括图论、杠杆法和D矩阵法等.如:Arnaudov等[5 ] 提出了一种新的基于杠杆模型的三端口图论模型,该模型可以分析行星齿轮机构的速度、扭矩和效率等,但计算较为复杂,效率较低;Chen等[6 ] 提出了一种基于几何结构的多级行星自动变速器设计方法,通过“效率”这一重要指标来筛选构型;Deng等[7 ] 针对单行星排的构型设计,提出了一种基于等效树图的模型,降低了构型的筛选难度,但是模型的表示方法较复杂,不能进一步拓展到多行星排的构型设计;Geng等[8 ] 提出了一种新的拓扑图,用于功率分流系统的构型设计,该方法能有效解决设计过程中机械结构的干涉问题;Gao等[9 -10 ] 提出了一种新型行星齿轮拓扑图表示方法,揭示了传动比与拓扑结构的关联关系,显著提升了传动系统的构型设计效率.拓扑图论法能清晰表达复杂行星排的连接关系,但现有拓扑模型侧重于几何连接,未与系统的运动学-动力学特征直接关联,并缺乏系统性的参数筛选准则,需结合人工经验剔除冗余构型.Yang等[11 ] 提出了一种改进的杠杆法,来设计具有高速比的最优构型,以满足高功率密度轮毂电机的需求;Kim等[12 -13 ] 提出了一种复合杠杆法,它是一种适用于寻找单行星排或两行星排混合动力系统最优构型方案的构型搜索方法;Song等[14 -15 ] 改进了复合杠杆法,在寻求最优的多模式构型中,从设计层面最大限度消除了冗余构型,减少了与优化相关的计算工作.杠杆法及其衍生方法适用于单行星排或两行星排混合动力系统,通过杠杆模型分析系统的转速、扭矩和效率特性,可直观反映行星排的力学关系,便于快速评估基础构型的运动学性能,但难以量化再生功率传递条件,无法在拓扑设计阶段筛选出无效构型.为了进一步降低电机功率,通过添加一组行星排,将发动机和发电机连入参考构型,生成了三行星排的基础拓扑结构方案[16 ] .而针对混合动力履带车辆三行星排构型方案的优化设计,秦兆博等[17 -18 ] 改进了Peng等[19 ] 提出的矩阵建模方法,分析了基于3排行星传动的多模式拓扑构型,结果表明,3排行星传动的多模式拓扑构型能更好地保证发动机工作点的配置,维持发动机工作在高效率区.D矩阵法适用于计算机快速筛选,具有一定的盲目性,且计算量较大.综上所述,现有方法在单一功能(如几何连接、效率评估)上具有一定优势,但均存在一定的局限:其一,无法在构型设计阶段有效剔除冗余方案;其二,模型复杂度较高,导致工程应用受限. ...
Kinematic analysis of planetary gear trains based on topology
1
2018
... 目前最常用的机电复合传动构型设计方法包括图论、杠杆法和D矩阵法等.如:Arnaudov等[5 ] 提出了一种新的基于杠杆模型的三端口图论模型,该模型可以分析行星齿轮机构的速度、扭矩和效率等,但计算较为复杂,效率较低;Chen等[6 ] 提出了一种基于几何结构的多级行星自动变速器设计方法,通过“效率”这一重要指标来筛选构型;Deng等[7 ] 针对单行星排的构型设计,提出了一种基于等效树图的模型,降低了构型的筛选难度,但是模型的表示方法较复杂,不能进一步拓展到多行星排的构型设计;Geng等[8 ] 提出了一种新的拓扑图,用于功率分流系统的构型设计,该方法能有效解决设计过程中机械结构的干涉问题;Gao等[9 -10 ] 提出了一种新型行星齿轮拓扑图表示方法,揭示了传动比与拓扑结构的关联关系,显著提升了传动系统的构型设计效率.拓扑图论法能清晰表达复杂行星排的连接关系,但现有拓扑模型侧重于几何连接,未与系统的运动学-动力学特征直接关联,并缺乏系统性的参数筛选准则,需结合人工经验剔除冗余构型.Yang等[11 ] 提出了一种改进的杠杆法,来设计具有高速比的最优构型,以满足高功率密度轮毂电机的需求;Kim等[12 -13 ] 提出了一种复合杠杆法,它是一种适用于寻找单行星排或两行星排混合动力系统最优构型方案的构型搜索方法;Song等[14 -15 ] 改进了复合杠杆法,在寻求最优的多模式构型中,从设计层面最大限度消除了冗余构型,减少了与优化相关的计算工作.杠杆法及其衍生方法适用于单行星排或两行星排混合动力系统,通过杠杆模型分析系统的转速、扭矩和效率特性,可直观反映行星排的力学关系,便于快速评估基础构型的运动学性能,但难以量化再生功率传递条件,无法在拓扑设计阶段筛选出无效构型.为了进一步降低电机功率,通过添加一组行星排,将发动机和发电机连入参考构型,生成了三行星排的基础拓扑结构方案[16 ] .而针对混合动力履带车辆三行星排构型方案的优化设计,秦兆博等[17 -18 ] 改进了Peng等[19 ] 提出的矩阵建模方法,分析了基于3排行星传动的多模式拓扑构型,结果表明,3排行星传动的多模式拓扑构型能更好地保证发动机工作点的配置,维持发动机工作在高效率区.D矩阵法适用于计算机快速筛选,具有一定的盲目性,且计算量较大.综上所述,现有方法在单一功能(如几何连接、效率评估)上具有一定优势,但均存在一定的局限:其一,无法在构型设计阶段有效剔除冗余方案;其二,模型复杂度较高,导致工程应用受限. ...
履带车辆传动机构实现转向再生功率传递的构型特征研究
2
2019
... 目前最常用的机电复合传动构型设计方法包括图论、杠杆法和D矩阵法等.如:Arnaudov等[5 ] 提出了一种新的基于杠杆模型的三端口图论模型,该模型可以分析行星齿轮机构的速度、扭矩和效率等,但计算较为复杂,效率较低;Chen等[6 ] 提出了一种基于几何结构的多级行星自动变速器设计方法,通过“效率”这一重要指标来筛选构型;Deng等[7 ] 针对单行星排的构型设计,提出了一种基于等效树图的模型,降低了构型的筛选难度,但是模型的表示方法较复杂,不能进一步拓展到多行星排的构型设计;Geng等[8 ] 提出了一种新的拓扑图,用于功率分流系统的构型设计,该方法能有效解决设计过程中机械结构的干涉问题;Gao等[9 -10 ] 提出了一种新型行星齿轮拓扑图表示方法,揭示了传动比与拓扑结构的关联关系,显著提升了传动系统的构型设计效率.拓扑图论法能清晰表达复杂行星排的连接关系,但现有拓扑模型侧重于几何连接,未与系统的运动学-动力学特征直接关联,并缺乏系统性的参数筛选准则,需结合人工经验剔除冗余构型.Yang等[11 ] 提出了一种改进的杠杆法,来设计具有高速比的最优构型,以满足高功率密度轮毂电机的需求;Kim等[12 -13 ] 提出了一种复合杠杆法,它是一种适用于寻找单行星排或两行星排混合动力系统最优构型方案的构型搜索方法;Song等[14 -15 ] 改进了复合杠杆法,在寻求最优的多模式构型中,从设计层面最大限度消除了冗余构型,减少了与优化相关的计算工作.杠杆法及其衍生方法适用于单行星排或两行星排混合动力系统,通过杠杆模型分析系统的转速、扭矩和效率特性,可直观反映行星排的力学关系,便于快速评估基础构型的运动学性能,但难以量化再生功率传递条件,无法在拓扑设计阶段筛选出无效构型.为了进一步降低电机功率,通过添加一组行星排,将发动机和发电机连入参考构型,生成了三行星排的基础拓扑结构方案[16 ] .而针对混合动力履带车辆三行星排构型方案的优化设计,秦兆博等[17 -18 ] 改进了Peng等[19 ] 提出的矩阵建模方法,分析了基于3排行星传动的多模式拓扑构型,结果表明,3排行星传动的多模式拓扑构型能更好地保证发动机工作点的配置,维持发动机工作在高效率区.D矩阵法适用于计算机快速筛选,具有一定的盲目性,且计算量较大.综上所述,现有方法在单一功能(如几何连接、效率评估)上具有一定优势,但均存在一定的局限:其一,无法在构型设计阶段有效剔除冗余方案;其二,模型复杂度较高,导致工程应用受限. ...
... 根据转向再生功率传递条件,应当满足式(3) ,将式(5) 至式(8) 代入(3),化简后可得[10 ] : ...
履带车辆传动机构实现转向再生功率传递的构型特征研究
2
2019
... 目前最常用的机电复合传动构型设计方法包括图论、杠杆法和D矩阵法等.如:Arnaudov等[5 ] 提出了一种新的基于杠杆模型的三端口图论模型,该模型可以分析行星齿轮机构的速度、扭矩和效率等,但计算较为复杂,效率较低;Chen等[6 ] 提出了一种基于几何结构的多级行星自动变速器设计方法,通过“效率”这一重要指标来筛选构型;Deng等[7 ] 针对单行星排的构型设计,提出了一种基于等效树图的模型,降低了构型的筛选难度,但是模型的表示方法较复杂,不能进一步拓展到多行星排的构型设计;Geng等[8 ] 提出了一种新的拓扑图,用于功率分流系统的构型设计,该方法能有效解决设计过程中机械结构的干涉问题;Gao等[9 -10 ] 提出了一种新型行星齿轮拓扑图表示方法,揭示了传动比与拓扑结构的关联关系,显著提升了传动系统的构型设计效率.拓扑图论法能清晰表达复杂行星排的连接关系,但现有拓扑模型侧重于几何连接,未与系统的运动学-动力学特征直接关联,并缺乏系统性的参数筛选准则,需结合人工经验剔除冗余构型.Yang等[11 ] 提出了一种改进的杠杆法,来设计具有高速比的最优构型,以满足高功率密度轮毂电机的需求;Kim等[12 -13 ] 提出了一种复合杠杆法,它是一种适用于寻找单行星排或两行星排混合动力系统最优构型方案的构型搜索方法;Song等[14 -15 ] 改进了复合杠杆法,在寻求最优的多模式构型中,从设计层面最大限度消除了冗余构型,减少了与优化相关的计算工作.杠杆法及其衍生方法适用于单行星排或两行星排混合动力系统,通过杠杆模型分析系统的转速、扭矩和效率特性,可直观反映行星排的力学关系,便于快速评估基础构型的运动学性能,但难以量化再生功率传递条件,无法在拓扑设计阶段筛选出无效构型.为了进一步降低电机功率,通过添加一组行星排,将发动机和发电机连入参考构型,生成了三行星排的基础拓扑结构方案[16 ] .而针对混合动力履带车辆三行星排构型方案的优化设计,秦兆博等[17 -18 ] 改进了Peng等[19 ] 提出的矩阵建模方法,分析了基于3排行星传动的多模式拓扑构型,结果表明,3排行星传动的多模式拓扑构型能更好地保证发动机工作点的配置,维持发动机工作在高效率区.D矩阵法适用于计算机快速筛选,具有一定的盲目性,且计算量较大.综上所述,现有方法在单一功能(如几何连接、效率评估)上具有一定优势,但均存在一定的局限:其一,无法在构型设计阶段有效剔除冗余方案;其二,模型复杂度较高,导致工程应用受限. ...
... 根据转向再生功率传递条件,应当满足式(3) ,将式(5) 至式(8) 代入(3),化简后可得[10 ] : ...
Configuration design of dual-input compound power-split mechanism for in-wheel motor-driven electrical vehicles based on an improved lever analogy method
1
2021
... 目前最常用的机电复合传动构型设计方法包括图论、杠杆法和D矩阵法等.如:Arnaudov等[5 ] 提出了一种新的基于杠杆模型的三端口图论模型,该模型可以分析行星齿轮机构的速度、扭矩和效率等,但计算较为复杂,效率较低;Chen等[6 ] 提出了一种基于几何结构的多级行星自动变速器设计方法,通过“效率”这一重要指标来筛选构型;Deng等[7 ] 针对单行星排的构型设计,提出了一种基于等效树图的模型,降低了构型的筛选难度,但是模型的表示方法较复杂,不能进一步拓展到多行星排的构型设计;Geng等[8 ] 提出了一种新的拓扑图,用于功率分流系统的构型设计,该方法能有效解决设计过程中机械结构的干涉问题;Gao等[9 -10 ] 提出了一种新型行星齿轮拓扑图表示方法,揭示了传动比与拓扑结构的关联关系,显著提升了传动系统的构型设计效率.拓扑图论法能清晰表达复杂行星排的连接关系,但现有拓扑模型侧重于几何连接,未与系统的运动学-动力学特征直接关联,并缺乏系统性的参数筛选准则,需结合人工经验剔除冗余构型.Yang等[11 ] 提出了一种改进的杠杆法,来设计具有高速比的最优构型,以满足高功率密度轮毂电机的需求;Kim等[12 -13 ] 提出了一种复合杠杆法,它是一种适用于寻找单行星排或两行星排混合动力系统最优构型方案的构型搜索方法;Song等[14 -15 ] 改进了复合杠杆法,在寻求最优的多模式构型中,从设计层面最大限度消除了冗余构型,减少了与优化相关的计算工作.杠杆法及其衍生方法适用于单行星排或两行星排混合动力系统,通过杠杆模型分析系统的转速、扭矩和效率特性,可直观反映行星排的力学关系,便于快速评估基础构型的运动学性能,但难以量化再生功率传递条件,无法在拓扑设计阶段筛选出无效构型.为了进一步降低电机功率,通过添加一组行星排,将发动机和发电机连入参考构型,生成了三行星排的基础拓扑结构方案[16 ] .而针对混合动力履带车辆三行星排构型方案的优化设计,秦兆博等[17 -18 ] 改进了Peng等[19 ] 提出的矩阵建模方法,分析了基于3排行星传动的多模式拓扑构型,结果表明,3排行星传动的多模式拓扑构型能更好地保证发动机工作点的配置,维持发动机工作在高效率区.D矩阵法适用于计算机快速筛选,具有一定的盲目性,且计算量较大.综上所述,现有方法在单一功能(如几何连接、效率评估)上具有一定优势,但均存在一定的局限:其一,无法在构型设计阶段有效剔除冗余方案;其二,模型复杂度较高,导致工程应用受限. ...
Comprehensive design methodology of input- and output-split hybrid electric vehicles: in search of optimal configuration
1
2016
... 目前最常用的机电复合传动构型设计方法包括图论、杠杆法和D矩阵法等.如:Arnaudov等[5 ] 提出了一种新的基于杠杆模型的三端口图论模型,该模型可以分析行星齿轮机构的速度、扭矩和效率等,但计算较为复杂,效率较低;Chen等[6 ] 提出了一种基于几何结构的多级行星自动变速器设计方法,通过“效率”这一重要指标来筛选构型;Deng等[7 ] 针对单行星排的构型设计,提出了一种基于等效树图的模型,降低了构型的筛选难度,但是模型的表示方法较复杂,不能进一步拓展到多行星排的构型设计;Geng等[8 ] 提出了一种新的拓扑图,用于功率分流系统的构型设计,该方法能有效解决设计过程中机械结构的干涉问题;Gao等[9 -10 ] 提出了一种新型行星齿轮拓扑图表示方法,揭示了传动比与拓扑结构的关联关系,显著提升了传动系统的构型设计效率.拓扑图论法能清晰表达复杂行星排的连接关系,但现有拓扑模型侧重于几何连接,未与系统的运动学-动力学特征直接关联,并缺乏系统性的参数筛选准则,需结合人工经验剔除冗余构型.Yang等[11 ] 提出了一种改进的杠杆法,来设计具有高速比的最优构型,以满足高功率密度轮毂电机的需求;Kim等[12 -13 ] 提出了一种复合杠杆法,它是一种适用于寻找单行星排或两行星排混合动力系统最优构型方案的构型搜索方法;Song等[14 -15 ] 改进了复合杠杆法,在寻求最优的多模式构型中,从设计层面最大限度消除了冗余构型,减少了与优化相关的计算工作.杠杆法及其衍生方法适用于单行星排或两行星排混合动力系统,通过杠杆模型分析系统的转速、扭矩和效率特性,可直观反映行星排的力学关系,便于快速评估基础构型的运动学性能,但难以量化再生功率传递条件,无法在拓扑设计阶段筛选出无效构型.为了进一步降低电机功率,通过添加一组行星排,将发动机和发电机连入参考构型,生成了三行星排的基础拓扑结构方案[16 ] .而针对混合动力履带车辆三行星排构型方案的优化设计,秦兆博等[17 -18 ] 改进了Peng等[19 ] 提出的矩阵建模方法,分析了基于3排行星传动的多模式拓扑构型,结果表明,3排行星传动的多模式拓扑构型能更好地保证发动机工作点的配置,维持发动机工作在高效率区.D矩阵法适用于计算机快速筛选,具有一定的盲目性,且计算量较大.综上所述,现有方法在单一功能(如几何连接、效率评估)上具有一定优势,但均存在一定的局限:其一,无法在构型设计阶段有效剔除冗余方案;其二,模型复杂度较高,导致工程应用受限. ...
Automatic generation of design space conversion maps and its application for the design of compound split hybrid powertrains
1
2018
... 目前最常用的机电复合传动构型设计方法包括图论、杠杆法和D矩阵法等.如:Arnaudov等[5 ] 提出了一种新的基于杠杆模型的三端口图论模型,该模型可以分析行星齿轮机构的速度、扭矩和效率等,但计算较为复杂,效率较低;Chen等[6 ] 提出了一种基于几何结构的多级行星自动变速器设计方法,通过“效率”这一重要指标来筛选构型;Deng等[7 ] 针对单行星排的构型设计,提出了一种基于等效树图的模型,降低了构型的筛选难度,但是模型的表示方法较复杂,不能进一步拓展到多行星排的构型设计;Geng等[8 ] 提出了一种新的拓扑图,用于功率分流系统的构型设计,该方法能有效解决设计过程中机械结构的干涉问题;Gao等[9 -10 ] 提出了一种新型行星齿轮拓扑图表示方法,揭示了传动比与拓扑结构的关联关系,显著提升了传动系统的构型设计效率.拓扑图论法能清晰表达复杂行星排的连接关系,但现有拓扑模型侧重于几何连接,未与系统的运动学-动力学特征直接关联,并缺乏系统性的参数筛选准则,需结合人工经验剔除冗余构型.Yang等[11 ] 提出了一种改进的杠杆法,来设计具有高速比的最优构型,以满足高功率密度轮毂电机的需求;Kim等[12 -13 ] 提出了一种复合杠杆法,它是一种适用于寻找单行星排或两行星排混合动力系统最优构型方案的构型搜索方法;Song等[14 -15 ] 改进了复合杠杆法,在寻求最优的多模式构型中,从设计层面最大限度消除了冗余构型,减少了与优化相关的计算工作.杠杆法及其衍生方法适用于单行星排或两行星排混合动力系统,通过杠杆模型分析系统的转速、扭矩和效率特性,可直观反映行星排的力学关系,便于快速评估基础构型的运动学性能,但难以量化再生功率传递条件,无法在拓扑设计阶段筛选出无效构型.为了进一步降低电机功率,通过添加一组行星排,将发动机和发电机连入参考构型,生成了三行星排的基础拓扑结构方案[16 ] .而针对混合动力履带车辆三行星排构型方案的优化设计,秦兆博等[17 -18 ] 改进了Peng等[19 ] 提出的矩阵建模方法,分析了基于3排行星传动的多模式拓扑构型,结果表明,3排行星传动的多模式拓扑构型能更好地保证发动机工作点的配置,维持发动机工作在高效率区.D矩阵法适用于计算机快速筛选,具有一定的盲目性,且计算量较大.综上所述,现有方法在单一功能(如几何连接、效率评估)上具有一定优势,但均存在一定的局限:其一,无法在构型设计阶段有效剔除冗余方案;其二,模型复杂度较高,导致工程应用受限. ...
Efficient design space exploration of multi-mode, two-planetary-gear, power-split hybrid electric powertrains via virtual levers
1
2020
... 目前最常用的机电复合传动构型设计方法包括图论、杠杆法和D矩阵法等.如:Arnaudov等[5 ] 提出了一种新的基于杠杆模型的三端口图论模型,该模型可以分析行星齿轮机构的速度、扭矩和效率等,但计算较为复杂,效率较低;Chen等[6 ] 提出了一种基于几何结构的多级行星自动变速器设计方法,通过“效率”这一重要指标来筛选构型;Deng等[7 ] 针对单行星排的构型设计,提出了一种基于等效树图的模型,降低了构型的筛选难度,但是模型的表示方法较复杂,不能进一步拓展到多行星排的构型设计;Geng等[8 ] 提出了一种新的拓扑图,用于功率分流系统的构型设计,该方法能有效解决设计过程中机械结构的干涉问题;Gao等[9 -10 ] 提出了一种新型行星齿轮拓扑图表示方法,揭示了传动比与拓扑结构的关联关系,显著提升了传动系统的构型设计效率.拓扑图论法能清晰表达复杂行星排的连接关系,但现有拓扑模型侧重于几何连接,未与系统的运动学-动力学特征直接关联,并缺乏系统性的参数筛选准则,需结合人工经验剔除冗余构型.Yang等[11 ] 提出了一种改进的杠杆法,来设计具有高速比的最优构型,以满足高功率密度轮毂电机的需求;Kim等[12 -13 ] 提出了一种复合杠杆法,它是一种适用于寻找单行星排或两行星排混合动力系统最优构型方案的构型搜索方法;Song等[14 -15 ] 改进了复合杠杆法,在寻求最优的多模式构型中,从设计层面最大限度消除了冗余构型,减少了与优化相关的计算工作.杠杆法及其衍生方法适用于单行星排或两行星排混合动力系统,通过杠杆模型分析系统的转速、扭矩和效率特性,可直观反映行星排的力学关系,便于快速评估基础构型的运动学性能,但难以量化再生功率传递条件,无法在拓扑设计阶段筛选出无效构型.为了进一步降低电机功率,通过添加一组行星排,将发动机和发电机连入参考构型,生成了三行星排的基础拓扑结构方案[16 ] .而针对混合动力履带车辆三行星排构型方案的优化设计,秦兆博等[17 -18 ] 改进了Peng等[19 ] 提出的矩阵建模方法,分析了基于3排行星传动的多模式拓扑构型,结果表明,3排行星传动的多模式拓扑构型能更好地保证发动机工作点的配置,维持发动机工作在高效率区.D矩阵法适用于计算机快速筛选,具有一定的盲目性,且计算量较大.综上所述,现有方法在单一功能(如几何连接、效率评估)上具有一定优势,但均存在一定的局限:其一,无法在构型设计阶段有效剔除冗余方案;其二,模型复杂度较高,导致工程应用受限. ...
Designing a super-fast prius: systematic design of multispeed eCVT via virtual design space
1
2024
... 目前最常用的机电复合传动构型设计方法包括图论、杠杆法和D矩阵法等.如:Arnaudov等[5 ] 提出了一种新的基于杠杆模型的三端口图论模型,该模型可以分析行星齿轮机构的速度、扭矩和效率等,但计算较为复杂,效率较低;Chen等[6 ] 提出了一种基于几何结构的多级行星自动变速器设计方法,通过“效率”这一重要指标来筛选构型;Deng等[7 ] 针对单行星排的构型设计,提出了一种基于等效树图的模型,降低了构型的筛选难度,但是模型的表示方法较复杂,不能进一步拓展到多行星排的构型设计;Geng等[8 ] 提出了一种新的拓扑图,用于功率分流系统的构型设计,该方法能有效解决设计过程中机械结构的干涉问题;Gao等[9 -10 ] 提出了一种新型行星齿轮拓扑图表示方法,揭示了传动比与拓扑结构的关联关系,显著提升了传动系统的构型设计效率.拓扑图论法能清晰表达复杂行星排的连接关系,但现有拓扑模型侧重于几何连接,未与系统的运动学-动力学特征直接关联,并缺乏系统性的参数筛选准则,需结合人工经验剔除冗余构型.Yang等[11 ] 提出了一种改进的杠杆法,来设计具有高速比的最优构型,以满足高功率密度轮毂电机的需求;Kim等[12 -13 ] 提出了一种复合杠杆法,它是一种适用于寻找单行星排或两行星排混合动力系统最优构型方案的构型搜索方法;Song等[14 -15 ] 改进了复合杠杆法,在寻求最优的多模式构型中,从设计层面最大限度消除了冗余构型,减少了与优化相关的计算工作.杠杆法及其衍生方法适用于单行星排或两行星排混合动力系统,通过杠杆模型分析系统的转速、扭矩和效率特性,可直观反映行星排的力学关系,便于快速评估基础构型的运动学性能,但难以量化再生功率传递条件,无法在拓扑设计阶段筛选出无效构型.为了进一步降低电机功率,通过添加一组行星排,将发动机和发电机连入参考构型,生成了三行星排的基础拓扑结构方案[16 ] .而针对混合动力履带车辆三行星排构型方案的优化设计,秦兆博等[17 -18 ] 改进了Peng等[19 ] 提出的矩阵建模方法,分析了基于3排行星传动的多模式拓扑构型,结果表明,3排行星传动的多模式拓扑构型能更好地保证发动机工作点的配置,维持发动机工作在高效率区.D矩阵法适用于计算机快速筛选,具有一定的盲目性,且计算量较大.综上所述,现有方法在单一功能(如几何连接、效率评估)上具有一定优势,但均存在一定的局限:其一,无法在构型设计阶段有效剔除冗余方案;其二,模型复杂度较高,导致工程应用受限. ...
一种履带车辆三行星排混合动力系统构型优化设计方案
1
2024
... 目前最常用的机电复合传动构型设计方法包括图论、杠杆法和D矩阵法等.如:Arnaudov等[5 ] 提出了一种新的基于杠杆模型的三端口图论模型,该模型可以分析行星齿轮机构的速度、扭矩和效率等,但计算较为复杂,效率较低;Chen等[6 ] 提出了一种基于几何结构的多级行星自动变速器设计方法,通过“效率”这一重要指标来筛选构型;Deng等[7 ] 针对单行星排的构型设计,提出了一种基于等效树图的模型,降低了构型的筛选难度,但是模型的表示方法较复杂,不能进一步拓展到多行星排的构型设计;Geng等[8 ] 提出了一种新的拓扑图,用于功率分流系统的构型设计,该方法能有效解决设计过程中机械结构的干涉问题;Gao等[9 -10 ] 提出了一种新型行星齿轮拓扑图表示方法,揭示了传动比与拓扑结构的关联关系,显著提升了传动系统的构型设计效率.拓扑图论法能清晰表达复杂行星排的连接关系,但现有拓扑模型侧重于几何连接,未与系统的运动学-动力学特征直接关联,并缺乏系统性的参数筛选准则,需结合人工经验剔除冗余构型.Yang等[11 ] 提出了一种改进的杠杆法,来设计具有高速比的最优构型,以满足高功率密度轮毂电机的需求;Kim等[12 -13 ] 提出了一种复合杠杆法,它是一种适用于寻找单行星排或两行星排混合动力系统最优构型方案的构型搜索方法;Song等[14 -15 ] 改进了复合杠杆法,在寻求最优的多模式构型中,从设计层面最大限度消除了冗余构型,减少了与优化相关的计算工作.杠杆法及其衍生方法适用于单行星排或两行星排混合动力系统,通过杠杆模型分析系统的转速、扭矩和效率特性,可直观反映行星排的力学关系,便于快速评估基础构型的运动学性能,但难以量化再生功率传递条件,无法在拓扑设计阶段筛选出无效构型.为了进一步降低电机功率,通过添加一组行星排,将发动机和发电机连入参考构型,生成了三行星排的基础拓扑结构方案[16 ] .而针对混合动力履带车辆三行星排构型方案的优化设计,秦兆博等[17 -18 ] 改进了Peng等[19 ] 提出的矩阵建模方法,分析了基于3排行星传动的多模式拓扑构型,结果表明,3排行星传动的多模式拓扑构型能更好地保证发动机工作点的配置,维持发动机工作在高效率区.D矩阵法适用于计算机快速筛选,具有一定的盲目性,且计算量较大.综上所述,现有方法在单一功能(如几何连接、效率评估)上具有一定优势,但均存在一定的局限:其一,无法在构型设计阶段有效剔除冗余方案;其二,模型复杂度较高,导致工程应用受限. ...
一种履带车辆三行星排混合动力系统构型优化设计方案
1
2024
... 目前最常用的机电复合传动构型设计方法包括图论、杠杆法和D矩阵法等.如:Arnaudov等[5 ] 提出了一种新的基于杠杆模型的三端口图论模型,该模型可以分析行星齿轮机构的速度、扭矩和效率等,但计算较为复杂,效率较低;Chen等[6 ] 提出了一种基于几何结构的多级行星自动变速器设计方法,通过“效率”这一重要指标来筛选构型;Deng等[7 ] 针对单行星排的构型设计,提出了一种基于等效树图的模型,降低了构型的筛选难度,但是模型的表示方法较复杂,不能进一步拓展到多行星排的构型设计;Geng等[8 ] 提出了一种新的拓扑图,用于功率分流系统的构型设计,该方法能有效解决设计过程中机械结构的干涉问题;Gao等[9 -10 ] 提出了一种新型行星齿轮拓扑图表示方法,揭示了传动比与拓扑结构的关联关系,显著提升了传动系统的构型设计效率.拓扑图论法能清晰表达复杂行星排的连接关系,但现有拓扑模型侧重于几何连接,未与系统的运动学-动力学特征直接关联,并缺乏系统性的参数筛选准则,需结合人工经验剔除冗余构型.Yang等[11 ] 提出了一种改进的杠杆法,来设计具有高速比的最优构型,以满足高功率密度轮毂电机的需求;Kim等[12 -13 ] 提出了一种复合杠杆法,它是一种适用于寻找单行星排或两行星排混合动力系统最优构型方案的构型搜索方法;Song等[14 -15 ] 改进了复合杠杆法,在寻求最优的多模式构型中,从设计层面最大限度消除了冗余构型,减少了与优化相关的计算工作.杠杆法及其衍生方法适用于单行星排或两行星排混合动力系统,通过杠杆模型分析系统的转速、扭矩和效率特性,可直观反映行星排的力学关系,便于快速评估基础构型的运动学性能,但难以量化再生功率传递条件,无法在拓扑设计阶段筛选出无效构型.为了进一步降低电机功率,通过添加一组行星排,将发动机和发电机连入参考构型,生成了三行星排的基础拓扑结构方案[16 ] .而针对混合动力履带车辆三行星排构型方案的优化设计,秦兆博等[17 -18 ] 改进了Peng等[19 ] 提出的矩阵建模方法,分析了基于3排行星传动的多模式拓扑构型,结果表明,3排行星传动的多模式拓扑构型能更好地保证发动机工作点的配置,维持发动机工作在高效率区.D矩阵法适用于计算机快速筛选,具有一定的盲目性,且计算量较大.综上所述,现有方法在单一功能(如几何连接、效率评估)上具有一定优势,但均存在一定的局限:其一,无法在构型设计阶段有效剔除冗余方案;其二,模型复杂度较高,导致工程应用受限. ...
混合动力履带车辆机电复合传动系统优化设计方法
1
2018
... 目前最常用的机电复合传动构型设计方法包括图论、杠杆法和D矩阵法等.如:Arnaudov等[5 ] 提出了一种新的基于杠杆模型的三端口图论模型,该模型可以分析行星齿轮机构的速度、扭矩和效率等,但计算较为复杂,效率较低;Chen等[6 ] 提出了一种基于几何结构的多级行星自动变速器设计方法,通过“效率”这一重要指标来筛选构型;Deng等[7 ] 针对单行星排的构型设计,提出了一种基于等效树图的模型,降低了构型的筛选难度,但是模型的表示方法较复杂,不能进一步拓展到多行星排的构型设计;Geng等[8 ] 提出了一种新的拓扑图,用于功率分流系统的构型设计,该方法能有效解决设计过程中机械结构的干涉问题;Gao等[9 -10 ] 提出了一种新型行星齿轮拓扑图表示方法,揭示了传动比与拓扑结构的关联关系,显著提升了传动系统的构型设计效率.拓扑图论法能清晰表达复杂行星排的连接关系,但现有拓扑模型侧重于几何连接,未与系统的运动学-动力学特征直接关联,并缺乏系统性的参数筛选准则,需结合人工经验剔除冗余构型.Yang等[11 ] 提出了一种改进的杠杆法,来设计具有高速比的最优构型,以满足高功率密度轮毂电机的需求;Kim等[12 -13 ] 提出了一种复合杠杆法,它是一种适用于寻找单行星排或两行星排混合动力系统最优构型方案的构型搜索方法;Song等[14 -15 ] 改进了复合杠杆法,在寻求最优的多模式构型中,从设计层面最大限度消除了冗余构型,减少了与优化相关的计算工作.杠杆法及其衍生方法适用于单行星排或两行星排混合动力系统,通过杠杆模型分析系统的转速、扭矩和效率特性,可直观反映行星排的力学关系,便于快速评估基础构型的运动学性能,但难以量化再生功率传递条件,无法在拓扑设计阶段筛选出无效构型.为了进一步降低电机功率,通过添加一组行星排,将发动机和发电机连入参考构型,生成了三行星排的基础拓扑结构方案[16 ] .而针对混合动力履带车辆三行星排构型方案的优化设计,秦兆博等[17 -18 ] 改进了Peng等[19 ] 提出的矩阵建模方法,分析了基于3排行星传动的多模式拓扑构型,结果表明,3排行星传动的多模式拓扑构型能更好地保证发动机工作点的配置,维持发动机工作在高效率区.D矩阵法适用于计算机快速筛选,具有一定的盲目性,且计算量较大.综上所述,现有方法在单一功能(如几何连接、效率评估)上具有一定优势,但均存在一定的局限:其一,无法在构型设计阶段有效剔除冗余方案;其二,模型复杂度较高,导致工程应用受限. ...
混合动力履带车辆机电复合传动系统优化设计方法
1
2018
... 目前最常用的机电复合传动构型设计方法包括图论、杠杆法和D矩阵法等.如:Arnaudov等[5 ] 提出了一种新的基于杠杆模型的三端口图论模型,该模型可以分析行星齿轮机构的速度、扭矩和效率等,但计算较为复杂,效率较低;Chen等[6 ] 提出了一种基于几何结构的多级行星自动变速器设计方法,通过“效率”这一重要指标来筛选构型;Deng等[7 ] 针对单行星排的构型设计,提出了一种基于等效树图的模型,降低了构型的筛选难度,但是模型的表示方法较复杂,不能进一步拓展到多行星排的构型设计;Geng等[8 ] 提出了一种新的拓扑图,用于功率分流系统的构型设计,该方法能有效解决设计过程中机械结构的干涉问题;Gao等[9 -10 ] 提出了一种新型行星齿轮拓扑图表示方法,揭示了传动比与拓扑结构的关联关系,显著提升了传动系统的构型设计效率.拓扑图论法能清晰表达复杂行星排的连接关系,但现有拓扑模型侧重于几何连接,未与系统的运动学-动力学特征直接关联,并缺乏系统性的参数筛选准则,需结合人工经验剔除冗余构型.Yang等[11 ] 提出了一种改进的杠杆法,来设计具有高速比的最优构型,以满足高功率密度轮毂电机的需求;Kim等[12 -13 ] 提出了一种复合杠杆法,它是一种适用于寻找单行星排或两行星排混合动力系统最优构型方案的构型搜索方法;Song等[14 -15 ] 改进了复合杠杆法,在寻求最优的多模式构型中,从设计层面最大限度消除了冗余构型,减少了与优化相关的计算工作.杠杆法及其衍生方法适用于单行星排或两行星排混合动力系统,通过杠杆模型分析系统的转速、扭矩和效率特性,可直观反映行星排的力学关系,便于快速评估基础构型的运动学性能,但难以量化再生功率传递条件,无法在拓扑设计阶段筛选出无效构型.为了进一步降低电机功率,通过添加一组行星排,将发动机和发电机连入参考构型,生成了三行星排的基础拓扑结构方案[16 ] .而针对混合动力履带车辆三行星排构型方案的优化设计,秦兆博等[17 -18 ] 改进了Peng等[19 ] 提出的矩阵建模方法,分析了基于3排行星传动的多模式拓扑构型,结果表明,3排行星传动的多模式拓扑构型能更好地保证发动机工作点的配置,维持发动机工作在高效率区.D矩阵法适用于计算机快速筛选,具有一定的盲目性,且计算量较大.综上所述,现有方法在单一功能(如几何连接、效率评估)上具有一定优势,但均存在一定的局限:其一,无法在构型设计阶段有效剔除冗余方案;其二,模型复杂度较高,导致工程应用受限. ...
Configuration design and control of hybrid tracked vehicle with three planetary gear sets
1
2021
... 目前最常用的机电复合传动构型设计方法包括图论、杠杆法和D矩阵法等.如:Arnaudov等[5 ] 提出了一种新的基于杠杆模型的三端口图论模型,该模型可以分析行星齿轮机构的速度、扭矩和效率等,但计算较为复杂,效率较低;Chen等[6 ] 提出了一种基于几何结构的多级行星自动变速器设计方法,通过“效率”这一重要指标来筛选构型;Deng等[7 ] 针对单行星排的构型设计,提出了一种基于等效树图的模型,降低了构型的筛选难度,但是模型的表示方法较复杂,不能进一步拓展到多行星排的构型设计;Geng等[8 ] 提出了一种新的拓扑图,用于功率分流系统的构型设计,该方法能有效解决设计过程中机械结构的干涉问题;Gao等[9 -10 ] 提出了一种新型行星齿轮拓扑图表示方法,揭示了传动比与拓扑结构的关联关系,显著提升了传动系统的构型设计效率.拓扑图论法能清晰表达复杂行星排的连接关系,但现有拓扑模型侧重于几何连接,未与系统的运动学-动力学特征直接关联,并缺乏系统性的参数筛选准则,需结合人工经验剔除冗余构型.Yang等[11 ] 提出了一种改进的杠杆法,来设计具有高速比的最优构型,以满足高功率密度轮毂电机的需求;Kim等[12 -13 ] 提出了一种复合杠杆法,它是一种适用于寻找单行星排或两行星排混合动力系统最优构型方案的构型搜索方法;Song等[14 -15 ] 改进了复合杠杆法,在寻求最优的多模式构型中,从设计层面最大限度消除了冗余构型,减少了与优化相关的计算工作.杠杆法及其衍生方法适用于单行星排或两行星排混合动力系统,通过杠杆模型分析系统的转速、扭矩和效率特性,可直观反映行星排的力学关系,便于快速评估基础构型的运动学性能,但难以量化再生功率传递条件,无法在拓扑设计阶段筛选出无效构型.为了进一步降低电机功率,通过添加一组行星排,将发动机和发电机连入参考构型,生成了三行星排的基础拓扑结构方案[16 ] .而针对混合动力履带车辆三行星排构型方案的优化设计,秦兆博等[17 -18 ] 改进了Peng等[19 ] 提出的矩阵建模方法,分析了基于3排行星传动的多模式拓扑构型,结果表明,3排行星传动的多模式拓扑构型能更好地保证发动机工作点的配置,维持发动机工作在高效率区.D矩阵法适用于计算机快速筛选,具有一定的盲目性,且计算量较大.综上所述,现有方法在单一功能(如几何连接、效率评估)上具有一定优势,但均存在一定的局限:其一,无法在构型设计阶段有效剔除冗余方案;其二,模型复杂度较高,导致工程应用受限. ...
Synthesis and analysis method for powertrain configuration of single motor hybrid electric vehicle
1
2020
... 目前最常用的机电复合传动构型设计方法包括图论、杠杆法和D矩阵法等.如:Arnaudov等[5 ] 提出了一种新的基于杠杆模型的三端口图论模型,该模型可以分析行星齿轮机构的速度、扭矩和效率等,但计算较为复杂,效率较低;Chen等[6 ] 提出了一种基于几何结构的多级行星自动变速器设计方法,通过“效率”这一重要指标来筛选构型;Deng等[7 ] 针对单行星排的构型设计,提出了一种基于等效树图的模型,降低了构型的筛选难度,但是模型的表示方法较复杂,不能进一步拓展到多行星排的构型设计;Geng等[8 ] 提出了一种新的拓扑图,用于功率分流系统的构型设计,该方法能有效解决设计过程中机械结构的干涉问题;Gao等[9 -10 ] 提出了一种新型行星齿轮拓扑图表示方法,揭示了传动比与拓扑结构的关联关系,显著提升了传动系统的构型设计效率.拓扑图论法能清晰表达复杂行星排的连接关系,但现有拓扑模型侧重于几何连接,未与系统的运动学-动力学特征直接关联,并缺乏系统性的参数筛选准则,需结合人工经验剔除冗余构型.Yang等[11 ] 提出了一种改进的杠杆法,来设计具有高速比的最优构型,以满足高功率密度轮毂电机的需求;Kim等[12 -13 ] 提出了一种复合杠杆法,它是一种适用于寻找单行星排或两行星排混合动力系统最优构型方案的构型搜索方法;Song等[14 -15 ] 改进了复合杠杆法,在寻求最优的多模式构型中,从设计层面最大限度消除了冗余构型,减少了与优化相关的计算工作.杠杆法及其衍生方法适用于单行星排或两行星排混合动力系统,通过杠杆模型分析系统的转速、扭矩和效率特性,可直观反映行星排的力学关系,便于快速评估基础构型的运动学性能,但难以量化再生功率传递条件,无法在拓扑设计阶段筛选出无效构型.为了进一步降低电机功率,通过添加一组行星排,将发动机和发电机连入参考构型,生成了三行星排的基础拓扑结构方案[16 ] .而针对混合动力履带车辆三行星排构型方案的优化设计,秦兆博等[17 -18 ] 改进了Peng等[19 ] 提出的矩阵建模方法,分析了基于3排行星传动的多模式拓扑构型,结果表明,3排行星传动的多模式拓扑构型能更好地保证发动机工作点的配置,维持发动机工作在高效率区.D矩阵法适用于计算机快速筛选,具有一定的盲目性,且计算量较大.综上所述,现有方法在单一功能(如几何连接、效率评估)上具有一定优势,但均存在一定的局限:其一,无法在构型设计阶段有效剔除冗余方案;其二,模型复杂度较高,导致工程应用受限. ...
履带车辆机电复合传动耦合机构数学特征的研究
1
2012
... 履带车辆直驶时,两侧的输入转速相同;转向时,一侧的输入转速升高,另一侧的输入转速降低.为了满足上述要求,耦合机构转速和转矩的自由度均为2.存在实数a 1 ,使得输入与输出的转速和转矩存在如下线性关系[20 ] : ...
履带车辆机电复合传动耦合机构数学特征的研究
1
2012
... 履带车辆直驶时,两侧的输入转速相同;转向时,一侧的输入转速升高,另一侧的输入转速降低.为了满足上述要求,耦合机构转速和转矩的自由度均为2.存在实数a 1 ,使得输入与输出的转速和转矩存在如下线性关系[20 ] : ...