新型桩架多级变幅机构运动学分析

doi:10.3785/j.issn.1006-754X.2024.14.06

新型桩架多级变幅机构运动学分析

邓华成^,¹, 康辉梅^,^,¹, 朱振新²^,³, 唐溪林¹

1.湖南师范大学工程与设计学院，湖南长沙 410081

2.山河智能装备股份有限公司国家级企业技术中心，湖南长沙 410100

3.地下工程装备湖南省工程研究中心，湖南长沙 410100

Kinematics analysis of novel multi-stage luffing mechanism of piling rig

DENG Huacheng^,¹, KANG Huimei^,^,¹, ZHU Zhenxin²^,³, TANG Xilin¹

1.College of Engineering and Design, Hunan Normal University, Changsha 410081, China

2.National Enterprise Technology Center, Sunward Intelligent Equipment Co. , Ltd. , Changsha 410100, China

3.Hunan Provincial Engineering Research Center for Underground Engineering Equipment, Changsha 410100, China

通讯作者: 康辉梅（1975—），女，副教授，硕士生导师，博士，从事机构动力学分析及优化设计等研究，E-mail: plum_007@sina.com, https://orcid.org/0009-0000-2689-2682

收稿日期: 2024-04-17 修回日期: 2024-05-20

基金资助:

国家自然科学基金资助项目. 51775185

Received: 2024-04-17 Revised: 2024-05-20

作者简介 About authors

邓华成（2001—），男，硕士生，从事机构动力学及仿真研究，E-mail:3046371611@qq.com , E-mail：3046371611@qq.com

摘要

为了改善桩架的受力情况，提出了一种新型桩架多级变幅机构。该机构能有效减小前液压缸的弯矩，提高桩架在作业时的稳定性。首先，建立了空间坐标系，分析了该机构空间位置的正解和反解，继而推导出速度雅可比矩阵和加速度海森矩阵，得到了该机构的运动学模型；其次，根据变幅条件设定了机构参数和液压缸位移函数后，采用MATLAB软件分析了机构的运动特性，确定了液压缸收缩动作的衔接方式，并进一步分析了机构参数对变幅运动的影响；最后，将机构变幅运动的ADAMS仿真结果与理论分析结果进行对比。结果表明：所构建的多级变幅机构的运动学模型正确；机构可以平稳地将立柱从水平变幅至竖直，变幅过程中滑块始终上移，变幅后连杆与前液压缸垂直；在前液压缸减速收缩的同时进行后液压缸加速收缩有利于变幅平稳。研究结果可为新型桩架多级变幅机构的动力学分析和优化设计提供参考。

关键词： 桩架 ; 变幅机构 ; 运动学分析 ; 参数设计 ; 仿真

Abstract

In order to improve the stress condition of piling rig, a novel multi-stage luffing mechanism of piling rig was proposed. The mechanism could effectively reduce the bending moment of the front hydraulic cylinder and improve the stability of piling rig during operation. Firstly, the spatial coordinate system was established, and the forward and inverse solutions of the spatial position of the mechanism were analyzed, and then the velocity Jacobian matrix and acceleration Hessian matrix were derived, and the kinematics model of the mechanism was obtained. Secondly, after the mechanism parameters and the displacement function of the hydraulic cylinder were set according to the luffing conditions, the motion characteristics of the mechanism were analyzed using MATLAB software, the connection mode of the hydraulic cylinder contraction was determined, and the influence of the mechanism parameters on the luffing motion was further analyzed. Finally, the ADAMS simulation results of luffing motion of the mechanism were compared with the theoretical analysis results. The results showed that the kinematics model of the multi-stage luffing mechanism was correct. The mechanism could steadily luff the column from horizontal to vertical, the slider always moved upward during the luffing process, and the connecting rod after luffing was vertical to the front hydraulic cylinder. Accelerating contraction of the rear hydraulic cylinder while decelerating contraction of the front hydraulic cylinder was conducive to stable luffing. The research results can provide a reference for the dynamics analysis and optimal design of the novel multi-stage luffing mechanism of piling rig.

Keywords： piling rig ; luffing mechanism ; kinematics analysis ; parameter design ; simulation

PDF (2123KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

邓华成, 康辉梅, 朱振新, 唐溪林. 新型桩架多级变幅机构运动学分析[J]. 工程设计学报, 2024, 31(6): 784-792 doi:10.3785/j.issn.1006-754X.2024.14.06

DENG Huacheng, KANG Huimei, ZHU Zhenxin, TANG Xilin. Kinematics analysis of novel multi-stage luffing mechanism of piling rig[J]. Chinese Journal of Engineering Design, 2024, 31(6): 784-792 doi:10.3785/j.issn.1006-754X.2024.14.06

桩架是桩基础施工中常用的工程装备^[1-3]，可作为母机搭载柴油锤、液压锤、套管钻机及长螺旋钻机等装置进行多种工法施工。在基础工程建设中，桩架承受着多种复杂载荷，整机稳定性及其零件的受力状况会对其工作寿命和施工效率造成很大影响。因此，许多学者对桩架的受力和稳定性进行了研究。如：张希恒等^[4-5]分析了桩架悬挂长螺旋钻机时立柱的受力状况，并讨论了斜撑的支撑位置对立柱稳定性的影响；曾礼平^[6]建立了三支点式履带打桩机的三维CAD模型，并进行了立柱变幅过程的动力学仿真、桩架结构的分析及优化设计；刘振东等^[7]分析了在桩架立柱的起架过程中起架油缸铰点的力变化情况，得到了起架油缸铰座的应力云图；安治鹏^[8]进行了桩架立柱斜撑结构的有限元建模与静态特性仿真，并对该结构进行屈曲分析，研究了其稳定性。以上研究主要集中在桩架构件强度的有限元分析上，没有设计有效的结构来提高桩架的稳定性。

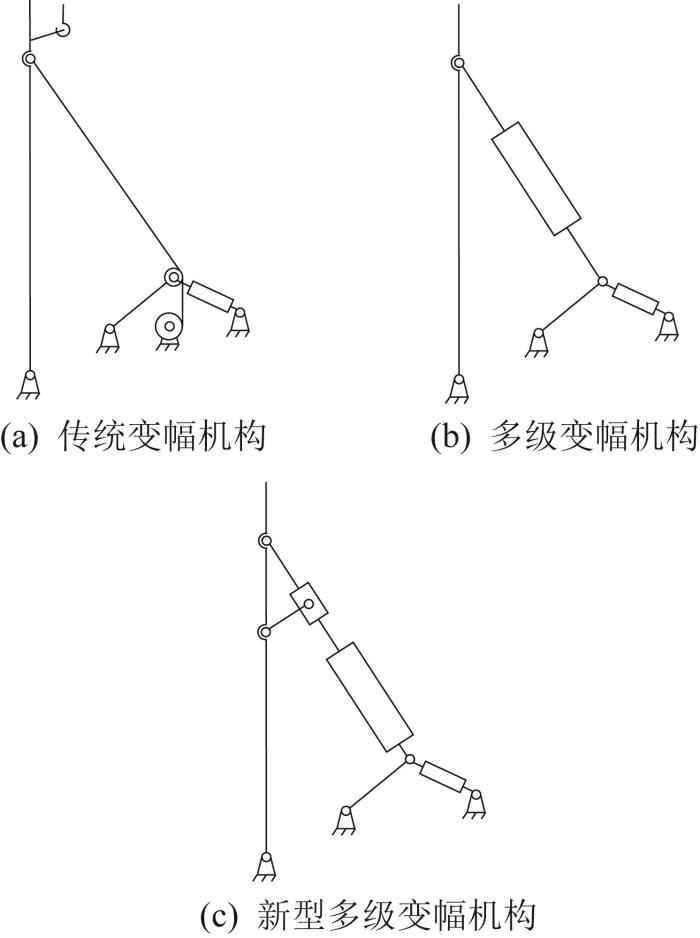
变幅机构是桩架的重要组成部分，起到调整立柱角度和支撑立柱的作用，对桩架的立桅便捷性和作业稳定性有重要影响。传统变幅机构的变幅范围有限，拆卸解体和重新安装都需要吊机辅助，无法进行自主立桅、倒桅作业。因此，钱奂云等^[9]提出了桩架多级变幅机构，有效消除了传统变幅机构变幅范围有限的弊端：采用2组液压缸代替传统的桩架斜撑，通过前、后液压缸两级变幅使立柱可以自主进行从水平到竖直的运动，解决了桩架立桅安全性低且操作繁琐的问题；顾林坤等^[10]对桩架多级变幅机构进行了参数设计和运动仿真，得到了一组能满足工程设计要求的机构参数；曹博等^[11]将桩架多级变幅机构简化为五杆机构，并建立了其动力学模型；朱振新等^[12-13]分别采用拉格朗日法和牛顿欧拉法对桩架多级变幅机构进行动力学分析，得到了前液压缸先收缩、后液压缸再收缩的变幅方式具有更优力学性能的结论。以上分析都将桩架多级变幅机构的空间机构转化为平面机构，所得结果与实际有较大差距。同时，当桩架受到水平方向的作用力时，桩架多级变幅机构中的2个前液压缸因两端铰点距离过长而产生较大弯矩。为了防止变形，前液压缸设计得比较粗笨，从而增大了桩架变幅的能量消耗。

为了实现桩架自主变幅，改善桩架在施工时的受力情况，提高桩架变幅机构的支撑稳定性，本文提出了一种新型桩架多级变幅机构。首先，建立了该机构的运动学模型，得到运动学解析解，以研究机构在变幅过程中的运动学特性^[14-17]和运动可行性；其次，设置变幅条件，进行机构参数设计，并利用 MATLAB软件进行分析和计算，以确定前、后液压缸收缩动作的衔接方式和机构参数对变幅运动可行性的影响；最后，利用ADAMS软件仿真得到该机构的速度、加速度、位置等曲线，来验证运动学模型的正确性。

1 新型桩架多级变幅机构的组成及工作原理

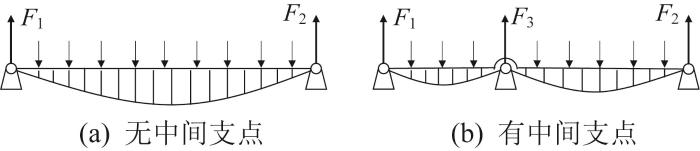
桩架变幅机构如图1所示。桩架多级变幅机构以前、后液压缸的收缩动作来代替传统变幅机构吊机和卷扬机的动作，无需外力辅助便可自主变幅。新型多级变幅机构在多级变幅机构的立柱和前液压缸之间添加了连杆和滑块，在前液压缸两端铰点之间增加了一个支点，减小了跨距的长度，从而显著减小前液压缸的弯矩，提高了桩架的稳定性。构件的弯矩如图2所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 桩架变幅机构示意图

Fig.1 Schematic diagram of luffing mechanism of piling rig

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 构件弯矩示意图

Fig.2 Schematic diagram of bending moment of component

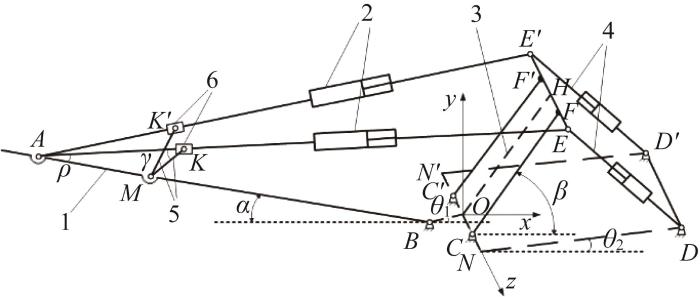
新型桩架多级变幅机构呈左右两侧对称分布，其运动简图如图3所示。机构主要由立柱、前液压缸、变幅架、后液压缸、连杆和滑块等组成，其中主动件分别为前液压缸和后液压缸。机架后侧分别铰接2个后液压缸筒于 $D$ 、 $D^{'}$ 两点，2条后液压缸活塞杆分别铰接变幅架于 $E$ 、 $E^{'}$ 两点；机架前侧铰接立柱于 $B$ 点，立柱铰接2个前液压缸筒于 $A$ 点，2条前液压缸活塞杆分别铰接变幅架于 $E$ 、 $E^{'}$ 两点；2条连杆一端均铰接于立柱的 $M$ 点，另一端分别铰接两滑块于 $K$ 、 $K^{'}$ 点，滑块可在对应的前液压缸筒上滑动。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 新型桩架多级变幅机构运动简图

1—立柱；2—前液压缸；3—变幅架；4—后液压缸；5—连杆；6—滑块。

Fig.3 Motion diagram of novel multi-stage luffing mechanism of piling rig

整个变幅过程分2步完成。第1步，后液压缸静止不动，通过2个前液压缸的同步收缩带动立柱绕铰点 $B$ 转动一定角度；第2步，前液压缸静止不动，通过2个后液压缸的同步收缩驱动变幅架转动，变幅架带动立柱继续转动，最终实现立柱从水平到竖直的变幅运动。立柱、前液压缸、连杆和滑块组成了2套导杆滑块机构，在变幅过程中通过立柱与前液压缸夹角的变化，驱动连杆绕铰点 $M$ 转动，滑块沿前液压缸方向移动。待立柱竖直并静止后，其上搭载的工作装置开始作业。

2 新型桩架多级变幅机构运动学模型的建立

如图3所示，以 $C C^{'}$ 的中点 $O$ 为原点，机构中间纵平面为 $x O y$ 面， $O C$ 为 $z$ 轴，建立空间直角坐标系O-xyz。定义点A、B之间的长度l_AB =l₁，l_CF =l₂，l_MK =l₃，l_OB =a₁，l_ND =a₂，l_ON = l_HE =a₃，l_AM =a₄；前液压缸长度l_AE =d₁，后液压缸长度l_DE = d₂；滑块到铰点 $A$ 的距离为 $s$ ；立柱与水平方向的夹角为 $α$ ，变幅架与水平方向的夹角为 $β$ ，立柱与前液压缸的夹角为 $ρ$ ，连杆与前液压缸的夹角为 $γ$ 。其中： $d_{1}$ 、 $d_{2}$ 为输入量， $α$ 、 $β$ 、 $ρ$ 、 $s$ 、 $γ$ 为输出量。

2.1　位置正解

求位置正解是通过已知的前、后液压缸长度 $d_{1}$ 和 $d_{2}$ ，求解机构的相关位姿参数 $α$ 、 $β$ 、 $ρ$ 、 $s$ 和 $γ$ 。

机构一侧各点的坐标可表示为：

[\begin{array}{l} x_{A} \\ y_{A} \\ z_{A} \end{array}] = [\begin{array}{l} - a_{1} c o s θ_{1} - l_{1} c o s α \\ - a_{1} s i n θ_{1} + l_{1} s i n α \\ 0 \end{array}]

，

[\begin{array}{l} x_{B} \\ y_{B} \\ z_{B} \end{array}] = [\begin{array}{l} - a_{1} c o s θ_{1} \\ - a_{1} s i n θ_{1} \\ 0 \end{array}]

[\begin{array}{l} x_{D} \\ y_{D} \\ z_{D} \end{array}] = [\begin{array}{l} a_{2} c o s θ_{2} \\ a_{2} s i n θ_{2} \\ a_{3} \end{array}]

，

[\begin{array}{l} x_{E} \\ y_{E} \\ z_{E} \end{array}] = [\begin{array}{l} l_{2} c o s β \\ l_{2} s i n β \\ a_{3} \end{array}]

[\begin{array}{l} x_{H} \\ y_{H} \\ z_{H} \end{array}] = [\begin{array}{l} l_{2} c o s β \\ l_{2} s i n β \\ 0 \end{array}]

经计算，可求得：

β = θ_{2} + a r c c o s (\frac{l_{2}^{2} + a_{2}^{2} - d_{2}^{2}}{2 l_{2} a_{2}})

(1)

l_{B H} = {[{(l_{2} c o s β + a_{1} c o s θ_{1})}^{2} + {(l_{2} s i n β + a_{1} s i n θ_{1})}^{2}]}^{\frac{1}{2}}

(2)

l_{B E} = {(l_{B H}^{2} + a_{3}^{2})}^{\frac{1}{2}}

(3)

∠ A B H = a r c c o s (\frac{l_{1}^{2} + l_{B H}^{2} - d_{1}^{2} + a_{3}^{2}}{2 l_{1} l_{B H}})

(4)

∠ H B O = a r c c o s (\frac{a_{1}^{2} + l_{B H}^{2} - l_{2}^{2}}{2 a_{1} l_{B H}})

(5)

α = π - θ_{1} - ∠ A B H - ∠ H B O

(6)

ρ = a r c c o s (\frac{l_{1}^{2} + d_{1}^{2} - l_{B E}^{2}}{2 l_{1} d_{1}})

(7)

s = a_{4} c o s ρ + \sqrt[]{l_{3}^{2} - a_{4}^{2} s i n^{2} ρ}

(8)

γ = a r c s i n (\frac{a_{4} s i n ρ}{l_{3}})

(9)

2.2　位置反解

求位置反解是根据输出量 $α$ 和 $β$ ，反向求解输入量 $d_{1}$ 和 $d_{2}$ 。

由模长公式，可得：

\begin{array}{l} d_{1} = [(l_{2} c o s β + a_{1} c o s θ_{1} + l_{1} {c o s α)}^{2} + \\ {(l_{2} s i n β + a_{1} s i n θ_{1} - l_{1} {s i n α)}^{2} + a_{3}^{2}]}^{\frac{1}{2}} \end{array}

(10)

d_{2} = {[(l_{2} c o s β - a_{2} c o s θ_{2})^{2} + (l_{2} s i n β - a_{2} s i n θ_{2})^{2}]}^{\frac{1}{2}}

(11)

2.3　速度雅可比矩阵

速度雅可比矩阵描述了输出与输入速度之间的映射关系，可表示为：

\dot{p} = J \dot{q}

(12)

式中： J 为 $5 \times 2$ 型雅可比矩阵； $\dot{p} = {[\dot{α} \dot{β} \dot{ρ} \dot{γ} \dot{s}]}^{T}$ ，为输出速度矢量； $\dot{q} = {[{\dot{d}}_{1} {\dot{d}}_{2}]}^{T}$ ，为输入速度矢量。

将式(10)对时间求导，可得：

\dot{α} = p_{1} {\dot{d}}_{1} + p_{2} \dot{β}

(13)

式中： $p_{1} = \frac{g_{1}}{g_{2}}$ ， $p_{2} = \frac{g_{3}}{g_{2}}$ ， $g_{1} = d_{1}$

g_{2} = - l_{1} l_{2} s i n (α + β) - a_{1} l_{1} s i n (α + θ_{1})

g_{3} = l_{1} l_{2} s i n (α + β) + a_{1} l_{2} s i n (β - θ_{1})

将式(11)对时间求导，可得：

\dot{β} = p_{3} {\dot{d}}_{2}

(14)

式中： $p_{3} = \frac{g_{4}}{g_{5}}$ ， $g_{4} = d_{2}$ ， $g_{5} = a_{2} l_{2} s i n (β - θ_{2})$ 。

将式(7)对时间求导，可得：

\dot{ρ} = p_{4} \dot{α} + p_{5} \dot{β} + p_{6} {\dot{d}}_{1}

(15)

式中： $p_{4} = \frac{g_{7}}{g_{6}}$ ， $p_{5} = \frac{g_{8}}{g_{6}}$ ， $p_{6} = \frac{g_{9}}{g_{6}}$ ， $g_{6} = l_{1} d_{1} s i n ρ$

g_{7} = l_{1} l_{2} s i n (α + β) + a_{1} l_{1} s i n (α + θ_{1})

g_{8} = l_{1} l_{2} s i n (α + β)

，

g_{9} = l_{1} c o s ρ

将式(8)对时间求导，可得：

\dot{s} = p_{7} \dot{ρ}

(16)

式中： $p_{7} = \frac{g_{11}}{g_{10}}$ ， $g_{10} = a_{4} c o s ρ - s$ ， $g_{11} = a_{4} s s i n ρ$ 。

将式(9)对时间求导，可得：

\dot{γ} = p_{8} \dot{ρ}

(17)

式中： $p_{8} = \frac{g_{13}}{g_{12}}$ ， $g_{12} = l_{3} c o s γ$ ， $g_{13} = a_{4} c o s ρ$ 。

由式(13)至式(17)可知， $\dot{β}$ 由 ${\dot{d}}_{2}$ 确定， $\dot{α}$ 由 ${\dot{d}}_{1}$ 、 $\dot{β}$ 确定， $\dot{ρ}$ 由 $\dot{α}$ 、 $\dot{β}$ 、 ${\dot{d}}_{1}$ 确定， $\dot{s}$ 和 $\dot{γ}$ 由 $\dot{ρ}$ 确定，最后 $\dot{α}$ 、 $\dot{β}$ 、 $\dot{ρ}$ 、 $\dot{s}$ 、 $\dot{γ}$ 都可递推成由 ${\dot{d}}_{1}$ 和 ${\dot{d}}_{2}$ 确定。将由 ${\dot{d}}_{1}$ 和 ${\dot{d}}_{2}$ 表示的 $\dot{α}$ 、 $\dot{β}$ 、 $\dot{ρ}$ 、 $\dot{s}$ 、 $\dot{γ}$ 代入式(12)，可解得雅可比矩阵方程为：

[\begin{array}{l} \dot{α} \\ \dot{β} \\ \dot{ρ} \\ \dot{s} \\ \dot{γ} \end{array}] = J [\begin{array}{l} {\dot{d}}_{1} \\ {\dot{d}}_{2} \end{array}] = [\begin{array}{l} j_{11} j_{12} \\ j_{21} j_{22} \\ j_{31} j_{32} \\ j_{41} j_{42} \\ j_{51} j_{52} \end{array}] [\begin{array}{l} {\dot{d}}_{1} \\ {\dot{d}}_{2} \end{array}]

(18)

式中： $j_{11} = p_{1}$ ， $j_{12} = p_{2} p_{3}$ ， $j_{21} = 0$ ， $j_{22} = p_{3}$

j_{31} = p_{1} p_{4} + p_{6}

，

j_{32} = p_{3} p_{5} + p_{2} p_{3} p_{4}

j_{41} = p_{6} p_{7} + p_{1} p_{4} p_{7}

，

j_{42} = p_{3} p_{5} p_{7} + p_{2} p_{3} p_{4} p_{7}

j_{51} = p_{6} p_{8} + p_{1} p_{4} p_{8}

，

j_{52} = p_{3} p_{5} p_{8} + p_{_{2}} p_{3} p_{4} p_{8}

2.4　加速度海森矩阵

加速度海森矩阵描述了输出与输入加速度之间的映射关系，可表示为：

\ddot{p} = J \ddot{q} + {\dot{q}}^{T} * H \dot{q}

(19)

式中： $H$ 为 $2 \times 2 \times 2$ 型海森矩阵； $\ddot{p} = {[\ddot{α} \ddot{β} \ddot{ρ} \ddot{s} \ddot{γ}]}^{T}$ ，为输出加速度矢量； $\ddot{q} = {[{\ddot{d}}_{1} {\ddot{d}}_{2}]}^{T}$ ，为输入加速度矢量。

将式(12)对时间求导并结合式(19)，可得：

\dot{J} = {\dot{q}}^{T} * H

(20)

式中： $\dot{J}$ 为 $J$ 的导数。

$\dot{J}$ 由 $J$ 求导得到，可表示为：

\begin{array}{l} [\begin{array}{l} {\dot{j}}_{11} {\dot{j}}_{12} \\ {\dot{j}}_{21} {\dot{j}}_{22} \\ {\dot{j}}_{31} {\dot{j}}_{32} \\ {\dot{j}}_{41} {\dot{j}}_{42} \\ {\dot{j}}_{51} {\dot{j}}_{52} \end{array}] = \\ [\begin{matrix} {\dot{p}}_{1} & {\dot{p}}_{2} p_{3} + p_{2} {\dot{p}}_{3} \\ 0 & {\dot{p}}_{3} \\ {\dot{p}}_{6} + {\dot{p}}_{1} p_{4} + p_{1} {\dot{p}}_{4} & \begin{array}{l} {\dot{p}}_{3} p_{5} + p_{3} {\dot{p}}_{5} + {\dot{p}}_{2} p_{3} p_{4} + \\ p_{2} {\dot{p}}_{3} p_{4} + p_{2} p_{3} {\dot{p}}_{4} \end{array} \\ {\dot{j}}_{31} p_{7} + j_{31} {\dot{p}}_{7} & {\dot{j}}_{32} p_{7} + j_{32} {\dot{p}}_{7} \\ {\dot{j}}_{31} p_{8} + j_{31} {\dot{p}}_{8} & {\dot{j}}_{32} p_{8} + j_{32} {\dot{p}}_{8} \end{matrix}] \end{array}

(21)

式中： ${\dot{p}}_{i} (i = 1, 2, \dots, 8)$ 为 $p_{i}$ 的导数。

${\dot{p}}_{i}$ 由 $p_{i}$ 求导得到，可表示为：

{\dot{p}}_{i} = f_{2 i - 1} {\dot{d}}_{1} + f_{2 i} {\dot{d}}_{2}

(22)

式中： $f_{1} = \frac{g_{2} - k_{1} g_{1} j_{11}}{g_{2}^{2}}$

f_{2} = \frac{- (k_{2} j_{22} + k_{1} j_{12}) g_{1}}{g_{2}^{2}}

f_{3} = \frac{- k_{1} g_{3} j_{11} + k_{3} g_{2} j_{11}}{g_{2}^{2}}

f_{4} = \frac{(k_{3} g_{2} - k_{1} g_{3}) j_{12} + (k_{4} g_{2} - k_{2} g_{3}) j_{22}}{g_{2}^{2}}

f_{5} = 0

，

f_{6} = \frac{g_{5} - k_{5} g_{4} j_{22}}{g_{5}^{2}}

f_{7} = \frac{k_{6} g_{6} j_{11} - k_{7} g_{7} j_{31} - k_{8} g_{7}}{g_{6}^{2}}

f_{8} = \frac{k_{6} g_{6} j_{12} + k_{3} g_{6} j_{22} - k_{7} g_{7} j_{32}}{g_{6}^{2}}

f_{9} = \frac{k_{3} g_{6} j_{11} - k_{7} g_{8} j_{31} - k_{8} g_{8}}{g_{6}^{2}}

f_{10} = \frac{k_{3} g_{6} (j_{12} + j_{22}) - k_{7} g_{8} j_{32}}{g_{6}^{2}}

f_{11} = \frac{k_{9} g_{6} j_{31} - k_{7} g_{9} j_{31} - k_{8} g_{9}}{g_{6}^{2}}

f_{12} = \frac{(k_{9} g_{6} - k_{9} g_{9}) j_{32}}{g_{6}^{2}}

f_{13} = \frac{g_{10} (k_{11} j_{31} - k_{10} j_{41}) - g_{11} (k_{10} j_{31} - j_{41})}{g_{10}^{2}}

f_{14} = \frac{g_{10} (k_{11} j_{32} - k_{10} j_{42}) - g_{11} (k_{10} j_{32} - j_{42})}{g_{10}^{2}}

f_{15} = \frac{k_{10} g_{12} j_{31} - k_{12} g_{13} j_{51}}{g_{12}^{2}}

f_{16} = \frac{k_{10} g_{12} j_{32} - k_{12} g_{13} j_{52}}{g_{12}^{2}}

k_{1} = - l_{1} l_{2} c o s (α + β) - a_{1} l_{1} c o s (α + θ_{1})

k_{2} = - l_{1} l_{2} c o s (α + β)

，

k_{3} = l_{1} l_{2} c o s (α + β)

k_{4} = l_{1} l_{2} c o s (α + β) + a_{1} l_{2} c o s (β - θ_{1})

k_{5} = a_{2} l_{2} c o s (β - θ_{2})

k_{6} = l_{1} l_{2} c o s (α + β) + a_{1} l_{1} c o s (α + θ_{1})

k_{7} = l_{1} d_{1} c o s ρ

，

k_{8} = l_{1} s i n ρ

k_{9} = - l_{1} s i n ρ

，

k_{10} = - a_{4} s i n ρ

k_{11} = a_{4} s c o s ρ

，

k_{12} = - l_{3} s i n γ

将式(22)代入式(21)得到 $\dot{J}$ ，将 $\dot{J}$ 代入式(20)得到 H，再将 H 代入式(19)得到海森矩阵方程，为：

[\begin{array}{l} \ddot{α} \\ \ddot{β} \\ \ddot{ρ} \\ \ddot{s} \\ \ddot{γ} \end{array}] = [\begin{array}{l} j_{11} j_{12} \\ j_{21} j_{22} \\ j_{31} j_{32} \\ j_{41} j_{42} \\ j_{51} j_{52} \end{array}] [\begin{array}{l} {\ddot{d}}_{1} \\ {\ddot{d}}_{2} \end{array}] + [{\dot{d}}_{1} {\dot{d}}_{2}] * [\begin{array}{l} (\begin{array}{l} h_{111} h_{112} \\ h_{121} h_{122} \end{array}) \\ (\begin{array}{l} h_{211} h_{212} \\ h_{221} h_{222} \end{array}) \\ (\begin{array}{l} h_{311} h_{312} \\ h_{321} h_{322} \end{array}) \\ (\begin{array}{l} h_{411} h_{412} \\ h_{421} h_{422} \end{array}) \\ (\begin{array}{l} h_{511} h_{512} \\ h_{521} h_{522} \end{array}) \end{array}] [\begin{array}{l} {\dot{d}}_{1} \\ {\dot{d}}_{2} \end{array}]

(23)

式中： $h_{111} = f_{1}$ , $h_{112} = f_{2}$ , $h_{121} = p_{3} f_{3}$ , $h_{122} = p_{3} f_{4} + p_{2} f_{5}$

h_{211} = 0

h_{212} = 0

h_{221} = f_{5}

h_{222} = f_{6}

h_{311} = f_{11} + p_{4} f_{1} + p_{1} f_{7}

h_{312} = f_{12} + p_{4} f_{2} + p_{1} f_{8}

h_{321} = p_{3} f_{9} + p_{3} p_{4} f_{3} + p_{2} p_{3} f_{7}

h_{322} = p_{5} f_{6} + p_{3} f_{10} + p_{3} p_{4} f_{4} + p_{2} p_{4} f_{6} + p_{2} p_{3} f_{8}

h_{411} = p_{7} h_{311} + f_{13} j_{31}

h_{412} = p_{7} h_{312} + f_{14} j_{31}

h_{421} = p_{7} h_{321} + f_{13} j_{32}

h_{422} = p_{7} h_{322} + f_{14} j_{32}

h_{511} = p_{8} h_{311} + f_{15} j_{31}

h_{512} = p_{8} h_{312} + f_{16} j_{31}

h_{521} = p_{8} h_{321} + f_{15} j_{32}

h_{522} = p_{8} h_{322} + f_{16} j_{32}

3 工程案例分析

3.1　变幅条件分析

新型桩架多级变幅机构的变幅条件如下。

条件1：为了保证变幅运动流畅，滑块的上移需持续，即滑块到 $A$ 点的距离 $s$ 单调递减。下面分别分析在前液压缸收缩和后液压缸收缩过程中 $s$ 的变化。

当前液压缸收缩时， $d_{1}$ 减小，l_BE 不变，由式(7)可知， $ρ$ 先增后减。当 $∠ A E B \leq 90 °$ 时， $ρ$ 递增；当 $∠ A E B > 90 °$ 时， $ρ$ 递减。由式(8)可知， $ρ$ 增大，则 $s$ 减小。因此，为了保证 $s$ 单调递减，在前液压缸收缩过程中需满足：

∠ A E B \leq 90 °

(24)

当后液压缸收缩时， $β$ 减小，由式(2)可知，l_BH 先增后减。当 $β \geq θ_{1}$ 时，l_BH 递增；当 $β < θ_{1}$ 时，l_BH 递减。由式(3)可知，l_BH 增大，则 $l_{B E}$ 增大。由式(7)可知， $l_{B E}$ 增大，则 $ρ$ 增大。由式(8)可知， $ρ$ 增大，则 $s$ 减小。因此，为了保证 $s$ 单调递减，在后液压缸收缩过程中需满足：

β \geq θ_{1}

(25)

条件2：2次变幅完成后，立柱从水平转成竖直，则在整个变幅过程中立柱最大可转动角度 $α_{m a x}$ 需满足：

α_{m a x} \geq 90 °

(26)

当立柱转动了 $α_{m a x}$ 时，在保证滑块运动方向不变的前提下，前、后液压缸需收缩到底。当前液压缸收缩到底时，由式(24)可知， $∠ A E B = 90 °$ ，则可由勾股定理得到前液压缸的最短长度 $d_{1}^{'}$ 。当后液压缸收缩到底时，由式(25)知， $β = θ_{1}$ ，则 $∠ H B O = 0$ ，将 $d_{1}^{'}$ 代入式(4)得到 $∠ A B H$ ，再将 $∠ A B H$ 代入式(6)，即可得立柱的最大可转动角度 $α_{m a x}$ 。

条件3：当立柱竖直时，连杆应与前液压缸垂直，即立柱竖直时连杆与前液压缸的夹角 $γ^{'}$ 需满足：

γ^{'} = 90 °

(27)

条件4：在前液压缸收缩停止和后液压缸收缩开始的衔接过程中，前、后液压缸的载荷波动较小，即衔接时多级变幅机构的加速度较小。

3.2　机构参数设定

根据工程实际要求，新型桩架多级变幅机构的参数如表1所示。表中： $α$ ₀为立柱与水平方向的初始夹角， $β$ ₀为变幅架与水平方向的初始夹角。

表1 多级变幅机构参数

Table1 Parameters of multi-stage luffing mechanism

参数	数值
$l_{1}$ /m	16.8
$l_{2}$ /m	3.054
$l_{3}$ /m	1.430 73
$a_{1}$ /m	1.276 79
$a_{2}$ /m	5.622 81
$a_{3}$ /m	2
$a_{4}$ /m	5.04
$α$ ₀/(°)	0
$β$ ₀/(°)	67
$θ_{1}$ /(°)	16.38
$θ_{2}$ /(°)	5.17

新窗口打开| 下载CSV

设定前、后液压缸匀速运动的速度分别为 $v_{1} = 46.8 m m / s$ ， $v_{2} = 42.6 m m / s$ ，加速过程和减速过程的平均速度均是其匀速过程速度的一半，则液压缸的位移函数可表示为：

d_{1} = \{\begin{array}{l} d_{01} - \frac{2}{3} v_{1} {t_{1}}^{3}, 0 < t_{1} \leq 0.5 s \\ d_{01} + \frac{2}{3} v_{1} (t_{1} {- 1)}^{3} - v_{1} t_{1} + \frac{v_{1}}{2}, 0.5 < t_{1} \leq 1 s \\ d_{01} - v_{1} t_{1} + \frac{v_{1}}{2}, 1 < t_{1} \leq 72 s \\ d_{01} + \frac{2}{3} v_{1} (t_{1} {- 72)}^{3} - v_{1} t_{1} + \frac{v_{1}}{2}, 72 < t_{1} \leq 72.5 s \\ d_{01} - \frac{2}{3} v_{1} (t_{1} {- 73)}^{3} - 72 v_{1}, 72.5 < t_{1} \leq 73 s \end{array}

(28)

d_{2} = \{\begin{array}{l} d_{02} - \frac{2}{3} v_{2} {t_{2}}^{3}, 0 < t_{2} \leq 0.5 s \\ d_{02} + \frac{2}{3} v_{2} (t_{2} {- 1)}^{3} - v_{2} t_{2} + \frac{v_{2}}{2}, 0.5 < t_{2} \leq 1 s \\ d_{02} - v_{2} t_{2} + \frac{v_{2}}{2}, 1 < t_{2} \leq 53 s \\ d_{02} + \frac{2}{3} v_{2} (t_{2} {- 53)}^{3} - v_{2} t_{2} + \frac{v_{2}}{2}, 53 < t_{2} \leq 53.5 s \\ d_{02} - \frac{2}{3} v_{2} (t_{2} {- 54)}^{3} - 53 v_{2}, 53.5 < t_{2} \leq 54 s \end{array}

(29)

式中： $d_{01}$ 为前液压缸变幅前长度， $d_{02}$ 为后液压缸变幅前长度， $t_{1}$ 为前液压缸收缩时间， $t_{2}$ 为后液压缸收缩时间。

3.3　MATLAB仿真分析

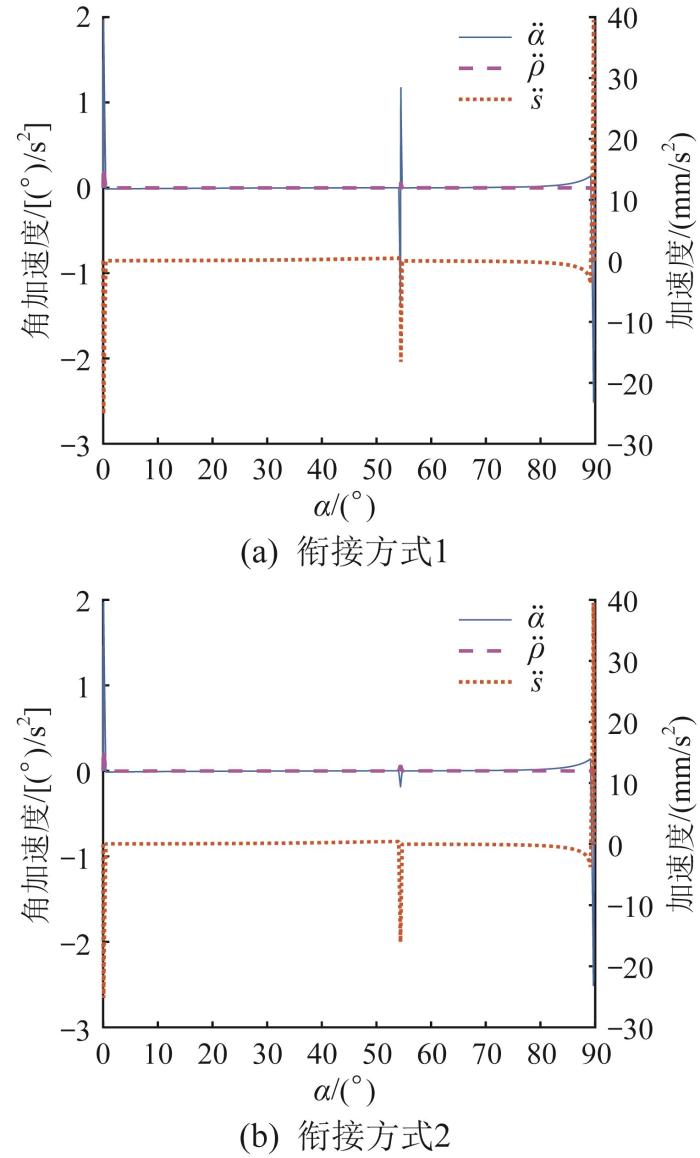
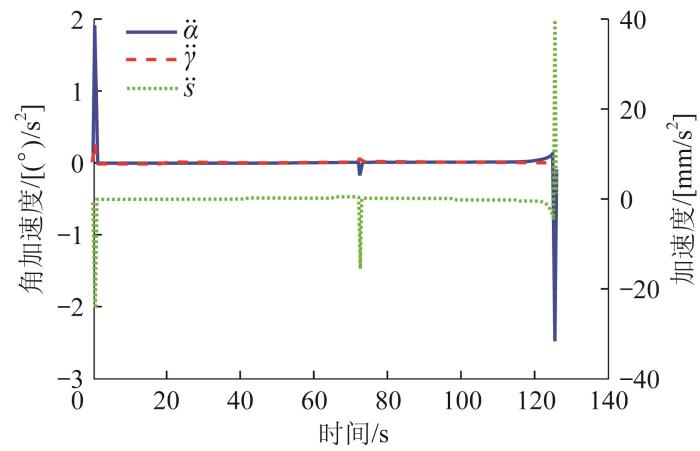
多级变幅机构前、后液压缸的动作衔接方式有2种，前液压缸收缩停止后再进行后液压缸收缩为衔接方式1，在前液压缸减速收缩的过程中进行后液压缸加速收缩为衔接方式2。基于上述多级变幅机构的运动学方程和液压缸位移函数进行MATLAB编程计算，可得多级变幅机构的加速度和角加速度曲线，如图4所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 多级变幅机构加速度和角加速度曲线

Fig.4 Acceleration and angular acceleration curves of multi-stage luffing mechanism

由图可知： $\ddot{α}$ 、 $\ddot{ρ}$ 、 $\ddot{s}$ 都在 $α$ = $0$ , $54 °$ , $90 °$ 时发生了突变，这是因为此时发生了前、后液压缸的启停；当 $α$ ≈ $54 °$ 时，衔接方式1下 $\ddot{α}$ 的突变大于衔接方式2，这是因为此时在衔接方式2下同时进行前液压缸停止和后液压缸启动，2种运动的突变部分抵消，所以在衔接方式1下立柱的角加速度较大；前液压缸的角加速度由 $\ddot{α}$ 和 $\ddot{ρ}$ 确定，而 $\ddot{ρ}$ 的突变较小，故前液压缸的突变角加速度主要由 $\ddot{α}$ 的突变决定，所以在衔接方式1下前液压缸的角加速度较大；当 $α = 54 °$ 时，衔接方式1下 $\ddot{s}$ 的突变略大于衔接方式2，表明衔接方式2下滑块的加速度较小，但衔接方式对滑块加速度的影响较小。多级变幅机构变幅时负载为其本身的质量，其主要集中在立柱及其搭载的工作装置和前液压缸上，衔接方式2下立柱和前液压缸的角加速度以及滑块的加速度更小，所以机构的惯性力更小。因此，为了保证变幅过程中前、后液压缸的衔接更加平稳，宜采用衔接方式2。

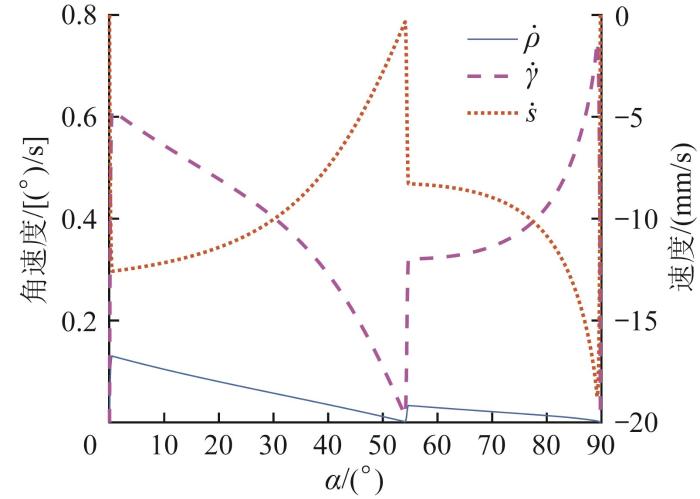
衔接方式2下多级变幅机构的速度和角速度曲线如图5所示。由图可知：当 $0 \leq α < 54 °$ 时， $\dot{ρ}$ 和 $\dot{γ}$ 先突增再减小到0附近， $\dot{s}$ 先突减再增大到0附近；当 $54 ° < α \leq 90 °$ 时， $\dot{ρ}$ 先突增再减小到0， $\dot{γ}$ 先突增再逐渐增大最后突减到0， $\dot{s}$ 先突减再逐渐减小最后突增到0。综上， $\dot{ρ}$ 和 $\dot{γ}$ 始终大于0， $\dot{s}$ 始终小于0，表明 $ρ$ 和 $γ$ 单调递增， $s$ 单调递减。因此，在变幅过程中，连杆持续绕 $M$ 点作逆时针旋转，滑块持续向上移动，在变幅过程中它们的运动方向没有改变，保证了导杆滑块机构运动的顺畅，从而保证了整个变幅过程的顺畅。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 衔接方式2下多级变幅机构速度和角速度曲线

Fig.5 Velocity and angular velocity curves of multi-stage luffing mechanism under connection mode 2

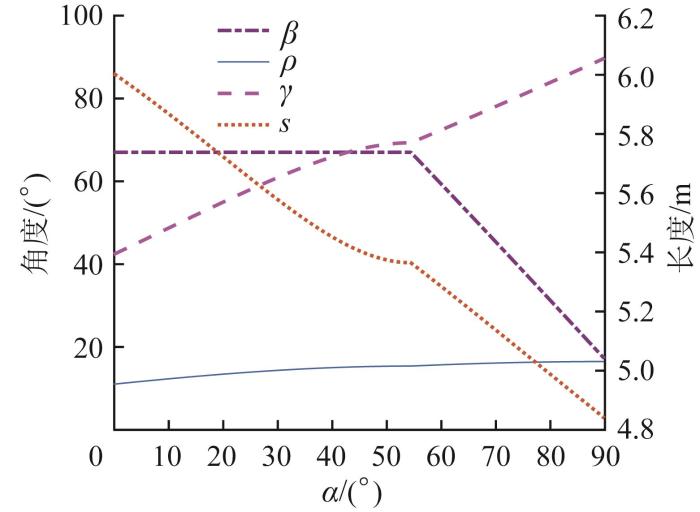
衔接方式2下变幅机构的位置曲线如图6所示。由图可知，当 $α = 90 °$ 时， $γ = 90 °$ ，即立柱竖直时连杆与前液压缸垂直，此时连杆减小弯矩的作用最大。同时，当 $γ = 90 °$ 时，前液压缸对连杆的力经过其回转中心点 $M$ ，导杆滑块机构处于死点位置，这就保证了在桩架作业时前液压缸能够稳定支撑立柱。桩架倒桅时，需导杆滑块机构先脱离死点才能进行正常的变幅过程，可在立柱和连杆之间添加一个小型液压缸，倒桅开始时液压缸驱动连杆绕 $M$ 点转动；或在前液压缸上添加弹簧，利用弹簧力将滑块推离死点。因此，该变幅机构可以完成立桅和倒桅的动作；立柱竖直时，连杆与前液压缸垂直，连杆能最大限度地减小前液压缸的弯矩。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 衔接方式2下多级变幅机构的位置曲线

Fig.6 Position curves of multi-stage luffing mechanism under connection mode 2

3.4　机构参数对 $α_{m a x}$ 的影响分析

$α_{m a x}$ 是决定多级变幅机构能否变幅成功的关键因素。对 $α_{m a x}$ 有影响的机构参数有 $B$ 点坐标（ $x_{B}$ ， $y_{B}$ ）、 $β_{0}$ 、 $l_{1}$ 、 $l_{2}$ 和 $a_{3}$ 。为了研究机构参数对机构变幅运动的影响，以（ $x_{B}$ ， $y_{B}$ ）、 $β_{0}$ 、 $l_{1}$ 、 $l_{2}$ 、 $a_{3}$ 为自变量，探究 $α_{m a x}$ 的变化规律。

以B(-1.225 m, -0.36 m)， $β = 67 °$ ， $l_{1} = 16.8 m$ ， $l_{2} = 3.054 m$ ， $a_{3} = 2 m$ 为基准，改变其中1个变量，保持其他变量不变，分析该变量对 $α_{m a x}$ 的影响。利用MATLAB软件进行计算和绘图，结果如图7所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 多级变幅机构参数对 $α_{m a x}$ 的影响

Fig.7 Influence of parameters of multi-stage luffing mechanism on $α_{m a x}$

由图7可知，在一定范围内， $α_{m a x}$ 随着 $x_{B}$ 的增大而减小，随着 $y_{B}$ 的增大而增大，随着 $β_{0}$ 的增大而减小，随着 $l_{1}$ 的增大而减小，随着 $l_{2}$ 的增大而增大，随着 $a_{3}$ 的增大而增大。由式(26)可知， $α_{m a x}$ ≥ $90 °$ 时立柱才能从水平转成竖直。因此，为了保证机构变幅成功， $y_{B}$ 、 $l_{2}$ 、 $a_{3}$ 应尽可能大， $x_{B}$ 、 $β_{0}$ 、 $l_{1}$ 尽可能小。

4 新型桩架多级变幅机构变幅仿真

在ADAMS软件中以大地为机架建立多级变幅机构仿真模型，如图8所示。添加约束如下：立柱、变幅架、后液压缸筒与大地之间均添加转动副；液压缸活塞杆与液压缸筒之间、滑块与前液压缸筒之间均添加移动副；除前液压缸筒与变幅架的铰点处添加转动副外，其余铰点处均添加球面副。完成后模型共有7个转动副、6个移动副和8个球面副。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 多级变幅机构ADAMS仿真模型

Fig.8 ADAMS simulation model of multi-stage luffing mechanism

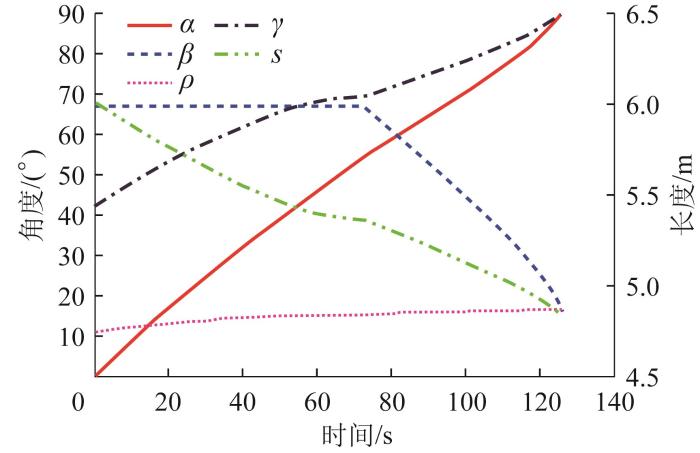
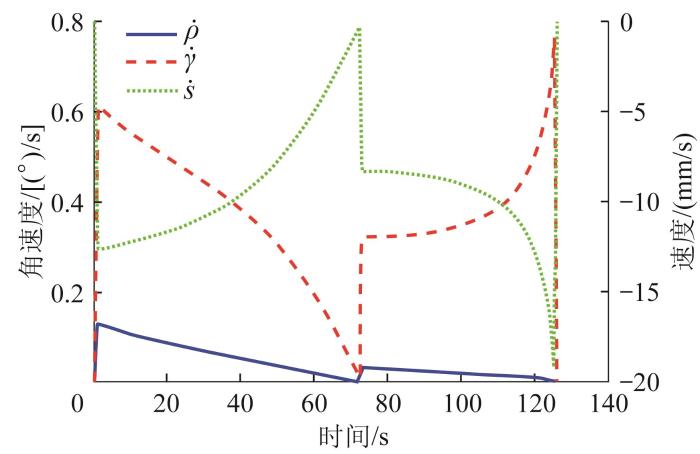
以前、后液压缸为原动件，对液压缸活塞杆和液压缸筒之间的移动副添加位移驱动函数。分别对衔接方式2下的 $d_{1}$ 和 $d_{2}$ 取点，组成时间—长度样条曲线SPLINE_1和SPLINE_2，则前、后液压缸的位移驱动函数分别为AKISPL（time，0，SPLINE_1，0）和AKISPL（time，0，SPLINE_2，0）。输入机构参数并建立测量，仿真126 s后得到多级变幅机构的位置曲线，微分处理可得到对应的速度、角速度、加速度和角加速度曲线，如图9至图11所示。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 多级变幅机构位置仿真曲线

Fig.9 Position simulation curves of multi-stage luffing mechanism

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 多级变幅机构速度和角速度仿真曲线

Fig.10 Velocity and angular velocity simulation curves of multi-stage luffing mechanism

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 多级变幅机构加速度和角加速度仿真曲线

Fig.11 Acceleration and angular acceleration simulation curves of multi-stage luffing mechanism

分别对比图4与图11、图5与图10、图6与图9可知，衔接方式2下机构变幅运动的仿真结果与理论分析结果一致，验证了本文提出的运动学模型的正确性和有效性。

5 结论

为了实现桩架在自主变幅的同时提高支撑稳定性，本文提出了一种新型桩架多级变幅机构，并对该机构进行了运动学分析。论文重点如下：

1）分析了新型桩架多级变幅机构的变幅条件，论证了该机构可以顺畅地将立柱从水平变幅至竖直。

2）分析了多级变幅机构的参数对变幅运动的影响，结果表明， $y_{B}$ 、 $l_{2}$ 、 $a_{3}$ 应尽可能大， $x_{B}$ 、 $β_{0}$ 、 $l_{1}$ 应尽可能小。

3）分析了多级变幅机构前、后液压缸的动作衔接方式，结果表明，在前液压缸减速收缩的过程中进行后液压缸加速收缩有利于机构变幅的平稳运行。

4）利用ADAMS软件搭建了多级变幅机构仿真模型，仿真结果验证了所构建的运动学模型的正确性和有效性。

5）后续可以所建立的机构运动学模型为基础，对机构的动力学特性作进一步分析，进行机构的优化和控制。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

刘古岷，王渝，胡国庆，等. 桩工机械［M］. 北京：机械工业出版社， 2001.