基于支重轮-履带-地面多体耦合的履带机器人振动响应研究

doi:10.3785/j.issn.1006-754X.2024.03.193

基于支重轮-履带-地面多体耦合的履带机器人振动响应研究

宋佳琪^,^,, 张宏^,, 王景宇, 殷国珠

太原科技大学机械工程学院，山西太原 030024

Study on vibration response of tracked robot based on multi-body coupling of supporting wheel-track-ground

SONG Jiaqi^,^,, ZHANG Hong^,, WANG Jingyu, YIN Guozhu

School of Mechanical Engineering, Taiyuan University of Science and Technology, Taiyuan 030024, China

通讯作者: 张　宏（1970—），男，山西太原人，教授，博士，从事机械动力学设计控制与健康监测研究，E-mail: hexie007@163.com

收稿日期: 2023-08-21 修回日期: 2023-12-21

基金资助:

国家自然科学基金资助项目.  52075355
中央引导地方科技发展资金项目.  YDZJSX20231A050
山西省重点研发计划项目.  202202100401012

Received: 2023-08-21 Revised: 2023-12-21

作者简介 About authors

宋佳琪（2000—），女，山西吕梁人，硕士生，从事履带机器人动力学研究，E-mail:1340458994@qq.com，https://orcid.org/0009-0003-4662-3115 , E-mail：1340458994@qq.com

摘要

构建支重轮-履带-地面多体耦合系统是研究履带机器人行驶平顺性的重要环节。以单侧五支重轮履带机器人为研究对象，在非线性悬挂系统模型以及考虑履带滤波作用的路面激励的基础上，建立了履带机器人振动理论估算模型。然后，基于履带机器人在不同等级路面及不同行驶速度工况下的仿真实验，利用均方根值定量分析了行驶速度、路面激励对机器人车体及其支重轮垂向振动的影响。最后，通过开展外路实验来验证七自由度半车的振动理论估算模型和动力学仿真模型。结果表明：随着行驶速度和路面不平度的提高，履带机器人车体的垂向振动近似呈线性增大，履带对路面激励有滤波作用。履带机器人车体质心及支重轮1，3，5的垂向振动加速度对路面激励最为敏感，车体垂向振动加速度功率谱密度幅值在频率为19 Hz左右时最大。由于支重轮5靠近驱动段，履带与主动轮啮合产生的多边形效应使其垂向振动相对于其他支重轮偏大。理论建模、仿真分析及外路实验相结合的方法为履带机器人在不同路况下的振动响应特性研究提供了新思路。

关键词： 履带机器人 ; 多体耦合 ; 支重轮 ; 垂向振动 ; 响应特性

Abstract

The construction of supporting wheel-track-ground multi-body coupling system is an important link for the travelling smoothness study of tracked robots. Taking the unilateral five- supporting wheel tracked robot as the study object, the theoretical estimation model for tracked robot vibration was established on the basis of the nonlinear suspension system model and the road excitation considering the track filtering effect. Then, based on the simulation experiments of the tracked robot under working conditons with different road levels and different driving speeds, the effects of driving speed and road excitation on the vertical vibration of the robot body and its supporting wheels were quantitatively analyzed by the root mean square value. Finally, the theoretical vibration estimation model and dynamics simulation model of the seven-degree-of-freedom semi-vehicle were verified by external road experiments. The results showed that the vertical vibration of the tracked robot body increased linearly with the increase of driving speed and road roughness, and the track had a filtering effect on the road excitation. The vertical vibration acceleration of the tracked robot body centroid and the supporting wheel 1, 3, 5 were most sensitive to the road excitation, and the power spectral density amplitude of the vertical vibration acceleration of the robot body was the largest when the frequency was about 19 Hz. As the supporting wheel 5 was close to the driving section, the polygonal effect generated by the track engaging with the active wheel made its vertical vibration larger than that of the other supporting wheels. The combination of theoretical modeling, simulation analysis and external experiment provides a new idea for the study of vibration response characteristics of tracked robots under different road conditions.

Keywords： tracked robot ; multi-body coupling ; supporting wheel ; vertical vibration ; response characteristics

PDF (4525KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

宋佳琪, 张宏, 王景宇, 殷国珠. 基于支重轮-履带-地面多体耦合的履带机器人振动响应研究[J]. 工程设计学报, 2024, 31(4): 456-464 doi:10.3785/j.issn.1006-754X.2024.03.193

SONG Jiaqi, ZHANG Hong, WANG Jingyu, YIN Guozhu. Study on vibration response of tracked robot based on multi-body coupling of supporting wheel-track-ground[J]. Chinese Journal of Engineering Design, 2024, 31(4): 456-464 doi:10.3785/j.issn.1006-754X.2024.03.193

本文链接：https://www.zjujournals.com/gcsjxb/CN/10.3785/j.issn.1006-754X.2024.03.193

煤矿井下巷道路面泥泞且凹凸不平，在救援履带机器人行驶过程中，其搭载的精密仪器会受到不同程度的振动影响。因此，研究履带机器人在不同路况下的适应性和振动响应特性具有重要意义。履带机器人所受的振动激励主要来源于地面与履带、履带与支重轮之间的接触碰撞，接触力通过悬挂系统传递到车身，故支重轮所受的激励会直接影响履带机器人的附着性能、牵引性能及行驶安全性^[1]。

近年来，国内外学者针对履带机器人的平顺性及其振动响应特性做了大量研究。马星国等^[2]、赵旗等^[3]、Ata等^[4]通过建立履带车辆的刚度-质量-阻尼振动模型，探讨了不同路面形态、不同悬架配置对履带车辆平顺性的影响。Miao等^[5]基于多体系统传递矩阵法对履带车辆系统的振动特性进行了分析。朱兴高等^[6]、张新等^[7]采用多体动力学仿真方法，研究了行驶速度、路面不平度和履带板参数对履带机器人动态特性的影响。Li等^[8]采用离散方法求解履带车辆的耦合动力学方程，得到了其质心的加速度和驱动链轮的牵引力。孟磊等^[9]建立了履带车辆-履带动力学模型和未考虑履带的履带车辆-试验台架动力学模型，探讨了有无履带状态下车辆振动响应的差异。Dchoi等^[10]建立了考虑履带影响的履带机器人三维实体模型，分析了履带与刚性地面之间的相互作用以及履带对路面激励的影响。乔新勇等^[11]在考虑履带环影响的条件下分析了履带车辆的振动响应，并对基于柔性履带模型与刚性履带模型的仿真结果进行了比较。李春明等^[12]建立了履带车辆的纵向-垂向耦合动力学模型，探讨了垂向、俯仰运动对履带车辆机动性的影响规律。上述文献针对履带机器人行驶系统的多体耦合关系以及履带机器人的振动响应特性进行了深入研究，但较少涉及履带机器人支重轮在不同行驶状态下的振动响应研究。

为此，笔者根据矿用救援履带机器人的行驶特点，分别建立履带机器人支重轮-履带-地面多体耦合系统的振动理论估算模型和动力学仿真模型，并开展外路实验，以分析行驶速度、路面激励对机器人车体及支重轮振动响应的影响，旨在为履带机器人的平顺性研究提供理论支撑。

1 支重轮-履带-地面多体耦合系统的振动理论估算模型

1.1　单支重轮非线性悬挂系统模型

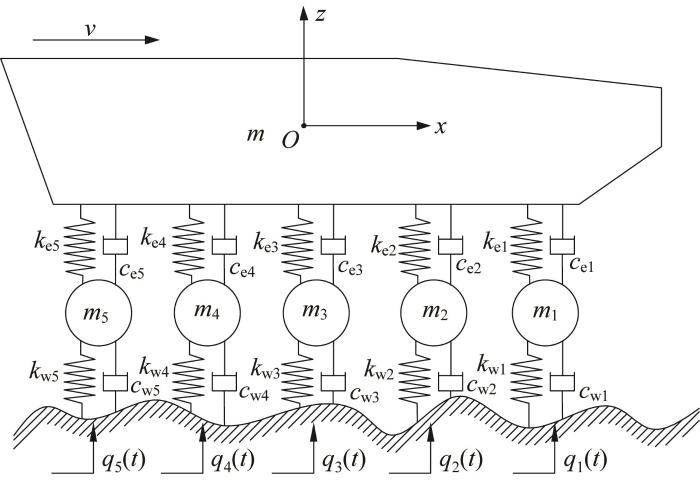
悬挂系统连接履带机器人的车体与支重轮，是机器人减振的关键部件，可保证支重轮载荷稳定^[13]。在履带机器人悬挂系统动力学研究中，常常将单个悬挂系统与支重轮及履带的相互作用简化为质量-刚度-阻尼形式。

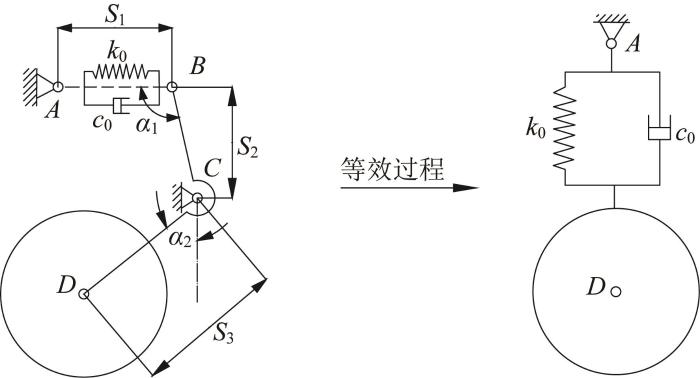
图1所示为履带机器人单支重轮悬挂系统的等效模型。图中：A点表示减振器与车体的固定连接点；杆BCD表示平衡肘，平衡肘通过螺栓与减振器连接于B点，B点位于限位槽内，可在限位槽范围内运动；支重轮中心与平衡肘连接于D点；平衡肘通过螺栓与车体连接于C点，连接点C处可转动。各参数定义如下： $k_{0}$ 、c₀为减振器的实际刚度、阻尼， $S_{1}$ 、 $S_{2}$ 、 $S_{3}$ 分别为各铰接点之间的距离， $α_{1}$ 为减振器与平衡肘支点的夹角， $α_{2}$ 为静平衡状态下平衡肘与竖直方向的夹角。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 单支重轮悬挂系统等效模型

Fig.1 Equivalent model of single supporting wheel suspension system

当行驶路面不平时，路面激励通过履带作用在支重轮上，平衡肘在减振器的作用下发生偏转（在限位槽范围内），使得支重轮上下移动，以提高履带机器人的行驶平顺性。假设平衡肘的偏转角度为 $Δ α$ ，支重轮的垂向移动距离为 $Δ x$ ，减振器的拉长/压缩量为 $Δ y$ ，求解悬挂系统的等效刚度 $k_{e}$ 和等效阻尼 $c_{e}$ 。根据力矩平衡原理，可得：

k_{e} Δ x S_{3} s i n (α_{2} + Δ α) = k_{0} Δ y S_{2} s i n [π - (α_{1} + Δ α)]

(1)

支重轮移动距离 $Δ x$ 与平衡肘偏转角度 $Δ α$ 之间的关系为：

Δ x = S_{3} [c o s α_{2} - c o s (α_{2} + Δ α)]

(2)

由余弦定理可得，减振器的拉长/压缩量 $Δ y$ 为：

\begin{array}{l} Δ y = \sqrt[]{S_{A C}^{2} + S_{2}^{2} - 2 S_{A C} S_{2} c o s ∠ B C A} - \\ \sqrt[]{S_{A C}^{2} + S_{2}^{2} - 2 S_{A C} S_{2} c o s (∠ B C A - Δ α)} \end{array}

(3)

式中：S_AC 为铰接点A、C之间的距离。

当减振器被拉长或压缩时，减振器与平衡肘支点的夹角 $α_{1}$ 会发生变化，而 $S_{2}$ 和铰接点A、C之间的距离 $S_{A C}$ 始终不变，则式(3)可简化为：

Δ y \approx S_{2} s i n Δ α

(4)

将式(2)与式(4)代入式(1)并进行一定的简化，可得到悬挂系统的等效刚度 $k_{e}$ ：

k_{e} = k_{0} \frac{S_{2}^{2} s i n (α_{2} + Δ α) s i n Δ α}{S_{3}^{2} [c o s α_{2} - c o s (α_{2} + Δ α)] s i n (α_{2} + Δ α)}

(5)

同理，根据力矩平衡原理，可得：

c_{e} Δ \dot{x} S_{3} s i n (α_{2} + Δ α) = c_{0} Δ \dot{y} S_{2} s i n (α_{1} + Δ α)

(6)

代入化简后，得到悬挂系统的等效阻尼 $c_{e}$ ：

c_{e} = c_{0} \frac{S_{2}^{2} c o s Δ α s i n (α_{1} + Δ α)}{S_{3}^{2} s i n^{2} (α_{2} + Δ α)}

(7)

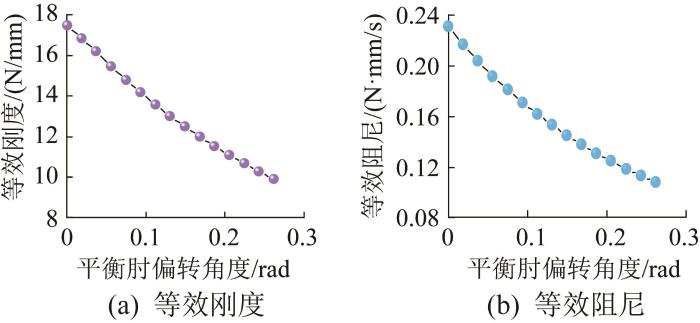
由于履带机器人限位槽的作用，平衡肘的最大偏转角度为 $π / 12$ （15°）。当平衡肘从静平衡状态转动到最大偏转角度时，履带机器人悬挂系统的等效刚度 $k_{e}$ 、等效阻尼 $c_{e}$ 与平衡肘偏转角度 $Δ α$ 之间的关系曲线如图2所示。由图2可以看出，悬挂系统的等效刚度、等效阻尼均随平衡肘偏转角度的增大而减小，这表明在限位槽允许范围内，悬挂系统在路面起伏较大时的减振效果更为突出。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 悬挂系统等效刚度、阻尼随平衡肘偏转角度的变化曲线

Fig.2 Variation curve of equivalent stiffness and damping of suspension system with deflection angle of balance elbow

通过上文分析可知，悬挂系统的等效刚度 $k_{e}$ 和等效阻尼 $c_{e}$ 与平衡肘偏转角度 $Δ α$ 呈非线性关系。由此可得，平衡肘偏转角度 $Δ α$ 表示为^[14]：

Δ α = a r c c o s (c o s α_{2} - \frac{Δ x}{S_{3}}) - α_{2}

(8)

其中，5个支重轮对应的减振器的拉长/压缩量 $∆ y_{i}$ (i=1, 2,…, 5)与履带机器人车体的垂向位移变化量 $Δ x_{z}$ 和俯仰角 $φ$ 的关系为：

\{\begin{array}{l} Δ y_{1} = Δ x_{z} + 2 l φ - q_{1} (t) \\ Δ y_{2} = Δ x_{z} + l φ - q_{2} (t) \\ Δ y_{3} = Δ x_{z} - q_{3} (t) \\ Δ y_{4} = Δ x_{z} + l φ - q_{4} (t) \\ Δ y_{5} = Δ x_{z} + 2 l φ - q_{5} (t) \end{array}

(9)

式中： $q_{i} (t)$ 为作用于5个支重轮的路面激励，l为各支重轮轮心的间距。

1.2　考虑履带滤波作用的路面激励模型

路面激励作为履带机器人振动系统的输入，其时间功率谱密度除了与空间功率谱密度相关外，还与机器人行驶速度相关^[15]。鉴于路面激励的功率谱密度在整个频率范围内为常数，其特性与白噪声功率谱特性一致，因此路面激励输入可用白噪声模拟，其时域模型可表示为^[16]：

\dot{Q} (t) = - 2 π n_{0} v Q (t) + 2 π n_{0} \sqrt[]{G_{q} (n_{0}) v} w (t)

(10)

式中： $Q (t)$ 为路面激励； $n_{0}$ 为参考空间频率，本文取 $n_{0} = 0.1 m^{- 1}$ ；v为履带机器人行驶速度； $G_{q} (n_{0})$ 为路面不平度系数； $w (t)$ 为均值为０和功率谱密度为1的理想白噪声。

在履带机器人行驶过程中，履带板对高频率的路面激励有良好的滤波作用。履带对路面激励的滤波作用类似于一阶低通滤波器。因此，本文采用一阶低通滤波器对基于白噪声生成的路面激励模型进行处理，以反映履带对路面激励高频成分的滤波作用。

根据一阶低通滤波器的幅频特性，得到履带的滤波函数 $G (n)$ ：

G (n) = \frac{G_{0}}{\sqrt[]{1 + {(n / n_{u})}^{2}}}

(11)

式中： $G_{0}$ 为滤波器的零频增益，n、n_u为空间频率及其上限。

由于履带滤掉了路面激励中比履带板节距空间频率 $n_{T}$ （ $n_{T} = 1 / t_{T}$ ，其中 $t_{T}$ 为履带板节距，本文取 $t_{T}$ =124 mm）高的成分，因此履带板节距空间频率 $n_{T}$ 成为路面激励空间频率的上限 $n_{u}$ ^[17]，即式(11)中 $n_{u} = n_{T}$ 。

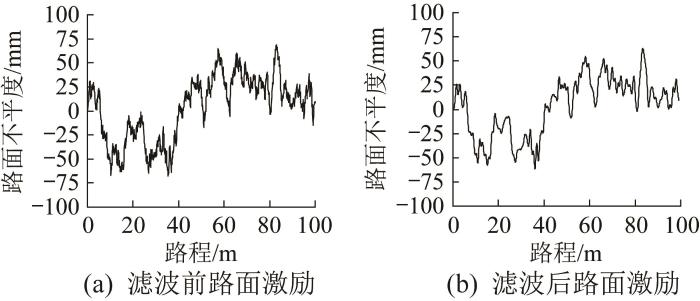
对长度为100 m的B级（沥青路面）、D级（压实土路）、E级（碎石路面）路面进行滤波处理分析。由于篇幅限制，仅给出考虑履带滤波作用前后的E级路面激励时域图，如图3所示。由图3可以看出，经履带滤波后E级路面激励中大于履带板节距空间频率的成分已被滤掉，该路面激励可直接作用于支重轮。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 滤波前后E级路面不平度对比

Fig.3 Comparison of E-class road unevenness before and after filtering

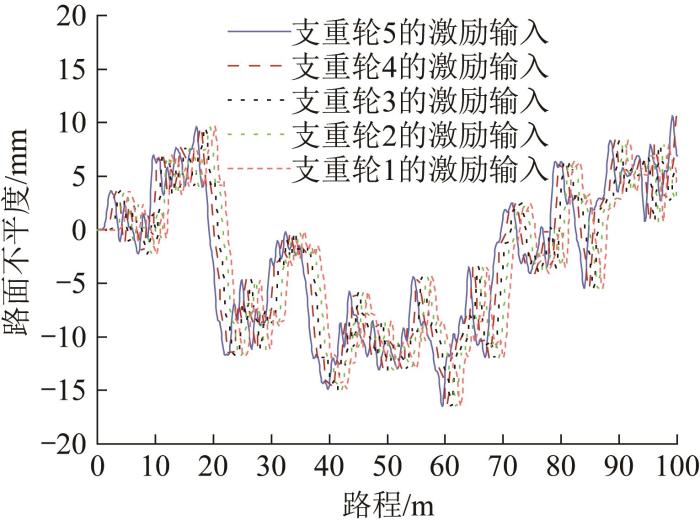
在构建履带机器人的路面激励模型时，还需考虑路面激励作用于各支重轮的延时性。假设每个支重轮所受的路面激励相同，但在履带机器人实际行驶过程中，5个支重轮依次通过不平路面，即路面激励对每个支重轮的作用时间不同^[18]。因此，在模拟路面激励时，应根据履带机器人的行驶速度以及支重轮之间的相对距离，对加载在各支重轮上的路面激励设置时间差，以更好地模拟路面激励对履带机器人行驶平顺性的影响。图4所示为B级路面下履带机器人行驶速度为1 m/s时，最终作用于单侧5个支重轮上的路面激励。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 考虑延时性的支重轮路面激励输入

Fig.4 Road excitation input of supporting wheel considering delay

1.3　七自由度半车模型

履带机器人是一个复杂的多自由度系统，在保证其动力学模型计算精度和完整性的前提下，作以下假设^[17]：

1）履带机器人所行驶的路面为刚性路面，且作用于两侧履带的路面激励相同，仅作用时间上存在延迟。

2）履带机器人各支重轮具有相同的刚度特性及阻尼特性，且各支重轮所受的力均作用于轮心。

3）整个履带机器人车体相对于质心对称，不计车体的侧摆运动。

图5所示为单侧五支重轮履带机器人的七自由度半车模型。图中：k_e1、k_e2、k_e3、k_e4、k_e5分别表示5个支重轮的悬挂系统的等效刚度，c_e1、c_e2、c_e3、c_e4、c_e5分别表示5个支重轮的悬挂系统的等效阻尼，k_w1、k_w2、k_w3、k_w4、k_w5分别表示5个支重轮的刚度，c_w1、c_w2、c_w3、c_w4、c_w5分别表示5个支重轮的阻尼，m₁、m₂、m₃、m₄、m₅分别表示5个支重轮的质量， $m$ 为机器人半车质量。半车模型的未知量为机器人车体质心处的垂向位移、机器人车体俯仰角以及5个支重轮的垂向位移。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 履带机器人的七自由度半车模型

Fig.5 Seven-degree-of-freedom semi-vehicle model of tracked robot

根据牛顿第二运动定律，可得履带机器人半车模型的振动微分方程：

\{\begin{array}{l} m Δ x_{z} = F_{e 1} + F_{e 2} + F_{e 3} + F_{e 4} + F_{e 5} \\ I \ddot{φ} = F_{e 1} l_{1} + F_{e 2} l_{2} + F_{e 3} l_{3} - F_{e 4} l_{4} - F_{e 5} l_{5} \\ m_{1} Δ {\ddot{x}}_{1} = F_{w 1} - F_{e 1} \\ m_{2} Δ {\ddot{x}}_{2} = F_{w 2} - F_{e 2} \\ m_{3} Δ {\ddot{x}}_{3} = F_{w 3} - F_{e 3} \\ m_{4} Δ {\ddot{x}}_{4} = F_{w 4} - F_{e 4} \\ m_{5} Δ {\ddot{x}}_{5} = F_{w 5} - F_{e 5} \end{array}

(12)

式中： $F_{e i}$ (i=1, 2, …, 5)为各悬挂系统作用于机器人车体的力， $F_{w i}$ 为各支重轮产生的动态力，l_i 为各支重轮到机器人车体质心的距离， $I$ 为机器人车体垂直于xOz平面的转动惯量， $Δ x_{i}$ 为各支重轮轮心处的垂向位移变化量，即垂向移动距离。

各悬挂系统作用于机器人车体的力 $F_{e i}$ 、各支重轮产生的动态力 $F_{w i}$ 可分别表示为：

\{\begin{array}{l} F_{e i} = k_{e i} (Δ x_{i} - Δ x_{b i}) + c_{e i} (Δ {\dot{x}}_{i} - Δ {\dot{x}}_{b i}) \\ F_{w i} = k_{w i} (q_{i} (t) - Δ x_{i}) \end{array}

(13)

其中：

Δ x_{b i} = Δ x_{z} - l_{i} φ

式中： $Δ x$ _b_i 为悬挂系统与机器人车体连接处的位移变化量。

将式(5)、式(7)、式(9)和式(12)代入式(13)，即可得到关于履带机器人车体及单侧支重轮垂向位移变化量 $Δ x_{z}$ 和车体俯仰角 $φ$ 的函数：

\{\begin{array}{l} Δ {\ddot{x}}_{z} (t) = f (Δ x_{z} (t), Δ {\dot{x}}_{z} (t), φ (t), \dot{φ} (t)) \\ \ddot{φ} (t) = g (Δ x_{z} (t), Δ {\dot{x}}_{z} (t), φ (t), \dot{φ} (t)) \\ Δ {\ddot{x}}_{1} (t) = y (Δ x_{z} (t), Δ {\dot{x}}_{z} (t), Δ x_{1} (t), φ (t), \dot{φ} (t)) \\ \dots \dots \\ Δ {\ddot{x}}_{5} (t) = y (Δ x_{z} (t), Δ {\dot{x}}_{z} (t), Δ x_{5} (t), φ (t), \dot{φ} (t)) \end{array}

(14)

2 履带机器人的动力学仿真模型

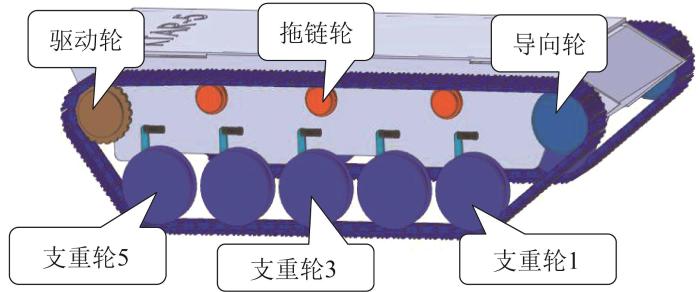
在SolidWorks软件中创建履带机器人车体部分的三维模型并将其导入多体动力学软件RecurDyn，添加其他结构后，建立各支重轮与车体之间的接触与约束。如图6所示，履带机器人的动力学仿真模型与其实际外形尺寸一致，其单侧履带结构的主要部件包括1个驱动轮、1个导向轮、3个拖链轮、5个支重轮以及73块履带板。建模时将悬挂系统的刚度、阻尼简化为平衡肘与车体铰接处弹簧的刚度、阻尼系数。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 履带机器人多体动力学仿真模型

Fig.6 Multi-body dynamics simulation model of tracked robot

采用step函数对驱动轮转动副定义速度—时间驱动函数。在本文中，履带机器人的行驶速度分别设置为0.5，1.0，1.5 m/s，驱动轮半径约为43.5 mm，则对应的驱动轮平均转速分别为110，220，330 r/min。因此，驱动函数分别定义为step(time, 0.1, 0, 1, -11.5)、step(time, 0.1, 0, 1, -23.3)、step(time, 0.1, 0, 1, -35.0)，表示在0—1 s内履带机器人驱动轮的转速从0 r/min增大到规定转速，1 s后保持该转速匀速运动。

为使仿真模型与理论模型的路面激励输入一致，将路面激励理论模型转化为多体动力学软件可识别的三维实体模型。采用三维等效容积法建立三维路面模型。将B级、D级、E级路面的不平度作为三维路面模型的z坐标，路面的宽度和长度分别为y、x坐标，利用MATLAB软件编程生成各个节点的三维坐标，并转换成含有节点向量矩阵与单元向量矩阵的文件^[19]，然后导入rdf格式的路面文件，生成可被多体动力学软件识别的三维路面模型。

3 履带机器人动力学仿真结果分析

3.1　行驶速度对履带机器人振动响应的影响

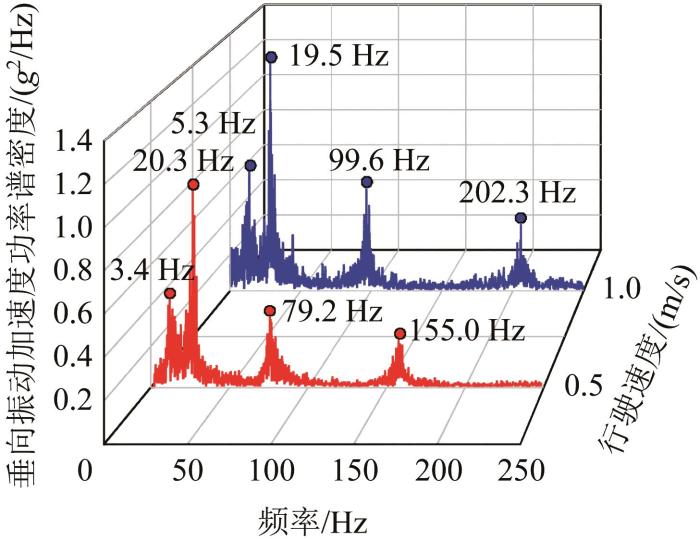
为分析行驶速度对履带机器人车体及支重轮振动响应的影响^[20]，通过动力学仿真分析得到履带机器人在B级路面上以0.5，1.0，1.5 m/s速度行驶时，其车体（质心处，下文同）的垂向振动加速度功率谱密度，如图7所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 不同行驶速度下履带机器人车体垂向振动加速度功率谱密度的仿真结果

Fig.7 Simulation result of vertical vibration acceleration power spectrum density of tracked robot body under different driving speeds

根据过往经验，履带机器人车体俯仰振动加速度的固有频率约为1.1 Hz，垂向振动加速度的固有频率约为1.5 Hz^[17]。由图7可以看出，在0~2 Hz频段内，履带机器人在B级路面上以不同速度行驶时，其车体的垂向振动加速度功率谱密度曲线均有峰值。车体垂向振动加速度功率谱密度主要峰值出现在19 Hz左右，该频段为路面不平度所引起的激励频率，由此说明路面激励对车体垂向振动的影响较大，不同行驶速度下对应的垂向振动加速度功率谱密度幅值分别为0.808，1.060，1.188 g²/Hz。

从图7中还可以看出，2~7 Hz的低频段主要为驱动轮的转动频率，该频率受履带机器人行驶速度的影响，该频段内不同行驶速度下对应的垂向振动加速度功率谱密度幅值为0.540，0.290，0.728 g²/Hz。75~117 Hz、150~230 Hz的高频段主要为由履带板节距造成的周期性激励频率以及驱动轮啮合频率的一倍频和二倍频，该频率与履带机器人行驶速度及履带板节距相关；随着行驶速度的增大，高频段内车体的垂向振动加速度功率谱密度峰值也增大。

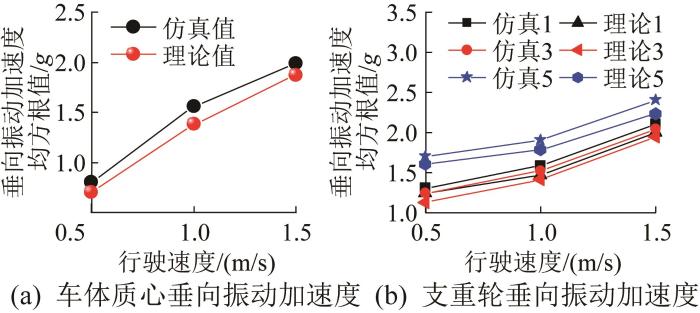
在5个支重轮所构成的5条振动传递路径中，履带机器人车体质心及支重轮1，3，5的垂向振动对路面激励最为敏感，故对车体质心及支重轮1，3，5的垂向振动加速度进行统计分析。利用均方根值定量分析支重轮-履带-地面多体耦合系统的振动响应特性，结果如图8所示。图中：仿真1，3，5与理论1，3，5分别表示支重轮1，3，5的垂向振动加速度均方根的仿真值与理论值。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 行驶速度对履带机器人车体及支重轮垂向振动的影响

Fig.8 Influence of driving speed on vertical vibration of tracked robot body and supporting wheel

由图8可知，履带机器人车体质心及支重轮1，3，5的垂向振动加速度均方根随行驶速度的提高而增大，整体上呈先慢后快的变化趋势。其中，支重轮5的垂向振动加速度均方根值略大于支重轮1，3，这是因为支重轮5靠近主动轮，处于履带的驱动段，履带与主动轮啮合产生的多边形效应使驱动段履带的牵引力发生变化，从而对位于驱动段的支重轮5造成影响。根据机器人车体质心及支重轮垂向振动加速度均方根理论值与仿真值的对比，可知振动理论估算模型与动力学仿真模型的计算结果接近，仿真值略大于理论值，这是因为理论模型未考虑履带板连接处不平整对支重轮造成的周期性激励。

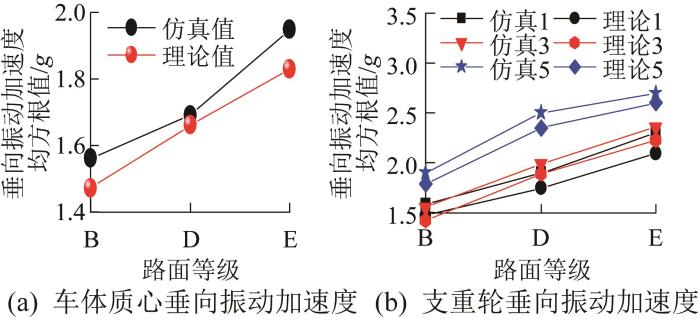
3.2　路面等级对履带机器人振动响应的影响

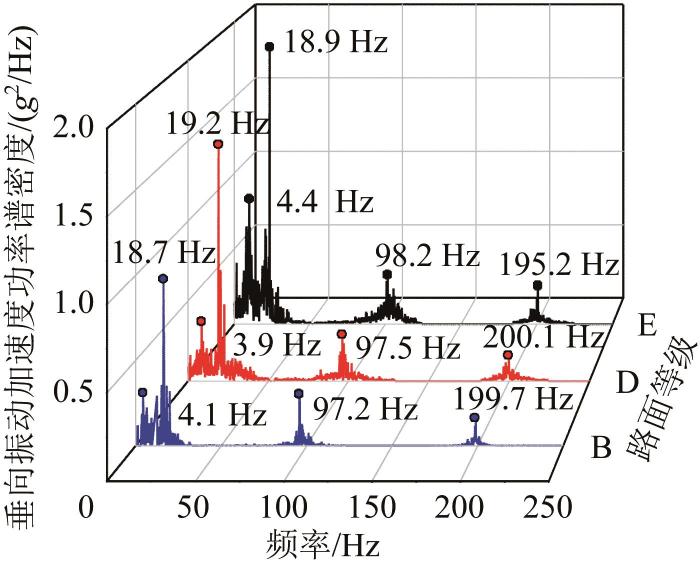
为了研究路面等级变化时履带机器人车体及支重轮垂向振动的变化规律，在保持行驶速度不变（1.0 m/s）的情况下分别设置B级、D级、E级路面，并进行动力学仿真分析。图9所示为3种路面下履带机器人车体的垂向振动加速度功率谱密度对比。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 不同路面下履带机器人车体垂向振动加速度功率谱密度的仿真结果

Fig.9 Simulation result of vertical vibration acceleration power spectrum density of tracked robot body under different roads

由图9可知，该履带机器人在不同路面上以1 m/s的速度行驶时，其车体的垂向振动加速度功率谱密度的主要峰值出现在19 Hz左右处，随着路面不平度的增大，该频段内垂向振动加速度功率谱密度幅值也在增大，分别为1.060，1.460，1.820 g²/Hz。4 Hz左右的低频段主要为驱动轮的转动频率，对应的车体垂向振动加速度功率谱密度幅值分别为0.350，0.438，0.713 g²/Hz。97 Hz以及200 Hz左右的高频段主要为履带板节距造成的周期性激励频率及驱动轮啮合频率的一倍频和二倍频，该频段内路面不平度的增大对车体垂向振动加速度功率谱密度幅值的影响不大。

同样，对不同路面下履带机器人车体质心及支重轮1，3，5的垂向振动加速度进行统计分析，结果如图10所示。图中仿真1，3，5和理论1，3，5的含义与图8同。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 路面等级对履带机器人车体及支重轮垂向振动的影响

Fig.10 Influence of road grade on vertical vibration of tracked robot body and supporting wheel

由图10可知，履带机器人车体质心及支重轮1，3，5的垂向振动加速度均方根值随路面等级的提高而增大，这主要是因为在相同行驶速度下，路面激励幅度的增大使履带的作用力增大。

4 实验验证

为进一步验证上文构建的振动理论估算模型与动力学仿真模型的正确性，在B级路面上开展实车测试，履带机器人分别以约0.5 m/s和1.0 m/s的行驶速度通过测试路面。

履带机器人的外路测试装置以及数据采集仪器的安装位置如图11所示。由于加速度传感器不能直接安装在支重轮上，将三向加速度传感器分别安装于支重轮1，3，5的悬挂系统与车体的连接处，从而间接测量支重轮的垂向振动加速度。将DH5902N坚固型数据采集分析系统与笔记本电脑连接，记录履带机器人行驶过程中车体质心及支重轮1，3，5的垂向振动加速度信号。此外，为确保履带机器人能在一段时间内保持0.5 m/s和1.0 m/s的行驶速度，将应变片贴于驱动轮上，并连接DH5905N无线扭矩测试分析系统以采集驱动轮的实时转速，以便在测试过程中对机器人行驶速度进行调整。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 履带机器人外路实验测试装置

Fig.11 Test device for external experiment of tracked robot

在履带机器人行驶速度分别为0.5 m/s和1.0 m/s的条件下，驱动轮的实测转速如图12所示。由图12可知，驱动轮的实测转速均值为111 r/min和220 r/min，说明履带机器人的行驶速度可保持为0.5 m/s和1.0 m/s。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 不同行驶速度下驱动轮的实测转速

Fig.12 Measured rotation speed of driving wheel under different driving speeds

通过实车测试得到履带机器人车体垂向振动加速度功率谱密度曲线，如图13所示。由图13可以看出，通过实验测得的履带机器人车体垂向振动加速度功率谱密度对应的高频成分频带较宽，这是因为实验中机器人驱动轮的转速并非恒定，而是在均值附近上下波动，这对与履带板节距相关的激励有较大扰动。通过对比图7和图13可知，在0~30 Hz的低频段内，履带机器人车体垂向振动加速度功率谱密度峰值对应频率的仿真结果与实测结果相吻合，均在19 Hz左右，由此说明所建立的动力学仿真模型较为合理。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 不同行驶速度下履带机器人车体垂向振动加速度功率谱密度的实验结果

Fig.13 Experimental result of vertical vibration acceleration power spectrum density of tracked robot body under different driving speeds

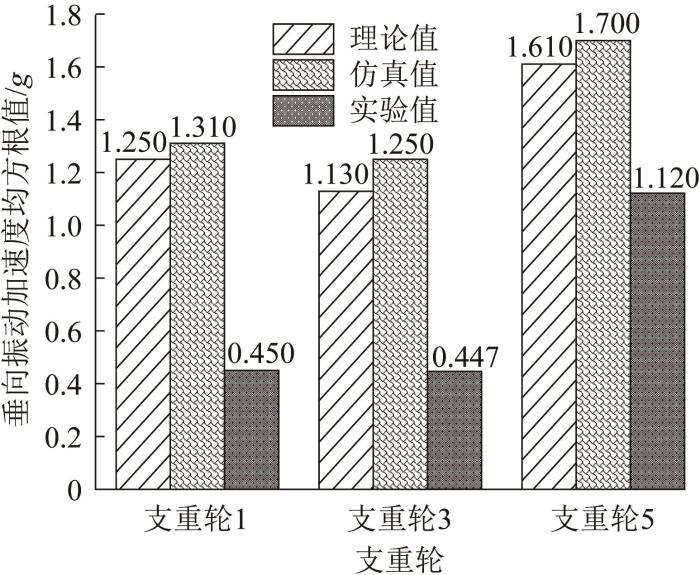
图14所示为履带机器人以0.5 m/s速度在B级路面上行驶时支重轮1，3，5的垂向振动加速度均方根值。由图14可以看出，支重轮5的垂向振动加速度比支重轮1，3的大，这与仿真结果和理论结果均一致；由于实验中测量的是各支重轮对应车体的垂向振动加速度，而悬挂系统有减振作用，故实测值小于仿真值和理论值，但仍可以间接验证所构建的振动理论估算模型与动力学仿真模型的正确性。

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 支重轮垂向振动加速度均方根值对比

Fig.14 Comparison of root mean square value of vertical vibration acceleration of supporting wheel

表1所示为0.5，1.0 m/s行驶速度下（B级路上）履带机器人车体质心垂向振动加速度均方根的理论值、仿真值与实测值的对比。由表1可以看出，履带机器人车体质心垂向振动加速度均方根的理论值与实测值的相对误差在25%以内，仿真值与实测值的相对误差在20%以内，说明仿真结果具有一定的参考价值。

表1 履带机器人车体质心垂向振动加速度均方根值对比

Table 1 Comparison of root mean square value of vertical vibration acceleration of tracked robot body centroid

对比项	行驶速度/(m/s)
对比项	0.5	1.0
理论值	0.69g	1.38g
仿真值	0.75g	1.56g
实测值	0.90g	1.70g
相对误差/%	23.3^①	18.8^①
相对误差/%	16.7^②	14.0^②

① 理论值与实测值的相对误差。

② 仿真值与实测值的相对误差。

新窗口打开| 下载CSV

5 结论

本文建立了支重轮-履带-地面多体耦合系统的振动理论估算模型，研究了行驶速度、路面等级对履带机器人车体及支重轮垂向振动的影响规律。主要结论如下：

1）采用功率谱密度分析了履带与路面激振频率、履带与主动轮啮合频率以及履带板的周期性激励对履带机器人车体垂向振动的影响。结果表明，随着履带机器人行驶速度的提高，其车体在高频段内的垂向振动加速度功率谱密度峰值所对应的频率增大，由主动轮啮合产生的激励与履带板激励主要受行驶速度的影响；车体垂向振动加速度功率谱密度幅值在19 Hz左右处最大，说明路面激励是影响车体垂向振动的主要因素。

2）利用均方根值定量分析了行驶速度、路面等级对履带机器人车体及支重轮垂向振动的影响。结果表明，随着行驶速度和路面不平度的提高，车体质心的垂向振动加速度近似呈线性增大；由于支重轮5位于履带的驱动段，履带与主动轮啮合产生的多边形效应使得支重轮5的垂向振动加速度略大于支重轮1，3，由此说明靠近驱动段的支重轮与悬挂系统的运行环境较恶劣。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

覃凌云，杨书仪，陈哲吾，等.

路面激励下的履带车辆负重轮动载荷研究

［J］.振动、测试与诊断，2021，41（4）：652-659，826-827. doi：10.16450/j.cnki.issn.1004-6801.2021.04.003