[1]
ZHANG S, SUN L, MAO X, et al Review on EEG-based authentication technology
[J]. Computational Intelligence and Neuroscience , 2021 , 2021 (1 ): 5229576
DOI:10.1155/2021/5229576
[本文引用: 1]
[2]
陈彬滨, 吴涛, 陈黎飞 基于缩放卷积注意力网络的跨多个体脑电情绪识别
[J]. 中国生物医学工程学报 , 2024 , 43 (5 ): 550 - 560
[本文引用: 1]
CHEN Binbin, WU Tao, CHEN Lifei Cross-subjects EEG emotion recognition based on scaled convolutional attention network
[J]. Chinese Journal of Biomedical Engineering , 2024 , 43 (5 ): 550 - 560
[本文引用: 1]
[3]
刘国文, 唐佳佳, 金宣妤, 等 基于多尺度卷积和身份子空间的脑纹识别
[J]. 杭州电子科技大学学报: 自然科学版 , 2025 , 45 (1 ): 82 - 88
[本文引用: 1]
LIU Guowen, TANG Jiajia, JIN Xuanyu, et al Brainprint recognition based on multi-scale convolution and subspace
[J]. Journal of Hangzhou Dianzi University: Natural Sciences , 2025 , 45 (1 ): 82 - 88
[本文引用: 1]
[4]
PALANIAPPAN R, MANDIC D P Biometrics from brain electrical activity: a machine learning approach
[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2007 , 29 (4 ): 738 - 742
DOI:10.1109/TPAMI.2007.1013
[本文引用: 1]
[5]
FALLANI F D V, VECCHIATO G, TOPPI J, et al. Subject identification through standard EEG signals during resting states [C]//Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society. Boston: IEEE, 2011: 2331–2333.
[本文引用: 1]
[6]
ALBASRI A, ABDALI-MOHAMMADI F, FATHI A EEG electrode selection for person identification thru a genetic-algorithm method
[J]. Journal of Medical Systems , 2019 , 43 (9 ): 297
DOI:10.1007/s10916-019-1364-8
[本文引用: 1]
[7]
YANG S, DERAVI F On the usability of electroencephalographic signals for biometric recognition: a survey
[J]. IEEE Transactions on Human-Machine Systems , 2017 , 47 (6 ): 958 - 969
DOI:10.1109/THMS.2017.2682115
[本文引用: 1]
[8]
SUN Y, LO F P W, LO B EEG-based user identification system using 1D-convolutional long short-term memory neural networks
[J]. Expert Systems with Applications , 2019 , 125 : 259 - 267
DOI:10.1016/j.eswa.2019.01.080
[本文引用: 5]
[9]
SCHONS T, MOREIRA G J P, SILVA P H L, et al. Convolutional network for EEG-based biometric [C]//Progress in Pattern Recognition, Image Analysis, Computer Vision, and Applications . Cham: Springer, 2018: 601–608.
[本文引用: 3]
[10]
WANG M, EL-FIQI H, HU J, et al Convolutional neural networks using dynamic functional connectivity for EEG-based person identification in diverse human states
[J]. IEEE Transactions on Information Forensics and Security , 2019 , 14 (12 ): 3259 - 3272
DOI:10.1109/TIFS.2019.2916403
[本文引用: 1]
[11]
FRASCHINI M, HILLEBRAND A, DEMURU M, et al An EEG-based biometric system using eigenvector centrality in resting state brain networks
[J]. IEEE Signal Processing Letters , 2015 , 22 (6 ): 666 - 670
DOI:10.1109/LSP.2014.2367091
[本文引用: 3]
[12]
KUMAR G P, DUTTA U, SHARMA K, et al. EEG-based biometrics: phase-locking value from gamma band performs well across heterogeneous datasets [C]//Proceedings of the International Conference of the Biometrics Special Interest Group . Darmstadt: IEEE, 2022: 1–6.
[本文引用: 5]
[13]
TIAN W, LI M, JU X, et al Applying multiple functional connectivity features in GCN for EEG-based human identification
[J]. Brain Sciences , 2022 , 12 (8 ): 1072
DOI:10.3390/brainsci12081072
[本文引用: 5]
[14]
MYUNG K, GU K, BUM P. Spectrogram and CNN based personal identification using EEG signal [C]//Proceedings of the IEEE International Conference on Consumer Electronics-Asia . Gangwon: IEEE, 2021: 1–4.
[本文引用: 1]
[15]
HOU Q, ZHOU D, FENG J. Coordinate attention for efficient mobile network design [C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Nashville: IEEE, 2021: 13708–13717.
[本文引用: 1]
[16]
LAWHERN V J, SOLON A J, WAYTOWICH N R, et al EEGNet: a compact convolutional neural network for EEG-based brain–computer interfaces
[J]. Journal of Neural Engineering , 2018 , 15 (5 ): 056013
DOI:10.1088/1741-2552/aace8c
[本文引用: 1]
[17]
LI H, LI J, WEI H, et al Slim-neck by GSConv: a lightweight-design for real-time detector architectures
[J]. Journal of Real-Time Image Processing , 2024 , 21 (3 ): 62
DOI:10.1007/s11554-024-01436-6
[本文引用: 1]
[18]
GARNOT V S F, LANDRIEU L, GIORDANO S, et al. Satellite image time series classification with pixel-set encoders and temporal self-attention [C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020: 12322–12331.
[本文引用: 1]
[19]
GOLDBERGER A L, AMARAL L A, GLASS L, et al PhysioBank, PhysioToolkit, and PhysioNet: components of a new research resource for complex physiologic signals
[J]. Circulation , 2000 , 101 (23 ): E215 - E220
[本文引用: 1]
[20]
KOELSTRA S, MUHL C, SOLEYMANI M, et al DEAP: a database for emotion Analysis;Using physiological signals
[J]. IEEE Transactions on Affective Computing , 2012 , 3 (1 ): 18 - 31
DOI:10.1109/T-AFFC.2011.15
[本文引用: 1]
[21]
ASHENAEI R, ASGHAR B A, YOUSEFI R T Stable EEG-based biometric system using functional connectivity based on time-frequency features with optimal channels
[J]. Biomedical Signal Processing and Control , 2022 , 77 : 103790
DOI:10.1016/j.bspc.2022.103790
[本文引用: 4]
[22]
ZHOU M, FANG Y, XIAO Z. Personal identification with exploiting competitive tasks in EEG signals [C]//Biometric Recognition . Cham: Springer, 2021: 11–19.
[本文引用: 2]
[23]
ALYASSERI Z A A, AHMAD ALOMARI O, MAKHADMEH S N, et al EEG channel selection for person identification using binary grey wolf optimizer
[J]. IEEE Access , 2022 , 10 : 10500 - 10513
DOI:10.1109/ACCESS.2021.3135805
[本文引用: 2]
[24]
JIN R, WANG Y, BAI R, et al. EPI-CGAN: robust EEG-based person identification using conditional generative adversarial network [C]//Proceedings of the IEEE International Joint Conference on Biometrics . Abu Dhabi: IEEE, 2023: 1–9.
[本文引用: 4]
[25]
ORTEGA-RODRÍGUEZ J, GÓMEZ-GONZÁLEZ J F, PEREDA E Selection of the minimum number of EEG sensors to guarantee biometric identification of individuals
[J]. Sensors , 2023 , 23 (9 ): 4239
DOI:10.3390/s23094239
[本文引用: 2]
[27]
ALSHEHRI L, HUSSAIN M A lightweight GCT-EEGNet for EEG-based individual recognition under diverse brain conditions
[J]. Mathematics , 2024 , 12 (20 ): 3286
DOI:10.3390/math12203286
[本文引用: 3]
[28]
LI D, ZENG Z, HUANG N, et al Brain topographic map: a visual feature for multi-view fusion design in EEG-based biometrics
[J]. Digital Signal Processing , 2025 , 164 : 105251
DOI:10.1016/j.dsp.2025.105251
[本文引用: 3]
[29]
DAS B B, KUMAR P, KAR D, et al A spatio-temporal model for EEG-based person identification
[J]. Multimedia Tools and Applications , 2019 , 78 (19 ): 28157 - 28177
DOI:10.1007/s11042-019-07905-6
[本文引用: 6]
[30]
ALYASSERI Z A A, AL-BETAR M A, AWADALLAH M A, et al. EEG feature fusion for person identification using efficient machine learning approach [C]//Proceedings of the Palestinian International Conference on Information and Communication Technology . Gaza: IEEE, 2021: 97–102.
[本文引用: 2]
[31]
KAUR B, SINGH D. Neuro signals: a future biomertic approach towards user identification [C]//Proceedings of the 7th International Conference on Cloud Computing, Data Science and Engineering - Confluence . Noida: IEEE, 2017: 112–117.
[本文引用: 3]
[32]
YAHYAEI R, ESAT ÖZKURT T Mean curve length: an efficient feature for brainwave biometrics
[J]. Biomedical Signal Processing and Control , 2022 , 76 : 103664
DOI:10.1016/j.bspc.2022.103664
[本文引用: 2]
[33]
LI D, ZENG Z, WANG Z, et al ESTformer: transformer utilising spatiotemporal dependencies for electroencephalogram super-resolution
[J]. Knowledge-Based Systems , 2025 , 317 : 113345
DOI:10.1016/j.knosys.2025.113345
[本文引用: 2]
[34]
BANDANA D B, KUMAR R S, SATHYA B K, et al Person identification using autoencoder-CNN approach with multitask-based EEG biometric
[J]. Multimedia Tools and Applications , 2024 , 83 (35 ): 83205 - 83225
DOI:10.1007/s11042-024-18693-z
[本文引用: 3]
[35]
WILAIPRASITPORN T, DITTHAPRON A, MATCHAPARN K, et al Affective EEG-based person identification using the deep learning approach
[J]. IEEE Transactions on Cognitive and Developmental Systems , 2020 , 12 (3 ): 486 - 496
DOI:10.1109/TCDS.2019.2924648
[本文引用: 3]
[36]
GÓMEZ-TAPIA C, BOZIC B, LONGO L On the minimal amount of EEG data required for learning distinctive human features for task-dependent biometric applications
[J]. Frontiers in Neuroinformatics , 2022 , 16 : 844667
DOI:10.3389/fninf.2022.844667
[本文引用: 4]
Review on EEG-based authentication technology
1
2021
... 生物识别系统已广泛应用于手机解锁、移动支付、安全监控等场景[1 ] . 目前主流技术如指纹、面部和虹膜识别,虽然便捷且精度较高,但活体检测能力不足,易被伪造,存在安全隐患[2 ] . 相比之下,脑电信号具有活体采集与不可伪造的特性,正逐步成为身份识别的新方向[3 ] . 过去十年中,传统机器学习方法如k近邻[4 ] 、朴素贝叶斯[5 ] 和支持向量机[6 ] 等被广泛应用于脑电生物特征研究. 这些方法依赖人工预处理与特征提取[7 ] ,不仅增加工作负担,而且限制模型泛化性能. ...
基于缩放卷积注意力网络的跨多个体脑电情绪识别
1
2024
... 生物识别系统已广泛应用于手机解锁、移动支付、安全监控等场景[1 ] . 目前主流技术如指纹、面部和虹膜识别,虽然便捷且精度较高,但活体检测能力不足,易被伪造,存在安全隐患[2 ] . 相比之下,脑电信号具有活体采集与不可伪造的特性,正逐步成为身份识别的新方向[3 ] . 过去十年中,传统机器学习方法如k近邻[4 ] 、朴素贝叶斯[5 ] 和支持向量机[6 ] 等被广泛应用于脑电生物特征研究. 这些方法依赖人工预处理与特征提取[7 ] ,不仅增加工作负担,而且限制模型泛化性能. ...
基于缩放卷积注意力网络的跨多个体脑电情绪识别
1
2024
... 生物识别系统已广泛应用于手机解锁、移动支付、安全监控等场景[1 ] . 目前主流技术如指纹、面部和虹膜识别,虽然便捷且精度较高,但活体检测能力不足,易被伪造,存在安全隐患[2 ] . 相比之下,脑电信号具有活体采集与不可伪造的特性,正逐步成为身份识别的新方向[3 ] . 过去十年中,传统机器学习方法如k近邻[4 ] 、朴素贝叶斯[5 ] 和支持向量机[6 ] 等被广泛应用于脑电生物特征研究. 这些方法依赖人工预处理与特征提取[7 ] ,不仅增加工作负担,而且限制模型泛化性能. ...
基于多尺度卷积和身份子空间的脑纹识别
1
2025
... 生物识别系统已广泛应用于手机解锁、移动支付、安全监控等场景[1 ] . 目前主流技术如指纹、面部和虹膜识别,虽然便捷且精度较高,但活体检测能力不足,易被伪造,存在安全隐患[2 ] . 相比之下,脑电信号具有活体采集与不可伪造的特性,正逐步成为身份识别的新方向[3 ] . 过去十年中,传统机器学习方法如k近邻[4 ] 、朴素贝叶斯[5 ] 和支持向量机[6 ] 等被广泛应用于脑电生物特征研究. 这些方法依赖人工预处理与特征提取[7 ] ,不仅增加工作负担,而且限制模型泛化性能. ...
基于多尺度卷积和身份子空间的脑纹识别
1
2025
... 生物识别系统已广泛应用于手机解锁、移动支付、安全监控等场景[1 ] . 目前主流技术如指纹、面部和虹膜识别,虽然便捷且精度较高,但活体检测能力不足,易被伪造,存在安全隐患[2 ] . 相比之下,脑电信号具有活体采集与不可伪造的特性,正逐步成为身份识别的新方向[3 ] . 过去十年中,传统机器学习方法如k近邻[4 ] 、朴素贝叶斯[5 ] 和支持向量机[6 ] 等被广泛应用于脑电生物特征研究. 这些方法依赖人工预处理与特征提取[7 ] ,不仅增加工作负担,而且限制模型泛化性能. ...
Biometrics from brain electrical activity: a machine learning approach
1
2007
... 生物识别系统已广泛应用于手机解锁、移动支付、安全监控等场景[1 ] . 目前主流技术如指纹、面部和虹膜识别,虽然便捷且精度较高,但活体检测能力不足,易被伪造,存在安全隐患[2 ] . 相比之下,脑电信号具有活体采集与不可伪造的特性,正逐步成为身份识别的新方向[3 ] . 过去十年中,传统机器学习方法如k近邻[4 ] 、朴素贝叶斯[5 ] 和支持向量机[6 ] 等被广泛应用于脑电生物特征研究. 这些方法依赖人工预处理与特征提取[7 ] ,不仅增加工作负担,而且限制模型泛化性能. ...
1
... 生物识别系统已广泛应用于手机解锁、移动支付、安全监控等场景[1 ] . 目前主流技术如指纹、面部和虹膜识别,虽然便捷且精度较高,但活体检测能力不足,易被伪造,存在安全隐患[2 ] . 相比之下,脑电信号具有活体采集与不可伪造的特性,正逐步成为身份识别的新方向[3 ] . 过去十年中,传统机器学习方法如k近邻[4 ] 、朴素贝叶斯[5 ] 和支持向量机[6 ] 等被广泛应用于脑电生物特征研究. 这些方法依赖人工预处理与特征提取[7 ] ,不仅增加工作负担,而且限制模型泛化性能. ...
EEG electrode selection for person identification thru a genetic-algorithm method
1
2019
... 生物识别系统已广泛应用于手机解锁、移动支付、安全监控等场景[1 ] . 目前主流技术如指纹、面部和虹膜识别,虽然便捷且精度较高,但活体检测能力不足,易被伪造,存在安全隐患[2 ] . 相比之下,脑电信号具有活体采集与不可伪造的特性,正逐步成为身份识别的新方向[3 ] . 过去十年中,传统机器学习方法如k近邻[4 ] 、朴素贝叶斯[5 ] 和支持向量机[6 ] 等被广泛应用于脑电生物特征研究. 这些方法依赖人工预处理与特征提取[7 ] ,不仅增加工作负担,而且限制模型泛化性能. ...
On the usability of electroencephalographic signals for biometric recognition: a survey
1
2017
... 生物识别系统已广泛应用于手机解锁、移动支付、安全监控等场景[1 ] . 目前主流技术如指纹、面部和虹膜识别,虽然便捷且精度较高,但活体检测能力不足,易被伪造,存在安全隐患[2 ] . 相比之下,脑电信号具有活体采集与不可伪造的特性,正逐步成为身份识别的新方向[3 ] . 过去十年中,传统机器学习方法如k近邻[4 ] 、朴素贝叶斯[5 ] 和支持向量机[6 ] 等被广泛应用于脑电生物特征研究. 这些方法依赖人工预处理与特征提取[7 ] ,不仅增加工作负担,而且限制模型泛化性能. ...
EEG-based user identification system using 1D-convolutional long short-term memory neural networks
5
2019
... 近年来,深度学习模型逐渐应用于EEG生物识别研究. 学者们为了提升识别率,采用更复杂的模型. Sun等[8 ] 结合卷积神经网络(CNN)和长短时记忆网络(LSTM),在Physionet数据集上的准确率大于98%,但模型参数量超过5.05亿. Schons等[9 ] 采用滑动窗口数据增强和CNN相结合,在相同数据集上实现 0.19%的等错误率(EER),但参数量超过7 800万. 这类方法虽然识别性能优异,但因参数庞大,难以实际部署. ...
... 针对数据集的测试,以Physionet-MI数据为主进行展开. 如表2 所示,对不同时间段及不同通道数N 下的分类准确率进行系统测试. 选取的时间段是1 s和4 s. 将通道数设为3、4、8、15、16、19、32、64. 4、16、32和64通道的分组参考文献[8 ],15通道和19通道的分组参考文献[21 ]. 3通道配置采用C3、C4和Cz,8通道配置包括F3、F4、C3、Cz、C4、P3、P4和Pz. ...
... Comparison of motor imagery data for Physionet dataset
Tab.5 方法 slot/s N ACC/% EER/% N p /106 COH_CNN[21 ] [21 ] 1 19 98.22 — — CNN-LSTM[8 ] 1 16 99.58 0.410 1927.50 多任务对抗学习[22 ] 1 64 99.20 — — BGWO-SVM[23 ] 1 23 94.13 — — EPI-CGAN[24 ] 1 64 99.02 — — PCA+SVM[25 ] 2 64 99.91 — — DNN[26 ] 4 64 97.81 — — GCT-EEGNet[27 ] 1 32 98.90 0.004 0.17 ResNet18[28 ] 1 64 99.59 — 11.25 提出方法 1 15 98.52 0.001 0.29
Ashenaei等[21 ] 使用COH提取特征,输入CNN分类,该模型在1 s时间段、19通道和1 s时间段、15通道的配置下,准确率分别达到98.22%和97.74%,本文方法在相同通道下分别提高了0.64%和0.78%. Sun等[8 ] 使用CNN-LSTM模型在64通道的配置下实现了99.58%的高识别准确率,比本文方法在64通道下的识别准确率低0.39%. 虽然文献[8 ]算法在16通道下的识别准确率略优于本文方法,但其结合了LSTM层,将参数量增加到1927.5 × 106 ,这增加了过拟合的风险,而本文模型的参数量远远小于该模型,且EER更低. Alyasseri等[23 ] 使用BGWO-SVM在23通道的配置下取得94.13%的准确率,相比之下,本文方法在更少通道数下表现更优. Ortega-Rodríguez等[25 ] 采用主成分分析结合SVM进行脑纹识别,在2 s时间段、64通道的配置下取得了99.91%的准确率. 本文方法仅在1 s时间段便能达到更优的识别效果,显示出更高的效率和实用性. Akbarnia等[26 ] 使用DNN对预处理脑电信号进行脑纹识别,在4 s时间段、64通道的配置下实现97.81%的准确率,明显低于所提方法的识别效果. Alshehri等[27 ] 提出轻量级GCT-EEGNet网络进行脑纹识别,在1 s时间段、32通道的配置下实现98.90%的识别准确率,虽然文献[27 ]方法采用的参数量仅为0.17×106 ,但识别性能低于本文方法. Li等[28 ] 构建多视图融合模型,使用ResNet18进行分类,在1 s时间段、64通道的配置下实现99.59%的准确率,参数量为11.25×106 . 相比之下,本文模型在参数量远小于文献[28 ]模型的情况下,识别准确率与其相当. Jin等[24 ] 采用EPI-CGAN模型,该模型在64通道下的准确率达到99.02%. Zhou等[22 ] 将LFCC特征与多任务对抗学习相结合,在64通道下取得99.20%的准确率. 这2种方法使用较多的通道数,且分类效果不及本文所提方法. 通过在Physionet-MI数据上的分类性能比较,验证了本文所提方法即便在参数量较少的情况下,仍能取得较好的分类效果. ...
... Ashenaei等[21 ] 使用COH提取特征,输入CNN分类,该模型在1 s时间段、19通道和1 s时间段、15通道的配置下,准确率分别达到98.22%和97.74%,本文方法在相同通道下分别提高了0.64%和0.78%. Sun等[8 ] 使用CNN-LSTM模型在64通道的配置下实现了99.58%的高识别准确率,比本文方法在64通道下的识别准确率低0.39%. 虽然文献[8 ]算法在16通道下的识别准确率略优于本文方法,但其结合了LSTM层,将参数量增加到1927.5 × 106 ,这增加了过拟合的风险,而本文模型的参数量远远小于该模型,且EER更低. Alyasseri等[23 ] 使用BGWO-SVM在23通道的配置下取得94.13%的准确率,相比之下,本文方法在更少通道数下表现更优. Ortega-Rodríguez等[25 ] 采用主成分分析结合SVM进行脑纹识别,在2 s时间段、64通道的配置下取得了99.91%的准确率. 本文方法仅在1 s时间段便能达到更优的识别效果,显示出更高的效率和实用性. Akbarnia等[26 ] 使用DNN对预处理脑电信号进行脑纹识别,在4 s时间段、64通道的配置下实现97.81%的准确率,明显低于所提方法的识别效果. Alshehri等[27 ] 提出轻量级GCT-EEGNet网络进行脑纹识别,在1 s时间段、32通道的配置下实现98.90%的识别准确率,虽然文献[27 ]方法采用的参数量仅为0.17×106 ,但识别性能低于本文方法. Li等[28 ] 构建多视图融合模型,使用ResNet18进行分类,在1 s时间段、64通道的配置下实现99.59%的准确率,参数量为11.25×106 . 相比之下,本文模型在参数量远小于文献[28 ]模型的情况下,识别准确率与其相当. Jin等[24 ] 采用EPI-CGAN模型,该模型在64通道下的准确率达到99.02%. Zhou等[22 ] 将LFCC特征与多任务对抗学习相结合,在64通道下取得99.20%的准确率. 这2种方法使用较多的通道数,且分类效果不及本文所提方法. 通过在Physionet-MI数据上的分类性能比较,验证了本文所提方法即便在参数量较少的情况下,仍能取得较好的分类效果. ...
... 使用CNN-LSTM模型在64通道的配置下实现了99.58%的高识别准确率,比本文方法在64通道下的识别准确率低0.39%. 虽然文献[8 ]算法在16通道下的识别准确率略优于本文方法,但其结合了LSTM层,将参数量增加到1927.5 × 106 ,这增加了过拟合的风险,而本文模型的参数量远远小于该模型,且EER更低. Alyasseri等[23 ] 使用BGWO-SVM在23通道的配置下取得94.13%的准确率,相比之下,本文方法在更少通道数下表现更优. Ortega-Rodríguez等[25 ] 采用主成分分析结合SVM进行脑纹识别,在2 s时间段、64通道的配置下取得了99.91%的准确率. 本文方法仅在1 s时间段便能达到更优的识别效果,显示出更高的效率和实用性. Akbarnia等[26 ] 使用DNN对预处理脑电信号进行脑纹识别,在4 s时间段、64通道的配置下实现97.81%的准确率,明显低于所提方法的识别效果. Alshehri等[27 ] 提出轻量级GCT-EEGNet网络进行脑纹识别,在1 s时间段、32通道的配置下实现98.90%的识别准确率,虽然文献[27 ]方法采用的参数量仅为0.17×106 ,但识别性能低于本文方法. Li等[28 ] 构建多视图融合模型,使用ResNet18进行分类,在1 s时间段、64通道的配置下实现99.59%的准确率,参数量为11.25×106 . 相比之下,本文模型在参数量远小于文献[28 ]模型的情况下,识别准确率与其相当. Jin等[24 ] 采用EPI-CGAN模型,该模型在64通道下的准确率达到99.02%. Zhou等[22 ] 将LFCC特征与多任务对抗学习相结合,在64通道下取得99.20%的准确率. 这2种方法使用较多的通道数,且分类效果不及本文所提方法. 通过在Physionet-MI数据上的分类性能比较,验证了本文所提方法即便在参数量较少的情况下,仍能取得较好的分类效果. ...
3
... 近年来,深度学习模型逐渐应用于EEG生物识别研究. 学者们为了提升识别率,采用更复杂的模型. Sun等[8 ] 结合卷积神经网络(CNN)和长短时记忆网络(LSTM),在Physionet数据集上的准确率大于98%,但模型参数量超过5.05亿. Schons等[9 ] 采用滑动窗口数据增强和CNN相结合,在相同数据集上实现 0.19%的等错误率(EER),但参数量超过7 800万. 这类方法虽然识别性能优异,但因参数庞大,难以实际部署. ...
... 如表6 所示为本文方法与其他方法在Physionet数据集中静息状态数据的分类表现,对于同一数据集,当前主流的算法性能与本文方法的比较如下. Das等[29 ] 使用CNN-LSTM模型进行测试,在4 s、8 s、12 s和16 s的实验中,12 s时段的效果最佳,EO和EC的识别准确率分别为98.00%和99.95%. 本文方法的EC识别准确率略低于文献[29 ]方法,但本文方法仅用2 s时间段,更适用于实际应用. Tian等[13 ] 应用基于GCN的方法,使用1 s数据,最高准确率达到98.56%,但在通道减少时准确率下降较快. 相比之下,本文方法在低通道数下保持较高的准确率. Schons等[9 ] 结合滑动窗口的数据增强技术和CNN,在最佳情况下EER为0.190%,本文所提方法在64通道下EER更低,使用的时间段更短. Li等[33 ] 提出ESTformer模型进行脑纹识别,在10 s时间段、64通道的条件下实现94.61%的准确率,模型参数量为33.7×106 . 相比之下,本文方法的准确率更高,参数量更少. Bandana等[34 ] 提出使用自动编码器对脑电信号进行重建,再使用CNN进行分类,在8 s时间段、64通道的配置下,睁眼和闭眼状态时分别达到99.45%和99.89%的准确率,但文献[34 ]方法使用的时间段比本文方法长. ...
... Comparison of resting state data for Physionet dataset
Tab.6 方法 slot/s N EO EC N p /106 ACC/% EER/% ACC/% EER/% 连通性网络[11 ] 12 64 96.90 4.400 92.60 6.500 — CNN-LSTM[29 ] [29 ] [29 ] [29 ] 4 64 95.00 — 95.33 — — COR+GCN[13 ] [13 ] [13 ] 1 64 98.56 — — — — FDF+SVM_RBF[30 ] 10 64 97.22 — — — — RF[31 ] 2 64 98.16 — 97.30 — — SVM[31 ] 2 64 97.64 — 96.02 — — MCL+马氏距离分类器[32 ] 10 64 99.40 6.330 98.80 10.500 — CNN+数据增强[9 ] 12 64 — — — 0.190 300.82 PLV+Gamma[12 ] [12 ] 4 56 99.40 — — — — ESTformer[33 ] 10 64 94.61 — — — 33.70 Autoencoder-CNN[34 ] 8 64 99.45 — 99.89 — — 提出方法 2 3 90.60 0.179 90.16 0.137 0.29
Fraschini等[11 ] 采用构建功能连通性脑网络的方法,使用12 s数据,在64通道的情况下,EO的识别准确率为96.90%,EC的识别准确率为92.60%. 相比之下,本文方法的准确率平均提高了2.55%和6.41%. Alyasseri等[30 ] 通过提取PSD和AR特征,送入SVM_RBF分类器进行分类,在64通道的条件下识别准确率达到97.22%,比本文方法低2.23%. Kaur等[31 ] 应用PCA提取特征,使用SVM分类的睁眼和闭眼状态的身份识别准确率分别为97.64%和96.02%,使用RF分类器的身份识别准确率分别为98.16%和97.30%,识别效果不如本文方法. Yahyaei等[32 ] 提取脑电信号的MCL特征,使用马氏距离分类器进行分类,在10 s时间段、64通道的条件下,EO识别准确率达到99.40%,EC识别准确率达到98.80%,但EER较高. Kumar等[12 ] 使用基于锁相值的SVM方法,在使用56通道时获得99.40%的准确率,当通道数减少至21时,准确率仅下降3.40%. 相比之下,本文方法在2 s时间段、16通道的配置下,准确率超过文献[12 ]方法在4 s时间段、21通道下的表现. 通过上述在睁眼和闭眼状态数据上的比较,本文方法在参数量较少,时间段较短的情况下,分类效果在多种性能评估下更好. ...
Convolutional neural networks using dynamic functional connectivity for EEG-based person identification in diverse human states
1
2019
... 部分算法致力于降低参数量,但通常需要更多的通道数或更长的时间段. Wang等[10 ] 在 Physionet数据集上采用相位锁定值和图卷积网络(GCN),在64通道、5.5 s时间段的条件下准确率超过98%,但在通道减少时性能显著下降. Fraschini等[11 ] 通过构建功能连通性脑网络进行身份识别,在睁眼静息态12 s的EEG数据上实现了96.9%的识别准确率,但该方法依赖较长时间段的脑电信号. Kumar等[12 ] 在Physionet数据集静息态数据中采用基于锁相值的SVM方法,在21通道下的准确率为96%. Tian等[13 ] 在同一数据集上应用基于GCN的方法,使用1 s时间段、16通道数据的识别准确率为53.41%. Myung等[14 ] 通过经验模态分解和频谱图提取特征,结合CNN在8通道静息态数据中达到75.7%的准确率. ...
An EEG-based biometric system using eigenvector centrality in resting state brain networks
3
2015
... 部分算法致力于降低参数量,但通常需要更多的通道数或更长的时间段. Wang等[10 ] 在 Physionet数据集上采用相位锁定值和图卷积网络(GCN),在64通道、5.5 s时间段的条件下准确率超过98%,但在通道减少时性能显著下降. Fraschini等[11 ] 通过构建功能连通性脑网络进行身份识别,在睁眼静息态12 s的EEG数据上实现了96.9%的识别准确率,但该方法依赖较长时间段的脑电信号. Kumar等[12 ] 在Physionet数据集静息态数据中采用基于锁相值的SVM方法,在21通道下的准确率为96%. Tian等[13 ] 在同一数据集上应用基于GCN的方法,使用1 s时间段、16通道数据的识别准确率为53.41%. Myung等[14 ] 通过经验模态分解和频谱图提取特征,结合CNN在8通道静息态数据中达到75.7%的准确率. ...
... Comparison of resting state data for Physionet dataset
Tab.6 方法 slot/s N EO EC N p /106 ACC/% EER/% ACC/% EER/% 连通性网络[11 ] 12 64 96.90 4.400 92.60 6.500 — CNN-LSTM[29 ] [29 ] [29 ] [29 ] 4 64 95.00 — 95.33 — — COR+GCN[13 ] [13 ] [13 ] 1 64 98.56 — — — — FDF+SVM_RBF[30 ] 10 64 97.22 — — — — RF[31 ] 2 64 98.16 — 97.30 — — SVM[31 ] 2 64 97.64 — 96.02 — — MCL+马氏距离分类器[32 ] 10 64 99.40 6.330 98.80 10.500 — CNN+数据增强[9 ] 12 64 — — — 0.190 300.82 PLV+Gamma[12 ] [12 ] 4 56 99.40 — — — — ESTformer[33 ] 10 64 94.61 — — — 33.70 Autoencoder-CNN[34 ] 8 64 99.45 — 99.89 — — 提出方法 2 3 90.60 0.179 90.16 0.137 0.29
Fraschini等[11 ] 采用构建功能连通性脑网络的方法,使用12 s数据,在64通道的情况下,EO的识别准确率为96.90%,EC的识别准确率为92.60%. 相比之下,本文方法的准确率平均提高了2.55%和6.41%. Alyasseri等[30 ] 通过提取PSD和AR特征,送入SVM_RBF分类器进行分类,在64通道的条件下识别准确率达到97.22%,比本文方法低2.23%. Kaur等[31 ] 应用PCA提取特征,使用SVM分类的睁眼和闭眼状态的身份识别准确率分别为97.64%和96.02%,使用RF分类器的身份识别准确率分别为98.16%和97.30%,识别效果不如本文方法. Yahyaei等[32 ] 提取脑电信号的MCL特征,使用马氏距离分类器进行分类,在10 s时间段、64通道的条件下,EO识别准确率达到99.40%,EC识别准确率达到98.80%,但EER较高. Kumar等[12 ] 使用基于锁相值的SVM方法,在使用56通道时获得99.40%的准确率,当通道数减少至21时,准确率仅下降3.40%. 相比之下,本文方法在2 s时间段、16通道的配置下,准确率超过文献[12 ]方法在4 s时间段、21通道下的表现. 通过上述在睁眼和闭眼状态数据上的比较,本文方法在参数量较少,时间段较短的情况下,分类效果在多种性能评估下更好. ...
... Fraschini等[11 ] 采用构建功能连通性脑网络的方法,使用12 s数据,在64通道的情况下,EO的识别准确率为96.90%,EC的识别准确率为92.60%. 相比之下,本文方法的准确率平均提高了2.55%和6.41%. Alyasseri等[30 ] 通过提取PSD和AR特征,送入SVM_RBF分类器进行分类,在64通道的条件下识别准确率达到97.22%,比本文方法低2.23%. Kaur等[31 ] 应用PCA提取特征,使用SVM分类的睁眼和闭眼状态的身份识别准确率分别为97.64%和96.02%,使用RF分类器的身份识别准确率分别为98.16%和97.30%,识别效果不如本文方法. Yahyaei等[32 ] 提取脑电信号的MCL特征,使用马氏距离分类器进行分类,在10 s时间段、64通道的条件下,EO识别准确率达到99.40%,EC识别准确率达到98.80%,但EER较高. Kumar等[12 ] 使用基于锁相值的SVM方法,在使用56通道时获得99.40%的准确率,当通道数减少至21时,准确率仅下降3.40%. 相比之下,本文方法在2 s时间段、16通道的配置下,准确率超过文献[12 ]方法在4 s时间段、21通道下的表现. 通过上述在睁眼和闭眼状态数据上的比较,本文方法在参数量较少,时间段较短的情况下,分类效果在多种性能评估下更好. ...
5
... 部分算法致力于降低参数量,但通常需要更多的通道数或更长的时间段. Wang等[10 ] 在 Physionet数据集上采用相位锁定值和图卷积网络(GCN),在64通道、5.5 s时间段的条件下准确率超过98%,但在通道减少时性能显著下降. Fraschini等[11 ] 通过构建功能连通性脑网络进行身份识别,在睁眼静息态12 s的EEG数据上实现了96.9%的识别准确率,但该方法依赖较长时间段的脑电信号. Kumar等[12 ] 在Physionet数据集静息态数据中采用基于锁相值的SVM方法,在21通道下的准确率为96%. Tian等[13 ] 在同一数据集上应用基于GCN的方法,使用1 s时间段、16通道数据的识别准确率为53.41%. Myung等[14 ] 通过经验模态分解和频谱图提取特征,结合CNN在8通道静息态数据中达到75.7%的准确率. ...
... Comparison of resting state data for Physionet dataset
Tab.6 方法 slot/s N EO EC N p /106 ACC/% EER/% ACC/% EER/% 连通性网络[11 ] 12 64 96.90 4.400 92.60 6.500 — CNN-LSTM[29 ] [29 ] [29 ] [29 ] 4 64 95.00 — 95.33 — — COR+GCN[13 ] [13 ] [13 ] 1 64 98.56 — — — — FDF+SVM_RBF[30 ] 10 64 97.22 — — — — RF[31 ] 2 64 98.16 — 97.30 — — SVM[31 ] 2 64 97.64 — 96.02 — — MCL+马氏距离分类器[32 ] 10 64 99.40 6.330 98.80 10.500 — CNN+数据增强[9 ] 12 64 — — — 0.190 300.82 PLV+Gamma[12 ] [12 ] 4 56 99.40 — — — — ESTformer[33 ] 10 64 94.61 — — — 33.70 Autoencoder-CNN[34 ] 8 64 99.45 — 99.89 — — 提出方法 2 3 90.60 0.179 90.16 0.137 0.29
Fraschini等[11 ] 采用构建功能连通性脑网络的方法,使用12 s数据,在64通道的情况下,EO的识别准确率为96.90%,EC的识别准确率为92.60%. 相比之下,本文方法的准确率平均提高了2.55%和6.41%. Alyasseri等[30 ] 通过提取PSD和AR特征,送入SVM_RBF分类器进行分类,在64通道的条件下识别准确率达到97.22%,比本文方法低2.23%. Kaur等[31 ] 应用PCA提取特征,使用SVM分类的睁眼和闭眼状态的身份识别准确率分别为97.64%和96.02%,使用RF分类器的身份识别准确率分别为98.16%和97.30%,识别效果不如本文方法. Yahyaei等[32 ] 提取脑电信号的MCL特征,使用马氏距离分类器进行分类,在10 s时间段、64通道的条件下,EO识别准确率达到99.40%,EC识别准确率达到98.80%,但EER较高. Kumar等[12 ] 使用基于锁相值的SVM方法,在使用56通道时获得99.40%的准确率,当通道数减少至21时,准确率仅下降3.40%. 相比之下,本文方法在2 s时间段、16通道的配置下,准确率超过文献[12 ]方法在4 s时间段、21通道下的表现. 通过上述在睁眼和闭眼状态数据上的比较,本文方法在参数量较少,时间段较短的情况下,分类效果在多种性能评估下更好. ...
... [
12 ]
4 56 99.40 — — — — ESTformer[33 ] 10 64 94.61 — — — 33.70 Autoencoder-CNN[34 ] 8 64 99.45 — 99.89 — — 提出方法 2 3 90.60 0.179 90.16 0.137 0.29 Fraschini等[11 ] 采用构建功能连通性脑网络的方法,使用12 s数据,在64通道的情况下,EO的识别准确率为96.90%,EC的识别准确率为92.60%. 相比之下,本文方法的准确率平均提高了2.55%和6.41%. Alyasseri等[30 ] 通过提取PSD和AR特征,送入SVM_RBF分类器进行分类,在64通道的条件下识别准确率达到97.22%,比本文方法低2.23%. Kaur等[31 ] 应用PCA提取特征,使用SVM分类的睁眼和闭眼状态的身份识别准确率分别为97.64%和96.02%,使用RF分类器的身份识别准确率分别为98.16%和97.30%,识别效果不如本文方法. Yahyaei等[32 ] 提取脑电信号的MCL特征,使用马氏距离分类器进行分类,在10 s时间段、64通道的条件下,EO识别准确率达到99.40%,EC识别准确率达到98.80%,但EER较高. Kumar等[12 ] 使用基于锁相值的SVM方法,在使用56通道时获得99.40%的准确率,当通道数减少至21时,准确率仅下降3.40%. 相比之下,本文方法在2 s时间段、16通道的配置下,准确率超过文献[12 ]方法在4 s时间段、21通道下的表现. 通过上述在睁眼和闭眼状态数据上的比较,本文方法在参数量较少,时间段较短的情况下,分类效果在多种性能评估下更好. ...
... Fraschini等[11 ] 采用构建功能连通性脑网络的方法,使用12 s数据,在64通道的情况下,EO的识别准确率为96.90%,EC的识别准确率为92.60%. 相比之下,本文方法的准确率平均提高了2.55%和6.41%. Alyasseri等[30 ] 通过提取PSD和AR特征,送入SVM_RBF分类器进行分类,在64通道的条件下识别准确率达到97.22%,比本文方法低2.23%. Kaur等[31 ] 应用PCA提取特征,使用SVM分类的睁眼和闭眼状态的身份识别准确率分别为97.64%和96.02%,使用RF分类器的身份识别准确率分别为98.16%和97.30%,识别效果不如本文方法. Yahyaei等[32 ] 提取脑电信号的MCL特征,使用马氏距离分类器进行分类,在10 s时间段、64通道的条件下,EO识别准确率达到99.40%,EC识别准确率达到98.80%,但EER较高. Kumar等[12 ] 使用基于锁相值的SVM方法,在使用56通道时获得99.40%的准确率,当通道数减少至21时,准确率仅下降3.40%. 相比之下,本文方法在2 s时间段、16通道的配置下,准确率超过文献[12 ]方法在4 s时间段、21通道下的表现. 通过上述在睁眼和闭眼状态数据上的比较,本文方法在参数量较少,时间段较短的情况下,分类效果在多种性能评估下更好. ...
... 使用基于锁相值的SVM方法,在使用56通道时获得99.40%的准确率,当通道数减少至21时,准确率仅下降3.40%. 相比之下,本文方法在2 s时间段、16通道的配置下,准确率超过文献[12 ]方法在4 s时间段、21通道下的表现. 通过上述在睁眼和闭眼状态数据上的比较,本文方法在参数量较少,时间段较短的情况下,分类效果在多种性能评估下更好. ...
Applying multiple functional connectivity features in GCN for EEG-based human identification
5
2022
... 部分算法致力于降低参数量,但通常需要更多的通道数或更长的时间段. Wang等[10 ] 在 Physionet数据集上采用相位锁定值和图卷积网络(GCN),在64通道、5.5 s时间段的条件下准确率超过98%,但在通道减少时性能显著下降. Fraschini等[11 ] 通过构建功能连通性脑网络进行身份识别,在睁眼静息态12 s的EEG数据上实现了96.9%的识别准确率,但该方法依赖较长时间段的脑电信号. Kumar等[12 ] 在Physionet数据集静息态数据中采用基于锁相值的SVM方法,在21通道下的准确率为96%. Tian等[13 ] 在同一数据集上应用基于GCN的方法,使用1 s时间段、16通道数据的识别准确率为53.41%. Myung等[14 ] 通过经验模态分解和频谱图提取特征,结合CNN在8通道静息态数据中达到75.7%的准确率. ...
... 如表6 所示为本文方法与其他方法在Physionet数据集中静息状态数据的分类表现,对于同一数据集,当前主流的算法性能与本文方法的比较如下. Das等[29 ] 使用CNN-LSTM模型进行测试,在4 s、8 s、12 s和16 s的实验中,12 s时段的效果最佳,EO和EC的识别准确率分别为98.00%和99.95%. 本文方法的EC识别准确率略低于文献[29 ]方法,但本文方法仅用2 s时间段,更适用于实际应用. Tian等[13 ] 应用基于GCN的方法,使用1 s数据,最高准确率达到98.56%,但在通道减少时准确率下降较快. 相比之下,本文方法在低通道数下保持较高的准确率. Schons等[9 ] 结合滑动窗口的数据增强技术和CNN,在最佳情况下EER为0.190%,本文所提方法在64通道下EER更低,使用的时间段更短. Li等[33 ] 提出ESTformer模型进行脑纹识别,在10 s时间段、64通道的条件下实现94.61%的准确率,模型参数量为33.7×106 . 相比之下,本文方法的准确率更高,参数量更少. Bandana等[34 ] 提出使用自动编码器对脑电信号进行重建,再使用CNN进行分类,在8 s时间段、64通道的配置下,睁眼和闭眼状态时分别达到99.45%和99.89%的准确率,但文献[34 ]方法使用的时间段比本文方法长. ...
... Comparison of resting state data for Physionet dataset
Tab.6 方法 slot/s N EO EC N p /106 ACC/% EER/% ACC/% EER/% 连通性网络[11 ] 12 64 96.90 4.400 92.60 6.500 — CNN-LSTM[29 ] [29 ] [29 ] [29 ] 4 64 95.00 — 95.33 — — COR+GCN[13 ] [13 ] [13 ] 1 64 98.56 — — — — FDF+SVM_RBF[30 ] 10 64 97.22 — — — — RF[31 ] 2 64 98.16 — 97.30 — — SVM[31 ] 2 64 97.64 — 96.02 — — MCL+马氏距离分类器[32 ] 10 64 99.40 6.330 98.80 10.500 — CNN+数据增强[9 ] 12 64 — — — 0.190 300.82 PLV+Gamma[12 ] [12 ] 4 56 99.40 — — — — ESTformer[33 ] 10 64 94.61 — — — 33.70 Autoencoder-CNN[34 ] 8 64 99.45 — 99.89 — — 提出方法 2 3 90.60 0.179 90.16 0.137 0.29
Fraschini等[11 ] 采用构建功能连通性脑网络的方法,使用12 s数据,在64通道的情况下,EO的识别准确率为96.90%,EC的识别准确率为92.60%. 相比之下,本文方法的准确率平均提高了2.55%和6.41%. Alyasseri等[30 ] 通过提取PSD和AR特征,送入SVM_RBF分类器进行分类,在64通道的条件下识别准确率达到97.22%,比本文方法低2.23%. Kaur等[31 ] 应用PCA提取特征,使用SVM分类的睁眼和闭眼状态的身份识别准确率分别为97.64%和96.02%,使用RF分类器的身份识别准确率分别为98.16%和97.30%,识别效果不如本文方法. Yahyaei等[32 ] 提取脑电信号的MCL特征,使用马氏距离分类器进行分类,在10 s时间段、64通道的条件下,EO识别准确率达到99.40%,EC识别准确率达到98.80%,但EER较高. Kumar等[12 ] 使用基于锁相值的SVM方法,在使用56通道时获得99.40%的准确率,当通道数减少至21时,准确率仅下降3.40%. 相比之下,本文方法在2 s时间段、16通道的配置下,准确率超过文献[12 ]方法在4 s时间段、21通道下的表现. 通过上述在睁眼和闭眼状态数据上的比较,本文方法在参数量较少,时间段较短的情况下,分类效果在多种性能评估下更好. ...
... [
13 ]
COR+GCN
[13 ] 1 64 98.56 — — — — FDF+SVM_RBF[30 ] 10 64 97.22 — — — — RF[31 ] 2 64 98.16 — 97.30 — — SVM[31 ] 2 64 97.64 — 96.02 — — MCL+马氏距离分类器[32 ] 10 64 99.40 6.330 98.80 10.500 — CNN+数据增强[9 ] 12 64 — — — 0.190 300.82 PLV+Gamma[12 ] [12 ] 4 56 99.40 — — — — ESTformer[33 ] 10 64 94.61 — — — 33.70 Autoencoder-CNN[34 ] 8 64 99.45 — 99.89 — — 提出方法 2 3 90.60 0.179 90.16 0.137 0.29 Fraschini等[11 ] 采用构建功能连通性脑网络的方法,使用12 s数据,在64通道的情况下,EO的识别准确率为96.90%,EC的识别准确率为92.60%. 相比之下,本文方法的准确率平均提高了2.55%和6.41%. Alyasseri等[30 ] 通过提取PSD和AR特征,送入SVM_RBF分类器进行分类,在64通道的条件下识别准确率达到97.22%,比本文方法低2.23%. Kaur等[31 ] 应用PCA提取特征,使用SVM分类的睁眼和闭眼状态的身份识别准确率分别为97.64%和96.02%,使用RF分类器的身份识别准确率分别为98.16%和97.30%,识别效果不如本文方法. Yahyaei等[32 ] 提取脑电信号的MCL特征,使用马氏距离分类器进行分类,在10 s时间段、64通道的条件下,EO识别准确率达到99.40%,EC识别准确率达到98.80%,但EER较高. Kumar等[12 ] 使用基于锁相值的SVM方法,在使用56通道时获得99.40%的准确率,当通道数减少至21时,准确率仅下降3.40%. 相比之下,本文方法在2 s时间段、16通道的配置下,准确率超过文献[12 ]方法在4 s时间段、21通道下的表现. 通过上述在睁眼和闭眼状态数据上的比较,本文方法在参数量较少,时间段较短的情况下,分类效果在多种性能评估下更好. ...
... [
13 ]
1 64 98.56 — — — — FDF+SVM_RBF[30 ] 10 64 97.22 — — — — RF[31 ] 2 64 98.16 — 97.30 — — SVM[31 ] 2 64 97.64 — 96.02 — — MCL+马氏距离分类器[32 ] 10 64 99.40 6.330 98.80 10.500 — CNN+数据增强[9 ] 12 64 — — — 0.190 300.82 PLV+Gamma[12 ] [12 ] 4 56 99.40 — — — — ESTformer[33 ] 10 64 94.61 — — — 33.70 Autoencoder-CNN[34 ] 8 64 99.45 — 99.89 — — 提出方法 2 3 90.60 0.179 90.16 0.137 0.29 Fraschini等[11 ] 采用构建功能连通性脑网络的方法,使用12 s数据,在64通道的情况下,EO的识别准确率为96.90%,EC的识别准确率为92.60%. 相比之下,本文方法的准确率平均提高了2.55%和6.41%. Alyasseri等[30 ] 通过提取PSD和AR特征,送入SVM_RBF分类器进行分类,在64通道的条件下识别准确率达到97.22%,比本文方法低2.23%. Kaur等[31 ] 应用PCA提取特征,使用SVM分类的睁眼和闭眼状态的身份识别准确率分别为97.64%和96.02%,使用RF分类器的身份识别准确率分别为98.16%和97.30%,识别效果不如本文方法. Yahyaei等[32 ] 提取脑电信号的MCL特征,使用马氏距离分类器进行分类,在10 s时间段、64通道的条件下,EO识别准确率达到99.40%,EC识别准确率达到98.80%,但EER较高. Kumar等[12 ] 使用基于锁相值的SVM方法,在使用56通道时获得99.40%的准确率,当通道数减少至21时,准确率仅下降3.40%. 相比之下,本文方法在2 s时间段、16通道的配置下,准确率超过文献[12 ]方法在4 s时间段、21通道下的表现. 通过上述在睁眼和闭眼状态数据上的比较,本文方法在参数量较少,时间段较短的情况下,分类效果在多种性能评估下更好. ...
1
... 部分算法致力于降低参数量,但通常需要更多的通道数或更长的时间段. Wang等[10 ] 在 Physionet数据集上采用相位锁定值和图卷积网络(GCN),在64通道、5.5 s时间段的条件下准确率超过98%,但在通道减少时性能显著下降. Fraschini等[11 ] 通过构建功能连通性脑网络进行身份识别,在睁眼静息态12 s的EEG数据上实现了96.9%的识别准确率,但该方法依赖较长时间段的脑电信号. Kumar等[12 ] 在Physionet数据集静息态数据中采用基于锁相值的SVM方法,在21通道下的准确率为96%. Tian等[13 ] 在同一数据集上应用基于GCN的方法,使用1 s时间段、16通道数据的识别准确率为53.41%. Myung等[14 ] 通过经验模态分解和频谱图提取特征,结合CNN在8通道静息态数据中达到75.7%的准确率. ...
1
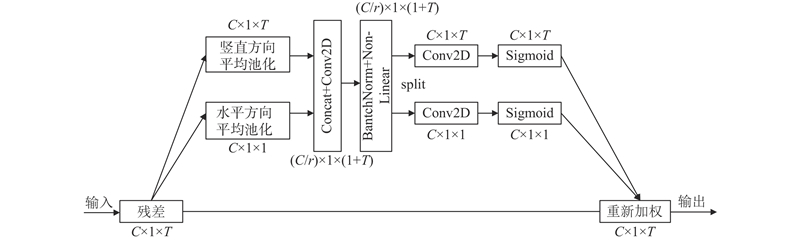
... 在多通道脑电信号处理领域,不同通道对识别任务的重要性存在显著差异,故而合理分配各通道的权重显得尤为关键. 引入CA模块[15 ] ,该模块不仅能够增强空间特征的建模能力,而且能够为不同通道赋予恰当的权重,从而有效地提取关键通道信息,进而提升脑电信号的判别性能. CA模块算法的实现结构如图2 所示. ...
EEGNet: a compact convolutional neural network for EEG-based brain–computer interfaces
1
2018
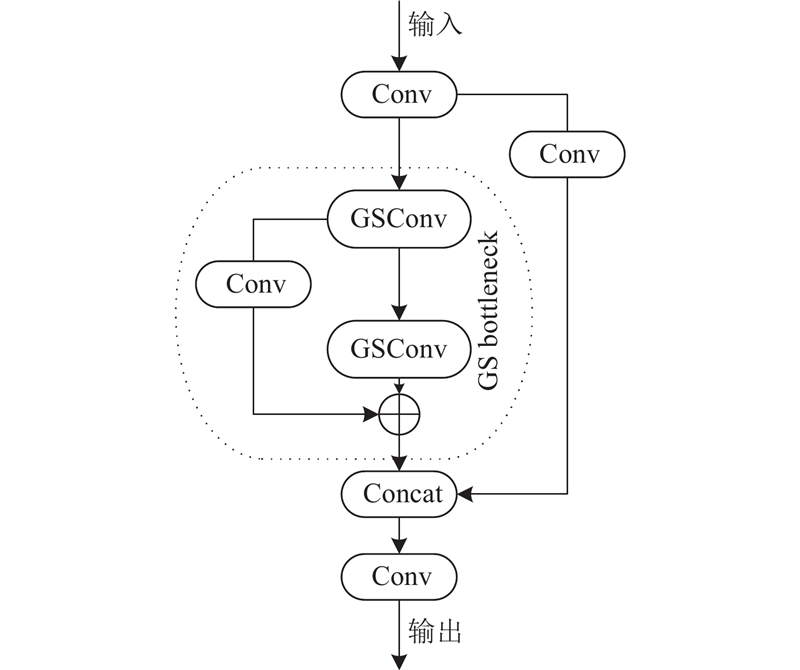
... EEGNet[16 ] 是专为脑电信号分类设计的轻量级神经网络,其架构精巧,通常由3层卷积结构构成,依次为二维卷积层、深度卷积层和可分离卷积层. 为了进一步提高模型对脑电信号的空间特征提取能力,将EEGNet中的原始二维卷积层替换为VoV-GSCSP模块[17 ] . 该模块融合了GSConv和CSP的优势,相较于传统卷积,在特征学习方面展现出更强大的表达能力,同时保持了较高的计算效率,未显著增加计算成本. ...
Slim-neck by GSConv: a lightweight-design for real-time detector architectures
1
2024
... EEGNet[16 ] 是专为脑电信号分类设计的轻量级神经网络,其架构精巧,通常由3层卷积结构构成,依次为二维卷积层、深度卷积层和可分离卷积层. 为了进一步提高模型对脑电信号的空间特征提取能力,将EEGNet中的原始二维卷积层替换为VoV-GSCSP模块[17 ] . 该模块融合了GSConv和CSP的优势,相较于传统卷积,在特征学习方面展现出更强大的表达能力,同时保持了较高的计算效率,未显著增加计算成本. ...
1
... 脑电信号不仅具有空间结构,而且包含重要的时间动态信息,不同时间步对识别任务的贡献不同. 为此,本文引入LTAE模块[18 ] . 该模块是高效的轻量级时间自注意力机制,旨在对输入数据进行时序建模,以捕捉长距离的时间依赖性,保持轻量化特性. ...
PhysioBank, PhysioToolkit, and PhysioNet: components of a new research resource for complex physiologic signals
1
2000
... 目前,脑电领域尚无专门针对脑纹识别的数据集,现有研究大多采用运动想象和情绪相关数据集作为实验数据. 为了验证脑纹识别方法的有效性,受试者数量应尽可能多,以确保模型的泛化能力. Physionet运动想象数据集[19 ] 包含109名受试者,DEAP情感数据集[20 ] 包含32名受试者,均具有较大规模的受试者数量,适用于脑纹识别研究. 选用Physionet数据集和DEAP数据集,评估模型的性能. ...
DEAP: a database for emotion Analysis;Using physiological signals
1
2012
... 目前,脑电领域尚无专门针对脑纹识别的数据集,现有研究大多采用运动想象和情绪相关数据集作为实验数据. 为了验证脑纹识别方法的有效性,受试者数量应尽可能多,以确保模型的泛化能力. Physionet运动想象数据集[19 ] 包含109名受试者,DEAP情感数据集[20 ] 包含32名受试者,均具有较大规模的受试者数量,适用于脑纹识别研究. 选用Physionet数据集和DEAP数据集,评估模型的性能. ...
Stable EEG-based biometric system using functional connectivity based on time-frequency features with optimal channels
4
2022
... 针对数据集的测试,以Physionet-MI数据为主进行展开. 如表2 所示,对不同时间段及不同通道数N 下的分类准确率进行系统测试. 选取的时间段是1 s和4 s. 将通道数设为3、4、8、15、16、19、32、64. 4、16、32和64通道的分组参考文献[8 ],15通道和19通道的分组参考文献[21 ]. 3通道配置采用C3、C4和Cz,8通道配置包括F3、F4、C3、Cz、C4、P3、P4和Pz. ...
... Comparison of motor imagery data for Physionet dataset
Tab.5 方法 slot/s N ACC/% EER/% N p /106 COH_CNN[21 ] [21 ] 1 19 98.22 — — CNN-LSTM[8 ] 1 16 99.58 0.410 1927.50 多任务对抗学习[22 ] 1 64 99.20 — — BGWO-SVM[23 ] 1 23 94.13 — — EPI-CGAN[24 ] 1 64 99.02 — — PCA+SVM[25 ] 2 64 99.91 — — DNN[26 ] 4 64 97.81 — — GCT-EEGNet[27 ] 1 32 98.90 0.004 0.17 ResNet18[28 ] 1 64 99.59 — 11.25 提出方法 1 15 98.52 0.001 0.29
Ashenaei等[21 ] 使用COH提取特征,输入CNN分类,该模型在1 s时间段、19通道和1 s时间段、15通道的配置下,准确率分别达到98.22%和97.74%,本文方法在相同通道下分别提高了0.64%和0.78%. Sun等[8 ] 使用CNN-LSTM模型在64通道的配置下实现了99.58%的高识别准确率,比本文方法在64通道下的识别准确率低0.39%. 虽然文献[8 ]算法在16通道下的识别准确率略优于本文方法,但其结合了LSTM层,将参数量增加到1927.5 × 106 ,这增加了过拟合的风险,而本文模型的参数量远远小于该模型,且EER更低. Alyasseri等[23 ] 使用BGWO-SVM在23通道的配置下取得94.13%的准确率,相比之下,本文方法在更少通道数下表现更优. Ortega-Rodríguez等[25 ] 采用主成分分析结合SVM进行脑纹识别,在2 s时间段、64通道的配置下取得了99.91%的准确率. 本文方法仅在1 s时间段便能达到更优的识别效果,显示出更高的效率和实用性. Akbarnia等[26 ] 使用DNN对预处理脑电信号进行脑纹识别,在4 s时间段、64通道的配置下实现97.81%的准确率,明显低于所提方法的识别效果. Alshehri等[27 ] 提出轻量级GCT-EEGNet网络进行脑纹识别,在1 s时间段、32通道的配置下实现98.90%的识别准确率,虽然文献[27 ]方法采用的参数量仅为0.17×106 ,但识别性能低于本文方法. Li等[28 ] 构建多视图融合模型,使用ResNet18进行分类,在1 s时间段、64通道的配置下实现99.59%的准确率,参数量为11.25×106 . 相比之下,本文模型在参数量远小于文献[28 ]模型的情况下,识别准确率与其相当. Jin等[24 ] 采用EPI-CGAN模型,该模型在64通道下的准确率达到99.02%. Zhou等[22 ] 将LFCC特征与多任务对抗学习相结合,在64通道下取得99.20%的准确率. 这2种方法使用较多的通道数,且分类效果不及本文所提方法. 通过在Physionet-MI数据上的分类性能比较,验证了本文所提方法即便在参数量较少的情况下,仍能取得较好的分类效果. ...
... [
21 ]
1 19 98.22 — — CNN-LSTM[8 ] 1 16 99.58 0.410 1927.50 多任务对抗学习[22 ] 1 64 99.20 — — BGWO-SVM[23 ] 1 23 94.13 — — EPI-CGAN[24 ] 1 64 99.02 — — PCA+SVM[25 ] 2 64 99.91 — — DNN[26 ] 4 64 97.81 — — GCT-EEGNet[27 ] 1 32 98.90 0.004 0.17 ResNet18[28 ] 1 64 99.59 — 11.25 提出方法 1 15 98.52 0.001 0.29 Ashenaei等[21 ] 使用COH提取特征,输入CNN分类,该模型在1 s时间段、19通道和1 s时间段、15通道的配置下,准确率分别达到98.22%和97.74%,本文方法在相同通道下分别提高了0.64%和0.78%. Sun等[8 ] 使用CNN-LSTM模型在64通道的配置下实现了99.58%的高识别准确率,比本文方法在64通道下的识别准确率低0.39%. 虽然文献[8 ]算法在16通道下的识别准确率略优于本文方法,但其结合了LSTM层,将参数量增加到1927.5 × 106 ,这增加了过拟合的风险,而本文模型的参数量远远小于该模型,且EER更低. Alyasseri等[23 ] 使用BGWO-SVM在23通道的配置下取得94.13%的准确率,相比之下,本文方法在更少通道数下表现更优. Ortega-Rodríguez等[25 ] 采用主成分分析结合SVM进行脑纹识别,在2 s时间段、64通道的配置下取得了99.91%的准确率. 本文方法仅在1 s时间段便能达到更优的识别效果,显示出更高的效率和实用性. Akbarnia等[26 ] 使用DNN对预处理脑电信号进行脑纹识别,在4 s时间段、64通道的配置下实现97.81%的准确率,明显低于所提方法的识别效果. Alshehri等[27 ] 提出轻量级GCT-EEGNet网络进行脑纹识别,在1 s时间段、32通道的配置下实现98.90%的识别准确率,虽然文献[27 ]方法采用的参数量仅为0.17×106 ,但识别性能低于本文方法. Li等[28 ] 构建多视图融合模型,使用ResNet18进行分类,在1 s时间段、64通道的配置下实现99.59%的准确率,参数量为11.25×106 . 相比之下,本文模型在参数量远小于文献[28 ]模型的情况下,识别准确率与其相当. Jin等[24 ] 采用EPI-CGAN模型,该模型在64通道下的准确率达到99.02%. Zhou等[22 ] 将LFCC特征与多任务对抗学习相结合,在64通道下取得99.20%的准确率. 这2种方法使用较多的通道数,且分类效果不及本文所提方法. 通过在Physionet-MI数据上的分类性能比较,验证了本文所提方法即便在参数量较少的情况下,仍能取得较好的分类效果. ...
... Ashenaei等[21 ] 使用COH提取特征,输入CNN分类,该模型在1 s时间段、19通道和1 s时间段、15通道的配置下,准确率分别达到98.22%和97.74%,本文方法在相同通道下分别提高了0.64%和0.78%. Sun等[8 ] 使用CNN-LSTM模型在64通道的配置下实现了99.58%的高识别准确率,比本文方法在64通道下的识别准确率低0.39%. 虽然文献[8 ]算法在16通道下的识别准确率略优于本文方法,但其结合了LSTM层,将参数量增加到1927.5 × 106 ,这增加了过拟合的风险,而本文模型的参数量远远小于该模型,且EER更低. Alyasseri等[23 ] 使用BGWO-SVM在23通道的配置下取得94.13%的准确率,相比之下,本文方法在更少通道数下表现更优. Ortega-Rodríguez等[25 ] 采用主成分分析结合SVM进行脑纹识别,在2 s时间段、64通道的配置下取得了99.91%的准确率. 本文方法仅在1 s时间段便能达到更优的识别效果,显示出更高的效率和实用性. Akbarnia等[26 ] 使用DNN对预处理脑电信号进行脑纹识别,在4 s时间段、64通道的配置下实现97.81%的准确率,明显低于所提方法的识别效果. Alshehri等[27 ] 提出轻量级GCT-EEGNet网络进行脑纹识别,在1 s时间段、32通道的配置下实现98.90%的识别准确率,虽然文献[27 ]方法采用的参数量仅为0.17×106 ,但识别性能低于本文方法. Li等[28 ] 构建多视图融合模型,使用ResNet18进行分类,在1 s时间段、64通道的配置下实现99.59%的准确率,参数量为11.25×106 . 相比之下,本文模型在参数量远小于文献[28 ]模型的情况下,识别准确率与其相当. Jin等[24 ] 采用EPI-CGAN模型,该模型在64通道下的准确率达到99.02%. Zhou等[22 ] 将LFCC特征与多任务对抗学习相结合,在64通道下取得99.20%的准确率. 这2种方法使用较多的通道数,且分类效果不及本文所提方法. 通过在Physionet-MI数据上的分类性能比较,验证了本文所提方法即便在参数量较少的情况下,仍能取得较好的分类效果. ...
2
... Comparison of motor imagery data for Physionet dataset
Tab.5 方法 slot/s N ACC/% EER/% N p /106 COH_CNN[21 ] [21 ] 1 19 98.22 — — CNN-LSTM[8 ] 1 16 99.58 0.410 1927.50 多任务对抗学习[22 ] 1 64 99.20 — — BGWO-SVM[23 ] 1 23 94.13 — — EPI-CGAN[24 ] 1 64 99.02 — — PCA+SVM[25 ] 2 64 99.91 — — DNN[26 ] 4 64 97.81 — — GCT-EEGNet[27 ] 1 32 98.90 0.004 0.17 ResNet18[28 ] 1 64 99.59 — 11.25 提出方法 1 15 98.52 0.001 0.29
Ashenaei等[21 ] 使用COH提取特征,输入CNN分类,该模型在1 s时间段、19通道和1 s时间段、15通道的配置下,准确率分别达到98.22%和97.74%,本文方法在相同通道下分别提高了0.64%和0.78%. Sun等[8 ] 使用CNN-LSTM模型在64通道的配置下实现了99.58%的高识别准确率,比本文方法在64通道下的识别准确率低0.39%. 虽然文献[8 ]算法在16通道下的识别准确率略优于本文方法,但其结合了LSTM层,将参数量增加到1927.5 × 106 ,这增加了过拟合的风险,而本文模型的参数量远远小于该模型,且EER更低. Alyasseri等[23 ] 使用BGWO-SVM在23通道的配置下取得94.13%的准确率,相比之下,本文方法在更少通道数下表现更优. Ortega-Rodríguez等[25 ] 采用主成分分析结合SVM进行脑纹识别,在2 s时间段、64通道的配置下取得了99.91%的准确率. 本文方法仅在1 s时间段便能达到更优的识别效果,显示出更高的效率和实用性. Akbarnia等[26 ] 使用DNN对预处理脑电信号进行脑纹识别,在4 s时间段、64通道的配置下实现97.81%的准确率,明显低于所提方法的识别效果. Alshehri等[27 ] 提出轻量级GCT-EEGNet网络进行脑纹识别,在1 s时间段、32通道的配置下实现98.90%的识别准确率,虽然文献[27 ]方法采用的参数量仅为0.17×106 ,但识别性能低于本文方法. Li等[28 ] 构建多视图融合模型,使用ResNet18进行分类,在1 s时间段、64通道的配置下实现99.59%的准确率,参数量为11.25×106 . 相比之下,本文模型在参数量远小于文献[28 ]模型的情况下,识别准确率与其相当. Jin等[24 ] 采用EPI-CGAN模型,该模型在64通道下的准确率达到99.02%. Zhou等[22 ] 将LFCC特征与多任务对抗学习相结合,在64通道下取得99.20%的准确率. 这2种方法使用较多的通道数,且分类效果不及本文所提方法. 通过在Physionet-MI数据上的分类性能比较,验证了本文所提方法即便在参数量较少的情况下,仍能取得较好的分类效果. ...
... Ashenaei等[21 ] 使用COH提取特征,输入CNN分类,该模型在1 s时间段、19通道和1 s时间段、15通道的配置下,准确率分别达到98.22%和97.74%,本文方法在相同通道下分别提高了0.64%和0.78%. Sun等[8 ] 使用CNN-LSTM模型在64通道的配置下实现了99.58%的高识别准确率,比本文方法在64通道下的识别准确率低0.39%. 虽然文献[8 ]算法在16通道下的识别准确率略优于本文方法,但其结合了LSTM层,将参数量增加到1927.5 × 106 ,这增加了过拟合的风险,而本文模型的参数量远远小于该模型,且EER更低. Alyasseri等[23 ] 使用BGWO-SVM在23通道的配置下取得94.13%的准确率,相比之下,本文方法在更少通道数下表现更优. Ortega-Rodríguez等[25 ] 采用主成分分析结合SVM进行脑纹识别,在2 s时间段、64通道的配置下取得了99.91%的准确率. 本文方法仅在1 s时间段便能达到更优的识别效果,显示出更高的效率和实用性. Akbarnia等[26 ] 使用DNN对预处理脑电信号进行脑纹识别,在4 s时间段、64通道的配置下实现97.81%的准确率,明显低于所提方法的识别效果. Alshehri等[27 ] 提出轻量级GCT-EEGNet网络进行脑纹识别,在1 s时间段、32通道的配置下实现98.90%的识别准确率,虽然文献[27 ]方法采用的参数量仅为0.17×106 ,但识别性能低于本文方法. Li等[28 ] 构建多视图融合模型,使用ResNet18进行分类,在1 s时间段、64通道的配置下实现99.59%的准确率,参数量为11.25×106 . 相比之下,本文模型在参数量远小于文献[28 ]模型的情况下,识别准确率与其相当. Jin等[24 ] 采用EPI-CGAN模型,该模型在64通道下的准确率达到99.02%. Zhou等[22 ] 将LFCC特征与多任务对抗学习相结合,在64通道下取得99.20%的准确率. 这2种方法使用较多的通道数,且分类效果不及本文所提方法. 通过在Physionet-MI数据上的分类性能比较,验证了本文所提方法即便在参数量较少的情况下,仍能取得较好的分类效果. ...
EEG channel selection for person identification using binary grey wolf optimizer
2
2022
... Comparison of motor imagery data for Physionet dataset
Tab.5 方法 slot/s N ACC/% EER/% N p /106 COH_CNN[21 ] [21 ] 1 19 98.22 — — CNN-LSTM[8 ] 1 16 99.58 0.410 1927.50 多任务对抗学习[22 ] 1 64 99.20 — — BGWO-SVM[23 ] 1 23 94.13 — — EPI-CGAN[24 ] 1 64 99.02 — — PCA+SVM[25 ] 2 64 99.91 — — DNN[26 ] 4 64 97.81 — — GCT-EEGNet[27 ] 1 32 98.90 0.004 0.17 ResNet18[28 ] 1 64 99.59 — 11.25 提出方法 1 15 98.52 0.001 0.29
Ashenaei等[21 ] 使用COH提取特征,输入CNN分类,该模型在1 s时间段、19通道和1 s时间段、15通道的配置下,准确率分别达到98.22%和97.74%,本文方法在相同通道下分别提高了0.64%和0.78%. Sun等[8 ] 使用CNN-LSTM模型在64通道的配置下实现了99.58%的高识别准确率,比本文方法在64通道下的识别准确率低0.39%. 虽然文献[8 ]算法在16通道下的识别准确率略优于本文方法,但其结合了LSTM层,将参数量增加到1927.5 × 106 ,这增加了过拟合的风险,而本文模型的参数量远远小于该模型,且EER更低. Alyasseri等[23 ] 使用BGWO-SVM在23通道的配置下取得94.13%的准确率,相比之下,本文方法在更少通道数下表现更优. Ortega-Rodríguez等[25 ] 采用主成分分析结合SVM进行脑纹识别,在2 s时间段、64通道的配置下取得了99.91%的准确率. 本文方法仅在1 s时间段便能达到更优的识别效果,显示出更高的效率和实用性. Akbarnia等[26 ] 使用DNN对预处理脑电信号进行脑纹识别,在4 s时间段、64通道的配置下实现97.81%的准确率,明显低于所提方法的识别效果. Alshehri等[27 ] 提出轻量级GCT-EEGNet网络进行脑纹识别,在1 s时间段、32通道的配置下实现98.90%的识别准确率,虽然文献[27 ]方法采用的参数量仅为0.17×106 ,但识别性能低于本文方法. Li等[28 ] 构建多视图融合模型,使用ResNet18进行分类,在1 s时间段、64通道的配置下实现99.59%的准确率,参数量为11.25×106 . 相比之下,本文模型在参数量远小于文献[28 ]模型的情况下,识别准确率与其相当. Jin等[24 ] 采用EPI-CGAN模型,该模型在64通道下的准确率达到99.02%. Zhou等[22 ] 将LFCC特征与多任务对抗学习相结合,在64通道下取得99.20%的准确率. 这2种方法使用较多的通道数,且分类效果不及本文所提方法. 通过在Physionet-MI数据上的分类性能比较,验证了本文所提方法即便在参数量较少的情况下,仍能取得较好的分类效果. ...
... Ashenaei等[21 ] 使用COH提取特征,输入CNN分类,该模型在1 s时间段、19通道和1 s时间段、15通道的配置下,准确率分别达到98.22%和97.74%,本文方法在相同通道下分别提高了0.64%和0.78%. Sun等[8 ] 使用CNN-LSTM模型在64通道的配置下实现了99.58%的高识别准确率,比本文方法在64通道下的识别准确率低0.39%. 虽然文献[8 ]算法在16通道下的识别准确率略优于本文方法,但其结合了LSTM层,将参数量增加到1927.5 × 106 ,这增加了过拟合的风险,而本文模型的参数量远远小于该模型,且EER更低. Alyasseri等[23 ] 使用BGWO-SVM在23通道的配置下取得94.13%的准确率,相比之下,本文方法在更少通道数下表现更优. Ortega-Rodríguez等[25 ] 采用主成分分析结合SVM进行脑纹识别,在2 s时间段、64通道的配置下取得了99.91%的准确率. 本文方法仅在1 s时间段便能达到更优的识别效果,显示出更高的效率和实用性. Akbarnia等[26 ] 使用DNN对预处理脑电信号进行脑纹识别,在4 s时间段、64通道的配置下实现97.81%的准确率,明显低于所提方法的识别效果. Alshehri等[27 ] 提出轻量级GCT-EEGNet网络进行脑纹识别,在1 s时间段、32通道的配置下实现98.90%的识别准确率,虽然文献[27 ]方法采用的参数量仅为0.17×106 ,但识别性能低于本文方法. Li等[28 ] 构建多视图融合模型,使用ResNet18进行分类,在1 s时间段、64通道的配置下实现99.59%的准确率,参数量为11.25×106 . 相比之下,本文模型在参数量远小于文献[28 ]模型的情况下,识别准确率与其相当. Jin等[24 ] 采用EPI-CGAN模型,该模型在64通道下的准确率达到99.02%. Zhou等[22 ] 将LFCC特征与多任务对抗学习相结合,在64通道下取得99.20%的准确率. 这2种方法使用较多的通道数,且分类效果不及本文所提方法. 通过在Physionet-MI数据上的分类性能比较,验证了本文所提方法即便在参数量较少的情况下,仍能取得较好的分类效果. ...
4
... Comparison of motor imagery data for Physionet dataset
Tab.5 方法 slot/s N ACC/% EER/% N p /106 COH_CNN[21 ] [21 ] 1 19 98.22 — — CNN-LSTM[8 ] 1 16 99.58 0.410 1927.50 多任务对抗学习[22 ] 1 64 99.20 — — BGWO-SVM[23 ] 1 23 94.13 — — EPI-CGAN[24 ] 1 64 99.02 — — PCA+SVM[25 ] 2 64 99.91 — — DNN[26 ] 4 64 97.81 — — GCT-EEGNet[27 ] 1 32 98.90 0.004 0.17 ResNet18[28 ] 1 64 99.59 — 11.25 提出方法 1 15 98.52 0.001 0.29
Ashenaei等[21 ] 使用COH提取特征,输入CNN分类,该模型在1 s时间段、19通道和1 s时间段、15通道的配置下,准确率分别达到98.22%和97.74%,本文方法在相同通道下分别提高了0.64%和0.78%. Sun等[8 ] 使用CNN-LSTM模型在64通道的配置下实现了99.58%的高识别准确率,比本文方法在64通道下的识别准确率低0.39%. 虽然文献[8 ]算法在16通道下的识别准确率略优于本文方法,但其结合了LSTM层,将参数量增加到1927.5 × 106 ,这增加了过拟合的风险,而本文模型的参数量远远小于该模型,且EER更低. Alyasseri等[23 ] 使用BGWO-SVM在23通道的配置下取得94.13%的准确率,相比之下,本文方法在更少通道数下表现更优. Ortega-Rodríguez等[25 ] 采用主成分分析结合SVM进行脑纹识别,在2 s时间段、64通道的配置下取得了99.91%的准确率. 本文方法仅在1 s时间段便能达到更优的识别效果,显示出更高的效率和实用性. Akbarnia等[26 ] 使用DNN对预处理脑电信号进行脑纹识别,在4 s时间段、64通道的配置下实现97.81%的准确率,明显低于所提方法的识别效果. Alshehri等[27 ] 提出轻量级GCT-EEGNet网络进行脑纹识别,在1 s时间段、32通道的配置下实现98.90%的识别准确率,虽然文献[27 ]方法采用的参数量仅为0.17×106 ,但识别性能低于本文方法. Li等[28 ] 构建多视图融合模型,使用ResNet18进行分类,在1 s时间段、64通道的配置下实现99.59%的准确率,参数量为11.25×106 . 相比之下,本文模型在参数量远小于文献[28 ]模型的情况下,识别准确率与其相当. Jin等[24 ] 采用EPI-CGAN模型,该模型在64通道下的准确率达到99.02%. Zhou等[22 ] 将LFCC特征与多任务对抗学习相结合,在64通道下取得99.20%的准确率. 这2种方法使用较多的通道数,且分类效果不及本文所提方法. 通过在Physionet-MI数据上的分类性能比较,验证了本文所提方法即便在参数量较少的情况下,仍能取得较好的分类效果. ...
... Ashenaei等[21 ] 使用COH提取特征,输入CNN分类,该模型在1 s时间段、19通道和1 s时间段、15通道的配置下,准确率分别达到98.22%和97.74%,本文方法在相同通道下分别提高了0.64%和0.78%. Sun等[8 ] 使用CNN-LSTM模型在64通道的配置下实现了99.58%的高识别准确率,比本文方法在64通道下的识别准确率低0.39%. 虽然文献[8 ]算法在16通道下的识别准确率略优于本文方法,但其结合了LSTM层,将参数量增加到1927.5 × 106 ,这增加了过拟合的风险,而本文模型的参数量远远小于该模型,且EER更低. Alyasseri等[23 ] 使用BGWO-SVM在23通道的配置下取得94.13%的准确率,相比之下,本文方法在更少通道数下表现更优. Ortega-Rodríguez等[25 ] 采用主成分分析结合SVM进行脑纹识别,在2 s时间段、64通道的配置下取得了99.91%的准确率. 本文方法仅在1 s时间段便能达到更优的识别效果,显示出更高的效率和实用性. Akbarnia等[26 ] 使用DNN对预处理脑电信号进行脑纹识别,在4 s时间段、64通道的配置下实现97.81%的准确率,明显低于所提方法的识别效果. Alshehri等[27 ] 提出轻量级GCT-EEGNet网络进行脑纹识别,在1 s时间段、32通道的配置下实现98.90%的识别准确率,虽然文献[27 ]方法采用的参数量仅为0.17×106 ,但识别性能低于本文方法. Li等[28 ] 构建多视图融合模型,使用ResNet18进行分类,在1 s时间段、64通道的配置下实现99.59%的准确率,参数量为11.25×106 . 相比之下,本文模型在参数量远小于文献[28 ]模型的情况下,识别准确率与其相当. Jin等[24 ] 采用EPI-CGAN模型,该模型在64通道下的准确率达到99.02%. Zhou等[22 ] 将LFCC特征与多任务对抗学习相结合,在64通道下取得99.20%的准确率. 这2种方法使用较多的通道数,且分类效果不及本文所提方法. 通过在Physionet-MI数据上的分类性能比较,验证了本文所提方法即便在参数量较少的情况下,仍能取得较好的分类效果. ...
... 如表7 所示为本文方法与其他方法在DEAP数据集上的分类性能对比. 选用10 s的时间段,分别针对5通道和32通道进行测试,均实现了99.00%以上的准确率. Wilaiprasitporn等[35 ] 提出结合CNN和GRU的混合模型,该方法将脑电信号划分为10 s长度,在5通道和32通道下分别达到99.17%和99.90%的平均准确率,分类准确率不如本文方法,且模型参数量较大. Gómez-Tapia等[36 ] 探究进行脑纹识别所需的最短时间段,在经过预处理的脑电信号中提取功率谱密度或小波能量特征,使用MLP进行分类,在1 s时间段下的识别准确率达到95.00%,在3 s时间段下进一步提升到99.00%,文献[36 ]方法所需的时间段短,但对信号质量的要求较高,信号预处理过程较复杂,且使用了完整的32通道数据. 相比之下,本文所提方法在仅使用5通道的情况下即可取得更优的性能. Jin等[24 ] 提出EPI-CGAN模型进行脑纹识别,实现了99.88%的高准确率,但采用的时间段较长,且分类性能略逊于本文方法. 通过在DEAP数据集上的比较可知,提出的网络模型在低通道数下的分类识别效果综合表现最优. ...
... Comparison of DEAP dataset
Tab.7 方法 slot/s N ACC/% N p /106 CNN-GRU[35 ] [35 ] 10 5 99.17 1.89 MLP[36 ] [36 ] 1 32 95.00 — EPI-CGAN[24 ] 12 32 99.88 — 提出方法 10 5 99.98 0.28
4. 结 语 提出基于轻量级时空注意力机制的卷积神经网络,能够在通道数少与时间段短的条件下实现高效的脑纹识别. 在参数量仅为0.29×106 的情况下,该方法在多个公开数据集上表现出优越的性能. 在通道数少于8或时间段短于1 s的条件下,模型性能有所下降,表明其对时空信息具有较强的依赖性. 未来的研究将进一步聚焦更少通道数、更短时间段下模型性能的提升,重点探索如何自适应地选择对脑纹识别贡献最大的关键通道子集. ...
Selection of the minimum number of EEG sensors to guarantee biometric identification of individuals
2
2023
... Comparison of motor imagery data for Physionet dataset
Tab.5 方法 slot/s N ACC/% EER/% N p /106 COH_CNN[21 ] [21 ] 1 19 98.22 — — CNN-LSTM[8 ] 1 16 99.58 0.410 1927.50 多任务对抗学习[22 ] 1 64 99.20 — — BGWO-SVM[23 ] 1 23 94.13 — — EPI-CGAN[24 ] 1 64 99.02 — — PCA+SVM[25 ] 2 64 99.91 — — DNN[26 ] 4 64 97.81 — — GCT-EEGNet[27 ] 1 32 98.90 0.004 0.17 ResNet18[28 ] 1 64 99.59 — 11.25 提出方法 1 15 98.52 0.001 0.29
Ashenaei等[21 ] 使用COH提取特征,输入CNN分类,该模型在1 s时间段、19通道和1 s时间段、15通道的配置下,准确率分别达到98.22%和97.74%,本文方法在相同通道下分别提高了0.64%和0.78%. Sun等[8 ] 使用CNN-LSTM模型在64通道的配置下实现了99.58%的高识别准确率,比本文方法在64通道下的识别准确率低0.39%. 虽然文献[8 ]算法在16通道下的识别准确率略优于本文方法,但其结合了LSTM层,将参数量增加到1927.5 × 106 ,这增加了过拟合的风险,而本文模型的参数量远远小于该模型,且EER更低. Alyasseri等[23 ] 使用BGWO-SVM在23通道的配置下取得94.13%的准确率,相比之下,本文方法在更少通道数下表现更优. Ortega-Rodríguez等[25 ] 采用主成分分析结合SVM进行脑纹识别,在2 s时间段、64通道的配置下取得了99.91%的准确率. 本文方法仅在1 s时间段便能达到更优的识别效果,显示出更高的效率和实用性. Akbarnia等[26 ] 使用DNN对预处理脑电信号进行脑纹识别,在4 s时间段、64通道的配置下实现97.81%的准确率,明显低于所提方法的识别效果. Alshehri等[27 ] 提出轻量级GCT-EEGNet网络进行脑纹识别,在1 s时间段、32通道的配置下实现98.90%的识别准确率,虽然文献[27 ]方法采用的参数量仅为0.17×106 ,但识别性能低于本文方法. Li等[28 ] 构建多视图融合模型,使用ResNet18进行分类,在1 s时间段、64通道的配置下实现99.59%的准确率,参数量为11.25×106 . 相比之下,本文模型在参数量远小于文献[28 ]模型的情况下,识别准确率与其相当. Jin等[24 ] 采用EPI-CGAN模型,该模型在64通道下的准确率达到99.02%. Zhou等[22 ] 将LFCC特征与多任务对抗学习相结合,在64通道下取得99.20%的准确率. 这2种方法使用较多的通道数,且分类效果不及本文所提方法. 通过在Physionet-MI数据上的分类性能比较,验证了本文所提方法即便在参数量较少的情况下,仍能取得较好的分类效果. ...
... Ashenaei等[21 ] 使用COH提取特征,输入CNN分类,该模型在1 s时间段、19通道和1 s时间段、15通道的配置下,准确率分别达到98.22%和97.74%,本文方法在相同通道下分别提高了0.64%和0.78%. Sun等[8 ] 使用CNN-LSTM模型在64通道的配置下实现了99.58%的高识别准确率,比本文方法在64通道下的识别准确率低0.39%. 虽然文献[8 ]算法在16通道下的识别准确率略优于本文方法,但其结合了LSTM层,将参数量增加到1927.5 × 106 ,这增加了过拟合的风险,而本文模型的参数量远远小于该模型,且EER更低. Alyasseri等[23 ] 使用BGWO-SVM在23通道的配置下取得94.13%的准确率,相比之下,本文方法在更少通道数下表现更优. Ortega-Rodríguez等[25 ] 采用主成分分析结合SVM进行脑纹识别,在2 s时间段、64通道的配置下取得了99.91%的准确率. 本文方法仅在1 s时间段便能达到更优的识别效果,显示出更高的效率和实用性. Akbarnia等[26 ] 使用DNN对预处理脑电信号进行脑纹识别,在4 s时间段、64通道的配置下实现97.81%的准确率,明显低于所提方法的识别效果. Alshehri等[27 ] 提出轻量级GCT-EEGNet网络进行脑纹识别,在1 s时间段、32通道的配置下实现98.90%的识别准确率,虽然文献[27 ]方法采用的参数量仅为0.17×106 ,但识别性能低于本文方法. Li等[28 ] 构建多视图融合模型,使用ResNet18进行分类,在1 s时间段、64通道的配置下实现99.59%的准确率,参数量为11.25×106 . 相比之下,本文模型在参数量远小于文献[28 ]模型的情况下,识别准确率与其相当. Jin等[24 ] 采用EPI-CGAN模型,该模型在64通道下的准确率达到99.02%. Zhou等[22 ] 将LFCC特征与多任务对抗学习相结合,在64通道下取得99.20%的准确率. 这2种方法使用较多的通道数,且分类效果不及本文所提方法. 通过在Physionet-MI数据上的分类性能比较,验证了本文所提方法即便在参数量较少的情况下,仍能取得较好的分类效果. ...
EEG-based identification system using deep neural networks with frequency features
2
2024
... Comparison of motor imagery data for Physionet dataset
Tab.5 方法 slot/s N ACC/% EER/% N p /106 COH_CNN[21 ] [21 ] 1 19 98.22 — — CNN-LSTM[8 ] 1 16 99.58 0.410 1927.50 多任务对抗学习[22 ] 1 64 99.20 — — BGWO-SVM[23 ] 1 23 94.13 — — EPI-CGAN[24 ] 1 64 99.02 — — PCA+SVM[25 ] 2 64 99.91 — — DNN[26 ] 4 64 97.81 — — GCT-EEGNet[27 ] 1 32 98.90 0.004 0.17 ResNet18[28 ] 1 64 99.59 — 11.25 提出方法 1 15 98.52 0.001 0.29
Ashenaei等[21 ] 使用COH提取特征,输入CNN分类,该模型在1 s时间段、19通道和1 s时间段、15通道的配置下,准确率分别达到98.22%和97.74%,本文方法在相同通道下分别提高了0.64%和0.78%. Sun等[8 ] 使用CNN-LSTM模型在64通道的配置下实现了99.58%的高识别准确率,比本文方法在64通道下的识别准确率低0.39%. 虽然文献[8 ]算法在16通道下的识别准确率略优于本文方法,但其结合了LSTM层,将参数量增加到1927.5 × 106 ,这增加了过拟合的风险,而本文模型的参数量远远小于该模型,且EER更低. Alyasseri等[23 ] 使用BGWO-SVM在23通道的配置下取得94.13%的准确率,相比之下,本文方法在更少通道数下表现更优. Ortega-Rodríguez等[25 ] 采用主成分分析结合SVM进行脑纹识别,在2 s时间段、64通道的配置下取得了99.91%的准确率. 本文方法仅在1 s时间段便能达到更优的识别效果,显示出更高的效率和实用性. Akbarnia等[26 ] 使用DNN对预处理脑电信号进行脑纹识别,在4 s时间段、64通道的配置下实现97.81%的准确率,明显低于所提方法的识别效果. Alshehri等[27 ] 提出轻量级GCT-EEGNet网络进行脑纹识别,在1 s时间段、32通道的配置下实现98.90%的识别准确率,虽然文献[27 ]方法采用的参数量仅为0.17×106 ,但识别性能低于本文方法. Li等[28 ] 构建多视图融合模型,使用ResNet18进行分类,在1 s时间段、64通道的配置下实现99.59%的准确率,参数量为11.25×106 . 相比之下,本文模型在参数量远小于文献[28 ]模型的情况下,识别准确率与其相当. Jin等[24 ] 采用EPI-CGAN模型,该模型在64通道下的准确率达到99.02%. Zhou等[22 ] 将LFCC特征与多任务对抗学习相结合,在64通道下取得99.20%的准确率. 这2种方法使用较多的通道数,且分类效果不及本文所提方法. 通过在Physionet-MI数据上的分类性能比较,验证了本文所提方法即便在参数量较少的情况下,仍能取得较好的分类效果. ...
... Ashenaei等[21 ] 使用COH提取特征,输入CNN分类,该模型在1 s时间段、19通道和1 s时间段、15通道的配置下,准确率分别达到98.22%和97.74%,本文方法在相同通道下分别提高了0.64%和0.78%. Sun等[8 ] 使用CNN-LSTM模型在64通道的配置下实现了99.58%的高识别准确率,比本文方法在64通道下的识别准确率低0.39%. 虽然文献[8 ]算法在16通道下的识别准确率略优于本文方法,但其结合了LSTM层,将参数量增加到1927.5 × 106 ,这增加了过拟合的风险,而本文模型的参数量远远小于该模型,且EER更低. Alyasseri等[23 ] 使用BGWO-SVM在23通道的配置下取得94.13%的准确率,相比之下,本文方法在更少通道数下表现更优. Ortega-Rodríguez等[25 ] 采用主成分分析结合SVM进行脑纹识别,在2 s时间段、64通道的配置下取得了99.91%的准确率. 本文方法仅在1 s时间段便能达到更优的识别效果,显示出更高的效率和实用性. Akbarnia等[26 ] 使用DNN对预处理脑电信号进行脑纹识别,在4 s时间段、64通道的配置下实现97.81%的准确率,明显低于所提方法的识别效果. Alshehri等[27 ] 提出轻量级GCT-EEGNet网络进行脑纹识别,在1 s时间段、32通道的配置下实现98.90%的识别准确率,虽然文献[27 ]方法采用的参数量仅为0.17×106 ,但识别性能低于本文方法. Li等[28 ] 构建多视图融合模型,使用ResNet18进行分类,在1 s时间段、64通道的配置下实现99.59%的准确率,参数量为11.25×106 . 相比之下,本文模型在参数量远小于文献[28 ]模型的情况下,识别准确率与其相当. Jin等[24 ] 采用EPI-CGAN模型,该模型在64通道下的准确率达到99.02%. Zhou等[22 ] 将LFCC特征与多任务对抗学习相结合,在64通道下取得99.20%的准确率. 这2种方法使用较多的通道数,且分类效果不及本文所提方法. 通过在Physionet-MI数据上的分类性能比较,验证了本文所提方法即便在参数量较少的情况下,仍能取得较好的分类效果. ...
A lightweight GCT-EEGNet for EEG-based individual recognition under diverse brain conditions
3
2024
... Comparison of motor imagery data for Physionet dataset
Tab.5 方法 slot/s N ACC/% EER/% N p /106 COH_CNN[21 ] [21 ] 1 19 98.22 — — CNN-LSTM[8 ] 1 16 99.58 0.410 1927.50 多任务对抗学习[22 ] 1 64 99.20 — — BGWO-SVM[23 ] 1 23 94.13 — — EPI-CGAN[24 ] 1 64 99.02 — — PCA+SVM[25 ] 2 64 99.91 — — DNN[26 ] 4 64 97.81 — — GCT-EEGNet[27 ] 1 32 98.90 0.004 0.17 ResNet18[28 ] 1 64 99.59 — 11.25 提出方法 1 15 98.52 0.001 0.29
Ashenaei等[21 ] 使用COH提取特征,输入CNN分类,该模型在1 s时间段、19通道和1 s时间段、15通道的配置下,准确率分别达到98.22%和97.74%,本文方法在相同通道下分别提高了0.64%和0.78%. Sun等[8 ] 使用CNN-LSTM模型在64通道的配置下实现了99.58%的高识别准确率,比本文方法在64通道下的识别准确率低0.39%. 虽然文献[8 ]算法在16通道下的识别准确率略优于本文方法,但其结合了LSTM层,将参数量增加到1927.5 × 106 ,这增加了过拟合的风险,而本文模型的参数量远远小于该模型,且EER更低. Alyasseri等[23 ] 使用BGWO-SVM在23通道的配置下取得94.13%的准确率,相比之下,本文方法在更少通道数下表现更优. Ortega-Rodríguez等[25 ] 采用主成分分析结合SVM进行脑纹识别,在2 s时间段、64通道的配置下取得了99.91%的准确率. 本文方法仅在1 s时间段便能达到更优的识别效果,显示出更高的效率和实用性. Akbarnia等[26 ] 使用DNN对预处理脑电信号进行脑纹识别,在4 s时间段、64通道的配置下实现97.81%的准确率,明显低于所提方法的识别效果. Alshehri等[27 ] 提出轻量级GCT-EEGNet网络进行脑纹识别,在1 s时间段、32通道的配置下实现98.90%的识别准确率,虽然文献[27 ]方法采用的参数量仅为0.17×106 ,但识别性能低于本文方法. Li等[28 ] 构建多视图融合模型,使用ResNet18进行分类,在1 s时间段、64通道的配置下实现99.59%的准确率,参数量为11.25×106 . 相比之下,本文模型在参数量远小于文献[28 ]模型的情况下,识别准确率与其相当. Jin等[24 ] 采用EPI-CGAN模型,该模型在64通道下的准确率达到99.02%. Zhou等[22 ] 将LFCC特征与多任务对抗学习相结合,在64通道下取得99.20%的准确率. 这2种方法使用较多的通道数,且分类效果不及本文所提方法. 通过在Physionet-MI数据上的分类性能比较,验证了本文所提方法即便在参数量较少的情况下,仍能取得较好的分类效果. ...
... Ashenaei等[21 ] 使用COH提取特征,输入CNN分类,该模型在1 s时间段、19通道和1 s时间段、15通道的配置下,准确率分别达到98.22%和97.74%,本文方法在相同通道下分别提高了0.64%和0.78%. Sun等[8 ] 使用CNN-LSTM模型在64通道的配置下实现了99.58%的高识别准确率,比本文方法在64通道下的识别准确率低0.39%. 虽然文献[8 ]算法在16通道下的识别准确率略优于本文方法,但其结合了LSTM层,将参数量增加到1927.5 × 106 ,这增加了过拟合的风险,而本文模型的参数量远远小于该模型,且EER更低. Alyasseri等[23 ] 使用BGWO-SVM在23通道的配置下取得94.13%的准确率,相比之下,本文方法在更少通道数下表现更优. Ortega-Rodríguez等[25 ] 采用主成分分析结合SVM进行脑纹识别,在2 s时间段、64通道的配置下取得了99.91%的准确率. 本文方法仅在1 s时间段便能达到更优的识别效果,显示出更高的效率和实用性. Akbarnia等[26 ] 使用DNN对预处理脑电信号进行脑纹识别,在4 s时间段、64通道的配置下实现97.81%的准确率,明显低于所提方法的识别效果. Alshehri等[27 ] 提出轻量级GCT-EEGNet网络进行脑纹识别,在1 s时间段、32通道的配置下实现98.90%的识别准确率,虽然文献[27 ]方法采用的参数量仅为0.17×106 ,但识别性能低于本文方法. Li等[28 ] 构建多视图融合模型,使用ResNet18进行分类,在1 s时间段、64通道的配置下实现99.59%的准确率,参数量为11.25×106 . 相比之下,本文模型在参数量远小于文献[28 ]模型的情况下,识别准确率与其相当. Jin等[24 ] 采用EPI-CGAN模型,该模型在64通道下的准确率达到99.02%. Zhou等[22 ] 将LFCC特征与多任务对抗学习相结合,在64通道下取得99.20%的准确率. 这2种方法使用较多的通道数,且分类效果不及本文所提方法. 通过在Physionet-MI数据上的分类性能比较,验证了本文所提方法即便在参数量较少的情况下,仍能取得较好的分类效果. ...
... 提出轻量级GCT-EEGNet网络进行脑纹识别,在1 s时间段、32通道的配置下实现98.90%的识别准确率,虽然文献[27 ]方法采用的参数量仅为0.17×106 ,但识别性能低于本文方法. Li等[28 ] 构建多视图融合模型,使用ResNet18进行分类,在1 s时间段、64通道的配置下实现99.59%的准确率,参数量为11.25×106 . 相比之下,本文模型在参数量远小于文献[28 ]模型的情况下,识别准确率与其相当. Jin等[24 ] 采用EPI-CGAN模型,该模型在64通道下的准确率达到99.02%. Zhou等[22 ] 将LFCC特征与多任务对抗学习相结合,在64通道下取得99.20%的准确率. 这2种方法使用较多的通道数,且分类效果不及本文所提方法. 通过在Physionet-MI数据上的分类性能比较,验证了本文所提方法即便在参数量较少的情况下,仍能取得较好的分类效果. ...
Brain topographic map: a visual feature for multi-view fusion design in EEG-based biometrics
3
2025
... Comparison of motor imagery data for Physionet dataset
Tab.5 方法 slot/s N ACC/% EER/% N p /106 COH_CNN[21 ] [21 ] 1 19 98.22 — — CNN-LSTM[8 ] 1 16 99.58 0.410 1927.50 多任务对抗学习[22 ] 1 64 99.20 — — BGWO-SVM[23 ] 1 23 94.13 — — EPI-CGAN[24 ] 1 64 99.02 — — PCA+SVM[25 ] 2 64 99.91 — — DNN[26 ] 4 64 97.81 — — GCT-EEGNet[27 ] 1 32 98.90 0.004 0.17 ResNet18[28 ] 1 64 99.59 — 11.25 提出方法 1 15 98.52 0.001 0.29
Ashenaei等[21 ] 使用COH提取特征,输入CNN分类,该模型在1 s时间段、19通道和1 s时间段、15通道的配置下,准确率分别达到98.22%和97.74%,本文方法在相同通道下分别提高了0.64%和0.78%. Sun等[8 ] 使用CNN-LSTM模型在64通道的配置下实现了99.58%的高识别准确率,比本文方法在64通道下的识别准确率低0.39%. 虽然文献[8 ]算法在16通道下的识别准确率略优于本文方法,但其结合了LSTM层,将参数量增加到1927.5 × 106 ,这增加了过拟合的风险,而本文模型的参数量远远小于该模型,且EER更低. Alyasseri等[23 ] 使用BGWO-SVM在23通道的配置下取得94.13%的准确率,相比之下,本文方法在更少通道数下表现更优. Ortega-Rodríguez等[25 ] 采用主成分分析结合SVM进行脑纹识别,在2 s时间段、64通道的配置下取得了99.91%的准确率. 本文方法仅在1 s时间段便能达到更优的识别效果,显示出更高的效率和实用性. Akbarnia等[26 ] 使用DNN对预处理脑电信号进行脑纹识别,在4 s时间段、64通道的配置下实现97.81%的准确率,明显低于所提方法的识别效果. Alshehri等[27 ] 提出轻量级GCT-EEGNet网络进行脑纹识别,在1 s时间段、32通道的配置下实现98.90%的识别准确率,虽然文献[27 ]方法采用的参数量仅为0.17×106 ,但识别性能低于本文方法. Li等[28 ] 构建多视图融合模型,使用ResNet18进行分类,在1 s时间段、64通道的配置下实现99.59%的准确率,参数量为11.25×106 . 相比之下,本文模型在参数量远小于文献[28 ]模型的情况下,识别准确率与其相当. Jin等[24 ] 采用EPI-CGAN模型,该模型在64通道下的准确率达到99.02%. Zhou等[22 ] 将LFCC特征与多任务对抗学习相结合,在64通道下取得99.20%的准确率. 这2种方法使用较多的通道数,且分类效果不及本文所提方法. 通过在Physionet-MI数据上的分类性能比较,验证了本文所提方法即便在参数量较少的情况下,仍能取得较好的分类效果. ...
... Ashenaei等[21 ] 使用COH提取特征,输入CNN分类,该模型在1 s时间段、19通道和1 s时间段、15通道的配置下,准确率分别达到98.22%和97.74%,本文方法在相同通道下分别提高了0.64%和0.78%. Sun等[8 ] 使用CNN-LSTM模型在64通道的配置下实现了99.58%的高识别准确率,比本文方法在64通道下的识别准确率低0.39%. 虽然文献[8 ]算法在16通道下的识别准确率略优于本文方法,但其结合了LSTM层,将参数量增加到1927.5 × 106 ,这增加了过拟合的风险,而本文模型的参数量远远小于该模型,且EER更低. Alyasseri等[23 ] 使用BGWO-SVM在23通道的配置下取得94.13%的准确率,相比之下,本文方法在更少通道数下表现更优. Ortega-Rodríguez等[25 ] 采用主成分分析结合SVM进行脑纹识别,在2 s时间段、64通道的配置下取得了99.91%的准确率. 本文方法仅在1 s时间段便能达到更优的识别效果,显示出更高的效率和实用性. Akbarnia等[26 ] 使用DNN对预处理脑电信号进行脑纹识别,在4 s时间段、64通道的配置下实现97.81%的准确率,明显低于所提方法的识别效果. Alshehri等[27 ] 提出轻量级GCT-EEGNet网络进行脑纹识别,在1 s时间段、32通道的配置下实现98.90%的识别准确率,虽然文献[27 ]方法采用的参数量仅为0.17×106 ,但识别性能低于本文方法. Li等[28 ] 构建多视图融合模型,使用ResNet18进行分类,在1 s时间段、64通道的配置下实现99.59%的准确率,参数量为11.25×106 . 相比之下,本文模型在参数量远小于文献[28 ]模型的情况下,识别准确率与其相当. Jin等[24 ] 采用EPI-CGAN模型,该模型在64通道下的准确率达到99.02%. Zhou等[22 ] 将LFCC特征与多任务对抗学习相结合,在64通道下取得99.20%的准确率. 这2种方法使用较多的通道数,且分类效果不及本文所提方法. 通过在Physionet-MI数据上的分类性能比较,验证了本文所提方法即便在参数量较少的情况下,仍能取得较好的分类效果. ...
... . 相比之下,本文模型在参数量远小于文献[28 ]模型的情况下,识别准确率与其相当. Jin等[24 ] 采用EPI-CGAN模型,该模型在64通道下的准确率达到99.02%. Zhou等[22 ] 将LFCC特征与多任务对抗学习相结合,在64通道下取得99.20%的准确率. 这2种方法使用较多的通道数,且分类效果不及本文所提方法. 通过在Physionet-MI数据上的分类性能比较,验证了本文所提方法即便在参数量较少的情况下,仍能取得较好的分类效果. ...
A spatio-temporal model for EEG-based person identification
6
2019
... 如表6 所示为本文方法与其他方法在Physionet数据集中静息状态数据的分类表现,对于同一数据集,当前主流的算法性能与本文方法的比较如下. Das等[29 ] 使用CNN-LSTM模型进行测试,在4 s、8 s、12 s和16 s的实验中,12 s时段的效果最佳,EO和EC的识别准确率分别为98.00%和99.95%. 本文方法的EC识别准确率略低于文献[29 ]方法,但本文方法仅用2 s时间段,更适用于实际应用. Tian等[13 ] 应用基于GCN的方法,使用1 s数据,最高准确率达到98.56%,但在通道减少时准确率下降较快. 相比之下,本文方法在低通道数下保持较高的准确率. Schons等[9 ] 结合滑动窗口的数据增强技术和CNN,在最佳情况下EER为0.190%,本文所提方法在64通道下EER更低,使用的时间段更短. Li等[33 ] 提出ESTformer模型进行脑纹识别,在10 s时间段、64通道的条件下实现94.61%的准确率,模型参数量为33.7×106 . 相比之下,本文方法的准确率更高,参数量更少. Bandana等[34 ] 提出使用自动编码器对脑电信号进行重建,再使用CNN进行分类,在8 s时间段、64通道的配置下,睁眼和闭眼状态时分别达到99.45%和99.89%的准确率,但文献[34 ]方法使用的时间段比本文方法长. ...
... 使用CNN-LSTM模型进行测试,在4 s、8 s、12 s和16 s的实验中,12 s时段的效果最佳,EO和EC的识别准确率分别为98.00%和99.95%. 本文方法的EC识别准确率略低于文献[29 ]方法,但本文方法仅用2 s时间段,更适用于实际应用. Tian等[13 ] 应用基于GCN的方法,使用1 s数据,最高准确率达到98.56%,但在通道减少时准确率下降较快. 相比之下,本文方法在低通道数下保持较高的准确率. Schons等[9 ] 结合滑动窗口的数据增强技术和CNN,在最佳情况下EER为0.190%,本文所提方法在64通道下EER更低,使用的时间段更短. Li等[33 ] 提出ESTformer模型进行脑纹识别,在10 s时间段、64通道的条件下实现94.61%的准确率,模型参数量为33.7×106 . 相比之下,本文方法的准确率更高,参数量更少. Bandana等[34 ] 提出使用自动编码器对脑电信号进行重建,再使用CNN进行分类,在8 s时间段、64通道的配置下,睁眼和闭眼状态时分别达到99.45%和99.89%的准确率,但文献[34 ]方法使用的时间段比本文方法长. ...
... Comparison of resting state data for Physionet dataset
Tab.6 方法 slot/s N EO EC N p /106 ACC/% EER/% ACC/% EER/% 连通性网络[11 ] 12 64 96.90 4.400 92.60 6.500 — CNN-LSTM[29 ] [29 ] [29 ] [29 ] 4 64 95.00 — 95.33 — — COR+GCN[13 ] [13 ] [13 ] 1 64 98.56 — — — — FDF+SVM_RBF[30 ] 10 64 97.22 — — — — RF[31 ] 2 64 98.16 — 97.30 — — SVM[31 ] 2 64 97.64 — 96.02 — — MCL+马氏距离分类器[32 ] 10 64 99.40 6.330 98.80 10.500 — CNN+数据增强[9 ] 12 64 — — — 0.190 300.82 PLV+Gamma[12 ] [12 ] 4 56 99.40 — — — — ESTformer[33 ] 10 64 94.61 — — — 33.70 Autoencoder-CNN[34 ] 8 64 99.45 — 99.89 — — 提出方法 2 3 90.60 0.179 90.16 0.137 0.29
Fraschini等[11 ] 采用构建功能连通性脑网络的方法,使用12 s数据,在64通道的情况下,EO的识别准确率为96.90%,EC的识别准确率为92.60%. 相比之下,本文方法的准确率平均提高了2.55%和6.41%. Alyasseri等[30 ] 通过提取PSD和AR特征,送入SVM_RBF分类器进行分类,在64通道的条件下识别准确率达到97.22%,比本文方法低2.23%. Kaur等[31 ] 应用PCA提取特征,使用SVM分类的睁眼和闭眼状态的身份识别准确率分别为97.64%和96.02%,使用RF分类器的身份识别准确率分别为98.16%和97.30%,识别效果不如本文方法. Yahyaei等[32 ] 提取脑电信号的MCL特征,使用马氏距离分类器进行分类,在10 s时间段、64通道的条件下,EO识别准确率达到99.40%,EC识别准确率达到98.80%,但EER较高. Kumar等[12 ] 使用基于锁相值的SVM方法,在使用56通道时获得99.40%的准确率,当通道数减少至21时,准确率仅下降3.40%. 相比之下,本文方法在2 s时间段、16通道的配置下,准确率超过文献[12 ]方法在4 s时间段、21通道下的表现. 通过上述在睁眼和闭眼状态数据上的比较,本文方法在参数量较少,时间段较短的情况下,分类效果在多种性能评估下更好. ...
... [
29 ]
CNN-LSTM
[29 ] CNN-LSTM
[29 ] 4 64 95.00 — 95.33 — — COR+GCN[13 ] [13 ] [13 ] 1 64 98.56 — — — — FDF+SVM_RBF[30 ] 10 64 97.22 — — — — RF[31 ] 2 64 98.16 — 97.30 — — SVM[31 ] 2 64 97.64 — 96.02 — — MCL+马氏距离分类器[32 ] 10 64 99.40 6.330 98.80 10.500 — CNN+数据增强[9 ] 12 64 — — — 0.190 300.82 PLV+Gamma[12 ] [12 ] 4 56 99.40 — — — — ESTformer[33 ] 10 64 94.61 — — — 33.70 Autoencoder-CNN[34 ] 8 64 99.45 — 99.89 — — 提出方法 2 3 90.60 0.179 90.16 0.137 0.29 Fraschini等[11 ] 采用构建功能连通性脑网络的方法,使用12 s数据,在64通道的情况下,EO的识别准确率为96.90%,EC的识别准确率为92.60%. 相比之下,本文方法的准确率平均提高了2.55%和6.41%. Alyasseri等[30 ] 通过提取PSD和AR特征,送入SVM_RBF分类器进行分类,在64通道的条件下识别准确率达到97.22%,比本文方法低2.23%. Kaur等[31 ] 应用PCA提取特征,使用SVM分类的睁眼和闭眼状态的身份识别准确率分别为97.64%和96.02%,使用RF分类器的身份识别准确率分别为98.16%和97.30%,识别效果不如本文方法. Yahyaei等[32 ] 提取脑电信号的MCL特征,使用马氏距离分类器进行分类,在10 s时间段、64通道的条件下,EO识别准确率达到99.40%,EC识别准确率达到98.80%,但EER较高. Kumar等[12 ] 使用基于锁相值的SVM方法,在使用56通道时获得99.40%的准确率,当通道数减少至21时,准确率仅下降3.40%. 相比之下,本文方法在2 s时间段、16通道的配置下,准确率超过文献[12 ]方法在4 s时间段、21通道下的表现. 通过上述在睁眼和闭眼状态数据上的比较,本文方法在参数量较少,时间段较短的情况下,分类效果在多种性能评估下更好. ...
... [
29 ]
CNN-LSTM
[29 ] 4 64 95.00 — 95.33 — — COR+GCN[13 ] [13 ] [13 ] 1 64 98.56 — — — — FDF+SVM_RBF[30 ] 10 64 97.22 — — — — RF[31 ] 2 64 98.16 — 97.30 — — SVM[31 ] 2 64 97.64 — 96.02 — — MCL+马氏距离分类器[32 ] 10 64 99.40 6.330 98.80 10.500 — CNN+数据增强[9 ] 12 64 — — — 0.190 300.82 PLV+Gamma[12 ] [12 ] 4 56 99.40 — — — — ESTformer[33 ] 10 64 94.61 — — — 33.70 Autoencoder-CNN[34 ] 8 64 99.45 — 99.89 — — 提出方法 2 3 90.60 0.179 90.16 0.137 0.29 Fraschini等[11 ] 采用构建功能连通性脑网络的方法,使用12 s数据,在64通道的情况下,EO的识别准确率为96.90%,EC的识别准确率为92.60%. 相比之下,本文方法的准确率平均提高了2.55%和6.41%. Alyasseri等[30 ] 通过提取PSD和AR特征,送入SVM_RBF分类器进行分类,在64通道的条件下识别准确率达到97.22%,比本文方法低2.23%. Kaur等[31 ] 应用PCA提取特征,使用SVM分类的睁眼和闭眼状态的身份识别准确率分别为97.64%和96.02%,使用RF分类器的身份识别准确率分别为98.16%和97.30%,识别效果不如本文方法. Yahyaei等[32 ] 提取脑电信号的MCL特征,使用马氏距离分类器进行分类,在10 s时间段、64通道的条件下,EO识别准确率达到99.40%,EC识别准确率达到98.80%,但EER较高. Kumar等[12 ] 使用基于锁相值的SVM方法,在使用56通道时获得99.40%的准确率,当通道数减少至21时,准确率仅下降3.40%. 相比之下,本文方法在2 s时间段、16通道的配置下,准确率超过文献[12 ]方法在4 s时间段、21通道下的表现. 通过上述在睁眼和闭眼状态数据上的比较,本文方法在参数量较少,时间段较短的情况下,分类效果在多种性能评估下更好. ...
... [
29 ]
4 64 95.00 — 95.33 — — COR+GCN[13 ] [13 ] [13 ] 1 64 98.56 — — — — FDF+SVM_RBF[30 ] 10 64 97.22 — — — — RF[31 ] 2 64 98.16 — 97.30 — — SVM[31 ] 2 64 97.64 — 96.02 — — MCL+马氏距离分类器[32 ] 10 64 99.40 6.330 98.80 10.500 — CNN+数据增强[9 ] 12 64 — — — 0.190 300.82 PLV+Gamma[12 ] [12 ] 4 56 99.40 — — — — ESTformer[33 ] 10 64 94.61 — — — 33.70 Autoencoder-CNN[34 ] 8 64 99.45 — 99.89 — — 提出方法 2 3 90.60 0.179 90.16 0.137 0.29 Fraschini等[11 ] 采用构建功能连通性脑网络的方法,使用12 s数据,在64通道的情况下,EO的识别准确率为96.90%,EC的识别准确率为92.60%. 相比之下,本文方法的准确率平均提高了2.55%和6.41%. Alyasseri等[30 ] 通过提取PSD和AR特征,送入SVM_RBF分类器进行分类,在64通道的条件下识别准确率达到97.22%,比本文方法低2.23%. Kaur等[31 ] 应用PCA提取特征,使用SVM分类的睁眼和闭眼状态的身份识别准确率分别为97.64%和96.02%,使用RF分类器的身份识别准确率分别为98.16%和97.30%,识别效果不如本文方法. Yahyaei等[32 ] 提取脑电信号的MCL特征,使用马氏距离分类器进行分类,在10 s时间段、64通道的条件下,EO识别准确率达到99.40%,EC识别准确率达到98.80%,但EER较高. Kumar等[12 ] 使用基于锁相值的SVM方法,在使用56通道时获得99.40%的准确率,当通道数减少至21时,准确率仅下降3.40%. 相比之下,本文方法在2 s时间段、16通道的配置下,准确率超过文献[12 ]方法在4 s时间段、21通道下的表现. 通过上述在睁眼和闭眼状态数据上的比较,本文方法在参数量较少,时间段较短的情况下,分类效果在多种性能评估下更好. ...
2
... Comparison of resting state data for Physionet dataset
Tab.6 方法 slot/s N EO EC N p /106 ACC/% EER/% ACC/% EER/% 连通性网络[11 ] 12 64 96.90 4.400 92.60 6.500 — CNN-LSTM[29 ] [29 ] [29 ] [29 ] 4 64 95.00 — 95.33 — — COR+GCN[13 ] [13 ] [13 ] 1 64 98.56 — — — — FDF+SVM_RBF[30 ] 10 64 97.22 — — — — RF[31 ] 2 64 98.16 — 97.30 — — SVM[31 ] 2 64 97.64 — 96.02 — — MCL+马氏距离分类器[32 ] 10 64 99.40 6.330 98.80 10.500 — CNN+数据增强[9 ] 12 64 — — — 0.190 300.82 PLV+Gamma[12 ] [12 ] 4 56 99.40 — — — — ESTformer[33 ] 10 64 94.61 — — — 33.70 Autoencoder-CNN[34 ] 8 64 99.45 — 99.89 — — 提出方法 2 3 90.60 0.179 90.16 0.137 0.29
Fraschini等[11 ] 采用构建功能连通性脑网络的方法,使用12 s数据,在64通道的情况下,EO的识别准确率为96.90%,EC的识别准确率为92.60%. 相比之下,本文方法的准确率平均提高了2.55%和6.41%. Alyasseri等[30 ] 通过提取PSD和AR特征,送入SVM_RBF分类器进行分类,在64通道的条件下识别准确率达到97.22%,比本文方法低2.23%. Kaur等[31 ] 应用PCA提取特征,使用SVM分类的睁眼和闭眼状态的身份识别准确率分别为97.64%和96.02%,使用RF分类器的身份识别准确率分别为98.16%和97.30%,识别效果不如本文方法. Yahyaei等[32 ] 提取脑电信号的MCL特征,使用马氏距离分类器进行分类,在10 s时间段、64通道的条件下,EO识别准确率达到99.40%,EC识别准确率达到98.80%,但EER较高. Kumar等[12 ] 使用基于锁相值的SVM方法,在使用56通道时获得99.40%的准确率,当通道数减少至21时,准确率仅下降3.40%. 相比之下,本文方法在2 s时间段、16通道的配置下,准确率超过文献[12 ]方法在4 s时间段、21通道下的表现. 通过上述在睁眼和闭眼状态数据上的比较,本文方法在参数量较少,时间段较短的情况下,分类效果在多种性能评估下更好. ...
... Fraschini等[11 ] 采用构建功能连通性脑网络的方法,使用12 s数据,在64通道的情况下,EO的识别准确率为96.90%,EC的识别准确率为92.60%. 相比之下,本文方法的准确率平均提高了2.55%和6.41%. Alyasseri等[30 ] 通过提取PSD和AR特征,送入SVM_RBF分类器进行分类,在64通道的条件下识别准确率达到97.22%,比本文方法低2.23%. Kaur等[31 ] 应用PCA提取特征,使用SVM分类的睁眼和闭眼状态的身份识别准确率分别为97.64%和96.02%,使用RF分类器的身份识别准确率分别为98.16%和97.30%,识别效果不如本文方法. Yahyaei等[32 ] 提取脑电信号的MCL特征,使用马氏距离分类器进行分类,在10 s时间段、64通道的条件下,EO识别准确率达到99.40%,EC识别准确率达到98.80%,但EER较高. Kumar等[12 ] 使用基于锁相值的SVM方法,在使用56通道时获得99.40%的准确率,当通道数减少至21时,准确率仅下降3.40%. 相比之下,本文方法在2 s时间段、16通道的配置下,准确率超过文献[12 ]方法在4 s时间段、21通道下的表现. 通过上述在睁眼和闭眼状态数据上的比较,本文方法在参数量较少,时间段较短的情况下,分类效果在多种性能评估下更好. ...
3
... Comparison of resting state data for Physionet dataset
Tab.6 方法 slot/s N EO EC N p /106 ACC/% EER/% ACC/% EER/% 连通性网络[11 ] 12 64 96.90 4.400 92.60 6.500 — CNN-LSTM[29 ] [29 ] [29 ] [29 ] 4 64 95.00 — 95.33 — — COR+GCN[13 ] [13 ] [13 ] 1 64 98.56 — — — — FDF+SVM_RBF[30 ] 10 64 97.22 — — — — RF[31 ] 2 64 98.16 — 97.30 — — SVM[31 ] 2 64 97.64 — 96.02 — — MCL+马氏距离分类器[32 ] 10 64 99.40 6.330 98.80 10.500 — CNN+数据增强[9 ] 12 64 — — — 0.190 300.82 PLV+Gamma[12 ] [12 ] 4 56 99.40 — — — — ESTformer[33 ] 10 64 94.61 — — — 33.70 Autoencoder-CNN[34 ] 8 64 99.45 — 99.89 — — 提出方法 2 3 90.60 0.179 90.16 0.137 0.29
Fraschini等[11 ] 采用构建功能连通性脑网络的方法,使用12 s数据,在64通道的情况下,EO的识别准确率为96.90%,EC的识别准确率为92.60%. 相比之下,本文方法的准确率平均提高了2.55%和6.41%. Alyasseri等[30 ] 通过提取PSD和AR特征,送入SVM_RBF分类器进行分类,在64通道的条件下识别准确率达到97.22%,比本文方法低2.23%. Kaur等[31 ] 应用PCA提取特征,使用SVM分类的睁眼和闭眼状态的身份识别准确率分别为97.64%和96.02%,使用RF分类器的身份识别准确率分别为98.16%和97.30%,识别效果不如本文方法. Yahyaei等[32 ] 提取脑电信号的MCL特征,使用马氏距离分类器进行分类,在10 s时间段、64通道的条件下,EO识别准确率达到99.40%,EC识别准确率达到98.80%,但EER较高. Kumar等[12 ] 使用基于锁相值的SVM方法,在使用56通道时获得99.40%的准确率,当通道数减少至21时,准确率仅下降3.40%. 相比之下,本文方法在2 s时间段、16通道的配置下,准确率超过文献[12 ]方法在4 s时间段、21通道下的表现. 通过上述在睁眼和闭眼状态数据上的比较,本文方法在参数量较少,时间段较短的情况下,分类效果在多种性能评估下更好. ...
... [
31 ]
2 64 97.64 — 96.02 — — MCL+马氏距离分类器[32 ] 10 64 99.40 6.330 98.80 10.500 — CNN+数据增强[9 ] 12 64 — — — 0.190 300.82 PLV+Gamma[12 ] [12 ] 4 56 99.40 — — — — ESTformer[33 ] 10 64 94.61 — — — 33.70 Autoencoder-CNN[34 ] 8 64 99.45 — 99.89 — — 提出方法 2 3 90.60 0.179 90.16 0.137 0.29 Fraschini等[11 ] 采用构建功能连通性脑网络的方法,使用12 s数据,在64通道的情况下,EO的识别准确率为96.90%,EC的识别准确率为92.60%. 相比之下,本文方法的准确率平均提高了2.55%和6.41%. Alyasseri等[30 ] 通过提取PSD和AR特征,送入SVM_RBF分类器进行分类,在64通道的条件下识别准确率达到97.22%,比本文方法低2.23%. Kaur等[31 ] 应用PCA提取特征,使用SVM分类的睁眼和闭眼状态的身份识别准确率分别为97.64%和96.02%,使用RF分类器的身份识别准确率分别为98.16%和97.30%,识别效果不如本文方法. Yahyaei等[32 ] 提取脑电信号的MCL特征,使用马氏距离分类器进行分类,在10 s时间段、64通道的条件下,EO识别准确率达到99.40%,EC识别准确率达到98.80%,但EER较高. Kumar等[12 ] 使用基于锁相值的SVM方法,在使用56通道时获得99.40%的准确率,当通道数减少至21时,准确率仅下降3.40%. 相比之下,本文方法在2 s时间段、16通道的配置下,准确率超过文献[12 ]方法在4 s时间段、21通道下的表现. 通过上述在睁眼和闭眼状态数据上的比较,本文方法在参数量较少,时间段较短的情况下,分类效果在多种性能评估下更好. ...
... Fraschini等[11 ] 采用构建功能连通性脑网络的方法,使用12 s数据,在64通道的情况下,EO的识别准确率为96.90%,EC的识别准确率为92.60%. 相比之下,本文方法的准确率平均提高了2.55%和6.41%. Alyasseri等[30 ] 通过提取PSD和AR特征,送入SVM_RBF分类器进行分类,在64通道的条件下识别准确率达到97.22%,比本文方法低2.23%. Kaur等[31 ] 应用PCA提取特征,使用SVM分类的睁眼和闭眼状态的身份识别准确率分别为97.64%和96.02%,使用RF分类器的身份识别准确率分别为98.16%和97.30%,识别效果不如本文方法. Yahyaei等[32 ] 提取脑电信号的MCL特征,使用马氏距离分类器进行分类,在10 s时间段、64通道的条件下,EO识别准确率达到99.40%,EC识别准确率达到98.80%,但EER较高. Kumar等[12 ] 使用基于锁相值的SVM方法,在使用56通道时获得99.40%的准确率,当通道数减少至21时,准确率仅下降3.40%. 相比之下,本文方法在2 s时间段、16通道的配置下,准确率超过文献[12 ]方法在4 s时间段、21通道下的表现. 通过上述在睁眼和闭眼状态数据上的比较,本文方法在参数量较少,时间段较短的情况下,分类效果在多种性能评估下更好. ...
Mean curve length: an efficient feature for brainwave biometrics
2
2022
... Comparison of resting state data for Physionet dataset
Tab.6 方法 slot/s N EO EC N p /106 ACC/% EER/% ACC/% EER/% 连通性网络[11 ] 12 64 96.90 4.400 92.60 6.500 — CNN-LSTM[29 ] [29 ] [29 ] [29 ] 4 64 95.00 — 95.33 — — COR+GCN[13 ] [13 ] [13 ] 1 64 98.56 — — — — FDF+SVM_RBF[30 ] 10 64 97.22 — — — — RF[31 ] 2 64 98.16 — 97.30 — — SVM[31 ] 2 64 97.64 — 96.02 — — MCL+马氏距离分类器[32 ] 10 64 99.40 6.330 98.80 10.500 — CNN+数据增强[9 ] 12 64 — — — 0.190 300.82 PLV+Gamma[12 ] [12 ] 4 56 99.40 — — — — ESTformer[33 ] 10 64 94.61 — — — 33.70 Autoencoder-CNN[34 ] 8 64 99.45 — 99.89 — — 提出方法 2 3 90.60 0.179 90.16 0.137 0.29
Fraschini等[11 ] 采用构建功能连通性脑网络的方法,使用12 s数据,在64通道的情况下,EO的识别准确率为96.90%,EC的识别准确率为92.60%. 相比之下,本文方法的准确率平均提高了2.55%和6.41%. Alyasseri等[30 ] 通过提取PSD和AR特征,送入SVM_RBF分类器进行分类,在64通道的条件下识别准确率达到97.22%,比本文方法低2.23%. Kaur等[31 ] 应用PCA提取特征,使用SVM分类的睁眼和闭眼状态的身份识别准确率分别为97.64%和96.02%,使用RF分类器的身份识别准确率分别为98.16%和97.30%,识别效果不如本文方法. Yahyaei等[32 ] 提取脑电信号的MCL特征,使用马氏距离分类器进行分类,在10 s时间段、64通道的条件下,EO识别准确率达到99.40%,EC识别准确率达到98.80%,但EER较高. Kumar等[12 ] 使用基于锁相值的SVM方法,在使用56通道时获得99.40%的准确率,当通道数减少至21时,准确率仅下降3.40%. 相比之下,本文方法在2 s时间段、16通道的配置下,准确率超过文献[12 ]方法在4 s时间段、21通道下的表现. 通过上述在睁眼和闭眼状态数据上的比较,本文方法在参数量较少,时间段较短的情况下,分类效果在多种性能评估下更好. ...
... Fraschini等[11 ] 采用构建功能连通性脑网络的方法,使用12 s数据,在64通道的情况下,EO的识别准确率为96.90%,EC的识别准确率为92.60%. 相比之下,本文方法的准确率平均提高了2.55%和6.41%. Alyasseri等[30 ] 通过提取PSD和AR特征,送入SVM_RBF分类器进行分类,在64通道的条件下识别准确率达到97.22%,比本文方法低2.23%. Kaur等[31 ] 应用PCA提取特征,使用SVM分类的睁眼和闭眼状态的身份识别准确率分别为97.64%和96.02%,使用RF分类器的身份识别准确率分别为98.16%和97.30%,识别效果不如本文方法. Yahyaei等[32 ] 提取脑电信号的MCL特征,使用马氏距离分类器进行分类,在10 s时间段、64通道的条件下,EO识别准确率达到99.40%,EC识别准确率达到98.80%,但EER较高. Kumar等[12 ] 使用基于锁相值的SVM方法,在使用56通道时获得99.40%的准确率,当通道数减少至21时,准确率仅下降3.40%. 相比之下,本文方法在2 s时间段、16通道的配置下,准确率超过文献[12 ]方法在4 s时间段、21通道下的表现. 通过上述在睁眼和闭眼状态数据上的比较,本文方法在参数量较少,时间段较短的情况下,分类效果在多种性能评估下更好. ...
ESTformer: transformer utilising spatiotemporal dependencies for electroencephalogram super-resolution
2
2025
... 如表6 所示为本文方法与其他方法在Physionet数据集中静息状态数据的分类表现,对于同一数据集,当前主流的算法性能与本文方法的比较如下. Das等[29 ] 使用CNN-LSTM模型进行测试,在4 s、8 s、12 s和16 s的实验中,12 s时段的效果最佳,EO和EC的识别准确率分别为98.00%和99.95%. 本文方法的EC识别准确率略低于文献[29 ]方法,但本文方法仅用2 s时间段,更适用于实际应用. Tian等[13 ] 应用基于GCN的方法,使用1 s数据,最高准确率达到98.56%,但在通道减少时准确率下降较快. 相比之下,本文方法在低通道数下保持较高的准确率. Schons等[9 ] 结合滑动窗口的数据增强技术和CNN,在最佳情况下EER为0.190%,本文所提方法在64通道下EER更低,使用的时间段更短. Li等[33 ] 提出ESTformer模型进行脑纹识别,在10 s时间段、64通道的条件下实现94.61%的准确率,模型参数量为33.7×106 . 相比之下,本文方法的准确率更高,参数量更少. Bandana等[34 ] 提出使用自动编码器对脑电信号进行重建,再使用CNN进行分类,在8 s时间段、64通道的配置下,睁眼和闭眼状态时分别达到99.45%和99.89%的准确率,但文献[34 ]方法使用的时间段比本文方法长. ...
... Comparison of resting state data for Physionet dataset
Tab.6 方法 slot/s N EO EC N p /106 ACC/% EER/% ACC/% EER/% 连通性网络[11 ] 12 64 96.90 4.400 92.60 6.500 — CNN-LSTM[29 ] [29 ] [29 ] [29 ] 4 64 95.00 — 95.33 — — COR+GCN[13 ] [13 ] [13 ] 1 64 98.56 — — — — FDF+SVM_RBF[30 ] 10 64 97.22 — — — — RF[31 ] 2 64 98.16 — 97.30 — — SVM[31 ] 2 64 97.64 — 96.02 — — MCL+马氏距离分类器[32 ] 10 64 99.40 6.330 98.80 10.500 — CNN+数据增强[9 ] 12 64 — — — 0.190 300.82 PLV+Gamma[12 ] [12 ] 4 56 99.40 — — — — ESTformer[33 ] 10 64 94.61 — — — 33.70 Autoencoder-CNN[34 ] 8 64 99.45 — 99.89 — — 提出方法 2 3 90.60 0.179 90.16 0.137 0.29
Fraschini等[11 ] 采用构建功能连通性脑网络的方法,使用12 s数据,在64通道的情况下,EO的识别准确率为96.90%,EC的识别准确率为92.60%. 相比之下,本文方法的准确率平均提高了2.55%和6.41%. Alyasseri等[30 ] 通过提取PSD和AR特征,送入SVM_RBF分类器进行分类,在64通道的条件下识别准确率达到97.22%,比本文方法低2.23%. Kaur等[31 ] 应用PCA提取特征,使用SVM分类的睁眼和闭眼状态的身份识别准确率分别为97.64%和96.02%,使用RF分类器的身份识别准确率分别为98.16%和97.30%,识别效果不如本文方法. Yahyaei等[32 ] 提取脑电信号的MCL特征,使用马氏距离分类器进行分类,在10 s时间段、64通道的条件下,EO识别准确率达到99.40%,EC识别准确率达到98.80%,但EER较高. Kumar等[12 ] 使用基于锁相值的SVM方法,在使用56通道时获得99.40%的准确率,当通道数减少至21时,准确率仅下降3.40%. 相比之下,本文方法在2 s时间段、16通道的配置下,准确率超过文献[12 ]方法在4 s时间段、21通道下的表现. 通过上述在睁眼和闭眼状态数据上的比较,本文方法在参数量较少,时间段较短的情况下,分类效果在多种性能评估下更好. ...
Person identification using autoencoder-CNN approach with multitask-based EEG biometric
3
2024
... 如表6 所示为本文方法与其他方法在Physionet数据集中静息状态数据的分类表现,对于同一数据集,当前主流的算法性能与本文方法的比较如下. Das等[29 ] 使用CNN-LSTM模型进行测试,在4 s、8 s、12 s和16 s的实验中,12 s时段的效果最佳,EO和EC的识别准确率分别为98.00%和99.95%. 本文方法的EC识别准确率略低于文献[29 ]方法,但本文方法仅用2 s时间段,更适用于实际应用. Tian等[13 ] 应用基于GCN的方法,使用1 s数据,最高准确率达到98.56%,但在通道减少时准确率下降较快. 相比之下,本文方法在低通道数下保持较高的准确率. Schons等[9 ] 结合滑动窗口的数据增强技术和CNN,在最佳情况下EER为0.190%,本文所提方法在64通道下EER更低,使用的时间段更短. Li等[33 ] 提出ESTformer模型进行脑纹识别,在10 s时间段、64通道的条件下实现94.61%的准确率,模型参数量为33.7×106 . 相比之下,本文方法的准确率更高,参数量更少. Bandana等[34 ] 提出使用自动编码器对脑电信号进行重建,再使用CNN进行分类,在8 s时间段、64通道的配置下,睁眼和闭眼状态时分别达到99.45%和99.89%的准确率,但文献[34 ]方法使用的时间段比本文方法长. ...
... 提出使用自动编码器对脑电信号进行重建,再使用CNN进行分类,在8 s时间段、64通道的配置下,睁眼和闭眼状态时分别达到99.45%和99.89%的准确率,但文献[34 ]方法使用的时间段比本文方法长. ...
... Comparison of resting state data for Physionet dataset
Tab.6 方法 slot/s N EO EC N p /106 ACC/% EER/% ACC/% EER/% 连通性网络[11 ] 12 64 96.90 4.400 92.60 6.500 — CNN-LSTM[29 ] [29 ] [29 ] [29 ] 4 64 95.00 — 95.33 — — COR+GCN[13 ] [13 ] [13 ] 1 64 98.56 — — — — FDF+SVM_RBF[30 ] 10 64 97.22 — — — — RF[31 ] 2 64 98.16 — 97.30 — — SVM[31 ] 2 64 97.64 — 96.02 — — MCL+马氏距离分类器[32 ] 10 64 99.40 6.330 98.80 10.500 — CNN+数据增强[9 ] 12 64 — — — 0.190 300.82 PLV+Gamma[12 ] [12 ] 4 56 99.40 — — — — ESTformer[33 ] 10 64 94.61 — — — 33.70 Autoencoder-CNN[34 ] 8 64 99.45 — 99.89 — — 提出方法 2 3 90.60 0.179 90.16 0.137 0.29
Fraschini等[11 ] 采用构建功能连通性脑网络的方法,使用12 s数据,在64通道的情况下,EO的识别准确率为96.90%,EC的识别准确率为92.60%. 相比之下,本文方法的准确率平均提高了2.55%和6.41%. Alyasseri等[30 ] 通过提取PSD和AR特征,送入SVM_RBF分类器进行分类,在64通道的条件下识别准确率达到97.22%,比本文方法低2.23%. Kaur等[31 ] 应用PCA提取特征,使用SVM分类的睁眼和闭眼状态的身份识别准确率分别为97.64%和96.02%,使用RF分类器的身份识别准确率分别为98.16%和97.30%,识别效果不如本文方法. Yahyaei等[32 ] 提取脑电信号的MCL特征,使用马氏距离分类器进行分类,在10 s时间段、64通道的条件下,EO识别准确率达到99.40%,EC识别准确率达到98.80%,但EER较高. Kumar等[12 ] 使用基于锁相值的SVM方法,在使用56通道时获得99.40%的准确率,当通道数减少至21时,准确率仅下降3.40%. 相比之下,本文方法在2 s时间段、16通道的配置下,准确率超过文献[12 ]方法在4 s时间段、21通道下的表现. 通过上述在睁眼和闭眼状态数据上的比较,本文方法在参数量较少,时间段较短的情况下,分类效果在多种性能评估下更好. ...
Affective EEG-based person identification using the deep learning approach
3
2020
... 如表7 所示为本文方法与其他方法在DEAP数据集上的分类性能对比. 选用10 s的时间段,分别针对5通道和32通道进行测试,均实现了99.00%以上的准确率. Wilaiprasitporn等[35 ] 提出结合CNN和GRU的混合模型,该方法将脑电信号划分为10 s长度,在5通道和32通道下分别达到99.17%和99.90%的平均准确率,分类准确率不如本文方法,且模型参数量较大. Gómez-Tapia等[36 ] 探究进行脑纹识别所需的最短时间段,在经过预处理的脑电信号中提取功率谱密度或小波能量特征,使用MLP进行分类,在1 s时间段下的识别准确率达到95.00%,在3 s时间段下进一步提升到99.00%,文献[36 ]方法所需的时间段短,但对信号质量的要求较高,信号预处理过程较复杂,且使用了完整的32通道数据. 相比之下,本文所提方法在仅使用5通道的情况下即可取得更优的性能. Jin等[24 ] 提出EPI-CGAN模型进行脑纹识别,实现了99.88%的高准确率,但采用的时间段较长,且分类性能略逊于本文方法. 通过在DEAP数据集上的比较可知,提出的网络模型在低通道数下的分类识别效果综合表现最优. ...
... Comparison of DEAP dataset
Tab.7 方法 slot/s N ACC/% N p /106 CNN-GRU[35 ] [35 ] 10 5 99.17 1.89 MLP[36 ] [36 ] 1 32 95.00 — EPI-CGAN[24 ] 12 32 99.88 — 提出方法 10 5 99.98 0.28
4. 结 语 提出基于轻量级时空注意力机制的卷积神经网络,能够在通道数少与时间段短的条件下实现高效的脑纹识别. 在参数量仅为0.29×106 的情况下,该方法在多个公开数据集上表现出优越的性能. 在通道数少于8或时间段短于1 s的条件下,模型性能有所下降,表明其对时空信息具有较强的依赖性. 未来的研究将进一步聚焦更少通道数、更短时间段下模型性能的提升,重点探索如何自适应地选择对脑纹识别贡献最大的关键通道子集. ...
... [
35 ]
10 5 99.17 1.89 MLP[36 ] [36 ] 1 32 95.00 — EPI-CGAN[24 ] 12 32 99.88 — 提出方法 10 5 99.98 0.28 4. 结 语 提出基于轻量级时空注意力机制的卷积神经网络,能够在通道数少与时间段短的条件下实现高效的脑纹识别. 在参数量仅为0.29×106 的情况下,该方法在多个公开数据集上表现出优越的性能. 在通道数少于8或时间段短于1 s的条件下,模型性能有所下降,表明其对时空信息具有较强的依赖性. 未来的研究将进一步聚焦更少通道数、更短时间段下模型性能的提升,重点探索如何自适应地选择对脑纹识别贡献最大的关键通道子集. ...
On the minimal amount of EEG data required for learning distinctive human features for task-dependent biometric applications
4
2022
... 如表7 所示为本文方法与其他方法在DEAP数据集上的分类性能对比. 选用10 s的时间段,分别针对5通道和32通道进行测试,均实现了99.00%以上的准确率. Wilaiprasitporn等[35 ] 提出结合CNN和GRU的混合模型,该方法将脑电信号划分为10 s长度,在5通道和32通道下分别达到99.17%和99.90%的平均准确率,分类准确率不如本文方法,且模型参数量较大. Gómez-Tapia等[36 ] 探究进行脑纹识别所需的最短时间段,在经过预处理的脑电信号中提取功率谱密度或小波能量特征,使用MLP进行分类,在1 s时间段下的识别准确率达到95.00%,在3 s时间段下进一步提升到99.00%,文献[36 ]方法所需的时间段短,但对信号质量的要求较高,信号预处理过程较复杂,且使用了完整的32通道数据. 相比之下,本文所提方法在仅使用5通道的情况下即可取得更优的性能. Jin等[24 ] 提出EPI-CGAN模型进行脑纹识别,实现了99.88%的高准确率,但采用的时间段较长,且分类性能略逊于本文方法. 通过在DEAP数据集上的比较可知,提出的网络模型在低通道数下的分类识别效果综合表现最优. ...
... 探究进行脑纹识别所需的最短时间段,在经过预处理的脑电信号中提取功率谱密度或小波能量特征,使用MLP进行分类,在1 s时间段下的识别准确率达到95.00%,在3 s时间段下进一步提升到99.00%,文献[36 ]方法所需的时间段短,但对信号质量的要求较高,信号预处理过程较复杂,且使用了完整的32通道数据. 相比之下,本文所提方法在仅使用5通道的情况下即可取得更优的性能. Jin等[24 ] 提出EPI-CGAN模型进行脑纹识别,实现了99.88%的高准确率,但采用的时间段较长,且分类性能略逊于本文方法. 通过在DEAP数据集上的比较可知,提出的网络模型在低通道数下的分类识别效果综合表现最优. ...
... Comparison of DEAP dataset
Tab.7 方法 slot/s N ACC/% N p /106 CNN-GRU[35 ] [35 ] 10 5 99.17 1.89 MLP[36 ] [36 ] 1 32 95.00 — EPI-CGAN[24 ] 12 32 99.88 — 提出方法 10 5 99.98 0.28
4. 结 语 提出基于轻量级时空注意力机制的卷积神经网络,能够在通道数少与时间段短的条件下实现高效的脑纹识别. 在参数量仅为0.29×106 的情况下,该方法在多个公开数据集上表现出优越的性能. 在通道数少于8或时间段短于1 s的条件下,模型性能有所下降,表明其对时空信息具有较强的依赖性. 未来的研究将进一步聚焦更少通道数、更短时间段下模型性能的提升,重点探索如何自适应地选择对脑纹识别贡献最大的关键通道子集. ...
... [
36 ]
1 32 95.00 — EPI-CGAN[24 ] 12 32 99.88 — 提出方法 10 5 99.98 0.28 4. 结 语 提出基于轻量级时空注意力机制的卷积神经网络,能够在通道数少与时间段短的条件下实现高效的脑纹识别. 在参数量仅为0.29×106 的情况下,该方法在多个公开数据集上表现出优越的性能. 在通道数少于8或时间段短于1 s的条件下,模型性能有所下降,表明其对时空信息具有较强的依赖性. 未来的研究将进一步聚焦更少通道数、更短时间段下模型性能的提升,重点探索如何自适应地选择对脑纹识别贡献最大的关键通道子集. ...