作为一种典型的无人驾驶物料搬运设备，自动导引车（automated guided vehicle，AGV）的调度优化研究往往结合各类生产场景，如制造车间^[1-3]、自动化仓库^[4-6] 、港口集装箱码头^[7-10]. AGV的调度往往需要考虑任务的分配、无冲突路由的路径规划^[11-12]及各种作业约束条件，以避免生产系统的生产事故风险，这极大地增加了AGV调度中任务执行方案优化的挑战性.

已有的AGV任务调度研究通过合理的任务执行顺序规划完成给定任务，以优化AGV任务调度方案，同时在不同程度上考虑AGV的作业约束. Zhang等^[3]针对给定的单AGV和一组运输任务（预设起点任务和终点任务固定），研究确定最优AGV路线的路径规划问题. De Ryck等^[13]针对AGV作业过程中的充电问题，扩展了经典的旅行商问题（traveling salesman problem，TSP）模型，使得访问节点数量可变，从而将充电站纳入指定的站点行程. 高文文等^[14]针对岸桥卸船作业中的AGV路径优化，考虑任务之间的偏序关系，建立混合整数规划模型进行求解，实现了较短时间内的可行解搜索. 祁璇等^[15]针对生产车间内的AGV路径规划与任务调度问题，提出基于改进近端优化策略算法的单AGV 多任务调度优化方法，避免了AGV空载或回程路线的浪费. 上述研究较少考虑任务执行顺序的限制，任务需求 （如任务访问节点、任务节点距离）多是静态的.

本文结合实际问题的业务需求，研究特定生产系统中单辆单载AGV在生产线和仓库之间运输托盘和成品工件的调度优化问题，旨在提供最大程度最小化AGV行驶总距离的优化调度方案. 调度方案的制定涉及任务选择策略和任务执行顺序规划. 在规划顺序限制的条件下，任务需求（起点、终点和到达时刻）随环境动态（工作点的托盘数量）变化. 建立基于有向无环图建模的动态旅行商问题（dynamic traveling salesman problem model based on directed acyclic graph modeling，DAGDTSP）模型，提出改进遗传算法（improved genetic algorithm，IGA）进行模型求解. 此外，考虑到任务选择策略多样性对优化调度方案求解的影响，提出基于二进制粒子群优化（binary particle swarm optimization，BPSO）的嵌套算法框架（以下简称为“BPSO嵌套框架”）. 基于随机生成的测试问题，通过实验验证所提方法的性能.

本文研究课题源于一家国内专业从事联轴器研发与制造的大型骨干企业. 该企业新建联轴器自动生产线，实现原料存储、生产加工和物流流转的自动化及生产管理的数字化. 机器人将工件从机器转移到仓库下料点后，AGV负责联轴器成品从生产线到仓库的运输和存储管理.

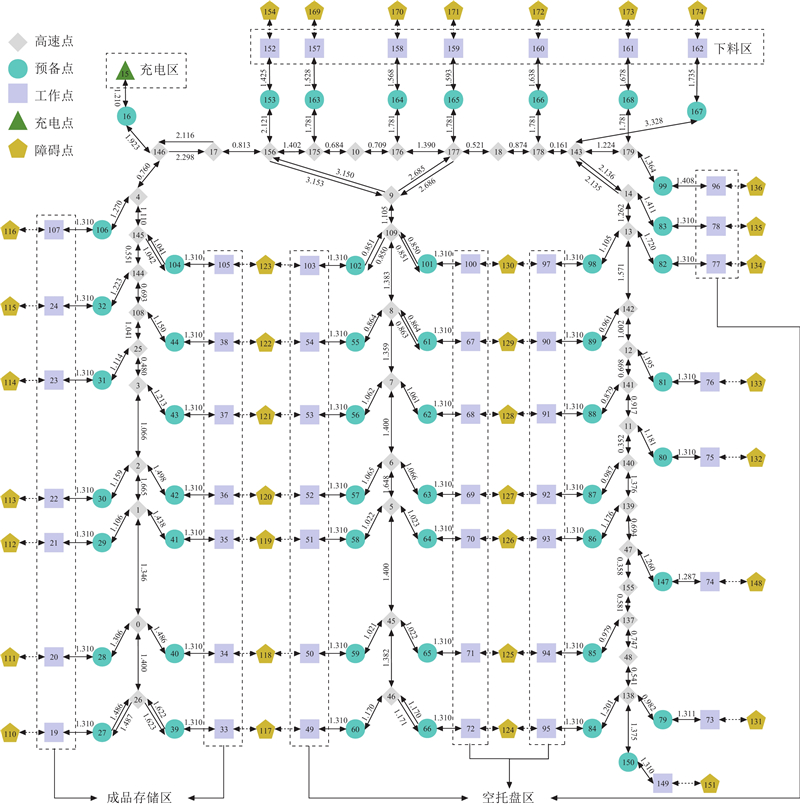
如图1所示为网络拓扑图，单载AGV在仓库区域运输托盘和工件，任意2个拓扑点之间存在唯一的最短路径，节点距离由拓扑图中边的权重表示. AGV在完成配送物料的一次性装载后，直接将物料运输到目的地. 定义AGV执行的出库任务为AGV将下料区的盛有工件的托盘运输到成品存储区，定义入库任务为AGV将空托盘区的空托盘运输至无托盘放置的下料点. 出库任务由工件加工完成所触发，即每一个工件的加工完成意味着一个出库任务到达. 在执行运输任务的过程中，AGV从充电点出发，在完成所有任务后停留在邻近高速点. AGV运输时应满足作业约束：AGV在下料点完成一次出库任务后，需要在下一个工件到达该点前，通过执行入库任务补充空托盘，以保证到达该点的后续工件被托盘盛放.

本文研究的问题如下：在工件的批量生产过程中，已知由工件加工完成所触发的多个出库任务的起点和到达时刻，为单辆单载AGV的任务调度提供优化调度方案，包括AGV待执行任务的起点、终点和开始执行时刻等信息. 优化调度方案以最小化AGV的行驶总距离为优化目标进行求解，保证AGV在执行任务的过程中满足作业要求，以避免引发生产事故. 除上述描述外，本文研究还基于以下假设条件.

(1)$ {{E}}_{\rm{AGV}}\left({t}\right){ > }{{E}}_{\rm{AGV}}^{{*}}. $

(2)$ {{v}}_{\rm{AGV}}\left({t}\right)={{v}}_{\rm{s}}. $

(3)$ \forall {p}\in {{P}}_{\rm{I}}{:}\,\,\left|{p}\right|={1},\left|{a}\right|={0}({a}\in {p}){.} $

(4)$ \forall {p}\in {{P}}_{\rm{G}}{:}\,\,\left|{p}\right|={R},\left|{a}\right|={0}({a}\in {p}). $

(5)$ \forall {p}\in {{P}}_{\rm{R}}{:}\left|{p}\right|={0}. $

(6)${{t}}_{\rm{load}}={{t}}_{\rm{unload}}={0}. $

式中：$ {{v}}_{\rm{AGV}}\left({t}\right) $为AGV在$ {t} $时刻的速度，恒为$ {{v}}_{\rm{s}} $；$ {{E}}_{\rm{AGV}}\left({t}\right) $为AGV在$ {t} $时刻剩余的电量；$ {{E}}_{\rm{AGV}}^{{*}} $为维持AGV作业的最小功耗；$ {{P}}_{\rm{I}} $、$ {{P}}_{\rm{G}} $、$ {{P}}_{\rm{R}} $分别为仓库的下料区、成品存储区和空托盘区的工作点集合；$ \left|{p}\right| $为仓库的任意工作点$ {p} $处堆放的托盘数量；$ \left|{a}\right| $为托盘$ a $盛放的工件数量；$ {{t}}_{\rm{load}}、 $$ {{t}}_{\rm{unload}} $分别为AGV装、卸操作的耗时时长.

调度方案的制定要求确定任务选择策略（给定AGV待执行的一组运输任务），以最小化AGV行驶总距离为目标，规划AGV执行给定任务的顺序，求解优化调度方案. 在一次连续的批量生产过程中，记任务集合$ {X}{=}\left\{{{x}}_{{1}},\cdots ,{{x}}_{{i}}\cdots ,{}{{x}}_{{N}},{}{{x}}_{{N}{+}{1}},\cdots , {}{{x}}_{{N}{+}{i}},\cdots ,{}{{x}}_{{2}{N}}\right\} $，其中$ {N} $为生产的工件总数，$ {{x}}_{\rm{1}},\cdots ,{}{{x}}_{{N}} $为依次到达下料区的出库任务，出库任务$ {{x}}_{{i}} $对应的入库任务为$ {{x}}_{{N}{+}{i}} $. 记任务选择策略给定的待执行任务集合$ {{X}}^{\mathrm{e}}{=}\left\{{{x}}_{{1}}^{\mathrm{e}},\cdots ,{}{{x}}_{{i}}^{\mathrm{e}},\cdots ,{}{{x}}_{{M}}^{\mathrm{e}},{}{{x}}_{{M}{+}{1}}^{\mathrm{e}},\cdots ,{}{{x}}_{{M}{+}{i}}^{\mathrm{e}},\cdots ,{}{{x}}_{{2}{M}}^{\mathrm{e}}\right\} $，其中出库任务$ {{x}}_{{i}}^{\mathrm{e}} $对应的入库任务为$ {{x}}_{{M}{+}{i}}^{\mathrm{e}} $. 记环境参数$ {C} $表示托盘最多可容纳的工件数量，当$ {C}{=}{1} $时，$ {X}{=}{{X}}^{\mathrm{e}} $；当$ {C}{ > }{1} $时，$ {{X}}^{\mathrm{e}} \subset {X} $. 调度方案可以表达为$ {{X}}^{\mathrm{e}} $中任务的排序.

托盘可以容纳多个工件，故AGV不需要在每个工件完成后都执行一次出库操作. 记下料区的工作点数量为$ {r} $，依次到达第$ {i} $个下料点的出库任务序列为$ {{X}}^{{i}}{=}\left({{x}}_{{1}}^{{i}},\cdots ,{}{{x}}_{{j}}^{{i}},\cdots ,{}{{x}}_{{{R}}_{{i}}}^{{i}}\right){,}\;{}{i}{}\,\,{\leqslant}{}\,\,{r} $. 其中，$ {{R}}_{{i}} $为到达第$ {i} $个下料点的工件数量，则$ \displaystyle {\sum} _{{i}{=}{1}}^{{r}}{{R}}_{{i}}{=}{N}{,}\left|{\bigcup} _{{i}{=}{1}}^{{r}}{{X}}^{{i}}\right|{=}{N} $. 在任务选择策略中，若选择任务$ {{x}}_{{j}}^{{i}}、{{x}}_{{k}}^{{i}}\in {{X}}^{{i}}{,}\text{ }{k}-{j}\text{ }{ < }\text{ }{C} $，则AGV需要在任务$ {{x}}_{{j}}^{{i}} $、$ {{x}}_{{k}}^{{i}} $到达后到达该工作点，将盛放有$ {k}-{j}{+}{1} $个工件的托盘运输至成品存储区. 为了最小化AGV在下料区各工作点执行的出库操作次数，可以采用常见的任务选择策略：$ \forall {{x}}_{{j}}^{{i}}\in {{X}}^{{i}} $，若$ {j}{\text{%}}{C}{=}{0} $或$ {j}{=}{{R}}_{{i}} $，则$ {{x}}_{{j}}^{{i}} $被选择. 将这种任务选择策略称为基准任务选择策略，将基准任务选择策略下按照顺序和即时原则执行任务的唯一调度方案称为基准调度方案. 顺序原则指被选择任务按照其到达顺序被AGV依次执行，即时原则指AGV每完成一项出库任务后，随即执行对应的入库任务. 将基准调度方案作为评价优化调度方案的参考对象.

为了最小化AGV在下料区每个工作点执行的出库任务数量，基准任务选择策略并非唯一的策略. 为了说明最小化待执行出库任务数量的原则下任务选择策略的多样性，记$ {{B}}^{{i}}{=} \left({{b}}_{{1}}^{{i}},\cdots ,{}{{b}}_{{j}}^{{i}},\cdots ,{}{{b}}_{{{R}}_{{i}}}^{{i}}\right),{} {{b}}_{{j}}^{{i}}\in \left\{{0},{1}\right\} $，表示任务序列$ {{X}}^{{i}}{=}\left({{x}}_{{1}}^{{i}},\cdots ,{}{{x}}_{{j}}^{{i}},\cdots ,{}{{x}}_{{{R}}_{{i}}}^{{i}}\right) $中任务的选择状态，$ i{=}{1},\cdots ,r $. 其中，$ {{b}}_{{j}}^{{i}}{=}{1} $表示出库任务$ {{x}}_{{j}}^{{i}} $被选择为DAGDTSP模型中的任务节点，$ {{x}}_{{j}}^{{i}}\in {{X}}^{\mathrm{e}} $；当$ {{b}}_{{j}}^{{i}}{=}{0} $时，$ {{x}}_{{j}}^{{i}}\notin {{X}}^{\mathrm{e}} $. 在下料区的第$ {i} $个工作点，AGV完成出库任务的数量至少为$ \left\lceil { {{{R}}_{{i}}}/{{C}}} \right\rceil $. 要保证AGV在下料区每个工作点执行的出库任务数量最少，$ {{B}}^{{i}} $应满足以下限制条件：

(7)$ \sum _{{i}{=1}}^{{r}}\sum _{{j}{=1}}^{{{R}}_{{i}}}{{b}}_{{j}}^{{i}}=\sum _{{k}={1}}^{{r}}\left\lceil { \frac{{{R}}_{{k}}}{{C}}} \right\rceil ;\;{{b}}_{{{R}}_{{i}}}^{{i}}={1}{,}\text{ }{1}{\leqslant}{i}{\leqslant}{r}. $

(8)$ \begin{split} &\forall {{b}}_{{j}}^{{i}}、{{b}}_{{k}}^{{i}}\in {{B}}^{{i}}{:}{{b}}_{{j}}^{{i}}={{b}}_{{k}}^{{i}}={1},{j}{ < }{k}{.}\text{ }\forall {l}\in \left\{{j}+{1},\cdots ,{}{k}-{1}\right\},\\ &{{b}}_{{l}}^{{i}}={0}.\Rightarrow {k}-{j}{ < }\text{ }{C}-{1}.\\[-1pt]\end{split} $

基于限制条件(7)、(8)，构建$ {{B}}^{{i}}\left(i={1},\cdots ,r\right) $中元素取值的排列组合向量空间子集$ {{ \varOmega }}_{\rm{1}}^{{i}} \cap {{ \varOmega }}_{\rm{2}}^{{i}} \left(i={1},\cdots ,r\right) $. 基于此，关于任务选择策略数量，有

(9)$\left.\begin{split} &{{ \varOmega }}^{{*}}=\left({{ \varOmega }}_{\rm{1}}^{{1}} \cap {{ \varOmega }}_{\rm{2}}^{{1}}\right){\times }\left({{ \varOmega }}_{\rm{1}}^{{2}} \cap {{ \varOmega }}_{\rm{2}}^{{2}}\right){\times }\cdots {\times }\left({{ \varOmega }}_{\rm{1}}^{{r}} \cap {{ \varOmega }}_{\rm{2}}^{{r}}\right){;}{} \\ &{1}{\leqslant}\left|{{ \varOmega }}^{{*}}\right|{ < }{\prod }_{{i=1}}^{{r}}\left(\begin{array}{c}{{R}}_{{i}}-{1}\\\left\lceil { {{R}}_{{i}}}/{{C}} \right\rceil -{1}\end{array}\right).\end{split} \right\}$

式中：$ {{ \varOmega }}^{{*}} $为向量空间$ {{ \varOmega }}_{\rm{1}}^{{1}} \cap {{ \varOmega }}_{\rm{2}}^{{1}},{{ \varOmega }}_{\rm{1}}^{{2}} \cap {{ \varOmega }}_{\rm{2}}^{{2}},\cdots {,}\text{ }{{ \varOmega }}_{\rm{1}}^{{r}} \cap {{ \varOmega }}_{\rm{2}}^{{r}} $构成的笛卡尔积，$ {{ \varOmega }}^{{*}} $中的元素数量等于任务选择策略数量.

DAGDTSP模型中的任务节点信息随环境动态变化. 这是因为随着AGV作业的进行，仓库成品存储区点位所堆放的托盘数量增至最大限额，空托盘区点位的空托盘数量减少为零，导致出库任务终点和入库任务起点的选择受限，影响AGV执行任务和转移至后续任务的行驶距离. 将任务选择策略给定的待执行任务集合$ {{X}}^{\mathrm{e}} $作为DAGDTSP模型中的节点. 具体地，将$ \forall {{x}}_{{j}}^{\mathrm{e}}\in {{X}}^{\mathrm{e}},{1}{}{\leqslant}{}{j}{}{\leqslant}{}{2}{M} $ 表示为四元组$ \left({{S}}_{{j}}^{\mathrm{e}},{}{{E}}_{{j}}^{\mathrm{e}},{}{{A}}_{{j}}^{\mathrm{e}},{}{{C}}_{{j}}^{\mathrm{e}}\right) $，即任务的运输起点、运输终点、到达时刻和完成时刻. 对于出库任务$ {{x}}_{{i}}^{\mathrm{e}}{=}\left({{S}}_{{i}}^{\mathrm{e}},{}{{E}}_{{i}}^{\mathrm{e}},{}{{A}}_{{i}}^{\mathrm{e}},{}{{C}}_{{i}}^{\mathrm{e}}\right){,} {{x}}_{{i}}^{\mathrm{e}}\in {{X}}^{\mathrm{e}},{{S}}_{{i}}^{\mathrm{e}}\in {{P}}_{{{\mathrm{I}}}} $. $ {{A}}_{{i}}^{\mathrm{e}} $随任务到达一起下发；$ {{C}}_{{i}}^{\mathrm{e}} $为AGV将载有工件的托盘运输至$ {{E}}_{{i}}^{\mathrm{e}} $的时刻；$ {{E}}_{{i}}^{\mathrm{e}} $为成品存储区$ {{P}}_{\rm{G}} $内距离$ {{S}}_{{i}}^{\mathrm{e}} $最近的工作点，

(10)$ {{E}}_{{i}}^{\mathrm{e}}=\underset{{p}\in {{P}}_{\rm{G}}{,}\left|p\right|{ < }{R}}{{{\mathrm{arg}}}{{\mathrm{min}}}}{D}\left({{S}}_{{i}}^{\mathrm{e}}{,}{}{p}\right). $

式中：$ D\left({{S}}_{{i}}^{\mathrm{e}}{,}{}{p}\right) $为工作点$ {{S}}_{{i}}^{\mathrm{e}} $、$ {p} $之间的最短路径距离；$ {R} $为环境参数，表示$ {{P}}_{\rm{G}} $、$ {{P}}_{\rm{R}} $内各工作点堆放托盘的最大层数.

对于入库任务$ {{x}}_{{M}{+}{i}}^{\mathrm{e}}{=}\left({{S}}_{{M}{+}{i}}^{\mathrm{e}}{,}{}{{E}}_{{M}{+}{i}}^{\mathrm{e}}{,}{}{{A}}_{{M}{+}{i}}^{\mathrm{e}}{,}{}{}{{C}}_{{M}{+}{i}}^{\mathrm{e}}\right), $$ {{x}}_{{M}{+}{i}}^{\mathrm{e}}\in {{X}}^{\mathrm{e}} $，$ {{E}}_{{M}{+}{i}}^{\mathrm{e}}{=}{{S}}_{{i}}^{\mathrm{e}} $. $ {{A}}_{{M}{+}{i}}^{\mathrm{e}} $为AGV将载有工件的托盘开始从$ {{S}}_{{i}}^{\mathrm{e}} $运输到$ {{E}}_{{i}}^{\mathrm{e}} $的时刻；$ {{C}}_{{M}{+}{i}}^{\mathrm{e}} $为AGV将空托盘运输至$ {{E}}_{{M}{+}{i}}^{\mathrm{e}} $的时刻；$ {{S}}_{{M}{+}{i}}^{\mathrm{e}} $为空托盘区内使得路径$ \left({p}_{\mathrm{A}\mathrm{G}\mathrm{V}}-{S}_{{M+i}}^{\mathrm{e}}-{S}_{{i}}^{\mathrm{e}}\right) $的距离最短的工作点，

(11)$ {{S}}_{{M+i}}^{\mathrm{e}}=\underset{{p}\in {{P}}_{\rm{R}}{,}\left|p\right|{\geqslant 1}}{{{\mathrm{arg}}}{{\mathrm{min}}}}{D}\left({{p}}_{\mathrm{A}\mathrm{G}\mathrm{V}}{,}\text{ }{p}\right)+{D}\left({p}{,}\text{ }{{S}}_{{i}}^{\mathrm{e}}\right). $

式中：$ {{p}}_{\mathrm{A}\mathrm{G}\mathrm{V}} $为AGV所在点位.

在$ {{X}}^{\mathrm{e}}{=}\left\{{{x}}_{{1}}^{\mathrm{e}},\cdots ,{}{{x}}_{{i}}^{\mathrm{e}},\cdots ,{}{{x}}_{{M}}^{\mathrm{e}},{}{{x}}_{{M}{+}{1}}^{\mathrm{e}},\cdots ,{}{{x}}_{{M}{+}{i}}^{\mathrm{e}},\cdots ,{{x}}_{{2M}}^{\mathrm{e}}\right\} $的基础上，建立有向无环$ {G}{=}\left\langle{{V},{E}}\right\rangle,{}{V}{=}{{X}}^{\mathrm{e}} $. 另记边集合$ {{E}}_{\rm{K}}{=}\left\{\left({{x}}_{{m}}^{\mathrm{e}}{,}\text{ }{{x}}_{{n}}^{\mathrm{e}}\right){|}{m}{,}\text{ }{1}{}{\leqslant}{}{n}{}{\leqslant}{}{2}{M}\right\} $表示已知的有向边，其中$ \left({{x}}_{{m}}^{\mathrm{e}}{,}{}{{x}}_{{n}}^{\mathrm{e}}\right) $表示任务$ {{x}}_{{m}}^{\mathrm{e}} $先于$ {{x}}_{{n}}^{\mathrm{e}} $被执行. 调度方案可以表达为$ {{X}}^{\mathrm{e}} $中任务的排序，即将$ {G} $中所有节点都遍历一次的路径. 关于路径中的边，基于问题描述中有关AGV的作业约束，分别定义第一约束（出库任务与入库任务之间的执行顺序限制）、第二约束（出库任务之间的执行顺序限制）和第三约束（出库任务完成时刻与入库任务到达时刻之间的先后关系），各约束如下所示.

(12)$ \begin{split} &\forall {{x}}_{{i}}^{\mathrm{e}}{、}\text{ }{{x}}_{{k}}^{\mathrm{e}}{、}\text{ }{{x}}_{{M}+{i}}^{\mathrm{e}}\in {{X}}^{\mathrm{e}}{,}\text{ }{i}{ < }{k}{\leqslant}{M}{:}\text{ }{{S}}_{{i}}^{\mathrm{e}}={{S}}_{{k}}^{\mathrm{e}}.\,\,\forall {{S}}_{{j}}^{\mathrm{e}}\in {{P}}_{{{\mathrm{I}}}}{,}\text{ }\\&{{S}}_{{j}}^{\mathrm{e}}{ \ne }{{S}}_{{i}}^{\mathrm{e}},{i}{ < }{j}{ < }{k}{.} \Rightarrow \left({{x}}_{{i}}^{\mathrm{e}}{,}\text{ }{{x}}_{{M}+{i}}^{\mathrm{e}}\right){、}\text{ }\left({{x}}_{{M}+{i}}^{\mathrm{e}}{,}\text{ }{}{{x}}_{{k}}^{\mathrm{e}}\right)\in {{E}}_{{{\mathrm{K}}}}.\end{split} $

(13)$\begin{split} &\forall {{x}}_{{i}}^{\mathrm{e}}{、}{{x}}_{{k}}^{\mathrm{e}}{、}{{x}}_{{l}}^{\mathrm{e}}\in {{X}}^{\mathrm{e}}{,}{i}{ < }{k}{ < }{l}{\leqslant}{M}{:}\text{ }{{S}}_{{i}}^{\mathrm{e}}={{S}}_{{k}}^{\mathrm{e}},{{S}}_{{i}}^{\mathrm{e}}{ \ne }{{S}}_{{l}}^{\mathrm{e}}{.}\text{ }\forall {{S}}_{{j}}^{\mathrm{e}}\in {{P}}_{{{\mathrm{I}}}}{,}\text{ }\\ &{{S}}_{{j}}^{\mathrm{e}}{ \ne }{{S}}_{{i}}^{\mathrm{e}}{,}\text{ }{i}{ < }{j}{ < }{k}{.} \Rightarrow \left({{x}}_{{i}}^{\mathrm{e}}{,}\text{ }{}{{x}}_{{l}}^{\mathrm{e}}\right)\in {{E}}_{{{\mathrm{K}}}}.\end{split}$

(14)$ \forall {{x}}_{{i}}^{\mathrm{e}}{、}\text{ }{{x}}_{{M}+{i}}^{\mathrm{e}}\in {{X}}^{\mathrm{e}}{,}\text{ }{i}{\leqslant}{M}{:}\text{ }{{C}}_{{i}}^{\mathrm{e}}{ < }{{A}}_{{M}+{i}}^{\mathrm{e}}. $

对于将$ {G} $中所有节点都遍历一次的路径，将满足第一约束和第二约束的路径定义为可能路径，满足第三约束的可能路径为有效路径，不满足第三约束的可能路径为无效路径. 在DAGDTSP模型中，关于基准调度方案所对应路径的类型，由于即时原则，路径满足第一约束. 由于顺序原则，路径满足第二约束. 由于即时原则及单个工件生产时间大于AGV单次任务执行时长，路径满足第三约束. 基准调度方案对应有效路径，具备可执行性.

将$ {G} $中任务节点之间的转移距离定义为前置任务终点和后续任务起点之间的最短路径距离. 求解DAGDTSP模型的目标是找到一条总距离最小的有效路径$ {{X}}^{{{\mathrm{v}}}} $，计算如下：

(15)$\begin{split} {{X}}^{\rm{v}}=&\underset{{{X}}_{{i}}^{\rm{v}}\in {{S}}_{\rm{v}}}{{{\mathrm{arg}} {\mathrm{min}}}}\bigg({D}\left({{p}}^{\rm{c}},{}{{S}}_{{i},{1}}^{\rm{v}}\right)+ \bigg.\\&\bigg.\displaystyle \sum _{{j}{=1}}^{{2}{M}}\left({D}\left({{S}}_{{i},{j}}^{\rm{v}}{,}{}{{E}}_{{i},{j}}^{\rm{v}}\right)+{D}\left({{E}}_{{i},{j}}^{\rm{v}},{}{{S}}_{{i},{j}+{1}}^{\rm{v}}\right)\right)\bigg).\end{split}$

式中：$ {{S}}_{\rm{p}} $和$ {{S}}_{\rm{v}} $分别为可能路径和有效路径的解空间，$ {{S}}_{\rm{v}}\in {{S}}_{\rm{p}} $；$ {{X}}_{{i}}^{\rm{v}} $为$ {{S}}_{\rm{v}} $中第$ {i} $条路径对应的AGV任务执行序列，$ {{X}}_{{i}}^{\rm{v}}{=}\left({{x}}_{{i},{1}}^{\rm{v}}, \cdots ,{}{{x}}_{{i},{j}}^{\rm{v}}, \cdots ,{}{{x}}_{{i},{2}{M}}^{\rm{v}}\right) $；$ {{p}}^{\rm{c}} $为充电点位；$ {{S}}_{{i},{2}{M}{+}{1}}^{\rm{v}}{=}{{{\mathrm{arg}}}{{\mathrm{min}}}}_{{p}\in {{P}}_{\rm{H}}}\,\,\,\,{D}\left({{E}}_{{i},{2}{M}}^{\rm{v}},{}{p}\right) $，其中$ {{P}}_{\rm{H}} $为仓库中的高速点集合.

基于对DAGDTSP模型的求解，设计改进遗传算法（IGA）和基于二进制粒子群优化的嵌套算法框架（BPSO嵌套框架），求解固定和多种任务选择策略下的优化调度方案.

遗传算法通过选择、交叉和突变的操作迭代优化求解^[16]. 为了求解DAGDTSP模型，采用改进遗传算法（IGA）对AGV执行任务的顺序进行编码，设计种群初始化机制、适应度评价方法和遗传算子. 当达到固定的迭代次数时，IGA算法终止.

染色体编码采用直接表示法，以任务节点序列表示求解DAGDTSP模型所得的固定长度路径，即AGV执行任务的顺序.

在种群初始化的过程中，随机生成一定数量的染色体，即DAGDTSP模型中任务节点的拓扑排序. 染色体即2.2节中有关DAGDTSP模型所定义的可能路径. 可能路径包括有效路径与无效路径. 在适应度的计算中，若染色体为有效路径，则适应度为染色体对应优化调度方案下AGV的行驶总距离；否则，适应度被指定为固定的惩罚值，记为$ {{V}}_{\rm{p}} $. $ {{V}}_{\rm{p}} $远远大于当前种群中所有有效路径的长度. 染色体的适应度越小，说明该个体越优秀. 染色体适应度的计算公式如下：

(16)$ \begin{split} & F\left({{X}}^{{{\mathrm{c}}}}\right)=\\ &\left\{ \begin{array}{c}{D} \left({{p}}^{{{\mathrm{c}}}},{{S}}_{\rm{1}}^{{{\mathrm{c}}}}\right) + \displaystyle \sum _{{j}{=1}}^{{2}{M}}\left({D}\left({{S}}_{{j}}^{{{\mathrm{c}}}},{}{{E}}_{{j}}^{{{\mathrm{c}}}}\right) + {D}\left({{E}}_{{j}}^{{{\mathrm{c}}}},{}{{S}}_{{j} + {1}}^{{{\mathrm{c}}}}\right)\right),{{X}}^{{{\mathrm{c}}}}\in {{S}}_{\mathrm{v}};\\ {{V}}_{\rm{p}}{,}\text{ }{{X}}^{{{\mathrm{c}}}}\notin {{S}}_{\mathrm{v}}.\end{array}\right.\end{split}$

式中：$ F\left({{X}}^{\rm{c}}\right) $为染色体$ {{X}}^{\rm{c}} $的适应度，$ {{X}}^{\rm{c}}\in {{S}}_{\rm{p}} $；$ {{S}}_{{j}}^{\rm{c}} $和$ {{E}}_{{j}}^{\rm{c}} $分别表示$ {{X}}^{\rm{c}} $对应的任务执行序列中第$ {j} $个任务的起点和终点；$ {{S}}_{{2}{M}{+}{1}}^{\rm{c}}{=}{{{\mathrm{arg}}}{{\mathrm{min}}}}_{{p}\in {{P}}_{\rm{H}}}\text{ }{D}\left({{E}}_{{2}{M}}^{{{\mathrm{c}}}},{}{p}\right) $.

利用IGA算法，设计选择、交叉和变异的遗传算子.

1）选择算子. 种群中的染色体为有效路径或无效路径，前者在求解空间内往往占较少数. 为了避免表示有效路径的染色体在进化过程中被大量淘汰，设计保留选择策略如下：选择父代种群中表示有效路径的染色体，对子代种群中的无效路径染色体进行替换.

2）交叉算子. 交叉操作为种群产生新的个体，保证种群的多样性. 记来自$ {{S}}_{\rm{p}} $空间的父代染色体$ {{P}}_{\rm{1}} $、$ {{P}}_{\rm{2}} $，以及交叉所得的子代染色体$ {{C}}_{\rm{1}} $、$ {{C}}_{\rm{2}} $. 其中，随机引入当前最佳的染色体作为父代. 算法的交叉过程如下.

a）随机选择$ {{}{x}}_{{i}}^{\mathrm{e}}{、}{{}{x}}_{{j}}^{\mathrm{e}}\in {{X}}^{\mathrm{e}}{,}\text{ }{}{i}{}{ < }{}{j}{}{\leqslant}{}{M} $. 记$ {{Y}}_{\rm{1}} $、$ {{Y}}_{\rm{2}} $分别为$ {{P}}_{\rm{1}} $、$ {{P}}_{\rm{2}} $上$ {{}{x}}_{{i}}^{\mathrm{e}} $和$ {{}{x}}_{{j}}^{\mathrm{e}} $之间的子序列.

b）对于$ \forall {y}\in {{Y}}_{\rm{1}} \cup {{Y}}_{\rm{2}} $，若编码顺序$ \left({{x}}_{{i}}^{\mathrm{e}},{}{y},{}{{x}}_{{j}}^{\mathrm{e}}\right) $在$ {{P}}_{\rm{1}} $、$ {{P}}_{\rm{2}} $上不成立，则根据最近原则，在染色体中将$ {y} $置换到$ {{}{x}}_{{i}}^{\mathrm{e}} $前或$ {{}{x}}_{{j}}^{\mathrm{e}} $后，得到$ {{P}}'_{\rm{1}} $、$ {{P}}'_{\rm{2}} $.

c）在$ {{P}}'_{\rm{1}} $、$ {{P}}'_{\rm{2}} $之间交换由$ \left\{{{x}}_{{i}}^{\mathrm{e}},{}{{}{x}}_{{j}}^{\mathrm{e}}\right\} \cup {{Y}}_{\rm{1}} \cup {{Y}}_{\rm{2}} $中的元素构成的子序列，得到$ {{P}}''_{\rm{1}} $、$ {{P}}''_{\rm{2}} $.

d）对于$ {{P}}''_{\rm{1}} $、$ {{P}}''_{\rm{2}} $，若染色体上任意2个基因的相对位置不满足第1约束或者第2约束，则调整对应基因的位置，使得其位置相邻并满足2项约束，得到子代染色体$ {{C}}_{\rm{1}} $、$ {{C}}_{\rm{2}} $.

3）变异算子. 变异操作为个体添加新的特征，保证种群变异性. 记来自$ {{S}}_{\rm{p}} $空间的父代和变异所得的子代染色体$ {{P}}_{\rm{1}} $、$ {{C}}_{\rm{1}} $，算法的变异过程如下.

a) 在$ {{P}}_{\rm{1}} $上随机选择若干个出库任务，改变任务在染色体上的编码位置. 基于第一约束选择$ {{P}}_{\rm{1}} $上的3个任务，记为$ {{x}}_{{M}{+}{i}}^{\mathrm{e}}{、}{{}{x}}_{{j}}^{\mathrm{e}}{、}{}{{x}}_{{M}{+}{j}}^{\mathrm{e}} $. 编码顺序$ \left({{x}}_{{M}{+}{i}}^{\mathrm{e}},{}{{x}}_{{j}}^{\mathrm{e}},{}{{x}}_{{M}{+}{j}}^{\mathrm{e}}\right) $在$ {{P}}_{\rm{1}} $上成立. 在$ {{P}}_{\rm{1}} $上，随机调整$ {{x}}_{{j}}^{\mathrm{e}} $在$ {{x}}_{{M}{+}{i}}^{\mathrm{e}} $和$ {}{{x}}_{{M}{+}{j}}^{\mathrm{e}} $之间的编码位置，得到$ {{P}}'_{\rm{1}} $. 若$ {{P}}'_{\rm{1}}\notin {{S}}_{\rm{p}} $，则调整$ {{P}}'_{\rm{1}}$的编码顺序，得到$ {{P}}''_{\rm{1}}\in {{S}}_{\rm{p}} $；否则，$ {{P}}''_{\rm{1}{}}{=}{}{{P}}'_{\rm{1}} $；

b) 在$ {{P}}_{\rm{1}}^{{''}} $上随机选择若干个入库任务，改变任务在染色体上的编码位置. 选择$ {{P}}_{\rm{1}}^{{''}} $上的任务$ {{}{x}}_{{i}}^{\mathrm{e}}、{}{{x}}_{{M}{+}{i}}^{\mathrm{e}} $，编码顺序$ \left({{x}}_{{i}}^{\mathrm{e}},{}{{x}}_{{M}{+}{i}}^{\mathrm{e}}\right) $在$ {{P}}_{\rm{1}}^{{''}} $上成立. 基于第一约束，若存在$ {{}{x}}_{{j}}^{\mathrm{e}}\in {{P}}_{{1}}^{{''}} $，使得编码顺序$ \left({{x}}_{{M}{+}{i}}^{\mathrm{e}},{}{{x}}_{{j}}^{\mathrm{e}}\right) $在$ {{P}}_{\rm{1}}^{{''}} $上成立，则随机调整$ {}{{x}}_{{M}{+}{i}}^{\mathrm{e}} $在$ {{}{x}}_{{i}}^{\mathrm{e}} $和$ {{}{x}}_{{j}}^{\mathrm{e}} $之间的编码位置，得到$ {{C}}_{\rm{1}} $；否则，随机调整$ {{x}}_{{M}{+}{i}}^{\mathrm{e}} $在$ {{}{x}}_{{i}}^{\mathrm{e}} $之后的编码位置，得到$ {{C}}_{\rm{1}} $.

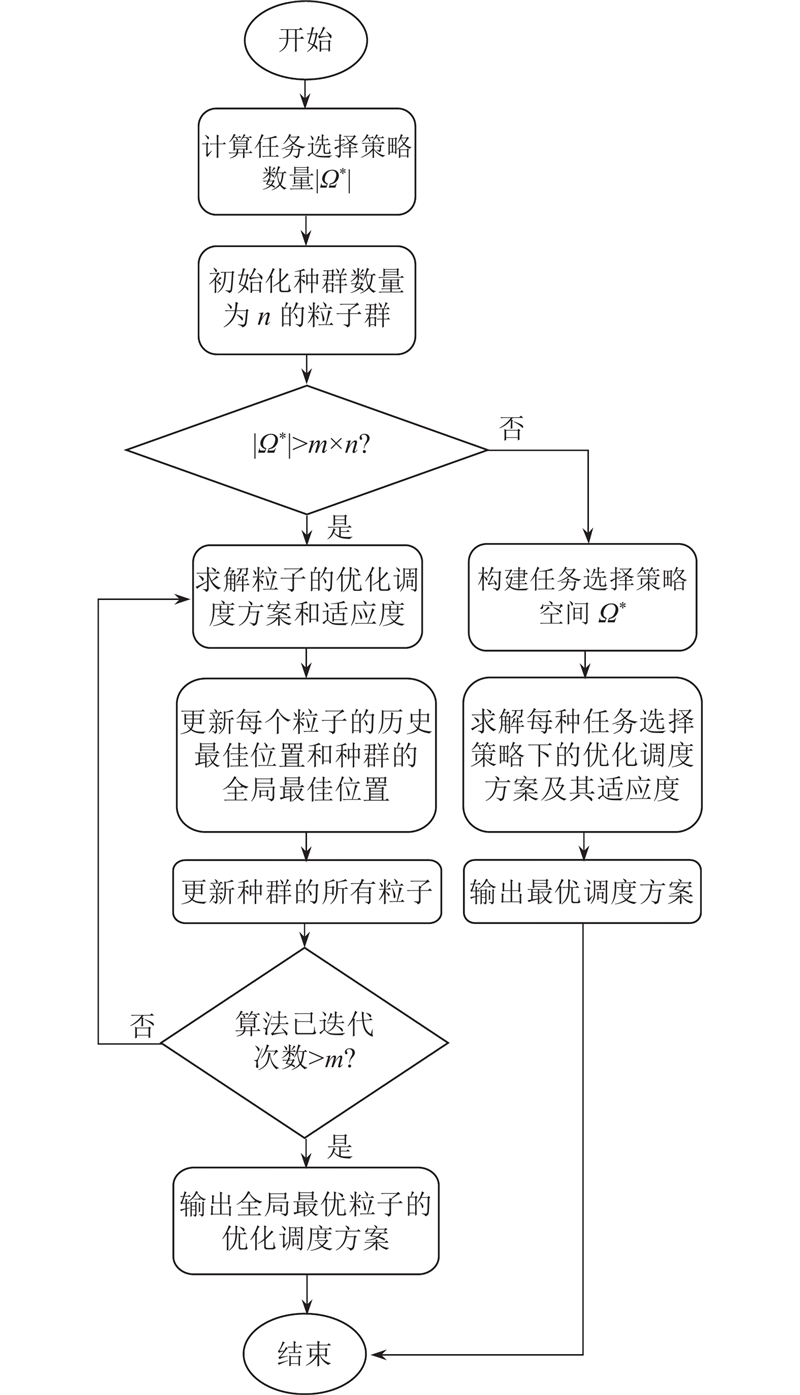
基于二进制粒子群优化的嵌套算法框架（BPSO嵌套框架）动态采取二进制粒子群优化策略（以下称为“BPSO优化策略”）或穷举策略，求解DAGDTSP模型，获取AGV任务调度的优化调度方案. BPSO嵌套框架的程序执行流程如图2所示. 其中，DAGDTSP模型的求解方法被称为内层优化组件（如3.1节的IGA算法）. BPSO优化策略基于二进制编码进行粒子表示，设计向量空间生成的粒子群初始化机制、适应度评价方法和粒子更新与矫正机制.

粒子的速度和位置表示为1个$ {N} $维向量，其中$ {N} $为计划生产的工件数量，即所有的出库任务数量. 粒子的位置向量可以映射到任务选择策略，向量空间$ {{ \varOmega }}^{{*}} $的定义如式(9)所示. 粒子位置向量各维度的值表示对应任务的选择状态. 如果被选择，则为1；否则为0. 在粒子的速度向量中，每个维度的值表示为概率形式，限制在0~1.0.

粒子群的随机初始化. 对于粒子的速度初始化，速度向量的每个维度被随机赋予一个0~1.0的值. 粒子的初始化位置为$ {{ \varOmega }}^{{*}} $中随机选择的二进制向量.

基于粒子位置向量与任务选择策略的映射关系，粒子的适应度定义如下. 求解DAGDTSP模型在所映射任务选择策略下的优化调度方案，若求解所得的优化调度方案对应为有效路径，则适应度为AGV在该方案中执行任务所需的行驶总距离；否则，适应度被指定为固定的惩罚值$ {{V}}_{\rm{p}} $. 粒子的适应度越小，说明该个体越优秀.

采用线性惯性权重^[3]，更新粒子位置为二进制向量^[17]. 记BPSO优化策略第$ {k} $次迭代后的种群中第$ {i} $个粒子的二进制位置向量为$ {\boldsymbol{x}}_{{i}}^{\left({k}{+}{1}\right)} $，若$ {\boldsymbol{x}}_{{i}}^{\left({k}{+}{1}\right)}\notin {{ \varOmega }}^{{*}} $，则需要进行矫正计算，从而使得$ {\boldsymbol{x}}_{{i}}^{\left({k}{+1}\right)}\in {{ \varOmega }}^{{*}} $. $ {\boldsymbol{x}}_{{i}}^{{(}{k}{+1)}} $由分别来自$ {{ \varOmega }}_{\rm{1}}^{{1}} \cap {{ \varOmega }}_{\rm{2}}^{{1}}, \cdots ,{}{{ \varOmega }}_{\rm{1}}^{{r}} \cap {{ \varOmega }}_{\rm{2}}^{{r}} $的$ {r} $个向量拼接而成，记$ {\boldsymbol{x}}_{{i}}^{\left({k}{+}{1}\right)}{=}\left[{\boldsymbol{x}}_{{i}{,}{}{1}}^{\left({k}{+}{1}\right)}{}{\boldsymbol{x}}_{{i},{2}}^{\left({k}{+}{1}\right)}, \cdots ,{}{\boldsymbol{x}}_{{i},{r}}^{\left({k}{+}{1}\right)}\right] $. 如果$\exists {\boldsymbol{x}}_{{i},{j}}^{\left({k}{+}{1}\right)} \notin {{ \varOmega }}_{\rm{1}}^{{j}} \cap {{ \varOmega }}_{\rm{2}}^{{j}},{1}{}{\leqslant}{}{j}{}\leqslant {}{r} $，则更新$ {\boldsymbol{x}}_{{i},{j}}^{\left({k}{+}{1}\right)} $为$ \underset{\boldsymbol{x}\in {{ \varOmega }}_{\rm{1}}^{{j}} \cap {{ \varOmega }}_{\rm{2}}^{{j}}}{{{\mathrm{arg}}}{}{{\mathrm{min}}}}{||{\boldsymbol{x}}_{{i},{j}}^{\left({k}{+}{1}\right)}-{{\boldsymbol{x}}}||}_{1} $.

通过实验验证利用IGA算法求解DAGDTSP模型的有效性，评价BPSO嵌套框架在不同规模的测试问题中的求解性能，验证BPSO优化策略的有效性. 分析所求优化调度方案对任务变化的适应性，验证DAGDTSP模型的准确性. 实验在11th Gen Intel(R) Core(TM) i7-11800H 2.30 GHz CPU计算机上进行，基于Python求解.

为了评价调度方案的优化效果，设计用于表征优化调度方案相比于基准调度方案的运输距离优化效果的指标. 记评估运输距离优化效果的指标为$ {F} $，$ {F} $越大，表明优化效果越好. $ {F} $计算为

(17)$ {F}=\frac{{{S}}_{\rm{bsc}}-{{S}}_{\rm{otm}}}{{{S}}_{\rm{bsc}}}. $

式中：$ {{S}}_{\rm{bsc}} $为基准调度方案中的AGV行驶总距离，$ {{S}}_{\rm{otm}} $为优化调度方案中的AGV行驶总距离.

通过随机生成出库任务的运输起点和到达时刻，设计4个测试问题，下发出库任务的数量分别为160、120、100和80. 在测试问题中，每隔45 min，每条生产线完成一个联轴器工件的加工，即一个出库任务到达.

为了验证改进遗传算法的性能，本节实验（以下称为“实验1”）在测试问题上对比了IGA算法与其他7种算法的运输距离优化效果，设计开展消融实验，以验证IGA算法各遗传算子的有效性. 其中，环境参数设置为：$ {C} $=12，$ {R} $=3.

为了验证利用IGA算法求解DAGDTSP模型的优越性，设计适用于DAGDTSP模型求解的改进粒子群优化算法（improved particle swarm optimization，IPSO）^[3]、改进蚁群算法（improved ant colony optimization，IACO）^[3,18]、改进鲸鱼优化算法（improved whale optimization algorithm，IWOA）^[19]、改进模拟退火算法（improved simulated annealing，ISA）^[20]、改进禁忌搜索算法（improved tabu search，ITS）^[21]、贪婪算法和随机算法，开展对比实验. 利用随机算法求解测试问题1、2和3、4，搜索规模分别设置为200 000、100 000.

如表1所示，在测试问题上运行IGA、IPSO和IACO、IWOA、ISA和ITS算法各50次，择优选取基准任务选择策略下的优化调度方案. 表中，$ {T}_{\rm{b}} $为算法求解优化调度方案的总运行时长. 如表1所示，IGA算法在4个测试问题上均取得了最佳的运输距离优化效果（$ {F} $指标值）. 相比于同样取得最佳运输距离优化效果的其他算法，IGA算法在4个测试问题上求解的总运行时长均最短. IGA算法相比于对比算法具备求解测试问题的优越性.

记不采用选择、交叉和变异算子的IGA算法分别为“IGA-NS”、“IGA-NC”和“IGA-NM”，在4个测试问题上，运行各算法50次，择优选取基准任务选择策略下的优化调度方案. 实验结果如表2所示，IGA算法的优化效果在测试问题1上优于IGA-NS，表明选择算子有效. 在测试问题1、2、3上优于IGA-NC，表明交叉算子有效. 在测试问题1、2、4上优于IGA-NM，表明变异算子有效. IGA算法的遗传算子有效性在消融实验结果中得到验证.

本节实验（以下称为“实验2”）对BPSO嵌套框架的BPSO优化策略和穷举策略的性能进行验证，分析所求解的优化调度方案对任务变化的适应性，环境参数的设置同实验1. 实验1表明，IGA算法针对固定任务选择策略下的优化策略求解更具备有效性. 实验2选择IGA算法为BPSO嵌套框架的内层优化组件，对每个粒子对应的任务选择策略求解10次粒子适应度和优化调度方案，择优选取求解结果. 实验使用多进程技术，并行加速计算各个粒子的适应度和优化调度方案.

根据任务选择策略空间规模$ \left|{ \varOmega }^{*}\right| $所采取的求解策略，将测试问题1、2和测试问题3、4分别记为BPSO优化策略求解组和穷举求解组. 在BPSO优化策略求解组中，针对各测试问题求解6次，择优选取最优任务选择策略下的优化调度方案. 实验结果如表3所示，记求解策略运行时长为$ {T}_{\rm{m}} $，相比于实验1的IGA算法，BPSO嵌套框架考虑了多种任务选择策略，搜索空间更大，耗时更长. 相比于穷举求解组，BPSO优化策略求解组的搜索空间更大，耗时更长. 相比于IGA算法在实验1中的求解结果，BPSO嵌套框架的求解结果的优化效果（$ F $指标值）在测试问题4上与之持平，在其余测试问题上表现更优. 由此可见，基于对任务选择策略多样性的考虑，BPSO嵌套框架以牺牲求解速度为代价，在更大的解空间中优化调度方案，减小了优化调度方案中的AGV行驶总距离$ {{S}}_{\rm{otm}} $，验证了BPSO优化和穷举求解策略的有效性.

为了验证BPSO优化策略及其粒子更新与矫正机制的有效性，设计采用0-1编码方案的二进制遗传算法（binary genetic algorithm，BGA）和二进制鲸鱼优化算法（binary whale optimization algorithm，BWOA）的优化策略. 设计BPSO-II优化策略，将粒子位置更新为连续向量. 如表4所示，在测试问题1、2上运行4种优化策略各6次，对$ {F} $进行统计. 表中，$ {F}_{\max} $、$ {F}_{{\mathrm{avg}}} $、$ {F}_{{\mathrm{med}}} $、$ {F}_{{\mathrm{mom}}} $分别为$ {F} $指标的最大值、均值、中位数、最大众数. 其中，BPSO优化策略仅在测试问题1上表现出略低于BPSO-II的$ {F}_{\max} $和$ {F}_{{\mathrm{avg}}} $，在其余情况下均表现最佳. BPSO优化策略的搜索能力及其粒子与更新机制的有效性得到了进一步的验证.

为了分析BPSO嵌套框架求解的优化调度方案对任务变化后的适用性，记$ {{X}}^{\mathrm{e}} $中的任务为“被选任务”，$ {X}-{{X}}^{\mathrm{e}} $中的任务为“非选任务”. 求解优化调度方案，即优化被选任务的执行顺序. 若任务变化不涉及原优化调度方案中的被选任务，则原优化调度方案针对新任务计划依旧可行. 分析任务减产和短暂延期时原任务调度方案对任务变化的适应性.

对测试问题随机选择10%的非选任务进行减产和延期处理，以任务变化的测试问题基准调度方案为基准，对比原优化调度方案和BPSO嵌套框架重新求解的优化效果. 实验结果见表5. 表中. $ {N}_{{\mathrm{tvc}}} $为任务变化数量. 从表5可知，原优化调度方案的运输距离优化效果（$ {F} $指标值）较重新求解稍差，但在总体上可观. 基于此，面对仅存在非选任务减产和延期的情况，BPSO嵌套框架求解的优化调度方案具备一定的适应性.

本节实验（以下称为“实验3”）通过设置不同的环境参数$ {C} $和$ {R} $，即托盘最多可容纳的工件数以及空托盘区和成品存储区每个工作点可堆放的最大托盘数，对DAGDTSP模型的准确性进行验证. 使用BPSO嵌套算法框架，求解不同环境参数设置下的测试问题，实验结果如表6所示. 结果显示，在不同的环境参数设置下，BPSO嵌套算法框架通过求解DAGDTSP模型均取得较好的运输距离优化效果，验证了DAGDTSP模型的准确性.

本文围绕单载AGV在生产线和仓库之间运输托盘和工件的任务调度问题，以最小化AGV执行任务的行驶总距离为优化目标，建立考虑任务执行顺序约束和任务节点信息随环境变化的DAGDTSP模型，提出固定任务选择策略下求解DAGDTSP模型的改进遗传算法（IGA）、考虑多种任务选择策略下求解优化调度方案的BPSO嵌套框架. 在测试问题上，通过实验验证了IGA算法和BPSO嵌套框架各自在求解速度、优化效果和任务变化适应性等方面的优越性和有效性以及DAGDTSP模型在面对环境变化时的准确性. 本文研究基于AGV作业过程中无电量不足情况的假设，未来工作将在问题建模中考虑AGV的充电问题. 此外，将围绕任务变化涉及被选任务时优化调度方案的适应性问题，开展进一步的研究.