微分博弈对策采用微分方程描述系统状态,可以求解多状态动态连续转变的最优对策[6]. 微分博弈最早由Isaacs[7]提出,并不断向随机微分博弈[8-9]、主从微分博弈[10]及合作微分博弈[11]等方向发展. 相比于其他博弈方法,微分博弈可以充分考虑各参与方的自主机动性能,使其更适合用于舰艇、航空制导这些对抗环境[12]. White等[13]基于线性二次型微分博弈问题,研究高速机动末端弹道的可拦截导引方法. 周俊峰[14]考虑航天器追逃对抗环境中系统状态不确定、对手目标函数或输入控制信息缺失的复杂状况,综合线性系统理论与微分对策设计自适应追逃博弈控制策略. Singh等[15]研究目标-攻击者-多防御者的微分博弈对策问题,建立参与各方在受限观测下的行为动态网络模型. Li等[16]在线性二次框架下,定义目标随机运动与逃逸综合的情况,计算集合随机项的防御方微分博弈策略. 当执行水下对抗拦截任务时,微分博弈理论可以应用于末端拦截导引、探测装置主被动工作模式下的动态对策导引及主动防御等多种情景[17].
本文针对包含目标、攻击者及防御者的三方攻防场景,基于随机微分博弈理论,设计适用于水下含噪、离散信息的博弈对策,形成不完全观测信息条件的机动导引律.
1. 完备信息条件下的微分对策设计
1.1. 运动方程关系
浅水环境中攻击方、目标、防御方运动可以简化为平面运动,在惯性坐标系内的基本运动学方程如下:
式中:x为惯性坐标系中的位置矢量,
以矩阵形式重新表述相对运动方程如下:
式中:
三方攻防TAD(target-attacker-defender)对抗由攻击-目标、防御-攻击2组追逃博弈组合而成,目标通常为高价值航行器,攻击方追踪目标,防御方须完成拦截、诱骗、毁伤等防御任务. 目标(target)的任务是摆脱攻击者(attacker)的追捕,以加速度
采用攻击方加速度矢量分解的方式,将三方博弈问题转化为两对双方追逃问题,以实现博弈求解. 三方各自的加速度形式可以分别表示为
式中:
1.2. 完备信息条件下的对抗博弈策略
完全信息条件指攻防各方时刻知道必要且准确的状态信息,不受观察、通信条件的限制,且系统的状态是确定性的,不考虑控制器在工作过程中产生的误差与延迟对运动状态的影响. 此外,认为博弈过程在有限且固定的时区
攻防博弈处于导引的末端过程,机动各方相对距离小,满足线性二次型的近似线性化处理条件[18]. 追踪方期望为以最小代价尽可能接近规避方,规避方则以最小代价远离. 博弈对策的性能指标设计为终端距离量,采用支付函数权重对加速度范围进行“软约束”,以惩罚项系数来表示博弈各方机动性能的差异. 构造有限时区的确定性微分博弈方程,支付函数如下所示:
式中:
定义哈密尔顿函数,通过Hamilton-Jacobi-Isaacs理论,结合微分方程的边界条件,获得最优策略的解析表达. 所构造的构造哈密尔顿函数H如下所示:
式中:
其中,
将式(9)、(10)代入哈密尔顿函数,并将控制项移至左侧,可得
将
为了求解P,将
式(17)要求对任何时刻的
采用式(15)~(18),可以根据目标、攻击者和防御者三者之间的相对运动状态,构建反馈控制博弈对策. 式(4)~(6)对应的加速度计算方程如下:
式(19)~(22)提供了完全信息条件的确定性攻防导引律,满足博弈纳什均衡式:
2. 不完全信息的随机微分对策设计
2.1. 不完全控制与观测偏差的对抗博弈策略
基于随机微分博弈理论,拓展对策形式,将随机过程引入状态方程中,实现对扰动的模拟. 在随机微分对策定义的追逃问题中,状态方程式为更一般的随机形式,如下所示:
式中:
包含无规律运动过程的状态方程为
追逃双方对状态的观测满足下式:
式中:
采用伊藤积分变换,可得
根据式(26),展开式
定义
其中物理系统的观测形式与卡尔曼滤波的估计形式相同,如下所示:
初值条件为
从式(30)~(32)可知,随机微分博弈策略的有效性取决于对于状态方程适用的预测模型. 在大多数情况下,需要获得合理的物理系统的预测感知策略,使预测模型达到接近最优的水平.
根据式(30),获得随机微分博弈的最优策略对为
从式(33)、(34)可知,随机条件下的最优策略对满足控制反馈过程,形式与完备条件近似.
2.2. 非完整间隔观测行为限制下的对抗博弈策略
考虑离散点化的序列观测估计场景,二次支付函数与运动状态方程满足式(25)、(26). 所获取的观测信息为
式中:
从式(37)、(38)可知,满足最优控制的条件为最优化
式中:
令
系统的运动方程改写为
对于任意某个观测间隔
获得某段离散观测间隔内的最优
式中:
由式(39)、(40)可得各段观测间隔内的最优博弈策略,整合获得连续策略. 通过离散间隔的估计转化,微分博弈的观测连续性重新得到满足,所得的策略对满足最优纳什均衡的特性.
3. 仿真实验
3.1. 仿真参数设置与数值方法
设定支付函数中的终端加权矩阵
采用数值方法开展近似迭代求解,常微分方程采用4阶经典Runge-Kutta方法,如下所示:
式中:
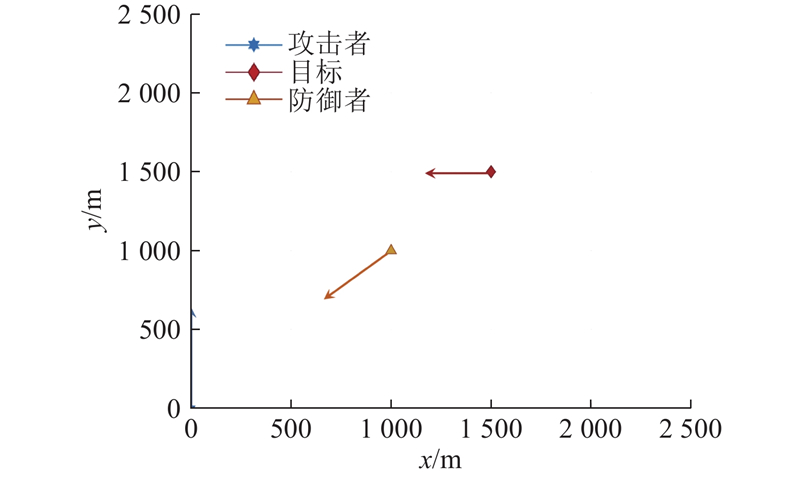
设置三方攻防博弈的仿真初始态势,如图1所示.
图 1
3.2. 对策演示与性能对比
3.2.1. 博弈对策模拟
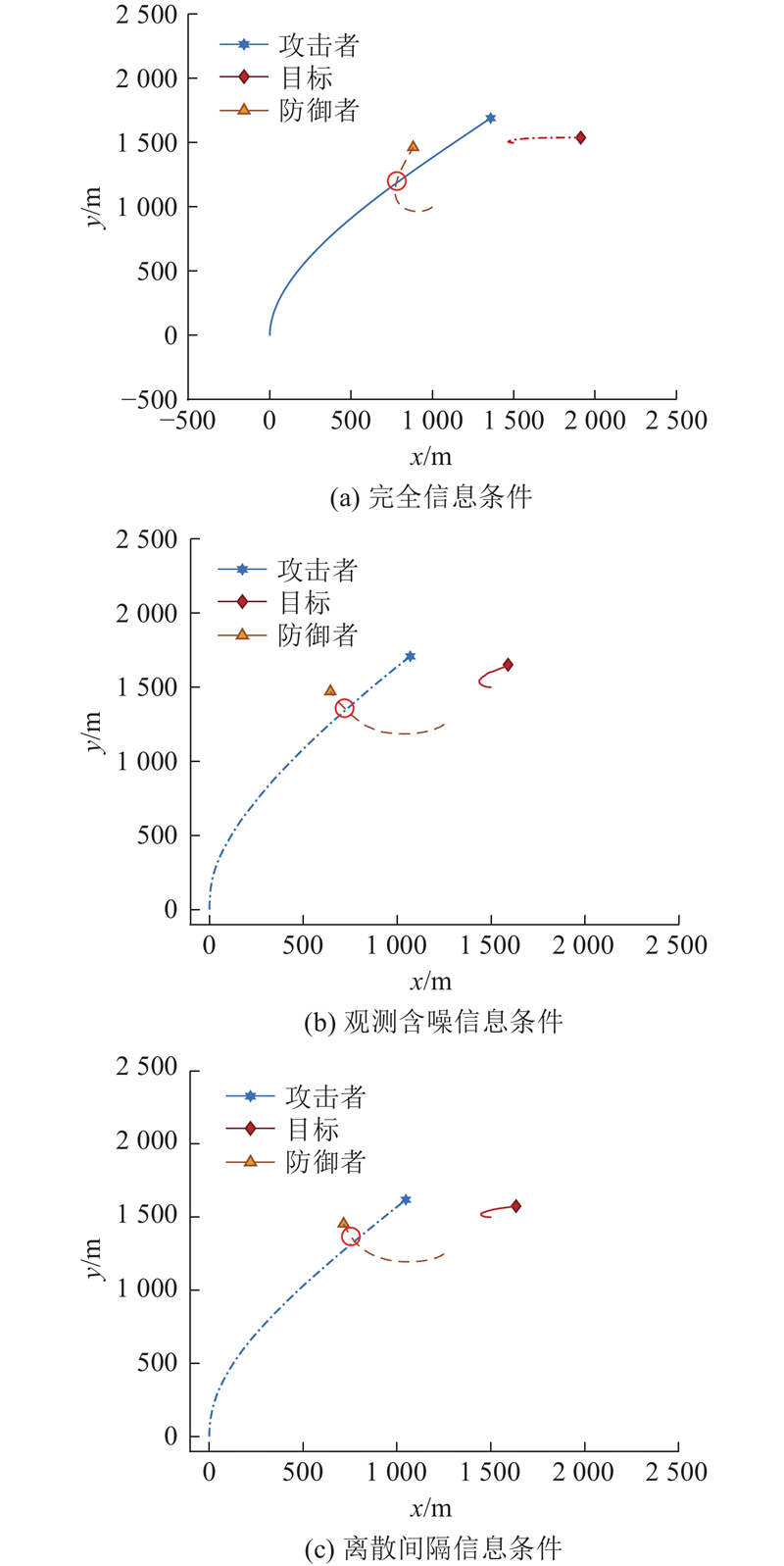
图 2
图 2 短博弈时长下的三方攻防运动轨迹
Fig.2 Motion of three-party attack-defense with short game duration
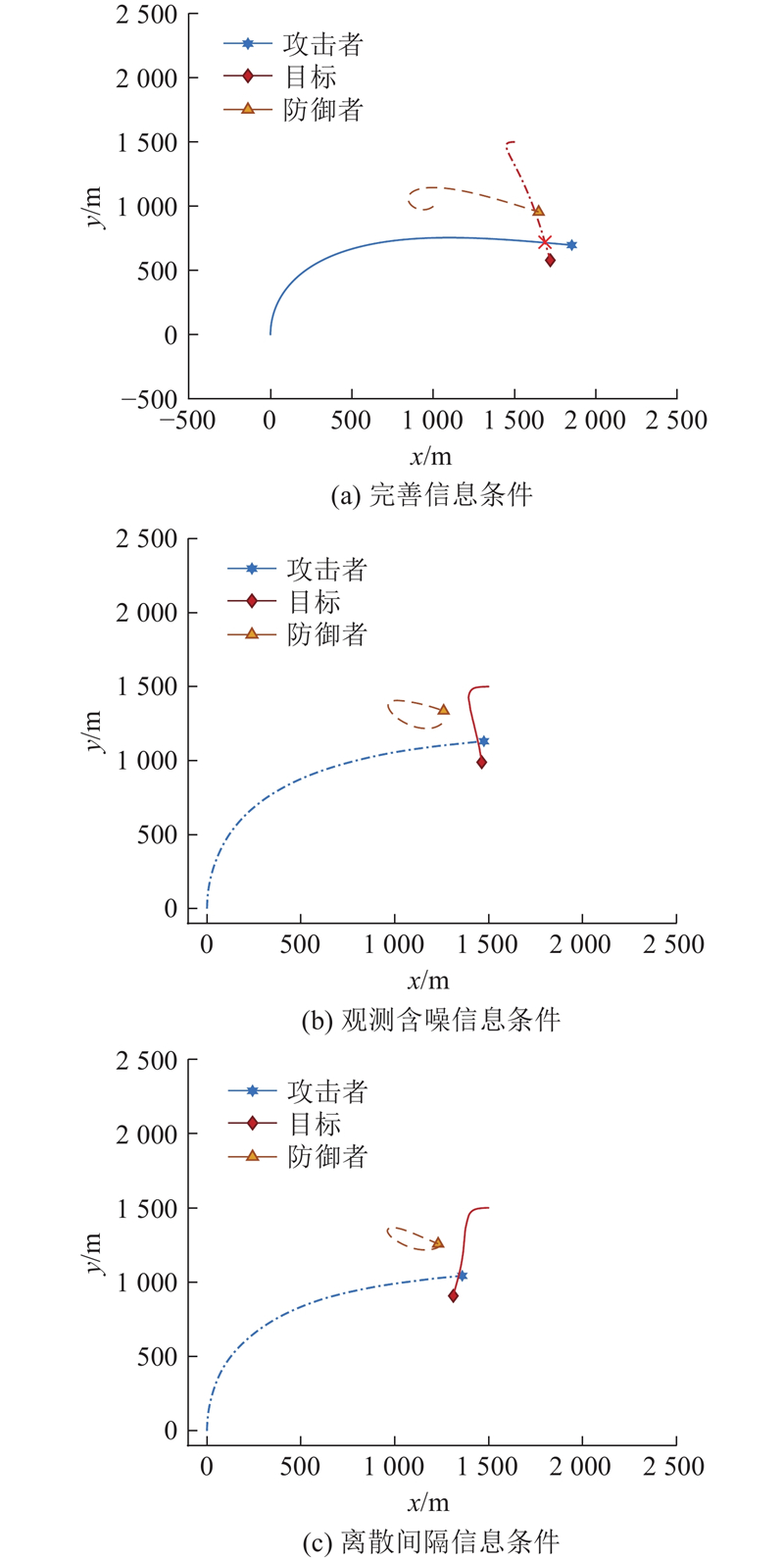
图 3
图 3 长博弈时长下的三方攻防运动轨迹
Fig.3 Motion of three-party attack-defense with long game duration
在短博弈时长场景下,防守方可以抵近攻击方,完成防御任务. 在长博弈时长场景下,完全信息条件下的攻击方成功攻击,在不完全观测含噪信息与离散间隔信息条件下,目标完成了规避任务.
3.2.2. 与其他运动导引策略的性能对比
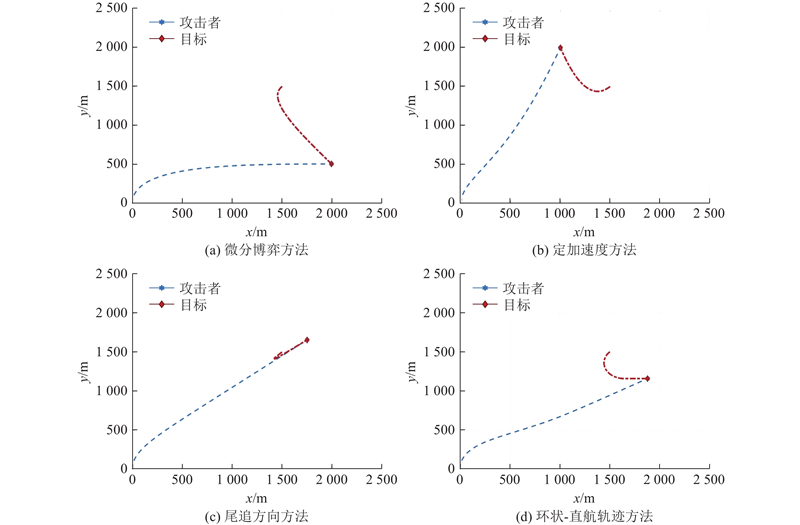
基于仿真结果,比较多类其他方法下的终端距离和总支付. 如图4所示为微分博弈导引方法与其他导引方法的运动轨迹对比.
图 4
在3种不同的信息条件下开展对比,每种条件运行10轮,结果取平均值,如表1所示. 微分博弈方法显著优于其他各类机动导引方法,突出了所提方法的性能优势. 在信息不完全场景下,各方自身的观测与控制随机特点使得机动控制的稳定性下降,微分博弈策略为各类方法最优,博弈方法的效益明显.
表 1 各类导引方法的博弈结果对比
Tab.1
| 博弈条件 | 微分博弈方法 | 定加速度方法 | 尾追方向方法 | 环状-直航方法 | |||||||
| 终端距离 | 总支付 | 终端距离 | 总支付 | 终端距离 | 总支付 | 终端距离 | 总支付 | ||||
| 完全信息 | 74.99 | 0 | 16.99 | 0 | 45.83 | 0 | 46.92 | ||||
| 观测含噪信息 | 79.78 | 0.523 | 20.38 | 54.32 | 46.82 | ||||||
| 离散间隔信息 | 76.12 | 18.58 | 42.00 | 48.17 | |||||||
3.2.3. 信息场景对比和鲁棒性分析
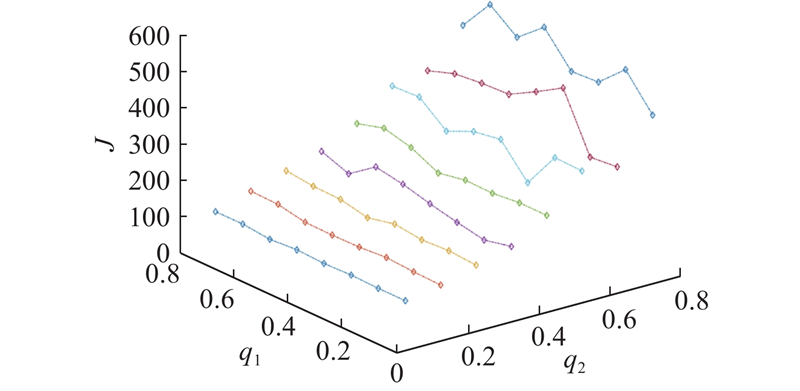
为了证明微分博弈算法在不完全信息条件下的改进效果,开展总支付对比试验,结果运行10轮取平均值. 完全信息条件下的博弈总支付为−324,观测含噪信息条件下的博弈总支付为−188,离散间隔信息条件下的博弈总支付进一步上升至705,证明了算法改进的效果.
考虑策略鲁棒问题. 计算控制误差系数
图 5
图 5 控制与观测误差系数的鲁棒性分析
Fig.5 Robustness analysis of control and observation error coefficient
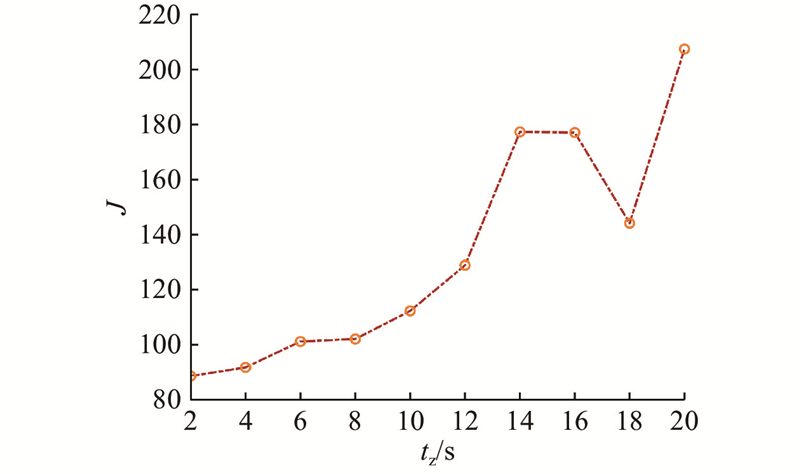
计算不同观测间隔下的10轮平均支付,如图6所示. 可知,当观测间隔tz小于12 s时,支付处于合理的性能偏差范围. 这表明策略具备有效处理观测信息间隔的能力.
图 6
4. 结 语
针对水下环境三方TAD机动攻防的博弈问题,本文建立运动学模型,设计完全信息、不完全随机与非完整离散间隔观测3种场景下的水下攻防机动行为对策. 通过仿真实验,展示递进信息限制下双方及三方的运动控制效果,并进行结果对比,验证了导引律在复杂信息环境下的有效性与鲁棒性,表明所提方法对强鲁棒性的水下机动对抗策略设计具有指导意义.
参考文献
Modeling and simulation of a robust energy efficient auv controller
[J].
Neural network guidance based on pursuit-evasion games with enhanced performance
[J].DOI:10.1016/j.conengprac.2005.03.001 [本文引用: 1]
基于矩阵博弈的智能水声对抗建模与仿真
[J].
Modeling and simulation of intelligent underwater acoustic countermeasure based on the matrix game
[J].
UUV攻防博弈的自适应攻击占位机动决策研究
[J].
Adaptive attack occupancy maneuver decision of UUV attack-defense game
[J].
时间定量微分对策最优性的充分条件
[J].
The sufficient condition for the optimality of a quantitative differential games
[J].
Discontinuous Nash equilibrium points for nonzero-sum stochastic differential games
[J].DOI:10.1016/j.spa.2020.07.003 [本文引用: 1]
传统零售商渠道选择策略微分博弈模型
[J].
Differential game model for channel selection strategies of traditional retailer
[J].
风电-光伏-抽蓄-电制氢多主体能源系统增益的合作博弈分配策略
[J].
A cooperative game allocation strategy for wind-solar-pumped storage-hydrogen muti-stakeholder energy system
[J].
Direct intercept guidance using differential geometry concepts
[J].DOI:10.1109/TAES.2007.4383574 [本文引用: 1]
Dynamic network analysis of a target defense differential game with limited observations
[J].
Defending an asset: a linear quadratic game approach
[J].DOI:10.1109/TAES.2011.5751240 [本文引用: 1]
多约束受扰追踪的微分对策滚动时域轨迹优化
[J].
Differential game trajectory optimization based on receding horizon control for multiple constraints tracking systems with additive disturbance
[J].
Role of information in the stochastic zero-sum differential game
[J].DOI:10.1007/BF00933801 [本文引用: 2]