多种理论和模型被用于出租汽车行业竞争关系研究. 有学者利用纳什均衡理论测算巡游出租车投放规模范围[4],建立考虑多种因素与条件的模型. 如罗清和等[5]构建古诺模型分析出租汽车市场最优状态;Van Vugt等[6]构建出行选择博弈模型,分析城市居民选择出行方式的博弈过程;Pedersen[7]构建鹰鸽模型,分析模型满足斯坦克尔伯格(Stackelberg)[8]均衡和古诺均衡所需条件;杨露萍等[9]构建演化博弈模型,考虑小汽车出行者类别,分析小汽车通勤向公交出行转移的演化过程. 考虑双方博弈时,Sun等[10]考虑政府监管,建立政府与网约车平台的二维博弈模型,提出监管对策;杨浩雄等[11]建立网约车与巡游出租车的博弈模型,认为巡游出租车不会因为网约车的高额补贴而退出市场. 交通运输领域学者关注并借鉴生态学模型. 如Sun等[12]引入Lotka-Volterra模型,构建基于Lotka-Volterra方程的系统动力学模型来预测新能源汽车市场演变;蒋慧峰等[13]从生物力学视角探讨公铁运输关系,运用Lotka-Volterra模型分析公铁运输间演化态势;Sun等[14]以Lotka-Volterra为基础构建网约车与巡游出租车的竞争模型,分析2种出行方式的竞争博弈程度. 在出租汽车运营实证领域,孙会君等[15]构建政府主导的双层规划模型框架,将大数据分析应用于模型参数校准和求解;陈启香等[16]通过对建成环境网格化研究,揭示了建成环境对巡游出租车的影响;奉鸣等[17]通过分析巡游出租车与其他交通方式的竞合、替代关系,预测未来出租汽车行业发展趋势;Grahn等[18]发现网约车与巡游出租车出行模式和服务能力在不同时空环境下存在显著差异;杨燕等[19]分析巡游出租车和网约车的行程距离、平均速度,通过热力图和莫兰指数(Moran’s I)检验探讨2种车辆的空间特征;韩印等[20]基于成都市网约车GPS轨迹数据,应用COPERT模型量化二氧化碳的排放量,分析网约车的时空分布特征. Michaelis-Menten(M-M)方程被应用在交通研究领域. 如Robinson等[21]利用偏移M-M方程获取动态疏散模拟中拥堵动态变化以及交通流量分配;Henry等[22]将车流速度差与流量关联,引入M-M方程进行交通网络分析;Shorshani等[23]研究道路交通对空气质量的影响,运用考虑车辆排放、功率和M-M方程的COPERT模型计算排放;Li等[24]运用本地化MOVES模型估算北京地区交通二氧化碳排放,引入M-M方程进行插值,获得连续二氧化碳数据. 传统M-M方程应对复杂交通系统存在局限性,不同交通方式间的动态博弈未被充分考虑.
本研究将博弈主体确定为政府、乘客、网约车和巡游出租车,基于博弈理论和Stackelberg模型,分析完全信息下动态博弈问题. 为了更好反映动态博弈对城市交通碳排放量的影响,对传统M-M方程进行改进,得到T-M-M方程,将碳排放量与不同博弈场景下车辆数量以及车辆行驶里程关联,克服传统M-M方程的局限性,准确反映出网约车与巡游出租车之间的相互作用、竞争关系及对交通碳排放的影响.
1. 四方博弈模型假设与构建
1.1. 基本假设
1)多方主体博弈与监管体系假设. 出租汽车市场多方互动与监管框架设定:主要参与者{
2)多方策略博弈假设. 政府策略集合包括严格监管
3)策略调整与多元效用博弈假设. 各博弈主体基于策略带来的收益进行调整. 在政府严格监管情况下,对于违规经营的巡游出租车和网约车,政府分别处以巡游出租车违规罚金
4)车辆经营效益与市场占有假设.
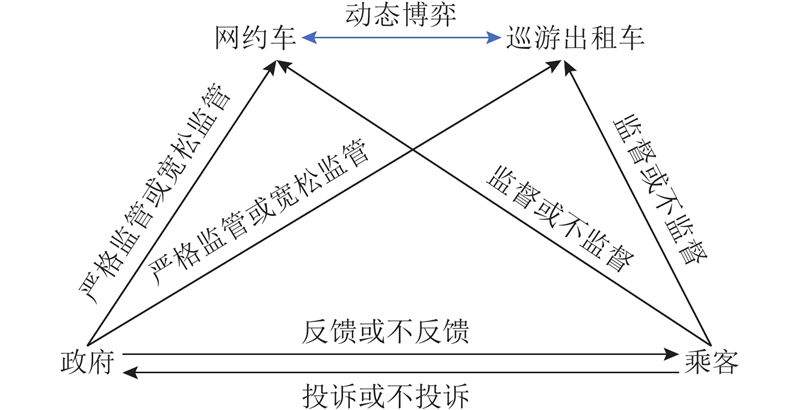
政府、乘客、网约车和巡游出租车四方博弈模型的逻辑关系如图1所示.
图 1
1.2. 博弈模型的构建
多方博弈主体的运营策略会受到其他参与者策略的影响,且策略实施存在先后. 后行动的参与者可以观察到先行者的策略,据此做出反应. 这意味着所有参与者都对可能的策略选择和相应收益有着清晰认识,可将这种博弈过程视为完全信息的动态博弈[26].
1.2.1. 斯坦克尔伯格模型
网约车和巡游出租车动态博弈受政府和乘客作用和影响, 选择Stackelberg模型作为工具,分析存在领导者和追随者关系的博弈情境,更好理解出租汽车行业相关各方市场策略互动及其对整体竞争格局的影响. 假设
1.2.2. 市场份额关系模型
令收益函数
表 1 不同博弈场景网约车和巡游出租车净收益
Tab.1
| 博弈场景 | ||
| 场景1. 严-监-合-合 | ||
| 场景2. 严-不-合-合 | ||
| 场景3. 宽-监-合-合 | ||
| 场景4. 宽-不-合-合 | ||
| 场景5. 严-监-合-违 | ||
| 场景6. 严-不-合-违 | ||
| 场景7. 宽-监-合-违 | ||
| 场景8. 宽-不-合-违 | ||
| 场景9. 严-监-违-合 | ||
| 场景10. 严-不-违-合 | ||
| 场景11. 宽-监-违-合 | ||
| 场景12. 宽-不-违-合 | ||
| 场景13. 严-监-违-违 | ||
| 场景14. 严-不-违-违 | ||
| 场景15. 宽-监-违-违 | ||
| 场景16. 宽-不-违-违 |
在构建Stackelberg模型和市场份额关系模型时,假设网约车先采取策略,巡游出租车后采取策略. 当巡游出租车先采取策略确定日均上线运营车辆数
表1中博弈主体网约车和巡游出租车净收益与式(5)、(6)对应,即网约车收益为
2. 博弈模型结果分析
2.1. 数据描述
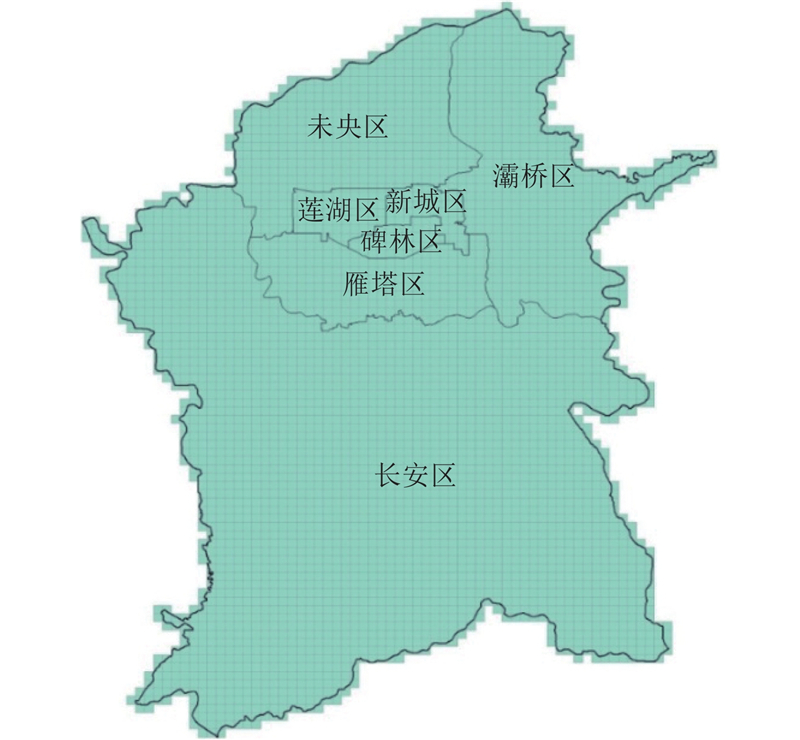
以陕西省西安市主城区7个行政区作为研究对象. 《西安市国民经济和社会发展第十二个五年规划纲要》确定新城、莲湖、碑林、雁塔、未央、灞桥和长安区为城市主城区. 采用2023年6月5日到6月11日连续7天网约车、巡游出租车订单数据以及从西安市出租汽车管理处获取的2023年网约车和巡游出租车每日上线运营数量和日均行驶里程数据,对所构建的博弈模型进行参数校准和实证验证. 订单数据主要包含车辆ID、订单编号、上下车时间、订单起讫点经纬度、载客里程、载客时间及支付金额等字段属性. 2023年,西安全市日均上线运营网约车16 094 辆,巡游出租车15 454 辆,出租汽车总量31 548 辆. 假设日均上线运营网约车和巡游出租车数量总和为32 000 辆.
2.2. 数据处理
对网约车和巡游出租车订单数据处理如下. 1)城市行政区划边界、道路网、网约车及巡游出租车订单数据统一采用WGS1984 Web Mercator投影坐标系,地理坐标系为GCS WGS1984 Major Auxiliary Sphere. 2)删减与研究内容无关字段,保留“订单编号”“上车时间”“下车时间”“车辆出发经度”“车辆出发纬度”“车辆到达经度”“车辆到达纬度”共7个字段. 3)删除异常值,剔除缺失上下车时间、经纬度坐标以及经纬度坐标在研究区域范围之外的订单数据;剔除单次出行时间小于2 min和大于2 h的订单教据. 4)得到1 362 424 条网约车和2 475 374条巡游出租车订单教据.
2.3. 网约车与巡游出租车在时空维度上的竞争
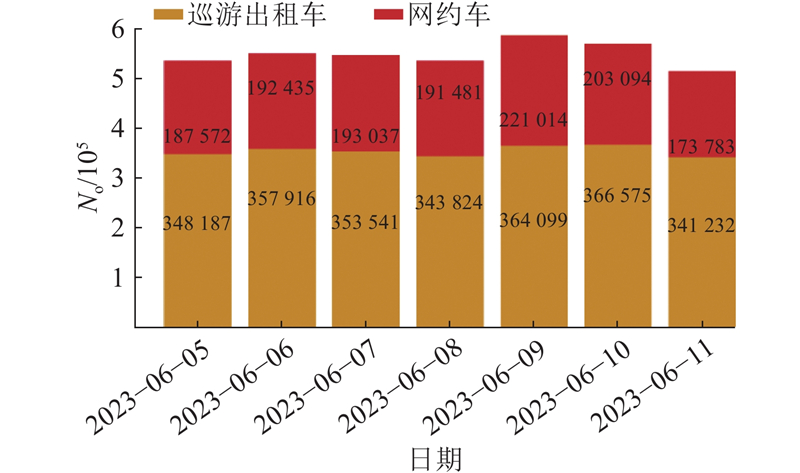
根据有效网约车与巡游出租车订单数据,汇总统计出日订单总量
图 2
式中:
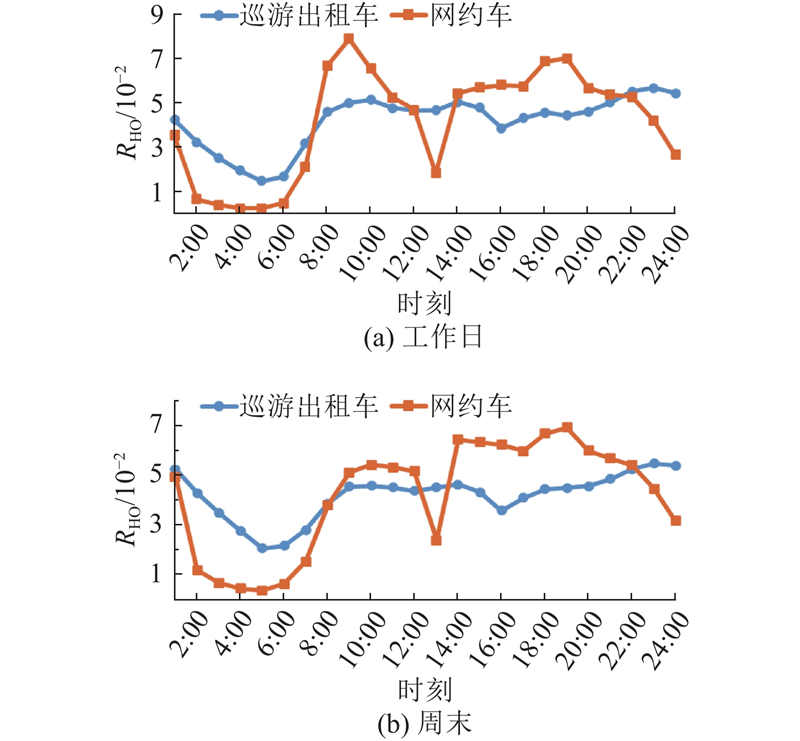
如图3所示,充分考虑工作日与周末居民出行模式的差异,分别统计巡游出租车与网约车在工作日期间(取5 d的平均值)与周末期间(取2 d的平均值)的小时订单率. 可以看出,网约车和巡游出租车小时订单率在工作日和周末均呈现明显波动和峰谷分布,反映不同时段市民的出行需求变化. 1)工作日7:00、11:00、13:00、21:00,周末8:00、12:00、14:00、22:00,网约车与巡游出租车订单率非常接近(2种方式订单量接近),表明这2组时间段内两者间竞争非常激烈,趋近于完全竞争[28]. 2)工作日12:00~14:00、22:00到第二天6:00,巡游出租车订单约占该时段总订单量的70.0%,网约车约为30.0%,该时段内巡游出租车订单率比网约车高出约40个百分点,即巡游出租车占有明显竞争优势[29];在7:00~10:00、15:00~21:00,网约车订单占该时段总订单量比例约为67.5%,而巡游出租车约为32.5%,该时段内网约车订单率比巡游出租车高出约35个百分点,即网约车占有明显竞争优势. 3)周末12:00~14:00、22:00到第二天8:00,巡游出租车订单约占该时段总订单的75.0%,网约车约为25.0%,该时段内巡游出租车订单率比网约车高出约50个百分点,即巡游出租车占有明显竞争优势;9:00~12:00、15:00~21:00,网约车订单约占该时段总订单量的70.0%,巡游出租车约为30.0%,该时段内网约车订单率比巡游出租车高出约40个百分点,即网约车占有明显竞争优势. 总体来说,网约车和巡游出租车的运力供给能较好匹配工作日与周末不同时段内居民多元化出行需求,共同组成满足市民多元化出行需求的城市出租汽车服务体系.
图 3
图 3 巡游出租车、网约车小时订单率分布
Fig.3 Distribution of hourly order rate for cruise taxis and ride-sourcing
为了度量给定空间范围网约车与巡游出租车的竞争关系,利用栅格化分析单元(单元格)统计网约车和巡游出租车的运营数据,主要指标包括上车次数和车辆竞争指数. 其中FID为栅格单元唯一标识;
图 4
表 2 西安市主城区内赫芬达尔-赫希曼指数统计(摘录)
Tab.2
| FID | R | T | Q | HHI |
| 2001 | 613 | 6 640 | 7 253 | 0.845 |
| 2002 | 1 089 | 3 762 | 4 851 | 0.652 |
| 2003 | 1 669 | 6 103 | 7 772 | 0.663 |
| 2004 | 516 | 449 | 965 | 0.502 |
| 2005 | 44 | 82 | 126 | 0.545 |
| 2006 | 87 | 33 | 120 | 0.601 |
| 2007 | 16 | 138 | 154 | 0.814 |
| 2008 | 4 | 0 | 4 | 1.000 |
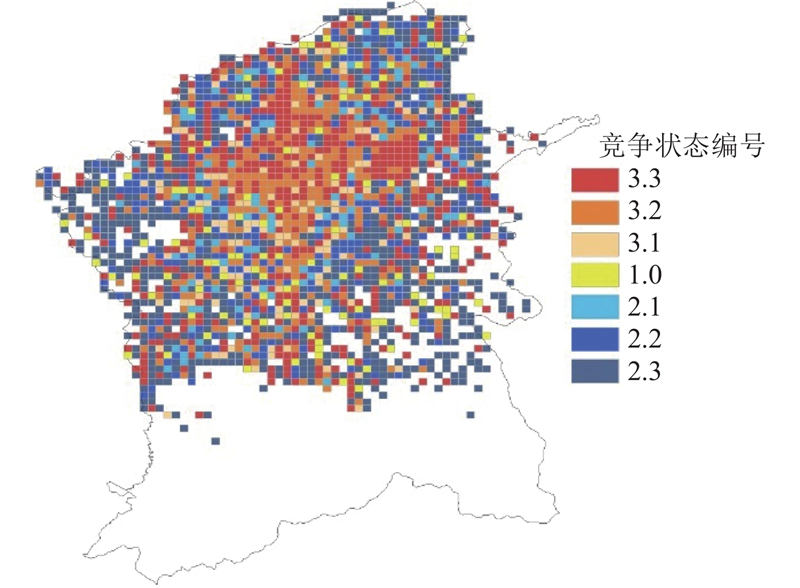
对HHI结果统计表进行筛选,得到2 171个有效数据栅格. 根据式(10)计算HHI,当HHI>0.501时,比较网约车与巡游出租车的上车次数,以确定哪个群体在竞争中存在优势乃至有垄断趋势. 网约车与巡游出租车竞争指数的比较标度如表3所示. 西安市主城区网约车与巡游出租车空间维度竞争程度如图5所示. 可以发现,网约车和巡游出租车在西安市主城区呈明显空间分异格局. 在城市中心区域,巡游出租车占据优势,部分区域甚至处于垄断状态. 这可能源于中心城区交通流量大、路网密集、地标众多等因素,乘客对司机熟悉路线和即时响应能力有较高需求,巡游出租车凭借线下叫车和巡游优势被青睐. 相比之下,远离城市中心郊区地带,网约车具有相对优势. 一方面,这些区域常年交通拥堵情况不太严重,实时路况不确定性较小,适合网约车预约服务模式;另一方面,网约车凭借供给弹性高、灵活定价和个性化服务等优势,在郊区市场占据了较强竞争地位. 部分偏远区域甚至呈现网约车垄断格局,可能与当地巡游出租车运力不足、覆盖程度有限有关. 竞争状态编号1.0~3.3的栅格数量(占比)分别为122(5.6%)、115(5.3%)、285(13.2%)、678(31.2%)、140(6.4%)、312(14.4%)、519(23.9%). 可以看出,网约车和巡游出租车各自在城市不同区域竞争力度存在较大差异. 网约车基本垄断的栅格数量占比为31.2%,巡游出租车基本垄断的栅格数量占比为23.9%. 这表明,尽管巡游出租车在城市中心区域占据优势,但网约车在许多其他区域已具更高程度的优势,显示其在出行服务便利性和灵活性方面竞争力更强. 总体来说,网约车和巡游出租车在西安市主城区7个行政区内空间分布格局呈现明显的中心城市化特征和城乡二元结构. 2种出行方式在不同区位上各具优势,通过市场机制实现空间上的相互渗透、竞争与功能分工,共同满足了市民多元化的出行需求[31]. 影响这种空间格局的因素具有多维特性,包括交通基础设施条件、人口分布特征、土地利用模式、消费偏好等因素.
表 3 网约车、巡游出租车竞争程度标度
Tab.3
| 竞争状态编号 | 状态描述 | HHI变化范围 | 网约车数量变化范围 | 巡游出租车数量变化范围 |
| 1.0 | 完全竞争 | 0.500≤HHI≤0.501 | [16 715, 15 285] | [16 715, 15 285] |
| 2.1 | 网约车轻微优势 | 0.501<HHIrs≤0.520 | (16 715, 19 200] | [12 800, 15 285) |
| 2.2 | 网约车优势竞争 | 0.520<HHIrs≤0.625 | (19 200, 24 000] | [8 000, 12 800) |
| 2.3 | 网约车基本垄断 | HHIrs>0.625 | (24 000, 32 000] | [0, 8 000) |
| 3.1 | 巡游出租车轻微优势 | 0.501<HHIct≤0.520 | [12 800, 15 285) | (16 715, 19 200] |
| 3.2 | 巡游出租车优势竞争 | 0.520<HHIct≤0.625 | [8 000, 12 800) | (19 200, 24 000] |
| 3.3 | 巡游出租车基本垄断 | HHIct>0.625 | [0, 8 000) | (24 000, 32 000] |
图 5
图 5 西安市主城区网约车与巡游出租车竞争程度分布
Fig.5 Distribution of competition degree between ride-sourcing and cruise taxis in main urban area of Xi’an
2.4. 纳什均衡结果分析
根据西安市出租汽车行业实际以及从西安市政府、市出租汽车管理处获取的数据,参考文献[32],对模型参数进行赋值,获得不同博弈策略场景下对应结果,如表4所示. 将博弈主体网约车和巡游出租车的净收益与式(5)、(6)联立,即网约车收益
表 4 博弈模型参数及赋值
Tab.4
| 参数 | 赋值 | 参数 | 赋值 | |
| 政府宽松监管成本 万元 | 10 | 政府严格监管成本 | 15 | |
| 网约车罚金 | 7 | 网约车运营成本 | 6 | |
| 巡游出租车罚金 | 7 | 巡游出租车运营成本 万元 | 6 | |
| 乘客监督奖励 | 4 | 乘客监督成本 | 2 | |
| 网约车合规收益 | 9 | 巡游出租车合规收益 万元 | 9 | |
| 网约车违规额外收益 | 3 | 巡游出租车违规额外收益 | 3 | |
| 政府严格监管概率 | 20 | 网约车合规经营概率 | 80 | |
| 乘客参与监督概率 | 20 | 巡游出租车合规经营概率 | 80 |
表 5 不同博弈场景下参数赋值纳什均衡结果(网约车优先实施策略)
Tab.5
| 博弈场景 | ||||||
| 场景1 | 9 | 6 | 9 | 6 | 1.5 | 0.75 |
| 场景2 | 9 | 6 | 9 | 6 | 1.5 | 0.75 |
| 场景3 | 9 | 6 | 9 | 6 | 1.5 | 0.75 |
| 场景4 | 9 | 6 | 9 | 6 | 1.5 | 0.75 |
| 场景5 | 12 | 13 | 9 | 6 | −2.5 | 2.75 |
| 场景6 | 12 | 13 | 9 | 6 | −2.5 | 2.75 |
| 场景7 | 12 | 9.5 | 9 | 6 | 1 | 1 |
| 场景8 | 12 | 6 | 9 | 6 | 4.5 | −0.75 |
| 场景9 | 9 | 6 | 12 | 13 | 3.5 | −2.25 |
| 场景10 | 9 | 6 | 12 | 13 | 3.5 | −2.25 |
| 场景11 | 9 | 6 | 12 | 9.5 | 1.75 | 0.375 |
| 场景12 | 9 | 6 | 12 | 6 | 0 | 3 |
| 场景13 | 12 | 13 | 12 | 13 | −0.5 | −0.25 |
| 场景14 | 12 | 13 | 12 | 13 | −0.5 | −0.25 |
| 场景15 | 12 | 9.5 | 12 | 9.5 | 1.25 | 0.625 |
| 场景16 | 12 | 6 | 12 | 6 | 3 | 1.5 |
表 6 博弈场景的纳什均衡结果
Tab.6
| 博弈场景 | ||
| 策略1 | 策略2 | |
| 场景1 | 1/2 | 2 |
| 场景2 | 1/2 | 2 |
| 场景3 | 1/2 | 2 |
| 场景4 | 1/2 | 2 |
| 场景7 | 1 | 14/3 |
| 场景11 | 3/14 | 1 |
| 场景15 | 1/2 | 2 |
| 场景16 | 1/2 | 2 |
表 7 不稳定博弈场景的删除说明
Tab.7
| 删除场景 | q1 | q2 | 说明 |
| 场景5 | 3.5 | −2.25 | q2为负值,表示市场无法有效运作 |
| 场景6 | 3.5 | −2.25 | q2为负值,表示市场无法有效运作 |
| 场景8 | 0 | 3 | q1=0,表示巡游出租车垄断市场 |
| 场景9 | −2.5 | 2.75 | q1为负值,表示市场无法有效运作 |
| 场景10 | −2.5 | 2.75 | q1为负值,表示市场无法有效运作 |
| 场景12 | 4.5 | −0.75 | q2为负值,表示市场无法有效运作 |
| 场景13 | −0.5 | −0.25 | q1、q2均为负值,表示市场完全失控 |
| 场景14 | −0.5 | −0.25 | q1、q2均为负值,表示市场完全失控 |
3. 碳排放结果分析
3.1. 车辆碳排放模型
车辆运营过程中产生的二氧化碳排放是全寿命碳排放总量的主要组成部分[34],采用网约车和巡游出租车运营期间的碳排放近似代替出租汽车行业所产生的交通碳排放总量. 构建混合策略下碳排放函数
式中:
式中:
考虑到群体内部竞争,根据西安市网约车、巡游出租车市场实际情况,改进M-M方程,得到T-M-M方程,改进过程如下. 1)原始M-M方程用于描述酶促反应速度,与底物浓度关系为
式中:
式中:
式中:
3.2. 不同模型理论下的碳排放结果分析
3.2.1. 碳排放函数理论解计算碳排放
根据式(16)构建的
图 6
图 6 总碳排放与网约车数量的关系
Fig.6 Relationship between total carbon emissions and number of ride-sourcing vehicles
3.2.2. 纳什均衡解计算碳排放
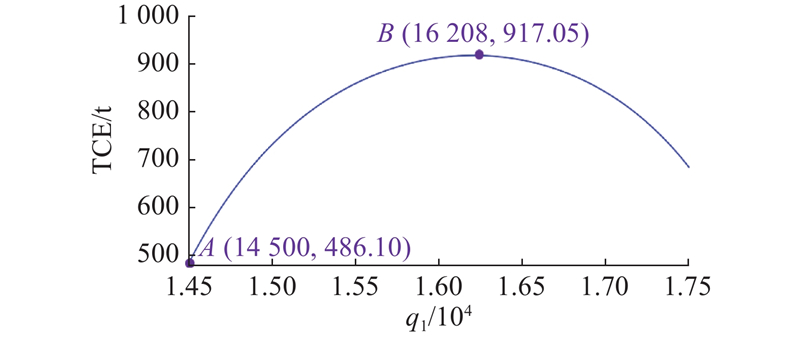
根据纳什均衡求解结果,博弈主体有2种决策顺序,共8种博弈场景. 网约车与巡游出租车的数量比有5种,分别为1、1/2、2、14/3、3/14. 为了防止市场垄断,式(15)要求
图 7
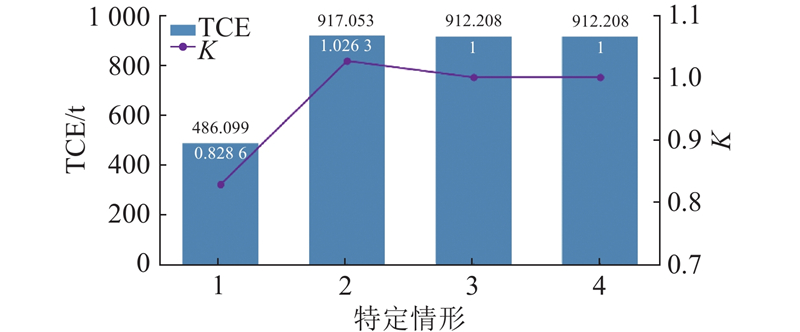
图 7 特定情形下的总碳排放比较
Fig.7 Comparison of total carbon emissions under particular cases
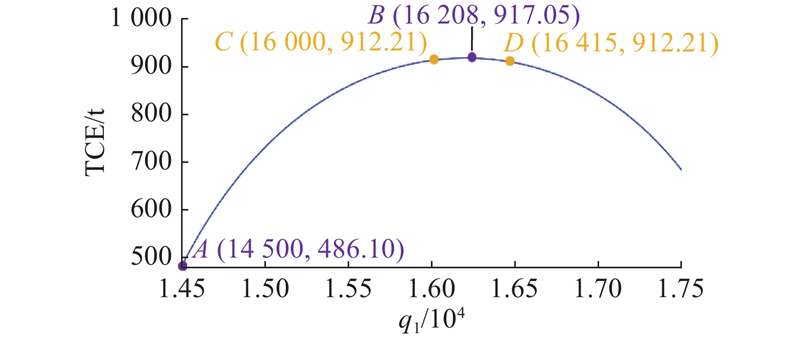
图 8
图 8 特定情形下碳排放随网约车数量的变化
Fig.8 Variation of carbon emissions with ride-sourcing vehicles under particular cases
综上,为了维持市场平衡和稳定,从低碳环保角度出发,政府可实施如限行、限号的政策,使得日均上线运营网约车数量略少于巡游出租车数量,将比值控制在0.828 6~
3.3. 参数分析
分析参数变化对碳排放结果的影响,揭示模型内在机理,为城市交通管理部门制定低碳发展战略及交通管理政策提供科学参考.
3.3.1. 参数敏感性分析
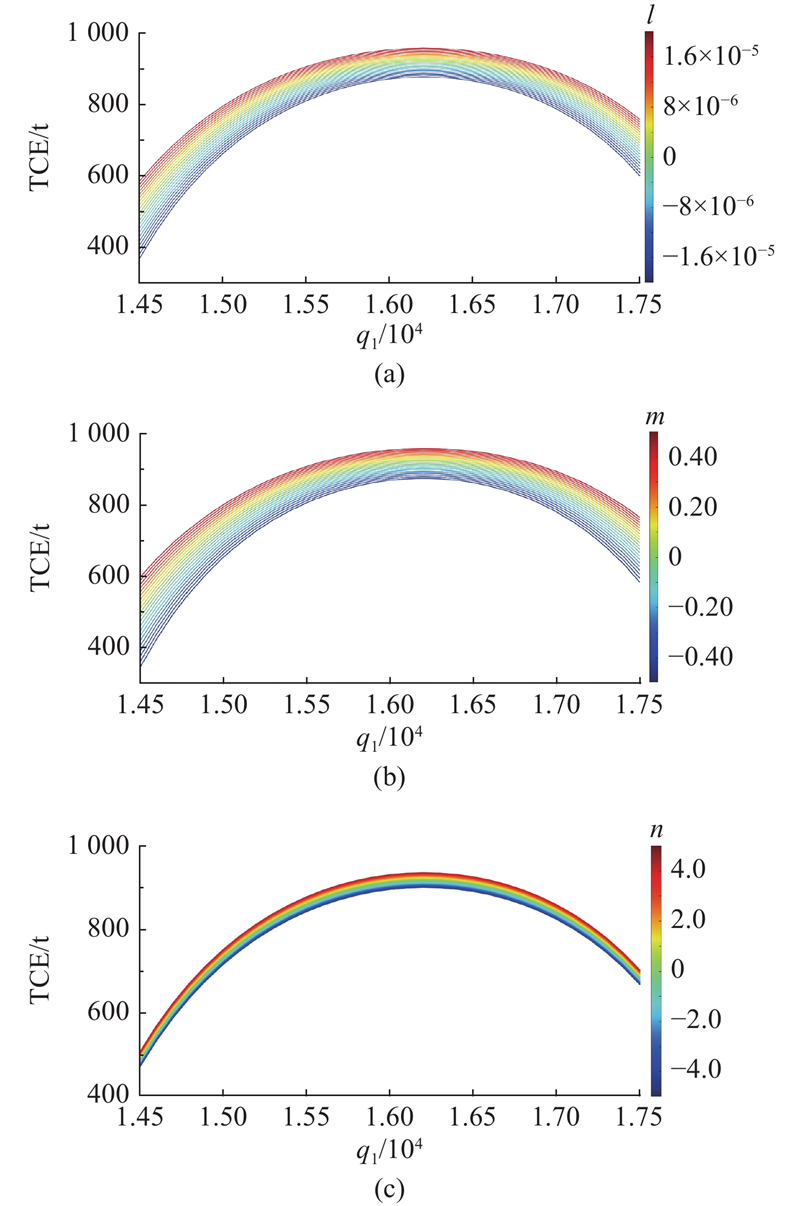
为了说明碳排放分析结果的有效性、稳健性,对模型中关键参数
图 9
3.3.2. 期望-方差分析
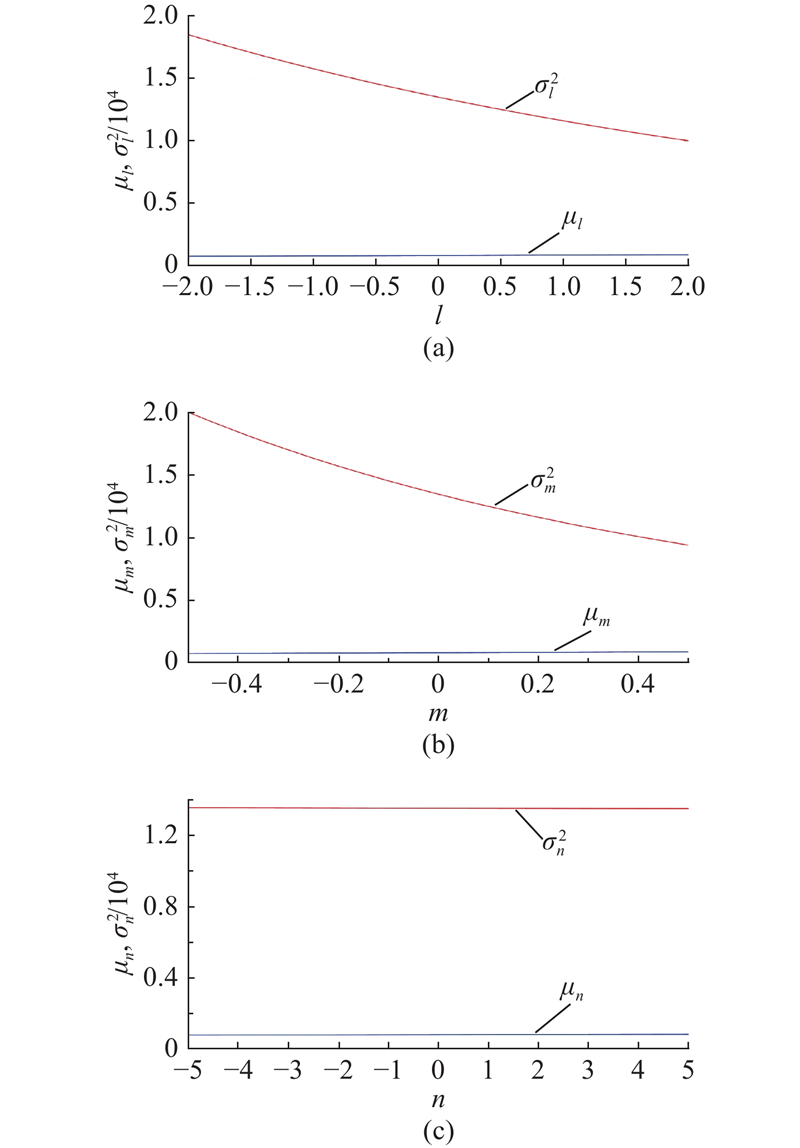
期望-方差分析用于进一步量化每个参数对碳排放的影响,全面理解参数变化对碳排放的影响,了解参数变化的影响幅度和稳定性. 图10(a)中,随着
图 10
综合分析结果:1)
4. 结 语
本研究基于共享出行出租汽车订单大数据分析城市网约车与巡游出租车的动态竞争关系,构建四方参与的完全信息动态博弈模型. 以西安市为例,将博弈结果与碳排放计算模型相结合,量化评估不同网约车与巡游出租车数量比例下交通碳排放水平. 在时空维度上,网约车与巡游出租车的竞争优势会动态变化,呈现中心城市化和城乡二元结构特征. 在不同时段和不同区域,出租汽车市场表现出不同博弈竞争格局. 在不同博弈策略下,网约车和巡游出租车数量比例、市场份额以及碳排放量的变化趋势均不同. 在不考虑外部因素影响前提下,当网约车与巡游出租车数量比值约为1.026 3时,市场达到失稳前最大忍受能力,交通碳排放最大;比值降低到0.828 6时,碳排放最小. 将网约车与巡游出租车数量比值维持在0.828 6~
参考文献
互联网对市场的改善和扰乱: 基于市场失灵理论的视角
[J].
Internet improvement and disruption to the market: from the perspective of market failure theory
[J].
出行共享中的用户价值共创机理: 基于优步的案例研究
[J].DOI:10.3969/j.issn.1002-5502.2017.08.013 [本文引用: 1]
The co-creation mechanism of user value in travel sharing: a case study based on Uber
[J].DOI:10.3969/j.issn.1002-5502.2017.08.013 [本文引用: 1]
平台经济视域下的商家舞弊治理: 博弈模型与政策建议
[J].
Analysis of sellers’ commercial fraud in platform economy based on evolutionary game theory
[J].
基于动态博弈的城市出租车投放量测算研究
[J].
Urban taxi quantity based on dynamic game theory
[J].
“专车” 进入后的出租车市场规制策略研究
[J].
Research on the regulation strategy of the taxi market after the “special car” entering
[J].
Car versus public transportation? The role of social value orientations in a real-life social dilemma
[J].DOI:10.1111/j.1559-1816.1995.tb01594.x [本文引用: 1]
Moral hazard in traffic games
[J].
Stackelberg games and multiple equilibrium behaviors on networks
[J].DOI:10.1016/j.trb.2007.03.002 [本文引用: 1]
小汽车通勤向公共交通转移演化博弈分析
[J].DOI:10.11860/j.issn.1673-0291.2014.04.27 [本文引用: 1]
Evolutionary game analysis on modal shift of car commuters to public transport
[J].DOI:10.11860/j.issn.1673-0291.2014.04.27 [本文引用: 1]
Evolutionary game between government and ride-hailing platform: evidence from China
[J].
网络约车与出租车的竞争博弈研究: 以平台补贴为背景
[J].
On the competition game between online tailored taxi and traditional taxi under platform’s subsidy policy
[J].
Analysis on the market evolution of new energy vehicle based on population competition model
[J].DOI:10.1016/j.trd.2018.08.005 [本文引用: 1]
基于时不变综合系数的运输方式动力学模型
[J].
Dynamic model of transportation modes based on time-invariant comprehensive coefficient
[J].
Modeling dynamic competition among urban taxis and the impact on carbon emissions
[J].DOI:10.1016/j.scs.2025.106258 [本文引用: 1]
数据驱动下共享出行资源配置的双层博弈问题研究
[J].
Research on data-driven bi-level game problems in resource allocation of sharing mobility systems
[J].
空间异质性建成环境对出租车与地铁竞合关系的影响
[J].
Impacts of built environment on competition and cooperation relationship between taxi and subway considering spatial heterogeneity
[J].
未来我国出租车发展趋势及市场化改革研究
[J].
Development trend and market reform of China’s taxi in the future
[J].
Socioeconomic and usage characteristics of transportation network company (TNC) riders
[J].DOI:10.1007/s11116-019-09989-3 [本文引用: 1]
出租车和网约车载客空间特征分析
[J].DOI:10.3969/j.issn.1672-4747.2020.01.009 [本文引用: 1]
Analysis the spatial characteristic of taxi and ridesourcing service trips
[J].DOI:10.3969/j.issn.1672-4747.2020.01.009 [本文引用: 1]
基于轨迹数据的网约车排放时空特征分析
[J].
Analyzing spatiotemporal characteristics of ridesourcing emissions based on trajectory data
[J].
Route change decision making by hurricane evacuees facing congestion
[J].
Approach to quantify the impact of disruptions on traffic conditions using dynamic weighted resilience metrics of transport networks
[J].DOI:10.1177/0361198121998663 [本文引用: 1]
Modelling chain for the effect of road traffic on air and water quality: techniques, current status and future prospects
[J].DOI:10.1016/j.envsoft.2014.11.020 [本文引用: 1]
Temporal variations of local traffic CO2 emissions and its relationship with CO2 flux in Beijing, China
[J].DOI:10.1016/j.trd.2018.10.007 [本文引用: 1]
大数据时代新型交通服务商业模式的监管——以网约车为例
[J].DOI:10.3969/j.issn.1002-5502.2019.06.010 [本文引用: 1]
The supervision of the new transport service business model in big data era: a case study of ride-hailing service
[J].DOI:10.3969/j.issn.1002-5502.2019.06.010 [本文引用: 1]
Dynamic game with perfect and complete information based dynamic channel assignment
[J].DOI:10.1007/s10489-012-0402-8 [本文引用: 1]
资产收益序列相依下的多阶段投资博弈模型
[J].DOI:10.3969/j.issn.1007-9807.2019.07.005 [本文引用: 1]
Multi-period portfolio game model with serially correlated returns
[J].DOI:10.3969/j.issn.1007-9807.2019.07.005 [本文引用: 1]
“完全竞争”的一种理论思考
[J].
A theoretical reflection on “perfect competition”
[J].
竞争优势与优势竞争: 后发地区的发展定位与竞争战略
[J].DOI:10.3969/j.issn.1006-2912.2003.04.008 [本文引用: 1]
To fixed competition advantage and advantage competition of development position and choice the competitive strategy in developing region
[J].DOI:10.3969/j.issn.1006-2912.2003.04.008 [本文引用: 1]
银行业务地理集中是否降低了金融风险? 基于中国城市商业银行微观数据的研究
[J].DOI:10.3969/j.issn.1002-5502.2021.05.008 [本文引用: 1]
Does the geographical concentration of banking business reduce financial risks? A study based on micro-level dataset of Chinese city commercial banks
[J].DOI:10.3969/j.issn.1002-5502.2021.05.008 [本文引用: 1]
基于电动汽车大数据的多等级充电站选址及服务能力研究
[J].
Location and service capability of multilevel charging stations based on electric vehicle big data
[J].
Regulation strategies of ride-hailing market in China: an evolutionary game theoretic perspective
[J].DOI:10.1007/s10660-020-09412-5 [本文引用: 1]
中国金融市场系统复杂性的演化机理与管理研究
[J].DOI:10.3969/j.issn.1007-9807.2017.01.008 [本文引用: 1]
Evolution mechanisms and management of systemic complexity in China’s financial markets
[J].DOI:10.3969/j.issn.1007-9807.2017.01.008 [本文引用: 1]
The importance of the use phase on the LCA of environmentally friendly solutions for asphalt road pavements
[J].DOI:10.1016/j.trd.2014.07.006 [本文引用: 1]
Traffic pollution modelling and emission data
[J].DOI:10.1016/j.envsoft.2004.06.013 [本文引用: 1]
Real-world fuel consumption and CO2 emissions of urban public buses in Beijing
[J].DOI:10.1016/j.apenergy.2013.09.017 [本文引用: 1]
中国低碳经济发展的协同效应研究
[J].DOI:10.3969/j.issn.1002-5502.2021.08.009 [本文引用: 1]
Research on the synergistic effect of low-carbon economy in China
[J].DOI:10.3969/j.issn.1002-5502.2021.08.009 [本文引用: 1]