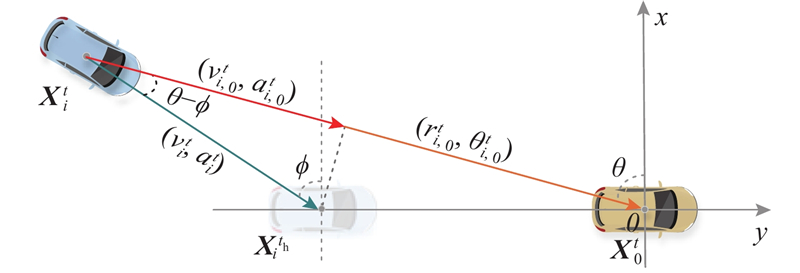
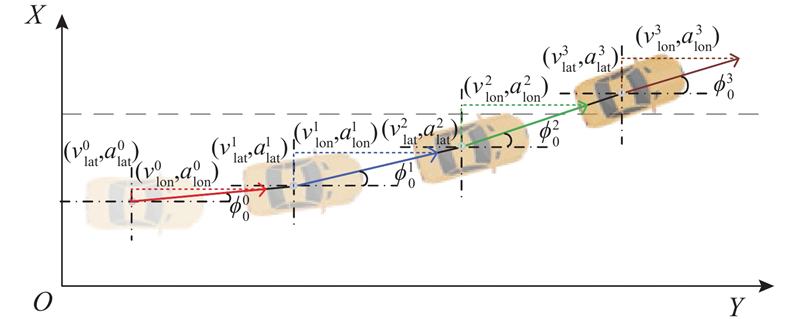
(6) ${\left.\begin{array}{l} r_{i,0}^t = \left[ {{{(y_i^t - y_0^t)}^2}+{{(x_i^t - x_0^t)}^2}}\right]^{1/2}, \\ \theta _{i,0}^t = {\text{arctan}}\;\dfrac{{y_i^t - y_0^t}}{{x_i^t - x_0^t}}, \qquad \phi _i^t = {\text{arctan}}\;\dfrac{{y_i^t - y_i^{{t_{{\text{h}}}}}}}{{x_i^t - x_i^{{t_{{\text{h}}}}}}}, \\ v_{i,0}^t = v_i^t \times {\text{cos}}\;(\theta _{i,0}^t - \phi _i^t), \quad a_{i,0}^t = a_i^t \times {\text{cos}}\;(\theta _{i,0}^t - \phi _i^t).\end{array}\right\}} $
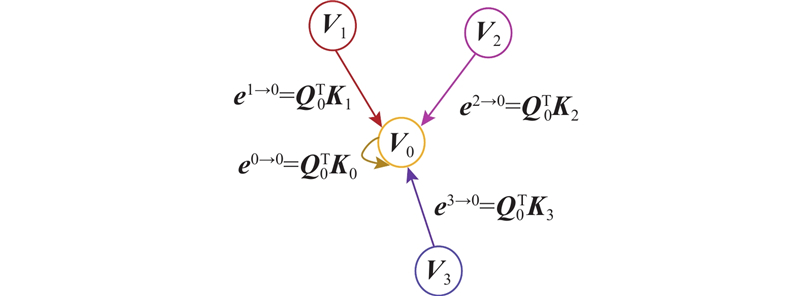
车辆在行驶中的行为与周围车辆运动状态高度相关. 利用图注意力网络表达周围车辆运动状态对目标车辆变道决策的影响,模型示意图如图4 所示. 图中,图注意力网络为有向图,方向表示周围车辆对目标车辆的影响,箭头所指节点为目标车辆,其余节点表示周围车辆. 图G= $ \{ V,E\} $ $ V = \{ {V_0},{V_1}, \cdot \cdot \cdot , {V_i}, \cdot \cdot \cdot ,{V_n}\} $ ${V_0}$ ${V_i}\;(1 \leqslant i \leqslant n)$ $ E = \{ {E_0}, {E_1}, \cdot \cdot \cdot , {E_i}, \cdot \cdot \cdot, {E_n}\} $ $ {{\boldsymbol{e}}^{i \to 0}} $ .
[1]
ISLAM M M, NEWAZ A A, SONG L, et al Connected autonomous vehicles: state of practice
[J]. Applied Stochastic Models in Business and Industry , 2023 , 39 (5 ): 684 - 700
DOI:10.1002/asmb.2772
[本文引用: 1]
[2]
HUANG Y J, DU J T, YANG Z R, et al A survey on trajectory-prediction methods for autonomous driving
[J]. IEEE Transactions on Intelligent Vehicles , 2022 , 7 (3 ): 652 - 674
DOI:10.1109/TIV.2022.3167103
[本文引用: 1]
[3]
BENRACHOU D E, GLASER S, ELHENAWY M, et al Use of social interaction and intention to improve motion prediction within automated vehicle framework: a review
[J]. IEEE Transactions on Intelligent Transportation Systems , 2022 , 23 (12 ): 22807 - 22837
DOI:10.1109/TITS.2022.3207347
[本文引用: 1]
[4]
李文礼, 韩迪, 石晓辉, 等. 基于时-空注意力机制的车辆轨迹预测[J]. 中国公路学报, 2023, 36: 226–239.
[本文引用: 1]
LI Wenli, HAN Di, SHI Xiaohui, et al, Vehicle trajectory prediction based on spatial-temporal attention mechanism[J]. China Journal of Highway and Transport , 2023, 36: 226–239.
[本文引用: 1]
[5]
ZHANG K P, LI L Explainable multimodal trajectory prediction using attention models
[J]. Transportation Research Part C: Emerging Technologies , 2022 , 143 : 103829
DOI:10.1016/j.trc.2022.103829
[本文引用: 1]
[6]
DING Z, ZHAO H Incorporating driving knowledge in deep learning based vehicle trajectory prediction: a survey
[J]. IEEE Transactions on Intelligent Vehicles , 2023 , 8 (8 ): 3996 - 4015
DOI:10.1109/TIV.2023.3266446
[本文引用: 1]
[7]
HOUENOU A, BONNIFAIT P, CHERFAOUI V, et al. Vehicle trajectory prediction based on motion model and maneuver recognition [C]// IEEE/RSJ International Conference on Intelligent Robots and Systems . Tokyo: IEEE, 2013: 4363–4369.
[本文引用: 1]
[8]
BARTH A, FRANKE U. Where will the oncoming vehicle be the next second? [C]// 2008 IEEE Intelligent Vehicles Symposium . Eindhoven: IEEE, 2008: 510–515.
[本文引用: 1]
[9]
JIANG Y, ZHU B, YANG S, et al Vehicle trajectory prediction considering driver uncertainty and vehicle dynamics based on dynamic bayesian network
[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems , 2023 , 53 (2 ): 689 - 703
DOI:10.1109/TSMC.2022.3186639
[本文引用: 1]
[10]
HUANG M, ZHU M, XIAO Y, et al Bayonet-corpus: a trajectory prediction method based on bayonet context and bidirectional GRU
[J]. Digital Communications and Networks , 2021 , 7 (1 ): 72 - 81
DOI:10.1016/j.dcan.2020.03.002
[本文引用: 1]
[11]
ALTCHé F, DE LA FORTELLE A, IEEE. An LSTM network for highway trajectory prediction [C]// IEEE International Conference on Intelligent Transportation Systems . New York: IEEE, 2017: 253–259.
[本文引用: 1]
[12]
LI X, YING X W, CHUAH M C, et al. GRIP: graph-based interaction-aware trajectory prediction [C]// IEEE Intelligent Transportation Systems Conference . Auckland: IEEE, 2019: 3960–3966.
[本文引用: 2]
[13]
MO X U, YANG X, CHEN L. Graph and recurrent neural network-based vehicle trajectory prediction for highway driving [C]// IEEE International Intelligent Transportation Systems Conference . Indianapolis: IEEE, 2021: 1934–1939.
[本文引用: 1]
[14]
GUPTA A, JOHNSON J, LI F F, et al. Social GAN: socially acceptable trajectories with generative adversarial networks [C]// IEEE/CVF Conference on Computer Vision and Pattern Recognition . Salt Lake City: IEEE, 2018: 2255–2264.
[本文引用: 4]
[15]
DEO N, TRIVEDI M M. Convolutional social pooling for vehicle trajectory prediction [C]// IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops . New York: IEEE, 2018: 1468–1476.
[本文引用: 6]
[16]
ALAHI A, GOEL K, RAMANATHAN V, et al. Social LSTM: human trajectory prediction in crowded spaces [C]// IEEE Conference on Computer Vision and Pattern Recognition . Seattle: IEEE, 2016: 961–971.
[本文引用: 4]
[17]
CHEN X, ZHANG H, ZHAO F, et al Intention-aware vehicle trajectory prediction based on spatial-temporal dynamic attention network for internet of vehicles
[J]. IEEE Transactions on Intelligent Transportation Systems , 2022 , 23 (10 ): 19471 - 19483
DOI:10.1109/TITS.2022.3170551
[本文引用: 4]
[18]
SONG H, DING W C, CHEN Y X, et al. PiP: planning-informed trajectory prediction for autonomous driving [C]// Computer Vision - ECCV 2020 16th European Conference Proceedings Lecture Notes in Computer Science . Glasgow: LNCS, 2020: 598–614.
[本文引用: 3]
[19]
COIFMAN B, LI L Z A critical evaluation of the next generation simulation (NGSIM) vehicle trajectory dataset
[J]. Transportation Research Part B - Methodological , 2017 , 105 : 362 - 377
DOI:10.1016/j.trb.2017.09.018
[本文引用: 2]
Connected autonomous vehicles: state of practice
1
2023
... 自动化驾驶技术有望重塑未来的交通系统,但在可预见的未来交通场景中,以不同渗透比例的人工驾驶车辆和自动驾驶车辆组成的混合交通流将长期存在[1 ] . 自动驾驶车辆之间能够通过数据共享获得彼此未来的轨迹,人工驾驶车辆轨迹只能通过预测手段获取[2 ] . 面对复杂的驾驶环境,人工驾驶车辆轨迹预测面临着诸多挑战[3 ] :车辆轨迹不仅取决于自身的历史轨迹,还受到车辆运动状态、交通流环境因素的影响[4 ] . 而且,车辆轨迹预测本质上是多模态的[5 ] ,即驾驶员操作和决策具有多样性,在同一场景下可能存在多种合理的驾驶方式. ...
A survey on trajectory-prediction methods for autonomous driving
1
2022
... 自动化驾驶技术有望重塑未来的交通系统,但在可预见的未来交通场景中,以不同渗透比例的人工驾驶车辆和自动驾驶车辆组成的混合交通流将长期存在[1 ] . 自动驾驶车辆之间能够通过数据共享获得彼此未来的轨迹,人工驾驶车辆轨迹只能通过预测手段获取[2 ] . 面对复杂的驾驶环境,人工驾驶车辆轨迹预测面临着诸多挑战[3 ] :车辆轨迹不仅取决于自身的历史轨迹,还受到车辆运动状态、交通流环境因素的影响[4 ] . 而且,车辆轨迹预测本质上是多模态的[5 ] ,即驾驶员操作和决策具有多样性,在同一场景下可能存在多种合理的驾驶方式. ...
Use of social interaction and intention to improve motion prediction within automated vehicle framework: a review
1
2022
... 自动化驾驶技术有望重塑未来的交通系统,但在可预见的未来交通场景中,以不同渗透比例的人工驾驶车辆和自动驾驶车辆组成的混合交通流将长期存在[1 ] . 自动驾驶车辆之间能够通过数据共享获得彼此未来的轨迹,人工驾驶车辆轨迹只能通过预测手段获取[2 ] . 面对复杂的驾驶环境,人工驾驶车辆轨迹预测面临着诸多挑战[3 ] :车辆轨迹不仅取决于自身的历史轨迹,还受到车辆运动状态、交通流环境因素的影响[4 ] . 而且,车辆轨迹预测本质上是多模态的[5 ] ,即驾驶员操作和决策具有多样性,在同一场景下可能存在多种合理的驾驶方式. ...
1
... 自动化驾驶技术有望重塑未来的交通系统,但在可预见的未来交通场景中,以不同渗透比例的人工驾驶车辆和自动驾驶车辆组成的混合交通流将长期存在[1 ] . 自动驾驶车辆之间能够通过数据共享获得彼此未来的轨迹,人工驾驶车辆轨迹只能通过预测手段获取[2 ] . 面对复杂的驾驶环境,人工驾驶车辆轨迹预测面临着诸多挑战[3 ] :车辆轨迹不仅取决于自身的历史轨迹,还受到车辆运动状态、交通流环境因素的影响[4 ] . 而且,车辆轨迹预测本质上是多模态的[5 ] ,即驾驶员操作和决策具有多样性,在同一场景下可能存在多种合理的驾驶方式. ...
1
... 自动化驾驶技术有望重塑未来的交通系统,但在可预见的未来交通场景中,以不同渗透比例的人工驾驶车辆和自动驾驶车辆组成的混合交通流将长期存在[1 ] . 自动驾驶车辆之间能够通过数据共享获得彼此未来的轨迹,人工驾驶车辆轨迹只能通过预测手段获取[2 ] . 面对复杂的驾驶环境,人工驾驶车辆轨迹预测面临着诸多挑战[3 ] :车辆轨迹不仅取决于自身的历史轨迹,还受到车辆运动状态、交通流环境因素的影响[4 ] . 而且,车辆轨迹预测本质上是多模态的[5 ] ,即驾驶员操作和决策具有多样性,在同一场景下可能存在多种合理的驾驶方式. ...
Explainable multimodal trajectory prediction using attention models
1
2022
... 自动化驾驶技术有望重塑未来的交通系统,但在可预见的未来交通场景中,以不同渗透比例的人工驾驶车辆和自动驾驶车辆组成的混合交通流将长期存在[1 ] . 自动驾驶车辆之间能够通过数据共享获得彼此未来的轨迹,人工驾驶车辆轨迹只能通过预测手段获取[2 ] . 面对复杂的驾驶环境,人工驾驶车辆轨迹预测面临着诸多挑战[3 ] :车辆轨迹不仅取决于自身的历史轨迹,还受到车辆运动状态、交通流环境因素的影响[4 ] . 而且,车辆轨迹预测本质上是多模态的[5 ] ,即驾驶员操作和决策具有多样性,在同一场景下可能存在多种合理的驾驶方式. ...
Incorporating driving knowledge in deep learning based vehicle trajectory prediction: a survey
1
2023
... 近年来,诸多学者对车辆轨迹预测问题进行了深入研究,其方法大体上可以分为模型驱动和数据驱动2种[6 ] . 基于模型驱动的方法依靠运动学和动力学定律,利用数学公式描述车辆的物理运动. 比如,Houenou等[7 ] 基于恒定角速度、加速度预测车辆轨迹,Barth等[8 ] 利用卡尔曼滤波和图像数据预测车辆的长期轨迹,Jiang等[9 ] 利用动态贝叶斯网络识别驾驶意图并预测车辆轨迹. 然而,基于模型驱动的轨迹预测难以挖掘数据的非线性关系,长期预测精度低. ...
1
... 近年来,诸多学者对车辆轨迹预测问题进行了深入研究,其方法大体上可以分为模型驱动和数据驱动2种[6 ] . 基于模型驱动的方法依靠运动学和动力学定律,利用数学公式描述车辆的物理运动. 比如,Houenou等[7 ] 基于恒定角速度、加速度预测车辆轨迹,Barth等[8 ] 利用卡尔曼滤波和图像数据预测车辆的长期轨迹,Jiang等[9 ] 利用动态贝叶斯网络识别驾驶意图并预测车辆轨迹. 然而,基于模型驱动的轨迹预测难以挖掘数据的非线性关系,长期预测精度低. ...
1
... 近年来,诸多学者对车辆轨迹预测问题进行了深入研究,其方法大体上可以分为模型驱动和数据驱动2种[6 ] . 基于模型驱动的方法依靠运动学和动力学定律,利用数学公式描述车辆的物理运动. 比如,Houenou等[7 ] 基于恒定角速度、加速度预测车辆轨迹,Barth等[8 ] 利用卡尔曼滤波和图像数据预测车辆的长期轨迹,Jiang等[9 ] 利用动态贝叶斯网络识别驾驶意图并预测车辆轨迹. 然而,基于模型驱动的轨迹预测难以挖掘数据的非线性关系,长期预测精度低. ...
Vehicle trajectory prediction considering driver uncertainty and vehicle dynamics based on dynamic bayesian network
1
2023
... 近年来,诸多学者对车辆轨迹预测问题进行了深入研究,其方法大体上可以分为模型驱动和数据驱动2种[6 ] . 基于模型驱动的方法依靠运动学和动力学定律,利用数学公式描述车辆的物理运动. 比如,Houenou等[7 ] 基于恒定角速度、加速度预测车辆轨迹,Barth等[8 ] 利用卡尔曼滤波和图像数据预测车辆的长期轨迹,Jiang等[9 ] 利用动态贝叶斯网络识别驾驶意图并预测车辆轨迹. 然而,基于模型驱动的轨迹预测难以挖掘数据的非线性关系,长期预测精度低. ...
Bayonet-corpus: a trajectory prediction method based on bayonet context and bidirectional GRU
1
2021
... 随着数据科学的发展,基于数据驱动的轨迹预测方法受到越来越多学者关注. 许多学者使用门控递归单元(gated recurrent unit,GRU)[10 ] 和长短期记忆(long short-term memory,LSTM)[11 ] 预测车辆轨迹. 但此类基于循环神经网络(recurrent neural network, RNN)的预测方法仅挖掘了时间维度上的轨迹特征,没有考虑车辆之间的空间交互影响. 图神经网络(graph neural network,GNN)将每个车辆视作图的节点,车辆之间的空间关系由边来表示[12 ] ,基于此,Mo等[13 ] 提出基于GNN-RNN的编码器-解码器网络的轨迹预测方法,使用GNN对车辆之间的交互进行编码. 但基于GNN的轨迹预测方法赋予了每个节点相同的重要性,无法表示车辆之间由位置不同而引起的交互差异. 此外,传统的GNN方法计算同一场景下所有车辆之间的相互作用,会造成算力浪费. ...
1
... 随着数据科学的发展,基于数据驱动的轨迹预测方法受到越来越多学者关注. 许多学者使用门控递归单元(gated recurrent unit,GRU)[10 ] 和长短期记忆(long short-term memory,LSTM)[11 ] 预测车辆轨迹. 但此类基于循环神经网络(recurrent neural network, RNN)的预测方法仅挖掘了时间维度上的轨迹特征,没有考虑车辆之间的空间交互影响. 图神经网络(graph neural network,GNN)将每个车辆视作图的节点,车辆之间的空间关系由边来表示[12 ] ,基于此,Mo等[13 ] 提出基于GNN-RNN的编码器-解码器网络的轨迹预测方法,使用GNN对车辆之间的交互进行编码. 但基于GNN的轨迹预测方法赋予了每个节点相同的重要性,无法表示车辆之间由位置不同而引起的交互差异. 此外,传统的GNN方法计算同一场景下所有车辆之间的相互作用,会造成算力浪费. ...
2
... 随着数据科学的发展,基于数据驱动的轨迹预测方法受到越来越多学者关注. 许多学者使用门控递归单元(gated recurrent unit,GRU)[10 ] 和长短期记忆(long short-term memory,LSTM)[11 ] 预测车辆轨迹. 但此类基于循环神经网络(recurrent neural network, RNN)的预测方法仅挖掘了时间维度上的轨迹特征,没有考虑车辆之间的空间交互影响. 图神经网络(graph neural network,GNN)将每个车辆视作图的节点,车辆之间的空间关系由边来表示[12 ] ,基于此,Mo等[13 ] 提出基于GNN-RNN的编码器-解码器网络的轨迹预测方法,使用GNN对车辆之间的交互进行编码. 但基于GNN的轨迹预测方法赋予了每个节点相同的重要性,无法表示车辆之间由位置不同而引起的交互差异. 此外,传统的GNN方法计算同一场景下所有车辆之间的相互作用,会造成算力浪费. ...
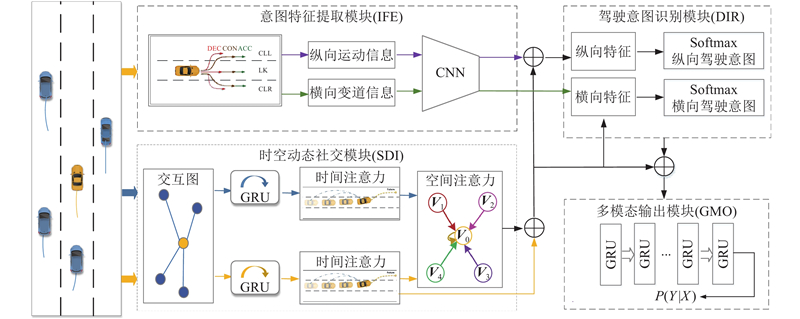
... 车辆时空特征信息的交互融合对车辆轨迹预测至关重要. 首先,利用多层感知机(multilayer perceptron,MLP)和GRU网络提取车辆运动特征. 其次,利用时间注意力网络捕捉不同时刻历史状态的重要信息,对车辆的时间维度轨迹信息进行加权处理. 最后,加入空间图注意力网络对车辆空间维度交互进行建模. 空间图注意力网络以车辆为节点,车辆之间的影响权重为边,弥补了关于车辆间相互影响的同质化表达缺陷[12 ,16 ] . ...
1
... 随着数据科学的发展,基于数据驱动的轨迹预测方法受到越来越多学者关注. 许多学者使用门控递归单元(gated recurrent unit,GRU)[10 ] 和长短期记忆(long short-term memory,LSTM)[11 ] 预测车辆轨迹. 但此类基于循环神经网络(recurrent neural network, RNN)的预测方法仅挖掘了时间维度上的轨迹特征,没有考虑车辆之间的空间交互影响. 图神经网络(graph neural network,GNN)将每个车辆视作图的节点,车辆之间的空间关系由边来表示[12 ] ,基于此,Mo等[13 ] 提出基于GNN-RNN的编码器-解码器网络的轨迹预测方法,使用GNN对车辆之间的交互进行编码. 但基于GNN的轨迹预测方法赋予了每个节点相同的重要性,无法表示车辆之间由位置不同而引起的交互差异. 此外,传统的GNN方法计算同一场景下所有车辆之间的相互作用,会造成算力浪费. ...
4
... 车辆未来轨迹具有多模态特性,如何准确表达这种特性尤为关键. 一些学者采用生成对抗网络(generative adversarial network,GAN)和高斯混合模型(Gaussian mixture model,GMM)生成多个不确定轨迹. Alahi等[14 ] 利用GAN模型捕捉未来预测轨迹的多模态. CS-LSTM[15 ] 将隐藏变量依据目标车辆的3种横向和2种纵向机动类别对未来的驾驶意图进行分类,利用GMM生成未来多个轨迹. 大多数基于GMM方法的轨迹多模态研究融合了编码上下文特征,但不足以精确预测不同的横向和纵向的驾驶意图,会影响车辆多模态轨迹预测精度. ...
... RMSE for different models in 5-second forecast range
Tab.1 数据集 RMSE t f /sS-LSTM[16 ] CS-LSTM[15 ] S-GAN[14 ] PIP[18 ] STDAN[17 ] STGAMT(w/o IFE) STGAMT HighD 1 0.22 0.22 0.20 0.17 0.19 0.07 0.07 2 0.62 0.61 0.57 0.52 0.27 0.19 0.19 3 1.27 1.24 1.14 1.05 0.48 0.35 0.32 4 2.15 2.10 1.90 1.76 0.91 0.65 0.61 5 3.14 3.27 2.91 2.63 1.66 1.20 1.14 NGSIM 1 0.65 0.61 0.57 0.55 0.42 0.22 0.21 2 1.31 1.27 1.32 1.18 1.01 0.80 0.78 3 2.16 2.09 2.22 1.94 1.69 1.52 1.49 4 3.25 3.10 3.26 2.88 2.56 2.47 2.40 5 4.55 4.37 4.40 4.04 3.67 3.69 3.58
1)S-LSTM[16 ] :使用全连接的社交池化层构建基于LSTM的编码器-解码器结构. ...
... 3)S-GAN[14 ] :该模型结合了序列到序列和生成对抗网络的模型来融合车辆交互信息并生成多模态轨迹预测. ...
... Comparison of training time per epoch for models
Tab.2 模型名称 t e /sS-LSTM[16 ] 0.0157 CS-LSTM[15 ] 0.0174 S-GAN[14 ] 0.0283 PIP[18 ] 0.0185 STDAN[17 ] 0.0214 STGAMT(w/o IFE) 0.0137 STGAMT 0.0139
本研究模型STGAMT较5个经典模型的平均耗时减少32.8%,较同样使用注意力机制的STDAN模型的消耗时间减少35.0%,表明本研究的时空图注意力网络较传统的注意力机制能够提升运行效率. 虽然STGAMT较STGAMT(w/o IFE)消耗时间增加1.5%,但误差降低4.1%,而且预测耗时依旧满足要求. 不同模型耗时的对比说明本研究模型在保证准确度的同时提升了推理效率. ...
6
... 车辆未来轨迹具有多模态特性,如何准确表达这种特性尤为关键. 一些学者采用生成对抗网络(generative adversarial network,GAN)和高斯混合模型(Gaussian mixture model,GMM)生成多个不确定轨迹. Alahi等[14 ] 利用GAN模型捕捉未来预测轨迹的多模态. CS-LSTM[15 ] 将隐藏变量依据目标车辆的3种横向和2种纵向机动类别对未来的驾驶意图进行分类,利用GMM生成未来多个轨迹. 大多数基于GMM方法的轨迹多模态研究融合了编码上下文特征,但不足以精确预测不同的横向和纵向的驾驶意图,会影响车辆多模态轨迹预测精度. ...
... 选取目标车辆一定距离范围内的车辆作为与目标车辆相互影响的周围车辆. 参照CS-LSTM[15 ] 模型参数标定,将目标车辆影响范围的横向距离设置为11.1 m(3条车道宽度),纵向距离设置为59.5 m(13辆轿车长度). ...
... 实验在NVIDIA GeForce RTX 2080 Ti上进行,代码在深度学习框架PyTorch下实现. 为了验证本研究模型的可行性,便于同其他模型进行对比,采用与CS-LSTM[15 ] 和STDAN[17 ] 类似的实验策略及实验环境. 利用2种损失函数训练策略,首先迭代5次均方误差损失函数,再利用3次迭代负对数似然损失函数训练轨迹数据. 优化器为Adam,学习率为0.001,批次为128,特征嵌入网络的维度为32,GRU特征编码的维度为64,空图注意力网络的注意力头数设置为4,GRU特征输出的维度为128. ...
... RMSE for different models in 5-second forecast range
Tab.1 数据集 RMSE t f /sS-LSTM[16 ] CS-LSTM[15 ] S-GAN[14 ] PIP[18 ] STDAN[17 ] STGAMT(w/o IFE) STGAMT HighD 1 0.22 0.22 0.20 0.17 0.19 0.07 0.07 2 0.62 0.61 0.57 0.52 0.27 0.19 0.19 3 1.27 1.24 1.14 1.05 0.48 0.35 0.32 4 2.15 2.10 1.90 1.76 0.91 0.65 0.61 5 3.14 3.27 2.91 2.63 1.66 1.20 1.14 NGSIM 1 0.65 0.61 0.57 0.55 0.42 0.22 0.21 2 1.31 1.27 1.32 1.18 1.01 0.80 0.78 3 2.16 2.09 2.22 1.94 1.69 1.52 1.49 4 3.25 3.10 3.26 2.88 2.56 2.47 2.40 5 4.55 4.37 4.40 4.04 3.67 3.69 3.58
1)S-LSTM[16 ] :使用全连接的社交池化层构建基于LSTM的编码器-解码器结构. ...
... 2)CS-LSTM[15 ] :将卷积运算引入社交池化层,以捕捉车辆间的交互. ...
... Comparison of training time per epoch for models
Tab.2 模型名称 t e /sS-LSTM[16 ] 0.0157 CS-LSTM[15 ] 0.0174 S-GAN[14 ] 0.0283 PIP[18 ] 0.0185 STDAN[17 ] 0.0214 STGAMT(w/o IFE) 0.0137 STGAMT 0.0139
本研究模型STGAMT较5个经典模型的平均耗时减少32.8%,较同样使用注意力机制的STDAN模型的消耗时间减少35.0%,表明本研究的时空图注意力网络较传统的注意力机制能够提升运行效率. 虽然STGAMT较STGAMT(w/o IFE)消耗时间增加1.5%,但误差降低4.1%,而且预测耗时依旧满足要求. 不同模型耗时的对比说明本研究模型在保证准确度的同时提升了推理效率. ...
4
... 车辆时空特征信息的交互融合对车辆轨迹预测至关重要. 首先,利用多层感知机(multilayer perceptron,MLP)和GRU网络提取车辆运动特征. 其次,利用时间注意力网络捕捉不同时刻历史状态的重要信息,对车辆的时间维度轨迹信息进行加权处理. 最后,加入空间图注意力网络对车辆空间维度交互进行建模. 空间图注意力网络以车辆为节点,车辆之间的影响权重为边,弥补了关于车辆间相互影响的同质化表达缺陷[12 ,16 ] . ...
... RMSE for different models in 5-second forecast range
Tab.1 数据集 RMSE t f /sS-LSTM[16 ] CS-LSTM[15 ] S-GAN[14 ] PIP[18 ] STDAN[17 ] STGAMT(w/o IFE) STGAMT HighD 1 0.22 0.22 0.20 0.17 0.19 0.07 0.07 2 0.62 0.61 0.57 0.52 0.27 0.19 0.19 3 1.27 1.24 1.14 1.05 0.48 0.35 0.32 4 2.15 2.10 1.90 1.76 0.91 0.65 0.61 5 3.14 3.27 2.91 2.63 1.66 1.20 1.14 NGSIM 1 0.65 0.61 0.57 0.55 0.42 0.22 0.21 2 1.31 1.27 1.32 1.18 1.01 0.80 0.78 3 2.16 2.09 2.22 1.94 1.69 1.52 1.49 4 3.25 3.10 3.26 2.88 2.56 2.47 2.40 5 4.55 4.37 4.40 4.04 3.67 3.69 3.58
1)S-LSTM[16 ] :使用全连接的社交池化层构建基于LSTM的编码器-解码器结构. ...
... 1)S-LSTM[16 ] :使用全连接的社交池化层构建基于LSTM的编码器-解码器结构. ...
... Comparison of training time per epoch for models
Tab.2 模型名称 t e /sS-LSTM[16 ] 0.0157 CS-LSTM[15 ] 0.0174 S-GAN[14 ] 0.0283 PIP[18 ] 0.0185 STDAN[17 ] 0.0214 STGAMT(w/o IFE) 0.0137 STGAMT 0.0139
本研究模型STGAMT较5个经典模型的平均耗时减少32.8%,较同样使用注意力机制的STDAN模型的消耗时间减少35.0%,表明本研究的时空图注意力网络较传统的注意力机制能够提升运行效率. 虽然STGAMT较STGAMT(w/o IFE)消耗时间增加1.5%,但误差降低4.1%,而且预测耗时依旧满足要求. 不同模型耗时的对比说明本研究模型在保证准确度的同时提升了推理效率. ...
Intention-aware vehicle trajectory prediction based on spatial-temporal dynamic attention network for internet of vehicles
4
2022
... 实验在NVIDIA GeForce RTX 2080 Ti上进行,代码在深度学习框架PyTorch下实现. 为了验证本研究模型的可行性,便于同其他模型进行对比,采用与CS-LSTM[15 ] 和STDAN[17 ] 类似的实验策略及实验环境. 利用2种损失函数训练策略,首先迭代5次均方误差损失函数,再利用3次迭代负对数似然损失函数训练轨迹数据. 优化器为Adam,学习率为0.001,批次为128,特征嵌入网络的维度为32,GRU特征编码的维度为64,空图注意力网络的注意力头数设置为4,GRU特征输出的维度为128. ...
... RMSE for different models in 5-second forecast range
Tab.1 数据集 RMSE t f /sS-LSTM[16 ] CS-LSTM[15 ] S-GAN[14 ] PIP[18 ] STDAN[17 ] STGAMT(w/o IFE) STGAMT HighD 1 0.22 0.22 0.20 0.17 0.19 0.07 0.07 2 0.62 0.61 0.57 0.52 0.27 0.19 0.19 3 1.27 1.24 1.14 1.05 0.48 0.35 0.32 4 2.15 2.10 1.90 1.76 0.91 0.65 0.61 5 3.14 3.27 2.91 2.63 1.66 1.20 1.14 NGSIM 1 0.65 0.61 0.57 0.55 0.42 0.22 0.21 2 1.31 1.27 1.32 1.18 1.01 0.80 0.78 3 2.16 2.09 2.22 1.94 1.69 1.52 1.49 4 3.25 3.10 3.26 2.88 2.56 2.47 2.40 5 4.55 4.37 4.40 4.04 3.67 3.69 3.58
1)S-LSTM[16 ] :使用全连接的社交池化层构建基于LSTM的编码器-解码器结构. ...
... 5)STDAN[17 ] :该模型综合运用了LSTM和注意力机制,提出用于车辆轨迹预测的时空动态注意力网络. ...
... Comparison of training time per epoch for models
Tab.2 模型名称 t e /sS-LSTM[16 ] 0.0157 CS-LSTM[15 ] 0.0174 S-GAN[14 ] 0.0283 PIP[18 ] 0.0185 STDAN[17 ] 0.0214 STGAMT(w/o IFE) 0.0137 STGAMT 0.0139
本研究模型STGAMT较5个经典模型的平均耗时减少32.8%,较同样使用注意力机制的STDAN模型的消耗时间减少35.0%,表明本研究的时空图注意力网络较传统的注意力机制能够提升运行效率. 虽然STGAMT较STGAMT(w/o IFE)消耗时间增加1.5%,但误差降低4.1%,而且预测耗时依旧满足要求. 不同模型耗时的对比说明本研究模型在保证准确度的同时提升了推理效率. ...
3
... RMSE for different models in 5-second forecast range
Tab.1 数据集 RMSE t f /sS-LSTM[16 ] CS-LSTM[15 ] S-GAN[14 ] PIP[18 ] STDAN[17 ] STGAMT(w/o IFE) STGAMT HighD 1 0.22 0.22 0.20 0.17 0.19 0.07 0.07 2 0.62 0.61 0.57 0.52 0.27 0.19 0.19 3 1.27 1.24 1.14 1.05 0.48 0.35 0.32 4 2.15 2.10 1.90 1.76 0.91 0.65 0.61 5 3.14 3.27 2.91 2.63 1.66 1.20 1.14 NGSIM 1 0.65 0.61 0.57 0.55 0.42 0.22 0.21 2 1.31 1.27 1.32 1.18 1.01 0.80 0.78 3 2.16 2.09 2.22 1.94 1.69 1.52 1.49 4 3.25 3.10 3.26 2.88 2.56 2.47 2.40 5 4.55 4.37 4.40 4.04 3.67 3.69 3.58
1)S-LSTM[16 ] :使用全连接的社交池化层构建基于LSTM的编码器-解码器结构. ...
... 4)PiP[18 ] :该模型以目标车辆的多个候选轨迹为条件,将轨迹预测与目标车辆的规划相结合. ...
... Comparison of training time per epoch for models
Tab.2 模型名称 t e /sS-LSTM[16 ] 0.0157 CS-LSTM[15 ] 0.0174 S-GAN[14 ] 0.0283 PIP[18 ] 0.0185 STDAN[17 ] 0.0214 STGAMT(w/o IFE) 0.0137 STGAMT 0.0139
本研究模型STGAMT较5个经典模型的平均耗时减少32.8%,较同样使用注意力机制的STDAN模型的消耗时间减少35.0%,表明本研究的时空图注意力网络较传统的注意力机制能够提升运行效率. 虽然STGAMT较STGAMT(w/o IFE)消耗时间增加1.5%,但误差降低4.1%,而且预测耗时依旧满足要求. 不同模型耗时的对比说明本研究模型在保证准确度的同时提升了推理效率. ...
A critical evaluation of the next generation simulation (NGSIM) vehicle trajectory dataset
2
2017
... 理想的预测结果需要高质量数据集的支持,然而,NGSIM数据集中存在噪声[19 ] ,影响了时间依赖性建模、车辆间交互提取和多模态表示学习,并最终干扰了预测结果,这使得本研究模型在NGSIM上的性能提升低于在HighD上的. NGSIM数据集包含了畅通、较拥堵和重度拥堵3种场景[19 ] ,在复杂交通场景下,驾驶意图的异质性较大,对长时序预测条件严苛,在一定程度上影响了本研究长时序预测精度的提升. 虽然在NGSIM数据集上长时序预测精度提升程度小于短时序的,但性能分析说明,本研究模型的时空动态交互模块改进了预测的性能. ...
... [19 ],在复杂交通场景下,驾驶意图的异质性较大,对长时序预测条件严苛,在一定程度上影响了本研究长时序预测精度的提升. 虽然在NGSIM数据集上长时序预测精度提升程度小于短时序的,但性能分析说明,本研究模型的时空动态交互模块改进了预测的性能. ...