目前,常用的机器人高精度控制方法有自适应控制、滑模控制、反步控制等,但是大多是渐进稳定的. Dian等[5]针对线驱动柔性机器人,提出基于滑模控制器和线性扩张观测器的新型抗扰控制方法,但滑模控制器采用的是指数趋近律. Ayala-Carrillo等[6]针对气驱动连续体机器人的鲁棒跟踪控制问题,提出基于有限时间的滑模控制器,实现跟踪误差在有限时间内收敛. 针对自由漂浮空间机器人的任务空间跟踪控制问题,Jin等[7]采用固定时间稳定性理论,保证跟踪误差的收敛时间有界且独立于系统初始状态. 固定时间控制器的时间与参数关系复杂,Sánchez-Torres等[8]提出预定义时间稳定理论,稳定时间上界显含于系统,简化控制器设计.
基于以上研究,本文提出柔性空间机器人预定义时间自适应滑模控制算法. 主要创新点如下. 1)结合柔性机器人与空间机器人,基于常曲率假设和拉格朗日法,建立柔性空间机器人的动力学模型. 2)针对柔性空间机器人的关节轨迹跟踪问题,提出基于预定义时间稳定性理论的滑模控制算法,简化了控制器的设计. 3)针对柔性空间机器人的建模误差和外界干扰,引入RBF神经网络进行补偿,提高了机器人系统的自适应性能. 通过仿真验证了所提出的预定义时间滑模控制器的有效性和RBF神经网络的自适应性.
1. 柔性空间机器人的动力学建模
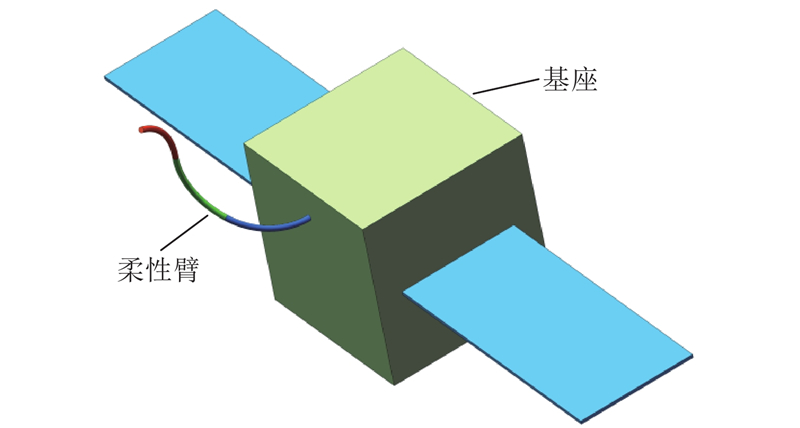
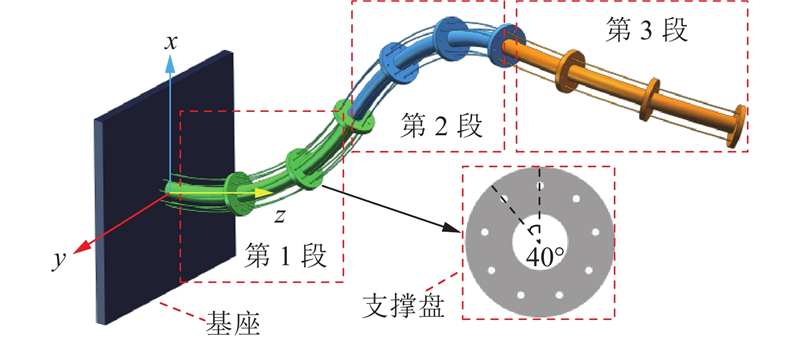
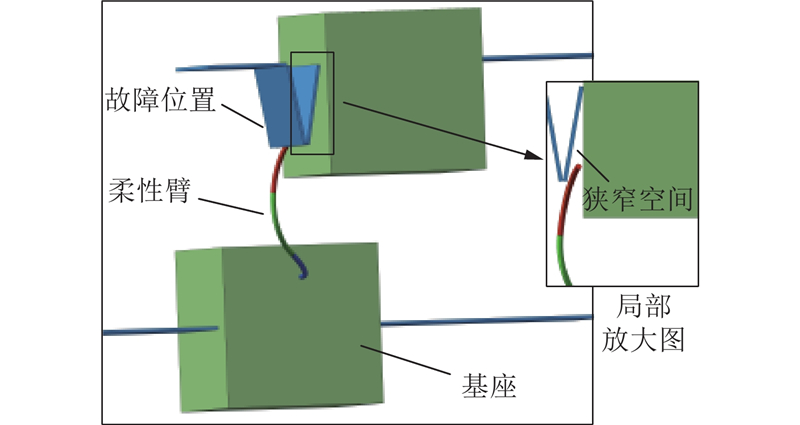
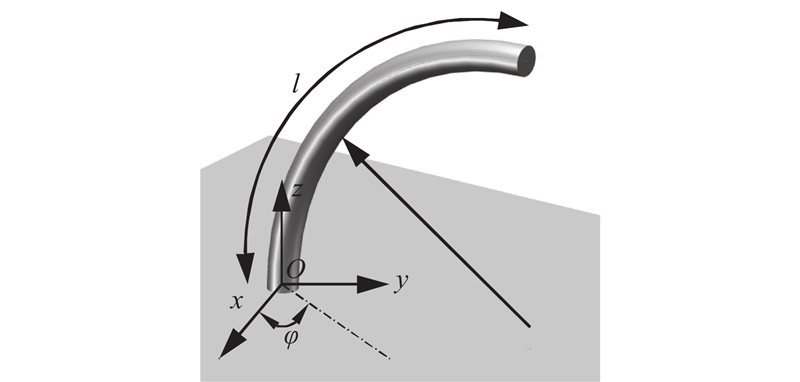
1.1. 柔性空间机器人的三维模型
图 1
图 2
图 3
1.2. 柔性机器人变形的描述
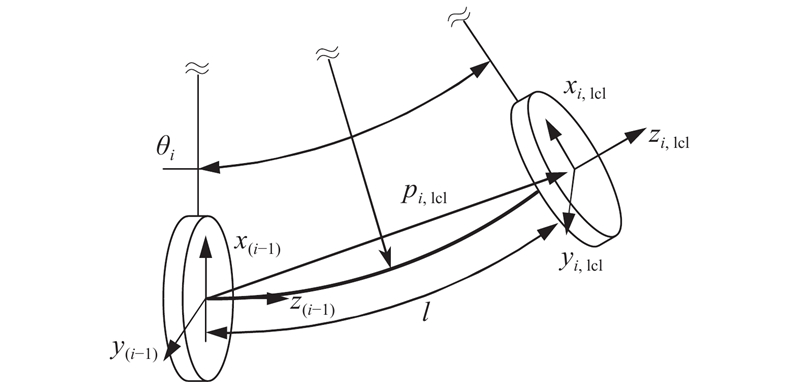
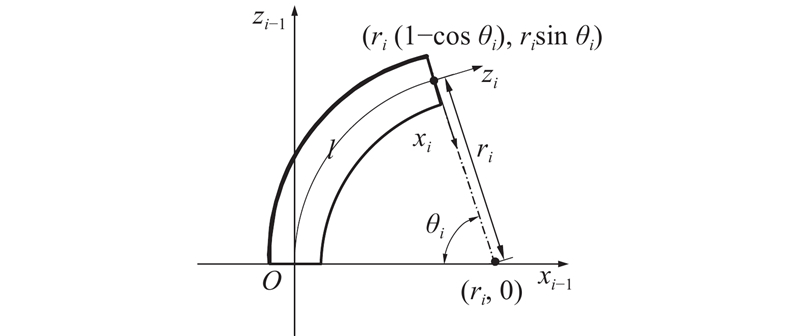
常用的柔性臂变形描述有常曲率法、有限元法、cosserat杆理论. 为了简化建模过程,将柔性机器人的控制作为研究重点,选择常曲率法作为柔性机器人的运动学建模基础. 根据常曲率假设可知,连续型的柔性机器人可以近似为一系列等曲率的子段.
图 4
定义旋转变换如下:
图 5
图 5
弯曲平面角
Fig.5
Bending plane angle
图 6
图 6 弯曲平面角为0时的坐标变换
Fig.6 Coordinate transformation when bending plane angle is 0
式中:下标
为了得到机械臂上每一点的位姿,提出使用弧长参数进行建模. 将机械臂的一个分段视为一段弧,定义弧长参数
当
姿态可以通过旋转变换矩阵表示为
线驱动连续体机械臂的运动学分析不仅包括上述关节空间(弯曲平面角、弯曲角)和工作空间(末端位姿)的映射关系,还包括驱动空间(绳索长度)和关节空间的映射关系,可见文献[17],不再详述.
1.3. 柔性空间机器人的动力学
定义如下符号:
由于在空间机器人在基座悬浮的状态下几乎不受外力,机器人系统的机械臂和基座位姿是相互耦合的,需要考虑整个系统的动量守恒. 系统的动量守恒方程可以表示为
式中:
系统总动能为
式中:
由于在太空环境下系统受到的重力势能等效为零,总势能只包含柔性杆的弹性势能,
式中:
动力学建模采用拉格朗日法建模,机器人系统的拉格朗日函数为
拉格朗日方程为
可得系统的运动方程为
式中:
化简得到
式中:
假设系统存在外部干扰,则动力学方程(13)可以修改为
式中:
对于柔性空间机器人这类复杂系统,难以获取模型的准确模型,但是可以得到机器人的名义模型. 考虑机器人的名义模型为
式中:
取状态变量
则系统为
式中:
2. 预定义时间滑模控制器设计
考虑如下的不确定动态系统:
式中:
定义1 若系统(18)是全局有限时间稳定的,且收敛时间上界与初始状态无关,则称系统为全局固定时间稳定的[19].
定义2 若系统(18)是全局固定时间稳定的,且收敛时间上界显含于系统函数中,则称系统为全局预定义时间稳定的[20].
系统(18)的预定义时间稳定的充分条件由以下引理给出.
引理1 如果存在径向无界的Lyapunov函数
则称该系统是预定义时间稳定的[21]. 式中:
式中:
针对式(17)描述的柔性空间机器人动力学模型,控制器设计的目的是使实际关节角
为了证明关节角误差能够在预定义时间内收敛,选取Lyapunov函数为
切换函数选择为
式中:
其中
该预定义时间滑模控制器对应的稳定时间分为以下2个阶段:第1个阶段为切换函数
滑动阶段:
对
根据引理1可知,
趋近阶段:
对
设控制量为
式中:
将式(27)代入式(26),可得
根据引理1可知,
综上可知,该系统为全局预定义时间稳定,收敛时间为
3. 基于RBF神经网络的预定义时间滑模控制器设计
在式(27)的控制量中,
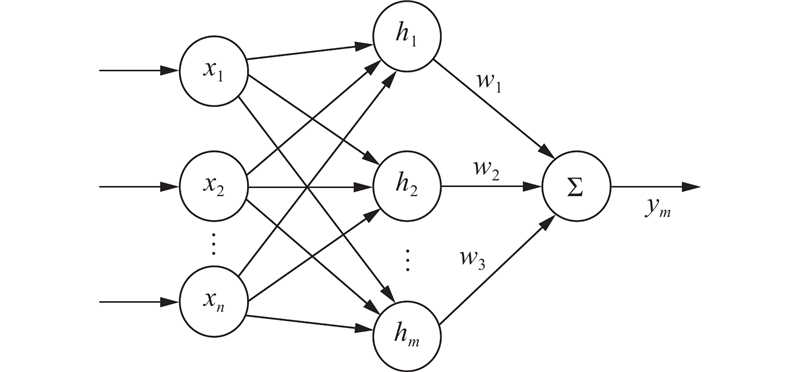
RBF神经网络是前向型神经网络,由于结构简单和非线性逼近能力较强,可以被应用于自适应非线性控制. 该网络的结构分为3层,如图7所示.
图 7
第1层为网络的输入层,
第2层为网络的隐藏层,激活函数采用径向基函数,输出为
式中:
第3层为网络的输出层,输出为
式中:
选择神经网络的输入为
式中:
式中:
选取Lyapunov函数为
式中:
由此,可以将自适应律设计为
则
由于RBF神经网络具有良好的逼近性能,误差
4. 仿真结果与分析
通过在SolidWorks软件中建立柔性空间机器人的三维模型,可以计算得到基座和连杆的形状、质量和转动惯量等模型参数. 柔性空间机器人的模型参数的测量值如表1所示.
表 1 柔性空间机器人的模型参数
Tab.1
| 参数 | 数值 | 说明 |
| 240 | 基座质量 | |
| 基座转动惯量 | ||
| 机械臂基座位置 | ||
| 中心杆密度 | ||
| 弹性模量 | ||
| 0.07 | 中心杆截面积 | |
| 0.45 | 中心杆长度 | |
| 中心杆惯性矩 | ||
| 0.117 | 圆盘质量 | |
| 圆盘转动惯量 |
4.1. 预定义时间控制器的性能
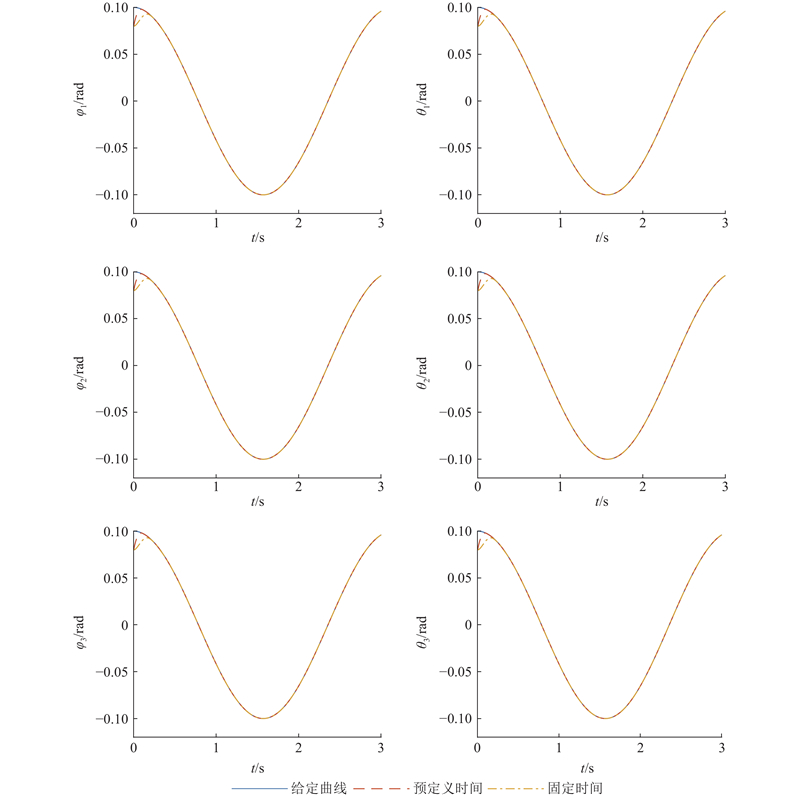
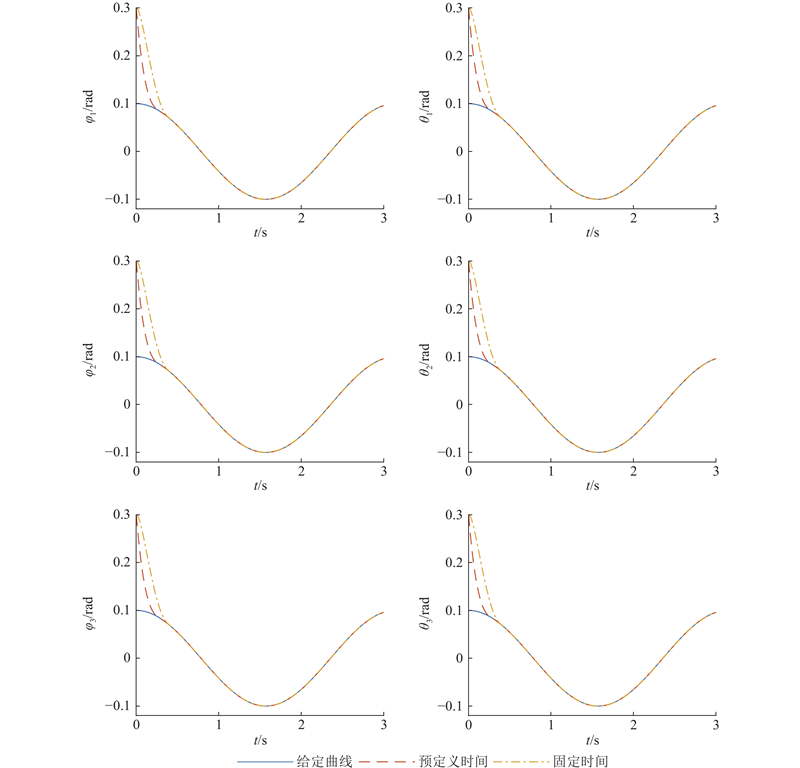
为了验证预定义时间控制器的性能,将其与文献[22]的固定时间控制器进行比较. 设柔性空间机器人各关节角的期望轨迹为
图 8
图 8
Fig.8
Angle tracking when
图 9
图 9
Fig.9
Angle tracking when
表 2
Tab.2
| 关节 | ||
| 0.099 | 0.357 | |
| 0.099 | 0.458 | |
| 0.099 | 0.357 | |
| 0.099 | 0.694 | |
| 0.099 | 0.851 | |
| 0.099 | 0.358 |
表 3
Tab.3
| 关节 | ||
| 0.259 | 0.392 | |
| 0.259 | 0.392 | |
| 0.259 | 0.392 | |
| 0.259 | 0.392 | |
| 0.259 | 0.761 | |
| 0.259 | 0.392 |
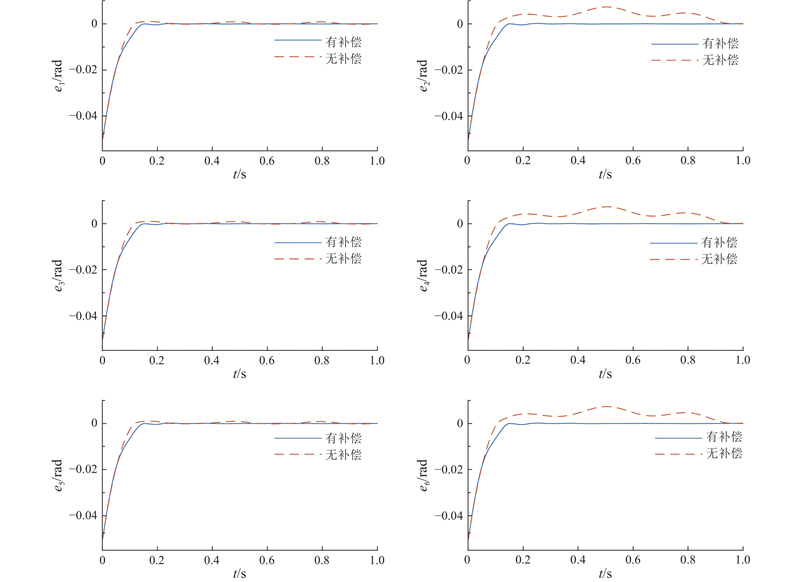
4.2. 神经网络的补偿性能
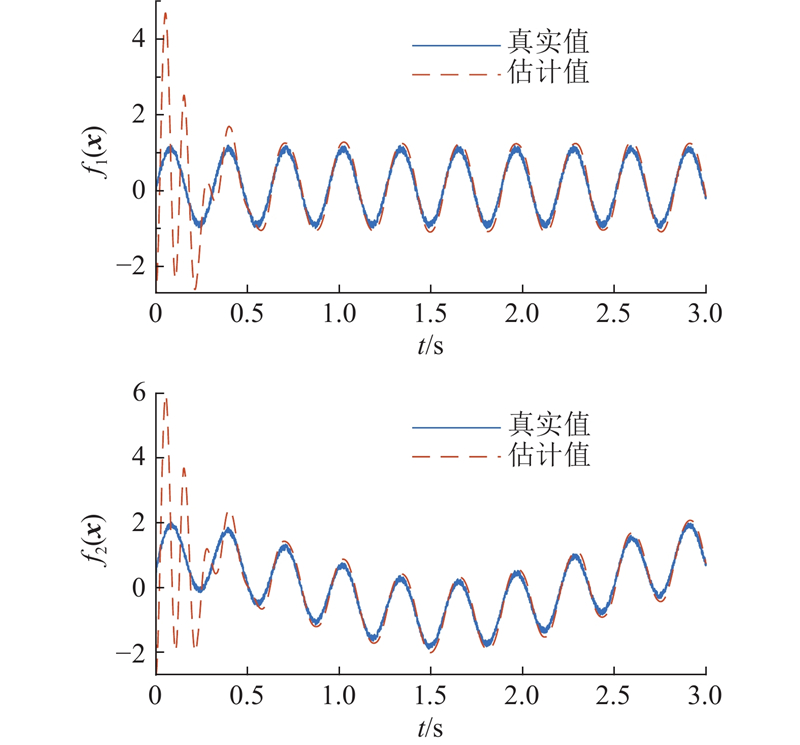
为了验证RBF神经网络的补偿性能,在预定义时间控制器有RBF神经网络补偿和无任何补偿的条件下,开展对比实验. 控制器参数
图 10
图 10 实际的干扰项和估计的干扰项
Fig.10 Actual disturbance term and estimated disturbance term
图 11
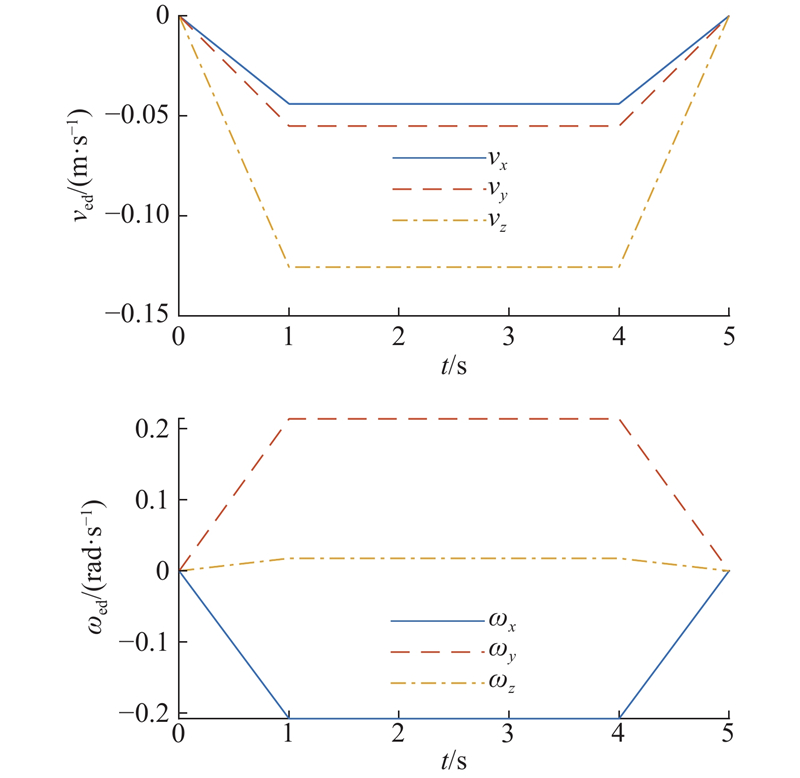
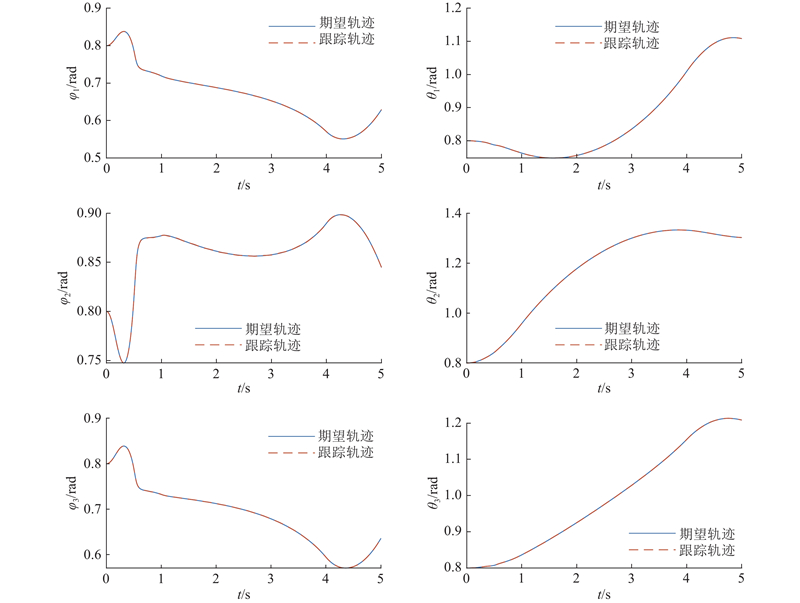
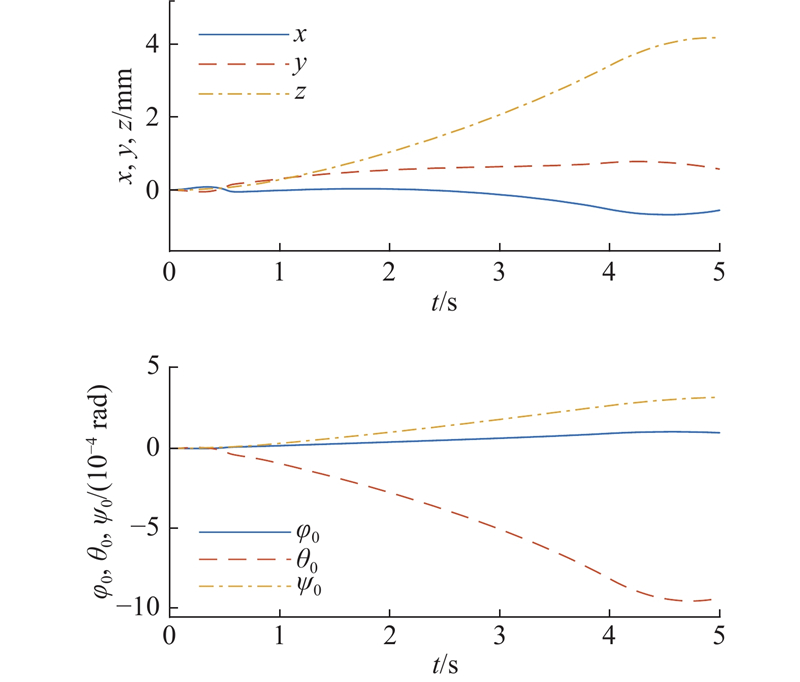
4.3. 轨迹规划与轨迹跟踪的联合仿真
针对提出的柔性空间机器人模型,为了验证轨迹跟踪的控制性能,将轨迹规划与轨迹跟踪进行联合仿真. 轨迹规划和轨迹跟踪时间均为5 s.
给定机器人基座的初始位姿为
图 12
式中:
柔性臂空间机器人的末端位姿误差反馈运动学模型可以表示为
式中:
综合式(6)、(38)和(39),可得位姿误差运动学的一般形式为
式中:
柔性空间机器人的关节速度可以规划为
式中:
图 13
图 14
5. 结 语
本文针对具有系统建模误差和外界干扰的柔性空间机器人轨迹跟踪问题,提出基于预定义时间的自适应滑模控制算法. 通过常曲率柔性杆假设、动量守恒方程和拉格朗日法,建立柔性空间机器人的动力学模型. 针对该模型,设计预定义时间收敛的滑模控制器. 针对系统的不确定项,采用RBF神经网络进行补偿,利用Lyapunov理论证明了系统误差可以在预定义时间内收敛. 通过在Matlab/Simulink上的数值仿真,证明了预定义时间控制方法能够在系统显含的预定时间内收敛,在收敛速度上优于固定时间控制. RBF神经网络可以较好地与预定义时间控制方法结合,补偿系统的不确定性. 在经过轨迹规划后,对关节角度进行轨迹跟踪控制,验证模型和控制器的有效性. 未来的工作将结合柔性空间机器人的实际应用进行进一步的研究.
参考文献
Space robot motion planning in the presence of nonconserved linear and angular momenta
[J].DOI:10.1007/s11044-020-09753-x [本文引用: 1]
Coordinated control of spacecraft's attitude and end-effector for space robots
[J].
Reinforcement learning in dual-arm trajectory planning for a free-floating space robot
[J].DOI:10.1016/j.ast.2019.105657 [本文引用: 1]
Progress, challenges, and prospects of soft robotics for space applications
[J].DOI:10.1002/aisy.202200071 [本文引用: 1]
A novel disturbance-rejection control framework for cable-driven continuum robots with improved state parameterizations
[J].DOI:10.1109/ACCESS.2022.3202934 [本文引用: 1]
Cascade control for robust tracking of continuum soft robots with finite-time convergence of pneumatic system
[J].
Observer-based fixed-time tracking control for space robots in task space
[J].DOI:10.1016/j.actaastro.2021.04.002 [本文引用: 1]
A class of predefined-time stable dynamical systems
[J].
Predefined-time predefined-bounded attitude tracking control for rigid spacecraft
[J].
Predefined-time control for free-floating space robots in task space
[J].DOI:10.1016/j.jfranklin.2021.09.030 [本文引用: 1]
Trajectory tracking for a dual-arm free-floating space robot with a class of general nonsingular predefined-time terminal sliding mode
[J].
A study on the design of error-based adaptive robust RBF neural network back-stepping controller for 2-DOF snake robot’s head
[J].DOI:10.1109/ACCESS.2023.3249346 [本文引用: 1]
Adaptive finite-time tracking control for output-constrained nonlinear systems with non-strict-feedback structure
[J].DOI:10.1002/acs.3099 [本文引用: 1]
Fixed-time adaptive neural tracking control for a class of uncertain nonlinear pure-feedback systems
[J].DOI:10.1109/ACCESS.2020.2972353 [本文引用: 1]
刚柔混合双臂空间机器人抓持-操作协同规划
[J].
Coordinated grasp and operation planning for hybrid rigid flexible dual arm space robot
[J].
Continuum robot dynamics utilizing the principle of virtual power
[J].
线驱动连续型机器人的运动学分析与仿真
[J].DOI:10.3901/JME.2010.19.001 [本文引用: 1]
Kinematic analysis and simulation for cable-driven continuum robot
[J].DOI:10.3901/JME.2010.19.001 [本文引用: 1]
基于模糊补偿的连续型空间机械臂预定时间控制
[J].
Predefined-time control of continuum space manipulator based on fuzzy compensation
[J].
An overview of finite/fixed-time control and its application in engineering systems
[J].DOI:10.1109/JAS.2022.105413 [本文引用: 1]
Predefined-time synchronization of chaotic systems with different dimensions and applications
[J].DOI:10.1016/j.chaos.2021.110988 [本文引用: 1]
Predefined-time attitude stabilization of receiver aircraft in aerial refueling
[J].
On SFTSM control with fixed‐time convergence
[J].DOI:10.1049/iet-cta.2016.1457 [本文引用: 1]
GA based adaptive singularity-robust path planning of space robot for on-orbit detection
[J].