Hudgins等[26 ] 提出最大允许时延是300 ms,因此本文设定$ w $ $ t $ $ n $ $ \alpha $ $ \beta $ [27 -28 ] .
[1]
BHAUMIK G, VERMA M, GOVIL M C, et al Hyfinet: hybrid feature attention network for hand gesture recognition
[J]. Multimedia Tools and Applications , 2023 , 82 (4 ): 4863 - 4882
DOI:10.1007/s11042-021-11623-3
[本文引用: 1]
[2]
都明宇, 鲍官军, 杨庆华, 等 基于改进支持向量机的人手动作模式识别方法
[J]. 浙江大学学报: 工学版 , 2018 , 52 (7 ): 1239 - 1246
[本文引用: 2]
DOU Mingyu, BAO Guanjun, YANG Qinghua, et al Novel method in pattern recognition of hand actions based on improved support vector machine
[J]. Journal of Zhejiang University: Engineering Science , 2018 , 52 (7 ): 1239 - 1246
[本文引用: 2]
[3]
赵翠莲, 徐浩宇, 罗林辉, 等 熵在不同等级偏瘫患者sEMG运动检测中的应用
[J]. 浙江大学学报: 工学版 , 2018 , 52 (4 ): 798 - 805
[本文引用: 1]
ZHAO Cuilian, XU Haoyu, LUO Linhui, et al SEMG activity detection of hemiplegic patients in different stages using entropy algorithms
[J]. Journal of Zhejiang University: Engineering Science , 2018 , 52 (4 ): 798 - 805
[本文引用: 1]
[4]
CHENG Y, LI G, YU M, et al Gesture recognition based on surface electromyography-feature image
[J]. Concurrency and Computation: Practice and Experience , 2021 , 33 (6 ): e6051
DOI:10.1002/cpe.6051
[本文引用: 2]
[5]
SUK H I, SIN B K, LEE S W Hand gesture recognition based on dynamic Bayesian network framework
[J]. Pattern Recognition , 2010 , 43 (9 ): 3059 - 3072
DOI:10.1016/j.patcog.2010.03.016
[本文引用: 1]
[6]
QI J, JIANG G, LI G, et al Intelligent human-computer interaction based on surface EMG gesture recognition
[J]. IEEE Access , 2019 , 7 : 61378 - 61387
DOI:10.1109/ACCESS.2019.2914728
[本文引用: 1]
[7]
BARGELLESI N, CARLETTI M, CENEDESE A, et al A random forest-based approach for hand gesture recognition with wireless wearable motion capture sensors
[J]. IFAC-PapersOnLine , 2019 , 52 (11 ): 128 - 133
DOI:10.1016/j.ifacol.2019.09.129
[本文引用: 1]
[8]
CHEN H, ZHANG Y, LI G, et al Surface electromyography feature extraction via convolutional neural network
[J]. International Journal of Machine Learning and Cybernetics , 2020 , 11 (1 ): 185 - 196
DOI:10.1007/s13042-019-00966-x
[本文引用: 5]
[9]
WANG H, ZHANG Y, LIU C, et al sEMG based hand gesture recognition with deformable convolutional network
[J]. International Journal of Machine Learning and Cybernetics , 2022 , 13 (6 ): 1729 - 1738
DOI:10.1007/s13042-021-01482-7
[本文引用: 1]
[10]
HU Y, WONG Y, WEI W, et al A novel attention-based hybrid CNN-RNN architecture for sEMG-based gesture recognition
[J]. PloS one , 2018 , 13 (10 ): e0206049
DOI:10.1371/journal.pone.0206049
[本文引用: 2]
[11]
TSINGANOS P, CORNELIS B, CORNELIS J, et al. Improved gesture recognition based on sEMG signals and TCN [C]// IEEE International Conference on Acoustics, Speech and Signal Processing . Brighton: IEEE, 2019: 1169-1173.
[本文引用: 1]
[12]
WANG W, YOU W, WANG Z, et al Feature fusion-based improved capsule network for sEMG signal recognition
[J]. Computational Intelligence and Neuroscience , 2022 , (1 ): 7603319
[本文引用: 1]
[13]
KUMAR V, MINZ S Feature selection: a literature review
[J]. SmartCR , 2014 , 4 (3 ): 211 - 229
[本文引用: 1]
[14]
CHEN G, WANG W, WANG Z, et al Two-dimensional discrete feature based spatial attention CapsNet for sEMG signal recognition
[J]. Applied Intelligence , 2020 , 50 : 3503 - 3520
DOI:10.1007/s10489-020-01725-0
[本文引用: 4]
[16]
KRIZHEVSKY A, SUTSKEVER I, HINTON G E ImageNet classification with deep convolutional neural networks
[J]. Communications of the ACM , 2017 , 60 (6 ): 84 - 90
DOI:10.1145/3065386
[本文引用: 1]
[17]
O'SHEA K, NASH R. An introduction to convolutional neural networks [EB/OL]. [2023-09-01]. https://arxiv.org/abs/1511.08458.
[本文引用: 1]
[18]
SHERSTINSKY A Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network
[J]. Physica D: Nonlinear Phenomena , 2020 , 404 : 132306
DOI:10.1016/j.physd.2019.132306
[本文引用: 1]
[19]
YU Y, SI X, HU C, et al A review of recurrent neural networks: LSTM cells and network architectures
[J]. Neural Computation , 2019 , 31 (7 ): 1235 - 1270
DOI:10.1162/neco_a_01199
[本文引用: 1]
[20]
SHEWALKAR A, NYAVANANDI D, LUDWIG S A Performance evaluation of deep neural networks applied to speech recognition: RNN, LSTM and GRU
[J]. Journal of Artificial Intelligence and Soft Computing Research , 2019 , 9 (4 ): 235 - 245
DOI:10.2478/jaiscr-2019-0006
[本文引用: 1]
[21]
CHO K, VAN M B, GULCEHRE C, et al. Learning phrase representations using RNN encoder-decoder for statistical machine translation [EB/OL]. [2023-09-01]. https://arxiv.org/abs/1406.1078.
[本文引用: 1]
[22]
BERGLUND M, RAIKO T, HONKALA M, et al. Bidirectional recurrent neural networks as generative models [EB/OL]. [2023-09-01]. https://proceedings.neurips.cc/paper/2015/hash/c75b6f114c23a4d7ea11331e7c00e73c-Abstract.html.
[本文引用: 1]
[23]
LI X, WANG W, HU X, et al. Selective kernel networks [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Long Beach: IEEE, 2019: 510-519.
[本文引用: 1]
[24]
ATZORI M, GIJSBERTS A, HEYNEN S, et al. Building the Ninapro database: a resource for the biorobotics community [C]// 4th IEEE RAS and EMBS International Conference on Biomedical Robotics and Biomechatronics . Rome: IEEE, 2012: 1258-1265.
[本文引用: 1]
[25]
NAZMI N, RAHMAN M A, YAMAMOTO S, et al Assessment on stationarity of EMG signals with different windows size during isotonic contractions
[J]. Applied Sciences , 2017 , 7 (10 ): 1050
DOI:10.3390/app7101050
[本文引用: 1]
[26]
HUDGINS B, PARKER P, SCOTT R N A new strategy for multifunction myoelectric control
[J]. IEEE Transactions on Biomedical Engineering , 1993 , 40 (1 ): 82 - 94
DOI:10.1109/10.204774
[本文引用: 1]
[27]
PHINYOMARK A, PHUKPATTARANONT P, LIMSAKUL C Feature reduction and selection for EMG signal classification
[J]. Expert Systems with Applications , 2012 , 39 (8 ): 7420 - 7431
DOI:10.1016/j.eswa.2012.01.102
[本文引用: 1]
[28]
ABBASPOUR S, LINDEN M, GHOLAMHOSSEINI H, et al Evaluation of surface EMG-based recognition algorithms for decoding hand movements
[J]. Medical and Biological Engineering and Computing , 2020 , 58 : 83 - 100
DOI:10.1007/s11517-019-02073-z
[本文引用: 1]
[29]
ZI L I, ZA X G, BI Z, et al Review of sEMG-based motion intent recognition methods in non-ideal conditions
[J]. Acta Automatica Sinica , 2021 , 47 (5 ): 955 - 969
[本文引用: 1]
[30]
PAUL Y, GOYAL V, JASWAL R A. Comparative analysis between SVM & KNN classifier for EMG signal classification on elementary time domain features [C]// 4th International Conference on Signal Processing, Computing and Control . Solan: IEEE, 2017: 169-175.
[本文引用: 3]
[31]
NARAYAN Y Comparative analysis of SVM and Naive Bayes classifier for the SEMG signal classification
[J]. Materials Today: Proceedings , 2021 , 37 : 3241 - 3245
DOI:10.1016/j.matpr.2020.09.093
[本文引用: 3]
[32]
HE K, ZHANG X, REN S, et al. Deep residual learning for image recognition [C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition . [S. l. ]: IEEE, 2016: 770-778.
[本文引用: 3]
[33]
ZHAO R, WANG D, YAN R, et al Machine health monitoring using local feature-based gated recurrent unit networks
[J]. IEEE Transactions on Industrial Electronics , 2017 , 65 (2 ): 1539 - 1548
[本文引用: 3]
[34]
GRAVES A, SCHMIDHUBER J Framewise phoneme classification with bidirectional LSTM and other neural network architectures
[J]. Neural Networks , 2005 , 18 (5/6 ): 602 - 610
[本文引用: 3]
[35]
SHEN S, WANG X, MAO F, et al Movements classification through sEMG with convolutional vision transformer and stacking ensemble learning
[J]. IEEE Sensors Journal , 2022 , 22 (13 ): 13318 - 13325
DOI:10.1109/JSEN.2022.3179535
[本文引用: 3]
[36]
WU Y, ZHENG B, ZHAO Y. Dynamic gesture recognition based on LSTM-CNN [C]// Chinese Automation Congress . Xi’an: IEEE, 2018: 2446-2450.
[本文引用: 3]
[37]
WEI W, DAI Q, WONG Y, et al Surface-electromyography-based gesture recognition by multi-view deep learning
[J]. IEEE Transactions on Biomedical Engineering , 2019 , 66 (10 ): 2964 - 2973
DOI:10.1109/TBME.2019.2899222
[本文引用: 1]
Hyfinet: hybrid feature attention network for hand gesture recognition
1
2023
... 肌电信号是肌肉收缩产生的皮下运动动作电位的总和,它代表运动单位动作电位在空间和时间上的叠加[1 ] . 目前人体仿生假肢的主要控制信号来源于表面肌电信号(sEMG)[2 ] . sEMG蕴含丰富的生物信息,且信号的采集通常是无创的,在康复医学和临床医学领域上常被当作仿生假肢的控制信号源,被广泛应用于人机交互领域[3 ] . ...
基于改进支持向量机的人手动作模式识别方法
2
2018
... 肌电信号是肌肉收缩产生的皮下运动动作电位的总和,它代表运动单位动作电位在空间和时间上的叠加[1 ] . 目前人体仿生假肢的主要控制信号来源于表面肌电信号(sEMG)[2 ] . sEMG蕴含丰富的生物信息,且信号的采集通常是无创的,在康复医学和临床医学领域上常被当作仿生假肢的控制信号源,被广泛应用于人机交互领域[3 ] . ...
... sEMG是较微弱的生物电信号[2 ] ,能够有效地提取肌电信号特征,是目前肌电领域的研究热点. 传统的特征提取方法大多以一个或多个统计值来表示sEMG所隐含的信息,可能会丢失更深层的特征信息[4 ] . 因为受试者的个体差异和电极偏移诸多外界因素的影响,常用的机器学习方法如贝叶斯分类法[5 ] 、线性判别分析法[6 ] 、随机森林[7 ] 等,它们的分类准确率受到较大的影响. ...
基于改进支持向量机的人手动作模式识别方法
2
2018
... 肌电信号是肌肉收缩产生的皮下运动动作电位的总和,它代表运动单位动作电位在空间和时间上的叠加[1 ] . 目前人体仿生假肢的主要控制信号来源于表面肌电信号(sEMG)[2 ] . sEMG蕴含丰富的生物信息,且信号的采集通常是无创的,在康复医学和临床医学领域上常被当作仿生假肢的控制信号源,被广泛应用于人机交互领域[3 ] . ...
... sEMG是较微弱的生物电信号[2 ] ,能够有效地提取肌电信号特征,是目前肌电领域的研究热点. 传统的特征提取方法大多以一个或多个统计值来表示sEMG所隐含的信息,可能会丢失更深层的特征信息[4 ] . 因为受试者的个体差异和电极偏移诸多外界因素的影响,常用的机器学习方法如贝叶斯分类法[5 ] 、线性判别分析法[6 ] 、随机森林[7 ] 等,它们的分类准确率受到较大的影响. ...
熵在不同等级偏瘫患者sEMG运动检测中的应用
1
2018
... 肌电信号是肌肉收缩产生的皮下运动动作电位的总和,它代表运动单位动作电位在空间和时间上的叠加[1 ] . 目前人体仿生假肢的主要控制信号来源于表面肌电信号(sEMG)[2 ] . sEMG蕴含丰富的生物信息,且信号的采集通常是无创的,在康复医学和临床医学领域上常被当作仿生假肢的控制信号源,被广泛应用于人机交互领域[3 ] . ...
熵在不同等级偏瘫患者sEMG运动检测中的应用
1
2018
... 肌电信号是肌肉收缩产生的皮下运动动作电位的总和,它代表运动单位动作电位在空间和时间上的叠加[1 ] . 目前人体仿生假肢的主要控制信号来源于表面肌电信号(sEMG)[2 ] . sEMG蕴含丰富的生物信息,且信号的采集通常是无创的,在康复医学和临床医学领域上常被当作仿生假肢的控制信号源,被广泛应用于人机交互领域[3 ] . ...
Gesture recognition based on surface electromyography-feature image
2
2021
... sEMG是较微弱的生物电信号[2 ] ,能够有效地提取肌电信号特征,是目前肌电领域的研究热点. 传统的特征提取方法大多以一个或多个统计值来表示sEMG所隐含的信息,可能会丢失更深层的特征信息[4 ] . 因为受试者的个体差异和电极偏移诸多外界因素的影响,常用的机器学习方法如贝叶斯分类法[5 ] 、线性判别分析法[6 ] 、随机森林[7 ] 等,它们的分类准确率受到较大的影响. ...
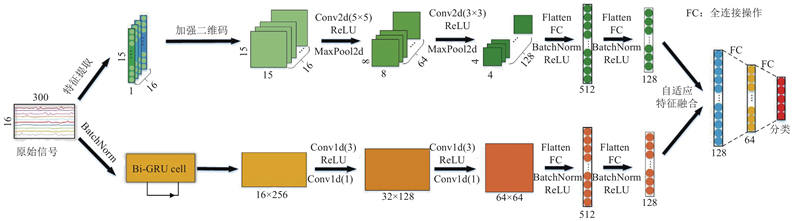
... 近年来,学者通常将提取原始肌电信号所得到的一维离散特征转换为高维特征图后,送入深度学习网络进行训练[12 ] . 现有的深度学习网络模型如CNN侧重捕捉肌电信号的空间信息,但忽视了肌电信号本质上是一连串时间序列数据,可能会忽视某些关键性特征[4 ] . 本文提出ETDTBN框架,整体结构如图1 所示. ...
Hand gesture recognition based on dynamic Bayesian network framework
1
2010
... sEMG是较微弱的生物电信号[2 ] ,能够有效地提取肌电信号特征,是目前肌电领域的研究热点. 传统的特征提取方法大多以一个或多个统计值来表示sEMG所隐含的信息,可能会丢失更深层的特征信息[4 ] . 因为受试者的个体差异和电极偏移诸多外界因素的影响,常用的机器学习方法如贝叶斯分类法[5 ] 、线性判别分析法[6 ] 、随机森林[7 ] 等,它们的分类准确率受到较大的影响. ...
Intelligent human-computer interaction based on surface EMG gesture recognition
1
2019
... sEMG是较微弱的生物电信号[2 ] ,能够有效地提取肌电信号特征,是目前肌电领域的研究热点. 传统的特征提取方法大多以一个或多个统计值来表示sEMG所隐含的信息,可能会丢失更深层的特征信息[4 ] . 因为受试者的个体差异和电极偏移诸多外界因素的影响,常用的机器学习方法如贝叶斯分类法[5 ] 、线性判别分析法[6 ] 、随机森林[7 ] 等,它们的分类准确率受到较大的影响. ...
A random forest-based approach for hand gesture recognition with wireless wearable motion capture sensors
1
2019
... sEMG是较微弱的生物电信号[2 ] ,能够有效地提取肌电信号特征,是目前肌电领域的研究热点. 传统的特征提取方法大多以一个或多个统计值来表示sEMG所隐含的信息,可能会丢失更深层的特征信息[4 ] . 因为受试者的个体差异和电极偏移诸多外界因素的影响,常用的机器学习方法如贝叶斯分类法[5 ] 、线性判别分析法[6 ] 、随机森林[7 ] 等,它们的分类准确率受到较大的影响. ...
Surface electromyography feature extraction via convolutional neural network
5
2020
... 近年来,不少学者将深度学习算法引入肌电手势识别中,取得了一定的效果. Chen等[8 ] 提出基于卷积神经网络(CNN)的特征提取方法,与传统特征相结合,提高手势识别的精度. Wang等[9 ] 提出结合可变形卷积层获得的高维特征映射与传统卷积层得到的低维特征映射,放入分类层分类,有效提高了手势识别的准确率. Hu等[10 ] 提出基于传统特征向量的新sEMG图像表示方法,能够挖掘肌电信号多个通道之间的隐式相关性. Tsinganos等[11 ] 提出使用时间卷积网络(TCN)来处理sEMG的问题,提高了识别准确率,但在实时性试验中表现欠佳,说明TCN无法满足实时性要求较高的手势识别系统. ...
... Recognition effect of each method under electrode displacement
Tab.2 方法 P c /%P o /%HC HO RF WE WF KNN+FE[30 ] 28.21±0.00 9.23±0.00 94.90±0.00 100±0.00 100±0.00 66.67±0.00 SVM+FE[31 ] 42.64±0.00 18.97±0.00 87.82±0.00 100±0.00 100±0.00 70.49±0.00 CNN[8 ] 90.72±6.97 13.42±7.82 23.21±10.15 96.79±2.58 96.75±5.29 64.18±2.73 CNN+FE 29.89±4.24 33.91±16.26 95.01±3.60 98.90±1.31 91.58±10.66 70.87±2.74 CNN+FE+ETD 85.56±4.44 40.33±13.50 75.20±8.05 98.85±1.18 86.18±5.24 78.24±2.26 RESNET+FE[32 ] 31.09±3.94 35.17±10.96 90.78±4.88 98.92±1.29 92.22±3.26 70.78±2.66 Bi-GRU[33 ] 84.10±8.19 5.41±5.09 72.67±10.26 100±0.00 99.34±1.09 72.04±2.35 LSTM[34 ] 73.64±11.84 4.33±1.99 71.13±18.33 100±0.00 99.40±1.02 70.88±3.55 TRANSFORMER[35 ] 80.64±5.84 20.15±3.53 66.17±8.62 98.55±1.38 89.14±2.19 66.14±3.25 LCNN[36 ] 93.13±2.98 12.51±3.53 81.03±6.54 98.26±0.52 91.08±4.90 76.38±0.94 TDACAPS[14 ] 97.59±2.62 74.87±15.71 95.18±4.42 98.56±1.82 55.39±16.87 84.77±0.82 ETDTBN 99.80±0.41 66.36±6.90 69.85±7.44 100±0.00 99.85±0.36 86.95±1.64
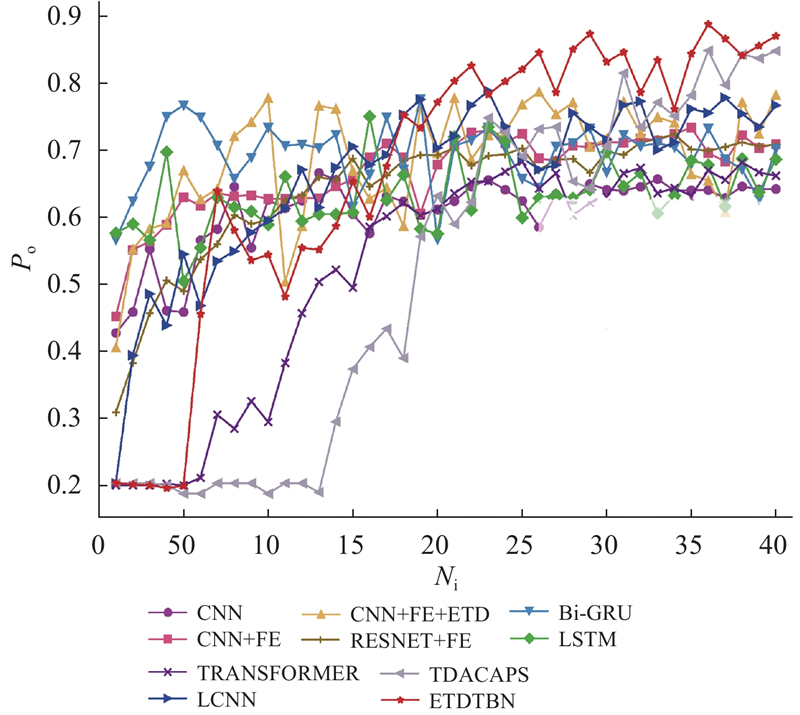
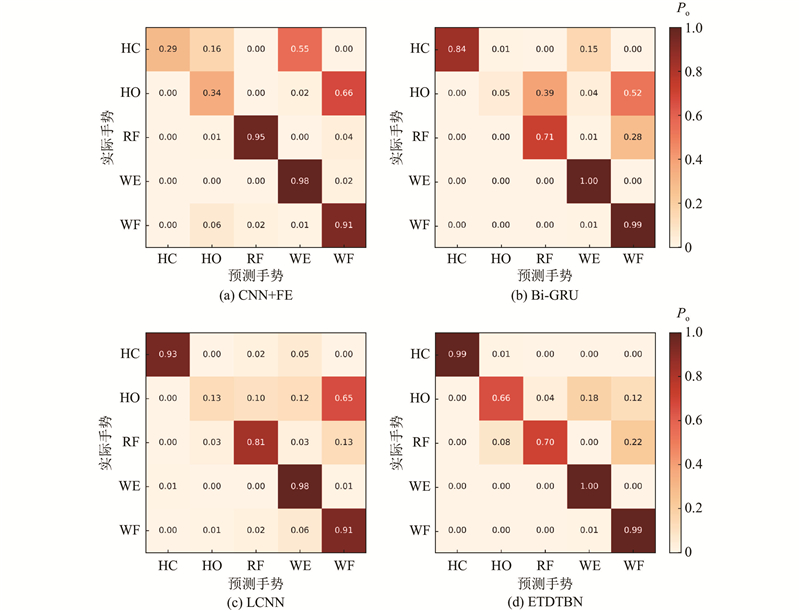
以KNN和SVM为代表的传统机器学习模型在动作WE和WF上的识别效果最好,均达到了100%的识别率,但对于其他手势动作的识别效果不理想. Bi-GRU的总体准确率略高于LSTM和TRANSFORMER,且Bi-GRU在模型结构上更简单,训练参数与时间更少,故选用Bi-GRU作为网络提取原信号时间特征的部分. 将提出的加强二维化方法用于CNN模型,与CNN+FE和RESNET+FE模型相比,整体识别率分别提高了7.37%和7.46%,在动作HO的识别上效果有所提升,说明利用该方法能够挖掘出HO的部分特性. 与LCNN相比,ETDTBN在保持动作HC、WE和WF接近100%识别率的情况下,对手势HO的分类准确率提高了53.85%,且该模型在12种方法中的总体识别率最高,达到86.95%,说明利用提出的方法能够有效地识别肌电信号. ...
... Recognition accuracy of each method under different subject
Tab.3 方法 P c /%P o /%HC HO RF WE WF KNN+FE[30 ] 97.18±0.00 72.99±0.00 47.95±0.00 93.50±0.00 42.14±0.00 70.75±0.00 SVM+FE[31 ] 64.27±0.00 86.24±0.00 51.71±0.00 100.00±0.00 52.99±0.00 71.04±0.00 CNN[8 ] 87.35±3.45 66.63±0.58 58.44±2.09 98.94±0.65 40.85±1.05 70.49±0.86 CNN+FE 71.99±4.16 90.51±1.85 80.87±7.59 99.82±0.49 31.39±7.51 75.06±0.18 CNN+FE+ETD 82.63±2.37 80.13±3.88 82.22±6.97 99.25±0.78 33.68±8.55 77.57±0.78 RESNET+FE[32 ] 73.79±3.96 85.22±2.78 81.17±6.19 99.22±0.65 32.11±6.95 74.96±0.26 Bi-GRU[33 ] 82.06±6.71 66.26±7.42 37.35±3.84 94.65±2.52 63.98±5.02 68.93±0.38 LSTM[34 ] 78.79±6.81 60.85±5.56 40.32±3.96 99.27±0.72 54.03±6.77 67.08±1.11 TRANSFORMER[35 ] 83.09±2.81 59.05±6.56 33.22±3.88 97.57±0.92 55.13±6.44 65.33±1.08 LCNN[36 ] 95.95±2.11 80.78±3.46 62.25±5.33 99.69±0.15 46.95±3.16 77.26±0.53 TDACAPS[14 ] 98.25±3.89 84.98±7.12 82.48±5.96 98.24±0.62 44.75±5.50 81.90±1.09 ETDTBN 99.75±0.15 75.51±1.85 95.27±2.54 99.93±0.05 50.21±0.45 84.15±0.41
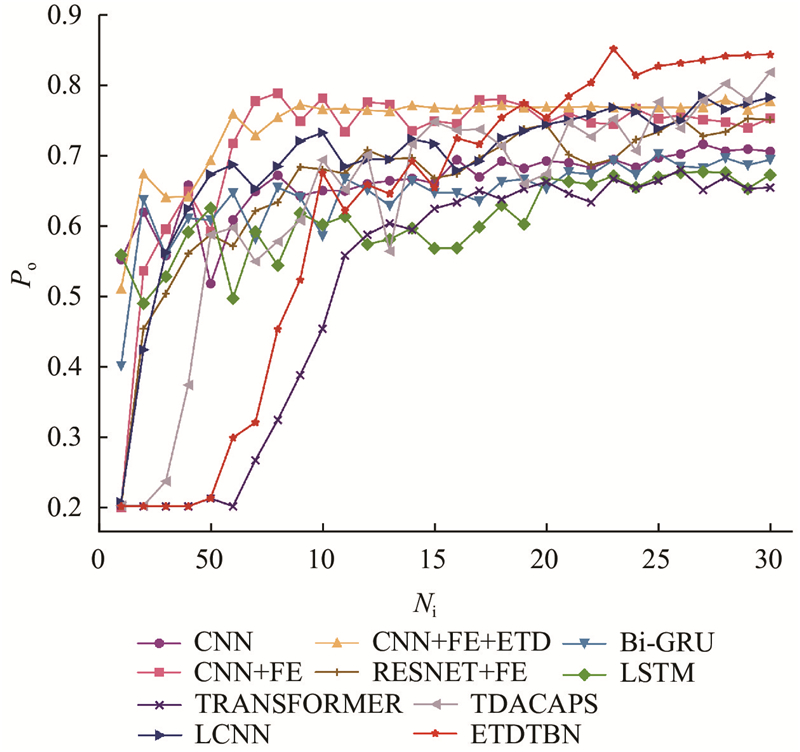
从表3 可以看出,当识别不同受试者的sEMG时,利用本实验的12种方法,能够较好地识别动作WE,但对动作WF的分类效果不理想. CNN模型通过加强二维化方法处理后,提升了总体准确率,对于除WF外的其他手势,均达到了大于80%的准确率. 以Bi-GRU和LSTM为代表的RNN在本实验中表现欠佳,但在动作WF的识别上优于其他模型. 与LCNN模型相比,ETDTBN模型的总体分类准确率提高了6.89%,ETDTBN模型是所有方法中效果最优的,总识别率为84.15%. 本文提出的方法对动作HC、RF、WE的识别效果均达到最佳,HO与WF的识别率虽然没有达到良好的预期,但高于大部分方法. ...
... Computational resource analysis for all methods
Tab.5 方法 N p /106 C /MBt e /st p /st r /msKNN+FE[30 ] — — 0.78±0.01 86.86±1.22 0.020±0.001 SVM+FE[31 ] — — 0.48±0.01 77.06±1.62 0.030±0.001 CNN[8 ] 4.98 162.73 22.65±0.98 148.61±3.38 0.078±0.003 CNN+FE 0.76 117.30 14.13±0.46 101.32±2.11 0.066±0.002 CNN+FE+ETD 1.15 184.48 20.19±0.65 153.51±3.65 0.086±0.002 RESNET+FE[32 ] 0.55 336.88 21.96±0.52 147.53±4.06 0.071±0.002 Bi-GRU[33 ] 1.41 118.10 16.76±0.50 160.49±2.98 0.078±0.002 LSTM[34 ] 1.52 146.35 17.14±0.59 168.25±3.16 0.082±0.002 TRANSFORMER[35 ] 2.49 335.68 24.16±0.66 187.23±4.56 0.079±0.002 LCNN[36 ] 1.77 533.50 21.06±0.62 180.85±4.29 0.082±0.003 TDACAPS[14 ] 0.87 741.38 216.45±6.16 1978.12 ±14.181.047±0.030 ETDTBN 3.73 321.41 17.85±0.48 156.28±3.99 0.076±0.002
从表6 可知,ETDTBN模型在3个NinaPro数据集中均取得了最高的识别准确率,在包含10个受试者数据中的NinaPro DB4数据集上,与其他算法相比,模型提升效果最明显. 可知,ETDTBN模型在手势分类问题上具备较好的泛化性和鲁棒性. ...
... Recognition effectiveness of each method on public dataset
Tab.6 方法 P o /%ChenNet[8 ] 68.23±2.07 71.74±3.67 67.25±4.49 HuNet[10 ] 81.18±5.69 82.21±5.69 69.52±3.94 WeiNet[37 ] 82.06±3.47 80.72±4.97 53.27±5.77 ETDTBN 82.59±4.46 83.01±3.42 77.16±3.98
4. 结 语 为了充分提取sEMG的有效特征,提高对相似手势的识别准确率,本文提出的ETDTBN模型利用加强二维化方法,将一维离散特征通过特征组合的形式构成二维规则特征图,加强了不同特征之间的联系,解决了原离散特征二维化方法生成的二维特征关系图参数重复冗余、特征信息稀疏的问题. 利用CNN在图像空间数据特征上的泛化能力,结合Bi-GRU网络善于提取信号时序特征的优势,利用2种网络同时挖掘sEMG信号的空间特征与时间特征. 利用SAFF策略对不同分支进行融合,组成时空特征,这样包含的信息更加全面,更有利于后续的分类. ...
sEMG based hand gesture recognition with deformable convolutional network
1
2022
... 近年来,不少学者将深度学习算法引入肌电手势识别中,取得了一定的效果. Chen等[8 ] 提出基于卷积神经网络(CNN)的特征提取方法,与传统特征相结合,提高手势识别的精度. Wang等[9 ] 提出结合可变形卷积层获得的高维特征映射与传统卷积层得到的低维特征映射,放入分类层分类,有效提高了手势识别的准确率. Hu等[10 ] 提出基于传统特征向量的新sEMG图像表示方法,能够挖掘肌电信号多个通道之间的隐式相关性. Tsinganos等[11 ] 提出使用时间卷积网络(TCN)来处理sEMG的问题,提高了识别准确率,但在实时性试验中表现欠佳,说明TCN无法满足实时性要求较高的手势识别系统. ...
A novel attention-based hybrid CNN-RNN architecture for sEMG-based gesture recognition
2
2018
... 近年来,不少学者将深度学习算法引入肌电手势识别中,取得了一定的效果. Chen等[8 ] 提出基于卷积神经网络(CNN)的特征提取方法,与传统特征相结合,提高手势识别的精度. Wang等[9 ] 提出结合可变形卷积层获得的高维特征映射与传统卷积层得到的低维特征映射,放入分类层分类,有效提高了手势识别的准确率. Hu等[10 ] 提出基于传统特征向量的新sEMG图像表示方法,能够挖掘肌电信号多个通道之间的隐式相关性. Tsinganos等[11 ] 提出使用时间卷积网络(TCN)来处理sEMG的问题,提高了识别准确率,但在实时性试验中表现欠佳,说明TCN无法满足实时性要求较高的手势识别系统. ...
... Recognition effectiveness of each method on public dataset
Tab.6 方法 P o /%ChenNet[8 ] 68.23±2.07 71.74±3.67 67.25±4.49 HuNet[10 ] 81.18±5.69 82.21±5.69 69.52±3.94 WeiNet[37 ] 82.06±3.47 80.72±4.97 53.27±5.77 ETDTBN 82.59±4.46 83.01±3.42 77.16±3.98
4. 结 语 为了充分提取sEMG的有效特征,提高对相似手势的识别准确率,本文提出的ETDTBN模型利用加强二维化方法,将一维离散特征通过特征组合的形式构成二维规则特征图,加强了不同特征之间的联系,解决了原离散特征二维化方法生成的二维特征关系图参数重复冗余、特征信息稀疏的问题. 利用CNN在图像空间数据特征上的泛化能力,结合Bi-GRU网络善于提取信号时序特征的优势,利用2种网络同时挖掘sEMG信号的空间特征与时间特征. 利用SAFF策略对不同分支进行融合,组成时空特征,这样包含的信息更加全面,更有利于后续的分类. ...
1
... 近年来,不少学者将深度学习算法引入肌电手势识别中,取得了一定的效果. Chen等[8 ] 提出基于卷积神经网络(CNN)的特征提取方法,与传统特征相结合,提高手势识别的精度. Wang等[9 ] 提出结合可变形卷积层获得的高维特征映射与传统卷积层得到的低维特征映射,放入分类层分类,有效提高了手势识别的准确率. Hu等[10 ] 提出基于传统特征向量的新sEMG图像表示方法,能够挖掘肌电信号多个通道之间的隐式相关性. Tsinganos等[11 ] 提出使用时间卷积网络(TCN)来处理sEMG的问题,提高了识别准确率,但在实时性试验中表现欠佳,说明TCN无法满足实时性要求较高的手势识别系统. ...
Feature fusion-based improved capsule network for sEMG signal recognition
1
2022
... 近年来,学者通常将提取原始肌电信号所得到的一维离散特征转换为高维特征图后,送入深度学习网络进行训练[12 ] . 现有的深度学习网络模型如CNN侧重捕捉肌电信号的空间信息,但忽视了肌电信号本质上是一连串时间序列数据,可能会忽视某些关键性特征[4 ] . 本文提出ETDTBN框架,整体结构如图1 所示. ...
Feature selection: a literature review
1
2014
... 在机器学习中,对于某个对象的属性特征通常会以特征向量的形式来表示[13 ] . 目前现有的提取原始肌电信号方法只能得到一维离散特征,若对一维离散特征不作处理,则容易遗漏不同离散特征之间的相关性,导致较难区分相似手势情况下的sEMG. Chen等[14 ] 提出离散特征二维化的方法,构建包含离散特征与合成特征的二维特征关系图,但该方法存在处理后特征信息稀疏、参数重复冗余的问题,由此本文提出加强二维化方法. ...
Two-dimensional discrete feature based spatial attention CapsNet for sEMG signal recognition
4
2020
... 在机器学习中,对于某个对象的属性特征通常会以特征向量的形式来表示[13 ] . 目前现有的提取原始肌电信号方法只能得到一维离散特征,若对一维离散特征不作处理,则容易遗漏不同离散特征之间的相关性,导致较难区分相似手势情况下的sEMG. Chen等[14 ] 提出离散特征二维化的方法,构建包含离散特征与合成特征的二维特征关系图,但该方法存在处理后特征信息稀疏、参数重复冗余的问题,由此本文提出加强二维化方法. ...
... Recognition effect of each method under electrode displacement
Tab.2 方法 P c /%P o /%HC HO RF WE WF KNN+FE[30 ] 28.21±0.00 9.23±0.00 94.90±0.00 100±0.00 100±0.00 66.67±0.00 SVM+FE[31 ] 42.64±0.00 18.97±0.00 87.82±0.00 100±0.00 100±0.00 70.49±0.00 CNN[8 ] 90.72±6.97 13.42±7.82 23.21±10.15 96.79±2.58 96.75±5.29 64.18±2.73 CNN+FE 29.89±4.24 33.91±16.26 95.01±3.60 98.90±1.31 91.58±10.66 70.87±2.74 CNN+FE+ETD 85.56±4.44 40.33±13.50 75.20±8.05 98.85±1.18 86.18±5.24 78.24±2.26 RESNET+FE[32 ] 31.09±3.94 35.17±10.96 90.78±4.88 98.92±1.29 92.22±3.26 70.78±2.66 Bi-GRU[33 ] 84.10±8.19 5.41±5.09 72.67±10.26 100±0.00 99.34±1.09 72.04±2.35 LSTM[34 ] 73.64±11.84 4.33±1.99 71.13±18.33 100±0.00 99.40±1.02 70.88±3.55 TRANSFORMER[35 ] 80.64±5.84 20.15±3.53 66.17±8.62 98.55±1.38 89.14±2.19 66.14±3.25 LCNN[36 ] 93.13±2.98 12.51±3.53 81.03±6.54 98.26±0.52 91.08±4.90 76.38±0.94 TDACAPS[14 ] 97.59±2.62 74.87±15.71 95.18±4.42 98.56±1.82 55.39±16.87 84.77±0.82 ETDTBN 99.80±0.41 66.36±6.90 69.85±7.44 100±0.00 99.85±0.36 86.95±1.64
以KNN和SVM为代表的传统机器学习模型在动作WE和WF上的识别效果最好,均达到了100%的识别率,但对于其他手势动作的识别效果不理想. Bi-GRU的总体准确率略高于LSTM和TRANSFORMER,且Bi-GRU在模型结构上更简单,训练参数与时间更少,故选用Bi-GRU作为网络提取原信号时间特征的部分. 将提出的加强二维化方法用于CNN模型,与CNN+FE和RESNET+FE模型相比,整体识别率分别提高了7.37%和7.46%,在动作HO的识别上效果有所提升,说明利用该方法能够挖掘出HO的部分特性. 与LCNN相比,ETDTBN在保持动作HC、WE和WF接近100%识别率的情况下,对手势HO的分类准确率提高了53.85%,且该模型在12种方法中的总体识别率最高,达到86.95%,说明利用提出的方法能够有效地识别肌电信号. ...
... Recognition accuracy of each method under different subject
Tab.3 方法 P c /%P o /%HC HO RF WE WF KNN+FE[30 ] 97.18±0.00 72.99±0.00 47.95±0.00 93.50±0.00 42.14±0.00 70.75±0.00 SVM+FE[31 ] 64.27±0.00 86.24±0.00 51.71±0.00 100.00±0.00 52.99±0.00 71.04±0.00 CNN[8 ] 87.35±3.45 66.63±0.58 58.44±2.09 98.94±0.65 40.85±1.05 70.49±0.86 CNN+FE 71.99±4.16 90.51±1.85 80.87±7.59 99.82±0.49 31.39±7.51 75.06±0.18 CNN+FE+ETD 82.63±2.37 80.13±3.88 82.22±6.97 99.25±0.78 33.68±8.55 77.57±0.78 RESNET+FE[32 ] 73.79±3.96 85.22±2.78 81.17±6.19 99.22±0.65 32.11±6.95 74.96±0.26 Bi-GRU[33 ] 82.06±6.71 66.26±7.42 37.35±3.84 94.65±2.52 63.98±5.02 68.93±0.38 LSTM[34 ] 78.79±6.81 60.85±5.56 40.32±3.96 99.27±0.72 54.03±6.77 67.08±1.11 TRANSFORMER[35 ] 83.09±2.81 59.05±6.56 33.22±3.88 97.57±0.92 55.13±6.44 65.33±1.08 LCNN[36 ] 95.95±2.11 80.78±3.46 62.25±5.33 99.69±0.15 46.95±3.16 77.26±0.53 TDACAPS[14 ] 98.25±3.89 84.98±7.12 82.48±5.96 98.24±0.62 44.75±5.50 81.90±1.09 ETDTBN 99.75±0.15 75.51±1.85 95.27±2.54 99.93±0.05 50.21±0.45 84.15±0.41
从表3 可以看出,当识别不同受试者的sEMG时,利用本实验的12种方法,能够较好地识别动作WE,但对动作WF的分类效果不理想. CNN模型通过加强二维化方法处理后,提升了总体准确率,对于除WF外的其他手势,均达到了大于80%的准确率. 以Bi-GRU和LSTM为代表的RNN在本实验中表现欠佳,但在动作WF的识别上优于其他模型. 与LCNN模型相比,ETDTBN模型的总体分类准确率提高了6.89%,ETDTBN模型是所有方法中效果最优的,总识别率为84.15%. 本文提出的方法对动作HC、RF、WE的识别效果均达到最佳,HO与WF的识别率虽然没有达到良好的预期,但高于大部分方法. ...
... Computational resource analysis for all methods
Tab.5 方法 N p /106 C /MBt e /st p /st r /msKNN+FE[30 ] — — 0.78±0.01 86.86±1.22 0.020±0.001 SVM+FE[31 ] — — 0.48±0.01 77.06±1.62 0.030±0.001 CNN[8 ] 4.98 162.73 22.65±0.98 148.61±3.38 0.078±0.003 CNN+FE 0.76 117.30 14.13±0.46 101.32±2.11 0.066±0.002 CNN+FE+ETD 1.15 184.48 20.19±0.65 153.51±3.65 0.086±0.002 RESNET+FE[32 ] 0.55 336.88 21.96±0.52 147.53±4.06 0.071±0.002 Bi-GRU[33 ] 1.41 118.10 16.76±0.50 160.49±2.98 0.078±0.002 LSTM[34 ] 1.52 146.35 17.14±0.59 168.25±3.16 0.082±0.002 TRANSFORMER[35 ] 2.49 335.68 24.16±0.66 187.23±4.56 0.079±0.002 LCNN[36 ] 1.77 533.50 21.06±0.62 180.85±4.29 0.082±0.003 TDACAPS[14 ] 0.87 741.38 216.45±6.16 1978.12 ±14.181.047±0.030 ETDTBN 3.73 321.41 17.85±0.48 156.28±3.99 0.076±0.002
从表6 可知,ETDTBN模型在3个NinaPro数据集中均取得了最高的识别准确率,在包含10个受试者数据中的NinaPro DB4数据集上,与其他算法相比,模型提升效果最明显. 可知,ETDTBN模型在手势分类问题上具备较好的泛化性和鲁棒性. ...
Recent advances in convolutional neural networks
1
2018
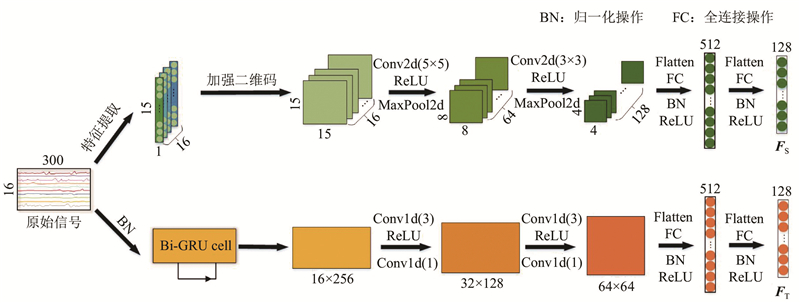
... 肌电原始信号经加强二维化后得到二维特征矩阵,需要放入深度学习模型中进一步训练. CNN模型是目前应用最广泛的深度学习算法之一,在基于sEMG的手势识别问题上有着良好的表现[15 ] . 肌电信号是时序信号,CNN不能有效地分析时序信号的历史信息. 门控循环神经网络与CNN最大的不同是它有记忆功能,当前的输出不仅依赖于当前的输入,而且依赖于前一次的输出,这使得它具有较强的处理时间序列的能力. CNN和RNN各自提取的特征信息侧重点不同,结合2种网络,有利于发挥各自的特点与优势. 本文提出双分支网络模型,具体结构如图2 所示. ...
ImageNet classification with deep convolutional neural networks
1
2017
... CNN是包含卷积计算且具备深度结构的前馈神经网络,从低层到高层逐步训练得到深层特征信息. 对输入数据进行分类,CNN具备局部连接与共享权重的特点,主要包括卷积层、池化层和全连接层[16 -17 ] . ...
1
... CNN是包含卷积计算且具备深度结构的前馈神经网络,从低层到高层逐步训练得到深层特征信息. 对输入数据进行分类,CNN具备局部连接与共享权重的特点,主要包括卷积层、池化层和全连接层[16 -17 ] . ...
Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network
1
2020
... RNN在处理时序性较强的信号时有着较好的效果[18 ] . RNN在训练过程中容易出现梯度消失或梯度爆炸的情况,存在长期依赖的问题[19 ] . 门限循环单元(GRU)是RNN的重要变体,能够较好地克服这些问题. GRU以原始信号作为输入,保留sEMG原始时间序列的相关性与时间依赖性,相较于长短期记忆网络(LSTM),GRU结构更简单,训练参数量更少,可以有效地减少训练时间,提高计算速率[20 ] . ...
A review of recurrent neural networks: LSTM cells and network architectures
1
2019
... RNN在处理时序性较强的信号时有着较好的效果[18 ] . RNN在训练过程中容易出现梯度消失或梯度爆炸的情况,存在长期依赖的问题[19 ] . 门限循环单元(GRU)是RNN的重要变体,能够较好地克服这些问题. GRU以原始信号作为输入,保留sEMG原始时间序列的相关性与时间依赖性,相较于长短期记忆网络(LSTM),GRU结构更简单,训练参数量更少,可以有效地减少训练时间,提高计算速率[20 ] . ...
Performance evaluation of deep neural networks applied to speech recognition: RNN, LSTM and GRU
1
2019
... RNN在处理时序性较强的信号时有着较好的效果[18 ] . RNN在训练过程中容易出现梯度消失或梯度爆炸的情况,存在长期依赖的问题[19 ] . 门限循环单元(GRU)是RNN的重要变体,能够较好地克服这些问题. GRU以原始信号作为输入,保留sEMG原始时间序列的相关性与时间依赖性,相较于长短期记忆网络(LSTM),GRU结构更简单,训练参数量更少,可以有效地减少训练时间,提高计算速率[20 ] . ...
1
... GRU是由Cho等[21 ] 提出的. GRU由更新门和重置门组成. 其中更新门代替了LSTM中的输入门和遗忘门,控制当前状态要从历史状态中保留多少有用信息以及要从候选状态中接受多少新信息. ...
1
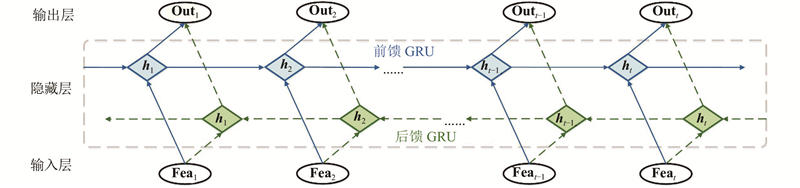
... 通常,完成一个连续手部动作所产生的电信号前后存在着某种依赖关系. 为了利用过去和未来的信息,采用Bi-GRU来分析连续动作中动作电位的变化关系[22 ] . Bi-GRU模型的结构如图3 所示. ...
1
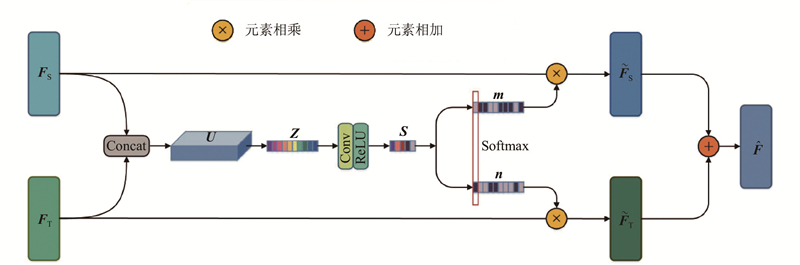
... 在多源信息问题上,现有的线性聚合方法难以根据输入内容调整不同分支的大小[23 ] . 本文提出自适应特征融合机制,该机制允许每个神经元根据输入信息的不同特征自适应地调整其在网络中的占比,采用非线性的方法融合两部分网络,实现对时间空间特征的学习. 该方法容易扩展到包含多个分支的网络中. 具体结构如图4 所示. ...
1
... 实验共邀请8名健康受试者(7名男性、1名女性,年龄为(25±5)岁,身高为(175±10) cm,体重为(65±10) kg),参与3 d(每天上午9时与下午15时,共6个时间段)的数据采集工作. 受试者在实验前均被告知本次采集的完整过程. 在采集前,使用酒精棉对受试者右前臂进行清洁,每位受试者将肌电采集袖套佩戴在右前臂,调节袖套使其紧贴肌肉,无法产生滑动,前臂与桌面呈45°角放置在桌面,根据指示完成相应动作. 每个人每个时间段分别演示5个手势动作,重复做3组,尽量保持每次手势的动作力度相当. 每个手势动作持续12 s,取中间10 s的稳定信号进行记录,每2个动作之间休息10 s. 这5种手势分别是握拳(hand closed, HC)、伸掌(hand open, HO)、手腕弯曲(radial flexion, RF)、手掌向下(wrist flexion, WF)、手腕展开(wrist extension, WE) [24 ] . 具体手势如图5 所示. ...
Assessment on stationarity of EMG signals with different windows size during isotonic contractions
1
2017
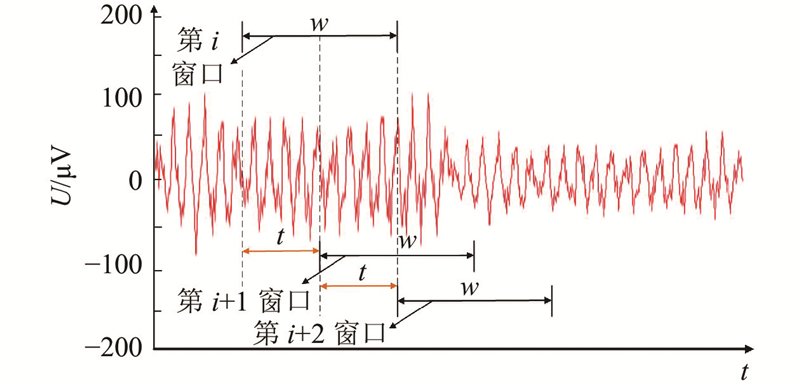
... 原始的sEMG可以看作是一连串连续的一维时间序列信号,而要实现通过sEMG对假肢的实时控制,输入延时是重点需要考虑的因素,因此采用窗口分析法对数据进行预处理. 该方法最重要的参数有2个,分别是滑动窗口长度和增量区间[25 ] . 滑动窗口的大小影响识别精度,增量区间对应影响系统的响应时间. 如图6 所示为窗口分析法的具体处理过程. 图中,$ w $ $ t $ $U $
A new strategy for multifunction myoelectric control
1
1993
... Hudgins等[26 ] 提出最大允许时延是300 ms,因此本文设定$ w $ $ t $ $ n $ $ \alpha $ $ \beta $ [27 -28 ] . ...
Feature reduction and selection for EMG signal classification
1
2012
... Hudgins等[26 ] 提出最大允许时延是300 ms,因此本文设定$ w $ $ t $ $ n $ $ \alpha $ $ \beta $ [27 -28 ] . ...
Evaluation of surface EMG-based recognition algorithms for decoding hand movements
1
2020
... Hudgins等[26 ] 提出最大允许时延是300 ms,因此本文设定$ w $ $ t $ $ n $ $ \alpha $ $ \beta $ [27 -28 ] . ...
Review of sEMG-based motion intent recognition methods in non-ideal conditions
1
2021
... 目前采集sEMG大多在理想条件下进行,而在现实生活中的采集存在诸多不可控因素,电极偏移和受试者个体差异是影响识别效果的2个重要因素[29 ] . 电极偏移指的是在采集过程中,由于电极袖套的穿戴与脱下,无法保证同一个电极对应之前皮肤的同一个位置,采集的数据会因检测点的变化在分布上有所差异. 不同受试者之间的浅层肌肉、运动神经元位置分布不同,在做出相同动作时产生的电位分布有所不同. ...
3
... Recognition effect of each method under electrode displacement
Tab.2 方法 P c /%P o /%HC HO RF WE WF KNN+FE[30 ] 28.21±0.00 9.23±0.00 94.90±0.00 100±0.00 100±0.00 66.67±0.00 SVM+FE[31 ] 42.64±0.00 18.97±0.00 87.82±0.00 100±0.00 100±0.00 70.49±0.00 CNN[8 ] 90.72±6.97 13.42±7.82 23.21±10.15 96.79±2.58 96.75±5.29 64.18±2.73 CNN+FE 29.89±4.24 33.91±16.26 95.01±3.60 98.90±1.31 91.58±10.66 70.87±2.74 CNN+FE+ETD 85.56±4.44 40.33±13.50 75.20±8.05 98.85±1.18 86.18±5.24 78.24±2.26 RESNET+FE[32 ] 31.09±3.94 35.17±10.96 90.78±4.88 98.92±1.29 92.22±3.26 70.78±2.66 Bi-GRU[33 ] 84.10±8.19 5.41±5.09 72.67±10.26 100±0.00 99.34±1.09 72.04±2.35 LSTM[34 ] 73.64±11.84 4.33±1.99 71.13±18.33 100±0.00 99.40±1.02 70.88±3.55 TRANSFORMER[35 ] 80.64±5.84 20.15±3.53 66.17±8.62 98.55±1.38 89.14±2.19 66.14±3.25 LCNN[36 ] 93.13±2.98 12.51±3.53 81.03±6.54 98.26±0.52 91.08±4.90 76.38±0.94 TDACAPS[14 ] 97.59±2.62 74.87±15.71 95.18±4.42 98.56±1.82 55.39±16.87 84.77±0.82 ETDTBN 99.80±0.41 66.36±6.90 69.85±7.44 100±0.00 99.85±0.36 86.95±1.64
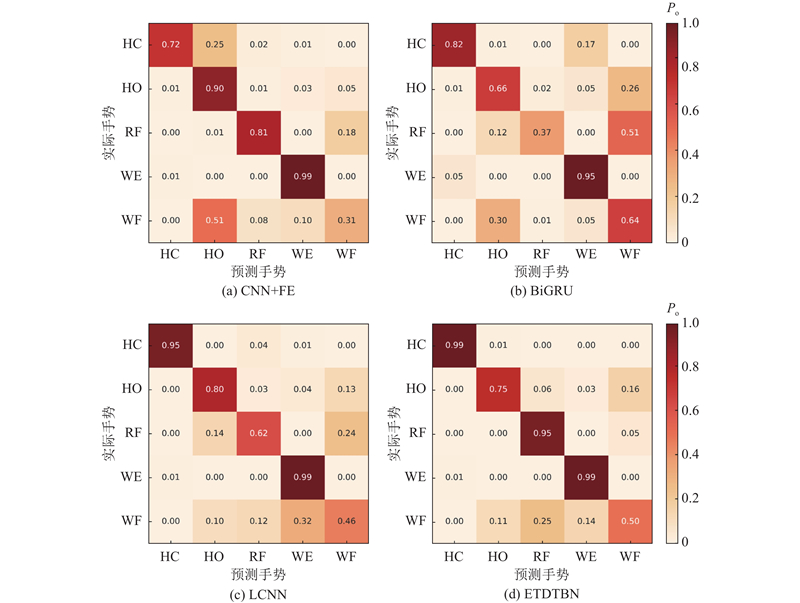
以KNN和SVM为代表的传统机器学习模型在动作WE和WF上的识别效果最好,均达到了100%的识别率,但对于其他手势动作的识别效果不理想. Bi-GRU的总体准确率略高于LSTM和TRANSFORMER,且Bi-GRU在模型结构上更简单,训练参数与时间更少,故选用Bi-GRU作为网络提取原信号时间特征的部分. 将提出的加强二维化方法用于CNN模型,与CNN+FE和RESNET+FE模型相比,整体识别率分别提高了7.37%和7.46%,在动作HO的识别上效果有所提升,说明利用该方法能够挖掘出HO的部分特性. 与LCNN相比,ETDTBN在保持动作HC、WE和WF接近100%识别率的情况下,对手势HO的分类准确率提高了53.85%,且该模型在12种方法中的总体识别率最高,达到86.95%,说明利用提出的方法能够有效地识别肌电信号. ...
... Recognition accuracy of each method under different subject
Tab.3 方法 P c /%P o /%HC HO RF WE WF KNN+FE[30 ] 97.18±0.00 72.99±0.00 47.95±0.00 93.50±0.00 42.14±0.00 70.75±0.00 SVM+FE[31 ] 64.27±0.00 86.24±0.00 51.71±0.00 100.00±0.00 52.99±0.00 71.04±0.00 CNN[8 ] 87.35±3.45 66.63±0.58 58.44±2.09 98.94±0.65 40.85±1.05 70.49±0.86 CNN+FE 71.99±4.16 90.51±1.85 80.87±7.59 99.82±0.49 31.39±7.51 75.06±0.18 CNN+FE+ETD 82.63±2.37 80.13±3.88 82.22±6.97 99.25±0.78 33.68±8.55 77.57±0.78 RESNET+FE[32 ] 73.79±3.96 85.22±2.78 81.17±6.19 99.22±0.65 32.11±6.95 74.96±0.26 Bi-GRU[33 ] 82.06±6.71 66.26±7.42 37.35±3.84 94.65±2.52 63.98±5.02 68.93±0.38 LSTM[34 ] 78.79±6.81 60.85±5.56 40.32±3.96 99.27±0.72 54.03±6.77 67.08±1.11 TRANSFORMER[35 ] 83.09±2.81 59.05±6.56 33.22±3.88 97.57±0.92 55.13±6.44 65.33±1.08 LCNN[36 ] 95.95±2.11 80.78±3.46 62.25±5.33 99.69±0.15 46.95±3.16 77.26±0.53 TDACAPS[14 ] 98.25±3.89 84.98±7.12 82.48±5.96 98.24±0.62 44.75±5.50 81.90±1.09 ETDTBN 99.75±0.15 75.51±1.85 95.27±2.54 99.93±0.05 50.21±0.45 84.15±0.41
从表3 可以看出,当识别不同受试者的sEMG时,利用本实验的12种方法,能够较好地识别动作WE,但对动作WF的分类效果不理想. CNN模型通过加强二维化方法处理后,提升了总体准确率,对于除WF外的其他手势,均达到了大于80%的准确率. 以Bi-GRU和LSTM为代表的RNN在本实验中表现欠佳,但在动作WF的识别上优于其他模型. 与LCNN模型相比,ETDTBN模型的总体分类准确率提高了6.89%,ETDTBN模型是所有方法中效果最优的,总识别率为84.15%. 本文提出的方法对动作HC、RF、WE的识别效果均达到最佳,HO与WF的识别率虽然没有达到良好的预期,但高于大部分方法. ...
... Computational resource analysis for all methods
Tab.5 方法 N p /106 C /MBt e /st p /st r /msKNN+FE[30 ] — — 0.78±0.01 86.86±1.22 0.020±0.001 SVM+FE[31 ] — — 0.48±0.01 77.06±1.62 0.030±0.001 CNN[8 ] 4.98 162.73 22.65±0.98 148.61±3.38 0.078±0.003 CNN+FE 0.76 117.30 14.13±0.46 101.32±2.11 0.066±0.002 CNN+FE+ETD 1.15 184.48 20.19±0.65 153.51±3.65 0.086±0.002 RESNET+FE[32 ] 0.55 336.88 21.96±0.52 147.53±4.06 0.071±0.002 Bi-GRU[33 ] 1.41 118.10 16.76±0.50 160.49±2.98 0.078±0.002 LSTM[34 ] 1.52 146.35 17.14±0.59 168.25±3.16 0.082±0.002 TRANSFORMER[35 ] 2.49 335.68 24.16±0.66 187.23±4.56 0.079±0.002 LCNN[36 ] 1.77 533.50 21.06±0.62 180.85±4.29 0.082±0.003 TDACAPS[14 ] 0.87 741.38 216.45±6.16 1978.12 ±14.181.047±0.030 ETDTBN 3.73 321.41 17.85±0.48 156.28±3.99 0.076±0.002
从表6 可知,ETDTBN模型在3个NinaPro数据集中均取得了最高的识别准确率,在包含10个受试者数据中的NinaPro DB4数据集上,与其他算法相比,模型提升效果最明显. 可知,ETDTBN模型在手势分类问题上具备较好的泛化性和鲁棒性. ...
Comparative analysis of SVM and Naive Bayes classifier for the SEMG signal classification
3
2021
... Recognition effect of each method under electrode displacement
Tab.2 方法 P c /%P o /%HC HO RF WE WF KNN+FE[30 ] 28.21±0.00 9.23±0.00 94.90±0.00 100±0.00 100±0.00 66.67±0.00 SVM+FE[31 ] 42.64±0.00 18.97±0.00 87.82±0.00 100±0.00 100±0.00 70.49±0.00 CNN[8 ] 90.72±6.97 13.42±7.82 23.21±10.15 96.79±2.58 96.75±5.29 64.18±2.73 CNN+FE 29.89±4.24 33.91±16.26 95.01±3.60 98.90±1.31 91.58±10.66 70.87±2.74 CNN+FE+ETD 85.56±4.44 40.33±13.50 75.20±8.05 98.85±1.18 86.18±5.24 78.24±2.26 RESNET+FE[32 ] 31.09±3.94 35.17±10.96 90.78±4.88 98.92±1.29 92.22±3.26 70.78±2.66 Bi-GRU[33 ] 84.10±8.19 5.41±5.09 72.67±10.26 100±0.00 99.34±1.09 72.04±2.35 LSTM[34 ] 73.64±11.84 4.33±1.99 71.13±18.33 100±0.00 99.40±1.02 70.88±3.55 TRANSFORMER[35 ] 80.64±5.84 20.15±3.53 66.17±8.62 98.55±1.38 89.14±2.19 66.14±3.25 LCNN[36 ] 93.13±2.98 12.51±3.53 81.03±6.54 98.26±0.52 91.08±4.90 76.38±0.94 TDACAPS[14 ] 97.59±2.62 74.87±15.71 95.18±4.42 98.56±1.82 55.39±16.87 84.77±0.82 ETDTBN 99.80±0.41 66.36±6.90 69.85±7.44 100±0.00 99.85±0.36 86.95±1.64
以KNN和SVM为代表的传统机器学习模型在动作WE和WF上的识别效果最好,均达到了100%的识别率,但对于其他手势动作的识别效果不理想. Bi-GRU的总体准确率略高于LSTM和TRANSFORMER,且Bi-GRU在模型结构上更简单,训练参数与时间更少,故选用Bi-GRU作为网络提取原信号时间特征的部分. 将提出的加强二维化方法用于CNN模型,与CNN+FE和RESNET+FE模型相比,整体识别率分别提高了7.37%和7.46%,在动作HO的识别上效果有所提升,说明利用该方法能够挖掘出HO的部分特性. 与LCNN相比,ETDTBN在保持动作HC、WE和WF接近100%识别率的情况下,对手势HO的分类准确率提高了53.85%,且该模型在12种方法中的总体识别率最高,达到86.95%,说明利用提出的方法能够有效地识别肌电信号. ...
... Recognition accuracy of each method under different subject
Tab.3 方法 P c /%P o /%HC HO RF WE WF KNN+FE[30 ] 97.18±0.00 72.99±0.00 47.95±0.00 93.50±0.00 42.14±0.00 70.75±0.00 SVM+FE[31 ] 64.27±0.00 86.24±0.00 51.71±0.00 100.00±0.00 52.99±0.00 71.04±0.00 CNN[8 ] 87.35±3.45 66.63±0.58 58.44±2.09 98.94±0.65 40.85±1.05 70.49±0.86 CNN+FE 71.99±4.16 90.51±1.85 80.87±7.59 99.82±0.49 31.39±7.51 75.06±0.18 CNN+FE+ETD 82.63±2.37 80.13±3.88 82.22±6.97 99.25±0.78 33.68±8.55 77.57±0.78 RESNET+FE[32 ] 73.79±3.96 85.22±2.78 81.17±6.19 99.22±0.65 32.11±6.95 74.96±0.26 Bi-GRU[33 ] 82.06±6.71 66.26±7.42 37.35±3.84 94.65±2.52 63.98±5.02 68.93±0.38 LSTM[34 ] 78.79±6.81 60.85±5.56 40.32±3.96 99.27±0.72 54.03±6.77 67.08±1.11 TRANSFORMER[35 ] 83.09±2.81 59.05±6.56 33.22±3.88 97.57±0.92 55.13±6.44 65.33±1.08 LCNN[36 ] 95.95±2.11 80.78±3.46 62.25±5.33 99.69±0.15 46.95±3.16 77.26±0.53 TDACAPS[14 ] 98.25±3.89 84.98±7.12 82.48±5.96 98.24±0.62 44.75±5.50 81.90±1.09 ETDTBN 99.75±0.15 75.51±1.85 95.27±2.54 99.93±0.05 50.21±0.45 84.15±0.41
从表3 可以看出,当识别不同受试者的sEMG时,利用本实验的12种方法,能够较好地识别动作WE,但对动作WF的分类效果不理想. CNN模型通过加强二维化方法处理后,提升了总体准确率,对于除WF外的其他手势,均达到了大于80%的准确率. 以Bi-GRU和LSTM为代表的RNN在本实验中表现欠佳,但在动作WF的识别上优于其他模型. 与LCNN模型相比,ETDTBN模型的总体分类准确率提高了6.89%,ETDTBN模型是所有方法中效果最优的,总识别率为84.15%. 本文提出的方法对动作HC、RF、WE的识别效果均达到最佳,HO与WF的识别率虽然没有达到良好的预期,但高于大部分方法. ...
... Computational resource analysis for all methods
Tab.5 方法 N p /106 C /MBt e /st p /st r /msKNN+FE[30 ] — — 0.78±0.01 86.86±1.22 0.020±0.001 SVM+FE[31 ] — — 0.48±0.01 77.06±1.62 0.030±0.001 CNN[8 ] 4.98 162.73 22.65±0.98 148.61±3.38 0.078±0.003 CNN+FE 0.76 117.30 14.13±0.46 101.32±2.11 0.066±0.002 CNN+FE+ETD 1.15 184.48 20.19±0.65 153.51±3.65 0.086±0.002 RESNET+FE[32 ] 0.55 336.88 21.96±0.52 147.53±4.06 0.071±0.002 Bi-GRU[33 ] 1.41 118.10 16.76±0.50 160.49±2.98 0.078±0.002 LSTM[34 ] 1.52 146.35 17.14±0.59 168.25±3.16 0.082±0.002 TRANSFORMER[35 ] 2.49 335.68 24.16±0.66 187.23±4.56 0.079±0.002 LCNN[36 ] 1.77 533.50 21.06±0.62 180.85±4.29 0.082±0.003 TDACAPS[14 ] 0.87 741.38 216.45±6.16 1978.12 ±14.181.047±0.030 ETDTBN 3.73 321.41 17.85±0.48 156.28±3.99 0.076±0.002
从表6 可知,ETDTBN模型在3个NinaPro数据集中均取得了最高的识别准确率,在包含10个受试者数据中的NinaPro DB4数据集上,与其他算法相比,模型提升效果最明显. 可知,ETDTBN模型在手势分类问题上具备较好的泛化性和鲁棒性. ...
3
... Recognition effect of each method under electrode displacement
Tab.2 方法 P c /%P o /%HC HO RF WE WF KNN+FE[30 ] 28.21±0.00 9.23±0.00 94.90±0.00 100±0.00 100±0.00 66.67±0.00 SVM+FE[31 ] 42.64±0.00 18.97±0.00 87.82±0.00 100±0.00 100±0.00 70.49±0.00 CNN[8 ] 90.72±6.97 13.42±7.82 23.21±10.15 96.79±2.58 96.75±5.29 64.18±2.73 CNN+FE 29.89±4.24 33.91±16.26 95.01±3.60 98.90±1.31 91.58±10.66 70.87±2.74 CNN+FE+ETD 85.56±4.44 40.33±13.50 75.20±8.05 98.85±1.18 86.18±5.24 78.24±2.26 RESNET+FE[32 ] 31.09±3.94 35.17±10.96 90.78±4.88 98.92±1.29 92.22±3.26 70.78±2.66 Bi-GRU[33 ] 84.10±8.19 5.41±5.09 72.67±10.26 100±0.00 99.34±1.09 72.04±2.35 LSTM[34 ] 73.64±11.84 4.33±1.99 71.13±18.33 100±0.00 99.40±1.02 70.88±3.55 TRANSFORMER[35 ] 80.64±5.84 20.15±3.53 66.17±8.62 98.55±1.38 89.14±2.19 66.14±3.25 LCNN[36 ] 93.13±2.98 12.51±3.53 81.03±6.54 98.26±0.52 91.08±4.90 76.38±0.94 TDACAPS[14 ] 97.59±2.62 74.87±15.71 95.18±4.42 98.56±1.82 55.39±16.87 84.77±0.82 ETDTBN 99.80±0.41 66.36±6.90 69.85±7.44 100±0.00 99.85±0.36 86.95±1.64
以KNN和SVM为代表的传统机器学习模型在动作WE和WF上的识别效果最好,均达到了100%的识别率,但对于其他手势动作的识别效果不理想. Bi-GRU的总体准确率略高于LSTM和TRANSFORMER,且Bi-GRU在模型结构上更简单,训练参数与时间更少,故选用Bi-GRU作为网络提取原信号时间特征的部分. 将提出的加强二维化方法用于CNN模型,与CNN+FE和RESNET+FE模型相比,整体识别率分别提高了7.37%和7.46%,在动作HO的识别上效果有所提升,说明利用该方法能够挖掘出HO的部分特性. 与LCNN相比,ETDTBN在保持动作HC、WE和WF接近100%识别率的情况下,对手势HO的分类准确率提高了53.85%,且该模型在12种方法中的总体识别率最高,达到86.95%,说明利用提出的方法能够有效地识别肌电信号. ...
... Recognition accuracy of each method under different subject
Tab.3 方法 P c /%P o /%HC HO RF WE WF KNN+FE[30 ] 97.18±0.00 72.99±0.00 47.95±0.00 93.50±0.00 42.14±0.00 70.75±0.00 SVM+FE[31 ] 64.27±0.00 86.24±0.00 51.71±0.00 100.00±0.00 52.99±0.00 71.04±0.00 CNN[8 ] 87.35±3.45 66.63±0.58 58.44±2.09 98.94±0.65 40.85±1.05 70.49±0.86 CNN+FE 71.99±4.16 90.51±1.85 80.87±7.59 99.82±0.49 31.39±7.51 75.06±0.18 CNN+FE+ETD 82.63±2.37 80.13±3.88 82.22±6.97 99.25±0.78 33.68±8.55 77.57±0.78 RESNET+FE[32 ] 73.79±3.96 85.22±2.78 81.17±6.19 99.22±0.65 32.11±6.95 74.96±0.26 Bi-GRU[33 ] 82.06±6.71 66.26±7.42 37.35±3.84 94.65±2.52 63.98±5.02 68.93±0.38 LSTM[34 ] 78.79±6.81 60.85±5.56 40.32±3.96 99.27±0.72 54.03±6.77 67.08±1.11 TRANSFORMER[35 ] 83.09±2.81 59.05±6.56 33.22±3.88 97.57±0.92 55.13±6.44 65.33±1.08 LCNN[36 ] 95.95±2.11 80.78±3.46 62.25±5.33 99.69±0.15 46.95±3.16 77.26±0.53 TDACAPS[14 ] 98.25±3.89 84.98±7.12 82.48±5.96 98.24±0.62 44.75±5.50 81.90±1.09 ETDTBN 99.75±0.15 75.51±1.85 95.27±2.54 99.93±0.05 50.21±0.45 84.15±0.41
从表3 可以看出,当识别不同受试者的sEMG时,利用本实验的12种方法,能够较好地识别动作WE,但对动作WF的分类效果不理想. CNN模型通过加强二维化方法处理后,提升了总体准确率,对于除WF外的其他手势,均达到了大于80%的准确率. 以Bi-GRU和LSTM为代表的RNN在本实验中表现欠佳,但在动作WF的识别上优于其他模型. 与LCNN模型相比,ETDTBN模型的总体分类准确率提高了6.89%,ETDTBN模型是所有方法中效果最优的,总识别率为84.15%. 本文提出的方法对动作HC、RF、WE的识别效果均达到最佳,HO与WF的识别率虽然没有达到良好的预期,但高于大部分方法. ...
... Computational resource analysis for all methods
Tab.5 方法 N p /106 C /MBt e /st p /st r /msKNN+FE[30 ] — — 0.78±0.01 86.86±1.22 0.020±0.001 SVM+FE[31 ] — — 0.48±0.01 77.06±1.62 0.030±0.001 CNN[8 ] 4.98 162.73 22.65±0.98 148.61±3.38 0.078±0.003 CNN+FE 0.76 117.30 14.13±0.46 101.32±2.11 0.066±0.002 CNN+FE+ETD 1.15 184.48 20.19±0.65 153.51±3.65 0.086±0.002 RESNET+FE[32 ] 0.55 336.88 21.96±0.52 147.53±4.06 0.071±0.002 Bi-GRU[33 ] 1.41 118.10 16.76±0.50 160.49±2.98 0.078±0.002 LSTM[34 ] 1.52 146.35 17.14±0.59 168.25±3.16 0.082±0.002 TRANSFORMER[35 ] 2.49 335.68 24.16±0.66 187.23±4.56 0.079±0.002 LCNN[36 ] 1.77 533.50 21.06±0.62 180.85±4.29 0.082±0.003 TDACAPS[14 ] 0.87 741.38 216.45±6.16 1978.12 ±14.181.047±0.030 ETDTBN 3.73 321.41 17.85±0.48 156.28±3.99 0.076±0.002
从表6 可知,ETDTBN模型在3个NinaPro数据集中均取得了最高的识别准确率,在包含10个受试者数据中的NinaPro DB4数据集上,与其他算法相比,模型提升效果最明显. 可知,ETDTBN模型在手势分类问题上具备较好的泛化性和鲁棒性. ...
Machine health monitoring using local feature-based gated recurrent unit networks
3
2017
... Recognition effect of each method under electrode displacement
Tab.2 方法 P c /%P o /%HC HO RF WE WF KNN+FE[30 ] 28.21±0.00 9.23±0.00 94.90±0.00 100±0.00 100±0.00 66.67±0.00 SVM+FE[31 ] 42.64±0.00 18.97±0.00 87.82±0.00 100±0.00 100±0.00 70.49±0.00 CNN[8 ] 90.72±6.97 13.42±7.82 23.21±10.15 96.79±2.58 96.75±5.29 64.18±2.73 CNN+FE 29.89±4.24 33.91±16.26 95.01±3.60 98.90±1.31 91.58±10.66 70.87±2.74 CNN+FE+ETD 85.56±4.44 40.33±13.50 75.20±8.05 98.85±1.18 86.18±5.24 78.24±2.26 RESNET+FE[32 ] 31.09±3.94 35.17±10.96 90.78±4.88 98.92±1.29 92.22±3.26 70.78±2.66 Bi-GRU[33 ] 84.10±8.19 5.41±5.09 72.67±10.26 100±0.00 99.34±1.09 72.04±2.35 LSTM[34 ] 73.64±11.84 4.33±1.99 71.13±18.33 100±0.00 99.40±1.02 70.88±3.55 TRANSFORMER[35 ] 80.64±5.84 20.15±3.53 66.17±8.62 98.55±1.38 89.14±2.19 66.14±3.25 LCNN[36 ] 93.13±2.98 12.51±3.53 81.03±6.54 98.26±0.52 91.08±4.90 76.38±0.94 TDACAPS[14 ] 97.59±2.62 74.87±15.71 95.18±4.42 98.56±1.82 55.39±16.87 84.77±0.82 ETDTBN 99.80±0.41 66.36±6.90 69.85±7.44 100±0.00 99.85±0.36 86.95±1.64
以KNN和SVM为代表的传统机器学习模型在动作WE和WF上的识别效果最好,均达到了100%的识别率,但对于其他手势动作的识别效果不理想. Bi-GRU的总体准确率略高于LSTM和TRANSFORMER,且Bi-GRU在模型结构上更简单,训练参数与时间更少,故选用Bi-GRU作为网络提取原信号时间特征的部分. 将提出的加强二维化方法用于CNN模型,与CNN+FE和RESNET+FE模型相比,整体识别率分别提高了7.37%和7.46%,在动作HO的识别上效果有所提升,说明利用该方法能够挖掘出HO的部分特性. 与LCNN相比,ETDTBN在保持动作HC、WE和WF接近100%识别率的情况下,对手势HO的分类准确率提高了53.85%,且该模型在12种方法中的总体识别率最高,达到86.95%,说明利用提出的方法能够有效地识别肌电信号. ...
... Recognition accuracy of each method under different subject
Tab.3 方法 P c /%P o /%HC HO RF WE WF KNN+FE[30 ] 97.18±0.00 72.99±0.00 47.95±0.00 93.50±0.00 42.14±0.00 70.75±0.00 SVM+FE[31 ] 64.27±0.00 86.24±0.00 51.71±0.00 100.00±0.00 52.99±0.00 71.04±0.00 CNN[8 ] 87.35±3.45 66.63±0.58 58.44±2.09 98.94±0.65 40.85±1.05 70.49±0.86 CNN+FE 71.99±4.16 90.51±1.85 80.87±7.59 99.82±0.49 31.39±7.51 75.06±0.18 CNN+FE+ETD 82.63±2.37 80.13±3.88 82.22±6.97 99.25±0.78 33.68±8.55 77.57±0.78 RESNET+FE[32 ] 73.79±3.96 85.22±2.78 81.17±6.19 99.22±0.65 32.11±6.95 74.96±0.26 Bi-GRU[33 ] 82.06±6.71 66.26±7.42 37.35±3.84 94.65±2.52 63.98±5.02 68.93±0.38 LSTM[34 ] 78.79±6.81 60.85±5.56 40.32±3.96 99.27±0.72 54.03±6.77 67.08±1.11 TRANSFORMER[35 ] 83.09±2.81 59.05±6.56 33.22±3.88 97.57±0.92 55.13±6.44 65.33±1.08 LCNN[36 ] 95.95±2.11 80.78±3.46 62.25±5.33 99.69±0.15 46.95±3.16 77.26±0.53 TDACAPS[14 ] 98.25±3.89 84.98±7.12 82.48±5.96 98.24±0.62 44.75±5.50 81.90±1.09 ETDTBN 99.75±0.15 75.51±1.85 95.27±2.54 99.93±0.05 50.21±0.45 84.15±0.41
从表3 可以看出,当识别不同受试者的sEMG时,利用本实验的12种方法,能够较好地识别动作WE,但对动作WF的分类效果不理想. CNN模型通过加强二维化方法处理后,提升了总体准确率,对于除WF外的其他手势,均达到了大于80%的准确率. 以Bi-GRU和LSTM为代表的RNN在本实验中表现欠佳,但在动作WF的识别上优于其他模型. 与LCNN模型相比,ETDTBN模型的总体分类准确率提高了6.89%,ETDTBN模型是所有方法中效果最优的,总识别率为84.15%. 本文提出的方法对动作HC、RF、WE的识别效果均达到最佳,HO与WF的识别率虽然没有达到良好的预期,但高于大部分方法. ...
... Computational resource analysis for all methods
Tab.5 方法 N p /106 C /MBt e /st p /st r /msKNN+FE[30 ] — — 0.78±0.01 86.86±1.22 0.020±0.001 SVM+FE[31 ] — — 0.48±0.01 77.06±1.62 0.030±0.001 CNN[8 ] 4.98 162.73 22.65±0.98 148.61±3.38 0.078±0.003 CNN+FE 0.76 117.30 14.13±0.46 101.32±2.11 0.066±0.002 CNN+FE+ETD 1.15 184.48 20.19±0.65 153.51±3.65 0.086±0.002 RESNET+FE[32 ] 0.55 336.88 21.96±0.52 147.53±4.06 0.071±0.002 Bi-GRU[33 ] 1.41 118.10 16.76±0.50 160.49±2.98 0.078±0.002 LSTM[34 ] 1.52 146.35 17.14±0.59 168.25±3.16 0.082±0.002 TRANSFORMER[35 ] 2.49 335.68 24.16±0.66 187.23±4.56 0.079±0.002 LCNN[36 ] 1.77 533.50 21.06±0.62 180.85±4.29 0.082±0.003 TDACAPS[14 ] 0.87 741.38 216.45±6.16 1978.12 ±14.181.047±0.030 ETDTBN 3.73 321.41 17.85±0.48 156.28±3.99 0.076±0.002
从表6 可知,ETDTBN模型在3个NinaPro数据集中均取得了最高的识别准确率,在包含10个受试者数据中的NinaPro DB4数据集上,与其他算法相比,模型提升效果最明显. 可知,ETDTBN模型在手势分类问题上具备较好的泛化性和鲁棒性. ...
Framewise phoneme classification with bidirectional LSTM and other neural network architectures
3
2005
... Recognition effect of each method under electrode displacement
Tab.2 方法 P c /%P o /%HC HO RF WE WF KNN+FE[30 ] 28.21±0.00 9.23±0.00 94.90±0.00 100±0.00 100±0.00 66.67±0.00 SVM+FE[31 ] 42.64±0.00 18.97±0.00 87.82±0.00 100±0.00 100±0.00 70.49±0.00 CNN[8 ] 90.72±6.97 13.42±7.82 23.21±10.15 96.79±2.58 96.75±5.29 64.18±2.73 CNN+FE 29.89±4.24 33.91±16.26 95.01±3.60 98.90±1.31 91.58±10.66 70.87±2.74 CNN+FE+ETD 85.56±4.44 40.33±13.50 75.20±8.05 98.85±1.18 86.18±5.24 78.24±2.26 RESNET+FE[32 ] 31.09±3.94 35.17±10.96 90.78±4.88 98.92±1.29 92.22±3.26 70.78±2.66 Bi-GRU[33 ] 84.10±8.19 5.41±5.09 72.67±10.26 100±0.00 99.34±1.09 72.04±2.35 LSTM[34 ] 73.64±11.84 4.33±1.99 71.13±18.33 100±0.00 99.40±1.02 70.88±3.55 TRANSFORMER[35 ] 80.64±5.84 20.15±3.53 66.17±8.62 98.55±1.38 89.14±2.19 66.14±3.25 LCNN[36 ] 93.13±2.98 12.51±3.53 81.03±6.54 98.26±0.52 91.08±4.90 76.38±0.94 TDACAPS[14 ] 97.59±2.62 74.87±15.71 95.18±4.42 98.56±1.82 55.39±16.87 84.77±0.82 ETDTBN 99.80±0.41 66.36±6.90 69.85±7.44 100±0.00 99.85±0.36 86.95±1.64
以KNN和SVM为代表的传统机器学习模型在动作WE和WF上的识别效果最好,均达到了100%的识别率,但对于其他手势动作的识别效果不理想. Bi-GRU的总体准确率略高于LSTM和TRANSFORMER,且Bi-GRU在模型结构上更简单,训练参数与时间更少,故选用Bi-GRU作为网络提取原信号时间特征的部分. 将提出的加强二维化方法用于CNN模型,与CNN+FE和RESNET+FE模型相比,整体识别率分别提高了7.37%和7.46%,在动作HO的识别上效果有所提升,说明利用该方法能够挖掘出HO的部分特性. 与LCNN相比,ETDTBN在保持动作HC、WE和WF接近100%识别率的情况下,对手势HO的分类准确率提高了53.85%,且该模型在12种方法中的总体识别率最高,达到86.95%,说明利用提出的方法能够有效地识别肌电信号. ...
... Recognition accuracy of each method under different subject
Tab.3 方法 P c /%P o /%HC HO RF WE WF KNN+FE[30 ] 97.18±0.00 72.99±0.00 47.95±0.00 93.50±0.00 42.14±0.00 70.75±0.00 SVM+FE[31 ] 64.27±0.00 86.24±0.00 51.71±0.00 100.00±0.00 52.99±0.00 71.04±0.00 CNN[8 ] 87.35±3.45 66.63±0.58 58.44±2.09 98.94±0.65 40.85±1.05 70.49±0.86 CNN+FE 71.99±4.16 90.51±1.85 80.87±7.59 99.82±0.49 31.39±7.51 75.06±0.18 CNN+FE+ETD 82.63±2.37 80.13±3.88 82.22±6.97 99.25±0.78 33.68±8.55 77.57±0.78 RESNET+FE[32 ] 73.79±3.96 85.22±2.78 81.17±6.19 99.22±0.65 32.11±6.95 74.96±0.26 Bi-GRU[33 ] 82.06±6.71 66.26±7.42 37.35±3.84 94.65±2.52 63.98±5.02 68.93±0.38 LSTM[34 ] 78.79±6.81 60.85±5.56 40.32±3.96 99.27±0.72 54.03±6.77 67.08±1.11 TRANSFORMER[35 ] 83.09±2.81 59.05±6.56 33.22±3.88 97.57±0.92 55.13±6.44 65.33±1.08 LCNN[36 ] 95.95±2.11 80.78±3.46 62.25±5.33 99.69±0.15 46.95±3.16 77.26±0.53 TDACAPS[14 ] 98.25±3.89 84.98±7.12 82.48±5.96 98.24±0.62 44.75±5.50 81.90±1.09 ETDTBN 99.75±0.15 75.51±1.85 95.27±2.54 99.93±0.05 50.21±0.45 84.15±0.41
从表3 可以看出,当识别不同受试者的sEMG时,利用本实验的12种方法,能够较好地识别动作WE,但对动作WF的分类效果不理想. CNN模型通过加强二维化方法处理后,提升了总体准确率,对于除WF外的其他手势,均达到了大于80%的准确率. 以Bi-GRU和LSTM为代表的RNN在本实验中表现欠佳,但在动作WF的识别上优于其他模型. 与LCNN模型相比,ETDTBN模型的总体分类准确率提高了6.89%,ETDTBN模型是所有方法中效果最优的,总识别率为84.15%. 本文提出的方法对动作HC、RF、WE的识别效果均达到最佳,HO与WF的识别率虽然没有达到良好的预期,但高于大部分方法. ...
... Computational resource analysis for all methods
Tab.5 方法 N p /106 C /MBt e /st p /st r /msKNN+FE[30 ] — — 0.78±0.01 86.86±1.22 0.020±0.001 SVM+FE[31 ] — — 0.48±0.01 77.06±1.62 0.030±0.001 CNN[8 ] 4.98 162.73 22.65±0.98 148.61±3.38 0.078±0.003 CNN+FE 0.76 117.30 14.13±0.46 101.32±2.11 0.066±0.002 CNN+FE+ETD 1.15 184.48 20.19±0.65 153.51±3.65 0.086±0.002 RESNET+FE[32 ] 0.55 336.88 21.96±0.52 147.53±4.06 0.071±0.002 Bi-GRU[33 ] 1.41 118.10 16.76±0.50 160.49±2.98 0.078±0.002 LSTM[34 ] 1.52 146.35 17.14±0.59 168.25±3.16 0.082±0.002 TRANSFORMER[35 ] 2.49 335.68 24.16±0.66 187.23±4.56 0.079±0.002 LCNN[36 ] 1.77 533.50 21.06±0.62 180.85±4.29 0.082±0.003 TDACAPS[14 ] 0.87 741.38 216.45±6.16 1978.12 ±14.181.047±0.030 ETDTBN 3.73 321.41 17.85±0.48 156.28±3.99 0.076±0.002
从表6 可知,ETDTBN模型在3个NinaPro数据集中均取得了最高的识别准确率,在包含10个受试者数据中的NinaPro DB4数据集上,与其他算法相比,模型提升效果最明显. 可知,ETDTBN模型在手势分类问题上具备较好的泛化性和鲁棒性. ...
Movements classification through sEMG with convolutional vision transformer and stacking ensemble learning
3
2022
... Recognition effect of each method under electrode displacement
Tab.2 方法 P c /%P o /%HC HO RF WE WF KNN+FE[30 ] 28.21±0.00 9.23±0.00 94.90±0.00 100±0.00 100±0.00 66.67±0.00 SVM+FE[31 ] 42.64±0.00 18.97±0.00 87.82±0.00 100±0.00 100±0.00 70.49±0.00 CNN[8 ] 90.72±6.97 13.42±7.82 23.21±10.15 96.79±2.58 96.75±5.29 64.18±2.73 CNN+FE 29.89±4.24 33.91±16.26 95.01±3.60 98.90±1.31 91.58±10.66 70.87±2.74 CNN+FE+ETD 85.56±4.44 40.33±13.50 75.20±8.05 98.85±1.18 86.18±5.24 78.24±2.26 RESNET+FE[32 ] 31.09±3.94 35.17±10.96 90.78±4.88 98.92±1.29 92.22±3.26 70.78±2.66 Bi-GRU[33 ] 84.10±8.19 5.41±5.09 72.67±10.26 100±0.00 99.34±1.09 72.04±2.35 LSTM[34 ] 73.64±11.84 4.33±1.99 71.13±18.33 100±0.00 99.40±1.02 70.88±3.55 TRANSFORMER[35 ] 80.64±5.84 20.15±3.53 66.17±8.62 98.55±1.38 89.14±2.19 66.14±3.25 LCNN[36 ] 93.13±2.98 12.51±3.53 81.03±6.54 98.26±0.52 91.08±4.90 76.38±0.94 TDACAPS[14 ] 97.59±2.62 74.87±15.71 95.18±4.42 98.56±1.82 55.39±16.87 84.77±0.82 ETDTBN 99.80±0.41 66.36±6.90 69.85±7.44 100±0.00 99.85±0.36 86.95±1.64
以KNN和SVM为代表的传统机器学习模型在动作WE和WF上的识别效果最好,均达到了100%的识别率,但对于其他手势动作的识别效果不理想. Bi-GRU的总体准确率略高于LSTM和TRANSFORMER,且Bi-GRU在模型结构上更简单,训练参数与时间更少,故选用Bi-GRU作为网络提取原信号时间特征的部分. 将提出的加强二维化方法用于CNN模型,与CNN+FE和RESNET+FE模型相比,整体识别率分别提高了7.37%和7.46%,在动作HO的识别上效果有所提升,说明利用该方法能够挖掘出HO的部分特性. 与LCNN相比,ETDTBN在保持动作HC、WE和WF接近100%识别率的情况下,对手势HO的分类准确率提高了53.85%,且该模型在12种方法中的总体识别率最高,达到86.95%,说明利用提出的方法能够有效地识别肌电信号. ...
... Recognition accuracy of each method under different subject
Tab.3 方法 P c /%P o /%HC HO RF WE WF KNN+FE[30 ] 97.18±0.00 72.99±0.00 47.95±0.00 93.50±0.00 42.14±0.00 70.75±0.00 SVM+FE[31 ] 64.27±0.00 86.24±0.00 51.71±0.00 100.00±0.00 52.99±0.00 71.04±0.00 CNN[8 ] 87.35±3.45 66.63±0.58 58.44±2.09 98.94±0.65 40.85±1.05 70.49±0.86 CNN+FE 71.99±4.16 90.51±1.85 80.87±7.59 99.82±0.49 31.39±7.51 75.06±0.18 CNN+FE+ETD 82.63±2.37 80.13±3.88 82.22±6.97 99.25±0.78 33.68±8.55 77.57±0.78 RESNET+FE[32 ] 73.79±3.96 85.22±2.78 81.17±6.19 99.22±0.65 32.11±6.95 74.96±0.26 Bi-GRU[33 ] 82.06±6.71 66.26±7.42 37.35±3.84 94.65±2.52 63.98±5.02 68.93±0.38 LSTM[34 ] 78.79±6.81 60.85±5.56 40.32±3.96 99.27±0.72 54.03±6.77 67.08±1.11 TRANSFORMER[35 ] 83.09±2.81 59.05±6.56 33.22±3.88 97.57±0.92 55.13±6.44 65.33±1.08 LCNN[36 ] 95.95±2.11 80.78±3.46 62.25±5.33 99.69±0.15 46.95±3.16 77.26±0.53 TDACAPS[14 ] 98.25±3.89 84.98±7.12 82.48±5.96 98.24±0.62 44.75±5.50 81.90±1.09 ETDTBN 99.75±0.15 75.51±1.85 95.27±2.54 99.93±0.05 50.21±0.45 84.15±0.41
从表3 可以看出,当识别不同受试者的sEMG时,利用本实验的12种方法,能够较好地识别动作WE,但对动作WF的分类效果不理想. CNN模型通过加强二维化方法处理后,提升了总体准确率,对于除WF外的其他手势,均达到了大于80%的准确率. 以Bi-GRU和LSTM为代表的RNN在本实验中表现欠佳,但在动作WF的识别上优于其他模型. 与LCNN模型相比,ETDTBN模型的总体分类准确率提高了6.89%,ETDTBN模型是所有方法中效果最优的,总识别率为84.15%. 本文提出的方法对动作HC、RF、WE的识别效果均达到最佳,HO与WF的识别率虽然没有达到良好的预期,但高于大部分方法. ...
... Computational resource analysis for all methods
Tab.5 方法 N p /106 C /MBt e /st p /st r /msKNN+FE[30 ] — — 0.78±0.01 86.86±1.22 0.020±0.001 SVM+FE[31 ] — — 0.48±0.01 77.06±1.62 0.030±0.001 CNN[8 ] 4.98 162.73 22.65±0.98 148.61±3.38 0.078±0.003 CNN+FE 0.76 117.30 14.13±0.46 101.32±2.11 0.066±0.002 CNN+FE+ETD 1.15 184.48 20.19±0.65 153.51±3.65 0.086±0.002 RESNET+FE[32 ] 0.55 336.88 21.96±0.52 147.53±4.06 0.071±0.002 Bi-GRU[33 ] 1.41 118.10 16.76±0.50 160.49±2.98 0.078±0.002 LSTM[34 ] 1.52 146.35 17.14±0.59 168.25±3.16 0.082±0.002 TRANSFORMER[35 ] 2.49 335.68 24.16±0.66 187.23±4.56 0.079±0.002 LCNN[36 ] 1.77 533.50 21.06±0.62 180.85±4.29 0.082±0.003 TDACAPS[14 ] 0.87 741.38 216.45±6.16 1978.12 ±14.181.047±0.030 ETDTBN 3.73 321.41 17.85±0.48 156.28±3.99 0.076±0.002
从表6 可知,ETDTBN模型在3个NinaPro数据集中均取得了最高的识别准确率,在包含10个受试者数据中的NinaPro DB4数据集上,与其他算法相比,模型提升效果最明显. 可知,ETDTBN模型在手势分类问题上具备较好的泛化性和鲁棒性. ...
3
... Recognition effect of each method under electrode displacement
Tab.2 方法 P c /%P o /%HC HO RF WE WF KNN+FE[30 ] 28.21±0.00 9.23±0.00 94.90±0.00 100±0.00 100±0.00 66.67±0.00 SVM+FE[31 ] 42.64±0.00 18.97±0.00 87.82±0.00 100±0.00 100±0.00 70.49±0.00 CNN[8 ] 90.72±6.97 13.42±7.82 23.21±10.15 96.79±2.58 96.75±5.29 64.18±2.73 CNN+FE 29.89±4.24 33.91±16.26 95.01±3.60 98.90±1.31 91.58±10.66 70.87±2.74 CNN+FE+ETD 85.56±4.44 40.33±13.50 75.20±8.05 98.85±1.18 86.18±5.24 78.24±2.26 RESNET+FE[32 ] 31.09±3.94 35.17±10.96 90.78±4.88 98.92±1.29 92.22±3.26 70.78±2.66 Bi-GRU[33 ] 84.10±8.19 5.41±5.09 72.67±10.26 100±0.00 99.34±1.09 72.04±2.35 LSTM[34 ] 73.64±11.84 4.33±1.99 71.13±18.33 100±0.00 99.40±1.02 70.88±3.55 TRANSFORMER[35 ] 80.64±5.84 20.15±3.53 66.17±8.62 98.55±1.38 89.14±2.19 66.14±3.25 LCNN[36 ] 93.13±2.98 12.51±3.53 81.03±6.54 98.26±0.52 91.08±4.90 76.38±0.94 TDACAPS[14 ] 97.59±2.62 74.87±15.71 95.18±4.42 98.56±1.82 55.39±16.87 84.77±0.82 ETDTBN 99.80±0.41 66.36±6.90 69.85±7.44 100±0.00 99.85±0.36 86.95±1.64
以KNN和SVM为代表的传统机器学习模型在动作WE和WF上的识别效果最好,均达到了100%的识别率,但对于其他手势动作的识别效果不理想. Bi-GRU的总体准确率略高于LSTM和TRANSFORMER,且Bi-GRU在模型结构上更简单,训练参数与时间更少,故选用Bi-GRU作为网络提取原信号时间特征的部分. 将提出的加强二维化方法用于CNN模型,与CNN+FE和RESNET+FE模型相比,整体识别率分别提高了7.37%和7.46%,在动作HO的识别上效果有所提升,说明利用该方法能够挖掘出HO的部分特性. 与LCNN相比,ETDTBN在保持动作HC、WE和WF接近100%识别率的情况下,对手势HO的分类准确率提高了53.85%,且该模型在12种方法中的总体识别率最高,达到86.95%,说明利用提出的方法能够有效地识别肌电信号. ...
... Recognition accuracy of each method under different subject
Tab.3 方法 P c /%P o /%HC HO RF WE WF KNN+FE[30 ] 97.18±0.00 72.99±0.00 47.95±0.00 93.50±0.00 42.14±0.00 70.75±0.00 SVM+FE[31 ] 64.27±0.00 86.24±0.00 51.71±0.00 100.00±0.00 52.99±0.00 71.04±0.00 CNN[8 ] 87.35±3.45 66.63±0.58 58.44±2.09 98.94±0.65 40.85±1.05 70.49±0.86 CNN+FE 71.99±4.16 90.51±1.85 80.87±7.59 99.82±0.49 31.39±7.51 75.06±0.18 CNN+FE+ETD 82.63±2.37 80.13±3.88 82.22±6.97 99.25±0.78 33.68±8.55 77.57±0.78 RESNET+FE[32 ] 73.79±3.96 85.22±2.78 81.17±6.19 99.22±0.65 32.11±6.95 74.96±0.26 Bi-GRU[33 ] 82.06±6.71 66.26±7.42 37.35±3.84 94.65±2.52 63.98±5.02 68.93±0.38 LSTM[34 ] 78.79±6.81 60.85±5.56 40.32±3.96 99.27±0.72 54.03±6.77 67.08±1.11 TRANSFORMER[35 ] 83.09±2.81 59.05±6.56 33.22±3.88 97.57±0.92 55.13±6.44 65.33±1.08 LCNN[36 ] 95.95±2.11 80.78±3.46 62.25±5.33 99.69±0.15 46.95±3.16 77.26±0.53 TDACAPS[14 ] 98.25±3.89 84.98±7.12 82.48±5.96 98.24±0.62 44.75±5.50 81.90±1.09 ETDTBN 99.75±0.15 75.51±1.85 95.27±2.54 99.93±0.05 50.21±0.45 84.15±0.41
从表3 可以看出,当识别不同受试者的sEMG时,利用本实验的12种方法,能够较好地识别动作WE,但对动作WF的分类效果不理想. CNN模型通过加强二维化方法处理后,提升了总体准确率,对于除WF外的其他手势,均达到了大于80%的准确率. 以Bi-GRU和LSTM为代表的RNN在本实验中表现欠佳,但在动作WF的识别上优于其他模型. 与LCNN模型相比,ETDTBN模型的总体分类准确率提高了6.89%,ETDTBN模型是所有方法中效果最优的,总识别率为84.15%. 本文提出的方法对动作HC、RF、WE的识别效果均达到最佳,HO与WF的识别率虽然没有达到良好的预期,但高于大部分方法. ...
... Computational resource analysis for all methods
Tab.5 方法 N p /106 C /MBt e /st p /st r /msKNN+FE[30 ] — — 0.78±0.01 86.86±1.22 0.020±0.001 SVM+FE[31 ] — — 0.48±0.01 77.06±1.62 0.030±0.001 CNN[8 ] 4.98 162.73 22.65±0.98 148.61±3.38 0.078±0.003 CNN+FE 0.76 117.30 14.13±0.46 101.32±2.11 0.066±0.002 CNN+FE+ETD 1.15 184.48 20.19±0.65 153.51±3.65 0.086±0.002 RESNET+FE[32 ] 0.55 336.88 21.96±0.52 147.53±4.06 0.071±0.002 Bi-GRU[33 ] 1.41 118.10 16.76±0.50 160.49±2.98 0.078±0.002 LSTM[34 ] 1.52 146.35 17.14±0.59 168.25±3.16 0.082±0.002 TRANSFORMER[35 ] 2.49 335.68 24.16±0.66 187.23±4.56 0.079±0.002 LCNN[36 ] 1.77 533.50 21.06±0.62 180.85±4.29 0.082±0.003 TDACAPS[14 ] 0.87 741.38 216.45±6.16 1978.12 ±14.181.047±0.030 ETDTBN 3.73 321.41 17.85±0.48 156.28±3.99 0.076±0.002
从表6 可知,ETDTBN模型在3个NinaPro数据集中均取得了最高的识别准确率,在包含10个受试者数据中的NinaPro DB4数据集上,与其他算法相比,模型提升效果最明显. 可知,ETDTBN模型在手势分类问题上具备较好的泛化性和鲁棒性. ...
Surface-electromyography-based gesture recognition by multi-view deep learning
1
2019
... Recognition effectiveness of each method on public dataset
Tab.6 方法 P o /%ChenNet[8 ] 68.23±2.07 71.74±3.67 67.25±4.49 HuNet[10 ] 81.18±5.69 82.21±5.69 69.52±3.94 WeiNet[37 ] 82.06±3.47 80.72±4.97 53.27±5.77 ETDTBN 82.59±4.46 83.01±3.42 77.16±3.98
4. 结 语 为了充分提取sEMG的有效特征,提高对相似手势的识别准确率,本文提出的ETDTBN模型利用加强二维化方法,将一维离散特征通过特征组合的形式构成二维规则特征图,加强了不同特征之间的联系,解决了原离散特征二维化方法生成的二维特征关系图参数重复冗余、特征信息稀疏的问题. 利用CNN在图像空间数据特征上的泛化能力,结合Bi-GRU网络善于提取信号时序特征的优势,利用2种网络同时挖掘sEMG信号的空间特征与时间特征. 利用SAFF策略对不同分支进行融合,组成时空特征,这样包含的信息更加全面,更有利于后续的分类. ...