路径规划是无人机(unmanned aerial vehicle, UAV)作业的核心问题[1]. 覆盖路径规划(coverage path planning, CPP)的主要任务是高效率地遍历任务区域并避开区域内的障碍物,该项应用在智能农业、遥感测绘、河流巡检和自主清洁等行业具有重要意义[2-5]. CPP算法可分为2种形式:经典式和启发式. 经典算法包括传统的路径规划算法,如随机漫步、动态规划. Pang等[6]设计的基于均方位移和截断随机游走的改进算法提升了搜索效率,Xie等[7]基于动态规划找到了覆盖区域的最优顺序. 经典算法在处理如旅行商问题(traveling salesman problem, TSP)的NP难[8]问题时,在适应复杂环境和提升覆盖效率方面显示出局限性[9]. 因此研究者越来越倾向于采用启发式算法,如蚁群算法(ant colony optimization, ACO)[10]、遗传算法(genetic algorithm, GA)[11]和基于强化学习的深度Q网络(deep Q network, DQN)、近端策略优化(proximal policy optimization, PPO)算法[12-13],以提高CPP任务的效率和适应性. 此外,杜楠楠等[14]提出基于无向图搜索方法的多无人机覆盖路径优化模型,通过有限遍历覆盖飞行的方向角,选择能流效率相对最优的飞行方向;Tnunay等[15]针对多无人机编队覆盖问题,基于虚拟引导者的最小网络拓扑生成具有动态约束的最小抖动时间参数轨迹和覆盖轨迹. 以上研究主要集中于旋翼UAV,而旋翼UAV的有效载荷小、续航时间短,难以完成大范围和远距离的CPP任务.
本研究聚焦倾转旋翼UAV (tilt-rotor UAV, TRUAV),这种新型无人机结合了旋翼UAV的垂直起降能力和固定翼UAV的高速长航时优点,能够适应多样化的复杂环境. TRUAV的非完整约束为CPP任务带来了新的挑战[16]. 已有研究基于改进的GA设计针对TRUAV的CPP算法,考虑了飞行动力学约束[17],但是没有考虑区域内可能存在的障碍物. 在现实任务环境中,阻碍正常飞行路线的不可穿越的障碍物常见,限制了该算法的现实应用. 本研究针对多障碍物约束下的凸多边形区域内的CPP任务,提出基于杜宾斯曲线的改进遗传算法(Dubins-based enhanced GA, DEGA). DEGA视CPP为TSP的变体,通过改进传统的GA,优化覆盖路径访问顺序,提高覆盖效率;结合杜宾斯路径生成符合TRUAV飞行动力学约束的平滑转弯路径. 为了保证飞行器避开区域内存在的障碍物,本研究提出适用于TRUAV特性的鱼尾形避障策略.
1. 问题描述和建模
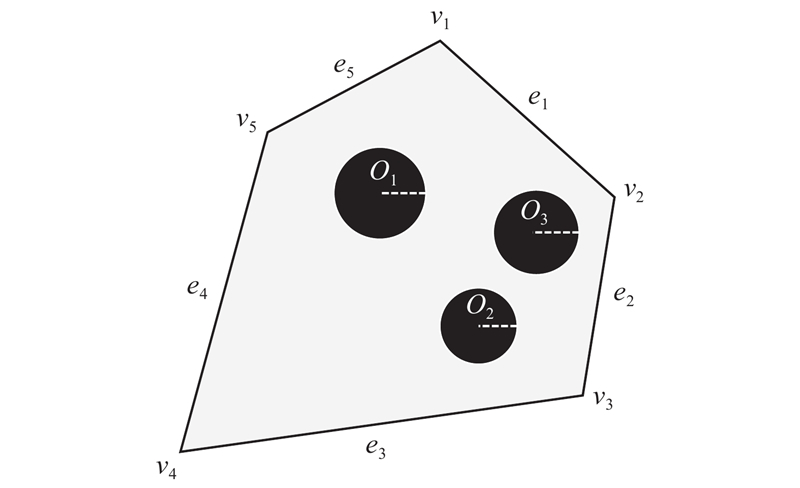
实际应用场景中的任务区域可能存在地形变化,为了简化问题,进行如下合理假设[18]. 1) 忽略TRUAV的大小和形状,在飞行过程中高度和俯仰角保持稳定,飞行速度稳定;2) 任务区域简化为凸多边形,忽略地形起伏;3) TRUAV在转弯和直线飞行中的误差在可接受范围,不考虑如阵风、侧滑的复杂因素. 在考虑TRUAV的构型特性和非完整约束时,须特别关注TRUAV在旋翼状态和固定翼状态间频繁切换带来的额外能耗以及倾转状态下复杂的气动特性对飞控系统的挑战. 为了减少能量消耗并提高飞行稳定性,TRUAV在起降过程中采用旋翼模式,在巡航和转弯过程中采用固定翼模式.
任务场景:装备机载相机的TRUAV从出发点
图 1
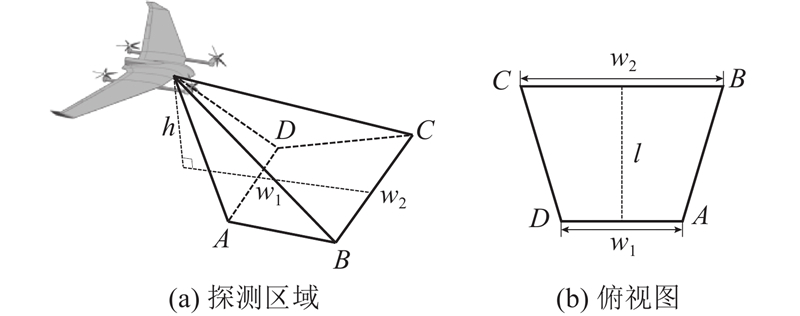
图 2
图 2 倾转旋翼无人机的相机视场
Fig.2 Camera field of view for tilt-rotor unmanned aerial vehicle
式中:
2. 障碍物约束下的区域覆盖路径规划
利用最小跨度算法确定TRUAV在区域内的最优飞行方向;根据最优飞行方向生成往返路径(back-and-forth path, BFP),从而得到任务区域的初规划覆盖路径;提出鱼尾形避障策略以应对区域内不可穿越的障碍物,从而生成区域内无碰撞的覆盖路径;DEGA用于优化覆盖路径的先后访问顺序,提高区域覆盖的任务效率,减少不必要的飞行距离.
2.1. 最小跨度算法
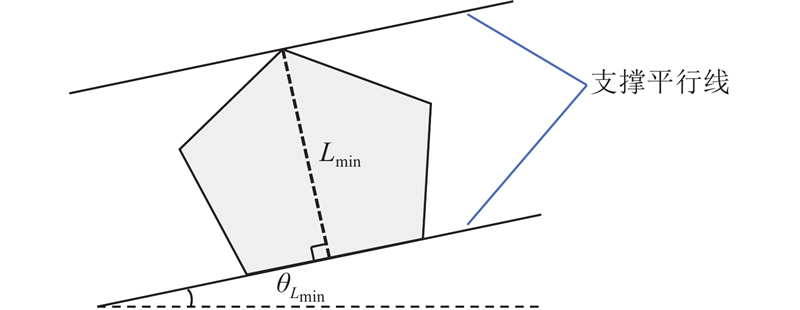
在固定的区域内执行覆盖任务时,TRUAV的飞行距离和能耗随转弯次数的增加而增加. TRUAV的航程有限,且转弯过程的耗能大于平飞过程,因此须找到区域内转弯总次数最少的飞行方向. 根据文献[20],基于减少转弯次数以优化覆盖任务距离的原则,当区域内的最优飞行方向平行于区域最小跨度
图 3
图 4
算法1 最小跨度
输入:凸多边形
输出:最小跨度
1. for
2. for
3. if
4.
5. end if;
6. end for;
7.
8. end for;
9.
10.
11.
2.2. 往返路径生成算法
对于给定的任务区域,常见的覆盖方法有螺旋形、之字形和往返形等. 在确定TRUAV的最优飞行方向后,采用BFP实现区域内的路径覆盖. BFP能够极大地简化路径计算过程,保证TRUAV在直线飞行时相机始终指向地面. 实现区域的完全覆盖须使第一条扫描路径与边界间的距离为扫描宽度
式中:
算法2 BFP生成算法
输入:凸多边形
输出:交点集
1. 将凸多边形
2. 找到旋转后
3. for
4.
5.
6. end for;
7. 将交点集
8. return
2.3. 鱼尾形避障策略
虽然算法2能够有效处理区域覆盖问题,但在多障碍物约束的区域内,基于BFP的覆盖路径可能受障碍物的影响,导致TRUAV无法依照原定的直线路线飞行. 比较障碍物的半径
图 5
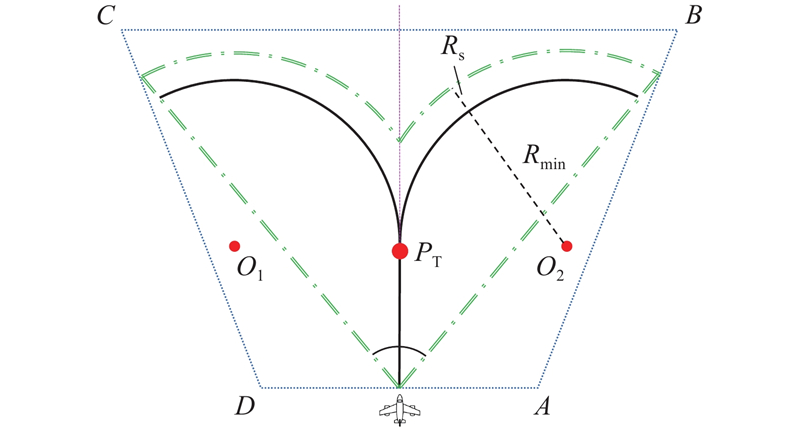
图 5 鱼尾形避障策略的探测范围
Fig.5 Detection range of fishtail-shaped obstacle avoidance strategy
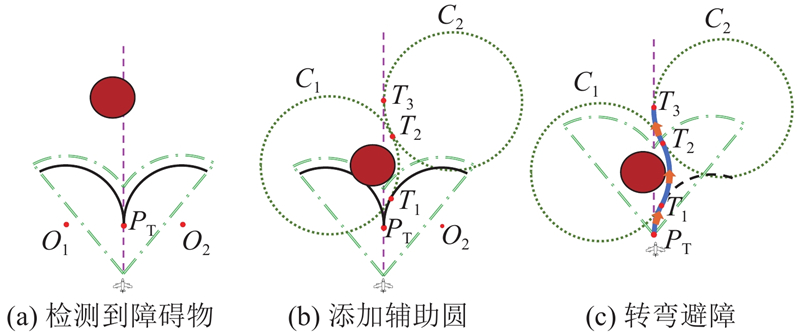
在区域内执行覆盖任务时,TRUAV进行当前规划路径障碍物探测,若探测到障碍物,则启动鱼尾形避障策略. 如图6(a)所示,设TRUAV在当前规划路径左侧检测到障碍物,TRUAV继续向前飞行,保持方向不变. 如图6(b)所示,当鱼尾形策略探测范围的边界圆弧形点划线与障碍物相切时,识别并添加2个半径为
图 6
图 6 鱼尾形避障策略的工作流程
Fig.6 Workflow of fishtail-shaped obstacle avoidance strategy
2.4. 基于杜宾斯曲线的改进遗传算法
对于给定的区域,覆盖路径长度为
式中:
传统CPP的算法依顺序覆盖任务区域,优点是算法逻辑简单、实现容易;缺点是方法存在很大的局限性,不足以应对复杂的环境,可能导致规划效率低下,尤其是当
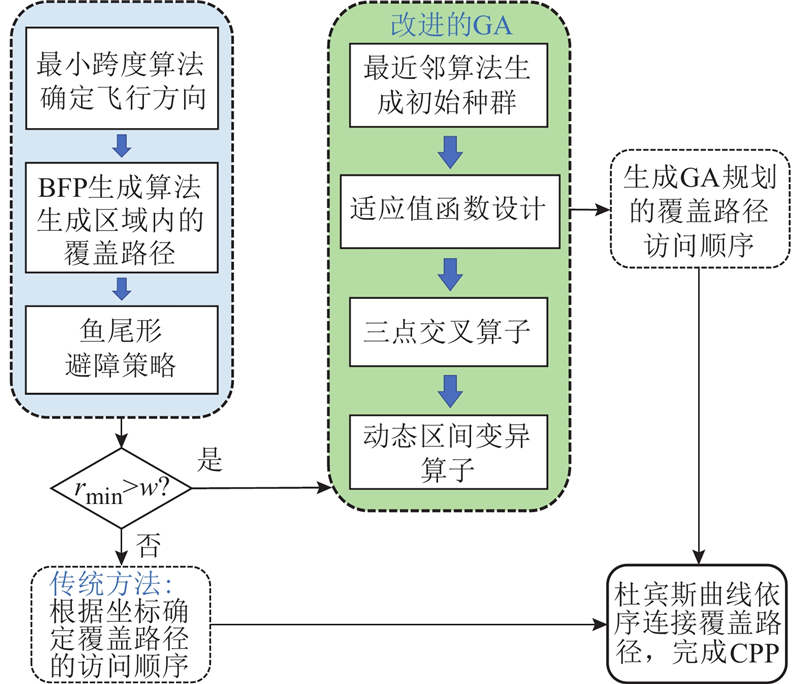
图 7
图 7 基于杜宾斯曲线的改进遗传算法流程
Fig.7 Workflow of Dubins-based enhanced genetic algorithm
2.4.1. 旅行商问题转化
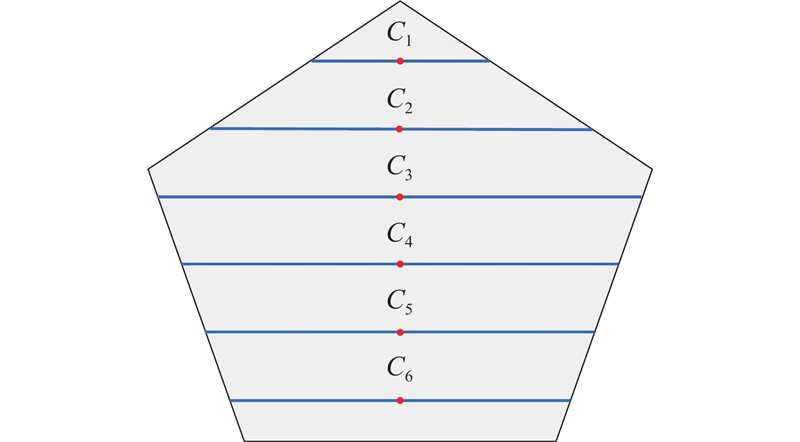
将BFP的访问顺序优化问题转化为TSP. CPP的任务特性决定了任务区域内的每条覆盖路径都必须被访问,且仅被访问一次. 因此,将区域内每条覆盖路径的中点视为TSP中必经的“城市”,并对这些“城市”按照顺序进行编号,编号方法如图8所示. BFP优化问题的TSP数学模型为
图 8
式中:
2.4.2. 改进的遗传算法
GA是基于生物遗传机制的启发式随机搜索算法,通过模拟自然选择、交叉、变异的过程,展现出强大的并行搜索和全局优化能力. 在GA种群中,染色体与潜在的覆盖路径访问顺序
1)初始种群的生成. 传统GA中的初始种群随机生成,可能生成大量低效或者非可行的解,无法捕捉到问题域中的先验知识和启发性信息,导致算法可能陷入局部最优解. 采用最近邻算法优化初始种群. 最近邻算法是有效的启发式搜索策略,常用于解决如TSP的组合优化问题. 如算法3所示,最近邻算法的核心思想是从某个随机的起始基因开始,逐步构建路径. 为了生成更均匀的初始种群,算法从距离当前基因最近的3个基因中择一添加到当前染色体中作为目标路径的一部分. 该过程重复进行,直到所有基因被访问一次,从而完成单个染色体的路径构建. 在此过程中,算法维护访问状态数组以确保每个基因只被访问一次,在选择下个“城市”时,已访问的“城市”不再被选中. 采用基于距离信息的启发式方法构建路径,优先选择相邻的基因,优化传统的随机生成种群策略,显著提高了初始种群的质量. 通过选择不同的起始基因,使解空间具有多样性,减少了早熟收敛的风险,能够避免算法陷入局部最优解.
算法3 最近邻算法
输入:所有覆盖路径间距离矩阵
输出:初始种群
1. for
2. 随机选取起始基因:
3. 初始化已访问列表:
4. 标记起始点为已访问:
5. for
6. 获取上一个基因到所有基因的距离:
7. 访问过的基因距离设为无穷:
8. 在距离最近的3个基因中随机选择作为下一个访问的基因:
9.
10. 标记该基因为已访问
11. end for;
12. end for;
13. return pop.
2) 适应度函数的设计. 适应度函数在优化过程中扮演着至关重要的角色,通过量化种群中个体性能的差异来指导优化的方向. 合理设计的适应值函数不仅可以加速算法的收敛过程,还能助力在全局搜索空间中发现更优解决方案. 在CPP任务中,核心的优化目标是最小化TRUAV的覆盖路径长度,为此适应度函数采用杜宾斯曲线距离作为衡量基因间距离的指标. 杜宾斯曲线距离的计算方法简洁且物理意义清晰,能够准确地反映CPP任务中的转弯距离. 适应度函数的表达式为
式中:
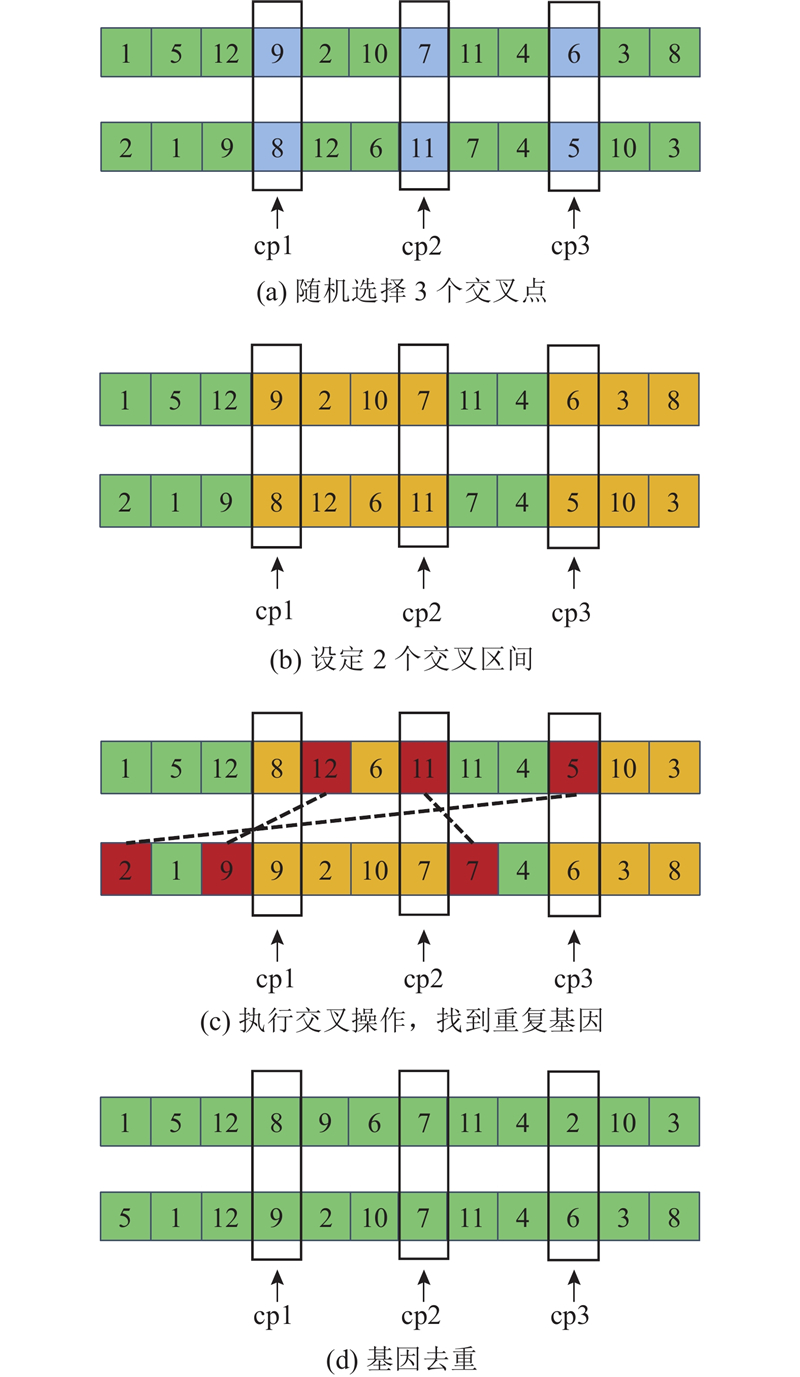
3) 交叉算子的改进. GA的交叉算子能够在解空间中进行全局搜索. 为了增强染色体间的信息交换,本研究提出三点交叉算子. 该算子不仅能够提高子代染色体的适应度,还继承了父代优秀的特性,具体的交叉操作如图9所示. 根据染色体的长度
图 9
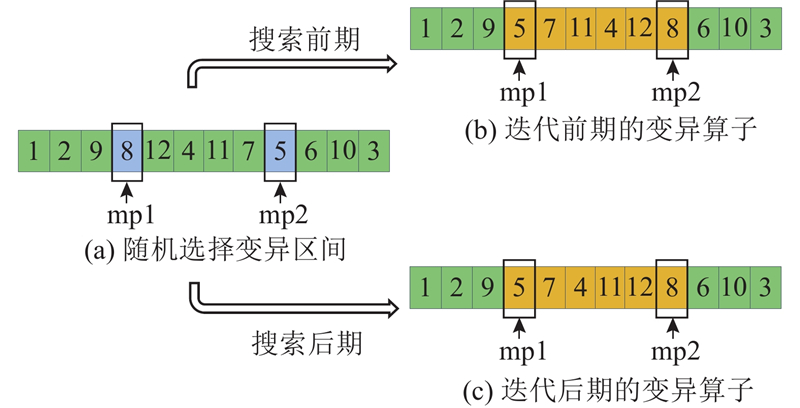
4) 变异算子的改进. 变异算子在当前解空间的局部邻域内引入随机扰动,旨在避免算法过早陷入局部最优并促进种群多样性的维持. 为了精细控制其对搜索过程的影响,变异概率应设定为较小值. 本研究提出的动态区间变异算子根据算法迭代的进程动态调整变异的强度,具体的变异算子操作如图10所示. 该算子根据
图 10
在迭代初期,变异算子施加较大强度的基因变异,区间内的所有基因进行前后互换以促进种群多样性的增加;在迭代的后期,随着算法接近收敛,区间内变异强度减弱,互换的基因长度按比例动态地减少,确保动态区间变异算子在接近全局最优解时的精细搜索. 动态区间变异算子通过当前迭代次数和预设的最大迭代次数之比来决定变异强度,实现探索与开发的动态平衡. 此策略的引入增加了搜索策略的灵活性,有效避免了算法过早收敛的问题,增强了算法在解空间中保持多样性的能力.
3. 实验验证
以Matlab为仿真实验工具,运行环境为Windows10, Intel(R) Core(TM) i5-7500 CPU @3.4 GHz. 实验主要包括1) 基于DEGA设计多个包含障碍物的任务区域作为测试案例;2) 以覆盖路径长度lt和执行时间te为评估指标,比较DEGA与现有CPP算法在覆盖效率和计算效率方面的性能. DEGA的主要参数如下:种群规模
图 11
3.1. 覆盖路径规划结果
DEGA根据TRUAV的扫描宽度
图 12
图 12 基于杜宾斯曲线的改进遗传算法的转弯策略
Fig.12 Turning strategy of Dubins-based enhanced genetic algorithm
图 13
图 13 不同算法的四边形区域覆盖路径规划
Fig.13 Paths planned by different algorithms covering quadrilateral region
图 14
图 14 不同算法的五边形区域覆盖路径规划
Fig.14 Paths planned by different algorithms covering pentagon region
3.2. 算法性能对比
对四边形区域和五边形区域进行仿真实验,引入3种扫描宽度,共6个测试场景. 设定的出发点
表 1 区域覆盖路径算法的性能对比(四边形区域)
Tab.1
| 算法 | lt/km | te/s | |||||
| n=10 | n=20 | n=50 | n=10 | n=20 | n=50 | ||
| DEGA | 8.491 | 18.924 | 80.665 | ||||
| GA | 8.356 | 18.708 | 77.156 | ||||
| SPC | 1.239 | 2.033 | 4.562 | ||||
表 2 区域覆盖路径算法的性能对比(五边形区域)
Tab.2
| 算法 | lt/km | te/s | |||||
| n=10 | n=20 | n=50 | n=10 | n=20 | n=50 | ||
| DEGA | 9.117 | 19.912 | 80.386 | ||||
| GA | 8.948 | 19.588 | 78.633 | ||||
| SPC | 1.418 | 1.998 | 4.567 | ||||
4. 结 语
研究倾转旋翼无人机在多障碍物约束下的规则区域覆盖路径规划问题,考虑倾转旋翼无人机的运动学特点,提出鱼尾形避障策略,并提出新型覆盖路径规划算法DEGA. 通过结合鱼尾形避障策略和杜宾斯曲线,所提算法显著提高了倾转旋翼无人机的区域覆盖效率. 在四边形和五边形任务区域内引入3种扫描宽度并开展不同路径规划算法的性能对比实验. 结果表明,在优化覆盖路径长度方面,DEGA相较于传统遗传算法和逐行路径覆盖算法表现更佳,在不明显增加计算成本的情况下,所规划的覆盖路径总长度远小于对比算法,充分证明DEGA在提升覆盖效率方面的显著效果. 后续研究将把DEGA应用于真实的倾转旋翼无人机飞行实验中,进一步验证该算法在实际应用中的效果和可行性.
参考文献
R-DFS: a coverage path planning approach based on region optimal decomposition
[J].DOI:10.3390/rs13081525 [本文引用: 1]
A new method using knowledge reasoning techniques for improving robot performance in coverage path planning
[J].
Optimal UAV route planning for coverage search of stationary target in river
[J].
A survey on the application of path-planning algorithms for multi-rotor UAVs in precision agriculture
[J].DOI:10.1017/S0373463321000825 [本文引用: 1]
Effect of random walk methods on searching efficiency in swarm robots for area exploration
[J].DOI:10.1007/s10489-020-02060-0 [本文引用: 1]
An integrated traveling salesman and coverage path planning problem for unmanned aircraft systems
[J].DOI:10.1109/LCSYS.2018.2851661 [本文引用: 1]
A comprehensive review of coverage path planning in robotics using classical and heuristic algorithms
[J].DOI:10.1109/ACCESS.2021.3108177 [本文引用: 1]
Coverage path planning of heterogeneous unmanned aerial vehicles based on ant colony system
[J].DOI:10.1016/j.swevo.2021.101005 [本文引用: 1]
Solution of an integrated traveling salesman and coverage path planning problem by using a genetic algorithm with modified operators
[J].DOI:10.33965/ijcsis_2019140206 [本文引用: 1]
Reinforcement learning-based energy-aware area coverage for reconfigurable hRombo tiling robot
[J].DOI:10.1109/ACCESS.2020.3038905 [本文引用: 1]
多太阳能无人机覆盖路径优化方法
[J].
Optimization method for coverage path planning of multi-solar powered UAVs
[J].
al. Global optimization of UAV area coverage path planning based on good point set and genetic algorithm
[J].DOI:10.3390/aerospace9020086 [本文引用: 1]
CARRILLO L R G, JIN L. Path planning for UAV to cover multiple separated convex polygonal regions
[J].DOI:10.1109/ACCESS.2020.2980203 [本文引用: 1]
基于最小转弯半径的无人机转弯航迹规划算法
[J].
UAV turning path planning algorithm based on minimum turning radius
[J].
Coverage path planning for UAVs based on enhanced exact cellular decomposition method
[J].DOI:10.1016/j.mechatronics.2010.10.009 [本文引用: 2]