Wang等[7]提出基于优势参与者-批评者(advantage actor-critic)算法的交通信号控制方法. 为了有效利用周边智能体的空间信息,Wang等[7]设计了基于图注意力网络的区域感知合作策略. 由于使用分散式控制,容易导致用于模型训练的环境状态不完整. Wang等[8]提出基于多智能体强化学习的交通信号控制方法. 为了能够更好地从相邻交叉口的历史数据中学习经验,Wang等[8]提出新的经验共享策略. Ma等[9]提出基于强化学习Actor-Critic模型的交通信号配时方法. 该方法在一定程度上避免了单纯基于值或策略的强化学习方法的缺陷,提高了交叉口的通行效率. Bouktif等[10]提出基于混合深度强化学习的交通信号控制方法,设计分层决策深度强化学习网络,优化下一个阶段待执行的相位及绿灯持续时间. Chu等[11]提出基于可扩展分散多智能体强化学习的交通信号控制方法. 虽然该方法通过提高环境的可观察性来稳定学习过程,但对所采样的经验信息的利用不够充分. 刘智敏等[12]提出基于改进深度强化学习的交通信号控制方法. 利用相邻时间步交叉口车辆数变化量构建新的奖励函数,能够及时跟踪和准确描述车道上交通状态的动态变化过程.
上述方法一般直接定义车辆速度和位置矩阵作为深度强化学习模型的输入,不仅因为涉及的参数多,增加了模型计算量,也忽略了速度矩阵和位置矩阵之间存在的冗余信息. 为了解决上述问题,本文提出基于车辆权重的A3C强化学习交通信号控制方法. 通过设计权重神经网络,对采集的交通状态进行预处理,提升强化学习模型的学习和决策能力. 在强化学习模型的输入端分别从交叉口和车道2个不同维度构建车辆权重增益网络,对车辆运动状态信息进行处理,网络输出的车辆权重系数可以更有效地反映不同运动状态下车辆的通行优先级. 以定时控制、模糊自适应控制及基于DQN和A3C的交通信号控制方法作为对照,在低、中、高3种不同交通流量模式下进行仿真测试,实验结果验证了本文所提方法的有效性.
1. 交通信号控制强化学习要素的定义
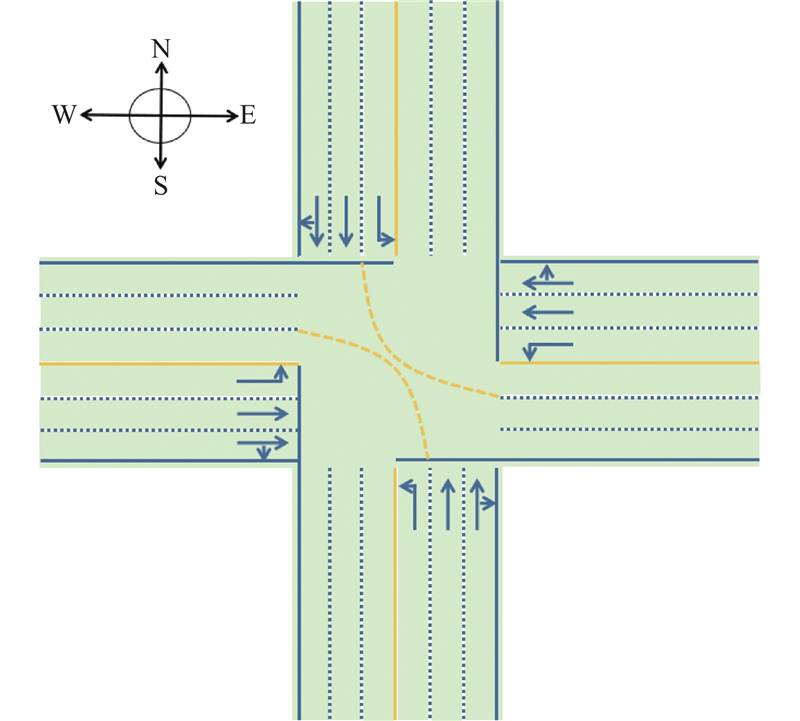
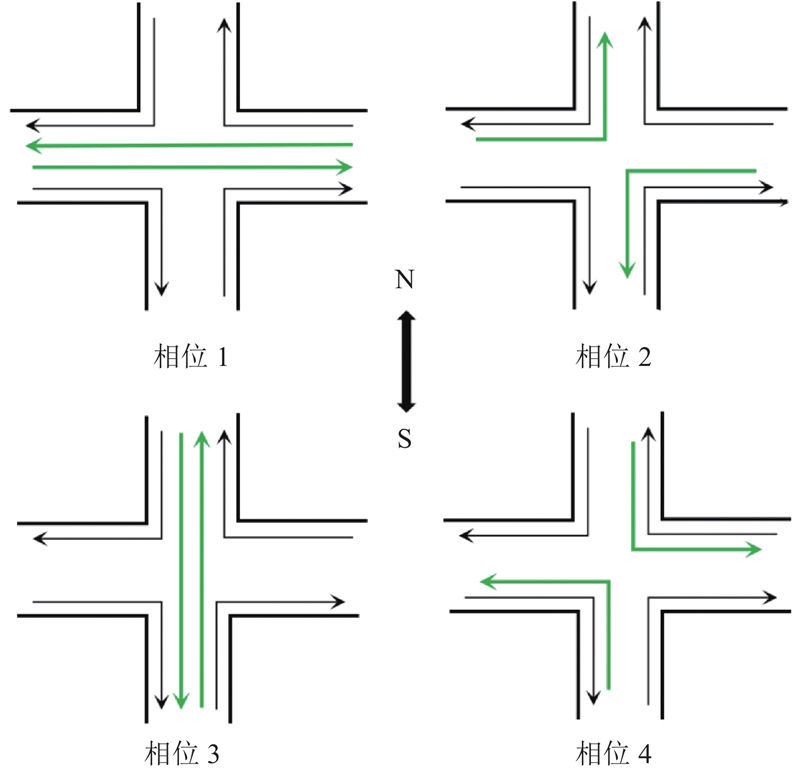
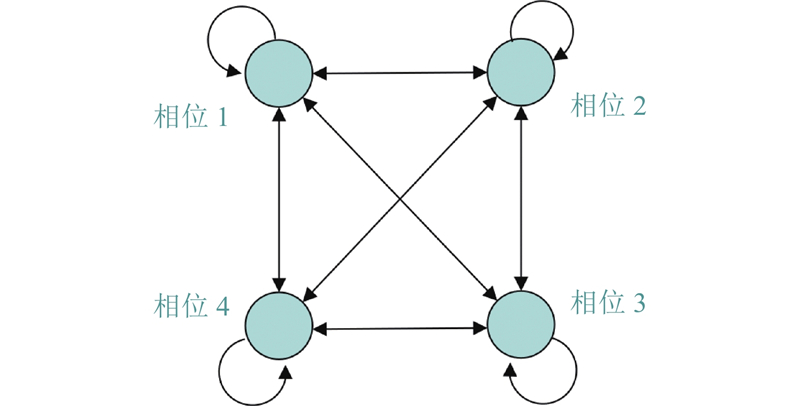
如图1所示,以典型十字交叉口为例进行具体描述. 该交叉口有4个进车方向,且每个进车方向上有3条车道,分别为1条直行右转车道、1条直行车道、1条左转车道. 为了便于描述,在交通信号控制框架下,分别定义强化学习的3个要素:状态、动作和奖励.
图 1
1.1. 输入状态和动作空间
在所构建的权重网络中,需要基于各个车道上的车辆数量和各个车道排队等待通行的车辆数量确定车辆的权重关系. 考虑到如图1所示的交叉口共有12条进口车道,可以将采集的该交叉口输入交通状态定义为矩阵M2×12. 从北进口方向的直行和右转共用车道开始,按顺时针方向依次采集各条车道的交通状态信息. 矩阵第1行中的各元素分别表示各条车道上的车辆总数,第2行中的各元素分别表示各条车道上排队等待通行的车辆数.
图 2
图 3
1.2. 奖励函数
综合考虑通过交叉口的车辆数和车辆等待时间这2个交通效益评价指标来设计奖励函数,能够更全面地评估当前输出动作决策的有效性. 根据多个指标来综合评定动作决策的优劣,可以激励强化学习算法进行多目标优化,使其在不同的交通状态下均能有良好的表现. 为了提高深度强化学习算法的决策能力,设计新的奖励函数,即采用当前采样时间步交叉口总的车辆等待时间的变化率和通过交叉口的车辆数的变化率来定义强化学习的奖励函数. 计算车辆等待时间的变化率
式中: wt为在第t个采样时间步交叉口各条车道上车辆的等待时间之和,wt−1为第t−1个采样时间步交叉口各条车道上车辆的等待时间之和.
式中: pt为在第t个采样时间步通过交叉口各车道的车辆数之和,pt−1为第t−1个采样时间步通过交叉路口各车道的车辆数之和.
在复杂系统中,连续的输入空间可能会导致控制策略过于复杂,难以优化和实施. 对得到的变化率进行处理,根据Wchange_rate和Pchange_rate确定等待时间的奖励值Rw和通过车辆数的奖励值Rp. 具体的分段计算规则如表1所示.
表 1 奖励分段规则
Tab.1
| Rw(Rp) | Wchange_rate (Pchange_rate) |
| 4 | (0.35, +∞) |
| 3 | (0.25, 0.35] |
| 2 | (0.15, 0.25] |
| 1 | [0, 0.15] |
| −1 | [−0.15, 0) |
| −2 | [−0.25, −0.15) |
| −3 | [−0.35, −0.25) |
| −4 | (−∞, −0.35) |
综上所述,设计的目标奖励函数定义如下:
式中:λ1和λ2分别为奖励Rw和Rp对应的权重系数. 设计上述奖励函数的目的是使深度强化学习智能体能够更好地响应车流的动态变化过程,使用变化率作为奖励来提高模型对突发事件的敏感度及强化学习算法的稳定性.
2. 车辆权重增益网络
对采样的交通状态信息进行处理和分析,提前获取一部分有代表性的交通特征信息,可以提高深度神经网络在挖掘深层次特征信息时的学习能力.
如图4所示,利用车辆权重增益网络对采集的交叉口车辆运动状态信息矩阵
图 4
图 4 车辆权重增益网络与A2C网络信息交互的示意图
Fig.4 Diagram of information exchange between vehicle weight gain network and network of A2C
从交叉口和车道2个不同维度上对车辆运动状态进行分析,构建交叉口级车辆权重增益网络(intersection vehicle weight gain network,IVWGN)和车道级车辆权重增益(lane vehicle weight gain network,LVWGN),对采集的车辆运动状态信息进行处理.
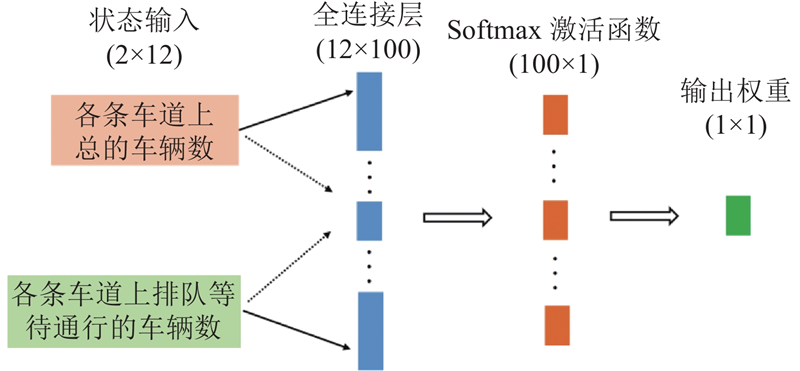
2.1. 交叉口级车辆权重增益网络
图 5
图 5 交叉口级车辆权重增益网络的示意图
Fig.5 Diagram of intersection vehicle weight gain network
在交叉口级车辆权重增益网络中,所有排队等待通行车辆的权重增益相同,因此输出权重矩阵的维度为1×1. 在得到增益权重后,利用下式计算各条车道上加权增益后的车辆数:
式中:
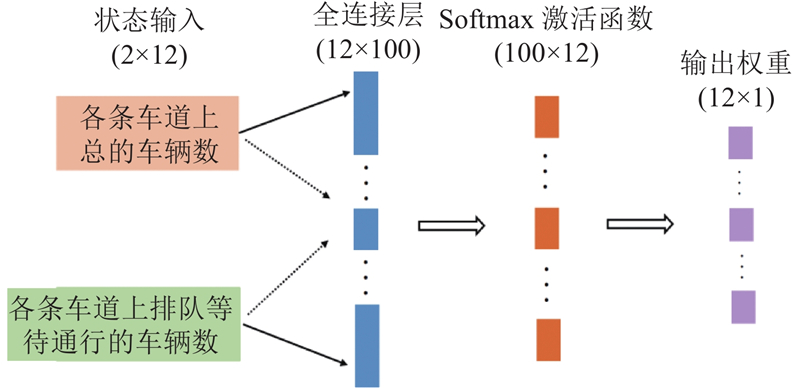
2.2. 车道级车辆权重增益网络
图 6
式中:
3. 基于融合车辆权重增益网络A3C的交通信号控制方法
3.1. 优势演员-评论家模型
式中:g
式中:
式中:
式中:
当训练策略网络时,对式(8)作近似,如下所示:
智能体执行动作at,环境会给出奖励rt和新的状态st+1,用观测到的奖励和新的状态对期望进行蒙特卡洛近似,得到
式中:
式中:θ为策略网络的参数,β为策略网络的学习率.
3.2. 车辆权重增益网络参数的更新
权重增益网络是基于A3C强化学习智能体的奖励来动态更新网络参数,更具体地说,车辆权重增益网络的参数是朝着使智能体产生正收益的方向进行动态更新.
在训练过程中,车辆权重的真实值无法直接得到,采用自举法对估计的车辆权重真实值进行更新计算. 在t时刻,环境状态为st,智能体执行动作at后,环境状态更新为st+1,智能体获得奖励rt . 假设t时刻车辆权重的估计值记为g(
式中:当rt−1 > 0时,rt−1/|rt−1|为正,表示车辆权重g(
式中:L(
式中:
3.3. 融合车辆权重增益的A3C算法(XVWG-A3C)
强化学习算法通常面临的共性问题是训练速度较慢[21]. 为了应对该问题,并行化训练被引入异步优势演员-评论家算法中. 该算法包括一个服务器和多个worker节点,通过并行化操作来提高训练速度.
在异步优势演员-评论家算法中,服务器维护策略网络和价值网络的最新参数,使用worker节点传来的梯度进行参数更新. 每个worker节点拥有独立的环境,通过本地策略网络控制智能体与环境进行交互,计算得到状态、动作和奖励对应的梯度,将梯度发送到服务器.
通过并行化训练流程,利用A3C算法能够同时训练多个子模型,大幅度减少训练时间,不受其他线程的干扰. 公共部分的网络模型是要学习的模型,线程中的网络模型主要用于与环境进行交互.
算法1 XVWG-A3C算法 1)设定全局共享参数向量 13 until T > Tmax
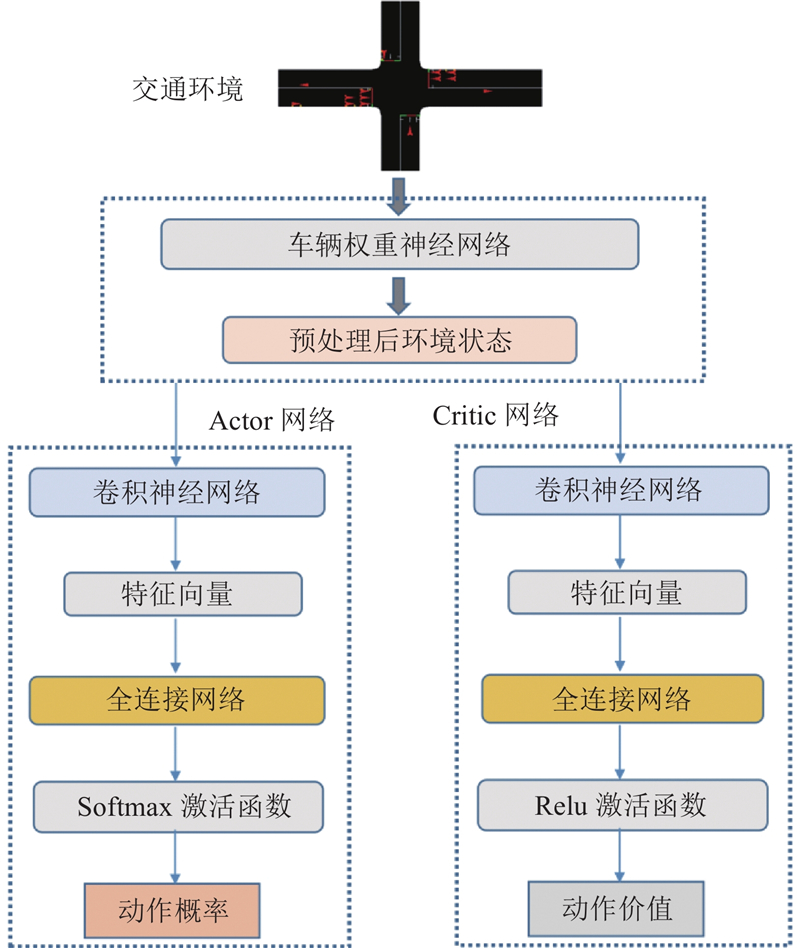
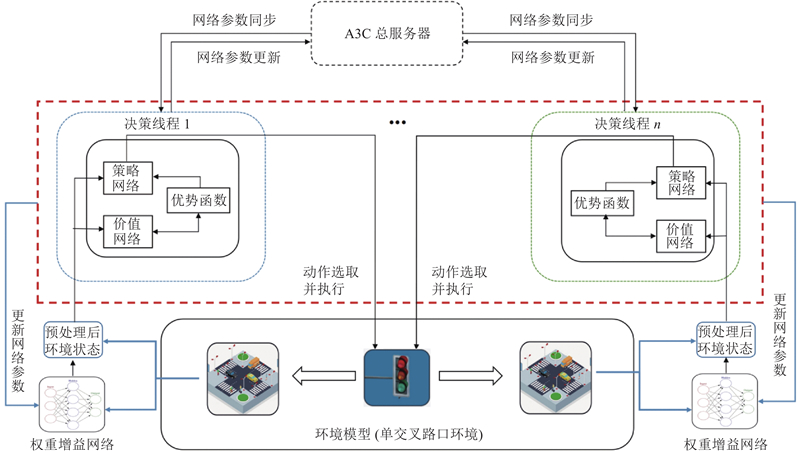
采样状态输入强化学习模型前需要进行预处理,对排队等待通行车辆权重进行动态增益. 算法1具体描述了融合车辆权重增益网络的A3C强化学习算法的具体执行步骤,图7展示了基于融合车辆权重增益网络的强化学习A3C的交通信号控制框架.
图 7
图 7 融合车辆权重增益网络的强化学习A3C交通信号控制框架
Fig.7 Framework of A3C based traffic signal control fused with vehicle weight gain network
4. 仿真与结果分析
4.1. 仿真环境与参数设置
为了验证所提方法的有效性,以如图1所示的交叉口为例开展仿真测试. 使用具备开源、微观和多模态特性的仿真软件SUMO作为测试平台,利用SUMO的Traci接口获取车辆实时交通状态信息.
将所提的基于融合车辆权重增益网络的A3C强化学习算法与DQN强化学习算法和基准A3C强化学习算法进行对比,具体参数如表2所示.
表 2 对比实验中各深度强化学习模型的参数设置
Tab.2
| 实验对比 | 参数 | 数值 |
| 融合权重增益网络的A3C 算法、传统A3C算法 | Actor网络学习率 | 0.000 02 |
| Critic网络学习率 | 0.000 2 | |
| Actor网络神经元数量 | 200 | |
| Critic网络神经元数量 | 100 | |
| 折扣因子 | 0.9 | |
| 训练步数 | 200 | |
| 训练时间/s | 7 200 | |
| DQN算法 | 学习率 | 0.000 02 |
| 神经元数量 | 200 | |
| 折扣因子 | 0.9 | |
| 训练步数 | 200 | |
| 训练时间/s | 7 200 |
为了测试交通信号控制在不同交通流量下的效果,设置低、中、高3种不同的车流量. 分别对应低流量(600辆/h)、中流量(1 000辆/h)和高流量(1 400辆/h),从4个不同进口方向随机生成车辆. 具体的参数设置如表3所示.
表 3 交通仿真环境的参数设置
Tab.3
| 参数 | 数值 |
| 车道长度/m | 100 |
| 平均车辆长度/m | 5 |
| 最小车辆间隔/m | 2.5 |
| 车辆最大速度/(m·s−1) | 13.89 |
| 车辆最大加速度/(m·s−2) | 2.6 |
| 车辆最大减速度/(m·s−2) | 4.6 |
| 黄灯时间/s | 3 |
| 相位保持时绿灯持续时间/s | 5 |
| 相位最小绿灯时间/s | 15 |
| 车辆直行概率 | 0.5 |
| 车辆左转概率 | 0.3 |
| 车辆右转概率 | 0.2 |
4.2. 实验结果与分析
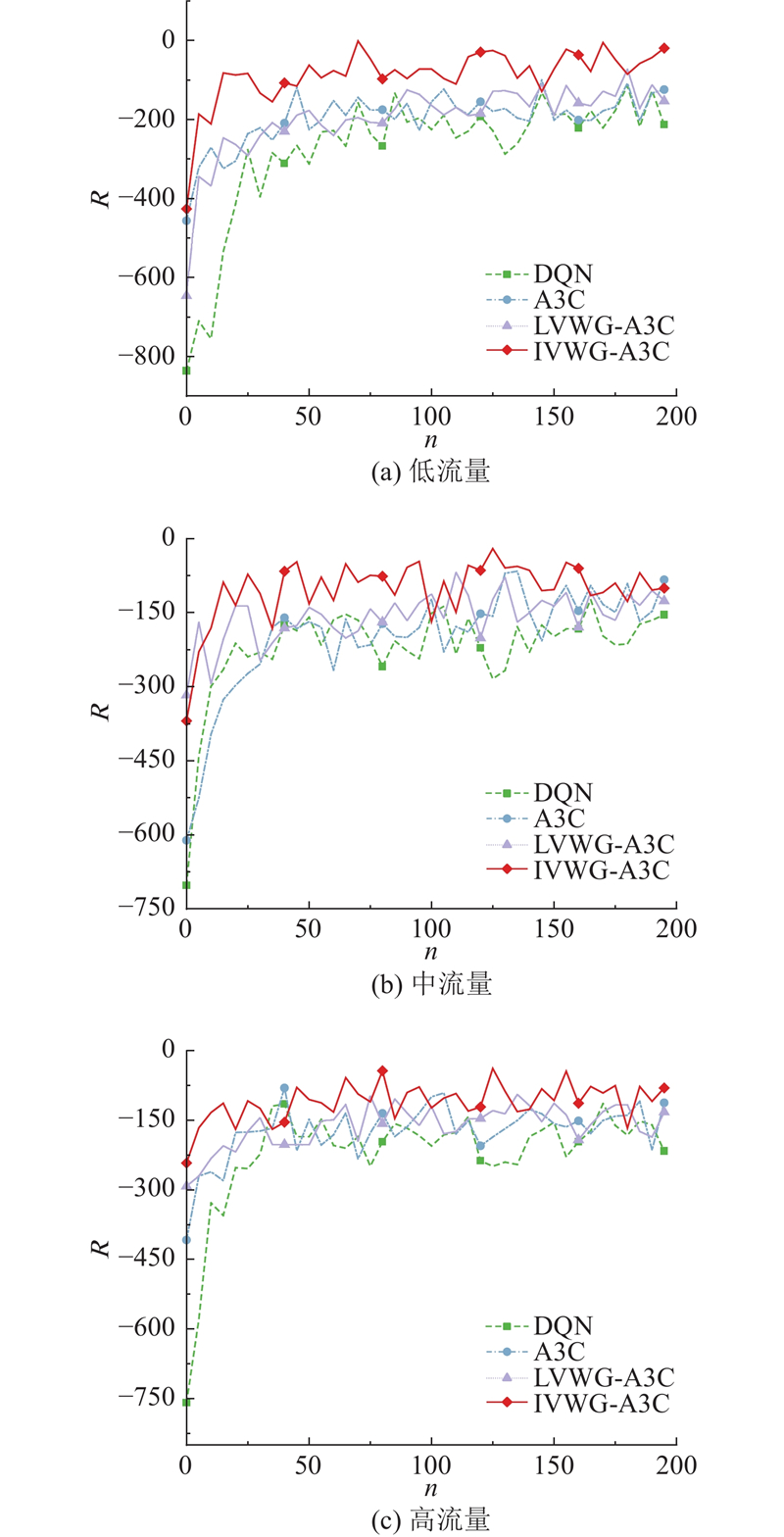
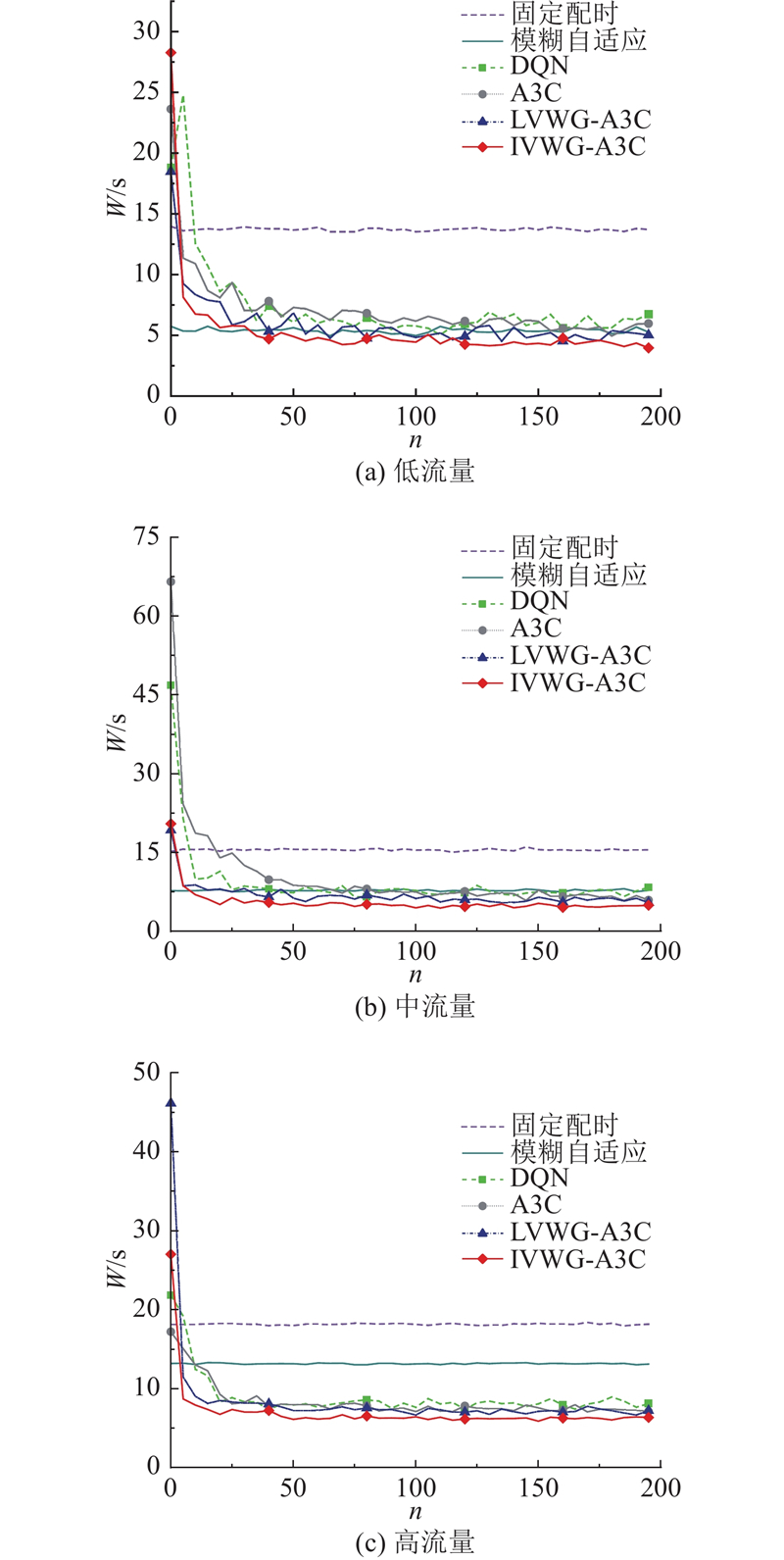
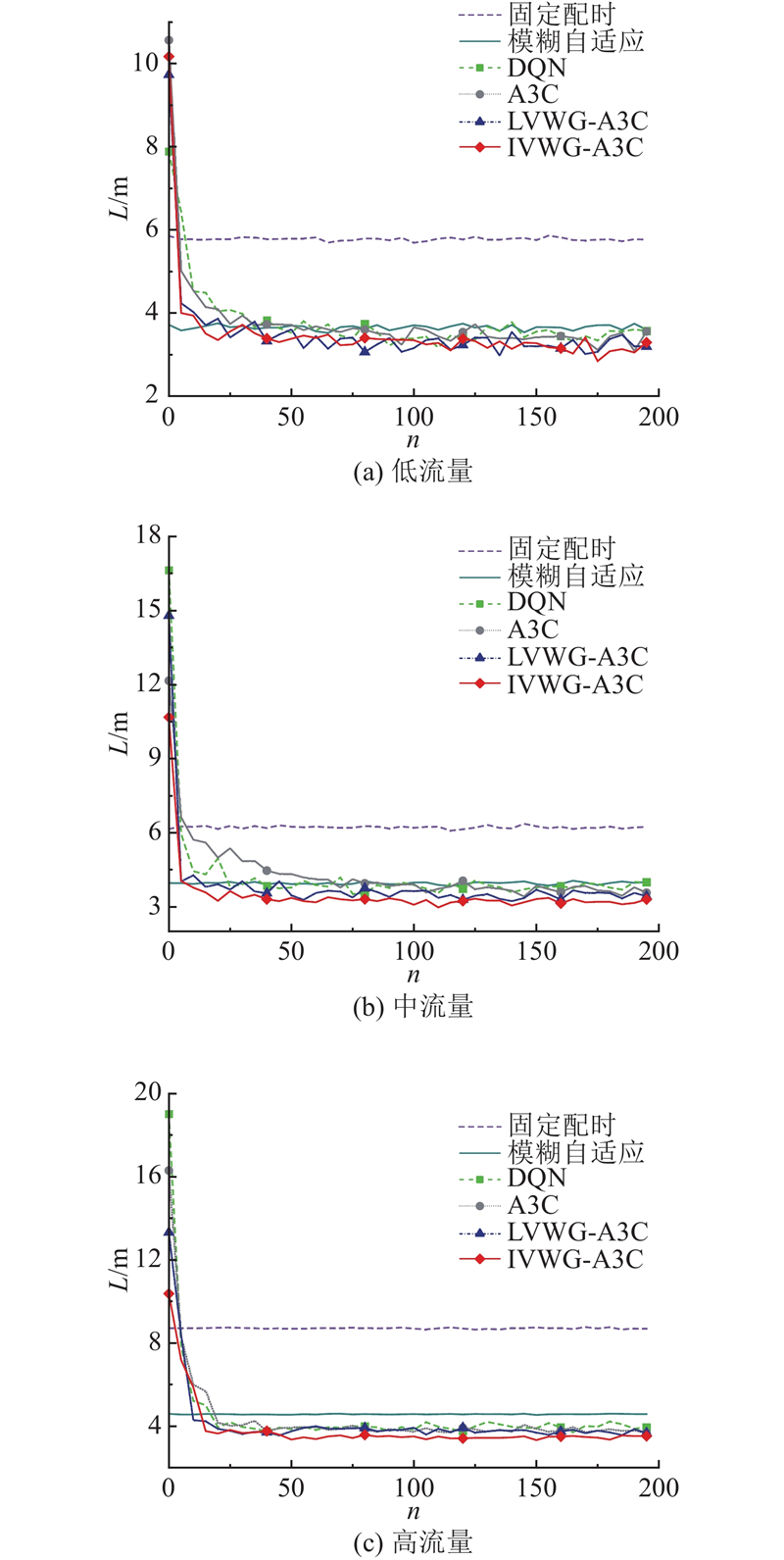
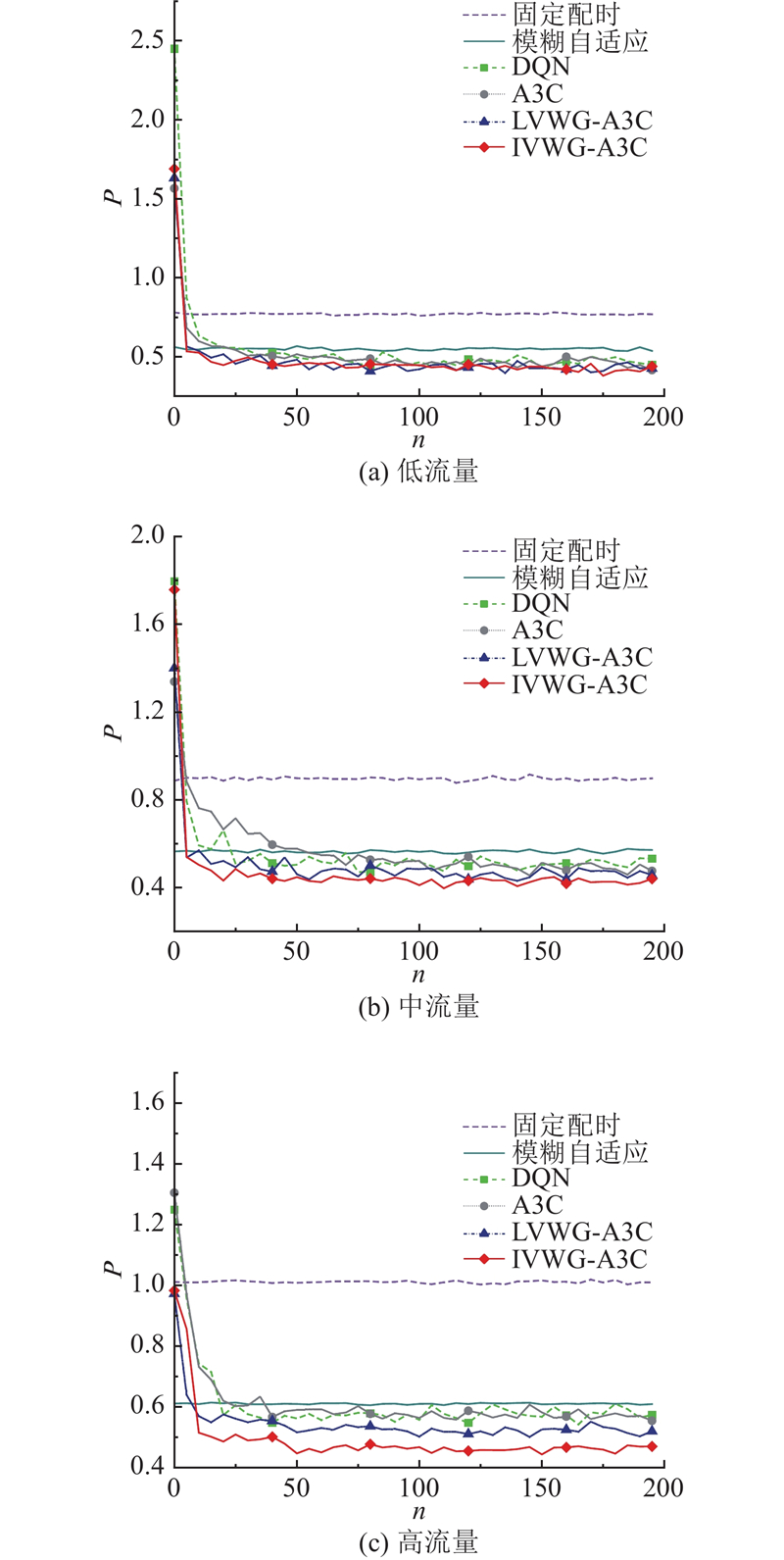
为了展示基于深度强化学习的交通信号控制方法相较于传统交通信号控制方法的优越性,选取传统的定时控制方法和模糊自适应方法作为对照组,开展仿真测试. 在定时控制下,交叉口各个相位的配时时间和顺序在不同的交通情况下保持不变. 模糊自适应方法依靠采集到的交通数据信息来调整模糊逻辑系统的参数,实时动态更新各个相位的绿灯时间,不改变相位的执行顺序. 为了分析和比较不同的交通信号控制方法在不同的交通流量条件下的控制效果,选择回合累积奖励、车辆平均等待时间、车辆平均排队长度和车辆平均停车次数4个评价指标,对各种交通信号控制方法进行评价,如图8~11所示. 图中,n为智能体的训练回合步数,R为智能体的累计回合奖励,W为车辆的平均等待时间,L为车辆的平均排队长度,P为车辆的平均停车次数. 在每个回合内,累积奖励越大,车辆平均等待时间越短,车辆平均排队长度和车辆停车次数越少,表示利用该方法确定交通信号配时方案的效果越好.
图 8
图 9
图 10
图 11
从图8(a)~(c)的结果可以看出,在基于深度强化学习的4种交通信号控制方法中,不同流量下各个强化学习模型都能收敛. 与深度强化学习模型DQN和基准A3C深度强化学习模型相比,融合了车辆权重增益网络的A3C深度强化学习模型LVWG-A3C和IVWG-A3C具有更好的模型收敛性能和更大的累计奖励. 与车道级车辆权重增益网络LVWG-A3C模型相比,交叉口级车辆权重增益网络的IVWG-A3C模型的收敛效果进一步增强. 上述实验结果表明,车辆权重增益网络可以显著改善深度强化学习A3C模型的收敛性能,采用交叉口级的车辆权重增益网络的效果更好.
与传统的交通信号控制方法相比,从图9~11所示的测试结果可知,定时控制和模糊自适应控制在低、中、高3种流量下的整体表现比较平稳,随着交通流量的增加,车辆平均等待时间、平均排队长度和平均停车次数均不断增大. 在各种流量条件下,模糊自适应控制算法在车辆平均等待时间、车辆平均排队长度和平均停车次数这3个指标上都优于定时控制. 在低流量交通状态下,模糊自适应在平均等待时间、平均排队长度和平均停车次数等指标上优于深度强化学习算法DQN,但弱于其他几种深度强化学习方法. 在中流量和高流量交通状态下,传统的定时控制方法和模糊自适应控制方法明显弱于所有参与对比的深度强化学习方法. 这表明随着车流量的不断增加,相比于传统控制方法,深度强化学习方法具有更好的控制效果.
如表4所示为不同交通信号控制方法的测试结果. 当采用LVWG-A3C算法时,与传统的DQN算法相比,在低、中、高流量下车辆的平均等待时间分别减少了16%、17%和14%,平均排队长度分别减少了7%、8%和7%,平均停车次数分别减少了8%、16%和11%. 与传统的DQN算法相比,采用IVWG-A3C算法得到的结果在低、中、高流量下的平均等待时间分别减少了23%、33%和37%,平均排队长度分别减少了13%、22%和24%,车辆平均停车次数减少了15%、21%和20%.
表 4 单路口情况下不同交通信号控制方法的测试结果
Tab.4
| 控制方法 | 低流量 | 中流量 | 高流量 | ||||||||||
| W/s | L/m | P | W/s | L/m | P | W/s | L/m | P | |||||
| 固定配时 | 13.85 | 5.83 | 0.77 | 15.68 | 6.28 | 0.91 | 17.31 | 8.62 | 1.01 | ||||
| 自适应 | 5.40 | 3.73 | 0.55 | 7.85 | 4.00 | 0.57 | 13.34 | 4.61 | 0.63 | ||||
| DQN | 6.14 | 3.54 | 0.47 | `7.38 | 3.81 | 0.55 | 8.32 | 4.05 | 0.59 | ||||
| A3C | 5.88 | 3.43 | 0.46 | 6.90 | 3.73 | 0.49 | 7.45 | 3.83 | 0.56 | ||||
| LVWG-A3C | 5.13 | 3.28 | 0.43 | 6.11 | 3.52 | 0.46 | 7.22 | 3.76 | 0.52 | ||||
| IVWG-A3C | 4.72 | 3.18 | 0.40 | 4.92 | 3.26 | 0.43 | 6.31 | 3.50 | 0.47 | ||||
当采用LVWG-A3C算法时,与传统的A3C算法相比,在低、中、高流量下车辆的平均等待时间分别减少了14%、11%和3%,平均排队长度分别减少了4%、5%和2%,车辆的平均停车次数减少了6%、6%和7%. 当采用IVWG-A3C算法时,与传统的A3C算法相比,在低、中、高流量下车辆的平均等待时间分别减少了19%、28%和15%,平均排队长度分别减少了7%、12%和8%,车辆平均停车次数分别减少了13%、12%和16%.
实验结果表明,与传统基于DQN和A3C强化学习的交通信号控制方法相比,基于融合车辆权重网络A3C强化学习的交通信号控制方法展现了更好的控制效果. 其中,以基于交叉口级车辆权重增益的A3C强化学习算法表现最出色,该方法有助于交通信号系统更均匀地分配绿灯时间给所有车道. 降低某些车道出现过度拥堵的风险,同时确保其他车道能够保持通畅,进而减少整体的车辆等待时间. 综上所述,基于深度强化学习的交通信号控制算法在评价指标方面,以交叉口车辆平均等待时间、车辆平均排队长度和平均停车次数为例,明显优于传统的定时控制和模糊自适应控制方法. 相较于传统的DQN和A3C深度强化学习方法,本研究提出的基于车辆权重增益的交通信号控制算法表现更好,尤其是基于融合交叉口级车辆权重增益网络的IVWG-A3C强化学习方法表现最佳.
5. 结 语
本文提出融合车辆权重增益的深度强化学习交通信号控制方法,通过提前捕捉关键交通特征信息,提升深度神经网络在特征提取过程中的学习能力. 该方法的核心是利用车辆权重增益网络对不同运动状态的车辆通行优先级进行区分. 当某车道存在大量排队等待通行车辆时,智能体会更倾向于让该车道上的车辆优先通行,提高了交叉口的通行效率. 为了验证本文方法的有效性,基于微观交通仿真软件SUMO,采用不同方法,对单交叉口在低流量、中流量、高流量3种不同交通状态下进行交通信号控制时的控制效果进行仿真测试. 测试结果表明,与其他基线方法相比,所提LVWG-A3C方法和IVWG-A3C方法具有更好的控制效果.
所提方法主要是针对单个交叉口,且在强化学习模型构建和训练过程中,尚未考虑诸如极端天气、交通事故等异常交通场景下的交通状态信息. 为了提高所提方法的实用性,未来研究工作的重点是拓展所提方法去解决区域交通信号协调控制问题.
参考文献
A survey of model predictive control methods for traffic signal control
[J].DOI:10.1109/JAS.2019.1911471 [本文引用: 1]
优化双向“绿波带”关键路口控制参数算法的研究
[J].
Research on the algorithm for optimizing the key intersection control parameters of two-way “Green Wave Belt”
[J].
基于值函数和策略梯度的深度强化学习综述
[J].DOI:10.11897/SP.J.1016.2019.01406 [本文引用: 1]
Review of deep reinforcement learning based on value functions and policy gradients
[J].DOI:10.11897/SP.J.1016.2019.01406 [本文引用: 1]
强化学习在城市交通信号灯控制方法中的应用
[J].
application of reinforcement learning in city traffic signal control methods.
[J].
A fast and accurate real-time vehicle detection method using deep learning for unconstrained environments
[J].
Human-level control through deep reinforcement learning
[J].DOI:10.1038/nature14236 [本文引用: 1]
Traffic signal control with reinforcement learning based on region-aware cooperative strategy
[J].
Traffic signal priority control based on shared experience multi-agent deep reinforcement learning
[J].
A deep reinforcement learning approach to traffic signal control with temporal traffic pattern mining
[J].
Traffic signal control using hybrid action space deep reinforcement learning
[J].DOI:10.3390/s21072302 [本文引用: 1]
Multi-agent deep reinforcement learning for large-scale traffic signal control
[J].
基于深度强化学习的交通信号控制方法
[J].
Traffic signal control methods based on deep reinforcement learning
[J].
Multi-agent deep reinforcement learning for urban traffic light control in vehicular networks
[J].DOI:10.1109/TVT.2020.2997896 [本文引用: 1]
双环相位结构约束下的强化学习交通信号控制方法
[J].
Reinforcement learning traffic signal control method under dual-ring phase structure constraints
[J].
一种基于通行优先度规则的城市交通信号自组织控制方法
[J].
A self-organized control method for urban traffic signals based on priority rules for passage
[J].
Controller exploitation-exploration reinforcement learning architecture for computing near-optimal policies
[J].DOI:10.1007/s00500-018-3225-7 [本文引用: 1]
On deep reinforcement learning for traffic engineering in SD-WAN
[J].
Robust deep reinforcement learning for traffic signal control
[J].DOI:10.1007/s42421-020-00029-6 [本文引用: 1]
Deep reinforcement learning-based vehicle driving strategy to reduce crash risks in traffic oscillations
[J].DOI:10.1177/0361198120937976 [本文引用: 1]
Multi-agent deep reinforcement learning for large-scale traffic signal control
[J].DOI:10.1109/TITS.2019.2901791 [本文引用: 1]
Deep reinforcement learning with spatio-temporal traffic forecasting for data-driven base station sleep control
[J].DOI:10.1109/TNET.2021.3053771 [本文引用: 1]