目前,大部分车道保持系统(lane keeping assist system, LKAS)都是将前轮转角或转向力矩作为控制量,未考虑驾驶人在环或将驾驶人操作视为外界扰动[9-10]. LKAS与驾驶人在转向任务中都拥有独立的控制方式,容易引发控制权上的冲突,需要对二者进行协调控制. 根据驾驶人与智能系统同时在环与否,将人机协同控制方式概括如下. 1)智能辅助驾驶. 2)特定场景下的驾驶控制权切换,如基于驾驶人生理特征与心理状态的切换准则研究[11]、基于驾驶意图、驾驶风格及驾驶能力裕度的切换准则研究[12]、综合考虑人-车-路的切换准则研究[13]. 3)共驾过程中的驾驶控制权动态分配,即通过合理设计权值分配策略来综合协调控制效果,但如何设计适宜的权值及明确介入准则缺少足够的理论支撑[14-15]. 现有研究更多的是在权值分配与跟踪精度之间寻求折中设计,优先保证横向偏差、横摆角偏差(方位偏差)、横向加速度等控制目标,这样容易导致智能系统对驾驶人操作过度干预的现象.
在变道决策、交叉口决策、超车决策等场景应用中,驾驶人与智能系统的输入是并行的,具有冗余与博弈的特征[2]. 与模糊控制[10] 、LPV-H∞[16]理论相比,博弈论是研究多个决策主体相互对抗与冲突时如何获得各自最佳策略的理论,能够更好地描述共驾过程中驾驶人与智能系统之间的交互行为,在车辆安全性、动力性、路面附着情况等约束条件下,让驾驶人与智能系统协同高效完成操作任务,达到纳什均衡(Nash equilibrium),实现全局优化控制的目标[17-18]. 为了减少共驾过程中的人机冲突,本文研究基于非合作博弈的人机共驾控制策略. 对车道保持共享控制问题进行数学描述. 基于非合作博弈理论,设计控制权博弈模型. 基于MPC框架,将共驾型LKAS前轮转角决策问题转化成带约束的在线二次规划问题. 设计不同的驾驶状态,利用驾驶人在环的集成仿真环境,对该控制算法与控制策略进行验证与探讨.
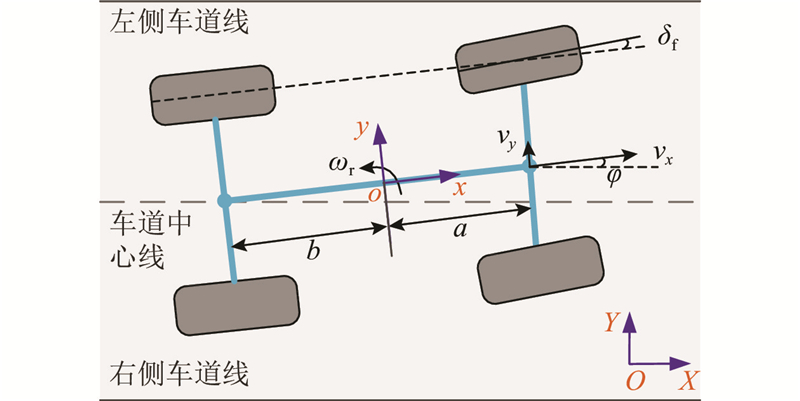
1. 车路模型
1.1. 数学建模
1.1.1. 状态空间方程
针对驾驶人与智能系统共同控制车辆转向,构建共驾型LKAS模型,并作如下约束.
1) 当车辆速度变化较小时,常纵向速度假设是近似成立的.
2) 忽略车辆的侧倾与俯仰运动.
3) 考虑到车辆质心随载荷、轮胎、路面等扰动因素而发生变化,工程应用时以车辆后轴中点作为参考点.
图 1
式中:
以
式中:各系数矩阵满足
以
式中:各系数矩阵满足
1.1.2. 多步预测模型
令当前时刻为k,预测时域为[k,k+p−1],控制时域为[k, k+c−1],其中c ≤ p. 由式(3)逐步迭代整理得到
式中:
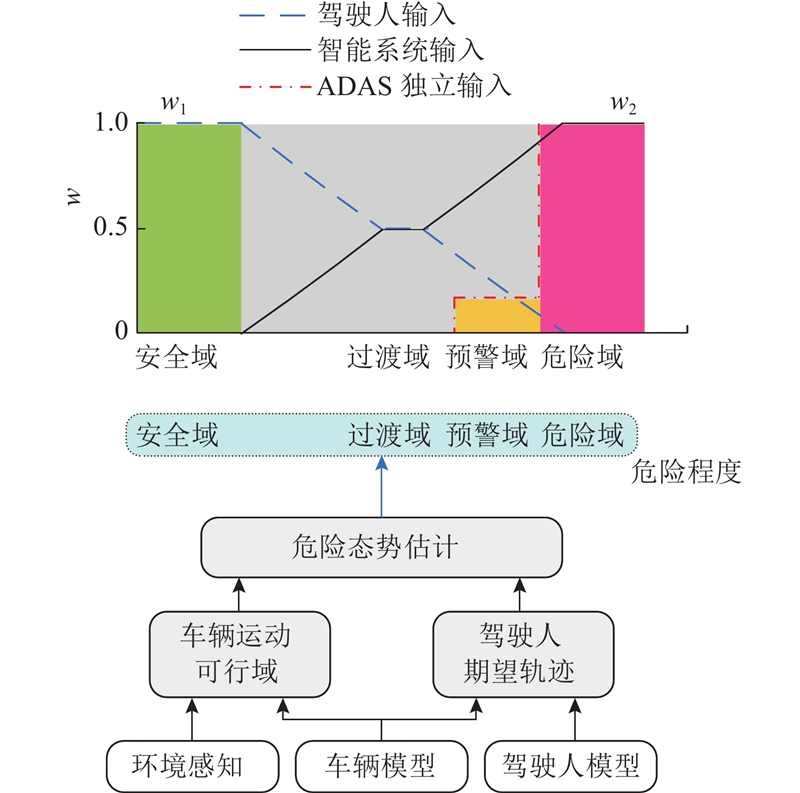
2. 非合作博弈共享控制
2.1. 人机共驾策略设计
2.1.1. 非合作人机共驾策略
图 2
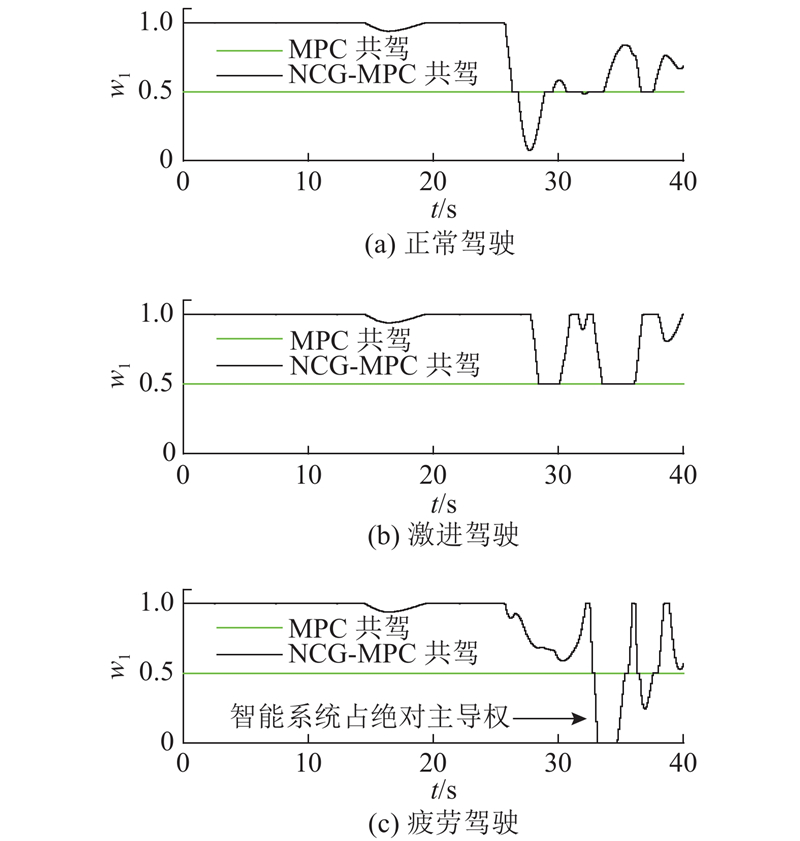
非合作人机共驾策略的作用是根据危险态势估计模型来综合协调驾驶人与智能系统的驾驶参与度,能够较好地兼顾驾乘舒适性与行驶安全性,保证驾驶人时刻在环. 当车辆处于安全域或过渡域前期时,在保证一定的横向运动控制精度的前提下,给予驾驶人足够的控制权裕度,以提升驾驶人的舒适体验. 当因驾驶人误操作、走神、疲劳等而导致车辆进入预警域或危险域时,该策略会逐步将驾驶控制权从驾驶人移交给智能系统.
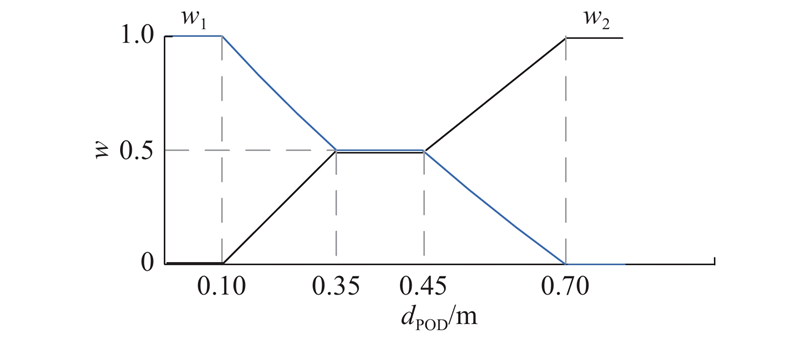
2.1.2. 控制权博弈模型
定义预瞄偏移距离(preview offset distance, POD)为车辆在预瞄点处偏移车道中心线的距离. 根据JTG B01-2014公路工程技术标准可知,我国高速公路车道的宽度为3.75 m,轿车宽度约为1.6~1.8 m. 基于POD距离,将车辆运动可行域划分成以下区域:1)安全域[0, 0.35] m,驾驶人占主导权;2) 过渡域(0.35, 0.6] m,逐渐提高智能系统的控制权值;3) 预警域(0.5, ∞) m,启动分级预警[22];4) 危险域(0.6, ∞) m,智能系统快速接管驾驶控制权.
图 3
驾驶人控制权的数学描述如下:
式中:
2.2. 共享控制算法的设计
2.2.1. 代价函数
车道保持的任务是使车辆横向位置应尽可能逼近期望路径,为了保证控制效果,控制输入宜尽可能小. 在非合作人机共驾策略中,包含2个决策者(即系统有2个控制输入):驾驶人、智能系统. 这2个决策者都期望自身在实现控制目标时所花费的成本最小,构造代价函数如下:
在代价函数中,第1项体现了对期望轨迹的跟踪能力,第2项反映了对控制平稳性的要求. 式中:
基于图3所示的控制权博弈模型,当车辆进入危险域时,通过逐步下调
2.2.2. 约束条件及松弛化处理
考虑到车辆自身的物理限制及实际应用场景,对由控制输入、系统状态所构成的控制器工作域进行边界约束:
式中:
将式(8)所示的硬约束条件所构成的约束空间称为求解可行域. 在MPC有限时域滚动优化过程中,可能会出现求解可行域内无可行解的问题. 采用松弛因子对硬约束条件进行松弛化处理,以扩展求解可行域[19],保证可行解存在.
式中:松弛因子满足
2.2.3. 算法演变
为了防止因引入松弛因子而导致对控制器工作域的边界约束作用失效,在代价函数中增加正则化项,以惩罚松弛因子扩展工作域边界的能力,从而在硬约束问题求解可行性与工作域边界的松弛程度之间寻求平衡[19]. 根据式(6)、(7)与(9),重构代价函数如下.
式中:C1、C2为常数项,
其中,
将共驾型LKAS算法设计问题转化为线性不等式约束的二次规划(quadratic programming, QP)问题. 对于每一个参与者来说,非合作博弈的均衡解,即纳什均衡,可以通过求解QP问题得到. 在滚动优化求解过程中,选取向量解的第1个数值作为下一步的输入,如此重复,实现滚动在线控制.
3. 实验验证
表 1 整车动力学参数
Tab.1
| 参数 | 数值 |
| 簧载质量/kg | 1 650 |
| 质心绕z轴的转动惯量/( kg·m2) | 3 234 |
| 前轴与车辆质心之间的距离/m | 1.4 |
| 后轴与车辆质心之间的距离/m | 1.65 |
| 车身宽度/m | 1.88 |
| 前轮的侧偏刚度/( kN·rad−1) | 80 |
| 后轮的侧偏刚度/( kN·rad−1) | 80 |
| 路面附着系数 | 0.8 |
| 迎风面积/m2 | 2.0 |
图 4
表 2 驾驶状态特性参数
Tab.2
| 驾驶状态 | 参数 | 数值 |
| 正常驾驶 | 反应时间/s | 0.5~1.2 |
| 正常驾驶 | 制动减速度/(m·s−2) | −2~0 |
| 正常驾驶 | 侧偏位移/m | −0.6~0.6 |
| 激进驾驶 | 反应时间/s | 0.1~0.7 |
| 激进驾驶 | 制动减速度/(m·s−2) | −3~0 |
| 激进驾驶 | 侧偏位移/m | −0.4~0.4 |
| 疲劳驾驶 | 反应时间/s | 0.8~2.0 |
| 疲劳驾驶 | 制动减速度/(m·s−2) | −4~0 |
| 疲劳驾驶 | 侧偏位移/m | −0.9~0.9 |
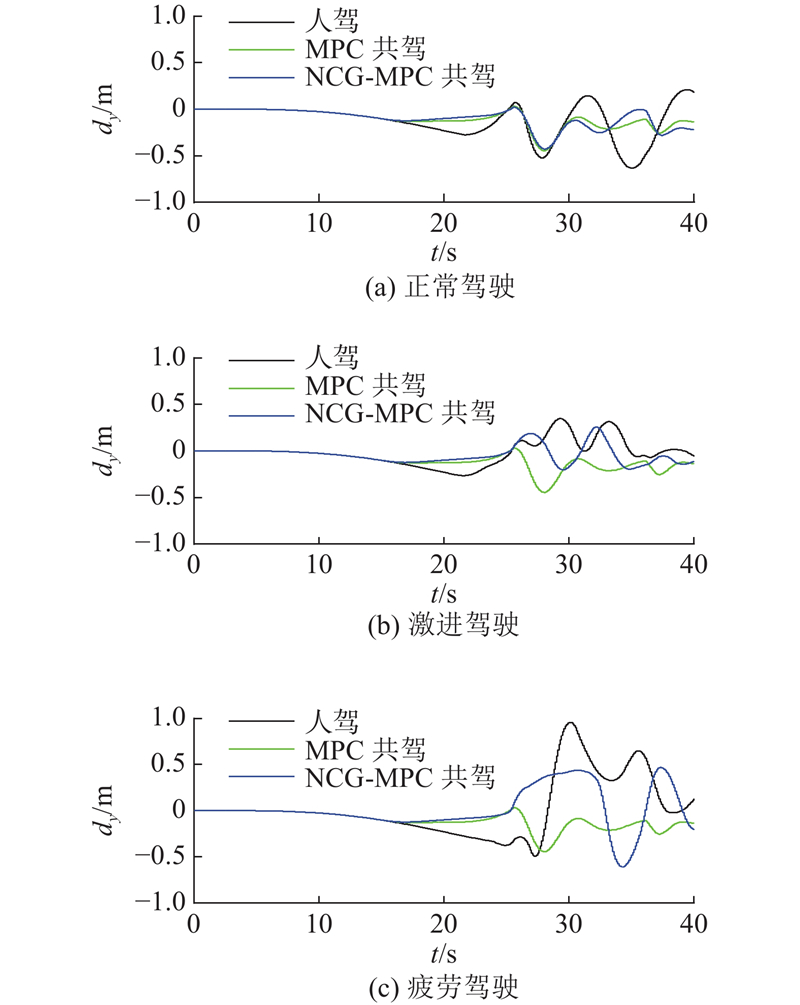
图 5
图 5 不同驾驶状态下的横向位移对比
Fig.5 Comparison of lateral displacements under different driving states
图 6
图 6 不同驾驶状态下驾驶人控制权的对比
Fig.6 Comparison of control authority under different driving states
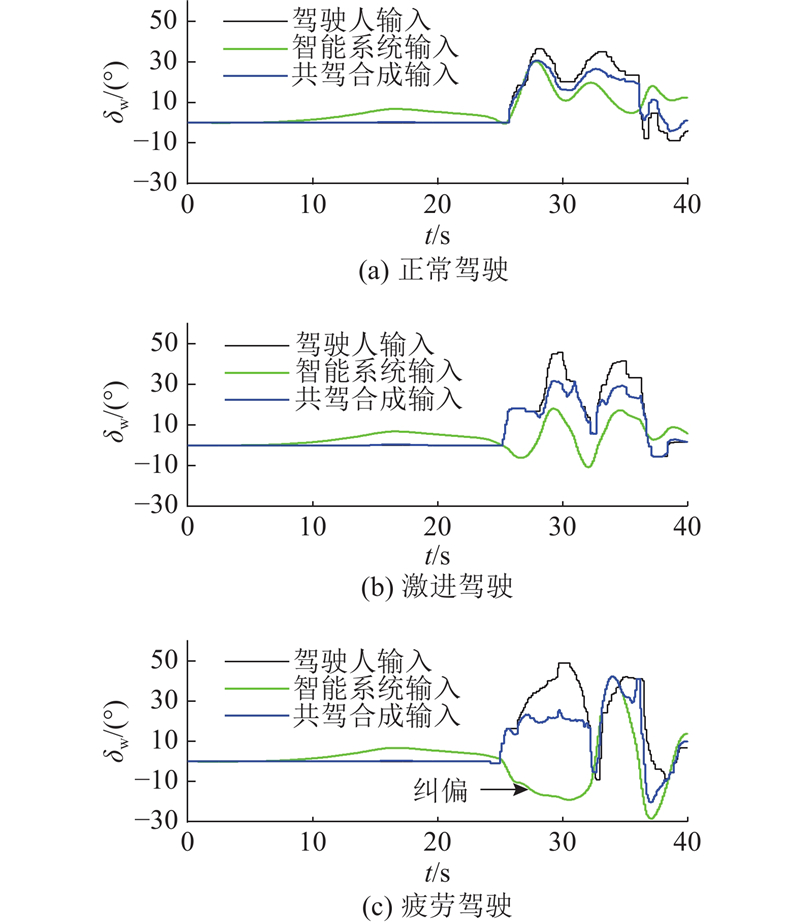
如图7所示,针对不同的驾驶状态,分别对NCG-MPC共驾模式下驾驶人、智能系统及共驾的方向盘转角δw进行仿真对比. 在0~25 s过程中, CarSim直道并非严格直线,故该过程中智能系统会有一定的输入. 由于该过程中的侧偏很小,控制权博弈模型给智能系统分配的输入权重很小甚至为0,这样使得合成输入接近于0. 在疲劳驾驶状态下,当驾驶人方向盘转向过大时,在控制权博弈模型的作用下智能驾驶系统将会及时介入,快速接管方向盘以纠正车辆的偏离行为,有效提高了车辆横向控制的抗扰动能力.
图 7
图 7 不同驾驶状态下方向盘转角的对比
Fig.7 Comparison of steering wheel angles under different driving states
4. 结 论
(1)基于MPC模型预测控制框架提出共驾型LKAS控制算法,采用二次型性能指标及线性不等式约束的形式,将前轮转角决策问题转化成带约束的在线二次规划问题.
(2)基于非合作博弈理论设计非合作人机共驾策略,以提高驾驶人与智能系统双驾双控过程中的友好性. 按照车道偏离程度,将车辆运动可行域划分成安全域、过渡域、预警域、危险域,综合车辆运动可行域与驾驶人期望轨迹进行危险态势估计. 采用POD距离对驾驶人与智能系统的置信度矩阵进行更新,以实现驾驶人与智能系统之间驾驶控制权的平稳交接,在保证驾驶人时刻在环的同时,能够有效避免因交接突兀而影响驾乘舒适性的不足.
(3)为了提高驾驶人的主观感受度及其对智能系统的信任感,设计控制权博弈模型. 在保证一定的横向运动控制精度的前提下,给予驾驶人足够的控制权裕度,以满足驾驶人的主观感受.
参考文献
智能汽车人机协同控制的研究现状与展望
[J].
Human-machine cooperative control of intelligent vehicle: recent developments and future perspectives
[J].
智能网联汽车(ICV)技术的发展现状及趋势
[J].
State-of-the-art and technical trends of intelligent and connected vehicles
[J].
Adaptive authority allocation of human-automation shared control for autonomous vehicle
[J].
基于人机协同的车道保持辅助系统研究进展
[J].
Overview of lane-keeping assist system based on human-machine cooperative control
[J].
基于预期偏移距离的人机权值分配策略研究
[J].
Weight allocation strategy between human and machine based on the preview distance to lane center
[J].
Human-machine shared steering control for vehicle lane keeping systems via a fuzzy observer-based event-triggered method
[J].
基于驾驶人风险响应机制的人机共驾模型
[J].
Man-machine shared driving model using risk-response mechanism of human driver
[J].
A two-layer potential-field-driven model predictive shared control towards driver-automation cooperation
[J].
基于人机共驾的车道保持辅助控制系统研究
[J].
Lane-keeping control systems based on human-machine cooperative driving
[J].
人机共驾智能车驾驶模式决策属性析取研究
[J].
Research on impact factors extraction for driving mode of intelligent vehicle
[J].
人-车-路交互下的驾驶人风险响应度建模
[J].
Modeling of driving risk response under human-vehicle-road interaction
[J].
Intention-based lane changing and lane keeping haptic guidance steering system
[J].DOI:10.1109/TIV.2020.3044180 [本文引用: 1]
Sensor reduction for driver-automation shared steering control via an adaptive authority allocation strategy
[J].DOI:10.1109/TMECH.2017.2698216 [本文引用: 1]
Preview-scheduled steering assistance control for copiloting vehicle: a human-like methodology
[J].DOI:10.1080/00423114.2019.1590607 [本文引用: 1]
A review of game theory models of lane changing
[J].DOI:10.1080/23249935.2020.1770368 [本文引用: 1]
Shared steering torque for lane change assistance: a stochastic game-theoretic approach
[J].DOI:10.1109/TIE.2018.2844784 [本文引用: 1]
实时多目标权重弯道跟随预测控制
[J].
Multi-objective real-time weighted model predictive control for car-following
[J].
Linear quadratic game and non-cooperative predictive methods for potential application to modelling driver–AFS interactive steering control
[J].DOI:10.1080/00423114.2012.715653 [本文引用: 2]
基于非合作模型预测控制的人机共驾策略
[J].
Cooperative driving strategy based on non-cooperative model predictive control
[J].