实时动态测量技术(real-time kinematic，RTK)是基于载波相位的动态差分技术，其工作原理为通过对观测量做差，减弱甚至消除公共误差，从而达到提升定位精度的目的. 对于高动态以及需要高精度定位的场景具有重要意义，广泛应用于测量领域，本研究即针对低轨卫星双星编队对RTK技术展开研究^[1-2]. 20世纪90年代，由日本宇宙事业开发集团(national space development agency of Japan，NASDA)指定的ETS-VII任务，首次使用星载GPS差分技术，以星载GPS伪距作为基本观测量用于后续的差分处理，并选择扩展卡尔曼滤波(extended Kalman filter，EKF)作为该任务的滤波算法，最终取得了小于10 m的实时相对位置精度(3DRMS)(3DRMS表示三维均方根)以及1 cm/s的速度精度(3DRMS)^[3]，远高于任务需求，证实了星载差分GPS技术在航天任务中的可行性和有效性. 随着技术的发展，不少学者开始借助半物理仿真平台开展星载GPS差分技术的研究. Ebinuma等^[4]借助GSS STR 4760模拟器，采用载波相位双差技术，对2颗基线距离为0~10 km的卫星展开研究，最终获得了小于5 cm的实时相对位置精度(3DRMS)以及1 mm/s的速度精度(3DRMS). Busse^[5]基于GPS模拟和分析工具包(GPS simulation and analysis toolkit，GSAT)对相距1 km的椭圆形卫星编队进行数据的分析与处理，使用载波相位单差技术，最终获得了小于2 cm (1 $\sigma $)的实时相对位置精度(3DRMS)以及小于0.5 mm/s的速度精度(3DRMS). Leung等^[6]提出分布式相对导航结构，并借助Spirent STR4760，使用载波相位双差技术，得出在1~10 km的基线范围内，可以达到小于1.5 mm的位置精度以及小于5 μm/s的速度精度. D′Amico等^[7]使用GSS7700模拟器对PRISMA主从星编队进行实时相对导航研究，对载波相位和伪距使用半和模型GRAPHIC (group and phase ionospheric correction)，并通过单差形式消除公共误差，最终达到了2.25 cm的实时相对位置精度(3DRMS)以及0.06 mm/s的速度精度(3DRMS).

卫星在太空中会有一些特殊的姿态要求，其中最常见的就是卫星侧摆，通常见于光学成像、对地凝视任务. 由于低轨卫星轨道高度较低，直接对地观测的成像幅宽较小，须调整卫星姿态，采用侧摆技术来提高对地观测效率^[8]. 这样就会对星间GPS测量产生负面影响，最直接的影响就是减少了共视星的数目，从而降低了相对定位的精度，在中长基线场景下甚至还会导致无法定位. 为了解决上述问题，本研究提出基于全视角星载GPS接收系统的低轨卫星实时相对定位方法. 该系统采用全视角天线，使可视卫星范围大大提高，从而提升相对定位性能. 针对星载高动态环境，提出基于几何无关(geometry free, GF)差分组合和衰减窗口的伪距粗差探测方法，同时基于抗差自适应扩展卡尔曼滤波(robust adaptive extended Kalmen filter, ARKF)，在短基线下使用基于新息向量的观测噪声协方差矩阵开窗估计法来代替传统方法.

接收系统采用基于全视角天线的星载GPS接收结构，用以增强相对定位性能，其中3副天线分别安装于等三角锥底座的3个侧面上，且三角锥的侧面与底面的夹角互呈60°，使得天线组件能够接收到的导航信号覆盖±120°空域范围. 具体结构如图1所示.

单根天线只能覆盖所在平面法线±60°范围，因此要实现全视角覆盖，至少需要3根天线，通过这种设计，全视角天线能够在±120°空域范围，即在低轨卫星轨道的全视角范围内保证较高的天线增益，从而保证有效接收全视角范围内的导航卫星信号. 同时，即使卫星执行较大幅度的机动，卫星定位或者卫星编队相对定位仍能收到足够多的导航星信号从而保证性能. 须说明的是，全视角天线的相位中心已在接收机内部进行了归一化处理. 作为对比，传统单天线方案是将一副天线安装于卫星对天面，GPS接收机仅能在相对较小的视角范围内收到导航信号，当卫星执行机动时，卫星定位或者卫星编队相对定位的性能有可能大幅下降甚至定位失败.

全视角星载GPS接收系统的伪距和载波相位观测方程可以表示为

(1) $ r = r+c(\text{δ} {t_{\rm{u}}} - \text{δ} {t^{(s)}})+I+{e_{\rm{r}}}, $

(2) $ f = {\lambda ^{ - 1}}(r+c(\text{δ} {t_{\rm{u}}} - \text{δ} {t^{(s)}}) - I)+N+{e_{\rm{f}}}. $

式中： $ r $为接收机与导航星间的几何距离， $ {t^{(s)}} $为某卫星（编号为s）发射时卫星钟对应的时刻， $\text{δ} {t_{\rm{u}}}$为接收机钟差， $ \text{δ} {t^{(s)}} $为卫星钟差， $ I $为电离层延迟， ${e_{\rm{r}}}$、 ${e_{\rm{f}}}$分别为伪距、载波相位的测量噪声，c为光在真空中的传播速度， $ \lambda $为对应载波相位的波长，N为载波相位模糊度.

电离层延迟为GPS信号传播过程中的主要误差源，目前基于双频接收机的主要处理方式为双频无电离层组合，表达式^[9-10]为

(3) $ {P_{\rm{c}}} = \alpha {P_1}+(1 - \alpha ){P_2} = \rho +c(\text{δ} {t_{\rm{u}}} - \text{δ} {t^{(s)}})+\varepsilon {P_{\rm{c}}}, $

(4) $ {L_{\rm{c}}} = \alpha {L_1}+(1 - \alpha ){L_2} = \rho +c(\text{δ} {t_{\rm{u}}} - \text{δ} {t^{(s)}})+{\lambda _{\rm{c}}}{N_{\rm{c}}}+\varepsilon {L_{\rm{c}}}. $

式中： $ {P_{\rm{c}}} $表示双频伪距消电离层组合观测量； $ {P_1} $、 $ {P_2} $分别为L1、L2频点的伪距测量值；L₁、L₂分别为L1、L2频点的载波相位测量值； $ {L_{\rm{c}}} $表示双频载波相位消电离层组合观测量；α为无电离层组合系数， $\alpha = f_1^2/(f_1^2 - f_2^2)$， ${f_1}$、 ${f_2}$分别表示GPS第1、2频点的频率； $ {\lambda _{\rm{c}}} $为双频无电离层组合波长； $ {N_{\rm{c}}} $为双频无电离层组合的模糊度； $ \varepsilon {P_{\rm{c}}} $为伪距测量噪声， $ \varepsilon {L_{\rm{c}}} $为载波相位测量噪声，组合后的 $ \varepsilon {P_{\rm{c}}} $和 $ \varepsilon {L_{\rm{c}}} $分别变为原单频测量噪声的3倍； $\,\rho$为卫星与接收机间的几何距离.

很多观测量的误差项具有空间、时间相关性，因此可以通过差分的方式消除掉公共误差，从而提升定位精度，本研究采用无电离层单差观测组合^[11]. 用户u和基准站b对卫星i的单差载波相位 $ \phi _{ub}^{(i)} $、单差伪距 $ \rho _{ub}^{(i)} $可以表示为

(5) $ \phi _{ub}^{(i)} = {\lambda ^{ - 1}}(r_{ub}^{(i)} - I_{ub}^{(i)})+f\text{δ} {t_{ub}}+N_{ub}^{(i)}+\varepsilon \phi _{ub}^{(i)}, $

(6) $ \rho _{ub}^{(i)} = r_{ub}^{(i)}+I_{ub}^{(i)}+c\text{δ} {t_{ub}}+\varepsilon \rho _{ub}^{(i)}. $

式中： $ r_{ub}^{(i)} $、 $ I_{ub}^{(i)} $、 $ \text{δ} {t_{ub}} $、 $ N_{ub}^{(i)} $分别为用户u和基准站b对卫星i的单差几何距离、单差电离层延迟、单差接收机钟差、单差模糊度；f表示对应载波相位频率；单差表达式中的卫星钟差项已被消除，相应的单差测量噪声 $ \varepsilon \phi _{ub}^{(i)} $、 $ \varepsilon \rho _{ub}^{(i)} $均变为原来的 $ \sqrt 2 $倍.

接收机观测数据质量的优劣直接影响卫星定位和星间基线测量结果，因此接收机观测质量分析与控制是获取高精度定位结果的基本前提^[12].

基于TurboEdit算法的改进^[13]提出基于几何无关(GF)差分组合和衰减窗口的伪距粗差探测方法，对较大粗差进行探测、剔除，对于较小粗差则使用抗差滤波算法进行处理. 其中GF组合 ${P_{\rm{G}}}$可以表示为

(7) $ {P_{\rm{G}}} = {P_1} - {P_2}. $

GF组合的一阶差分项 $\Delta {P_{\rm{G}}}$表达式为

(8) $ \begin{split} \Delta {P_{\rm{G}}}(t) =& {P_{\rm{G}}}(t) - {P_{\rm{G}}}(t - 1)= \\& \frac{{f_2^2 - f_1^2}}{{f_2^2}}{I_1}(t) - \frac{{f_2^2 - f_1^2}}{{f_2^2}}{I_1}(t - 1)+\Delta \varepsilon . \end{split}$

式中： $ {I_1}(t) $、 ${P_{\rm{G}}}(t)$、 $ {I_1}(t - 1) $、 ${P_{\rm{G}}}(t - 1)$分别表示t和t−1时刻的电离层延迟以及伪距几何无关组合， $ \Delta \varepsilon $为GF组合的一阶差分项的组合噪声. 由于须在满足实时性的同时较为准确地反映出数据的整体水平，故选择前向衰减窗口计算. 表达式如下：

(9) $ \beta (t) = {b}/(a+t), $

(10) $ {P_{\rm{A}}}(k) = \frac{1}{m}\sum\limits_{t = k - m}^{k - 1} {\Delta {P_{\rm{G}}}(t)}, $

(11) $ {P_{\beta}}(k) = \sum\limits_{t = k - m+1}^k {\beta (t)\Delta {P_{\rm{G}}}(t)}\Biggr/{{\displaystyle\sum\limits_{t = k - m+1}^k {\beta (t)} }}, $

(12) $ {P_{{\rm{W}}} }(k) = {P_{\beta} }(k) - {P_{\rm{A}}}(k). $

式中： ${P_{\rm{A}}}$为前向滑动窗口平均值，为当前历元t之前的m个历元的伪距几何无关一阶差分项的平均值,这里选用前向滑动窗口计算； ${P_{\beta} }$为前向衰减窗口加权平均值，为当前历元(包括本历元)的伪距几何无关一阶差分项的加权平均值，着重反映出当前历元数据的变化； ${P_{{\rm{W}}} }$为粗差检验量；为 ${P_{\beta} }$与 ${P_{\rm{A}}}$的差值； $ \;\beta (t) $为衰退因子，用以降低之前测量值对当前时刻的贡献；t为当前历元，根据误差传播规律，以不放大组合后的方差； a、b为衰减系数. a、b的取值满足以下条件^[14]：

(13) $ {\sigma _{{{\rm{W}}_{}}}}^2 = \left[{\left(\frac{b}{{a+1}}\right)^2}+{\left(\frac{b}{{a+2}}\right)^2}+\cdots+{\left(\frac{b}{{a+m}}\right)^2}\right]{\sigma _{\rm{p}}}^2. $

式中：σ_W为粗差检验量的标准差，σ_p为伪距噪声标准差.

简化得到

(14) $ \sum\limits_{k = 1}^m {{{\left(\frac{b}{{a+k}}\right)}^2}} < 1. $

本研究中取a=9, b=3, m=20.

前向衰减窗口平均值 $ {P_{\rm{A}}} $的标准差 $ {\sigma _{\rm{A}}} $约等于0.45 $ {\sigma _{\rm{p}}} $，前向衰减窗口加权平均值 $ {P_{\beta } } $的标准差 $ {\sigma _{\rm{B}}} $约等于0.18 $ {\sigma _{\rm{p}}} $，粗差检验量 $ {P_{\rm{W}}} $的标准差 $ {\sigma _{\rm{W}}} $约等于0.48 $ {\sigma _{\rm{p}}} $，可以写成如下形式.

(15) $ {\sigma _{\rm{W}}} = 0.48{\sigma _{\rm{p}}}. $

则基于衰减窗口的伪距GF组合一阶差分项只须满足以下条件即可认为此历元的伪距测量值为粗差：

(16) $ |{P_{\rm{W}}}(k) - {\rm{mean}}\;({P_{\rm{W}}}(k))| \geqslant 3{\sigma _{\rm{W}}}. $

式中： ${P_{\rm{W}}}(k)$表示k历元的粗差检验量，mean表示平均运算.

考虑到电离层在每个时段的变化趋势不一样，以当前时段的电离层变化量作为参考，可以增加粗差探测的成功率，如果单纯以伪距GF组合一阶差分项作为判别标准，在电离层活动较为频繁的情况下，难免会发生粗差探测错误、甚至失败的情况，进而影响定位解算质量.

借助半物理平台进行验证，采用思博伦GSS9000型号的导航信号模拟器产生轨道高度500 km 的GPS L1C/A、GPS L2C 双频民码信号，通过射频线连接到L1/L2双频星载GPS接收机进行数据采集. 在某些卫星的连续观测历元可能存在粗差，进而导致该卫星模糊度重新初始化，影响收敛时间，因此，规定只有在连续锁定历元大于5且不存在粗差的情况下，才可参与定位解算.

采用高度角剔除法作为对比试验以验证本研究所提方法的优势，其中对于单天线接收系统，截止高度角一般选择 5°~10°. 本研究使用的全视角接收系统可视区域为±120°，对应截止高度角范围为−25°~−20°，本研究选取截止高度角为−20°. 如表1所示展示了2种方法的探测效果. 表中，N表示伪距粗差探测采样点个数，n表示探测粗差总个数， $ {P_{\rm{M}}} $、 $ {P_{\rm{m}}} $ 分别表示探测到的最大和最小伪距粗差.可以看出，基于GF差分组合和衰减窗口的伪距粗差探测方法相较于传统方法在粗差探测数以及粗差探测最小值上均有所提升，侧面说明了本研究所提方法具有相对较强的探测能力，验证了本研究所提出的粗差探测法在全视角情况下的有效性. 以上提到的粗差探测方法只能对较大粗差进行探测，对于较小的粗差则须联合使用抗差滤波方法进行抑制处理.

周跳是接收机在连续跟踪信号的过程中，接收机计数器中断或者信号传播途中被障碍物遮挡亦或是卫星仰角过低致使观测质量变差，最终导致载波相位发生跳变. 目前在导航领域常用的周跳探测手段为TurboEdit算法^[15]，主要基于Melbourne-Wübbena(MW)组合和GF组合对测量值进行处理，可以覆盖大部分的周跳情况，从而剔除超过判别门限的数据.

低轨卫星所处空间环境较为复杂，并且全视角接收系统的信号覆盖范围较大，很难保证所有卫星信号质量，为此本研究选用抗差自适应扩展卡尔曼滤波作为研究的滤波算法^[16].

在观测值可靠的情况下，预测残差向量能反映动力学模型误差的大小，可以通过比较理论预测残差协方差 ${\rm{Cov}}({\overline {\boldsymbol{V}} _k})$以及实际预测残差协方差 $\hat {{\rm{Cov}}} ({\overline {\boldsymbol{V}} _k})$的大小，确定自适应因子的取值，具体可以表示为

(17) $ {\rm{Cov}}({\overline {\boldsymbol{V}} _k}) = {{\boldsymbol{H}}_k}{\rm{Cov}}({\overline {\boldsymbol{X}} _k}){{\boldsymbol{H}}_k}^{\rm{T}}{+}{\rm{Cov}}({{\boldsymbol{R}}_k}), $

(18) $ {\hat {\bar {\boldsymbol{V}}} _k} = {{\boldsymbol{y}}_k}{\boldsymbol{ - }}{{\boldsymbol{C}}_k}{\overline {\boldsymbol{X}} _k}, $

(19) $ \hat {{\rm{Cov}}} ({\overline {\boldsymbol{V}} _k}) = {\hat{\bar {\boldsymbol{V}}} _k}\hat{\bar {\boldsymbol{V}}} _k^{\rm{T}}, $

(20) $ {\alpha }_{k}\approx \left\{ \begin{array}{l}1,\qquad \qquad \quad 其他;\\ \dfrac{{\rm{tr}}\;({\rm{Cov}}({\overline{{\boldsymbol{V}}}}_{k}))}{{\rm{tr}}\;(\hat{{\rm{Cov}}}({\overline{{\boldsymbol{V}}}}_{k}))},\;{\rm{tr}}\;(\hat{{\rm{Cov}}}({\overline{{\boldsymbol{V}}}}_{k})) > {\rm{tr}}\;({\rm{Cov}}({\overline{{\boldsymbol{V}}}}_{k})).\end{array}\right. $

式中： ${\rm{tr}}$表示对矩阵求迹， ${\rm{Cov}}$表示变量的协方差矩阵， $ {\overline {\boldsymbol{V}} _k} $表示理论预测残差， $ {\overline {\boldsymbol{X}} _k} $表示k时刻的预测状态向量， $ {{\hat {\overline {\boldsymbol{V}} }_k}} $表示实际预测残差， $ {{\boldsymbol{H}}_k} $表示k时刻的设计矩阵， ${{\boldsymbol{R}}_k}$表示观测噪声协方差矩阵， $ {{\boldsymbol{y}}_k} $表示k时刻的测量值.

由式(17)~(20)可以看出，在ARKF算法中，当系统模型出现异常干扰时，会通过自适应因子对系统模型的协方差矩阵进行方差膨胀，从而降低预测信息对系统状态变量的影响. 当模型无异常干扰时， $ {\alpha _k} $的理论值为1，一旦模型出现扰动，就会根据扰动的大小，自适应降低动力学模型在状态量中的预测权重.

自适应因子的求解是在测量值可靠的前提下进行的，一旦测量值存在粗差，就会将误差引入到最终的状态量中. 为了防止滤波发散，应时刻调整测量值噪声大小.

类似于预测残差，观测残差 $ {{\boldsymbol{V}}_k} $由k时刻的状态估计向量 $ {\hat {\boldsymbol{x}} _k} $求得，参考IGG-Ⅲ方案^[17]，调整后的 $ {{\boldsymbol{V}}_k} $以及观测噪声等价协方差矩阵 $ {\overline {\boldsymbol{R}} _k} $可以表示为

(21) $ {{\boldsymbol{V}}_k} = {{\boldsymbol{y}}_k}{\boldsymbol{ - }}{{\boldsymbol{H}}_k}{\hat {\boldsymbol{x}} _k}{{.}} $

(22) $ \begin{split} & {\overline {\boldsymbol{R}} _{k(i,i)}} =\\ & \left\{ \begin{array}{ll} {{\boldsymbol{R}}_{k(i,i)}},&\left| {{{\boldsymbol{V}}_{k,(i)}}} \right| \leqslant {k_0}; \\ {{\boldsymbol{R}}_{_{k(i,i)}}}\dfrac{{\left| {{{\boldsymbol{V}}_{k,(i)}}} \right|}}{{{k_0}}}{\left(\dfrac{{({k_1} - {k_0})}}{{{k_1} - \left| {{{\boldsymbol{V}}_{k,(i)}}} \right|}}\right)^2},&{k_0}{\text{ < }}\left| {{{\boldsymbol{V}}_{k,(i)}}} \right| \leqslant {k_1}; \\ {10^4},&\left| {{{\boldsymbol{V}}_{k,(i)}}} \right| > {k_1}. \end{array} \right. \end{split} $

式中： $ {k_0} $、 $ {k_1} $为调和系数，本算法取 $ {k_0} $=1、 $ {k_1} $=3.

(23) $ {{\boldsymbol{V}}_{k,(i)}} = \frac{{\left| {{{\boldsymbol{V}}_i} - E({{\boldsymbol{V}}_k})} \right|}}{{D({{\boldsymbol{V}}_k})}}. $

式中： $E({{\boldsymbol{V}}_k})$和 $D({{\boldsymbol{V}}_k})$分别表示观察残差的均值和标准差.

上述方法是基于观测向量残差来进行质量区分的，然而观测向量残差仅能作为评判定位结果好坏的必要条件，而不能成为充分条件. 并且，当观测向量同时出现恒值干扰时，基于观测残差的观测噪声等价协方差矩阵估计法并不能很好的检测和处理. 因此，Mehera提出基于新息序列的自适应卡尔曼滤波^[18]，新息向量定义为观测量的预测值与理论值之差，也就是实际预测残差，具体参见式(18). 其基本原理是基于方差匹配原则，通过调整过程噪声协方差矩阵Q和观测噪声协方差矩阵R，使新息序列的理论方差与实际方差基本一致^[19] .

新息序列的实际协方差 $ {{{\hat {\boldsymbol{C}}}}_k} $可以在特定的窗口内，通过对样本残差取平均的方式来预测，具体可以表示为

(24) $ {\hat{{\boldsymbol{C}}}}_{k}=\frac{1}{N_{\rm{w}}}\left(\sum _{i={i}_{0}}^{k}{{\boldsymbol{e}}}_{i}{{\boldsymbol{e}}}_{i}^{{\rm{T}}}\right);\;{i}_{0}=k-N_{\rm{w}}+1,k\geqslant N_{\rm{w}}. $

式中： ${{\boldsymbol{e}}}_{i}$表示第i个样本残差，N_w为窗口大小，k为当前历元，进一步可以得到

(25) $ {{{\bar {\boldsymbol{R}}}}_k} = {{{\hat {\boldsymbol{C}}}}_k} - {{\boldsymbol{H}}_k}{{\boldsymbol{P}}_{k\mid k - 1}}{\boldsymbol{H}}_k^{\rm{T}}, $

(26) $ {{{\bar {\boldsymbol{Q}}}}_k} \approx {{\boldsymbol{K}}_k}{{{\hat {\boldsymbol{C}}}}_k}{{\boldsymbol{K}}_k}. $

式中： $ {{\boldsymbol{P}}_{k\mid k - 1}} $表示k−1历元到k历元的预测状态协方差， $ {{\boldsymbol{K}}_k} $表示k历元的卡尔曼滤波增益矩阵， $\bar Q_k $表示过程噪声等价协方差矩阵.

然而，新息序列实际协方差的预测过程各历元残差要满足同类、同维且同分布，否则不能按照式(24)计算 ${{{\hat {\boldsymbol{C}}}}_k}$^[20]. 对于低轨卫星来说，由于其高动态特性，不可能保证每个历元观测到相同数量且相同编号的卫星，因此，在一般情况下很难应用于卫星定位. 由于本例中模拟器输出卫星间的信号质量差异不大，采用基于高度角的观测噪声模型代替 $ {{\boldsymbol{R}}_k} $， $ {{\boldsymbol{P}}_{k\mid k - 1}} $则由前N个历元 $ {{\boldsymbol{P}}_{k\mid k - 1}} $的平均值得到，N的选取一般根据经验确定，之后代入式(24)，得到优化后的 ${{{\hat {\boldsymbol{C}}}}_k}$，最后按照式(25)、(26)进行观测噪声协方差矩阵的开窗估计，其中基于高度角的伪距观测噪声 $ \sigma _{\rm{P}}^2 $^[21]可以表示为

(27) $ \sigma _{\rm{P}}^2 = {{c}^2}+{{d}^2}/{\sin ^2}\;E. $

式中：c、d为噪声系数，按照经验并结合开源软件rtklib相关部分，一般取0.3；E为高度角，经多次测试，选择与实际情况最符合，精度最高的arcsin 0.1 rad 作为本次测试的高度角参数. 对于载波相位测量噪声 $ \sigma _{\rm{C}}^2 $来说，一般与伪距测量噪声差2~3个数量级，即

(28) $ \sigma _{\rm{C}}^2 = ({10^{ - 2}}\sim {10^{ - 3}})\sigma _{\rm{P}}^2. $

在ARKF算法中，通过自适应因子的调节以及抗差滤波算法分别降低单历元下异常动力学模型以及异常观测数据对最终定位结果的影响.

在ARKF算法中选取状态变量 $ {\boldsymbol{x}} $为

(29) $ {\boldsymbol{x}} = \left[ {\boldsymbol{r}}(t),{\boldsymbol{v}}(t),{\boldsymbol{\delta t}}(t),{\boldsymbol{p}}(t)\right]^{{\rm{T}}}. $

式中：r、v分别为卫星的相对位置、速度； ${\boldsymbol{\delta t}}$为接收机钟差；p为动力学参数，包括太阳光压系数 ${{\boldsymbol{C}}_{\rm{R}}}$、大气阻力系数 ${{\boldsymbol{C}}_{\rm{D}}}$以及三轴经验加速度 ${{\boldsymbol{a}}_{{\rm{emp}}}}$. 本研究采用的轨道动力学模型如表2所示.

双星编队的相对动力学模型将两星的各自运动状态做差即可，其相对状态转移矩阵 $ {{\boldsymbol{\varPhi}} _{\rm{R}}} $与相对敏感矩阵 $ {{\boldsymbol{S}}_{\rm{R}}} $^[22]可以表示为

(30) $ {{\boldsymbol{\varPhi }}_{\rm{R}}}\left( {t,{t_0}} \right) = {{\boldsymbol{\varPhi}} _{\rm{B}}}\left( {t,{t_0}} \right), $

(31) $ {{\boldsymbol{S}}_{\rm{R}}}(t) = {{\boldsymbol{S}}_{\rm{B}}}(t). $

式中： ${{\boldsymbol{S}}_{\rm{B}}}(t)$、 ${{\boldsymbol{\varPhi}} _{\rm{B}}}\left( {t,{t_0}} \right)$分别表示B星 $ t $时刻的敏感矩阵以及 $ {t_0} $到 $ t $时刻的状态转移矩阵.

ARKF算法流程图如图2所示.在实时相对定位算法开始阶段，首先进行EKF参数的初始化以及时间更新，之后计算导航星的位置以及钟差，并对观测数据进行预处理以及差分组合，接着计算自适应因子的大小，并选择合适的观测噪声协方差估计方法，最后进行量测更新并输出本历元的定位结果，同时进行下一历元的时间更新，具体流程如图3所示.

使用半物理平台对实时相对定位算法进行验证，模拟器采用思博伦GSS9000型号的导航信号模拟器产生绝对功率为−130 dbm的 GPS L1C/A、GPS L2C 双频民码信号，通过射频线连接到L1/L2双频星载GPS接收机进行数据采集，仿真实验环境以及流程图分别如图4、 5所示. 本次实验根据实际卫星任务分别设置轨道高度约为500 km，同轨基线分别为5、50、300 km的3组对比试验.

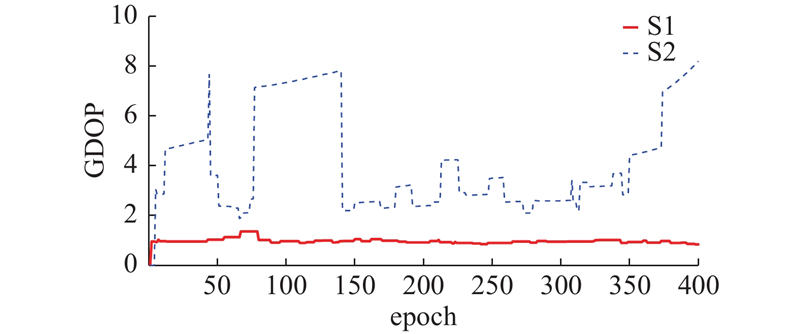
卫星几何分布优劣可以通过几何精度因子(geometric dilution precision，GDOP)表示，假设存在一个各颗可见卫星与GPS接收机为顶点所组成的单位边长的锥形多面体，则此锥面体的体积大致与GDOP成反比. 不难得出，接收机的可视范围越大，可视卫星越多，则卫星的几何分布越好，GDOP越小.

以基线50 km的双星为例，GDOP随时间的分布如图6所示. 图中，S1表示基于全视角接收系统测量数据的GDOP，S2表示基于传统单天线测量数据的GDOP.可以看出，S1的数据每个历元都集中在约1.0，相比于S2的数据，其卫星几何构型更加稳定且对测量误差的放大程度更小，测量数据质量更加稳定，有利于提高定位解算性能^[23].

全视角接收系统数据的测试结果以及作为对比实验的单天线接收系统的测试结果，如表3、图7所示. 表中，A_R、A_T、A_N、A_3D分别为向径方向、飞行器运动方向、轨道面正法向方向的相对定位精度， ${P_{\rm{n}}} $为粗差探测率. 由于单天线下300 km基线数据无法正确定位，故没有对比展示. 本次实验的测试区间长度为1.5 h，解算间隔为10 s，滤波算法统一为EKF.

对于中长基线数据(300 km)，单天线差分无法正确差分定位，全视角差分则可以达到分米级的相对定位精度，但是由于基线过长，有些误差不再具有很强的时间、空间上的相关性，且在侧摆情况下，观测星数受限，因此差分的优势无法最大程度地发挥.

对于短基线数据(5 、50 km)，单天线差分虽然可以正确地定位解算，但是由于共视星数的限制，精度只能达到分米级水平. 全视角差分则增加了一倍左右的共视星数，在观测方程上有一定的冗余，分别可以达到厘米级、近厘米级的相对定位精度.

针对全视角接收系统数据，应用基于GF差分组合和衰减窗口的伪距粗差探测方法，进行不同观测噪声估计法对比实验. 测试结果如表4以及图8、 9所示. 表中， $\Delta L $为基线长度. Case-(a)、(b)、(c)的定义分别如下. Case-(a): EKF+基于高度角定权的观测噪声等价协方差矩阵估计法；Case-(b): ARKF+基于观察残差的观测噪声等价协方差矩阵估计法；Case-(c): ARKF+基于新息向量的观测噪声协方差矩阵开窗估计法. 由于基于观测残差的抗差估计须进行至少2次量测更新，考虑到算法的实时性，其中Case-(c)的计算窗口取10，迭代次数取1.

根据仿真结果可以得到以下结论：

1) 整体对比3种基线定位结果，基线越短，相对定位精度越高，且其受基线长度影响程度较大，本次算法侧重实时性，并未使用精密星历、精密钟差事后产品，主要误差源除了模型修正外，主要依靠差分算法来抑制或者消除，基线越短，差分效果越明显，因此基线长度是实时算法中的重要因素.

2) 观察图8，定义从某历元起连续10个历元定位偏差满足3σ原则，该历元即为收敛时刻^[24]，则5、50、300 km的收敛历元分别为100、150、250历元，同理对比观察图7，可以得出全视角数据的收敛速度优于单天线的收敛速度，且随基线的缩短，收敛速度的提升效果越显著，收敛时间也相对变短.

3)对比3种基线的case-(a)和case-(b)，相对定位精度提升分别在12.68%、22.08%和5.89%，证明基于观察残差的观测噪声等价协方差矩阵估计法可以适应大部分基线长度，且相对定位精度提升与基线长度没有明显关系.

4) 对比3种基线的case-(a)和case-(c)，相对定位精度提升分别在36.60%、23.49%和0%，且基线长度越短，相对定位精度提升效果越好. 基线长度的增加，会导致部分误差时间、空间相关性下降，并且共视星平均高度角下降，进一步导致作为差分算法中主要误差源的多径效应带来的误差增大，从而使新息序列的理论方差预测难度增大，预测精度下降，在长基线情况下体现不出其明显优势.

5) 综合对比不同基线定位精度图，可以看出，在短基线情况下使用基于新息向量的观测噪声协方差矩阵开窗估计法可以得到较好的相对定位结果，最终定位精度可以达到厘米级；在长基线情况下，基于观察残差的观测噪声等价协方差矩阵估计法拥有比基于新息向量的观测噪声协方差矩阵开窗估计法更好的适用性，最终相对定位精度可以达到分米级.

上述分析场景建立在极端场景下，即全弧段侧摆，旨在验证算法可行性. 为了进一步验证实际卫星编队任务，建立机动仿真场景，在正常对地姿态情况下，在第350历元附近，以 $ {1^ \circ }/{\rm{s}} $速度执行侧摆(横滚角)45°指令，侧摆到位后保持5 min，之后以 $ {1^ \circ }/{\rm{s}} $速度恢复到正常对地姿态. 在此过程中可用星数对比图与自适应因子变化图分别如图10、 11所示. 图中，num_f、num_s分别表示全视角接收系统和单天线系统中定轨可用星数. 可以看出，全视角接收系统相对于单天线系统在可用星数方面有着显著的优势，对于单天线系统来说，在侧摆区间随着卫星姿态的改变，在某些卫星失锁的同时，也会捕获新的卫星，但由于地球的遮挡，总体呈现阶梯式的下降趋势，而对于全视角接收系统，由于其广阔的观测视角，几乎不受影响.

图11反映了自适应因子随时间变化的情况. 除了收敛段个别历元，自适应因子调节历元大多集中在侧摆区间，这主要是由于卫星在侧摆区间，姿态发生较大变化，从而使得动力学模型误差增大. 但本研究对象为轨道高度为500 km的低轨卫星，其轨道高度大于GRACE、GOCE典型低轨卫星轨道高度，大气阻力模型之类的其他动力学模型更加精准，且研究平台为半实物平台，动力学模型均为已知状态，结合自适应因子的调节作用，使得动力学模型对定位结果的影响降到了最小.

相对定位测试结果如表5、6以及图12、 13所示. 图中，Case-(1)～Case-(4)定义如下. Case-(1): EKF(单天线接收系统)；Case-(2): EKF(全视角接收系统)；Case-(3): ARKF+基于观察残差的观测噪声等价协方差矩阵估计法(全视角接收系统)；Case-(4): ARKF+基于新息向量的观测噪声协方差矩阵开窗估计法(全视角接收系统). 其中，Case-(4)的计算窗口取10.

根据仿真结果可以得到以下结论.

1) 对比表3、5，粗差探测率集中在约1%，侧面反映了粗差探测方法的稳定性与有效性，且区间“侧摆-回正”过程整体探测率低于全弧度侧摆过程，这是由于区间“侧摆-回正”过程中机动区间仅存在一个较短的时间间隔，其余大部分历元下卫星处于正常对地姿态，天线接收系统可以收到更多来自于高仰角卫星的信号，从而降低了发生粗大误差的概率.

2) 对比图12中各基线长度下case-(1)与case-(2)~ case-(4)，单天线接收系统对部分可观测卫星来说在侧摆区间会经历由失锁到重新捕获的过程，而接收机重新捕获则需要一个过程，因此观测星数不能及时随侧摆阶段的结束而恢复正常，进而导致定位精度存在较长时间大幅度抖动，而全视角接收系统则由于其较多的观测星数而基本不受影响，进一步证明了本研究提出的新方法在应用场景的可行性.

3) 分别对比图9. 各基线下case-(a)~ case-(c)与图13各基线中case-(2)~ case-(4)，相对定位精度均有小幅度提升，且变化趋势基本一致. 由于区间“侧摆-回正”过程相对于“全弧度侧摆”，绝大部分历元下可视卫星的范围增加约33.3%，伴随可用星数的增加，差分性能得到提升. 短基线下基于新息向量的观测噪声协方差矩阵开窗估计法拥有比基于新息向量的观测噪声等价协方差矩阵估计法更高的相对定位精度，但随着基线长度的增加，上述情况反之，这一点与3.2.1节的结论4) 一致.

4) 对比图13各基线下case-(3)、 case-(4)，2种情况下相对定位精度差别较小，证明在低轨卫星高动态场景下，可用星数仍是制约相对定位精度的主要因素，本研究提出的伪距粗差探测方法以及使用的2种观测噪声协方差矩阵估计法仅起辅助作用，且随着整体相对定位精度的提升，观测质量以及观测噪声协方差矩阵对相对定位精度影响的权重逐渐降低.

半物理仿真结果表明，在全弧段侧摆与机动条件下，本研究所提出的新方法相比于单天线方案，可用星数大幅增加、相对定位精度大幅提升；在短基线情况下，使用基于新息向量的观测噪声协方差矩阵开窗估计法可以达到厘米级的相对定位精度，在长基线情况下，使用基于观察残差的观测噪声等价协方差矩阵估计法可以达到分米级相对定位精度. 本研究的目的在于突出全视角接收系统相对于单天线接收系统的优势以及抗差滤波算法的优越性，为了在简化算法的同时达到实验目的，选择了浮点解作为量化指标. 出于本项目特殊的应用场景以及独特的接收系统设计构造，模糊度的固定方法与常规固定方法有所不同，后续将单独对此进行更深入的研究. 本研究提出的新方法适用于搭载全视角接收系统的微纳卫星编队实时相对定位，并可在全弧段侧摆与机动条件下，实现高精度、稳定的编队相对定位. 未来有望应用于微纳卫星编队光学成像、对地凝视之类的特殊姿态任务中.