[21]
CHOLLET F. Xception: deep learning with depthwise separable convolutions [C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition . Honolulu: IEEE, 2017: 1251-1258.
[22]
HOWARD A G, ZHU M, CHEN B, et al. MobileNets: efficient convolutional neural networks for mobile vision applications [EB/OL]. (2017-04-17) [2022-12-10]. https: arxiv.org/pdf/1704.04861. pdf.
[本文引用: 1]
[23]
HE Y H, LIN J, LIU Z J, et al. AMC: AutoML for model compression and acceleration on mobile devices [C]// Proceedings of the European Conference on Computer Vision . [S. l.]: Springer, 2018: 815-832.
[本文引用: 1]
[24]
ASHOK A, RHINEHART N, BEAINY F, et al. N2N learning: network to network compression via policy gradient reinforcement learning [EB/OL]. (2017-12-17)[2022-12-10]. https://arxiv.org/pdf/1709.06030v1.pdf.
[本文引用: 1]
[25]
LIU Z C, MU H Y, ZHANG X Y, et al. MetaPruning: meta learning for automatic neural network channel pruning [C]// Proceedings of the IEEE/CVF International Conference on Computer Vision. Seoul: IEEE, 2019: 3296-3305.
[本文引用: 1]
[26]
LILLICRAP T P, HUNT J J, PRITZEL A, et al. Continuous control with deep reinforcement learning [EB/OL]. (2019-07-15)[2022-12-12]. https://arxiv.org/pdf/1509.02971.pdf.
[本文引用: 1]
[27]
LIN M B, JI R R, ZHANG Y X. Channel pruning via automatic structure search [EB/OL]. (2020-06-29)[2022-12-16]. https://arxiv.org/pdf/2001.08565.pdf.
[本文引用: 2]
[28]
HUANG Z Z, SHAO W Q, WANG X J. Rethinking the pruning criteria for convolutional neural network [C]// Conference and Workshop on Neural Information Processing Systems . Montreal: MIT Press, 2021, 34: 16305-16318.
[本文引用: 2]
[29]
盛骤, 谢式千, 潘承毅. 概率论与数理统计[M]. 北京高等教育出版社, 2008: 112-114.
[本文引用: 1]
[30]
LIN S H, JI R R, YAN C Q, et al. Towards optimal structured CNN pruning via generative adversarial learning [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Long Beach: IEEE, 2019: 2790-2799.
[本文引用: 3]
[31]
LI H, KADAV A, DURDANOVIC I, et al. Pruning filters for efficient convnets [EB/OL]. (2017-03-10)[2022-12-20]. https://arxiv.org/pdf/1608.08710.pdf.
[本文引用: 3]
[32]
LUO J H, WU J X. An entropy-based pruning method for CNN compression [EB/OL]. (2017-06-19)[2022-12-20]. https: arxiv.org/pdf/1706.05791.pdf.
[本文引用: 2]
[1]
KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet classification with deep convolutional neural networks [C]// Proceedings of the 25th International Conference on Neural Information Processing Systems . Lake Tahoe: Curran Associates Inc, 2012: 1097-1105.
[本文引用: 1]
[2]
ZHANG L B, HUANG S L, LIU W. Intra-class part swapping for fine-grained image classification [C]// Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision . Waikoloa: IEEE, 2021: 3209-3218.
[本文引用: 1]
[33]
HU H Y, PENG R, TAI Y W, et al. Network trimming: a data-driven neuron pruning approach towards efficient deep architectures [EB/OL]. (2016-07-12)[2022-12-20]. https://arxiv.org/pdf/1607.03250.pdf.
[本文引用: 1]
[34]
LIN M B, JI R R, WANG Y. HRank: filter pruning using high-rank feature map [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Seattle: IEEE, 2020: 1529-1538.
[本文引用: 1]
[3]
REN S K, HE K M, GIRSHICK R, et al. Object detection networks on convolutional feature maps [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence . 2017, 39(7): 1476-1481.
[本文引用: 1]
[4]
REDMON J, DIVVALA S, GIRSHICK R, et al. You only look once: unified, real-time object detection [C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition . Las Vegas: IEEE, 2016: 779-788.
[5]
BLAIVAS M, ARNTFIELD R, WHITE M Creation and testing of a deep learning algorithm to automatically identify and label vessels, nerves, tendons, and bones on cross-sectional point-of-care ultrasound scans for peripheral intravenous catheter placement by novices
[J]. Journal of Ultrasound in Medicine , 2020 , 39 (9 ): 1721 - 1727
DOI:10.1002/jum.15270
[本文引用: 1]
[6]
LONG J, SHELHAMER E, DARRELL T. Fully convolutional networks for semantic segmentation [C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition . Boston: IEEE, 2015: 3431-3440.
[本文引用: 1]
[7]
TANZI L, PIAZZOLLA P, PORPIGLIA F, et al Real-time deep learning semantic segmentation during intra-operative surgery for 3D augmented reality assistance
[J]. International Journal of Computer Assisted Radiology and Surgery , 2021 , 16 : 1435 - 1445
DOI:10.1007/s11548-021-02432-y
[8]
张哲晗, 方薇, 杜丽丽, 等 基于编码-解码卷积神经网络的遥感图像语义分割
[J]. 光学学报 , 2020 , 40 (3 ): 46 - 55
[本文引用: 1]
ZHANG Zhe-han, FANG Wei, DU Li-li, et al Semantic segmentation of remote sensing image based on coding-decoding convolutional neural network
[J]. Acta Optica Sinica , 2020 , 40 (3 ): 46 - 55
[本文引用: 1]
[9]
吕永发. 基于深度学习的手机表面缺陷检测算法[D]. 郑州: 郑州大学, 2020.
[本文引用: 1]
LV Yong-fa. Mobile phone surface detect detection algorithm based on deep learning [D]. Zhengzhou: Zhengzhou University, 2020.
[本文引用: 1]
[10]
JIANG Y, WANG W, ZHAO C. A machine vision-based realtime anomaly detection method for industrial products using deep learning [C]// 2019 Chinese Automation Congress . Hangzhou: IEEE, 2019: 4842-4847.
[本文引用: 1]
[11]
GONG R H, LIU X L, JIANG S H, et al. Differentiable soft quantization: bridging full-precision and low-bit neural networks [C]// Proceedings of the IEEE/CVF International Conference on Computer Vision . Seoul: IEEE, 2019: 4852-4861.
[本文引用: 1]
[12]
COURBARIAUX M, HUBARA I, SOUDRY D, et al. Binarized neural networks: training neural networks with weights and activations constrained to +1 or −1 [EB/OL]. (2016-03-17)[2022-12-10]. https:arxiv.org/pdf/1602.02830.pdf.
[本文引用: 1]
[13]
LI F F, LIU B, WANG X X. Ternary weight networks [EB/OL]. (2022-11-20)[2022-12-10]. https://arxiv.org/pdf/1605.04711.pdf.
[本文引用: 1]
[15]
KIM Y D, PARK E, YOO S, et al. Compression of deep convolutional neural networks for fast and low power mobile applications [EB/OL]. (2016-12-24) [2022-12-10]. https://arxiv.org/pdf/1511.06530.pdf.
[本文引用: 1]
[16]
LATHAUWER L D Decompositions of a higher-order tensor in block terms
[J]. SIAM Journal on Matrix Analysis and Applications , 2008 , 30 (3 ): 1022 - 1032
DOI:10.1137/060661685
[本文引用: 1]
[17]
ZAGORUYKO S, KOMODAKIS N. Paying more attention to attention: improving the performance of convolutional neural networks via attention transfer [EB/OL]. (2017-12-12)[2022-12-10]. https://arxiv.org/pdf/1612.03928.pdf.
[本文引用: 1]
[18]
ZHANG L F, SONG J B, GAO A, et al. Be your own teacher: improve the performance of convolutional neural networks via self distillation [C]// Proceedings of the IEEE/CVF International Conference on Computer Vision . Seoul: IEEE, 2019: 3713-3722.
[本文引用: 1]
[19]
IANDOLA F N, HAN S, MOSKEWICZ M W, et al. SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and<0.5MB model size [EB/OL]. (2016-11-04)[2022-12-10]. https:arxiv.org/pdf/1602.07360.pdf.
[本文引用: 1]
[20]
ZHANG X Y, ZHOU X Y, LIN M X, et al. ShuffleNet: an extremely efficient convolutional neural network for mobile devices [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Salt Lake City: IEEE, 2018: 6848-6856.
1
... 深度神经网络在图像分类[1 -2 ] 、物体检测[3 -5 ] 、语义分割[6 -8 ] 等领域的应用效果良好. 随着深度学习的发展,神经网络的层数越来越深,参数越来越多. 由于将神经网络部署在资源受限的嵌入式设备上有一定的困难,导致庞大的神经网络模型在实时性要求较高的工业现场的应用受阻. 模型压缩可以有效地减少网络参数,降低网络复杂度,拓展深度神经网络在工业现场的应用[9 -10 ] . 模型压缩的方法主要有量化、低秩分解、知识蒸馏、轻量化网络设计和剪枝等. 模型量化[11 ] 是将高比特的浮点运算转换为低比特的定点运算,如网络二值化方法[12 ] 、三值神经网络[13 ] ,但这类方法在压缩模型的同时损失了较大的网络精度. 低秩分解是通过奇异值分解(singular value decomposition, SVD)[14 ] 、Tucker分解[15 ] 、Block Term分解[16 ] 等方法将网络结构中复杂的张量用精简的张量表示,这类方法能够压缩网络,但矩阵分解成本高,并且分解后需要逐层微调,一定程度上减缓了模型训练速度. 知识蒸馏方法虽然性能较好,但存在效率低以及教师模型难设计、难选择的问题[17 -18 ] . 轻量化网络设计[19 -22 ] 是在保持模型精度的基础上,根据技巧和经验设计的性能较优的小型网络,但轻量化网络模型固定,该方法不适用于特定网络结构的压缩. ...
1
... 剪枝是最常用的模型压缩方法. 在传统的剪枝方法中,剪枝率和阈值通常由经验丰富的专家根据模型大小和准确率人为设定,不仅耗时而且主观性较强,在大规模的网络结构中容易导致局部最优. 因此,自动寻找稀疏的网络结构成为新的研究热点. 强化学习可以在节省人力的情况下,通过自动探索和学习,更好地实现复杂的任务自动化和大规模的空间搜索. He等[23 ] 提出用强化学习对模型进行压缩,利用深度确定性策略梯度算法自动搜索每层的压缩率;根据压缩率逐层进行通道剪枝.该方法可将网络VGG16实现4倍加速,且剪枝后的准确率比手工设定的剪枝方法高2.7%. 全连接层仍然存在一定的冗余,而且卷积层由于稀疏率固定为50%,导致压缩率不高. Ashok等[24 ] 提出基于策略梯度先剪枝网络层,再剪枝网络层参数的方法. 该方法可以在保持较高压缩率的情况下,使准确率基本不变,但剪枝过程中网络搜索时间较长. Liu等[25 ] 通过训练元网络对通道进行自动化剪枝. 该方法搜索时不需要微调,搜索效率高、性能优越,但在剪枝网络编码的过程中需要反复迭代. ...
1
... 剪枝是最常用的模型压缩方法. 在传统的剪枝方法中,剪枝率和阈值通常由经验丰富的专家根据模型大小和准确率人为设定,不仅耗时而且主观性较强,在大规模的网络结构中容易导致局部最优. 因此,自动寻找稀疏的网络结构成为新的研究热点. 强化学习可以在节省人力的情况下,通过自动探索和学习,更好地实现复杂的任务自动化和大规模的空间搜索. He等[23 ] 提出用强化学习对模型进行压缩,利用深度确定性策略梯度算法自动搜索每层的压缩率;根据压缩率逐层进行通道剪枝.该方法可将网络VGG16实现4倍加速,且剪枝后的准确率比手工设定的剪枝方法高2.7%. 全连接层仍然存在一定的冗余,而且卷积层由于稀疏率固定为50%,导致压缩率不高. Ashok等[24 ] 提出基于策略梯度先剪枝网络层,再剪枝网络层参数的方法. 该方法可以在保持较高压缩率的情况下,使准确率基本不变,但剪枝过程中网络搜索时间较长. Liu等[25 ] 通过训练元网络对通道进行自动化剪枝. 该方法搜索时不需要微调,搜索效率高、性能优越,但在剪枝网络编码的过程中需要反复迭代. ...
1
... 剪枝是最常用的模型压缩方法. 在传统的剪枝方法中,剪枝率和阈值通常由经验丰富的专家根据模型大小和准确率人为设定,不仅耗时而且主观性较强,在大规模的网络结构中容易导致局部最优. 因此,自动寻找稀疏的网络结构成为新的研究热点. 强化学习可以在节省人力的情况下,通过自动探索和学习,更好地实现复杂的任务自动化和大规模的空间搜索. He等[23 ] 提出用强化学习对模型进行压缩,利用深度确定性策略梯度算法自动搜索每层的压缩率;根据压缩率逐层进行通道剪枝.该方法可将网络VGG16实现4倍加速,且剪枝后的准确率比手工设定的剪枝方法高2.7%. 全连接层仍然存在一定的冗余,而且卷积层由于稀疏率固定为50%,导致压缩率不高. Ashok等[24 ] 提出基于策略梯度先剪枝网络层,再剪枝网络层参数的方法. 该方法可以在保持较高压缩率的情况下,使准确率基本不变,但剪枝过程中网络搜索时间较长. Liu等[25 ] 通过训练元网络对通道进行自动化剪枝. 该方法搜索时不需要微调,搜索效率高、性能优越,但在剪枝网络编码的过程中需要反复迭代. ...
1
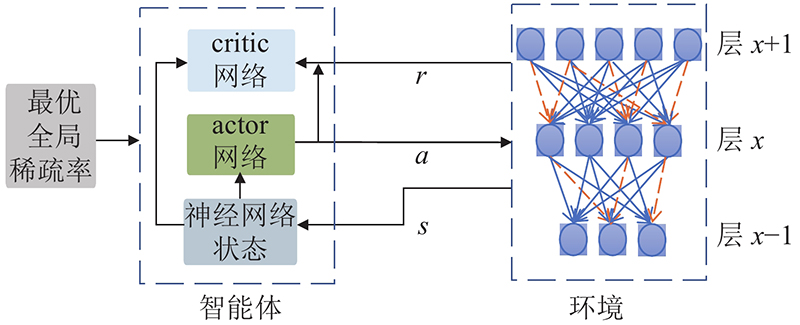
... 强化学习在训练智能体与环境交互中进行学习. 如何在智能体不断地尝试学习后,执行可以获得最大奖励的行动,是优化问题. 深度确定性策略梯度(deep deterministic policy gradient, DDPG[26 ] )算法是基于行动者-评论家(actor-critic)算法和确定性策略梯度(DPG)的算法.它既能够单步更新值,又能够用于处理高维连续动作,使奖励值最大化. 基于DDPG搭建强化学习下的自动化剪枝结构框架,如图1 所示. 图中, actor、critic为DDPG的2个网络,s 为环境的状态,a 为下一步要采取的动作,r 为产生的奖励,x 为神经网络的层数. ...
2
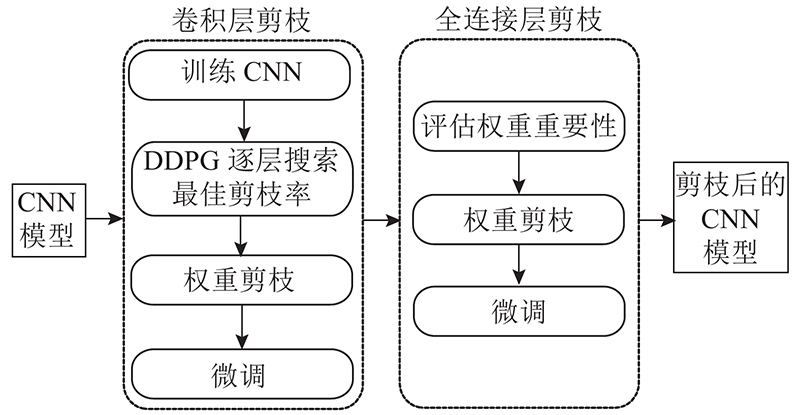
... 在权重剪枝过程中,有连续稀疏比和权重数2个操作空间. 连续稀疏比可以直观地反映网络结构的稀疏程度,稀疏度越低,冗余参数越多. 由权重数可以直观了解须修剪的参数数量,但每层网络结构的权重数不同,若直接输出需剪枝的权重数,会导致搜索空间不固定,加大计算量. 已有部分实验使用权重数作为动作空间[27 ] ,权重数可用于复杂的网络结构,用于普通的网络架构可能会出现损失爆炸问题. 模型压缩对稀疏比很敏感,为了避免损失爆炸问题,采用连续的动作空间a ∈(0,1.0],以实现更加精确的模型压缩. ...
... ResNet50共50层,其中卷积层为49层,全连接层为1层. 该网络由2个基本块Conv Block和Identity Block组成,Conv Block用来改变网络的维度,不能连续串联;Identity Block输入输出维度一样,能串联用来加深网络. 在数据集ILSVRC-2012 ImageNet上对ResNet50进行剪枝实验. 根据图4 ,设置强化学习搜索权重剪枝的目标全局稀疏率为80%. 数据集ILSVRC-2012 ImageNet在ResNet50上进行评估的Top1准确率为76.02%,Top5准确率为92.94%. 组合剪枝微调后的Top1准确率为74.16%, Top5准确率为91.96%,各块具体剪枝后的结果如表7 所示. 表中,∆p T1 为Top1准确率变化量. 由表可知,在卷积层强化学习权重剪枝后,对全连接层进行3σ 权重剪枝可进一步压缩网络. 为了验证本研究所提组合剪枝方法的有效性,与GAL[30 ] 、ABCPruner[27 ] 、HRank[34 ] 剪枝算法进行对比,结果如表8 所示. 由表可知,在压缩80.9%参数的情况下,组合剪枝方法仅导致1.86%的精度损失,明显优于其他剪枝算法. ...
2
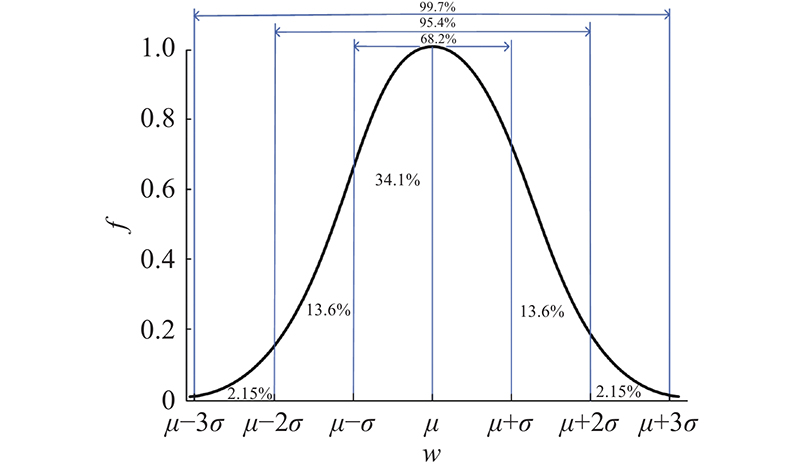
... 在网络训练过程中,每层的权重不同,因此对网络剪枝时,每层设置不同的阈值有利于减少准确性损失、避免层垮塌. 全连接层参数众多,随着训练次数增加,模型的参数分布近似正态分布[28 ] ,符合3σ 准则. 3σ 准则[29 ] 分布如图3 所示. 图中,w 为权重值,f 为概率密度,µ 为均值,σ 为标准差. 3σ 准则准确的数值分布为 ...
... 由图3 可知,对于任意近似正态分布的权重参数集合,权重大部分分布在(µ−3σ ,µ+3σ ),只有0.27%的权重参数超出该范围. 深度神经网络存在大量的冗余权重,在已有的权重剪枝方法中,权重阈值一般由权重标准差决定. 本研究根据3σ 准则,通过均值和方差确定阈值. 均值反映权重参数的整体趋势,标准差反映每个权重值相对于样本中心的离散程度[28 ] . 通过均值和标准差相结合的统计准则,可以选出大量性能较差的权重值并移除,以压缩网络. ...
1
... 在网络训练过程中,每层的权重不同,因此对网络剪枝时,每层设置不同的阈值有利于减少准确性损失、避免层垮塌. 全连接层参数众多,随着训练次数增加,模型的参数分布近似正态分布[28 ] ,符合3σ 准则. 3σ 准则[29 ] 分布如图3 所示. 图中,w 为权重值,f 为概率密度,µ 为均值,σ 为标准差. 3σ 准则准确的数值分布为 ...
3
... 分别使用强化学习权重剪枝和3σ 准则确定阈值权重剪枝方法对整个VGG16网络进行实验,并将组合剪枝方法与GAL-0.05[30 ] 、L1正则化[31 ] 、Entropy-based[32 ] 方法进行性能对比. 各方法在CIFAR10数据集的实验结果如表4 所示. 从表可知,当仅使用强化学习自动化搜索压缩率对VGG16网络进行剪枝时,虽然误差最小,但剪枝率为28.08%. 原因是强化学习搜索剪枝法只对卷积层进行剪枝,全连接层由于层数较少,不能提供足够的环境供强化学习搜索,因此仍留有大量冗余参数. 用3σ 准则确定阈值对整个网络进行剪枝的剪枝率最高,但是相比本研究所提方法,误差较大. 与其他方法进行比较,发现当GAL-0.05压缩77.46%的权重参数时,会导致6.86%的损失,使用本研究所提方法可以将参数压缩83.33%,且仅有1.55%的误差. 比GAL-0.05多压缩5.87%,误差大大降低. Entropy-based下的实验误差虽然比GAL-0.05和LI正则化的实验误差小,但是其性能不及组合剪枝方法. 组合剪枝方法可以比Entropy-based方法剪去更多的冗余参数,具有更小的误差. 实验结果表明,本研究所提的组合剪枝方法性能较好. ...
... Comparison of combination pruning method with other methods on VGG16
Tab.4 方法 a o /% ∆p /% 强化学习权重剪枝 28.08 −0.75 3σ 权重剪枝 99.05 −6.11 GAL-0.05[30 ] 77.46 −6.86 LI正则化[31 ] 64.08 −7.13 Entropy-based[32 ] 43.00 −2.06 组合剪枝 83.33 −1.55
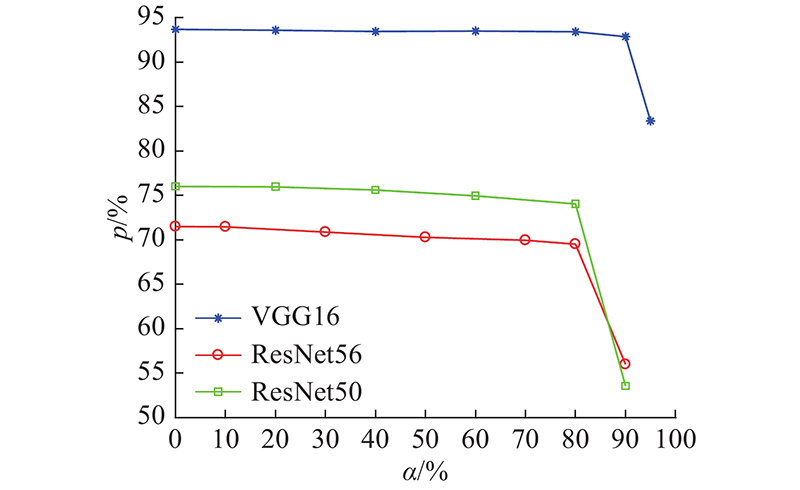
3.2. ResNet56实验结果 ResNet56是56层的残差网络,由残差块和残差连接组成. 在数据集CIFAR100上进行训练和剪枝,基线准确率为71.5%. 如图4 所示,ResNet56随着稀疏率的增大,准确率下降比VGG16严重. 原因是ResNet56残差网络有很多支线将输入与后面的层相连,部分层与层的联系紧密,提取的大部分为重要特征,冗余度较小. 当α =80%时,能够保证一定的压缩率,且准确率损失相对较少,为1.98%. 在稀疏率为80%,用DDPG搜索卷积层最佳权重剪枝率时,最大奖励下获得的剪枝结果如表5 所示. 表中,a b 为网络各块的剪枝率. 由表可知,DDPG自动化框架将ResNet56网络结构剪去了70.1%的参数,准确率为69.52%. ...
... ResNet50共50层,其中卷积层为49层,全连接层为1层. 该网络由2个基本块Conv Block和Identity Block组成,Conv Block用来改变网络的维度,不能连续串联;Identity Block输入输出维度一样,能串联用来加深网络. 在数据集ILSVRC-2012 ImageNet上对ResNet50进行剪枝实验. 根据图4 ,设置强化学习搜索权重剪枝的目标全局稀疏率为80%. 数据集ILSVRC-2012 ImageNet在ResNet50上进行评估的Top1准确率为76.02%,Top5准确率为92.94%. 组合剪枝微调后的Top1准确率为74.16%, Top5准确率为91.96%,各块具体剪枝后的结果如表7 所示. 表中,∆p T1 为Top1准确率变化量. 由表可知,在卷积层强化学习权重剪枝后,对全连接层进行3σ 权重剪枝可进一步压缩网络. 为了验证本研究所提组合剪枝方法的有效性,与GAL[30 ] 、ABCPruner[27 ] 、HRank[34 ] 剪枝算法进行对比,结果如表8 所示. 由表可知,在压缩80.9%参数的情况下,组合剪枝方法仅导致1.86%的精度损失,明显优于其他剪枝算法. ...
3
... 分别使用强化学习权重剪枝和3σ 准则确定阈值权重剪枝方法对整个VGG16网络进行实验,并将组合剪枝方法与GAL-0.05[30 ] 、L1正则化[31 ] 、Entropy-based[32 ] 方法进行性能对比. 各方法在CIFAR10数据集的实验结果如表4 所示. 从表可知,当仅使用强化学习自动化搜索压缩率对VGG16网络进行剪枝时,虽然误差最小,但剪枝率为28.08%. 原因是强化学习搜索剪枝法只对卷积层进行剪枝,全连接层由于层数较少,不能提供足够的环境供强化学习搜索,因此仍留有大量冗余参数. 用3σ 准则确定阈值对整个网络进行剪枝的剪枝率最高,但是相比本研究所提方法,误差较大. 与其他方法进行比较,发现当GAL-0.05压缩77.46%的权重参数时,会导致6.86%的损失,使用本研究所提方法可以将参数压缩83.33%,且仅有1.55%的误差. 比GAL-0.05多压缩5.87%,误差大大降低. Entropy-based下的实验误差虽然比GAL-0.05和LI正则化的实验误差小,但是其性能不及组合剪枝方法. 组合剪枝方法可以比Entropy-based方法剪去更多的冗余参数,具有更小的误差. 实验结果表明,本研究所提的组合剪枝方法性能较好. ...
... Comparison of combination pruning method with other methods on VGG16
Tab.4 方法 a o /% ∆p /% 强化学习权重剪枝 28.08 −0.75 3σ 权重剪枝 99.05 −6.11 GAL-0.05[30 ] 77.46 −6.86 LI正则化[31 ] 64.08 −7.13 Entropy-based[32 ] 43.00 −2.06 组合剪枝 83.33 −1.55
3.2. ResNet56实验结果 ResNet56是56层的残差网络,由残差块和残差连接组成. 在数据集CIFAR100上进行训练和剪枝,基线准确率为71.5%. 如图4 所示,ResNet56随着稀疏率的增大,准确率下降比VGG16严重. 原因是ResNet56残差网络有很多支线将输入与后面的层相连,部分层与层的联系紧密,提取的大部分为重要特征,冗余度较小. 当α =80%时,能够保证一定的压缩率,且准确率损失相对较少,为1.98%. 在稀疏率为80%,用DDPG搜索卷积层最佳权重剪枝率时,最大奖励下获得的剪枝结果如表5 所示. 表中,a b 为网络各块的剪枝率. 由表可知,DDPG自动化框架将ResNet56网络结构剪去了70.1%的参数,准确率为69.52%. ...
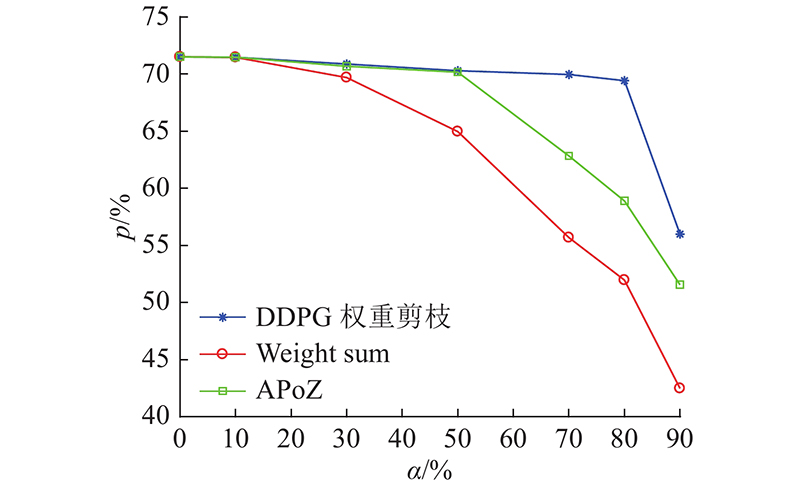
... 对ResNet56全连接层确定不同阈值,进行权重剪枝并评估数据集CIFAR100在剪枝后ResNet56上的性能. 通过确定不同阈值,对网络剪枝、微调,再训练和预训练一样的epoch,详细的实验结果如表6 所示. 由表可知,无论阈值取何值,ResNet56剪枝后的准确率均急剧下降. 当阈值为μ +3σ 时,压缩率最大,但损失为35.61%. 原因是ResNet56为残差网络,由1层输入、3个残差模块和1个分类的全连接层组成,全连接层有6 400个神经元,数目相对较少. 当使用3σ 准则作为阈值进行剪枝时,会剪去大部分参数,导致准确率偏低. 因此对ResNet56,本研究仅采用DDPG自动化搜索卷积层权重并剪枝的方法. 该方法与Weight sum[31 ] 和APoZ[33 ] 方法的性能对比如图5 所示. 由图可知,在这些方法中, DDPG权重剪枝方法性能最优,在稀疏率为80%时,仍能保持一定的准确率. 但在Weight sum方法和APoZ方法的稀疏率为80%时,准确率分别为51.96%和58.89%. 相比DDPG权重剪枝方法,性能分别下降了17.46%和10.53%. 原因是Weight sum方法根据计算滤波器权重绝对值之和进行剪枝,当稀疏率为80%时,剪去大量参数后准确率下降. APoZ方法根据输出通道通过激活函数后的非零比值进行剪枝,在稀疏率小于50%时,准确率与DDPG权重剪枝方法相差较小,表示已正确移除零值通道. 但当稀疏率超过50%时,准确率下降是由于剪枝后的通道包含丰富且不同的特征信息,在此基础上进一步剪枝,非零比值小的通道将会被剪去,导致准确率下降. DDPG根据提供的全局稀疏率,自动化学习搜索每层的最佳剪枝率,在反馈奖励最大时,进行剪枝. ...
2
... 分别使用强化学习权重剪枝和3σ 准则确定阈值权重剪枝方法对整个VGG16网络进行实验,并将组合剪枝方法与GAL-0.05[30 ] 、L1正则化[31 ] 、Entropy-based[32 ] 方法进行性能对比. 各方法在CIFAR10数据集的实验结果如表4 所示. 从表可知,当仅使用强化学习自动化搜索压缩率对VGG16网络进行剪枝时,虽然误差最小,但剪枝率为28.08%. 原因是强化学习搜索剪枝法只对卷积层进行剪枝,全连接层由于层数较少,不能提供足够的环境供强化学习搜索,因此仍留有大量冗余参数. 用3σ 准则确定阈值对整个网络进行剪枝的剪枝率最高,但是相比本研究所提方法,误差较大. 与其他方法进行比较,发现当GAL-0.05压缩77.46%的权重参数时,会导致6.86%的损失,使用本研究所提方法可以将参数压缩83.33%,且仅有1.55%的误差. 比GAL-0.05多压缩5.87%,误差大大降低. Entropy-based下的实验误差虽然比GAL-0.05和LI正则化的实验误差小,但是其性能不及组合剪枝方法. 组合剪枝方法可以比Entropy-based方法剪去更多的冗余参数,具有更小的误差. 实验结果表明,本研究所提的组合剪枝方法性能较好. ...
... Comparison of combination pruning method with other methods on VGG16
Tab.4 方法 a o /% ∆p /% 强化学习权重剪枝 28.08 −0.75 3σ 权重剪枝 99.05 −6.11 GAL-0.05[30 ] 77.46 −6.86 LI正则化[31 ] 64.08 −7.13 Entropy-based[32 ] 43.00 −2.06 组合剪枝 83.33 −1.55
3.2. ResNet56实验结果 ResNet56是56层的残差网络,由残差块和残差连接组成. 在数据集CIFAR100上进行训练和剪枝,基线准确率为71.5%. 如图4 所示,ResNet56随着稀疏率的增大,准确率下降比VGG16严重. 原因是ResNet56残差网络有很多支线将输入与后面的层相连,部分层与层的联系紧密,提取的大部分为重要特征,冗余度较小. 当α =80%时,能够保证一定的压缩率,且准确率损失相对较少,为1.98%. 在稀疏率为80%,用DDPG搜索卷积层最佳权重剪枝率时,最大奖励下获得的剪枝结果如表5 所示. 表中,a b 为网络各块的剪枝率. 由表可知,DDPG自动化框架将ResNet56网络结构剪去了70.1%的参数,准确率为69.52%. ...
1
... 深度神经网络在图像分类[1 -2 ] 、物体检测[3 -5 ] 、语义分割[6 -8 ] 等领域的应用效果良好. 随着深度学习的发展,神经网络的层数越来越深,参数越来越多. 由于将神经网络部署在资源受限的嵌入式设备上有一定的困难,导致庞大的神经网络模型在实时性要求较高的工业现场的应用受阻. 模型压缩可以有效地减少网络参数,降低网络复杂度,拓展深度神经网络在工业现场的应用[9 -10 ] . 模型压缩的方法主要有量化、低秩分解、知识蒸馏、轻量化网络设计和剪枝等. 模型量化[11 ] 是将高比特的浮点运算转换为低比特的定点运算,如网络二值化方法[12 ] 、三值神经网络[13 ] ,但这类方法在压缩模型的同时损失了较大的网络精度. 低秩分解是通过奇异值分解(singular value decomposition, SVD)[14 ] 、Tucker分解[15 ] 、Block Term分解[16 ] 等方法将网络结构中复杂的张量用精简的张量表示,这类方法能够压缩网络,但矩阵分解成本高,并且分解后需要逐层微调,一定程度上减缓了模型训练速度. 知识蒸馏方法虽然性能较好,但存在效率低以及教师模型难设计、难选择的问题[17 -18 ] . 轻量化网络设计[19 -22 ] 是在保持模型精度的基础上,根据技巧和经验设计的性能较优的小型网络,但轻量化网络模型固定,该方法不适用于特定网络结构的压缩. ...
1
... 深度神经网络在图像分类[1 -2 ] 、物体检测[3 -5 ] 、语义分割[6 -8 ] 等领域的应用效果良好. 随着深度学习的发展,神经网络的层数越来越深,参数越来越多. 由于将神经网络部署在资源受限的嵌入式设备上有一定的困难,导致庞大的神经网络模型在实时性要求较高的工业现场的应用受阻. 模型压缩可以有效地减少网络参数,降低网络复杂度,拓展深度神经网络在工业现场的应用[9 -10 ] . 模型压缩的方法主要有量化、低秩分解、知识蒸馏、轻量化网络设计和剪枝等. 模型量化[11 ] 是将高比特的浮点运算转换为低比特的定点运算,如网络二值化方法[12 ] 、三值神经网络[13 ] ,但这类方法在压缩模型的同时损失了较大的网络精度. 低秩分解是通过奇异值分解(singular value decomposition, SVD)[14 ] 、Tucker分解[15 ] 、Block Term分解[16 ] 等方法将网络结构中复杂的张量用精简的张量表示,这类方法能够压缩网络,但矩阵分解成本高,并且分解后需要逐层微调,一定程度上减缓了模型训练速度. 知识蒸馏方法虽然性能较好,但存在效率低以及教师模型难设计、难选择的问题[17 -18 ] . 轻量化网络设计[19 -22 ] 是在保持模型精度的基础上,根据技巧和经验设计的性能较优的小型网络,但轻量化网络模型固定,该方法不适用于特定网络结构的压缩. ...
1
... 对ResNet56全连接层确定不同阈值,进行权重剪枝并评估数据集CIFAR100在剪枝后ResNet56上的性能. 通过确定不同阈值,对网络剪枝、微调,再训练和预训练一样的epoch,详细的实验结果如表6 所示. 由表可知,无论阈值取何值,ResNet56剪枝后的准确率均急剧下降. 当阈值为μ +3σ 时,压缩率最大,但损失为35.61%. 原因是ResNet56为残差网络,由1层输入、3个残差模块和1个分类的全连接层组成,全连接层有6 400个神经元,数目相对较少. 当使用3σ 准则作为阈值进行剪枝时,会剪去大部分参数,导致准确率偏低. 因此对ResNet56,本研究仅采用DDPG自动化搜索卷积层权重并剪枝的方法. 该方法与Weight sum[31 ] 和APoZ[33 ] 方法的性能对比如图5 所示. 由图可知,在这些方法中, DDPG权重剪枝方法性能最优,在稀疏率为80%时,仍能保持一定的准确率. 但在Weight sum方法和APoZ方法的稀疏率为80%时,准确率分别为51.96%和58.89%. 相比DDPG权重剪枝方法,性能分别下降了17.46%和10.53%. 原因是Weight sum方法根据计算滤波器权重绝对值之和进行剪枝,当稀疏率为80%时,剪去大量参数后准确率下降. APoZ方法根据输出通道通过激活函数后的非零比值进行剪枝,在稀疏率小于50%时,准确率与DDPG权重剪枝方法相差较小,表示已正确移除零值通道. 但当稀疏率超过50%时,准确率下降是由于剪枝后的通道包含丰富且不同的特征信息,在此基础上进一步剪枝,非零比值小的通道将会被剪去,导致准确率下降. DDPG根据提供的全局稀疏率,自动化学习搜索每层的最佳剪枝率,在反馈奖励最大时,进行剪枝. ...
1
... ResNet50共50层,其中卷积层为49层,全连接层为1层. 该网络由2个基本块Conv Block和Identity Block组成,Conv Block用来改变网络的维度,不能连续串联;Identity Block输入输出维度一样,能串联用来加深网络. 在数据集ILSVRC-2012 ImageNet上对ResNet50进行剪枝实验. 根据图4 ,设置强化学习搜索权重剪枝的目标全局稀疏率为80%. 数据集ILSVRC-2012 ImageNet在ResNet50上进行评估的Top1准确率为76.02%,Top5准确率为92.94%. 组合剪枝微调后的Top1准确率为74.16%, Top5准确率为91.96%,各块具体剪枝后的结果如表7 所示. 表中,∆p T1 为Top1准确率变化量. 由表可知,在卷积层强化学习权重剪枝后,对全连接层进行3σ 权重剪枝可进一步压缩网络. 为了验证本研究所提组合剪枝方法的有效性,与GAL[30 ] 、ABCPruner[27 ] 、HRank[34 ] 剪枝算法进行对比,结果如表8 所示. 由表可知,在压缩80.9%参数的情况下,组合剪枝方法仅导致1.86%的精度损失,明显优于其他剪枝算法. ...
1
... 深度神经网络在图像分类[1 -2 ] 、物体检测[3 -5 ] 、语义分割[6 -8 ] 等领域的应用效果良好. 随着深度学习的发展,神经网络的层数越来越深,参数越来越多. 由于将神经网络部署在资源受限的嵌入式设备上有一定的困难,导致庞大的神经网络模型在实时性要求较高的工业现场的应用受阻. 模型压缩可以有效地减少网络参数,降低网络复杂度,拓展深度神经网络在工业现场的应用[9 -10 ] . 模型压缩的方法主要有量化、低秩分解、知识蒸馏、轻量化网络设计和剪枝等. 模型量化[11 ] 是将高比特的浮点运算转换为低比特的定点运算,如网络二值化方法[12 ] 、三值神经网络[13 ] ,但这类方法在压缩模型的同时损失了较大的网络精度. 低秩分解是通过奇异值分解(singular value decomposition, SVD)[14 ] 、Tucker分解[15 ] 、Block Term分解[16 ] 等方法将网络结构中复杂的张量用精简的张量表示,这类方法能够压缩网络,但矩阵分解成本高,并且分解后需要逐层微调,一定程度上减缓了模型训练速度. 知识蒸馏方法虽然性能较好,但存在效率低以及教师模型难设计、难选择的问题[17 -18 ] . 轻量化网络设计[19 -22 ] 是在保持模型精度的基础上,根据技巧和经验设计的性能较优的小型网络,但轻量化网络模型固定,该方法不适用于特定网络结构的压缩. ...
Creation and testing of a deep learning algorithm to automatically identify and label vessels, nerves, tendons, and bones on cross-sectional point-of-care ultrasound scans for peripheral intravenous catheter placement by novices
1
2020
... 深度神经网络在图像分类[1 -2 ] 、物体检测[3 -5 ] 、语义分割[6 -8 ] 等领域的应用效果良好. 随着深度学习的发展,神经网络的层数越来越深,参数越来越多. 由于将神经网络部署在资源受限的嵌入式设备上有一定的困难,导致庞大的神经网络模型在实时性要求较高的工业现场的应用受阻. 模型压缩可以有效地减少网络参数,降低网络复杂度,拓展深度神经网络在工业现场的应用[9 -10 ] . 模型压缩的方法主要有量化、低秩分解、知识蒸馏、轻量化网络设计和剪枝等. 模型量化[11 ] 是将高比特的浮点运算转换为低比特的定点运算,如网络二值化方法[12 ] 、三值神经网络[13 ] ,但这类方法在压缩模型的同时损失了较大的网络精度. 低秩分解是通过奇异值分解(singular value decomposition, SVD)[14 ] 、Tucker分解[15 ] 、Block Term分解[16 ] 等方法将网络结构中复杂的张量用精简的张量表示,这类方法能够压缩网络,但矩阵分解成本高,并且分解后需要逐层微调,一定程度上减缓了模型训练速度. 知识蒸馏方法虽然性能较好,但存在效率低以及教师模型难设计、难选择的问题[17 -18 ] . 轻量化网络设计[19 -22 ] 是在保持模型精度的基础上,根据技巧和经验设计的性能较优的小型网络,但轻量化网络模型固定,该方法不适用于特定网络结构的压缩. ...
1
... 深度神经网络在图像分类[1 -2 ] 、物体检测[3 -5 ] 、语义分割[6 -8 ] 等领域的应用效果良好. 随着深度学习的发展,神经网络的层数越来越深,参数越来越多. 由于将神经网络部署在资源受限的嵌入式设备上有一定的困难,导致庞大的神经网络模型在实时性要求较高的工业现场的应用受阻. 模型压缩可以有效地减少网络参数,降低网络复杂度,拓展深度神经网络在工业现场的应用[9 -10 ] . 模型压缩的方法主要有量化、低秩分解、知识蒸馏、轻量化网络设计和剪枝等. 模型量化[11 ] 是将高比特的浮点运算转换为低比特的定点运算,如网络二值化方法[12 ] 、三值神经网络[13 ] ,但这类方法在压缩模型的同时损失了较大的网络精度. 低秩分解是通过奇异值分解(singular value decomposition, SVD)[14 ] 、Tucker分解[15 ] 、Block Term分解[16 ] 等方法将网络结构中复杂的张量用精简的张量表示,这类方法能够压缩网络,但矩阵分解成本高,并且分解后需要逐层微调,一定程度上减缓了模型训练速度. 知识蒸馏方法虽然性能较好,但存在效率低以及教师模型难设计、难选择的问题[17 -18 ] . 轻量化网络设计[19 -22 ] 是在保持模型精度的基础上,根据技巧和经验设计的性能较优的小型网络,但轻量化网络模型固定,该方法不适用于特定网络结构的压缩. ...
Real-time deep learning semantic segmentation during intra-operative surgery for 3D augmented reality assistance
0
2021
基于编码-解码卷积神经网络的遥感图像语义分割
1
2020
... 深度神经网络在图像分类[1 -2 ] 、物体检测[3 -5 ] 、语义分割[6 -8 ] 等领域的应用效果良好. 随着深度学习的发展,神经网络的层数越来越深,参数越来越多. 由于将神经网络部署在资源受限的嵌入式设备上有一定的困难,导致庞大的神经网络模型在实时性要求较高的工业现场的应用受阻. 模型压缩可以有效地减少网络参数,降低网络复杂度,拓展深度神经网络在工业现场的应用[9 -10 ] . 模型压缩的方法主要有量化、低秩分解、知识蒸馏、轻量化网络设计和剪枝等. 模型量化[11 ] 是将高比特的浮点运算转换为低比特的定点运算,如网络二值化方法[12 ] 、三值神经网络[13 ] ,但这类方法在压缩模型的同时损失了较大的网络精度. 低秩分解是通过奇异值分解(singular value decomposition, SVD)[14 ] 、Tucker分解[15 ] 、Block Term分解[16 ] 等方法将网络结构中复杂的张量用精简的张量表示,这类方法能够压缩网络,但矩阵分解成本高,并且分解后需要逐层微调,一定程度上减缓了模型训练速度. 知识蒸馏方法虽然性能较好,但存在效率低以及教师模型难设计、难选择的问题[17 -18 ] . 轻量化网络设计[19 -22 ] 是在保持模型精度的基础上,根据技巧和经验设计的性能较优的小型网络,但轻量化网络模型固定,该方法不适用于特定网络结构的压缩. ...
基于编码-解码卷积神经网络的遥感图像语义分割
1
2020
... 深度神经网络在图像分类[1 -2 ] 、物体检测[3 -5 ] 、语义分割[6 -8 ] 等领域的应用效果良好. 随着深度学习的发展,神经网络的层数越来越深,参数越来越多. 由于将神经网络部署在资源受限的嵌入式设备上有一定的困难,导致庞大的神经网络模型在实时性要求较高的工业现场的应用受阻. 模型压缩可以有效地减少网络参数,降低网络复杂度,拓展深度神经网络在工业现场的应用[9 -10 ] . 模型压缩的方法主要有量化、低秩分解、知识蒸馏、轻量化网络设计和剪枝等. 模型量化[11 ] 是将高比特的浮点运算转换为低比特的定点运算,如网络二值化方法[12 ] 、三值神经网络[13 ] ,但这类方法在压缩模型的同时损失了较大的网络精度. 低秩分解是通过奇异值分解(singular value decomposition, SVD)[14 ] 、Tucker分解[15 ] 、Block Term分解[16 ] 等方法将网络结构中复杂的张量用精简的张量表示,这类方法能够压缩网络,但矩阵分解成本高,并且分解后需要逐层微调,一定程度上减缓了模型训练速度. 知识蒸馏方法虽然性能较好,但存在效率低以及教师模型难设计、难选择的问题[17 -18 ] . 轻量化网络设计[19 -22 ] 是在保持模型精度的基础上,根据技巧和经验设计的性能较优的小型网络,但轻量化网络模型固定,该方法不适用于特定网络结构的压缩. ...
1
... 深度神经网络在图像分类[1 -2 ] 、物体检测[3 -5 ] 、语义分割[6 -8 ] 等领域的应用效果良好. 随着深度学习的发展,神经网络的层数越来越深,参数越来越多. 由于将神经网络部署在资源受限的嵌入式设备上有一定的困难,导致庞大的神经网络模型在实时性要求较高的工业现场的应用受阻. 模型压缩可以有效地减少网络参数,降低网络复杂度,拓展深度神经网络在工业现场的应用[9 -10 ] . 模型压缩的方法主要有量化、低秩分解、知识蒸馏、轻量化网络设计和剪枝等. 模型量化[11 ] 是将高比特的浮点运算转换为低比特的定点运算,如网络二值化方法[12 ] 、三值神经网络[13 ] ,但这类方法在压缩模型的同时损失了较大的网络精度. 低秩分解是通过奇异值分解(singular value decomposition, SVD)[14 ] 、Tucker分解[15 ] 、Block Term分解[16 ] 等方法将网络结构中复杂的张量用精简的张量表示,这类方法能够压缩网络,但矩阵分解成本高,并且分解后需要逐层微调,一定程度上减缓了模型训练速度. 知识蒸馏方法虽然性能较好,但存在效率低以及教师模型难设计、难选择的问题[17 -18 ] . 轻量化网络设计[19 -22 ] 是在保持模型精度的基础上,根据技巧和经验设计的性能较优的小型网络,但轻量化网络模型固定,该方法不适用于特定网络结构的压缩. ...
1
... 深度神经网络在图像分类[1 -2 ] 、物体检测[3 -5 ] 、语义分割[6 -8 ] 等领域的应用效果良好. 随着深度学习的发展,神经网络的层数越来越深,参数越来越多. 由于将神经网络部署在资源受限的嵌入式设备上有一定的困难,导致庞大的神经网络模型在实时性要求较高的工业现场的应用受阻. 模型压缩可以有效地减少网络参数,降低网络复杂度,拓展深度神经网络在工业现场的应用[9 -10 ] . 模型压缩的方法主要有量化、低秩分解、知识蒸馏、轻量化网络设计和剪枝等. 模型量化[11 ] 是将高比特的浮点运算转换为低比特的定点运算,如网络二值化方法[12 ] 、三值神经网络[13 ] ,但这类方法在压缩模型的同时损失了较大的网络精度. 低秩分解是通过奇异值分解(singular value decomposition, SVD)[14 ] 、Tucker分解[15 ] 、Block Term分解[16 ] 等方法将网络结构中复杂的张量用精简的张量表示,这类方法能够压缩网络,但矩阵分解成本高,并且分解后需要逐层微调,一定程度上减缓了模型训练速度. 知识蒸馏方法虽然性能较好,但存在效率低以及教师模型难设计、难选择的问题[17 -18 ] . 轻量化网络设计[19 -22 ] 是在保持模型精度的基础上,根据技巧和经验设计的性能较优的小型网络,但轻量化网络模型固定,该方法不适用于特定网络结构的压缩. ...
1
... 深度神经网络在图像分类[1 -2 ] 、物体检测[3 -5 ] 、语义分割[6 -8 ] 等领域的应用效果良好. 随着深度学习的发展,神经网络的层数越来越深,参数越来越多. 由于将神经网络部署在资源受限的嵌入式设备上有一定的困难,导致庞大的神经网络模型在实时性要求较高的工业现场的应用受阻. 模型压缩可以有效地减少网络参数,降低网络复杂度,拓展深度神经网络在工业现场的应用[9 -10 ] . 模型压缩的方法主要有量化、低秩分解、知识蒸馏、轻量化网络设计和剪枝等. 模型量化[11 ] 是将高比特的浮点运算转换为低比特的定点运算,如网络二值化方法[12 ] 、三值神经网络[13 ] ,但这类方法在压缩模型的同时损失了较大的网络精度. 低秩分解是通过奇异值分解(singular value decomposition, SVD)[14 ] 、Tucker分解[15 ] 、Block Term分解[16 ] 等方法将网络结构中复杂的张量用精简的张量表示,这类方法能够压缩网络,但矩阵分解成本高,并且分解后需要逐层微调,一定程度上减缓了模型训练速度. 知识蒸馏方法虽然性能较好,但存在效率低以及教师模型难设计、难选择的问题[17 -18 ] . 轻量化网络设计[19 -22 ] 是在保持模型精度的基础上,根据技巧和经验设计的性能较优的小型网络,但轻量化网络模型固定,该方法不适用于特定网络结构的压缩. ...
1
... 深度神经网络在图像分类[1 -2 ] 、物体检测[3 -5 ] 、语义分割[6 -8 ] 等领域的应用效果良好. 随着深度学习的发展,神经网络的层数越来越深,参数越来越多. 由于将神经网络部署在资源受限的嵌入式设备上有一定的困难,导致庞大的神经网络模型在实时性要求较高的工业现场的应用受阻. 模型压缩可以有效地减少网络参数,降低网络复杂度,拓展深度神经网络在工业现场的应用[9 -10 ] . 模型压缩的方法主要有量化、低秩分解、知识蒸馏、轻量化网络设计和剪枝等. 模型量化[11 ] 是将高比特的浮点运算转换为低比特的定点运算,如网络二值化方法[12 ] 、三值神经网络[13 ] ,但这类方法在压缩模型的同时损失了较大的网络精度. 低秩分解是通过奇异值分解(singular value decomposition, SVD)[14 ] 、Tucker分解[15 ] 、Block Term分解[16 ] 等方法将网络结构中复杂的张量用精简的张量表示,这类方法能够压缩网络,但矩阵分解成本高,并且分解后需要逐层微调,一定程度上减缓了模型训练速度. 知识蒸馏方法虽然性能较好,但存在效率低以及教师模型难设计、难选择的问题[17 -18 ] . 轻量化网络设计[19 -22 ] 是在保持模型精度的基础上,根据技巧和经验设计的性能较优的小型网络,但轻量化网络模型固定,该方法不适用于特定网络结构的压缩. ...
1
... 深度神经网络在图像分类[1 -2 ] 、物体检测[3 -5 ] 、语义分割[6 -8 ] 等领域的应用效果良好. 随着深度学习的发展,神经网络的层数越来越深,参数越来越多. 由于将神经网络部署在资源受限的嵌入式设备上有一定的困难,导致庞大的神经网络模型在实时性要求较高的工业现场的应用受阻. 模型压缩可以有效地减少网络参数,降低网络复杂度,拓展深度神经网络在工业现场的应用[9 -10 ] . 模型压缩的方法主要有量化、低秩分解、知识蒸馏、轻量化网络设计和剪枝等. 模型量化[11 ] 是将高比特的浮点运算转换为低比特的定点运算,如网络二值化方法[12 ] 、三值神经网络[13 ] ,但这类方法在压缩模型的同时损失了较大的网络精度. 低秩分解是通过奇异值分解(singular value decomposition, SVD)[14 ] 、Tucker分解[15 ] 、Block Term分解[16 ] 等方法将网络结构中复杂的张量用精简的张量表示,这类方法能够压缩网络,但矩阵分解成本高,并且分解后需要逐层微调,一定程度上减缓了模型训练速度. 知识蒸馏方法虽然性能较好,但存在效率低以及教师模型难设计、难选择的问题[17 -18 ] . 轻量化网络设计[19 -22 ] 是在保持模型精度的基础上,根据技巧和经验设计的性能较优的小型网络,但轻量化网络模型固定,该方法不适用于特定网络结构的压缩. ...
1
... 深度神经网络在图像分类[1 -2 ] 、物体检测[3 -5 ] 、语义分割[6 -8 ] 等领域的应用效果良好. 随着深度学习的发展,神经网络的层数越来越深,参数越来越多. 由于将神经网络部署在资源受限的嵌入式设备上有一定的困难,导致庞大的神经网络模型在实时性要求较高的工业现场的应用受阻. 模型压缩可以有效地减少网络参数,降低网络复杂度,拓展深度神经网络在工业现场的应用[9 -10 ] . 模型压缩的方法主要有量化、低秩分解、知识蒸馏、轻量化网络设计和剪枝等. 模型量化[11 ] 是将高比特的浮点运算转换为低比特的定点运算,如网络二值化方法[12 ] 、三值神经网络[13 ] ,但这类方法在压缩模型的同时损失了较大的网络精度. 低秩分解是通过奇异值分解(singular value decomposition, SVD)[14 ] 、Tucker分解[15 ] 、Block Term分解[16 ] 等方法将网络结构中复杂的张量用精简的张量表示,这类方法能够压缩网络,但矩阵分解成本高,并且分解后需要逐层微调,一定程度上减缓了模型训练速度. 知识蒸馏方法虽然性能较好,但存在效率低以及教师模型难设计、难选择的问题[17 -18 ] . 轻量化网络设计[19 -22 ] 是在保持模型精度的基础上,根据技巧和经验设计的性能较优的小型网络,但轻量化网络模型固定,该方法不适用于特定网络结构的压缩. ...
A singularly valuable decomposition: the SVD of a matrix
1
1996
... 深度神经网络在图像分类[1 -2 ] 、物体检测[3 -5 ] 、语义分割[6 -8 ] 等领域的应用效果良好. 随着深度学习的发展,神经网络的层数越来越深,参数越来越多. 由于将神经网络部署在资源受限的嵌入式设备上有一定的困难,导致庞大的神经网络模型在实时性要求较高的工业现场的应用受阻. 模型压缩可以有效地减少网络参数,降低网络复杂度,拓展深度神经网络在工业现场的应用[9 -10 ] . 模型压缩的方法主要有量化、低秩分解、知识蒸馏、轻量化网络设计和剪枝等. 模型量化[11 ] 是将高比特的浮点运算转换为低比特的定点运算,如网络二值化方法[12 ] 、三值神经网络[13 ] ,但这类方法在压缩模型的同时损失了较大的网络精度. 低秩分解是通过奇异值分解(singular value decomposition, SVD)[14 ] 、Tucker分解[15 ] 、Block Term分解[16 ] 等方法将网络结构中复杂的张量用精简的张量表示,这类方法能够压缩网络,但矩阵分解成本高,并且分解后需要逐层微调,一定程度上减缓了模型训练速度. 知识蒸馏方法虽然性能较好,但存在效率低以及教师模型难设计、难选择的问题[17 -18 ] . 轻量化网络设计[19 -22 ] 是在保持模型精度的基础上,根据技巧和经验设计的性能较优的小型网络,但轻量化网络模型固定,该方法不适用于特定网络结构的压缩. ...
1
... 深度神经网络在图像分类[1 -2 ] 、物体检测[3 -5 ] 、语义分割[6 -8 ] 等领域的应用效果良好. 随着深度学习的发展,神经网络的层数越来越深,参数越来越多. 由于将神经网络部署在资源受限的嵌入式设备上有一定的困难,导致庞大的神经网络模型在实时性要求较高的工业现场的应用受阻. 模型压缩可以有效地减少网络参数,降低网络复杂度,拓展深度神经网络在工业现场的应用[9 -10 ] . 模型压缩的方法主要有量化、低秩分解、知识蒸馏、轻量化网络设计和剪枝等. 模型量化[11 ] 是将高比特的浮点运算转换为低比特的定点运算,如网络二值化方法[12 ] 、三值神经网络[13 ] ,但这类方法在压缩模型的同时损失了较大的网络精度. 低秩分解是通过奇异值分解(singular value decomposition, SVD)[14 ] 、Tucker分解[15 ] 、Block Term分解[16 ] 等方法将网络结构中复杂的张量用精简的张量表示,这类方法能够压缩网络,但矩阵分解成本高,并且分解后需要逐层微调,一定程度上减缓了模型训练速度. 知识蒸馏方法虽然性能较好,但存在效率低以及教师模型难设计、难选择的问题[17 -18 ] . 轻量化网络设计[19 -22 ] 是在保持模型精度的基础上,根据技巧和经验设计的性能较优的小型网络,但轻量化网络模型固定,该方法不适用于特定网络结构的压缩. ...
Decompositions of a higher-order tensor in block terms
1
2008
... 深度神经网络在图像分类[1 -2 ] 、物体检测[3 -5 ] 、语义分割[6 -8 ] 等领域的应用效果良好. 随着深度学习的发展,神经网络的层数越来越深,参数越来越多. 由于将神经网络部署在资源受限的嵌入式设备上有一定的困难,导致庞大的神经网络模型在实时性要求较高的工业现场的应用受阻. 模型压缩可以有效地减少网络参数,降低网络复杂度,拓展深度神经网络在工业现场的应用[9 -10 ] . 模型压缩的方法主要有量化、低秩分解、知识蒸馏、轻量化网络设计和剪枝等. 模型量化[11 ] 是将高比特的浮点运算转换为低比特的定点运算,如网络二值化方法[12 ] 、三值神经网络[13 ] ,但这类方法在压缩模型的同时损失了较大的网络精度. 低秩分解是通过奇异值分解(singular value decomposition, SVD)[14 ] 、Tucker分解[15 ] 、Block Term分解[16 ] 等方法将网络结构中复杂的张量用精简的张量表示,这类方法能够压缩网络,但矩阵分解成本高,并且分解后需要逐层微调,一定程度上减缓了模型训练速度. 知识蒸馏方法虽然性能较好,但存在效率低以及教师模型难设计、难选择的问题[17 -18 ] . 轻量化网络设计[19 -22 ] 是在保持模型精度的基础上,根据技巧和经验设计的性能较优的小型网络,但轻量化网络模型固定,该方法不适用于特定网络结构的压缩. ...
1
... 深度神经网络在图像分类[1 -2 ] 、物体检测[3 -5 ] 、语义分割[6 -8 ] 等领域的应用效果良好. 随着深度学习的发展,神经网络的层数越来越深,参数越来越多. 由于将神经网络部署在资源受限的嵌入式设备上有一定的困难,导致庞大的神经网络模型在实时性要求较高的工业现场的应用受阻. 模型压缩可以有效地减少网络参数,降低网络复杂度,拓展深度神经网络在工业现场的应用[9 -10 ] . 模型压缩的方法主要有量化、低秩分解、知识蒸馏、轻量化网络设计和剪枝等. 模型量化[11 ] 是将高比特的浮点运算转换为低比特的定点运算,如网络二值化方法[12 ] 、三值神经网络[13 ] ,但这类方法在压缩模型的同时损失了较大的网络精度. 低秩分解是通过奇异值分解(singular value decomposition, SVD)[14 ] 、Tucker分解[15 ] 、Block Term分解[16 ] 等方法将网络结构中复杂的张量用精简的张量表示,这类方法能够压缩网络,但矩阵分解成本高,并且分解后需要逐层微调,一定程度上减缓了模型训练速度. 知识蒸馏方法虽然性能较好,但存在效率低以及教师模型难设计、难选择的问题[17 -18 ] . 轻量化网络设计[19 -22 ] 是在保持模型精度的基础上,根据技巧和经验设计的性能较优的小型网络,但轻量化网络模型固定,该方法不适用于特定网络结构的压缩. ...
1
... 深度神经网络在图像分类[1 -2 ] 、物体检测[3 -5 ] 、语义分割[6 -8 ] 等领域的应用效果良好. 随着深度学习的发展,神经网络的层数越来越深,参数越来越多. 由于将神经网络部署在资源受限的嵌入式设备上有一定的困难,导致庞大的神经网络模型在实时性要求较高的工业现场的应用受阻. 模型压缩可以有效地减少网络参数,降低网络复杂度,拓展深度神经网络在工业现场的应用[9 -10 ] . 模型压缩的方法主要有量化、低秩分解、知识蒸馏、轻量化网络设计和剪枝等. 模型量化[11 ] 是将高比特的浮点运算转换为低比特的定点运算,如网络二值化方法[12 ] 、三值神经网络[13 ] ,但这类方法在压缩模型的同时损失了较大的网络精度. 低秩分解是通过奇异值分解(singular value decomposition, SVD)[14 ] 、Tucker分解[15 ] 、Block Term分解[16 ] 等方法将网络结构中复杂的张量用精简的张量表示,这类方法能够压缩网络,但矩阵分解成本高,并且分解后需要逐层微调,一定程度上减缓了模型训练速度. 知识蒸馏方法虽然性能较好,但存在效率低以及教师模型难设计、难选择的问题[17 -18 ] . 轻量化网络设计[19 -22 ] 是在保持模型精度的基础上,根据技巧和经验设计的性能较优的小型网络,但轻量化网络模型固定,该方法不适用于特定网络结构的压缩. ...
1
... 深度神经网络在图像分类[1 -2 ] 、物体检测[3 -5 ] 、语义分割[6 -8 ] 等领域的应用效果良好. 随着深度学习的发展,神经网络的层数越来越深,参数越来越多. 由于将神经网络部署在资源受限的嵌入式设备上有一定的困难,导致庞大的神经网络模型在实时性要求较高的工业现场的应用受阻. 模型压缩可以有效地减少网络参数,降低网络复杂度,拓展深度神经网络在工业现场的应用[9 -10 ] . 模型压缩的方法主要有量化、低秩分解、知识蒸馏、轻量化网络设计和剪枝等. 模型量化[11 ] 是将高比特的浮点运算转换为低比特的定点运算,如网络二值化方法[12 ] 、三值神经网络[13 ] ,但这类方法在压缩模型的同时损失了较大的网络精度. 低秩分解是通过奇异值分解(singular value decomposition, SVD)[14 ] 、Tucker分解[15 ] 、Block Term分解[16 ] 等方法将网络结构中复杂的张量用精简的张量表示,这类方法能够压缩网络,但矩阵分解成本高,并且分解后需要逐层微调,一定程度上减缓了模型训练速度. 知识蒸馏方法虽然性能较好,但存在效率低以及教师模型难设计、难选择的问题[17 -18 ] . 轻量化网络设计[19 -22 ] 是在保持模型精度的基础上,根据技巧和经验设计的性能较优的小型网络,但轻量化网络模型固定,该方法不适用于特定网络结构的压缩. ...