近年来，伴随着自主移动机器人、无人机、智能汽车以及AR/VR 等智能产品与设备逐步融入人们的生产生活之中^[1]，同步地图构建和定位技术(simultaneous localization and mapping, SLAM)成为研究热点之一^[2]. 经过多年的理论发展，SLAM技术的研究框架和理论方法取得了较大的进步，出现了多种基于不同传感器的SLAM技术，其中视觉SLAM算法因低功耗、低成本、小型化等优势^[3]，是目前SLAM技术研究的重点.

Mur-Artal等^[4]提出基于点特征的视觉SLAM算法，构建具有代表意义的完整SLAM系统，在此基础上，有不少学者提出了改进算法. 李国竣等^[5]依据图像灰度调节点特征的提取阈值，平衡系统在不同光照场景下的点特征数量，提高了系统的建图成功率. Li等^[6]根据相邻2帧图像的像素均值与标准差，调整点特征提取阈值，基于网格运动统计(grid-based motion statistics, GMS)算法进行匹配筛选，提升了系统的鲁棒性与实时性. 胡山山等^[7]通过构建Hessian矩阵优化点特征的提取过程，使得点特征具有更好的跟踪特征，有效提高了系统的准确性. 张一等^[8]提出基于亚像素均衡化的点特征提取方法，使得点特征的分布更加均匀、准确，提升了系统的准确性与实时性.

为了提高ORB-SLAM算法在动态场景中的系统精度与鲁棒性，Gan等^[9]提出基于目标检测的改进算法，通过剔除场景中动态对象上的点特征，有效提高了系统在动态场景下的准确性与鲁棒性. Ai等^[10]通过新增动态目标的概率模型，增强了目标识别效率，提高了系统在动态环境下的准确性与实时性. 视觉SLAM系统的性能与相机特性、机器人运动性能息息相关. 曹力科等^[11]提出基于卷帘快门相机的改进SLAM算法，通过控制特征的速度对卷帘快门效应进行校正，提高了系统的准确性. 刘贵涛等^[12]使用多个相机紧耦合的改进SLAM方法，增强了系统的稳定性与鲁棒性. Yang等^[13]通过控制运动平台的运动特性，将匀速运动状态作为已知量引入SLAM系统中，有效缩短了系统的初始化时间. 在绝大多数的工程实际中，系统无法预知相机特性与机器人的运动性能. 本文考虑相机自身运动对系统的影响，提出基于运动预测的改进ORB-SLAM算法，解决运动场景下固定点特征提取与匹配策略失效的问题，在保证系统实时性和漂移量的情况下，提升系统的准确性.

在基于点特征的视觉SLAM系统中，点特征提取的好坏直接关系到系统定位和建图的准确性和鲁棒性^[14]. 若点特征数量较少，则容易出现跟踪丢失的情况；若无限增加点特征数量，则会产生较多的错误匹配信息，影响系统的实时性与准确性.

在相邻2帧图像整体纹理与对比度不发生突变的前提下，提出基于点特征利用率的检测阈值调整方法. 点特征利用率为

(1) $ {R_{\rm{e}}} = \begin{array}{*{20}{c}} {\dfrac{{{N_{{\rm{effect}}}}}}{{{N_{{\rm{all}}}}}}}. \end{array} $

式中：N_all为上一帧图像提取出来的所有点特征数量之和，N_effect为上一帧图像中的有效点特征数量之和. 一个有效点特征应该具有以下条件.

1）该点特征具有正深度. 当使用深度相机时，该特征点在深度图上对应的深度为正. 当使用双目相机时，通过双目立体视觉匹配^[15]后计算出的深度为正.

2）该点特征具有良好的匹配信息. 该匹配关系包括与上一帧及参考关键帧建立的匹配关系，在进行局部地图位姿优化时，可以与局部地图点建立匹配关系.

3）该点特征不为离群点. 在进行位姿估计时，该点特征的重投影误差^[16]小于误差阈值.

基于点特征利用率的阈值调整可以描述为

(2) $ \left.\begin{split} & {\xi ^*} = \xi +\rho (r)\{ {k_{\rm{p}}} e(k)+{k_{\rm{d}}}(e(k) - e(k - 1))\} , \\ & e(k) = {R_{\rm{e}}} - {R_{\rm{e}}}^\prime . \end{split} \right\}$

式中：ξ*、ξ分别为当前帧和上一帧的图像点特征检测阈值；R_e'与R_e分别为上一帧图像的点特征利用率与当前帧图像的期望点特征利用率；e(k)为当前帧的期望点特征利用率与上一帧的点特征利用率差值；ρ(r)为转换函数，将点特征利用率的差值转换为点特征检测阈值；k_p、k_d为表达式的控制参数.

当点特征利用率较低时，表示无效点特征偏多，此时需要提高检测阈值，保证系统的实时性及准确性. 当点特征利用率过高时，表示可用的跟踪点偏少，容易出现追踪丢失的情况，此时应该降低检测阈值，保证系统的准确性与稳定性.

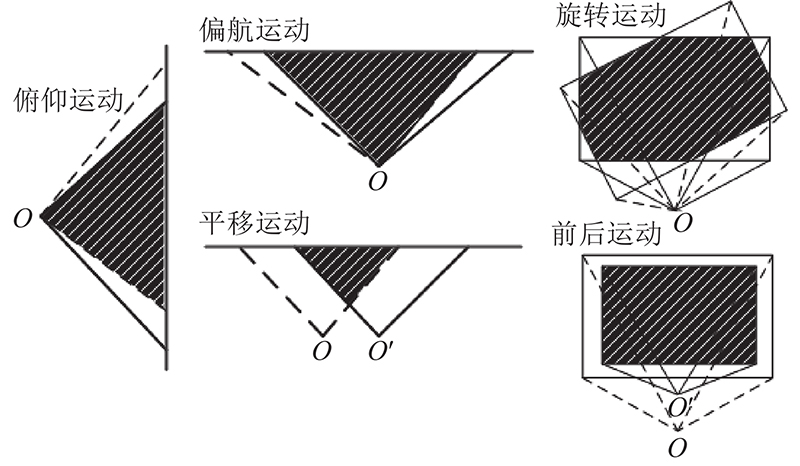
通常相邻2帧图像存在一定的共视范围，可以用于建立帧与帧之间的匹配关系. 构建t−2时刻到t−1时刻的相机匀速运动模型，预测出t−1时刻与当前t时刻的共视范围，优化点特征的提取. 不同位姿变化下图像的共视范围示意图如图1所示. 图中，O、O'分别为上一帧与当前帧的相机光心，实线为上一帧的视角范围，虚线为当前帧的视角范围，阴影部分为2帧之间的共视范围.

为了直观地描述不同位姿变化下图像的共视范围，采用欧拉角^[17]和平移向量的方式来表述三维空间的连续运动. 欧拉角与旋转矩阵之间的变换关系如下：

(3) $ \left. \begin{aligned} & {\theta} = \arctan \left( { - {{{r_{31}}} \mathord{\left/ {\vphantom {{{r_{31}}} {\sqrt {r_{32}^2+r_{33}^2} }}} \right. } {\sqrt {r_{32}^2+r_{33}^2} }}} \right), \\ & {\phi} = \arctan \; \left( {{{{r_{32}}} \mathord{\left/ {\vphantom {{{r_{32}}} {{r_{33}}}}} \right. } {{r_{33}}}}} \right), \\ & {\psi} = \arctan \; \left( {{{{r_{21}}} \mathord{\left/ {\vphantom {{{r_{21}}} {{r_{11}}}}} \right. } {{r_{11}}}}} \right) . \end{aligned}\right\} $

式中：θ为俯仰角，ϕ为翻滚角，ψ为偏航角，r_ij为旋转矩阵中对应行列上的元素.

由于将三维空间的连续运动逐一分解来求取共视范围是十分复杂的，提出不同位姿变化情况下的共视范围求取方法. 下面将讨论共视范围的求取过程.

假设已知t−2到t−1时刻的位姿变换矩阵^[18]为

(4) $ \begin{array}{*{20}{c}} {{\boldsymbol{T}}' = \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{R}}'}&{{\boldsymbol{t}}'} \\ {{{\boldsymbol{0}}^{\rm{T}}}}&1 \end{array}} \right]}. \end{array} $

式中：R'、t'分别为t−2时刻到t−1时刻的旋转矩阵与平移向量.

根据相机投影模型^[19]，可以得到t−1时刻图像上的某一像素坐标在t时刻图像上的像素坐标：

(5) $ \begin{array}{*{20}{c}} {{{\boldsymbol{p}}_i} = {\boldsymbol{K}} {\boldsymbol{R}}' {{\boldsymbol{K}}^{ - 1}}{{{\boldsymbol{p}}}_i'}+{\boldsymbol{K}} {\boldsymbol{t}}'}. \end{array} $

式中：K为相机内参矩阵，p_i'为t−1时刻的某一像素坐标，p_i为当前t时刻的对应投影像素坐标.

若将相邻2帧的图像顶点坐标转换到同一坐标系下，则将问题转换为：已知2个多边形的顶点集为C₁={p₁,p₂,···,p_m}和C₂={q₁,q₂,···,q_n}，求解这2个多边形的交集. 算法的整体思想如下. 1)将2个多边形的顶点及交点放入集合S中. 2)遍历集合S，保留同时属于这2个多边形范围内的点，将无序点集整理成有序点集. 3)根据有序点集，确定共视范围与比例.

求取多边形的交点，即求取多边形之间每条边的交点，求取任意2条线段之间的交点.

假设线段l₁的两端点坐标以向量形式表示为p=[x,y]^T与p+r=[x',y']^T，线段l₂的端点坐标为q = [z,w]^T与q + s = [z',w']^T，则线段上任意一点的坐标可以描述为

(6) $ \left. {\begin{array}{c}{{\boldsymbol{p}}}_{i}={{\boldsymbol{p}}}+t {{\boldsymbol{r}}},\begin{array}{cc}& t\in [0\text{，}1.0]\begin{array}{cc}\text{，}& {{\boldsymbol{p}}}_{i}\in {l}_{1};\end{array}\end{array}\\ {{\boldsymbol{q}}}_{j}={{\boldsymbol{q}}}+u {{\boldsymbol{s}}},\begin{array}{cc}& u\in [0\text{，}1.0]\begin{array}{cc}\text{，}& {{\boldsymbol{q}}}_{j}\in {l}_{2}.\end{array}\end{array}\end{array} } \right\}$

若2条线段相交，则有

(7) $ \left.\begin{aligned} & {\boldsymbol{q}}+u {\boldsymbol{s}} = {\boldsymbol{p}}+t {\boldsymbol{r}}, \\ & {\boldsymbol{q}} \times {\boldsymbol{s}}+u \cdot {\boldsymbol{s}} \times {\boldsymbol{s}} = {\boldsymbol{p}} \times {\boldsymbol{s}}+t \cdot ( {\boldsymbol{r}} \times {\boldsymbol{s}}), \\ & d = \frac{{|( {\boldsymbol{p}} - {\boldsymbol{q}}) \times {\boldsymbol{s}}|}}{{ | {\boldsymbol{s}} \times {\boldsymbol{r}}|}} . \end{aligned} \right\}$

同理，可得

(8) $ {u = \frac{{|( {\boldsymbol{p}} - {\boldsymbol{q}}) \times {\boldsymbol{r}}|}}{{ |{\boldsymbol{s}} \times {\boldsymbol{r}}|}}}. $

当s×r≠0且t、u ∈[0,1.0]时，有且仅有一个交点，该交点用p+tr或者q+us表示. 当s×r=0且(p−q)×s=0或(p−q)×r=0时，线段重叠，存在无数个交点. 结合运用场景，取共线4个顶点中的倒数第2个顶点作为最终的共视交点.

基于Ray- Shooting方法^[20]，可以判断点是否在多边形内. 其中，只需要判断C₁点集是否在当前t时刻的图像范围内，C₂点集是否在t−1时刻的投影图像范围内，得到无序点集S' = {p₁, p₂, ···, p_n}. 通过构造向量夹角进行无序点的排序，原理示意图如图2所示.

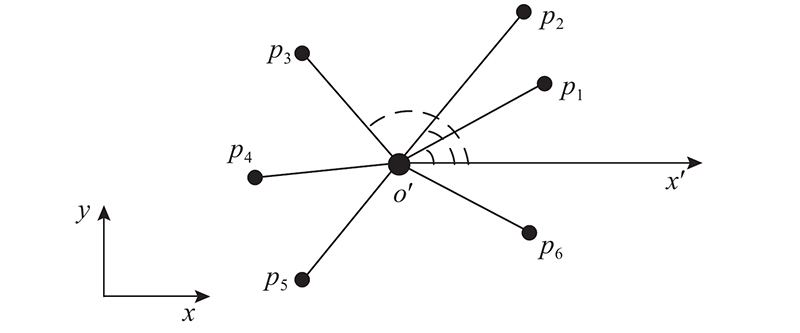
图2中，点p₁、p₂、p₃、p₄、p₅、p₆为无序点集中的点，点o'为点集的重心，坐标为

(9) $ {x_{o'}} = m^{-1}{{\displaystyle\sum\limits_{i = 1}^m {{x_{{p_i}}}} }} ,\;{{y_{o'}} = m^{-1}{{\displaystyle\sum\limits_{i = 1}^m {{y_{{p_i}}}} }}} . $

以点集重心o'做一条平行于x轴的向量 $\overrightarrow{o'x'}$，各点与重心构成向量 $\overrightarrow{o'p_i} $，计算向量 $\overrightarrow{o'p_i} $与向量 $\overrightarrow{o'x'} $之间的夹角，根据夹角大小确定点的连接顺序. 根据凸多边形的定义^[21]可知，S'点集组成的闭合多边形为凸多边形，可得一个闭合的多边形.

下面以图像共视面积比来表征共视比例，根据相邻2帧之间的共视比例确定优化程度. 基于叉乘的快速面积计算方法描述为

(10) $ S = \frac{1}{2}\left|\sum\limits_{i = 1}^n {({x_i}{y_{i+1}} - {x_{i+1}}{y_i}} )\right| {x_{n+1}} = {x_1},\;{y_{n+1}} = {y_1} . $

式中：S为多边形的面积，x_i、y_i为多边形上某一顶点的二维坐标值. 式(10)的证明过程详见附录1.

综上所述，基于运动预测的点特征提取算法的检测阈值可以描述为

(11) $ {\xi ^*} = \xi +h(s)\rho (r)\{ {k_{\rm{p}}} e(k)+{k_{\rm{d}}}(e(k) - e(k - 1))\} ,\; e(k) = {R_{\rm{e}}} - {R_{\rm{e}}}^\prime . $

式中：h(s)为共视范围内的检测阈值优化函数，

(12) $ {h(s) = \left\{ {\begin{array}{*{20}{c}} {1},&{S \notin {S_{{\rm{mut}}}}};\\ {1 + \ln \;(1 + s'),s' = s - {s_{{\rm{set}}}},}&{S \in {S_{{\rm{mut}}}}}. \end{array}} \right.} $

其中S_mut和s分别为当前帧的共视面积、当前帧的共视比例，s_set为共视比例阈值.

针对不同运动场景下以固定的匹配策略导致的匹配运算量大及误匹配多的问题，提出基于运动预测的点特征匹配优化策略. 该方法通过匀速运动模型，快速确定出共视范围内的有效待匹配点，推算出相机的运动情况，结合图像金字塔^[4]缩小匹配搜索范围，减少大量的无效匹配过程，改善误匹配问题.

假设已知t−2时刻到t−1时刻的位姿变换阵T'以及t−1时刻的相机位姿矩阵T_lw，则可以通过匀速运动模型推算出当前位姿矩阵T_cw. 将t−1时刻的点特征投影到当前帧中，则有

(13) $\left. { \begin{array}{*{20}{c}} \begin{gathered} {{\boldsymbol{P}}_{{\rm{w}}i}} = \left[ {\begin{array}{*{20}{c}} {{x_i}} \\ {{y_i}} \\ {{z_i}} \end{array}} \right] = {{\boldsymbol{R}}_{{\rm{wl}}}}\left[ {\begin{array}{*{20}{c}} {({{u}_i}' - {c_x}/{f_x}) {{d}_i}}' \\ {({{v}_i}' - {c_y}/{f_y}) {{d}_i}}' \\ {{{d}_i}}' \end{array}} \right]+{{\boldsymbol{t}}_{{\rm{wl}}}}, \\ {{\boldsymbol{P}}_{{\rm{c}}i}} = \left[ {\begin{array}{*{20}{c}} {{{x}_i}}' \\ {{{y}_i}}' \\ {{{z}_i}}' \end{array}} \right] = {{\boldsymbol{R}}_{{\rm{cw}}}}\left[ {\begin{array}{*{20}{c}} {{x_i}} \\ {{y_i}} \\ {{z_i}} \end{array}} \right]+{{\boldsymbol{t}}_{{\rm{cw}}}}, \\ {{\boldsymbol{p}}_i} = \left[ {\begin{array}{*{20}{c}} {{u_i}} \\ {{v_i}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{f_x} {x_i}^\prime /{z_i}^\prime +{c_x}} \\ {{f_y} {y_i}^\prime /{z_i}^\prime +{c_y}} \end{array}} \right]. \\ \end{gathered} & \end{array} } \right\}$

式中：R_wl、t_wl分别为t−1时刻相机坐标系转换到世界坐标系的旋转矩阵与平移向量，R_cw、t_cw分别为世界坐标系转换到当前t时刻相机坐标系的旋转矩阵和平移向量，[u_i′,v_i′]^T为t−1时刻下的某一点特征像素坐标，P_wi为该点特征在世界坐标系下的三维空间坐标，P_ci为该点特征在当前t时刻相机观察下的三维空间坐标，f_x、f_y、c_x、c_y分别为相机的内参参数.

通过判断p_i是否在当前t时刻的图像范围内，可以确定是否为共视范围内的有效待匹配点.

利用匀速运动模型，推算得到t−1时刻到当前t时刻的相机平移量t_lc为

(14) $ \left. {\begin{array}{*{20}{c}} {{\boldsymbol{t}}_{{\rm{wc}}}} = - {\boldsymbol{R}}_{{\rm{cw}}}^{\rm{T}}{\boldsymbol{t}}_{\rm{cw}},\\ {{\boldsymbol{t}}_{{\rm{lc}}}} = {{\boldsymbol{T}}_{{\rm{lw}}}} {{\boldsymbol{t}}_{{\rm{wc}}}} = {{\boldsymbol{R}}_{\rm{l}}}_{\rm{w}}( - {\boldsymbol{R}}_{{\rm{cw}}}^{\rm{T}}{\boldsymbol{t}}_{\rm{cw}}) + {{\boldsymbol{t}}_{\rm{l}}}_{\rm{w}} . \end{array} } \right\}$

式中：t_wc为相机坐标系转换到当前t时刻世界坐标系的平移向量， ${{\boldsymbol{R}}_{\rm{l}}}_{\rm{w}} $、 ${{\boldsymbol{t}}_{\rm{l}}}_{\rm{w}} $分别为t−1时刻世界坐标系转换到相机坐标系的旋转矩阵与平移向量.

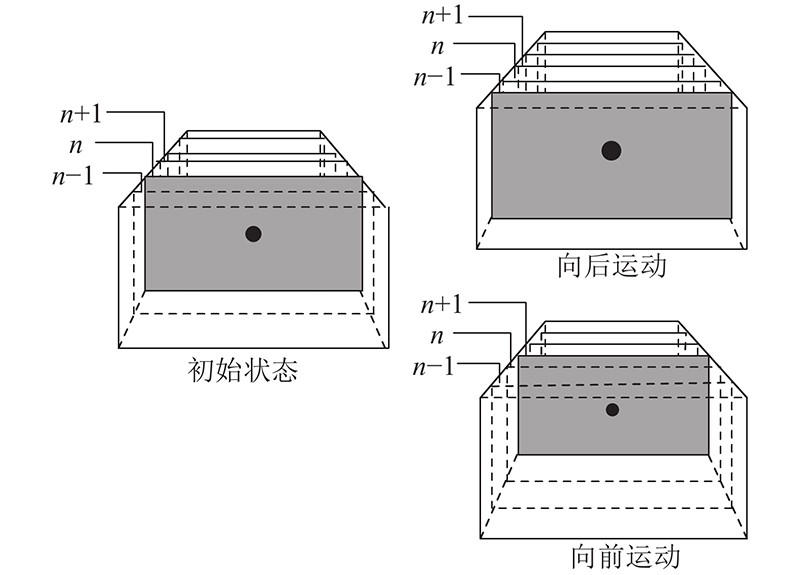
根据匀速运动模型推算出的t_lc判断相机的运动状态，通过图像金字塔缩小匹配搜索范围. 图像金字塔在点特征匹配中的原理示意图如图3所示.

图3所示的黑色圆点为图像金字塔第n层(灰色部分表示)中具有一定像素面积的点特征. 当相机向前运动时，黑色点特征在原图层中所占的面积增大，需要在更高层级的图像金字塔中才能保持面积不变，实现该点特征的搜索与匹配. 当相机向后运动时，需要在更低层级的图像金字塔中实现该点特征的搜索与匹配.

根据匀速运动模型，可以推算出相机的运动情况，缩小匹配搜索范围. 若向前运动，则在待匹配点所在层至图像金字塔最高层中进行搜索与匹配. 若向后运动，则在图像金字塔最低层至有效待匹配点所在层中进行搜索与匹配.

为了提高匹配准确率，利用最近邻匹配法^[22]进行匹配筛选，该方法的判别表达式为

(15) $ {d}/{{d'}} < {L};\;{L \in (0,1.0)} . $

式中：d、d'分别为最佳与次佳匹配距离，L为比例阈值. 比例阈值越高，匹配数量越多，但匹配正确率越低；反之，比例阈值越低，匹配正确率越高，匹配数量越少.

当图像整体发生旋转时，待匹配点特征之间会存在角度变化值，称为主旋转方向. 利用匹配点特征之间的主旋转方向，可以筛选掉一些旋转异常的匹配对. 具体流程如下.

1）建立旋转角度直方图，12°每簇，共30簇.

2）计算每个匹配对中的点特征旋转角度，按点特征旋转角度归入对应簇内，记录下该匹配点对并增加对应簇的计数量.

3）统计得到旋转角度直方图中计数量最多的前3簇，作为主旋方向，剔除不属于主旋方向中的错误匹配对.

为了验证改进算法的有效性，与ORB- SLAM2算法在公开的TUM数据集上进行对比实验，分别从系统准确性、实时性及漂移量3个评价指标进行分析验证. 使用的实验数据序列详细情况及主要的参数设置如表1所示，其中D_n、T_r、v_d和ω_a分别表示为数据序列的时长、轨迹长度、位移速度及运动角速度. 表1所列的参数可以在一定程度上体现算法的性能与先进性，但不为最优参数，可以调整参数来进一步提升算法性能.

为了避免实验结果的不确定性，所有实验均在Intel Core i5-8300H@2.30 GHz、内存为16 GB的计算机上开展，每个数据序列运行30次，与出现频次最多的运行结果进行对比分析.

利用绝对轨迹误差(absolute trajectory error, ATE)评估轨迹的一致性，比较系统估计轨迹与真实轨迹之间的绝对距离差值. 使用相对位姿误差(relative pose error, RPE)评估系统的漂移量，即比较一段时间间隔内的位姿变换量差值^[23].

表2、3中，ATE₁、ATE₂分别为利用ORB-SLAM2算法和本文算法得到的ATE，RPE₁、RPE₂分别为利用ORB-SLAM2算法和本文算法得到的RPE，η为提升率，RMSE(root mean square error)为均方根误差，Mean为误差均值，Median为误差中值，Std(standard deviation)为标准差. 结合表2、3的数据可知，相机运动越剧烈，本文算法对系统准确性的改善效果越明显.

对比2种算法的绝对轨迹误差RMSE可知，本文算法的RMSE均远低于原算法的RMSE，其中本文算法的平均RMSE约为0.018 79 m，ORB-SLAM2算法的平均RMSE约为0.029 75 m，说明本文算法的估计轨迹更加准确. 结合表3可知，本文算法在改善系统精度的同时，减少了一定的系统漂移量.

为了更加直观地显示本文算法在长时间运动状态下的优化效果，使用表1中所述数据集中时间最久、轨迹最长的数据集fr1/room的运行结果进行对比分析，如图4所示为该数据集下的ATE运行结果.

从图4可知，系统在长时间运动状态下，存在一定的误差波动，利用本文算法可以有效地减小误差波动范围，保证总体误差处于可接受范围内，使得估计轨迹更贴合真实轨迹. 轨迹误差均值、误差中值及标准差等都明显减小，其中均方根误差减小了约46%，误差最小值约为3.522 mm.

系统的实时性是评价SLAM系统的关键指标. 如表4所示为本文算法与ORB-SLAM2算法对于每帧处理时间的对比情况. 表中，t₁、t₂分别为ORB-SLAM2算法和本文算法对于每帧的处理时间. 本文算法相比于ORB-SLAM2算法在每帧的处理时间上更快，平均处理每帧的时间约为25 ms，具有更好的实时性，可以较好地应用于真实场景之中.

针对不同运动场景下以固定的点特征提取与匹配策略的ORB-SLAM算法存在系统跟踪误差较大的问题，通过考虑相机自身运动的影响，提出基于运动预测的改进ORB-SLAM算法. 在公开的TUM数据集上，将本文算法与标准的ORB-SLAM2算法进行对比实验. 实验结果表明，所提算法不仅实时性好，而且提高了系统的精度. 本文算法的思路可以应用于其他的视觉SLAM系统中，为视觉SLAM的改进方向提供了新思路.