自主水下航行器(autonomous underwater vehicle, AUV) 是进行海洋探索的重要工具,依靠携带的动力与导航系统自主航行,在军事和民用诸多领域中都有广泛的应用价值.航迹跟踪是AUV完成各种水下作业任务的基本前提,因此研究精准的航迹跟踪控制算法用来减小航行过程中的超调具有重要意义.航迹跟踪控制算法包括跟踪算法和控制算法,跟踪算法是根据AUV的实时位置和期望航线获取期望航向;控制算法是根据期望航向和期望航速操纵舵机角度和电机转速,使得AUV从任意位置出发,驶入期望航迹,并以期望航速按照期望航迹航行.
在控制算法方面,PID及其优化算法[4-5]结构简单并且鲁棒性和适应性较强,对于系统的具体模型依赖程度较低,但常规PID控制在执行器幅值受限情况下,积分器容易饱和导致系统超调和震荡. 田勇等[6]在航向控制上采用负反馈设计的抗积分饱和,PID控制器解决航向超调和震荡的问题.陈世利等[7]针对AUV在高速下转向时航迹跟踪效果差的缺点,将航向控制闭环和航速控制闭环设计成双闭环控制,在调整航向的同时依据航向环偏航角差实时控制航速环转向目标速度,实验表明相较于常规控制算法,双闭环控制算法在AUV转向时,可以更好地实现航迹跟踪控制. 随着计算机技术的发展,以状态空间为基础的先进控制理论日趋完善,控制器还可以采用神经网络控制[8]、滑模控制[9]、模糊控制[10]、最优控制[11]、自适应控制[12-13]、反步控制[14]、非线性H∞控制[15]以及多种控制算法的结合[16-17].先进控制在多工况下相比PID控制有较大的优势,但算法要求数学模型精确,运算复杂度高,参数整定困难. 目前研究大多停留在仿真计算上,将先进控制理论融合到PID控制器中,既可以保持PID控制的优点,又可以通过先进控制技术在线调整PID控制器的参数,以适应被控对象特性的变化.
针对声学模拟功能的自主水下航行器,以航行器缩比模型结构很接近的典型AUV为具体研究对象,提出时变前视距离的视线导引算法和控制器设计上结合抗积分饱和PID控制算法,并引入参数自适应PID算法以适应多种航行工况,设计一种新型航向航速双闭环控制算法,根据AUV到期望航迹段终点的距离偏差实时调整AUV期望转向速度.将文献[7]双闭环PID算法进行仿真对比,可以得出此算法在AUV大角度转向时,有效减小航迹超调以提升跟踪效果.
1. 模型介绍和问题描述
1.1. 模型介绍
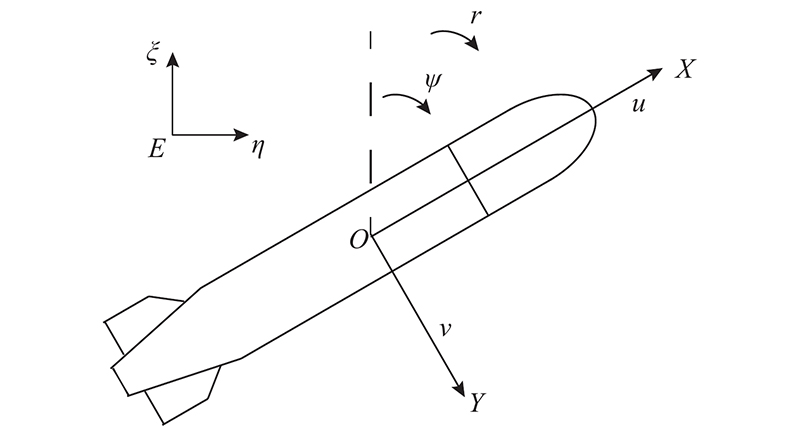
图 1
式中:MRB为刚体本身的惯性矩阵,
考虑到水平面或某一特定深度平面的航迹跟踪,十字形舵的垂直舵和水平舵的作用相互独立,忽略AUV横滚效应,可以建立水平面的动力学模型式:
式中:u、v、r分别为AUV在随体坐标系XOY(原点O为AUV的浮心)下的纵向、横向线速度和偏航角速度,
运动学模型为
式中:x,y,ψ分别为大地坐标系ξEη下AUV的水平位置坐标和航向角.
1.2. 问题描述
如图2所示,在大地坐标系ξEη平面中,由目标点Pi (i=0, 1, 2
图 2
AUV水平面直线航迹跟踪控制目标是设计跟踪算法和控制算法,使AUV从初始位置出发,到达预设的期望航迹,以期望航速沿期望航迹航行,并尽量减小转弯航行过程中的航迹超调.控制上目标分为以下2部分:1)控制AUV的航行速度保持期望航速,即
2. 航迹跟踪控制算法设计
2.1. 视线导引法
视线导引算法是经典有效的导引跟踪策略. 本研究采用基于前视距离的LOS算法,原理图如图2所示,将位置偏差转化成航向偏差,控制AUV的合速度方向始终对准期望航向上的LOS矢量点Plos,引导AUV逼近期望航迹. 在大地坐标系下,期望航迹的航向方位角为期望航迹与大地坐标系纵轴间的夹角.定义四象限反正切计算(y,x)坐标原点为起点,指向点(y,x)的射线在坐标平面上与x轴正方向的夹角. 点PkPk+1组成期望航迹的航向方位角:
AUV实时位置Pt(xt,yt)至期望航迹PkPk+1的垂直偏差为
定义AUV实时位置在期望航迹上的垂足至视线点Plos的距离为前视距离Δ,一般选为艇长的整数倍,即Δ = nL,其中n ≥ 1,一般取2~6,L为AUV长度,
由上述可知,前视距离Δ的选取会影响期望航向角的大小. 当Δ较大时,矢量点选取得较远,AUV将慢慢接近期望航线,随着Δ减小,AUV收敛至期望航线的速度加快,但容易产生震荡、超调和不稳定.考虑到AUV在离期望航迹较远时,首要是快速逼近期望航迹,减小横向误差,此时应选取较小的前视距离;而AUV在期望航迹附近时,应选取较大的前视距离,使AUV慢慢接近期望航迹,尽量减少超调. 因此引入垂直距离ye(t),采用简单的时变前视距离:
式中:Δmin和Δmax分别为设计前视距离,一般选取为L的整数倍;λ为设计系数,λ>0.
当AUV距离期望航线较远即ye(t)较大时,Δ=Δmin,促使AUV快速逼近期望航线,随着AUV接近期望航迹,ye(t)减小,Δ变大并接近Δmax,可使AUV较为平滑地接近期望航线,有效减小位置误差的超调. LOS算法只与实时位置和期望航迹有关,在切换期望航迹时会出现阶跃信号,因此对期望航向角加入一阶惯性滤波加以平滑,滤波器参数为
2.2. 控制器设计
图 3
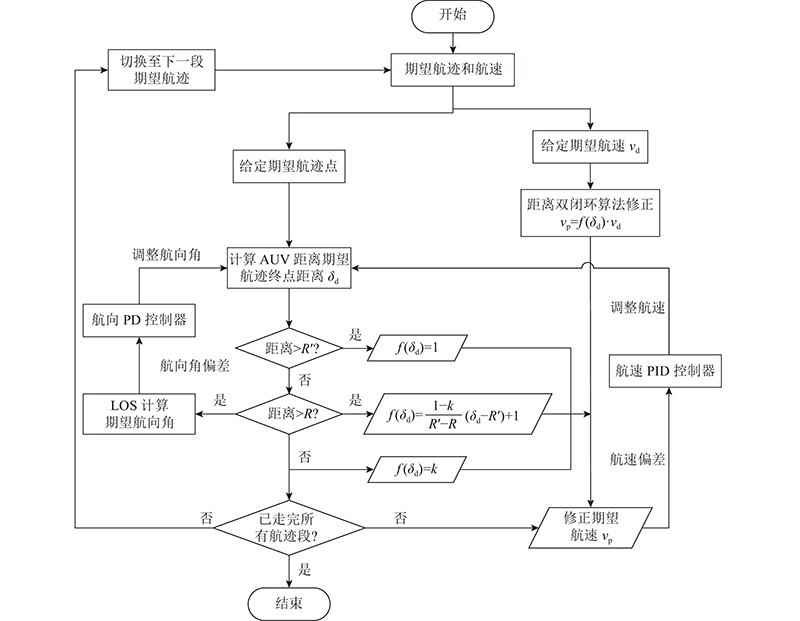
图 3 AUV平面直线航迹跟踪控制算法流程图
Fig.3 AUV plane path tracking control algorithm diagram
图 4
图 5
式中:n为不经限幅的控制器输出,输出限幅上限和下限分别为nmax和nmin,sat (n)为限幅运算.
AUV在期望航迹上航行,若航速较大,当切换期望航迹时将产生较大的航迹超调量.因此如图6所示,设计航向航速双闭环控制器:当AUV航行时,依据AUV至期望航迹段终点的距离差实时调节AUV转向目标航速;当AUV将要切换期望航迹时,降低期望航速,AUV低速切换航迹,减小航迹超调;当航迹切换完成后,加速至期望航速航行.
图 6
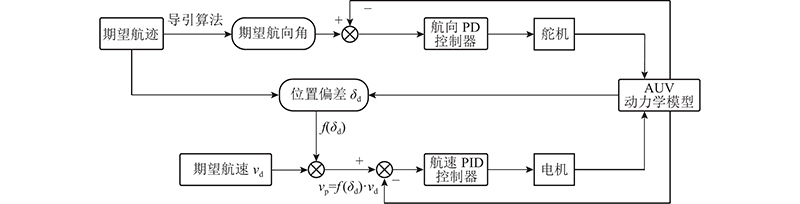
图 6 AUV航向航速双闭环控制框图
Fig.6 AUV heading/speeding double loop control block diagram
航向环控制器的输入变量为期望航向角和实际航向角,输出为舵机舵角.速度环控制器的输入为AUV期望航速和实际航速,以及AUV与期望航迹段终点的位置偏差δd.设计位置偏差和航速环输入目标速度关系为
式中:vp为随位置偏差变化调整的修正期望航速,即最终航速环的期望目标值;系数f(δd)为位置偏差δd的函数.
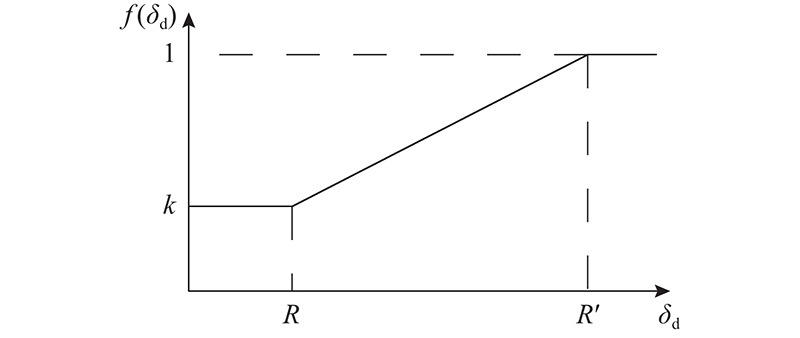
为使AUV转向时速度逐渐下降,不损坏AUV的整体机械性能且不使问题复杂化,设计修正期望速度随着距离偏差的变化呈线性变化,具体关系如图7所示. R、R′均为常量,R为同航迹更新原则中的R,依赖回旋半径设计;R′为预备减速距离偏差,即当AUV距离期望航迹段终点的距离偏差为R′时,AUV开始减速. k为设计转向时期望航速的倍数,称为转向航速系数,取值为0~1.0. 1)当AUV距离期望航迹段终点的偏差大于R′时,说明AUV离期望航迹段终点较远,暂不会切换航迹,期望航速不改变,此时f(δd) = 1.0,即vp = vd,修正期望航速即给定任务期望航速. 2)当AUV距离期望航迹段终点的偏差小于等于R时,说明AUV准备开始切换期望航迹,此时应降低航速,使AUV低速转向,设计f(δd) = k,0 < k < 1.0,即 vp =kvd. 3)当距离偏差R < δd < R′ 时,设计修正期望航速随距离偏差实时线性变化,由图7可以得出AUV在此距离偏差范围内,
图 7
图 7 距离双闭环算法中期望航速系数与位置偏差的变化关系
Fig.7 Relationship between coefficient and position deviation of distance double closed loop algorithm
由上述可知,在AUV航行过程中,航向航速控制器形成双闭环控制;在转向过程中,转向系数f(δd)从1.0到k线性变化;在转向完成后,随着距离差的增大,系数由k到1.0线性变化,航速环不断调节期望航速,实现“转向低速航行,直行高速航行”.
3. 仿真结果与分析
为验证提出算法的有效性,基于Matlab/Simulink软件对AUV模型进行直线航迹跟踪控制仿真,AUV模型参数见文献[18]. 在仿真过程中,电机转速变化过程设为线性变化,在15 s中增长率设置为2 500 r/min,舵机一阶惯性时间常数为0.1 s. 选取坐标原点为起始点,AUV初始状态为:x = 0,y = 0,u = 0,v = 0,ψ = 0,r = 0. 规划多角度航迹,且加入常用弓字形航迹:给定目标点坐标(单位:m)为(200, 0),(0, −200),(200, −200),(400, 0),(600, 0),(600, −100),(400, −100),(400, −200),(600, −200),给定期望航速2.5 m/s.对于跟踪算法设计最小前视距离 Δmin= 8 m,最大前视距离Δmax= 18 m,设计系数λ = 4.0,轨迹更新原则R = 3.0,预备减速距离偏差R′ = 10.0,转向航速系数k = 0.4,分别采用文献[7]提出的航向角偏差双闭环PID控制算法(角度双闭环)和本研究提出的距离偏差双闭环自适应PID控制算法(距离双闭环)进行仿真,参照实际应用情况并且为增强系统稳定性,对AUV执行器进行限幅处理:舵机舵角限幅±8°,电机转速限幅2 500 r/min,在Matlab/Simulink仿真调试选取PID参数. 对于角度双闭环控制,航向PD控制器比例系数kp = 0.2,微分系数kd = 0.2,航速PID控制器比例系数kp = 8.0,积分系数ki = 1.2,微分系数kd = −5.0. 对于距离双闭环控制,航向PD控制器自适应比例航速系数 kp = 0.5−0.1u,微分系数kd = 0.2;航速PID控制器比例系数kp = 10−u,积分系数ki= 1.2,抗饱和反馈系数kf = 10,微分系数kd = −5,仿真结果如 图8所示.
图 8
图 8 角度双闭环和距离双闭环航迹跟踪仿真结果对比
Fig.8 Simulation results comparison of angle double closed loop and distance double closed loop path tracking algorithm
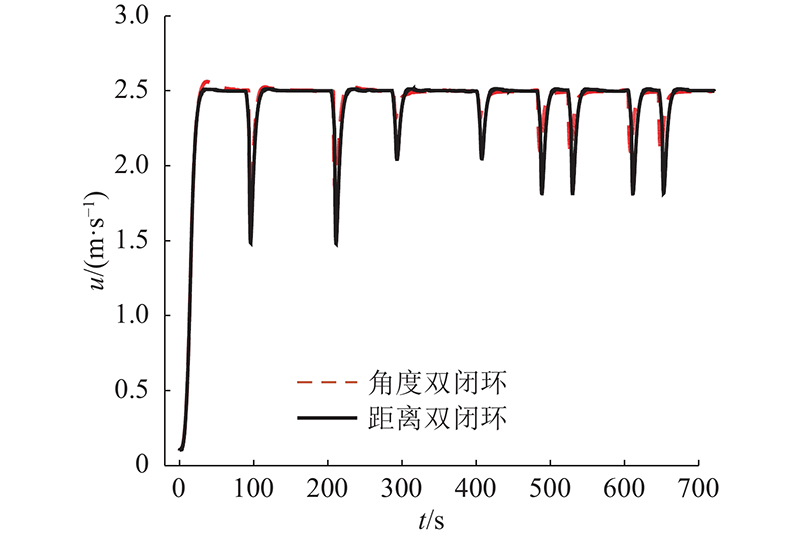
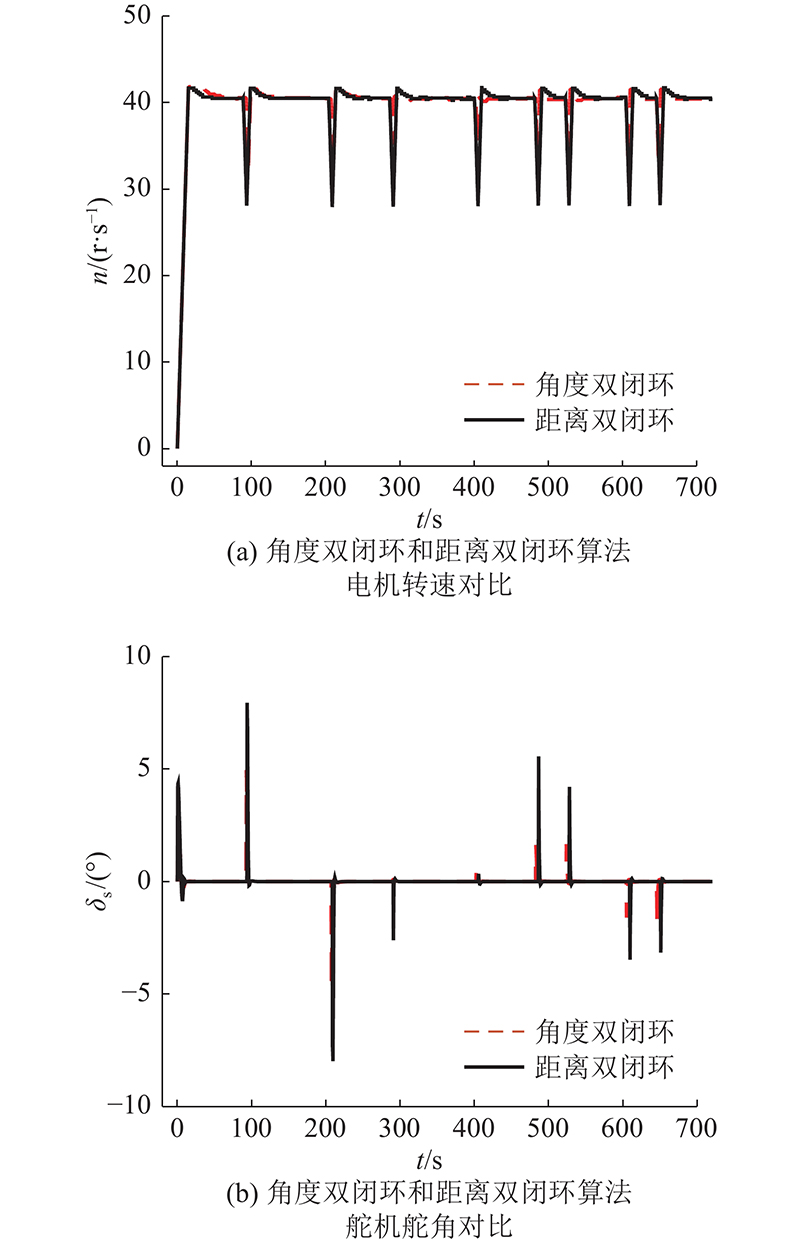
从图8(a)航迹跟踪曲线和图8(c)跟踪过程中的实际航向角可看出,2种双闭环控制算法均能使AUV在整个航迹跟踪过程中达到较好的跟踪控制效果,实际航迹可以很好地收敛至期望航迹上. 从图8(b)拐角处航迹跟踪曲线和图8(d)跟踪过程中的航迹误差变化可看出,距离偏差双闭环自适应PID控制算法在(0, −200)处大角度转向时跟踪控制效果得到较大改善,实际航迹切换更为平滑,超调量明显减小,在整个航迹跟踪过程中,最大超调量在1.0 m,2种控制算法的AUV航速变化如 图9所示. 由图可知,2种控制算法均会使AUV切换期望航迹时降低航速,距离偏差双闭环算法可使AUV提前降速,以更小的航速转向,减小航迹超调,且算法加入抗饱和反馈,避免积分器持续饱和导致航速超调,航速控制效果更好. 电机转速和舵机舵角的输出值如图10所示.
图 9
图 9 角度双闭环和距离双闭环算法航速变化对比
Fig.9 Speed change comparison of angle double closed loop and distance double closed loop algorithm
图 10
图 10 角度双闭环和距离双闭环算法电机和舵机输出值对比
Fig.10 Motor and servos output comparison of angle double closed loop and distance double closed loop algorithm
转向航速系数k应为0~1.0,理论上k越小,转向时速度越小,转弯半径越小,转向航迹越平滑,航迹超调也会越小.转向速度太小会导致转弯时间过长,电机升速降速频繁造成能源耗费与机器耗损,此次仿真过程折中选择0.4. 在实际航行中根据航行速度、航迹长度、转向角度和频率来确定具体数值.
4. 结 论
针对自主水下航行器在平面直线航迹跟踪过程中的航迹超调问题,开发一种AUV平面直线航迹跟踪控制算法,有效减小了航迹超调. 主要结论如下:
(1)通过时变前视距离的视线导引法获取期望航向,并引入一阶惯性滤波对期望航向角加以平滑,以抑制期望航向角的阶跃变化.
(2)引入参数自适应算法以适应多种航行工况,结合抗积分饱和以避免电机持续输出导致航速超调,将航向航速设计成双闭环控制,根据AUV至期望航迹段终点的距离偏差调整航速环期望速度,提前减速至低速转向,减小AUV转向过程中的航迹超调.
(3)对于典型AUV模型相比以航向角为偏差的双闭环PID算法,仿真结果表明,所提出的距离双闭环算法具有更好的航迹跟踪控制效果,在大角度转向时可有效减小转向过程中的航迹超调.
(4)本研究设计的平面直线跟踪控制算法考虑水平面或某一特定深度平面的航迹跟踪,后续计划引入深度控制,并针对减小三维空间AUV航迹跟踪过程中的航迹超调问题进行研究.
参考文献
Line-of-sight path following of underactuated marine craft
[J].DOI:10.1016/S1474-6670(17)37809-6 [本文引用: 1]
Line-of-sight path following for dubins paths with adaptive sideslip compensation of drift forces
[J].DOI:10.1109/TCST.2014.2338354 [本文引用: 1]
海洋环境下欠驱动无人艇航迹跟踪控制算法
[J].DOI:10.11918/j.issn.0367-6234.201709067 [本文引用: 1]
Path tracking control algorithm for the underactuated USV in the marine environment
[J].DOI:10.11918/j.issn.0367-6234.201709067 [本文引用: 1]
PID control system analysis, design and technology
[J].DOI:10.1109/TCST.2005.847331 [本文引用: 1]
具有 PID反馈增益的自主水下航行器反步法变深控制
[J].
Backstepping method with PID gain tuning in diving control of autonomous underwater vehicle
[J].
无人水面艇直线航迹跟踪控制器的设计与验证
[J].DOI:10.16411/j.cnki.issn1006-7736.2015.04.017 [本文引用: 1]
Design and validation of path tracking controller for USV along straight-lines
[J].DOI:10.16411/j.cnki.issn1006-7736.2015.04.017 [本文引用: 1]
基于双闭环的矢量推进器的AUV转向控制方法
[J].
Steering control strategy of AUV with vectored thruster based on double-loop mode
[J].
基于 RBF神经网络的作业型 AUV自适应终端滑模控制方法及实验研究
[J].
Adaptive terminal sliding mode control method based on RBF neural network for operational AUV and its experimental research
[J].
水下自主机器人航向控制算法应用研究
[J].DOI:10.3404/j.issn.1672-7649.2020.02.021 [本文引用: 1]
Application research of heading control algorithm for AUV
[J].DOI:10.3404/j.issn.1672-7649.2020.02.021 [本文引用: 1]
不确定 AUV系统的鲁棒最优滑模控制
[J].
Robust optimal sliding mode control for AUV system with uncertainties
[J].
Serret-Frenet坐标系下AUV自适应路径跟踪控制
[J].DOI:10.12341/jssms12955 [本文引用: 1]
Adaptive path following control of autonomous underwear vehicles in Serret-Frenet coordinate
[J].DOI:10.12341/jssms12955 [本文引用: 1]
Adaptive coordinated tracking control of multiple autonomous underwater vehicles
[J].DOI:10.1016/j.oceaneng.2014.08.019 [本文引用: 1]
基于滤波反步法的欠驱动 AUV三维路径跟踪控制
[J].
Three-dimensional path-following control of underactuated autonomous underwater vehicle with command filtered backstepping
[J].
Nonlinear H∞ state and output feedback control schemes for an autonomous underwater vehicle in the dive plane
[J].DOI:10.1177/0142331217695671 [本文引用: 1]
基于模糊自适应滑模方法的 AUV轨迹跟踪控制
[J].DOI:10.3404/j.issn.1672-7649.2017.12.012 [本文引用: 1]
Trajectory-tracking control of autonomous underwater vehicles based on fuzzy adaptive sliding mode method
[J].DOI:10.3404/j.issn.1672-7649.2017.12.012 [本文引用: 1]
欠驱动AUV自适应神经网络反步滑模跟踪控制
[J].
Path following of an underactuated AUV based on adaptive neural network backstepping sliding mode control
[J].