全球人口老龄化问题日益突出，同时劳动人口短缺导致养老护工严重不足^[1-2]， 科技发展使服务机器人为老年人提供养老服务成为可能^[3-4]. 但是养老服务机器人功能单一，被服务对象的任务需求通常需要由多个不同功能（异构）的服务机器人配合完成. 同时，养老情境下的服务任务通常具有不同的优先级^[5]，优先级越高的任务，响应速度应该越快. 此外，服务机器人的系统在进行任务分配时必须考虑被服务对象的主观满意度. 如何在考虑任务的优先级与主观满意度的同时，合理分配异构多机器人系统的动态多任务，是亟待解决的科学问题.

Das等^[6]提出应用于异构多机器人系统的分布式任务分配方案，采用并行拍卖及协商一致机制分配护理任务. 该方案中的服务机器人基于任务的优先级及自身状态对任务进行投标，通过协商一致算法确定任务分配方案. 虽然该方案可以有效解决动态环境下的任务分配问题，但这些任务都是可以由1个机器人完成的，并未考虑异构服务机器人的协作问题. Hunt等^[7]提出基于协商一致分组算法的多智能体协作任务分配方案. 该方案基于协商一致的打包算法提出多个异构机器人的组队机制，将单个任务分配给多个异构智能体相互协作. Lee^[8]充分考虑机器人在任务执行过程中自身资源消耗对新任务分配的影响，提出机器人个体资源限制的任务分配算法. 该算法中的多机器人系统采用分布式组织结构并基于市场机制的任务拍卖算法分配任务，研究者为执行智能体设置自身资源约束，该约束影响着机器人的任务执行效果. 上述任务分配算法虽然较全面地解决了多机器人系统任务分配中的问题，但未考虑多异构机器人协作存在严格先后约束的任务情况。为此，Tereshchuk等^[9]提出柔性任务进程约束的多机器人调度规划方法. 考虑到在飞机装配生产线上，不同组装工序有不同的工具需求，任务分配需要进行不同工序的有限顺序，研究者提出将基于市场机制的任务拍卖算法与机器学习算法结合的任务分配方案，确定了最节约时间的装配工序. Lee等^[8-9]均未考虑当服务对象为人时，人的主观感受. 李勇等^[10]提出智能体Petri网融合的多机器人-多任务协调框架. 该框架对养老机构中服务机器人执行任务的过程建模；考虑被服务对象的个人主观因素差异，提出满意度模型，并基于满意度模型得出使被服务对象总体满意度最大的任务执行顺序. 在处理异构服务机器人时，该框架将处于相同任务的机器人进行“捆绑”，直至任务完成. 此外，该框架无法动态分配养老情景中不断出现的新任务.

本研究基于多智能体的异构多服务机器人系统（heterogeneous multi service robot system based on multi-agent，HMSRMA）提出动态任务分配机制，对类型相对固定的异构多机器人的多个任务进行动态分配；以满意度函数为基础，建立投标值计算模型；根据拓扑排序算法提出智能体自身、智能体间的死锁检测及处理方法.

多智能体系统应具有较好的稳定性和可扩展性：1）功能分解待执行任务，2）将任务分配给具有不同服务能力的智能体进行任务协商. HMSRMA采用分布式和集中式结构相结合的组织结构.

中央智能体负责任务分解. 根据任务调研结果，分解养老机构中日常出现的被服务对象需求并建立任务库. 基于各子任务间的时序关系与机器人功能，将养老院频繁出现的任务分解成多个子任务. 养老院中出现较为频繁的3种任务为被服务对象吃饭、去卫生间、摔倒救援，子任务分解为拉/放、运送、拉/放. 本研究以吃饭、摔倒救援为例进行分析. 中央智能体还负责发布待执行子任务，对各执行智能体分布协商出的任务分配方案进行互锁检测与解锁.

执行智能体采用分布式架构。该类智能体给出各子任务的投标值并协商确定任务执行方案，进行自锁检测与解锁后，将任务执行方案发送给中央智能体. 在本研究中1个执行智能体对应于一类服务机器人中的1个. 如图1所示，执行智能体主要有2类：1）实现拉起和放下被服务对象功能的人形护理机器人（assistance robot，AR），2）实现运送被服务对象功能的智能轮椅机器人（wheelchair robot，WR）. 系统中AR、WR的数量由任务分配过程是否进行自适应调节确定. 在任务分配过程中，若出现当前智能体数无法完成当前任务数的情况，可以增加一定量的智能体.

区别于其他情境，养老机构中的任务分配具有以下特点. 1）任务类型相对固定，被服务对象每天的生活需求内容有限；2）任务多为并发，同时刻会出现多个被服务对象提出多个需求的情况；3）养老机构为动态环境，被服务对象的需求随机出现. 为此，提出的动态任务分配机制描述如下.

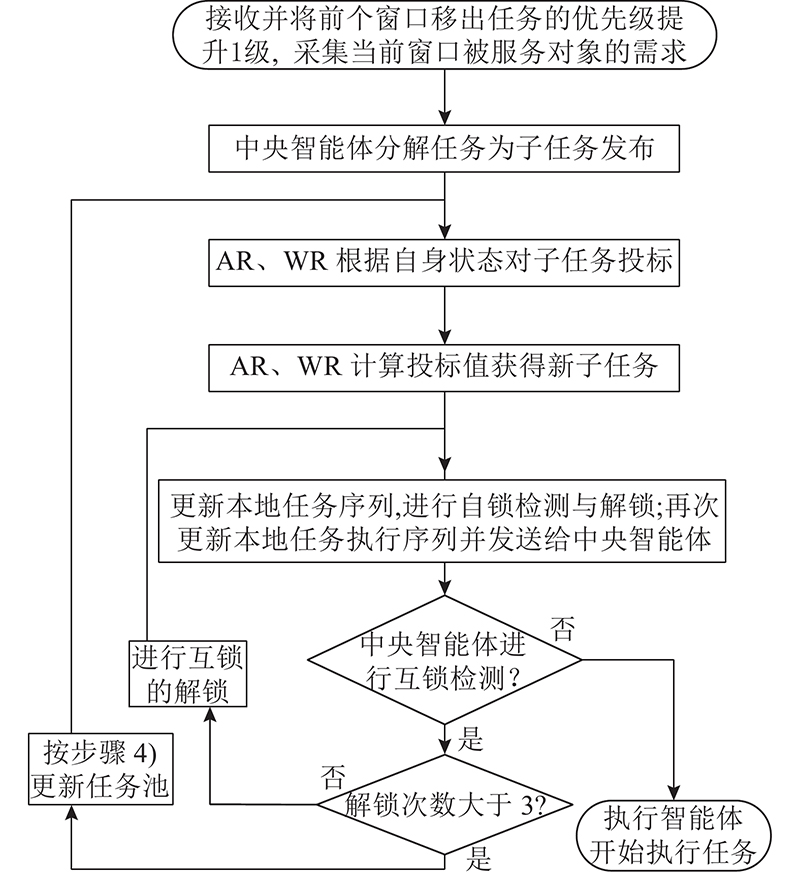
1）设定固定时间间隔作为时间窗口. 每经过1个时间窗口，中央智能体收集当前时间窗口内新产生的任务需求，根据任务分解机制将这些任务分解为多个子任务，将子任务连续发布给所有的执行智能体.

2）各执行智能体分别依次接收子任务，根据自身功能约束 ${c}_{\mathrm{r}}$判断自身是否与任务需求匹配. 若功能匹配，基于实时状态（所处物理位置信息、正在执行以及将要执行任务信息）根据投标值 ${b}_{i,j}$函数计算对该子任务的投标值.

3）执行智能体进行信息交换，确定赢得该子任务的执行智能体，并更新自身的任务执行序列 ${T}_{\mathrm{s}}$. 自锁检测与解锁后，执行智能体再次更新任务执行序列，将更新后的执行序列发送给中央智能体.

4）中央智能体基于拓扑排序算法对更新后的任务执行序列进行互锁检测和解锁，并判断成功与否. 当解锁失败次数达到阈值（本研究设定为3），将当前时间窗口内任务优先级最低的任务移至下个时间窗口，并将优先级提升1级. 如果最低优先级任务数大于1，则根据任务需求提出的时刻，选择后提出的低优先级任务.

时间窗口触发的动态任务分配机制在某一时间窗口的流程如图2所示.

养老情景下的机器人由多个被服务对象分时共享，1个执行智能体会分时执行多个子任务，形成本地任务执行序列 ${T}_{\mathrm{s}}$^[11-13]. 本地序列存储子任务信息，执行智能体根据实时信息调整任务执行序列. 养老院中任务分配及执行规划问题的数学描述为

(1) $ \left.\begin{array}{l}\mathrm{max}\left({\displaystyle \sum\nolimits_{i}^{N}{\displaystyle \sum\nolimits _{j}^{M}{b}_{i,j}}}\right); \\ {{{\rm{s}}.{\rm{t}}.\;}}\left\{{{c}}_{\text{r}}^{}\right\}, \left\{{c}_{\text{s}}^{}\right\}. \end{array}\right\} $

式中：M为待处理子任务数，N为执行这些子任务的服务机器人数， ${b}_{i,j}$为第i个机器人对第j个子任务的投标值， ${c}_{\mathrm{s}}$为子任务时序约束.

多智能体系统的目标是减小任务执行成本以扩大收益^[14-16]. 养老情景下将被服务对象的感受作为收益，引用李勇等^[10]提出的满意度模型来计算任务分配投标值. 基于文献[10]的满意度模型，提出AR、WR计算满意度的模型，在本研究场景下， AR完成拉/放任务时不存在运行速度的参数. 为了保证满意度值为正，将AR、WR的满意度计算公式分别修改为

(2) $\begin{split} {S _{{{\rm{AR}}} }} =& \left| {{\alpha _0}{{P}} - {\alpha _1}{{I}}{{\rm{exp}}}\,({\alpha _2}{{t_{\rm{w}}}}/{t_{\rm{wm}}}) - } \right.\\ &\left. { {\alpha _3}{{\rm{exp}}\,({{\alpha _4}\left( {{t_{\rm{e}}} - {t_{{\rm{es}}}}} \right)/{\alpha _5}}}}) \right|^{-1} , \end{split} $

(3) $ \begin{split} {S _{{\rm{WR}}}} =& \left| {\alpha_{{0}}}{{P } -}{\alpha _1}{I}{{\rm{exp}}}\,({\alpha _2}{t_{\rm{w}}}/{{{t_{{\rm{wm}}}}}}) -\right. \\ &\left.{\alpha _3}{{\rm{exp}}\,({{\alpha _4}\left( {v - {v_{\rm{s}}}} \right)}}) \right|^{-1}.\quad \end{split} $

式中： $ {\alpha }_{0} $~ $ {\alpha }_{5} $为可调参数； $ P $服务任务的优先级，其中吃饭任务优先级 $ P\in \left\{0,\mathrm{1,2},\mathrm{3,4}\right\} $，摔倒任务优先级 $ P\in \left\{10,\mathrm{11,12,13,14}\right\} $，摔倒任务的优先级远大于吃饭； $ I $为被服务对象的性格急躁系数， $I\in \left\{\mathrm{1.0,} \mathrm{1.1,1.2,1.3,1.4}\right\}$； $ {t}_{\mathrm{w}} $为被服务对象提出服务需求至服务智能体开始任务执行的时间； $ {t}_{\mathrm{w}\mathrm{m}} $为被服务对象能忍受的最大等待时间； $ {t}_{\mathrm{e}} $为AR执行拉/放任务的时间，该参数为AR的固定属性； ${t}_{\mathrm{es}}$为被服务对象感到舒适的拉/放时间； $ v $为WR执行运送任务的速度； ${v}_{\mathrm{s}}$为被服务对象感到舒适的运送速度^[10].

$ {t}_{\mathrm{w}} $是影响满意度的主要参数. 若智能体本地任务执行序列中有 $ l $个子任务，则第 $ n $个子任务的等待时间计算公式为

(4) $ {t_{{\rm{w}},{n}}} = \left( {{t_{{\rm{b}}}} - {t_{\rm{p}}}} \right)+{t_{{{\rm{a}}},n}}+{t_{{{\rm{c}}},n}}+{t_{{{\rm{t}}}}}. $

(5) $ {t_{{{\rm{a}}},n}} = {D}/{v}. $

(6) $ {t}_{\text{c},n}=\left\{\begin{array}{l}0,\quad\quad\quad\quad\quad \text{无前件子任务};\\ 0,\quad\quad\quad\quad\quad {t}_{\text{a},n}+{t}_{\text{t}} < {t}_{\text{ep}};\\ {t}_{\text{a},n}+{t}_{\text{t}}-{t}_{\text{ep}},\;\;\;\;{t}_{\text{a},n}+{t}_{\text{t}}\geqslant {t}_{\text{ep}}.\end{array}\right. $

(7) $ {t_{{{\rm{ep}}}}} = {t_{{{\rm{w}},{{n}}-1}}}+t_{{{\rm{e}},{{n}}-1}}. $

(8) $ {t_{\rm{t}}} = \sum\nolimits_{i = 1}^{ n - 1} {{t_{{{\rm{w}}},{i}}}+{t_{{{\rm{e}}},i}}} . $

式中：D为执行智能体本地任务序列中第n个子任务与第（n−1）个子任务间的距离； $ {t}_{\mathrm{b}} $为投标时间， ${t}_{\mathrm{p}}$为子任务发布时间， ${（t}_{\mathrm{b}}-{t}_{\mathrm{p}}）$表示该子任务从发布到投标的时间； ${t}_{\mathrm{a},n}$为该智能体本地序列中第 $ n $个子任务与第（n−1）个子任务间的到达时间； ${t}_{{\rm{c}},n}$为第 $ n $个子任务与第（n−1）个子任务交接的等待时间； $ {t}_{\mathrm{e}\mathrm{p}} $为序列中（n−1）个子任务的执行时间； ${t}_{\mathrm{w},n-1}$为第（n−1）个的等待时间； ${t}_{\mathrm{e},n-1}$为第（n−1）个子任务的执行时间； $ {t}_{{\rm{t}}} $为智能体本地任务执行序列中前 $ n $个子任务的执行与等待时间总和； $ {t}_{\mathrm{w},i} $为序列中第 $ i $个子任务的等待时间，可根据式（4）求出； $ {t}_{\mathrm{e},i} $为第 $ i $个子任务的执行时间，由不同执行智能体的预设信息得出.

兼顾整体与个体的投标值计算模型为

(9) $ {{b}}_{i,j}= {{{L}}_{\text{1}}}\left( {S^\prime { - }S} \right){\text+}{{{L}}_{\text{2}}}\left( {{s_{i,j}^\prime }{{ - }}{s}_{i,j}} \right), $

(10) $ S^\prime = \sum\nolimits_{k = 1}^{L'} {{S_k}} , $

(11) $ {S = \sum\nolimits_{k = 1}^L {{S_k}} .} $

式中： ${S}^{{'}}$为执行智能体本地任务执行序列调整后序列中所有任务的满意度之和； $ {L}{{'}} $为调整后在任务序列中的任务数； $ S $为执行智能体本地任务执行序列调整前（尚未对新任务投标时）序列中所有任务的满意度之和； $ L $为调整前在任务序列中的任务数； $ {\mathrm{S}}_{k} $为序列中第 $ k $个任务的满意度； ${s}_{i,j}$、 $ {s}{{'}}_{i,j} $分别为调整前后的智能体本地任务执行序列的最小满意度； $ {L}_{1} $、 $ {L}_{2} $为可调系数. 当执行智能体的功能不满足子任务需求时，智能体无法对新任务投标，规定此时投标值为0，即无效投标. 可以看出，执行智能体投标值计算公式由子任务满意度计算得到，被服务对象满意度由子任务满意度加和得到，因此式（9）可以有效反映被服务对象的满意度情况.

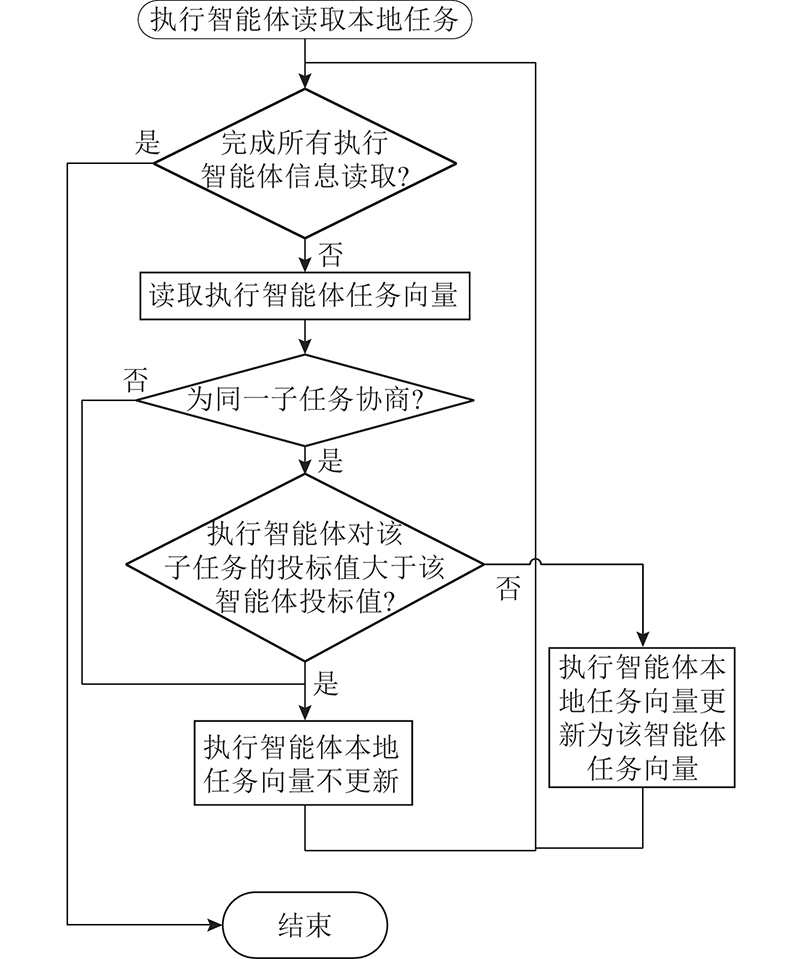
新的子任务投标结束后，所有执行智能体进行分布式协商以确定投标值最大的智能体. 为了方便执行智能体存储本地投标信息，引入任务向量 $ {\boldsymbol{T}}_{\rm{v}} $^[6]. 任务向量中的信息存储格式为

(12) $ {{{\boldsymbol{T}}}_{\rm{v}}}{ = }\left[ {{{{T}}_{{\rm{ID}}}}{,{{T}}}_{{\rm{id}}},{{b}}_{{i,j}},\,{{{a}} _{{\rm{ID}}}},\,{{{t}}_{\rm{b}}}} \right]{.} $

式中： ${T}_{\mathrm{I}\mathrm{D}}$为主体任务标号， ${T}_{\mathrm{i}\mathrm{d}}$为子任务标号， $ {a}_{\mathrm{I}\mathrm{D}} $为给出投标值的智能体标号. 各智能体的本地任务向量在对子任务投标及智能体间协商完成后进行更新. 设定4种执行智能体任务执行状态为空闲、响应、任务执行中、任务锁定. 当某子任务正在被执行时，执行该子任务的智能体会向准备执行后件子任务的智能体发出锁定命令，接到该命令后负责执行后件子任务的智能体不再投标新任务. 协商过程的算法流程图如图3所示.

死锁是分布式系统中的常见问题^[17-18]. 当某个执行智能体须执行多个子任务时，最优执行序列中的子任务可能不满足子任务时序约束；以该顺序执行时，无法完成的任务便陷入无限等待，这种执行智能体自身任务序列的死锁称为执行智能体自锁. 当某个智能体执行的任务须以另一个智能体陷入等待的子任务完成为前提时的死锁称为多执行智能体间互锁.

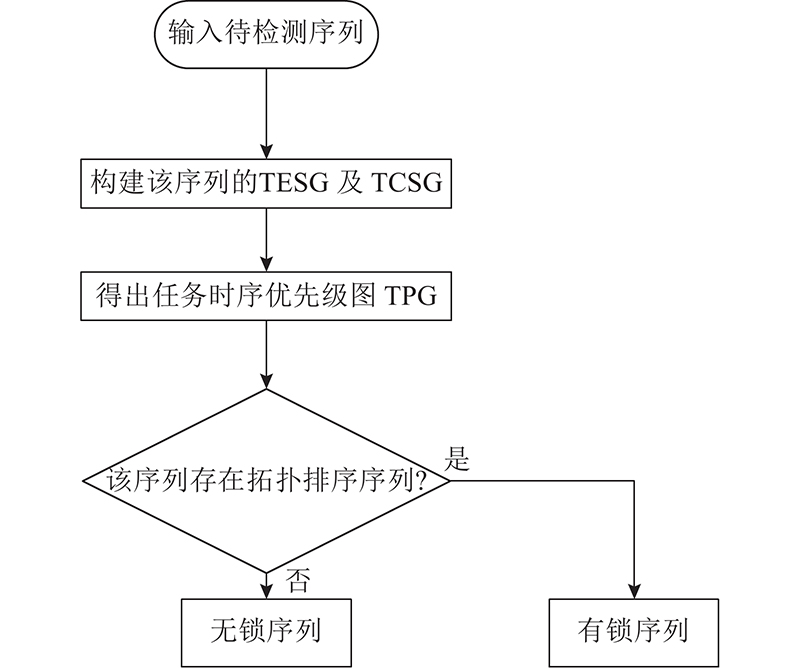
引入基于拓扑排序算法（topological sort）的死锁检测与解锁算法^[18]. 该算法基于任务时序优先级图(task precedence graph，TPG). TPG由任务执行子图(task executing subgraph, TESG)和任务约束子图(task constraint subgraph, TCSG)构成. 其中TESG反应执行智能体本地任务执行序列的约束，TCSG反应1个服务任务包含的子任务时序约束. 使用拓扑排序算法对TPG排序，判断任务分配方案是否存在死锁，若存在，则调整存在死锁的执行智能体任务序列.

如图4所示，基于自锁检测算法检测各执行智能体的本地任务序列，若存在自锁，则执行如下解锁流程. 1）改变本地任务执行序列中的子任务执行顺序，采用遍历法生成所有可能的新的本地任务序列集1. 2）基于拓扑排序算法检测集1中各个序列是否存在自锁。删除自锁序列后，得到本地任务序列集2. 3）执行智能体计算集2每个序列的满意度和. 4）选择某个满意度和最大序列作为该执行智能体解锁后的本地任务执行序列.

若多智能体间出现互锁，往往仅需调整某个智能体的任务序列，为此需要准确定位死锁的任务节点. 由于各执行智能体中只包含局部任务分配信息，采用基于拓扑排序算法检测全局分配方案须在中央智能体中运行. 若某种任务分配方案存在互锁，则其任务时序优先级图中存在强连通分量（strongly connected components，SCC），SCC与TESG的交集构成可变子图. 可变子图可以调整，且包含死锁子任务节点间的有向边，由此实现对死锁节点的准确定位. 通过转置可变子图的邻接矩阵得到无锁子任务间的依赖关系，再由新的任务时序优先级图得到调整后的执行智能体本地任务执行序列.

为了提高多机协作机制的决策效率，对任务分配结果中的互锁问题进行多次解锁操作. 当多智能体系统某次出现死锁并进行解锁后，更新本地任务执行序列，再次检测解锁后的任务分配方案是否解锁成功. 在任务分配机制流程中，死锁情况下最低优先级的任务被移至下个时间窗口后，与该时间窗口中被服务对象提出的新需求一起进行新的任务分配. 此时，该时间窗口下的任务序列若依然出现死锁，则与前个时间窗口下的解锁流程进行相同的解锁操作，以此类推. 若多次解锁操作失败，说明对于现有规模的多执行智能体来说，须处理的任务规模太大。引入空闲的备用资源或减少当前时间窗口下多智能体系统接受的任务数，使系统正常运行（在养老机构中，通常不会有空闲机器人，多数情况下采用减少任务规模的方式）后，更新多智能体系统执行方案中的任务池.

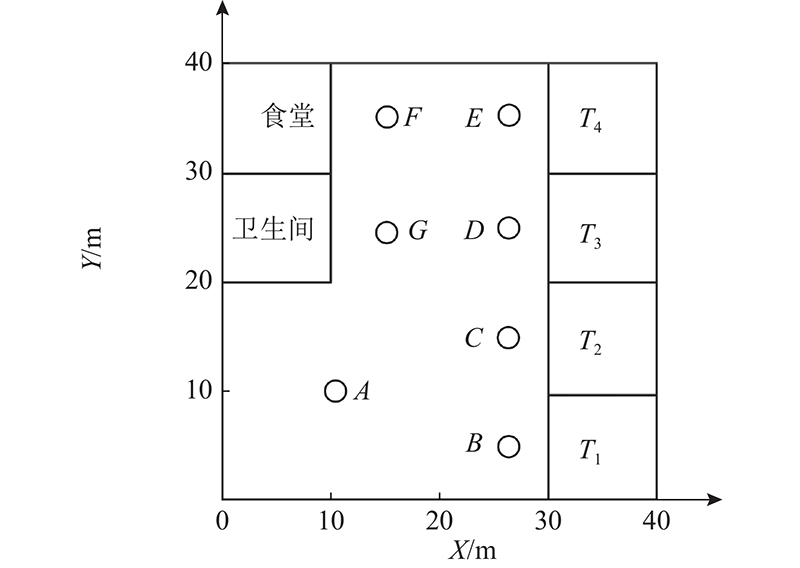
如图5所示为仿真场景各房间及固定点坐标。其中 A（10，10）、B（25，5）、C（25，15）、D（25，25）、E（25，35）、F（15，35）、G（15，25），食堂（5，35），卫生间（5，25），T₁（35，5）、T₂（35，15）、T₃（35，25）、T₄（35，35），上述信息均存储在各执行智能体中.

为了简化研究，规定起始点、被服务对象的房间、卫生间等仿真场景都有对应的固定点，即点A、B、C等. 在不考虑执行智能体间碰撞问题的前提下，将所有智能体均视为点，设系统初始状态的执行智能体均处于点A位置. 以任务T1智能体AR为例，在初始状态下，当某个执行智能体收到任务并要前往该任务所在位置时，AR确定当前所处位置坐标点A，确定点B为T1任务位置对应的固定点，则AR在当前位置沿直线AB行驶至点B，再从点B直线行驶到点T₁. 在非初始状态下，执行智能体按照其自身任务序列前往下个任务所在位置时（执行完T3，后序任务为T4），AR确定当前所处位置坐标点T₃，确定点D为T3任务位置对应的固定点，确定点E为T4任务位置对应的固定点. 则AR从点T₃沿直线行驶到点D，再从点D直线行驶到点E，由点E直线行驶到点T₄. 以此类推，所有智能体均按上述机制行驶.

设多智能体系统由1个中央智能体及4个执行智能体组成，执行智能体的编号分别为AR1（技能为拉/放，空载速度1 m/s，服务时间20 s）、AR2（技能为拉/放，空载速度1 m/s，服务时间15 s）、WR1（技能为运送，空载速度1.5 m/s，服务速度0.6 m/s）、WR2（技能为运送，空载速度1.8 m/s，服务速度0.5 m/s）. 在该情况中模拟1个任务收集时间窗口内同时出现2个同类型任务的情况，设时间窗口为60 s，此时多执行智能体系统在点A位置，各智能体的本地任务执行序列为空. 任务的具体信息如下：任务T1，位置为（35，5），任务类型为吃饭，任务优先级为1，被服务对象性格急躁系数为1.1，最大忍受等待时间为70 s；任务T2，位置为（35，15），任务类型为吃饭，优先级为1，老人急躁系数为1.2，最大忍受等待时间为75 s. 服务任务的子任务信息如表1所示.

如表2所示为各智能体对子任务的投标值. 表中，不带括号的投标值为当 $ {L}_{1}=1、{L}_{2}=0 $时由式（9）计算得出的结果，带括号的投标值为 $ \mathrm{当}{L}_{1}=1\mathrm{、} {L}_{2}=10 $时由式（9）计算得出的结果. 可以看出，在完成某个子任务投标后，执行智能体能协商出对该子任务投标值最大的智能体，得出使任务T1、T2中所有子任务获得最大投标值的方案. 任务分配结果如下：AR1本地任务执行序列为T1_3(T1_3,T1_1,T2_3); AR2本地任务执行序列为T1_1, T2_1, T2_3(T2_1); WR1本地任务执行序列为T2_2(T2_2)；WR2本地任务执行序列为 T1_2(T1_2). T1_1、T1_2、T1_3、T2_1、T2_2、T2_3的满意度分别为0.112 0(0.060 0)，0.056 0(0.083 0)，0.0006(0.0008)，0.018 0(0.097 0)，0.010 0(0.0008)，0.0006(0.0004)，总体满意度为0.199 0(0.242 0).

为了进一步证明多异构服务机器人协作机制可以提高被服务对象的满意度，分别采用先到先得及随机分配机制，进行养老服务任务的分配并计算完成各子任务时被服务对象的满意度. 先到先得机制的任务分配结果：AR1的本地任务执行序列为（T1_1, T2_1），AR2的本地任务执行序列为（T1_3, T2_3），WR1的本地任务执行序列为（T1_2），WR2的本地任务执行序列为（T2_2）. 按该方案执行任务时，T1_1、T1_2、T1_3、T2_1、T2_2、T2_3的满意度分别为0.087、0.014、4.421×10⁻⁵、8.837×10⁻⁶、1.701×10⁻⁶、8.204×10⁻⁹ ，总体满意度为0.101. 随机机制的任务分配结果：AR1的本地任务序列为（T2_1, T1_3），AR2的本地任务序列为（T1_1, T2_3），WR1的本地任务序列为（T2_2），WR2的本地任务序列为（T1_2），按该方案执行任务时，T1_1、T1_2、T1_3、T2_1、T2_2、T2_3的满意度分别为9.243×10⁻⁶、1.877×10⁻⁶、2.678×10⁻⁹、0.106、0.006，0.001×10⁻¹.

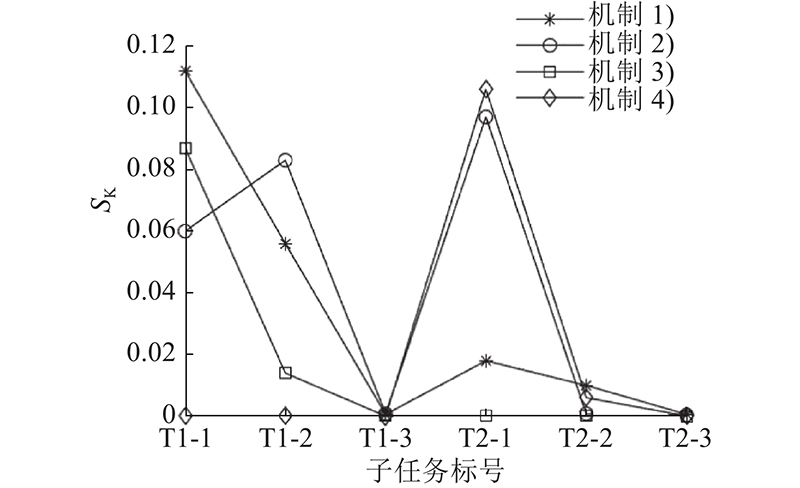
各种分配机制下各子任务的满意度对比图如图6所示. 图中，机制1）表示 $ {L}_{1}=1、{L}_{2}=0 $时的多协作机制，机制2）表示 $ {L}_{1}=1、{L}_{2}=10 $时的多协作机制，机制3）表示先到先得机制，机制4）表示随机分配机制. 可以看出，采用机制3）分配任务时，后发布的任务等待时间过长，导致后发布任务的各子任务满意度始终较低，本研究所提多异构服务机器人协作机制可以显著提高被服务老人的满意度. 采用机制4）分配任务时，只有子任务T2_1的满意度高于本研究所提机制进行分配时的满意度. 机制4）各子任务满意度之和为0.113，使用本研究所提机制时各子任务的满意度之和为0.199，表明应用本研究所提机制可以使各子任务的满意度之和较大.

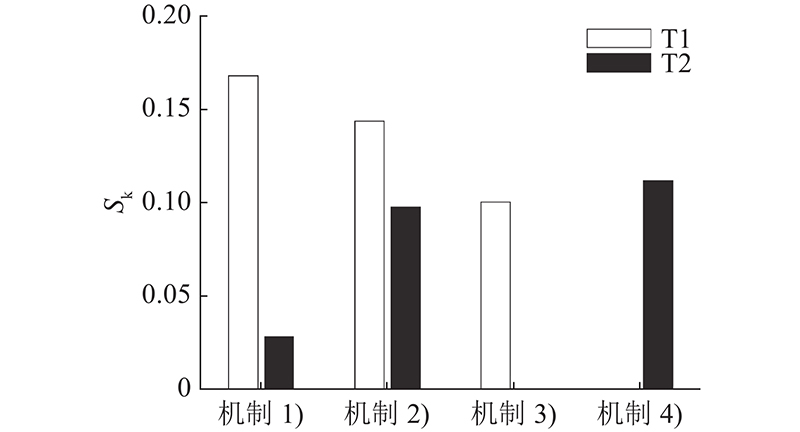
提出任务需求的2个被服务对象满意度对比图如图7所示. 可以看出，不采用本研究所提机制进行分配时，会出现总体满意度和个体满意度很小的情况. 使用本研究所提机制时， 机制1）偏重总体满意度，机制2）偏重提升个体满意度的最小值. 因此，可以根据使用者偏好，调整投标值函数中的 $ {L}_{1} $、 $ {L}_{2} $，实现兼顾使用者偏好和整体个体满意度的任务分配机制.

假设在前个任务收集时间窗口完成的下个时间窗口内出现新任务T3，将T3定义为摔倒救援任务，任务优先级为最高，T3的具体信息如下：任务位置为（5，25），任务优先级为4，被服务对象的性格急躁系数为1.2，最大可忍受等待时间为50 s. T3所包含的子任务为T3_1（所需技能为拉/放，最佳服务时间为16 s），T3_2（所需技能为运送，最佳服务速度为0.5 m/s），T3_3（所需技能为拉/放，最佳服务时间为15 s）. T3出现时，多智能体系统完成上个时间窗口的任务T1、T2的分配，各智能体状态已经改变，基于新的状态，各智能体对T3中子任务的投标结果如表3所示. 分配结果：AR1的任务执行序列（T1_3），AR2的任务执行序列（T3_1, T2_3, T3_3），WR1的任务执行序列（T2_2），WR2的任务执行序列为（T3_2）. 可以看出， 当T3出现时，上个时间窗口任务的子任务T1_1已完成，T1_2、T2_1正在执行，因此更新智能体本地序列。根据执行智能体状态可知，此时AR1、WR1为锁定状态，无法投标新任务，因此其投标值为0. 同时高优先级任务的子任务总是处于任务序列靠前的位置.

通过模拟实验验证同个时间窗口出现大规模（相对于智能体数量）需求时，本研究所提机制的有效性. 在某时间窗口内出现任务T1、T2的基础上，将该时间窗口内出现的任务数增加到4个，即T1、T2、T4、T5. T4的具体信息如下：位置为（35，25），任务类型为吃饭，优先级为1，被服务对象的性格急躁系数为1.1，最大忍受等待时间为70 s. T5的具体信息如下：任务位置为（35，35），任务类型为吃饭，优先级为1，被服务对象的性格急躁系数为1.0，最大忍受等待时间为75 s. 子任务信息如表4所示. 此时子任务总数为12个，仅有4个执行智能体，每个智能体的子任务数量较多.

当基于未添加死锁处理及预防机制的多机协作机制进行任务分配时，分配结果如下：AR1的本地任务执行序列为T1_3, T2_1, T4_1, T4_3, T5_1；AR2的本地任务执行序列为T2_3, T1_1, T5_3；WR1的本地任务执行序列为T1_2, T2_2；WR2的本地任务执行序列为T4_2, T5_2. 当同个时间窗口出现4个任务时，AR1 本地序列的第1个子任务及 AR2 本地任务序列中第1个子任务均有2个前件子任务，它们的首个前件子任务又不在对方本地序列的第1位，这使 AR1 、AR2 陷入无限等待，因此该方案无法运行. 死锁处理后任务分配结果如下：AR1的本地任务执行序列为T1_3, T2_1, T4_1, T4_3, T5_1；AR2的本地任务执行序列为T1_1, T2_3, T5_3；WR1的本地任务执行序列为T1_2, T2_2；WR2的本地任务执行序列为T4_2, T5_2. 即经过处理后，AR2先执行子任务T1_1（AR1中第1个任务的前件子任务），便不会出现死锁. 可以看出，在为本研究所提机制增加互锁的处理及预防功能后，得出了可以正常执行的无锁任务分配方案.

本研究基于多智能体系统，针对养老情景下的异构多服务机器人任务分配问题，提出动态任务分配机制. 以被服务对象的满意度函数为基础，建立投标值计算模型，在完成养老情境下被服务对象提出的需求的同时，提高了被服务对象的满意度. 解决了多智能体系统在进行动态任务分配过程中出现的执行智能体自身和各执行智能体间的死锁问题. 由仿真结果可以看出，所提机制可以基于任务的不同类型及被服务对象的个体差异进行动态任务分配，有效提高了被服务对象的总体满意度. 由于被服务对象满意度是根据常识建立的数学模型，其真实性还有待研究。后续计划采集真实数据，建立更符合实际的被服务对象满意度模型.