连续型机械臂依靠柔性结构进行弯曲运动,此柔性结构易引发振动,属于高度复杂的非线性系统. Ivanescu等 [ 6] 将连续型机械臂分解为解耦控制系统,以曲率及曲率梯度作为控制参数,采用滑模变结构控制方法研究机械臂的形态. Alqumsan等 [ 7] 针对Cosserat杆模型设计了基于滑模的鲁棒控制器,同时考虑控制饱和输入以避免张力剧烈变化.在考虑系统存在不匹配不确定性的情况下,该团队利用多面滑模控制方法设计了鲁棒控制器,使机械臂到达目标位姿 [ 8] . Qi等 [ 9] 设计的基于模糊控制器的智能控制方法,完成了轨迹跟踪任务,使机械臂系统具有良好的稳定性与抗干扰能力. Piltan等 [ 10] 为了提高手术机器人的可靠性与故障容错精度,提出基于自适应模糊观测器的反馈线性控制方法. 由于系统高度复杂,智能控制器须调节、训练大量参数,导致该方法难以满足快速轨迹跟踪的要求.尽管上述基于滑模控制方法的连续型机械臂系统具有较强鲁棒性能与抗扰能力,但它们的系统是渐进稳定的,对这类系统的快速收敛、精准控制的动态性能有了更高的要求,因此,现有方法难以同时满足抗干扰与快速精确跟踪的控制要求.
与非有限时间控制方法相比,有限、固定时间控制方法具有更优的收敛性能以及更好的鲁棒和抗扰动性能,在航天器的快速姿态机动与振动抑制问题中有较好的应用 [ 11- 12] . 有限时间控制方法的稳定时间是与系统初始状态有关的无界函数,固定时间控制方法的稳定时间与系统参数有关,且无法直接建立控制参数与稳定时间的数学表达式,为此Sánchez-Torres等 [ 13] 提出预定时间控制方法,将稳定时间作为控制参数,该参数可根据系统设计需求提前设置,并被认作为固定稳定时间的最小上界. Wang等 [ 14] 已将预定时间稳定性理论应用于刚性航天器的姿态机动问题中,确保姿态跟踪误差和角速度在预先设定的时间内收敛到零.
为了提高线驱连续型空间机械臂系统的姿态收敛和抗扰动性能,本研究在存在外界时变干扰与系统参数不确定性的情况下,设计模糊估计器估计并补偿上界未知的干扰,再基于滑模变结构方法设计预定时间控制器. 基于Lyapunov稳定理论证明线驱连续型机械臂系统误差能在设定时间内达到预定时间稳定,并给出仿真结果验证算法的有效性.
1. 多节线驱连续型机械臂的动力学模型
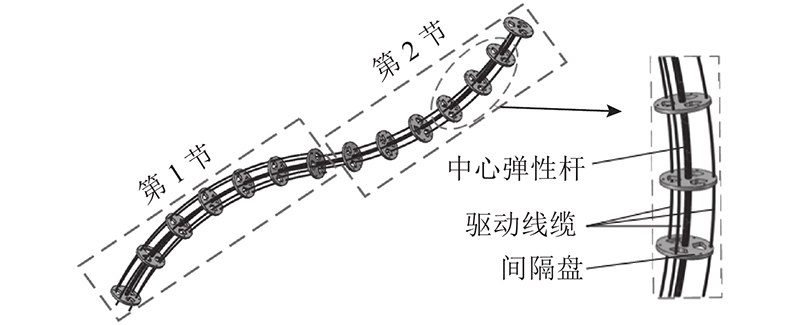
本研究的对象为多节线驱连续型空间机械臂,如 图1所示为2节机械臂示意图. 机械臂每节长度相等,每节由3根线缆驱动中心弹性杆弯曲变形,等距分布的间隔盘为机械臂保持弯曲形态提供刚度支撑.
图 1
图 1 2节线驱动连续型机械臂示意图
Fig.1 Schematic diagram of two-section cable-driven continuum manipulator
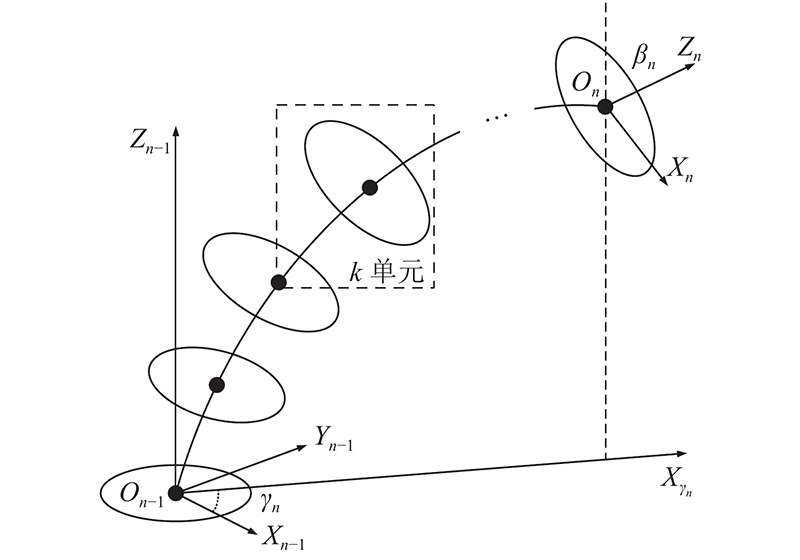
如 图2所示,对第
图 2
式中:
考虑到连续型空间机械臂处于微重力环境,忽略其重力势能影响,其弹性势能为
式中:
多节线驱连续型机械臂的广义力
式中:
将动能、势能以及广义力表达式(1)~(6)代入拉格朗日第二类方程,得到多节线驱连续型机械臂的动力学方程为
结合式(7),考虑存在外界时变干扰与系统参数不确定性
式中:
2. 基于模糊补偿的连续型空间机械臂预定时间控制
针对存在外界未知扰动的多节线驱连续型机械臂系统,设计基于模糊补偿的预定时间控制方法,研究机械臂的快速姿态稳定与抗扰问题.
2.1. 控制目标
定义机械臂系统的姿态角误差
假设1 多节线驱连续型机械臂系统受到的总干扰力矩有界但界值未知,即
控制目标:针对多节线驱连续型机械臂系统式(8),在假设1的条件下,设计基于模糊补偿的预定时间控制律 u ,使得线驱机械臂姿态角
2.2. 控制律设计
定义1 对于非线性自治系统:
式中: x 为系统状态,
引理1 对于非线性自治系统式(9),假设存在连续径向无界函数
式中:
选取滑模面:
式中:
式中:
设计预定时间控制律为
式中:
定理1 对于多节线驱连续型空间机械臂系统式(8),在存在外界时变干扰和参数不确定性时,在假设1的条件下,采用预定时间控制律式(13),机械臂系统姿态角误差 e 将在预定时间
证明:在系统误差状态未到达滑模面阶段,选取Lyapunov函数:
将式(14)对时间求导,并将式(12)、(13)代入,整理得到
依据Cauchy-Schwarz不等式,进一步得到
根据引理1,系统误差状态将在
当系统误差状态到达滑模面时,有
根据引理1,系统误差状态将在
综上所述,该连续型空间机械臂系统姿态角能在用户预先设定时间
由预定时间控制律式(13)可知,切换增益 k易引发抖振,考虑到模糊系统具有万能逼近特性 [ 16] ,采用模糊规则估计切换增益,补偿未知有界干扰项,消除抖振.
滑模存在的条件为
式中: K为由经验值确定的比例系数.
控制参数的选取依据如下. 1) 用户预先设定的时间
3. 数值仿真与结果分析
对2节线驱连续型空间机械臂系统进行仿真,研究系统在基于模糊补偿的预定时间控制方法下的姿态稳定性能,并对比基于非奇异终端滑模(nonsingular terminal sliding mode control,NTSMC)的有限时间控制方法 [ 11] . 假设期望姿态角
图 3
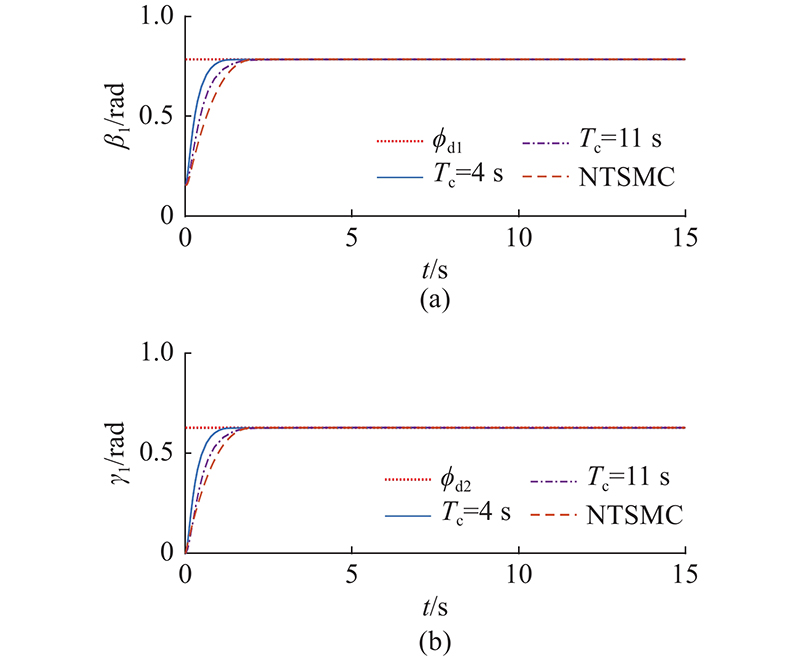
图 3 不同控制策略下的第1节机械臂姿态响应曲线
Fig.3 Attitude response curves of section 1 manipulator under different control strategies
图 4
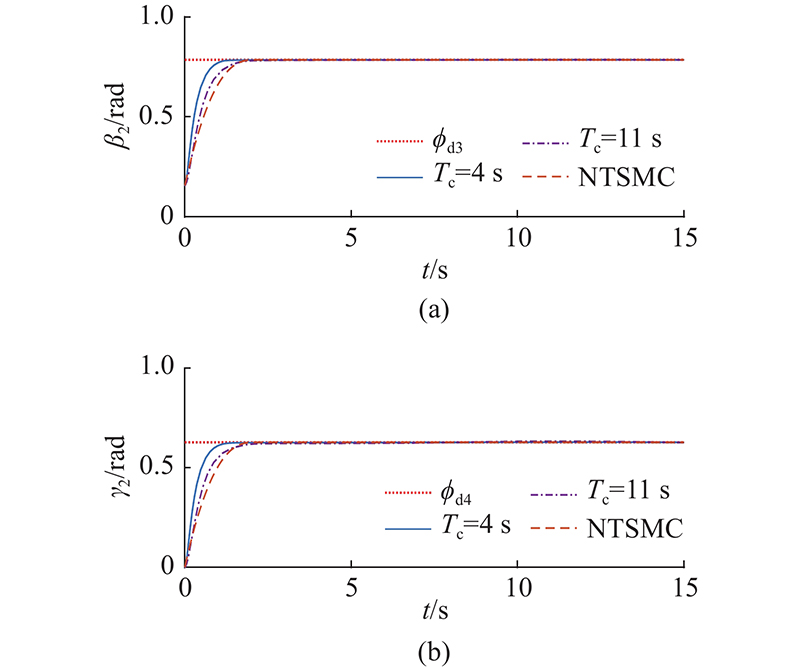
图 4 不同控制策略下的第2节机械臂姿态响应曲线
Fig.4 Attitude response curves of section 2 manipulator under different control strategies
图 5
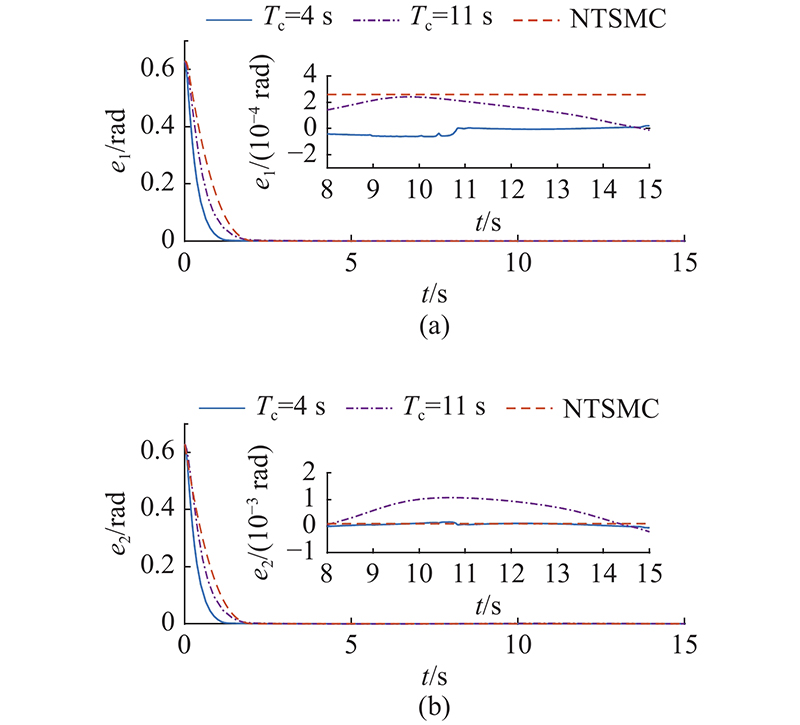
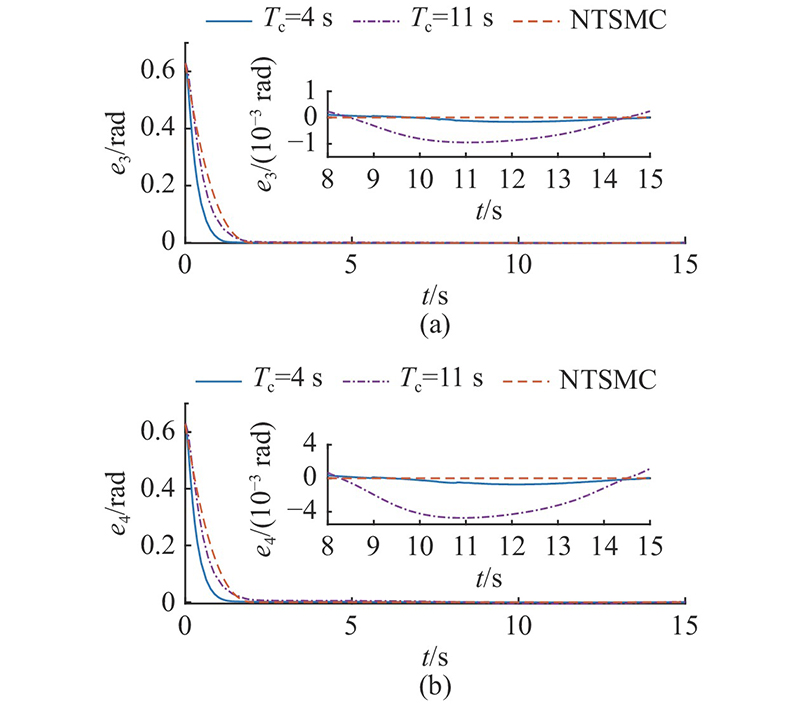
图 5 不同控制策略下的第1节机械臂姿态误差曲线
Fig.5 Attitude error curves of section 1 manipulator under different control strategies
图 6
图 6 不同控制策略下的第2节机械臂姿态误差曲线
Fig.6 Attitude error curves of section 2 manipulator under different control strategies
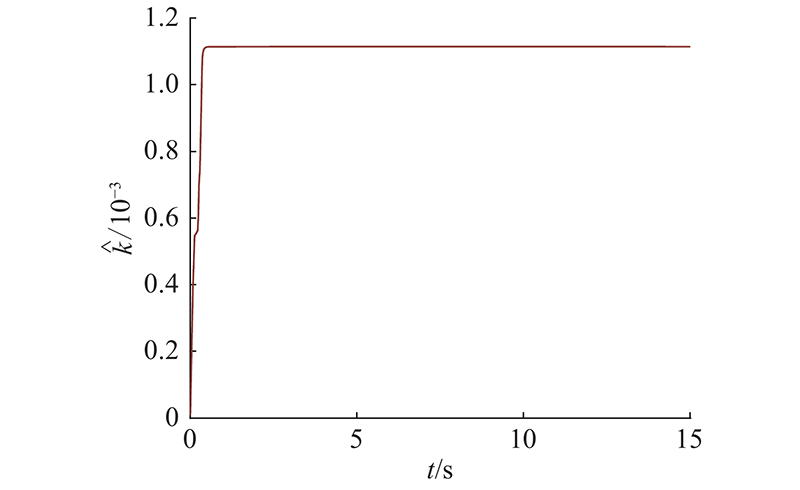
图 7
虽然姿态角在不同设定时间内均能有效收敛,但两者的控制性能是不同的. 定义控制能量消耗指标
式中:
经计算,当
4. 结 语
本研究针对受外界时变干扰且具有参数不确定性的多节线驱连续型空间机械臂系统的姿态稳定控制问题,设计了基于模糊补偿的预定时间控制器,使机械臂系统能够在预先设定的时间范围内到达稳定状态,且稳定时间与系统初始状态无关. 所设计的模糊估计器较好地抑制了总干扰对机械臂系统的不利影响. 本研究所提控制方法可以满足机械臂系统的快速收敛与较高精度控制要求,更贴合实际应用需求. 在工程应用中,为了高效运行被控系统,常需要在线调节控制参数以满足实际需求与应用,如何自适应调节系统控制参数是下一步计划开展的研究.
参考文献
On the guidance, navigation and control of in-orbit space robotic missions: a survey and prospective vision
[J].DOI:10.1016/j.actaastro.2021.03.029 [本文引用: 1]
Hybrid rigid-continuum dual-arm space robots: modeling, coupling analysis, and coordinated motion planning
[J].DOI:10.1016/j.ast.2021.106861 [本文引用: 1]
Active uncoiling and feeding of a continuum arm robot
[J].DOI:10.1016/j.rcim.2018.09.003
Coordinated control based on reinforcement learning for dual-arm continuum manipulators in space capture missions
[J].DOI:10.1061/(ASCE)AS.1943-5525.0001335 [本文引用: 1]
A decoupled sliding mode control for a continuum arm
[J].DOI:10.1080/01691864.2015.1035323 [本文引用: 1]
Robust control of continuum robots using Cosserat rod theory
[J].DOI:10.1016/j.mechmachtheory.2018.09.011 [本文引用: 1]
Multi-surface sliding mode control of continuum robots with mismatched uncertainties
[J].DOI:10.1007/s11012-019-01072-6 [本文引用: 1]
Kinematic control of continuum manipulators using a fuzzy model-based approach
[J].DOI:10.1109/TIE.2016.2554078 [本文引用: 1]
Adaptive fuzzy-based fault-tolerant control of a continuum robotic system for maxillary sinus surgery
[J].DOI:10.3390/app9122490 [本文引用: 1]
Finite-time attitude control for flexible spacecraft with unknown bounded disturbance
[J].DOI:10.1177/0142331214566223 [本文引用: 2]
Fixed-time attitude control for rigid spacecraft with actuator saturation and faults
[J].DOI:10.1109/TCST.2016.2519838 [本文引用: 1]
Attitude control of rigid spacecraft with predefined-time stability
[J].DOI:10.1016/j.jfranklin.2020.01.001 [本文引用: 1]
A class of predefined-time stable dynamical systems
[J].DOI:10.1093/imamci/dnx004 [本文引用: 2]