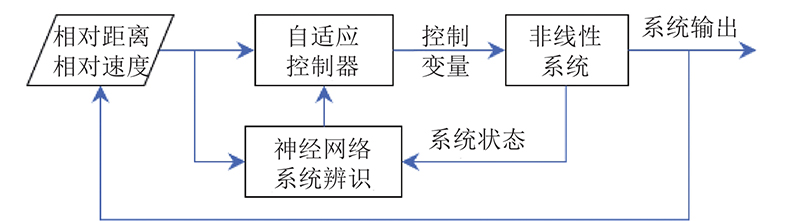
式中: ${ {\boldsymbol{Z}}} = {[{\bar {\boldsymbol{z}}},1]^{\rm{T}}} \in$ R n +1${{\boldsymbol{\bar z}}} = [{z_1},\cdots,{z_n}]$ ${{ {\boldsymbol{W}} }}\in$ R l +1${{\boldsymbol{V}}} \in$ R n ×l ${{\boldsymbol{W}}} = $ $ {[{w_{^1}},\cdots,{w_{l + 1}}]^{{\rm{T}}}},$ ${{\boldsymbol{V}}} = {[{{\boldsymbol{v}}_{^1}},\cdots,{{\boldsymbol{v}}_l}]}$ ${{{\boldsymbol{v}}}_j} = {[{v_{j1}},\cdots,{v_{jn}}]}^{{\rm{T}}}$ $j = 1, $ $ \cdots, l$ ${\boldsymbol{S}} = {[s({{\boldsymbol{v}}}_1^{{\rm{T}}}{{\boldsymbol{Z}}}),\cdots,s({{\boldsymbol{v}}}_l^{{\rm{T}}}{{\boldsymbol{Z}}}),1]^{{\rm{T}}}}$ $ s $
[1]
MAZAL L, PEREZ D, BEVILACQUA R, et al Spacecraft rendezvous by differential drag under uncertainties
[J]. Journal of Guidance, Control, and Dynamics , 2016 , 39 (8 ): 1721 - 1733
[本文引用: 1]
[2]
HE S, WANG J, LIN D Elliptical orbital spacecraft rendezvous without velocity measurement
[J]. Journal of Aerospace Engineering , 2016 , 29 (4 ): 04015084
[3]
BRENTARI M, URBINA S, ARZELIER D, et al A hybrid control framework for impulsive control of satellite rendezvous
[J]. IEEE Transactions on Control Systems Technology , 2019 , 27 (4 ): 1537 - 1551
[4]
ZANETTI R Optimal glideslope guidance for spacecraft rendezvous
[J]. AIAA Journal of Guidance, Control, and Dynamics , 2011 , 34 (5 ): 1593 - 1597
[本文引用: 1]
[5]
谭天乐. 航天器交会对接的模型预测与反演制导控制[J]. 控制与决策, 2019, 34(4): 793-798.
[本文引用: 1]
TAN Tian-le. Model predictive and inversive guidance and control for spacecraft rendezvous and docking [J]. Control and Decision , 2019, 34(4): 793-798.
[本文引用: 1]
[7]
胡勇, 徐李佳, 解永春. 针对失控翻滚目标航天器的交会对接控制[J]. 宇航学报, 2015, 36(1): 47-57.
[本文引用: 1]
HU Yong, XU Li-jia, XIE Yong-chun. Control for rendezvous and docking with a tumbling target spacecraft [J]. Journal of Astronautics , 2015, 36(1): 47-57.
[本文引用: 1]
[8]
靳锴, 罗建军, 郑茂章, 等 考虑导航误差和摄动影响的椭圆轨道最优交会制导
[J]. 控制理论与应用 , 2018 , 35 (10 ): 1484 - 1493
[本文引用: 1]
JIN Kai, LUO Jian-jun, ZHENG Mao-zhang, et al Guidance design with navigation errors for relative motion in noncircular perturbed orbits
[J]. Control Theory and Application , 2018 , 35 (10 ): 1484 - 1493
[本文引用: 1]
[9]
ZHANG K, DEMETRIOU M A. Synthesis of adaptive controllers for spacecraft rendezvous maneuvers using nonlinear models of relative motion [C]// Proceedings of the IEEE Conference on Decision and Control . Las Vegas: IEEE, 2016: 12-14.
[本文引用: 1]
[10]
ZHANG K, DEMETRIOU M A. Adaptive controllers for spacecraft rendezvous based on nonlinear model with unknown parameters [C]// Proceedings of AIAA Guidance, Navigation, and Control Conference . Grapevine: AIAA, 2017: 9-13.
[本文引用: 1]
[11]
KALUR A, SHIVAKUMAR K, SCHMID M, et al. Adaptive control for spacecraft formation flying with solar radiation pressure and reduction of secular drift [C]// Proceedings of the American Control Conference . Boston: [s. n. ], 2016: 6-8.
[本文引用: 1]
[12]
IMANI A, BEIGZADEH B Robust control of spacecraft rendezvous on elliptical orbits: optimal sliding mode and backstepping sliding mode approaches
[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering , 2016 , 230 (10 ): 1975 - 1989
[本文引用: 1]
[13]
INNOCENTI M, TARTAGLIA V. Game theoretic strategies for spacecraft rendezvous and motion synchronization [C]//Proceedings of AIAA Guidance, Navigation, and Control Conference . San Diego: AIAA, 2016: 4-8.
[本文引用: 1]
[14]
ZHANG G, YE D Optimal short-range rendezvous using on–off constant thrust
[J]. Aerospace Science and Technology , 2017 , 69 : 209 - 217
[本文引用: 1]
[15]
FARRELL J A, POLYCARPOU M M. Adaptive approximation based control: unifying neural, fuzzy and traditional adaptive approximation approaches [M]. New York: Wiley, 2006: 46-48.
[本文引用: 1]
[16]
ROVITHAKIS G A, CHRISTODOULOU M A. Adaptive control with recurrent high-order neural networks: theory and industrial applications [M]. [S. l. ]: Springer, 2012: 9-27.
[17]
GE S, HANG C, LEE T, et al. Stable adaptive neural network control [M]. New York: Springer, 2013: 27-46.
[本文引用: 1]
[18]
SPOONER J, MAGGIORE M, ORDONEZ R, et al. Stable adaptive control and estimation for nonlinear systems: neural and fuzzy approximator techniques [M]. New York: Wiley, 2002: 6-10.
[本文引用: 1]
[19]
ALFRIEND K, VADALI R, GURFIL P, et al. Spacecraft formation flying: dynamics, control and navigation [M]. Oxford: Butterworth-Heinemann, 2009: 60-64.
[本文引用: 2]
[20]
CURTIS H D. Orbital mechanics for engineering students [M]. Oxford: Butterworth-Heinemann, 2013: 66-72.
[本文引用: 1]
[21]
KAPLAN M H. Modern spacecraft dynamics and control [M]. [S. l. ]: Wiley, 1976.
[本文引用: 1]
[22]
ZHANG T, GE S S, HANG C C Adaptive neural network control for strict-feedback nonlinear systems using backstepping design
[J]. Automatica , 2000 , 36 (12 ): 1835 - 1846
[本文引用: 1]
[23]
LEWIS F L, YESILDIREK A, LIU K Multilayer neural-net robot controller with guaranteed tracking performance
[J]. IEEE Transactions on Neural Networks , 1996 , 7 (2 ): 388 - 399
[本文引用: 2]
[24]
WANG D, HUANG J Adaptive neural network control for a class of uncertain nonlinear systems in pure-feedback form
[J]. Automatica , 2002 , 38 (8 ): 1365 - 1372
[本文引用: 1]
[25]
HORN R A, JOHNSON C R. Matrix analysis [M]. 2nd ed. Cambridge: Cambridge University Press, 2013.
[本文引用: 1]
[26]
KRSTIC M, KANELLAKOPOULOS I, KOKOTOVIC P V. Nonlinear and adaptive control design [M]. New York: Wiley, 1995: 99-110.
[本文引用: 2]
[27]
CORLESS M, LEITMANN G Continuous state feedback guaranteeing uniform ultimate boundedness for uncertain dynamic systems
[J]. IEEE Transactions on Automatic Control , 1981 , 26 (5 ): 1139 - 1144
[本文引用: 1]
Spacecraft rendezvous by differential drag under uncertainties
1
2016
... 航天器相对运动的线性模型结构简洁,基于线性模型提出的交会对接控制方法有很多[1 -4 ] . 例如,谭天乐[5 ] 利用状态模型预测与反演控制方法,基于线性离散系统模型,实现了航天器柔顺平滑的高精度交会对接. 李蒙等[6 ] 通过初值计算和精确迭代求解变轨策略,利用变轨控制实现航天器远程自主交会. 胡勇等[7 ] 基于特征模型控制方法,设计相对位置跟踪控制器及姿态同步控制器,实现了针对慢速翻滚目标的末段精确交会对接. 靳锴等[8 ] 采用状态转移矩阵求解方法建立导航误差模型,探究在外部扰动下的航天器交会制导最优解. 总的来说,采用相对运动线性模型能够使控制设计变得简单,但使其应用范围受到了局限. ...
Elliptical orbital spacecraft rendezvous without velocity measurement
0
2016
A hybrid control framework for impulsive control of satellite rendezvous
0
2019
Optimal glideslope guidance for spacecraft rendezvous
1
2011
... 航天器相对运动的线性模型结构简洁,基于线性模型提出的交会对接控制方法有很多[1 -4 ] . 例如,谭天乐[5 ] 利用状态模型预测与反演控制方法,基于线性离散系统模型,实现了航天器柔顺平滑的高精度交会对接. 李蒙等[6 ] 通过初值计算和精确迭代求解变轨策略,利用变轨控制实现航天器远程自主交会. 胡勇等[7 ] 基于特征模型控制方法,设计相对位置跟踪控制器及姿态同步控制器,实现了针对慢速翻滚目标的末段精确交会对接. 靳锴等[8 ] 采用状态转移矩阵求解方法建立导航误差模型,探究在外部扰动下的航天器交会制导最优解. 总的来说,采用相对运动线性模型能够使控制设计变得简单,但使其应用范围受到了局限. ...
1
... 航天器相对运动的线性模型结构简洁,基于线性模型提出的交会对接控制方法有很多[1 -4 ] . 例如,谭天乐[5 ] 利用状态模型预测与反演控制方法,基于线性离散系统模型,实现了航天器柔顺平滑的高精度交会对接. 李蒙等[6 ] 通过初值计算和精确迭代求解变轨策略,利用变轨控制实现航天器远程自主交会. 胡勇等[7 ] 基于特征模型控制方法,设计相对位置跟踪控制器及姿态同步控制器,实现了针对慢速翻滚目标的末段精确交会对接. 靳锴等[8 ] 采用状态转移矩阵求解方法建立导航误差模型,探究在外部扰动下的航天器交会制导最优解. 总的来说,采用相对运动线性模型能够使控制设计变得简单,但使其应用范围受到了局限. ...
1
... 航天器相对运动的线性模型结构简洁,基于线性模型提出的交会对接控制方法有很多[1 -4 ] . 例如,谭天乐[5 ] 利用状态模型预测与反演控制方法,基于线性离散系统模型,实现了航天器柔顺平滑的高精度交会对接. 李蒙等[6 ] 通过初值计算和精确迭代求解变轨策略,利用变轨控制实现航天器远程自主交会. 胡勇等[7 ] 基于特征模型控制方法,设计相对位置跟踪控制器及姿态同步控制器,实现了针对慢速翻滚目标的末段精确交会对接. 靳锴等[8 ] 采用状态转移矩阵求解方法建立导航误差模型,探究在外部扰动下的航天器交会制导最优解. 总的来说,采用相对运动线性模型能够使控制设计变得简单,但使其应用范围受到了局限. ...
航天器远程自主交会方法设计与实现
1
2017
... 航天器相对运动的线性模型结构简洁,基于线性模型提出的交会对接控制方法有很多[1 -4 ] . 例如,谭天乐[5 ] 利用状态模型预测与反演控制方法,基于线性离散系统模型,实现了航天器柔顺平滑的高精度交会对接. 李蒙等[6 ] 通过初值计算和精确迭代求解变轨策略,利用变轨控制实现航天器远程自主交会. 胡勇等[7 ] 基于特征模型控制方法,设计相对位置跟踪控制器及姿态同步控制器,实现了针对慢速翻滚目标的末段精确交会对接. 靳锴等[8 ] 采用状态转移矩阵求解方法建立导航误差模型,探究在外部扰动下的航天器交会制导最优解. 总的来说,采用相对运动线性模型能够使控制设计变得简单,但使其应用范围受到了局限. ...
航天器远程自主交会方法设计与实现
1
2017
... 航天器相对运动的线性模型结构简洁,基于线性模型提出的交会对接控制方法有很多[1 -4 ] . 例如,谭天乐[5 ] 利用状态模型预测与反演控制方法,基于线性离散系统模型,实现了航天器柔顺平滑的高精度交会对接. 李蒙等[6 ] 通过初值计算和精确迭代求解变轨策略,利用变轨控制实现航天器远程自主交会. 胡勇等[7 ] 基于特征模型控制方法,设计相对位置跟踪控制器及姿态同步控制器,实现了针对慢速翻滚目标的末段精确交会对接. 靳锴等[8 ] 采用状态转移矩阵求解方法建立导航误差模型,探究在外部扰动下的航天器交会制导最优解. 总的来说,采用相对运动线性模型能够使控制设计变得简单,但使其应用范围受到了局限. ...
1
... 航天器相对运动的线性模型结构简洁,基于线性模型提出的交会对接控制方法有很多[1 -4 ] . 例如,谭天乐[5 ] 利用状态模型预测与反演控制方法,基于线性离散系统模型,实现了航天器柔顺平滑的高精度交会对接. 李蒙等[6 ] 通过初值计算和精确迭代求解变轨策略,利用变轨控制实现航天器远程自主交会. 胡勇等[7 ] 基于特征模型控制方法,设计相对位置跟踪控制器及姿态同步控制器,实现了针对慢速翻滚目标的末段精确交会对接. 靳锴等[8 ] 采用状态转移矩阵求解方法建立导航误差模型,探究在外部扰动下的航天器交会制导最优解. 总的来说,采用相对运动线性模型能够使控制设计变得简单,但使其应用范围受到了局限. ...
1
... 航天器相对运动的线性模型结构简洁,基于线性模型提出的交会对接控制方法有很多[1 -4 ] . 例如,谭天乐[5 ] 利用状态模型预测与反演控制方法,基于线性离散系统模型,实现了航天器柔顺平滑的高精度交会对接. 李蒙等[6 ] 通过初值计算和精确迭代求解变轨策略,利用变轨控制实现航天器远程自主交会. 胡勇等[7 ] 基于特征模型控制方法,设计相对位置跟踪控制器及姿态同步控制器,实现了针对慢速翻滚目标的末段精确交会对接. 靳锴等[8 ] 采用状态转移矩阵求解方法建立导航误差模型,探究在外部扰动下的航天器交会制导最优解. 总的来说,采用相对运动线性模型能够使控制设计变得简单,但使其应用范围受到了局限. ...
考虑导航误差和摄动影响的椭圆轨道最优交会制导
1
2018
... 航天器相对运动的线性模型结构简洁,基于线性模型提出的交会对接控制方法有很多[1 -4 ] . 例如,谭天乐[5 ] 利用状态模型预测与反演控制方法,基于线性离散系统模型,实现了航天器柔顺平滑的高精度交会对接. 李蒙等[6 ] 通过初值计算和精确迭代求解变轨策略,利用变轨控制实现航天器远程自主交会. 胡勇等[7 ] 基于特征模型控制方法,设计相对位置跟踪控制器及姿态同步控制器,实现了针对慢速翻滚目标的末段精确交会对接. 靳锴等[8 ] 采用状态转移矩阵求解方法建立导航误差模型,探究在外部扰动下的航天器交会制导最优解. 总的来说,采用相对运动线性模型能够使控制设计变得简单,但使其应用范围受到了局限. ...
考虑导航误差和摄动影响的椭圆轨道最优交会制导
1
2018
... 航天器相对运动的线性模型结构简洁,基于线性模型提出的交会对接控制方法有很多[1 -4 ] . 例如,谭天乐[5 ] 利用状态模型预测与反演控制方法,基于线性离散系统模型,实现了航天器柔顺平滑的高精度交会对接. 李蒙等[6 ] 通过初值计算和精确迭代求解变轨策略,利用变轨控制实现航天器远程自主交会. 胡勇等[7 ] 基于特征模型控制方法,设计相对位置跟踪控制器及姿态同步控制器,实现了针对慢速翻滚目标的末段精确交会对接. 靳锴等[8 ] 采用状态转移矩阵求解方法建立导航误差模型,探究在外部扰动下的航天器交会制导最优解. 总的来说,采用相对运动线性模型能够使控制设计变得简单,但使其应用范围受到了局限. ...
1
... 为了更精确地描述航天器之间的相对运动,Zhang等[9 -10 ] 采用非线性模型进行控制设计. Kalur等[11 ] 使用摄动方法校正引起非线性动力学项的初始条件,提出自适应控制律保持航天器编队飞行. Imani等[12 ] 基于滑模控制理论开发了2个鲁棒控制器,用于保证不确定性系统的鲁棒性和稳定性. Innocenti等[13 ] 将2个航天器之间的交会对接描述为非零和差分博弈问题,采用线性二次微分博弈方法计算反馈控制律. Zhang等[14 ] 利用优化方法,将航天器交会对接问题转换为非线性规划问题,实现最小燃料和时间的航天器交会对接机动. 针对非线性模型的不确定性而言,系统鲁棒性和稳定性一直是控制设计中的关键问题,对非线性系统采用自适应控制策略是有效的方法. 其中,自适应神经网络方法在非线性控制上得到了广泛应用[15 -18 ] . ...
1
... 为了更精确地描述航天器之间的相对运动,Zhang等[9 -10 ] 采用非线性模型进行控制设计. Kalur等[11 ] 使用摄动方法校正引起非线性动力学项的初始条件,提出自适应控制律保持航天器编队飞行. Imani等[12 ] 基于滑模控制理论开发了2个鲁棒控制器,用于保证不确定性系统的鲁棒性和稳定性. Innocenti等[13 ] 将2个航天器之间的交会对接描述为非零和差分博弈问题,采用线性二次微分博弈方法计算反馈控制律. Zhang等[14 ] 利用优化方法,将航天器交会对接问题转换为非线性规划问题,实现最小燃料和时间的航天器交会对接机动. 针对非线性模型的不确定性而言,系统鲁棒性和稳定性一直是控制设计中的关键问题,对非线性系统采用自适应控制策略是有效的方法. 其中,自适应神经网络方法在非线性控制上得到了广泛应用[15 -18 ] . ...
1
... 为了更精确地描述航天器之间的相对运动,Zhang等[9 -10 ] 采用非线性模型进行控制设计. Kalur等[11 ] 使用摄动方法校正引起非线性动力学项的初始条件,提出自适应控制律保持航天器编队飞行. Imani等[12 ] 基于滑模控制理论开发了2个鲁棒控制器,用于保证不确定性系统的鲁棒性和稳定性. Innocenti等[13 ] 将2个航天器之间的交会对接描述为非零和差分博弈问题,采用线性二次微分博弈方法计算反馈控制律. Zhang等[14 ] 利用优化方法,将航天器交会对接问题转换为非线性规划问题,实现最小燃料和时间的航天器交会对接机动. 针对非线性模型的不确定性而言,系统鲁棒性和稳定性一直是控制设计中的关键问题,对非线性系统采用自适应控制策略是有效的方法. 其中,自适应神经网络方法在非线性控制上得到了广泛应用[15 -18 ] . ...
Robust control of spacecraft rendezvous on elliptical orbits: optimal sliding mode and backstepping sliding mode approaches
1
2016
... 为了更精确地描述航天器之间的相对运动,Zhang等[9 -10 ] 采用非线性模型进行控制设计. Kalur等[11 ] 使用摄动方法校正引起非线性动力学项的初始条件,提出自适应控制律保持航天器编队飞行. Imani等[12 ] 基于滑模控制理论开发了2个鲁棒控制器,用于保证不确定性系统的鲁棒性和稳定性. Innocenti等[13 ] 将2个航天器之间的交会对接描述为非零和差分博弈问题,采用线性二次微分博弈方法计算反馈控制律. Zhang等[14 ] 利用优化方法,将航天器交会对接问题转换为非线性规划问题,实现最小燃料和时间的航天器交会对接机动. 针对非线性模型的不确定性而言,系统鲁棒性和稳定性一直是控制设计中的关键问题,对非线性系统采用自适应控制策略是有效的方法. 其中,自适应神经网络方法在非线性控制上得到了广泛应用[15 -18 ] . ...
1
... 为了更精确地描述航天器之间的相对运动,Zhang等[9 -10 ] 采用非线性模型进行控制设计. Kalur等[11 ] 使用摄动方法校正引起非线性动力学项的初始条件,提出自适应控制律保持航天器编队飞行. Imani等[12 ] 基于滑模控制理论开发了2个鲁棒控制器,用于保证不确定性系统的鲁棒性和稳定性. Innocenti等[13 ] 将2个航天器之间的交会对接描述为非零和差分博弈问题,采用线性二次微分博弈方法计算反馈控制律. Zhang等[14 ] 利用优化方法,将航天器交会对接问题转换为非线性规划问题,实现最小燃料和时间的航天器交会对接机动. 针对非线性模型的不确定性而言,系统鲁棒性和稳定性一直是控制设计中的关键问题,对非线性系统采用自适应控制策略是有效的方法. 其中,自适应神经网络方法在非线性控制上得到了广泛应用[15 -18 ] . ...
Optimal short-range rendezvous using on–off constant thrust
1
2017
... 为了更精确地描述航天器之间的相对运动,Zhang等[9 -10 ] 采用非线性模型进行控制设计. Kalur等[11 ] 使用摄动方法校正引起非线性动力学项的初始条件,提出自适应控制律保持航天器编队飞行. Imani等[12 ] 基于滑模控制理论开发了2个鲁棒控制器,用于保证不确定性系统的鲁棒性和稳定性. Innocenti等[13 ] 将2个航天器之间的交会对接描述为非零和差分博弈问题,采用线性二次微分博弈方法计算反馈控制律. Zhang等[14 ] 利用优化方法,将航天器交会对接问题转换为非线性规划问题,实现最小燃料和时间的航天器交会对接机动. 针对非线性模型的不确定性而言,系统鲁棒性和稳定性一直是控制设计中的关键问题,对非线性系统采用自适应控制策略是有效的方法. 其中,自适应神经网络方法在非线性控制上得到了广泛应用[15 -18 ] . ...
1
... 为了更精确地描述航天器之间的相对运动,Zhang等[9 -10 ] 采用非线性模型进行控制设计. Kalur等[11 ] 使用摄动方法校正引起非线性动力学项的初始条件,提出自适应控制律保持航天器编队飞行. Imani等[12 ] 基于滑模控制理论开发了2个鲁棒控制器,用于保证不确定性系统的鲁棒性和稳定性. Innocenti等[13 ] 将2个航天器之间的交会对接描述为非零和差分博弈问题,采用线性二次微分博弈方法计算反馈控制律. Zhang等[14 ] 利用优化方法,将航天器交会对接问题转换为非线性规划问题,实现最小燃料和时间的航天器交会对接机动. 针对非线性模型的不确定性而言,系统鲁棒性和稳定性一直是控制设计中的关键问题,对非线性系统采用自适应控制策略是有效的方法. 其中,自适应神经网络方法在非线性控制上得到了广泛应用[15 -18 ] . ...
1
... 神经网络近似方法由于具有良好的函数逼近能力,通常被用作在不确定性情况下对非线性函数建模. 假设连续函数 $ f(\bar z) $ $ f(\bar z) $ [17 ,22 -23 ] : ...
1
... 为了更精确地描述航天器之间的相对运动,Zhang等[9 -10 ] 采用非线性模型进行控制设计. Kalur等[11 ] 使用摄动方法校正引起非线性动力学项的初始条件,提出自适应控制律保持航天器编队飞行. Imani等[12 ] 基于滑模控制理论开发了2个鲁棒控制器,用于保证不确定性系统的鲁棒性和稳定性. Innocenti等[13 ] 将2个航天器之间的交会对接描述为非零和差分博弈问题,采用线性二次微分博弈方法计算反馈控制律. Zhang等[14 ] 利用优化方法,将航天器交会对接问题转换为非线性规划问题,实现最小燃料和时间的航天器交会对接机动. 针对非线性模型的不确定性而言,系统鲁棒性和稳定性一直是控制设计中的关键问题,对非线性系统采用自适应控制策略是有效的方法. 其中,自适应神经网络方法在非线性控制上得到了广泛应用[15 -18 ] . ...
2
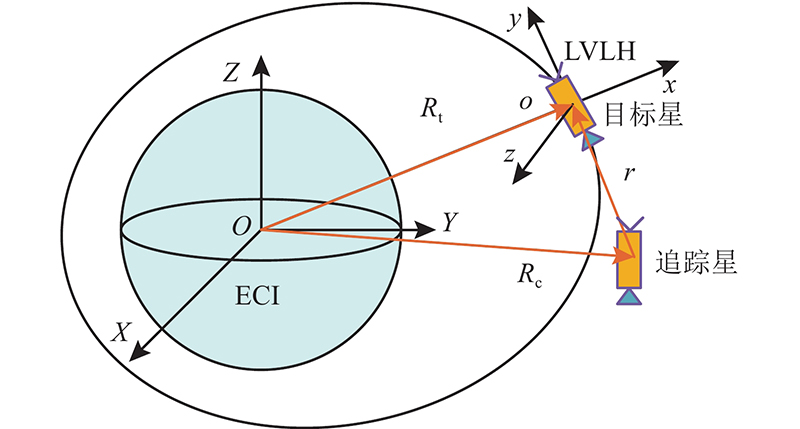
... 为了得到追踪星相对于目标星的运动方程,需要分析它们在惯性系中的相对运动,再转换为基于目标星LVLH的模型表达[19 -20 ] . 定义追踪星和目标星之间的相对距离 ${\boldsymbol{r}} = {{\boldsymbol{R}}_{\rm{c}}} - {{\boldsymbol{R}}_{\rm{t}}}$
... 针对航天器的交会对接任务,建立基于目标星LVLH坐标系下的相对运动模型. 令 ${\boldsymbol{r}} = [x,y,z]$ ${{\boldsymbol{R}}_{\rm{t}}} = [{r_{\rm{t}}},0,0]$ ${\boldsymbol{\omega}} _{\rm{E}}^{\rm{L}} = [0,0,{\dot \theta _{\rm{t}}}]$ ${\theta _{\rm{t}}}$ $ {\boldsymbol{r}} $ ${{\boldsymbol{R}}_{\rm{t}}}$ ${\boldsymbol{\omega}} _{\rm{E}}^{\rm{L}}$ [19 -21 ] : ...
1
... 为了得到追踪星相对于目标星的运动方程,需要分析它们在惯性系中的相对运动,再转换为基于目标星LVLH的模型表达[19 -20 ] . 定义追踪星和目标星之间的相对距离 ${\boldsymbol{r}} = {{\boldsymbol{R}}_{\rm{c}}} - {{\boldsymbol{R}}_{\rm{t}}}$
1
... 针对航天器的交会对接任务,建立基于目标星LVLH坐标系下的相对运动模型. 令 ${\boldsymbol{r}} = [x,y,z]$ ${{\boldsymbol{R}}_{\rm{t}}} = [{r_{\rm{t}}},0,0]$ ${\boldsymbol{\omega}} _{\rm{E}}^{\rm{L}} = [0,0,{\dot \theta _{\rm{t}}}]$ ${\theta _{\rm{t}}}$ $ {\boldsymbol{r}} $ ${{\boldsymbol{R}}_{\rm{t}}}$ ${\boldsymbol{\omega}} _{\rm{E}}^{\rm{L}}$ [19 -21 ] : ...
Adaptive neural network control for strict-feedback nonlinear systems using backstepping design
1
2000
... 神经网络近似方法由于具有良好的函数逼近能力,通常被用作在不确定性情况下对非线性函数建模. 假设连续函数 $ f(\bar z) $ $ f(\bar z) $ [17 ,22 -23 ] : ...
Multilayer neural-net robot controller with guaranteed tracking performance
2
1996
... 神经网络近似方法由于具有良好的函数逼近能力,通常被用作在不确定性情况下对非线性函数建模. 假设连续函数 $ f(\bar z) $ $ f(\bar z) $ [17 ,22 -23 ] : ...
... 引入变量 $\hat {\boldsymbol{W}}$ $\hat {\boldsymbol{V}}$ ${\boldsymbol{W}}$ ${\boldsymbol{V}}$ $\tilde {\boldsymbol{W}} = \hat {\boldsymbol{W}} - {\boldsymbol{W}}$ $\tilde {\boldsymbol{V}} = \hat {\boldsymbol{V}} - {\boldsymbol{V}}$ . 神经网络的估计误差满足以下关系式[23 -24 ] : ...
Adaptive neural network control for a class of uncertain nonlinear systems in pure-feedback form
1
2002
... 引入变量 $\hat {\boldsymbol{W}}$ $\hat {\boldsymbol{V}}$ ${\boldsymbol{W}}$ ${\boldsymbol{V}}$ $\tilde {\boldsymbol{W}} = \hat {\boldsymbol{W}} - {\boldsymbol{W}}$ $\tilde {\boldsymbol{V}} = \hat {\boldsymbol{V}} - {\boldsymbol{V}}$ . 神经网络的估计误差满足以下关系式[23 -24 ] : ...
1
... 其中下标 $ {\rm{F}} $ [25 ] . ...
2
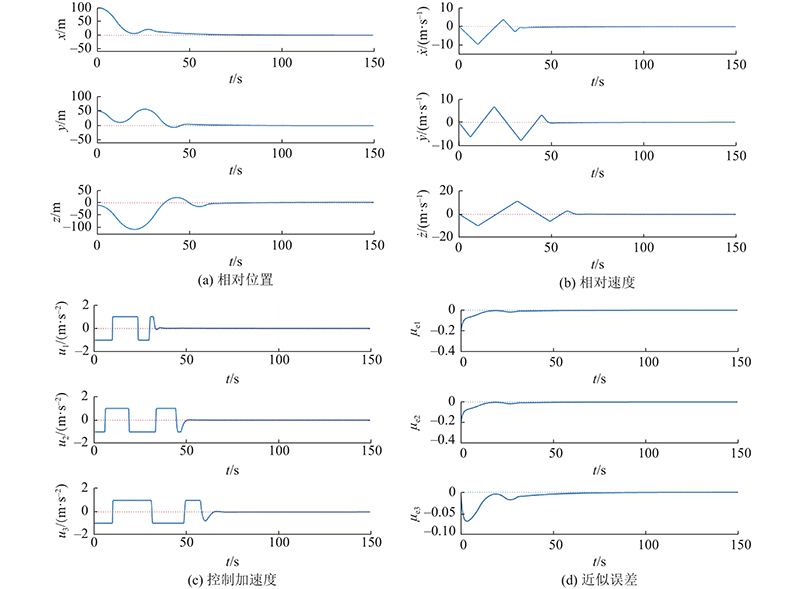
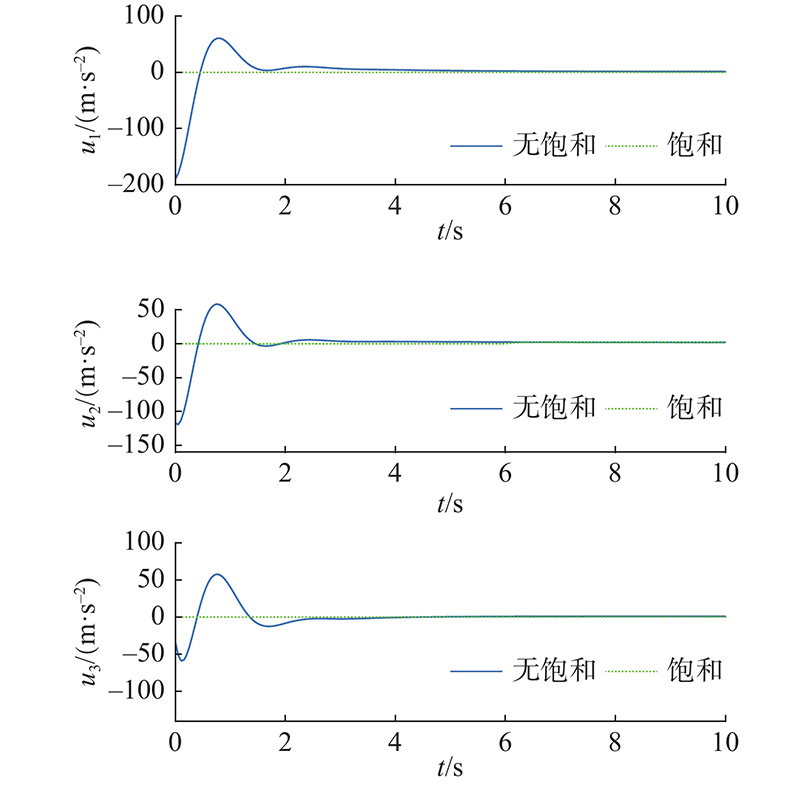
... 模型(4)中的不确定项来自于目标星的绕行参数 ${\dot \theta _{\rm{t}}}$ ${\ddot \theta _{\rm{t}}}$ ${r_{\rm{t}}}$ $ {d_i} $ [26 ] . 定义状态空间向量 $ [{x_1},{x_2},{x_3},{x_4},{x_5},{x_6}] $ $ = [x,y,z,\dot x,\dot y,\dot z] $
... 式中: $\lambda = \min \ \{ {k_i},{\varepsilon _i},{\gamma _{{\rm{w}}i}},{\gamma _{{\rm{v}}i}},{\lambda _{\min }}({{\boldsymbol{\varGamma}} _{{\rm{w}}i}}),{\lambda _{\min }}({{\boldsymbol{\varGamma}} _{{\rm{v}}i}})\}$ . 式(21)表明[26 ] ...
Continuous state feedback guaranteeing uniform ultimate boundedness for uncertain dynamic systems
1
1981
... 对于有界的初始条件,系统信号最终一致有界[27 ] ,且收敛到由 $ {a_{{\rm{v}}1}} $ $ {x_i} $