浙江大学学报(工学版)

浙江大学学报(工学版), 2021, 55(12): 2359-2364 doi: 10.3785/j.issn.1008-973X.2021.12.016

电子、通信与自动控制技术

基于微分跟踪器的共轴反桨无人机串级TD-PID控制算法

王思孝,, 赵文军, 张浩,, 高永, 李普森

1. 中国海洋大学 信息科学与工程学部，山东 青岛266100

2. 北京卫星导航中心，北京 100094

3. 青岛海洋科学与技术试点国家实验室，山东 青岛266100

Cascade TD-PID control algorithm for coaxial anti-propeller unmanned aerial vehicle based on tracking differentiator

WANG Si-xiao,, ZHAO Wen-jun, ZHANG Hao,, GAO Yong, LI Pu-sen

1. Faculty of Information Science and Engineering, Ocean University of China, Qingdao 266100, China

2. Beijing Satellite Navigation Center, Beijing 100094, China

3. Pilot National Laboratory for Marine Science and Technology, Qingdao 266100, China

通讯作者: 张浩，男，教授. orcid.org/0000-0002-6454-0239. E-mail： zhanghao@ouc.edu.cn

收稿日期: 2021-01-25  

基金资助: 国家自然科学基金资助项目（91938204，41527901，61701462）；山东省支持青岛海洋科学与技术试点国家实验室重大科技专项（2018SDKJ0210）；中央军委装备发展部装备预研领域基金重点项目（61404160502）

Received: 2021-01-25  

Fund supported: 国家自然科学基金资助项目（91938204，41527901，61701462）；山东省支持青岛海洋科学与技术试点国家实验室重大科技专项（2018SDKJ0210）；中央军委装备发展部装备预研领域基金重点项目（61404160502）

作者简介 About authors

王思孝（1995—），男，硕士生，从事海洋通信及无人飞行器研究.orcid.org/0000-0002-2779-5945.E-mail：wangsixiao1516@163.com , E-mail：wangsixiao1516@163.com

摘要

针对传统PID控制算法对共轴反桨无人机的欠驱动、强耦合非线性系统控制效果不理想的问题，提出基于微分跟踪器的串级TD-PID控制算法，以提高无人机飞行稳定性. 设计共轴反桨无人机飞行系统，针对无人机的姿态控制提出基于微分跟踪器的串级TD-PID控制算法：外环为传统PID算法，内环使用2个微分跟踪器，通过串级控制改善系统动态性能. 在Matlab/Simulink中搭建控制系统的仿真模型进行仿真试验. 仿真结果表明：相较于传统串级PID控制算法，所提控制算法超调量更小，系统稳定性有较大提高. 对比串级TD-PID控制算法与串级PID控制算法控制效果的飞行试验结果表明：所提控制算法能有效减少系统超调量，提升系统稳定性和抗干扰能力.

关键词： 共轴反桨 ; 无人机(UAV) ; 姿态控制 ; 微分跟踪器(TD) ; 串级TD-PID控制算法 ; 超调量

Abstract

A cascade TD-PID control algorithm based on the tracking differentiator was proposed to improve unmanned aerial vehicle (UAV) flight stability, in view of the problem that the traditional PID control algorithm was not ideal for the under-driven and highly coupled nonlinear system control effect of coaxial anti-propeller UAV. The coaxial anti-propeller UAV flight system was designed, and the cascade TD-PID control algorithm based on the tracking differentiator was proposed for the attitude control of the UAV. The outer loop was the traditional PID algorithm, and the inner loop used two tracking differentiators to improve the dynamic performance of the system through cascade control. The simulation model of the control system was set up in Matlab /Simulink for simulation testing. Simulation results show that compared with the traditional cascade PID control algorithm, the overtone of the proposed control algorithm is smaller , and the system stability is greatly improved. The control effect of cascade TD-PID control algorithm and cascade PID control algorithm was compared through flight test. Test results show that the proposed control algorithm can effectively reduce the system overtone, and improve system stability and anti-jamming ability.

Keywords： coaxial anti-propeller ; unmanned aerial vehicle (UAV) ; attitude control ; tracking differentiator(TD) ; cascade TD-PID control algorithm ; overtone

PDF (1149KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

王思孝, 赵文军, 张浩, 高永, 李普森. 基于微分跟踪器的共轴反桨无人机串级TD-PID控制算法. 浙江大学学报(工学版)[J], 2021, 55(12): 2359-2364 doi:10.3785/j.issn.1008-973X.2021.12.016

WANG Si-xiao, ZHAO Wen-jun, ZHANG Hao, GAO Yong, LI Pu-sen. Cascade TD-PID control algorithm for coaxial anti-propeller unmanned aerial vehicle based on tracking differentiator. Journal of Zhejiang University(Engineering Science)[J], 2021, 55(12): 2359-2364 doi:10.3785/j.issn.1008-973X.2021.12.016

无人机（unmanned aerial vehicle， UAV）的控制方法种类繁多，主要包括PID（ proportional integral derivative）控制、LQR（linear quadratic regulator）控制、反步控制、滑模控制、鲁棒控制等[1-5]. 国内外对无人机的研究工作多针对固定翼或多旋翼，对共轴反桨无人机的研究起步较晚，取得的研究成果包括：Teh等[6]基于卡尔曼滤波器和降阶的Luenberger观测器，设计研发小型共轴双旋翼无人机的控制系统；Husnic[7]提出基于新的有限时间收敛扰动观测器的分层控制器，以解决小型共轴旋翼式无人机在未知气动力作用下的路径跟踪问题；陈保国等[8]提出基于模糊控制的共轴飞行器姿态自稳算法；王长龙等[9]基于反步法设计鲁棒跟踪控制器，实现共轴旋翼无人机的姿态控制；陈汉等[10]针对共轴双旋翼飞行器的悬停控制提出滑模PID控制算法；Xu等[11]针对具有2个可倾转同轴转子的无人机机器人推导计算力矩控制器，实现双自由度倾转机构的多功能运动模式.

共轴反桨无人机的结构复杂度高、耦合性强，在飞行过程中是不稳定的系统[12-13]，外部环境也会干扰无人机的运行. 传统PID控制算法存在积分饱和、超调量过大以及微分作用对高频干扰过于敏感等问题[14-15]，很难实现对共轴反桨无人机的平稳控制，有必要设计适合应用于共轴反桨无人机的飞行控制算法以提高控制稳定性. 本研究基于共轴反桨无人机整体结构，设计飞行姿态控制系统，并提出基于微分跟踪器的串级TD-PID控制算法.

1. 无人机整体设计

1.1. 设计指标

如表1所示，在对共轴反桨无人机的设计中，无人机飞行质量、总体布局及姿态控制有明确的设计指标. 表中，mmax为最大飞行质量，meff为有效任务荷载，L为整机长度，R为无人机外径，Hmax为最大飞行高度，vmax为最大飞行速度，θmax为机头最大偏转角, θerr机头偏转时可允许最大角度抖动量.

表 1   共轴反桨无人机设计指标

Tab.1  Coaxial anti-propeller UAV design index

指标 指标值 指标 指标值
mmax/kg ≤15 Hmax/m 10
meff/kg 2 vmax/(m·s−1) 20
L/mm ≤1 200 θmax/(°) 俯仰/横滚：−15~15
偏航：−90~90
R/mm ≤160 θerr/(°) ±1

新窗口打开| 下载CSV


1.2. 飞行系统设计

共轴反桨无人机为竖直对称式结构，姿态控制结构分为共轴电机和舵机平台共2个部分，舵机平台采用两轴云台结构设计方案，共轴电机安装于舵机平台上，使用桨夹结构固定无人机旋翼. 共轴反桨无人机飞行结构如图1所示.

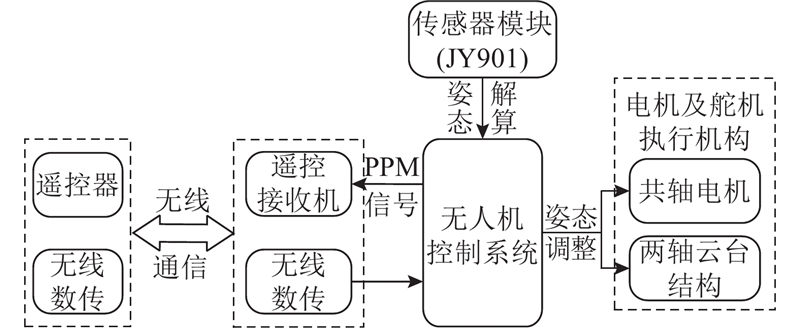
共轴反桨无人机系统采用模块化设计方案，包括主控制器模块、传感器模块、远程遥控模块、电机及舵机执行机构以及无线数据收发模块6部分. 无人机以微处理器STM32F407VGT6作为主控芯片，通过遥控设备及无线通信设备完成无人机的远程通信，实现人机交互，并通过传感器在动态环境下实时测算机体的运动姿态，由主控制器对电机及舵机执行机构进行实时控制，实现无人机的稳定飞行. 无人机系统控制框图如图2所示，图中，JY901为所选用传感器模块型号，PPM为脉位调制信号.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   共轴反桨无人机飞行结构

Fig.1   Coaxial anti-propeller UAV flight structure


图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   无人机系统控制框图

Fig.2   Control block diagram of UAV system


2. 串级TD-PID控制器设计

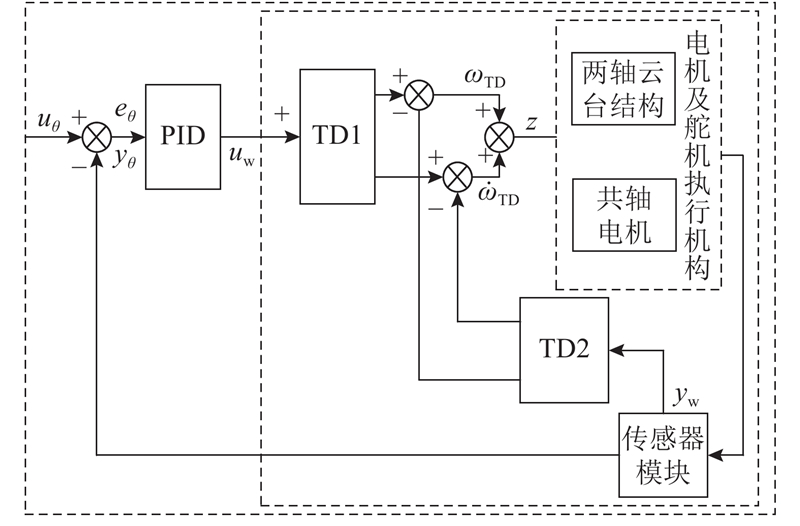
串级TD-PID控制算法是内外嵌套的双环结构，其中外环选用传统PID控制器实现对角度环的控制，内环选用微分跟踪器实现对角速度环的控制. 微分跟踪器视为具有滤波作用的PD控制器，既能对输入信号进行滤波，又能给出该信号的微分信号，有效抑制高频噪声，避免将其带入系统[16]. 这种控制器不仅通过串级控制克服进入副回路的二次扰动，提高系统控制质量，也可以发挥微分跟踪器的优势，抑制响应时的超调现象，改善系统的动态特性.

控制器的角度环以传统PID控制器实现，以遥控信号为期望值 ${u_\theta }(k)$，无人机系统中姿态传感器解算的姿态信息为反馈值 ${y_\theta }(k)$，控制偏差为

$ {e_\theta }\left( k \right) = {u_\theta }\left( k \right) - {y_\theta }\left( k \right). $

控制律为

$ {u_{\rm{w}}}\left( k \right) = {k_{{\rm{p}}\theta }}{e_\theta }\left( k \right) + {k_{{\rm{i}}\theta }}{e_{{\rm{i}}\theta }}\left( k \right) + {k_{{\rm{d}}\theta }}{e_{{\rm{d}}\theta }}\left( k \right), $

$ {e_{{\rm{i}}\theta }}\left( k \right) = \sum\limits_{j=1}^k {{e_\theta }} \left( j \right), $

$ {e_{{\rm{d}}\theta }}\left( k \right) = {e_\theta }\left( k \right) - {e_\theta }\left( {k - 1} \right). $

式中： ${u_{\rm{w}}}(k)$为角度环控制器的输出， ${e_{{\rm{i}}\theta }(k)} $、 ${e_{{\rm{d}}\theta }(k)} $分别为对控制偏差 ${e_{\theta }(k)} $的积分、微分计算结果， ${k_{{\rm{p}}\theta }}$为角度环的比例系数， ${k_{{\rm{i}}\theta }}$为角度环的积分系数， ${k_{{\rm{d}}\theta }}$为角度环的微分系数[17-18].

控制器的角速度环使用2个微分跟踪器实现对角速度的控制，微分跟踪器TD1的输入为角度环控制器的输出 ${u_{\rm{w}}}(k)$，微分跟踪器TD2作用于反馈通道，反馈通道输入为传感器解算出的实时角速度 ${y_{\rm{w}}}(k)$. 微分跟踪器TD1在控制目标时可以柔化指令姿态的变化，以免初始控制力太大产生超调，微分跟踪器TD2对传感器测得的角速度信号分别进行滤波、微分处理，以减小反馈所得的姿态信号和对应微分信号中的噪声. 角速度环的控制律为

$ z\left(k\right)={\omega }_{{\rm{TD}}}+{\stackrel{·}{\omega }}_{{\rm{TD}}}. $

式中： $z\left( k \right)$为角速度环输出， $ {\omega _{{\text{TD}}}} $、 ${\stackrel{·}{\omega }}_{{\rm{TD}}}$为微分跟踪器TD1经反馈通道后的输出.

微分跟踪器使用离散系统快速最优控制综合函数 ${F_{{\rm{fhan}}}}$，可以有效提取原始信号，消除在数字计算中产生的高频干扰，得到较好的微分信号[19]，其原理为

$ \left. \begin{gathered} {F_{{\rm{fh}}}} = {F_{{\rm{fhan}}}}\left( {{e_1}\left( {k - 1} \right) - {e_0}\left( k \right),{e_2}\left( {k - 1} \right),{r_0},{h_0}} \right), \hfill \\ {e_1}\left( k \right) = {e_1}\left( {k - 1} \right) + h{e_2}\left( {k - 1} \right), \hfill \\ {e_2}\left( k \right) = {e_2}\left( {k - 1} \right) + h {F_{{\rm{fh}}}}. \hfill \\ \end{gathered} \right\} $

式中： ${e_0}(k)$为输入信号，即微分跟踪器的目标值; ${e_1}(k)$、 ${e_2}(k)$均为微分跟踪器的输出信号，其中 ${e_1}(k)$为对 ${e_0}(k)$的跟踪信号， ${e_2}(k)$为对 ${e_0}(k)$的微分信号； ${r_0}$为决定跟踪速度的速度因子，值越大，跟踪速度越快； $h$、 ${h_0}$为数字控制器计算的积分步长，当 $h$与 ${h_0}$的值相同时，系统产生超调和震荡，当 ${h_0}$的取值较大时，可以有效减少震荡，因此 ${h_0}$也被称为滤波因子. 若将函数 ${F_{{\rm{fhan}}}}$的定义为

$ {F_{{\rm{fh}}}} = {F_{{\rm{fhan}}}}\left( {{x_1},{x_2},r,h} \right). $

则 ${F_{{\rm{fhan}}}}$的计算过程为

$ \left. \begin{gathered} d = rh,\,{a_0} = h{x_2},\,y = {x_1} + {a_0}, \hfill \\ {a_1} = \sqrt {d\left( {d + 8\left| y \right|} \right)} , \hfill \\ {a_2} = {a_0} + {\rm{sgn}}\,\left( y \right){{\left( {{a_1} - d} \right)} \mathord{\left/ {\vphantom {{\left( {{a_1} - d} \right)} 2}} \right. } 2}, \hfill \\ {S_y} = {{\left( {{\rm{sgn}}\,\left( {y + d} \right) - {\rm{sgn}}\,\left( {y - d} \right)} \right)} \mathord{\left/ {\vphantom {{\left( {{\rm{sgn}}\,\left( {y + d} \right) - {\rm{sgn}}\,\left( {y - d} \right)} \right)} 2}} \right. } 2}, \hfill \\ a = \left( {{a_0} + y} \right){S_y} + {a_2}\left( {1 - {S_y}} \right), \hfill \\ {S_a} = {{\left( {{\rm{sgn}}\,\left( {a + d} \right) - {\rm{sgn}}\,\left( {a - d} \right)} \right)} \mathord{\left/ {\vphantom {{\left( {{\rm{sgn}}\,\left( {a + d} \right) - {\rm{sgn}}\,\left( {a - d} \right)} \right)} {2,}}} \right. } {2,}} \hfill \\ {F_{{\rm{fh}}}} = - r\left( {{a \mathord{\left/ {\vphantom {a d}} \right. } d} - {{\rm{sgn}}}\, a} \right){S_a} - r{{\rm{sgn}}}\,a. \hfill \\ \end{gathered} \right\} $

式中： $ {x_1} $， $ {x_2} $分别为输入信号的跟踪信号、微分信号， $ a $、 $ {a_0} $、 $ {a_1} $、 $ {a_2} $、 $ {S_y} $、 $ {S_a} $及 $ y $均为中间变量. $r$值作为速度因子，在值增大时可以获得更好的跟踪效果，虽然在这个过程中会导致微分信号被噪声污染，但选取适当的 $h$值，可以起到良好的滤波效果，滤除微分信号 ${e_0}(k)$中的高频噪声[20].

共轴反桨无人机对于控制器的响应时间有较高要求，对微分跟踪器安排过渡过程会导致控制器的控制延时加大，因此在实际设计中放弃对微分跟踪器安排过渡过程，以微分跟踪器实现角速度环的非线性PD控制. 串级TD-PID控制器原理框图如图3所示.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   串级TD-PID控制器原理图

Fig.3   Schematic diagram of cascade TD-PID controller


3. 控制系统仿真

共轴反桨无人机有较复杂的机械传动结构和非线性、强耦合的动力学特性，很难建立精确的数学模型，因此本研究使用Matlab中的系统辨识工具箱辨识无人机的传递函数.

采集共轴反桨无人机飞行时各通道输入输出数据，将姿态调节中获取的角度数据导入Matlab中的系统辨识工具箱，得到无人机俯仰、滚转及偏航3个通道角度环的传递函数. 对于该共轴反桨无人机而言，舵机控制平台是由平行平面构成的两轴云台对称结构，在实现对无人机的俯仰通道及滚转通道的控制时，其传递函数一致. 所得角度环传递函数为

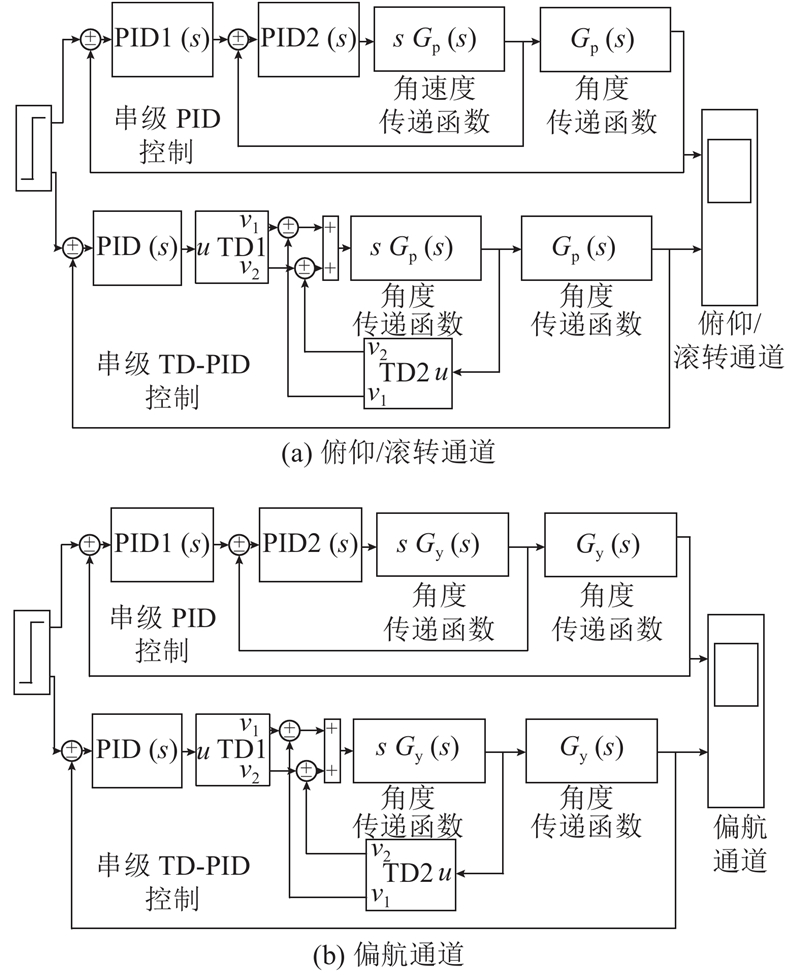
$ {G_{\rm{p}}}\left( s \right) = {G_{\rm{r}}}\left( s \right) = \frac{{ - 0.06s - 0.2}}{{{s^3} + 0.8{s^2} + 5.1s + 4.1}}, $

$ {G_{\rm{y}}}\left( s \right) = \frac{{ - 0.14s + 1.06}}{{{s^3} + 5.3{s^2} + 33.9s + 7}}. $

为了验证所提出的TD-PID算法的可行性，在Matlab/Simulink中以阶跃信号为输入信号，并将辨识所得到的传递函数导入已经搭建好的控制模型中，实现对共轴反桨无人机控制算法的建模仿真. 在Matlab/Simulink环境下2种控制算法的仿真模型如图4所示. 图中，u为微分跟踪器的目标值，v1和v2均为微分跟踪器的输出信号，其中v1是对u的跟踪信号，v2是对u的微分信号.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   Matlab/Simulink环境下2种控制算法的仿真模型

Fig.4   Simulation model of two control algorithms in Matlab/Simulink environment


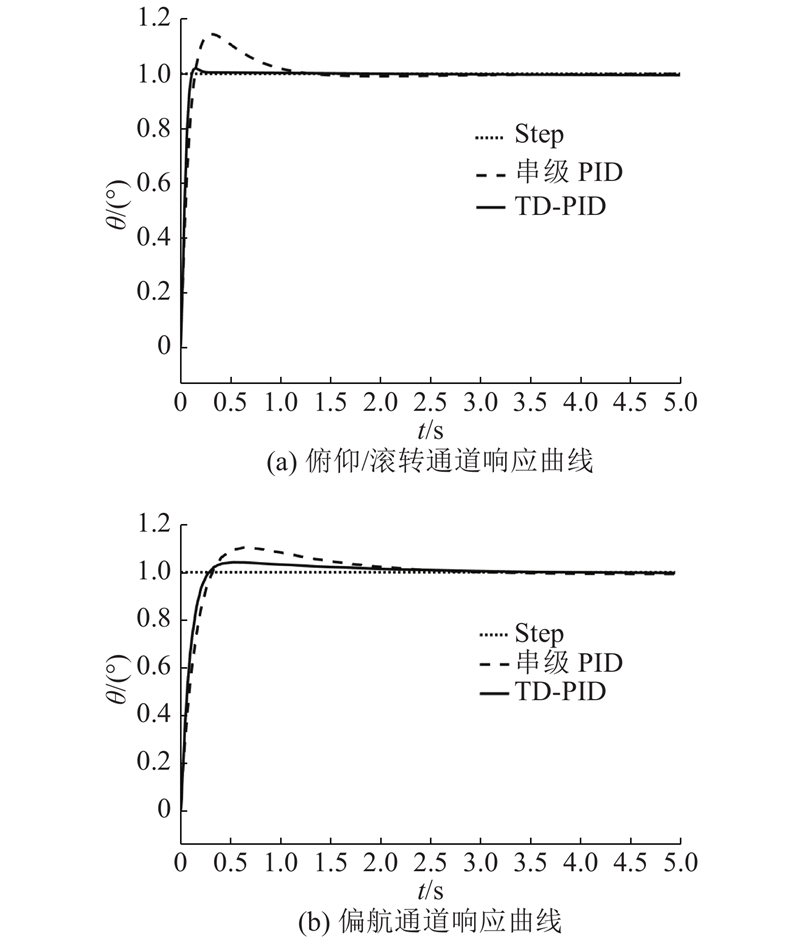
将串级TD-PID控制算法与传统串级PID控制算法的响应曲线进行对比，2种控制法的姿态跟踪仿真结果如图5所示. 图中，Step为0 s时阶跃值为1°的阶跃信号，t为仿真时间， ${\theta } $为仿真过程中的信号角度变化. 共轴反桨无人机的俯仰/滚转通道与偏航通道的结构设计方案不同，其控制方式也有一定区别. 俯仰/滚转通道的控制主要通过对两轴云台结构的倾转实现，偏航通道的控制是对共轴电机中上下2个电机的差速控制，因此对俯仰/滚转通道及偏航通道的控制将采用不同的控制参数，实际控制效果也有一定区别. 分析图5可得，与传统串级PID控制算法相比，串级TD-PID控制算法的系统响应速度更快，且超调量更小，其具体仿真结果对比如表2所示. 表中，Tr为响应时间，QO为超调量. 与传统串级PID控制算法相比，串级TD-PID控制算法在俯仰/滚转数与通道的控制中，控制系统响应时间缩短0.030 s，超调量降低3.9%；串级TD-PID控制算法在偏航通道的控制中，控制系统响应时间缩短0.065 s，超调量降低3.34%. 由此可见，串级TD-PID控制算法对共轴反桨无人机具有更好的控制效果.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   Matlab/Simulink环境下2种控制算法的仿真结果对比

Fig.5   Comparison of simulation results of two control algorithms in Matlab/Simulink environment


表 2   阶跃响应仿真结果对比

Tab.2  Comparison of step response simulation results

通道 控制算法 Tr QO/%
俯仰/滚转通道 串级PID 0.248 16.20
TD-PID 0.218 2.30
偏航通道 串级PID 0.321 10.20
TD-PID 0.265 6.86

新窗口打开| 下载CSV


4. 飞行试验

分别采用传统串级PID控制算法和串级TD-PID控制算法，对无人机进行姿态的实时控制，分析对比2种方法得到的试验数据.

试验前对串级TD-PID控制器进行参数整定，如表3所示. 表中，r01、r02分别表示微分跟踪器TD1、TD2的速度因子，h01、h1为微分跟踪器TD1计算的积分步长，h02、h2微分跟踪器TD2计算的积分步长。无人机飞行试验如图6所示. 分别使用2种算法进行实际飞行控制试验，在无人机飞行过程中，每20 ms进行一次数据采集，记录无人机飞行数据. 调用飞行日志，将无人机的飞行数据导入Matlab，描绘无人机在不同控制算法下各通道的角度变化，所得到的角度变化波形图如图7所示. 图中，T为飞行时间， $ {\textit{ϕ}}$为飞行过程中各通道的角度变化。

表 3   共轴反桨无人机串级TD-PID控制器参数表

Tab.3  Coaxial anti-propeller UAV cascade TD-PID controller parameter table

控制器 ${k_{{\rm{p}}\theta }} $ ${k_{{\rm{i}}\theta }} $ ${k_{{\rm{d}}\theta }} $ ${r_{01}}$ ${h_{01}}$ ${h_{1}}$ ${r_{02}}$ ${h_{02}}$ ${h_{2}}$
俯仰/滚转通道 4.5 0.012 0.010 550 0.032 0.002 200 0.020 0.002
偏航通道 3.0 0.009 0.015 550 0.015 0.001 200 0.013 0.001

新窗口打开| 下载CSV


图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6   无人机飞行示意图

Fig.6   Flight diagram of UAV


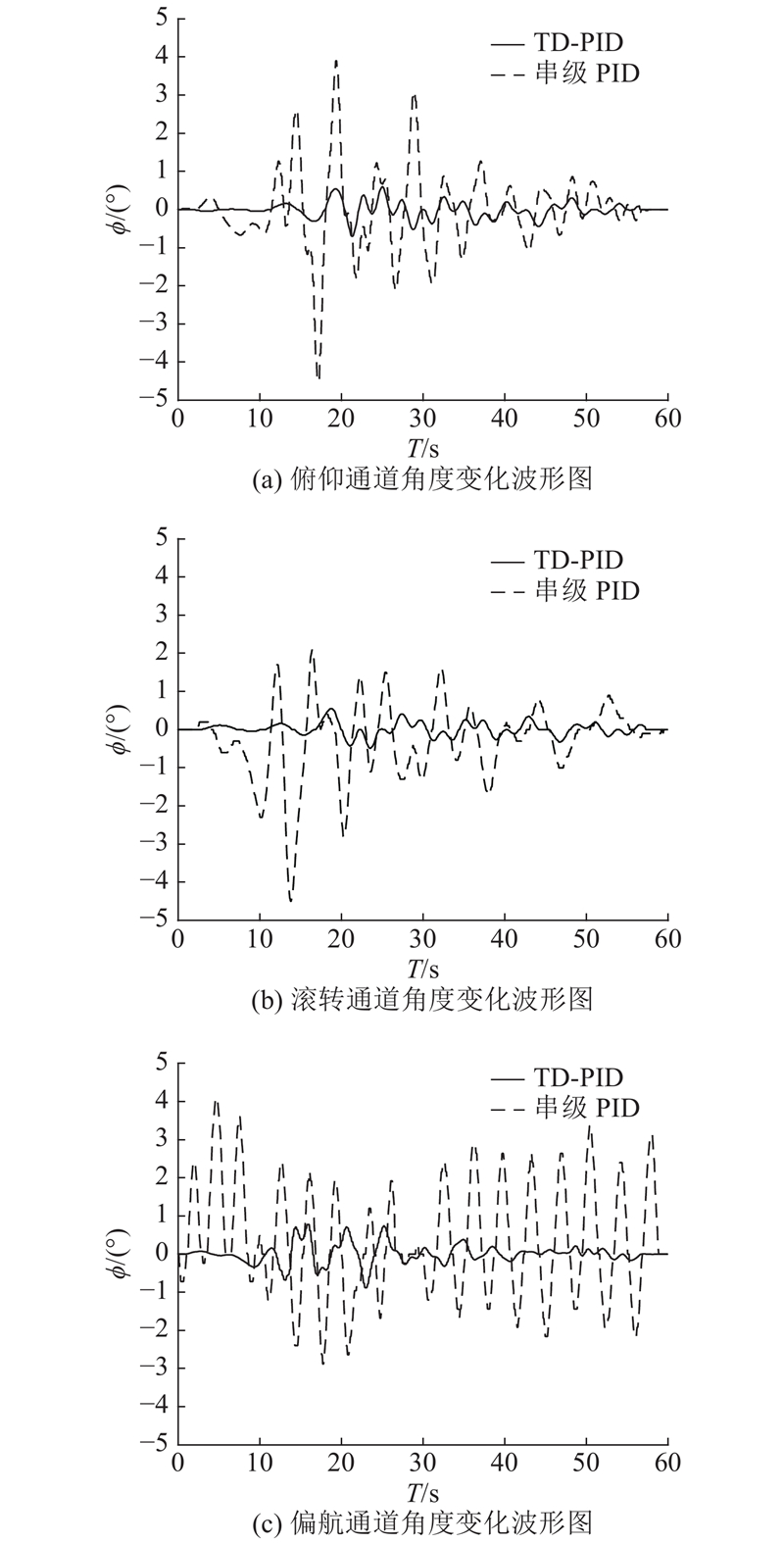
分析飞行试验数据可得，在串级TD-PID控制算法的控制下，共轴反桨无人机的整体飞行过程稳定. 由于飞行结构存在设计精度及外部环境扰动问题，无人机在飞行时会出现抖动现象. 结合图7分析，在使用串级PID控制算法时，无人机抖动明显、出现一定自旋现象，其中俯仰/滚转通道最大抖动角度控制误差超过4°，偏航通道角度控制误差为−3°~4°，且存在角度超过4°的连续抖动；在使用串级TD-PID控制算法时，无人机姿态角虽有小幅波动出现，但系统最大控制偏差小于0.90°，其中俯仰/滚转通道的角度抖动量最大为0.70°，偏航通道的角度抖动量最大为0.88°，其轻微抖动不影响飞行效果，整体飞行过程平稳，且满足设计指标中±1°的角度抖动量.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7   2种控制算法下飞行数据的波形对比

Fig.7   Waveform comparison of flight data under two control algorithms


5. 结　语

本研究提出基于微分跟踪器的串级TD-PID控制算法，对角速度环控制进行优化，减少系统的超调和震荡，实现共轴反桨无人机的稳定飞行. 通过仿真及飞行试验对比：串级TD-PID 控制算法的控制效果优于串级PID 控制算法，串级TD-PID控制器可实现姿态调节中系统响应时间和超调量之间的平衡，系统响应时间短，抗扰动能力强. 本研究仅使用离线辨识方法确定无人机传递函数，仿真试验未考虑时变性因素对无人机运行的影响. 本研究提出的串级TD-PID 控制算法，角度环使用传统PID控制器，其积分项易引起过饱和现象，下一步计划加入积分自适应因子优化角度环控制器，进一步提升系统稳态性能和抗扰动能力.

参考文献

王成, 杨杰, 姚辉, 等

四旋翼无人机飞行控制算法综述

[J]. 电光与控制, 2018, 25 (12): 53- 58

DOI:10.3969/j.issn.1671-637X.2018.12.012      [本文引用: 1]

WANG Cheng, YANG Jie, YAO Hui, et al

An overview of flight control algorithms for quadrotors

[J]. Electronics Optics and Control, 2018, 25 (12): 53- 58

DOI:10.3969/j.issn.1671-637X.2018.12.012      [本文引用: 1]

YUAN T, GUO G Y, DU B Y, et al

The adaptive sliding mode control using improved genetic algorithm tuning PID controller for the planetary rover

[J]. Aircraft Engineering and Aerospace Technology, 2021, 93 (1): 218- 226

DOI:10.1108/AEAT-05-2019-0096     

AHMAD F, KUMAR P, BHANDARI A, et al

Simulation of the quadcopter dynamics with LQR based control

[J]. Materials Today: Proceedings, 2020, 24: 326- 332

DOI:10.1016/j.matpr.2020.04.282     

杨雷恒, 李继广, 杨璐, 等

飞翼无人机机动飞行非线性反步控制律设计

[J]. 航空工程进展, 2020, 11 (5): 645- 650

URL    

YANG Lei-heng, LI Ji-guang, YANG Lu, et al

Design of nonlinear backstepping controller for flying wing UAV maneuvering flight

[J]. Advances in Aeronautical Science and Engineering, 2020, 11 (5): 645- 650

URL    

YANG S Y, HAN J, XIA L, et al

Adaptive robust servo constraint tracking control for an underactuated quadrotor UAV with mismatched uncertainties

[J]. ISA Transactions, 2020, 106: 12- 30

DOI:10.1016/j.isatra.2020.07.007      [本文引用: 1]

TEH S H, NASSIRHARAND A

Design of dual-range linear multivariable controllers for nonlinear systems with application to UAV control

[J]. Journal of Aerospace Engineering, 2014, 27 (2): 215- 224

DOI:10.1061/(ASCE)AS.1943-5525.0000233      [本文引用: 1]

HUSNIC Z. Micro coaxial helicopter controller design[D]. Philadelphia: Drexel University, 2015: 47-54.

[本文引用: 1]

陈保国, 史春景, 王磊, 等

基于模糊控制的共轴飞行器姿态自稳算法

[J]. 探测与控制学报, 2018, 40 (6): 37- 42

URL     [本文引用: 1]

CHEN Bao-guo, SHI Chun-jing, WANG Lei, et al

Coaxial aircraft auto-stabilization algorithm based on fuzzy control

[J]. Journal of Detection and Control, 2018, 40 (6): 37- 42

URL     [本文引用: 1]

王长龙, 武斌, 李永科, 等

共轴旋翼无人飞行器姿态控制

[J]. 装甲兵工程学院学报, 2019, 33 (1): 57- 62

DOI:10.3969/j.issn.1672-1497.2019.01.010      [本文引用: 1]

WANG Chang-long, WU Bin, LI Yong-ke, et al

Attitude control of coaxial-rotor unmanned aerial vehicle

[J]. Journal of Academy of Armored Force Engineering, 2019, 33 (1): 57- 62

DOI:10.3969/j.issn.1672-1497.2019.01.010      [本文引用: 1]

陈汉, 李科伟, 邓宏彬, 等

一种共轴双旋翼飞行器悬停控制联合仿真

[J]. 兵工学报, 2019, 40 (2): 303- 313

URL     [本文引用: 1]

CHEN Han, LI Ke-wei, DENG Hong-bin, et al

Hover control co-simulation of a coaxial dual-rotor aircraft

[J]. Acta Armamentarii, 2019, 40 (2): 303- 313

URL     [本文引用: 1]

XU X S, WATANABE K, NAGAI I

Feedback linearization control for a tandem rotor UAV robot equipped with two 2-DOF tiltable coaxial-rotors

[J]. Artificial Life and Robotics, 2021, 26: 259- 268

DOI:10.1007/s10015-020-00655-x      [本文引用: 1]

黄迅

一种新型串列式双旋翼飞行器

[J]. 机械工程师, 2019, (10): 96- 99

URL     [本文引用: 1]

HUANG Xun

A new type of tandem double-rotor copter

[J]. Mechanical Engineer, 2019, (10): 96- 99

URL     [本文引用: 1]

刘志军, 赵文艺, 魏亮, 等

共轴双旋翼结构在多旋翼无人机教学活动中的应用分析

[J]. 中国教育技术装备, 2018, (4): 30- 32

DOI:10.3969/j.issn.1671-489X.2018.04.030      [本文引用: 1]

LIU Zhi-jun, ZHAO Wen-yi, WEI Liang, et al

Analysis of coaxial double rotor structure of multi rotor UAV using in teaching activities

[J]. China Educational Technology and Equipment, 2018, (4): 30- 32

DOI:10.3969/j.issn.1671-489X.2018.04.030      [本文引用: 1]

周祖鹏, 甘良棋, 张晓东

带机械臂四旋翼飞行器的控制方法研究

[J]. 机械设计与制造, 2021, (2): 62- 66

URL     [本文引用: 1]

ZHOU Zu-peng, GAN Liang-qi, ZHANG Xiao-dong

Research on control method for a quadrotor with mechanical arm

[J]. Machinery Design and Manufacture, 2021, (2): 62- 66

URL     [本文引用: 1]

HAO C, ZHOU Q L

Research on fuzzy mathematics in PID control

[J]. Applied Mechanics and Materials, 2014, 608/609: 875- 879

DOI:10.4028/www.scientific.net/AMM.608-609.875      [本文引用: 1]

张海丽, 张宏立

微分跟踪器的研究与应用

[J]. 化工自动化及仪表, 2013, 40 (4): 474- 477

DOI:10.3969/j.issn.1000-3932.2013.04.012      [本文引用: 1]

ZHANG Hai-li, ZHANG Hong-li

Research and application of differential tracker

[J]. Control and Instruments in Chemical Industry, 2013, 40 (4): 474- 477

DOI:10.3969/j.issn.1000-3932.2013.04.012      [本文引用: 1]

白金凤, 金正焕, 金湜

基于PID控制的多用途无人机模拟器的设计

[J]. 数据通信, 2020, (6): 16- 18

DOI:10.3969/j.issn.1002-5057.2020.06.004      [本文引用: 1]

BAI Jin-feng, JIN Zheng-huan, JIN Shi

Design of a multi-purpose drone simulator based on PID control

[J]. Data Communications, 2020, (6): 16- 18

DOI:10.3969/j.issn.1002-5057.2020.06.004      [本文引用: 1]

NAJM A A, IBRAHEEM I K

Nonlinear PID controller design for a 6-DOF UAV quadrotor system

[J]. Engineering Science and Technology, an International Journal, 2019, 22 (4): 1087- 1097

DOI:10.1016/j.jestch.2019.02.005      [本文引用: 1]

WANG H W, WANG H P

A comparison study of advanced tracking differentiator design techniques

[J]. Procedia Engineering, 2015, 99: 1005- 1013

DOI:10.1016/j.proeng.2014.12.634      [本文引用: 1]

石嘉, 裴忠才, 唐志勇, 等. 改进型自抗扰四旋翼无人机控制系统设计与实现[J]. 北京航空航天大学学报, 2021, 47(9): 1823-1831.

[本文引用: 1]

SHI Jia, PEI Zhong-cai, TANG Zhi-yong, et al. Design and realization of an improved active disturbance rejection quadrotor control system [J]. Journal of Beijing University of Aeronautics and Astronautics: 2021, 47(9): 1823-1831.

[本文引用: 1]

/

〈 〉