现代有轨电车因为节能、环保、成本低廉等特性,受到越来越多城市的青睐. 截至2018年底,中国现代有轨电车线路长度总计406.2 km,规划中的总里程则达到7 000 km[1]. 作为未来城市轨道交通的重要组成部分,有轨电车轨道的运营维护任务也将日趋繁重. 与此同时,有轨电车线路本身的曲线半径小、坡度大、车辆启制动频繁,会加速轨道的损伤,进而影响线路轨道的使用寿命和运营安全[2]. 传统按计划的周期性检修方式的效率较低,容易造成维护资源的浪费. 使用基于激光位移传感器的非接触式轨道检测系统可以动态获取轨道几何参数,实时指导有轨电车线路的运营维护,能有效减轻运营维护的成本和人力. 在有轨电车不断发展的背景下,设计适用于有轨电车轨道的非接触式轨道检测系统具有重要的工程意义.
近年来基于激光位移传感器的非接触式检测技术被广泛应用于轨道检测系统中. Alippi等[3]提出使用激光视觉检测技术实现钢轨轮廓动态测量;Popov等[4]提出基于线性模型的激光位移传感器标定方法,并应用于轨道检测系统;Liu等[5]提出卡尔曼滤波和黑塞矩阵相结合的激光光条中心线快速提取方法,并使用基于特征点的轮廓匹配算法计算钢轨磨耗;Sun等[6-7]提出应用于激光视觉检测技术的运动偏差校正方法,减少了由于光平面不垂直轨道导致的测量误差;Li等[8]利用廓形中钢轨颚点和相邻的内线作为粗匹配特征,以此避免轨腰区域可能的异常数据影响;冯凯等[9]利用钢轨廓形的斜率切线值提取特征点,并通过特征点匹配和最近点迭代算法(iterative closest point,ICP)相结合的方式完成轮廓的精确匹配;陆英杰等[10]在特征点粗匹配的基础上,提出基于时间序列对应关系的精匹配方法,实现高精度廓形匹配;Yang等[11-12]采用激光位移传感器设计出钢轨轨距检测算法,实现钢轨轨距参数的动态检测;熊仕勇等[13]在基于轮廓特征点匹配的基础上,实现钢轨轨底坡参数的动态检测.
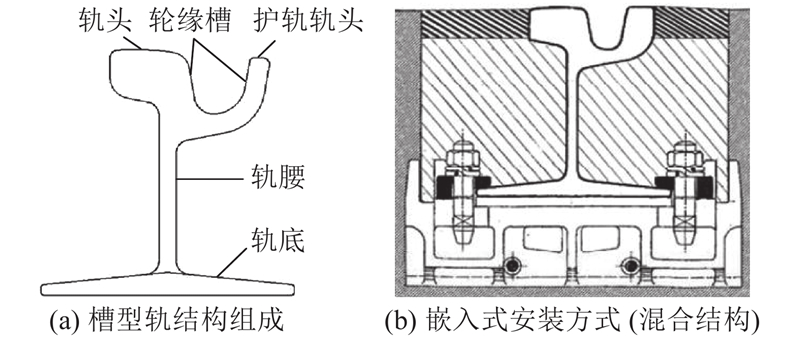
目前关于非接触式轨道检测系统的研究以工字轨轨道(如高铁轨道)为主. 考虑到路权共享和道路美观,有轨电车轨道多采用低地板车辆结构和嵌入式槽型轨轨道[14],目前针对槽型轨检测方法的研究较少. 槽型轨的结构和安装方式给检测工作带来很大的困难,其中最大的问题在于钢轨廓形匹配方法的不适用. 动态检测过程中,轨道几何参数检测系统会相对轨道产生多自由度的随机振动,采集到廓形数据后,须先用廓形匹配算法将数据归算到统一的测量坐标系中. 因此,如何完成实测轮廓与标准轮廓的高精度自动匹配,是轨道几何参数高精度动态检测面临的关键问题. 由于槽型轨的嵌入式安装方式,可获取的轮廓数据极少,传统工字轨检测方法中用于匹配的轨腰区域在有轨电车轨道中位于地面以下,无法直接测量. 同时,槽型轨的轮缘槽结构极易堆积异物,更增加了匹配算法的难度.
针对这一问题,本文重点研究槽型轨匹配基准区域的定位和分割方法:根据磨损规律和轨道结构特征,在可检测区段内定义匹配基准区域并设计基于距离和斜率特征值的区域自动分割方法. 设计与之相适应的两段式ICP匹配算法,利用初匹配完成匹配基准区域定位后,使用分割得到的匹配区段实现点云数据的精确匹配. 通过卡尔曼滤波器对匹配算法中的旋转平移参数进行跟踪预测,解决道岔处和存在表面异物等特殊情况的匹配问题. 通过实际线路实验检验该匹配算法在工程应用中的有效性和应用在轨距检测时的检测性能.
1. 检测系统原理
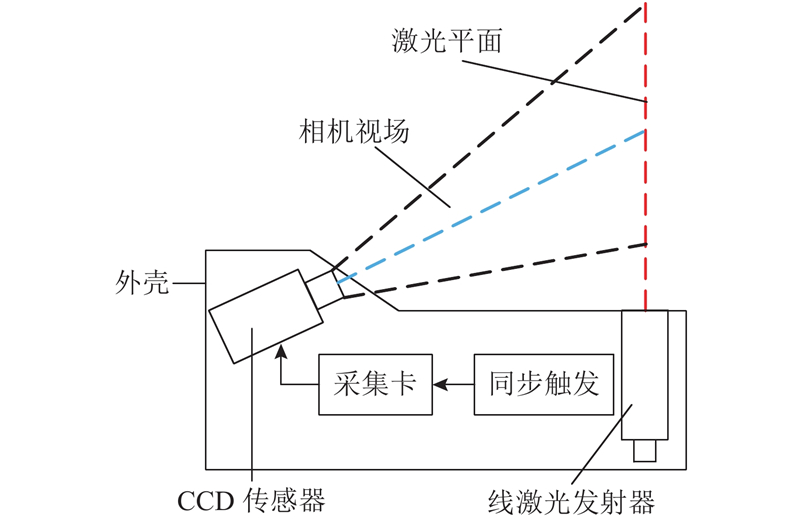
激光位移传感器因系统结构简单、检测速度快、实时处理能力强等优点,被广泛应用于长度、距离、三维形貌等工业检测中. 传感器由成固定几何关系的激光光源和CCD传感器封装而成,内部结构如图1所示.
图 1
图 1 激光位移传感器内部结构示意图
Fig.1 Schematic diagram of internal structure for laser displacement sensor
传感器采用激光三角检测原理,由光源发出的一束激光照射在待测物体平面上,并通过反射光线在CCD传感器上成像. 当物体表面的位置发生改变时,其所成的像在检测器上也发生相应的位移,由像移和实际位移的关系式即可知道真实物体的位移或形貌[15].
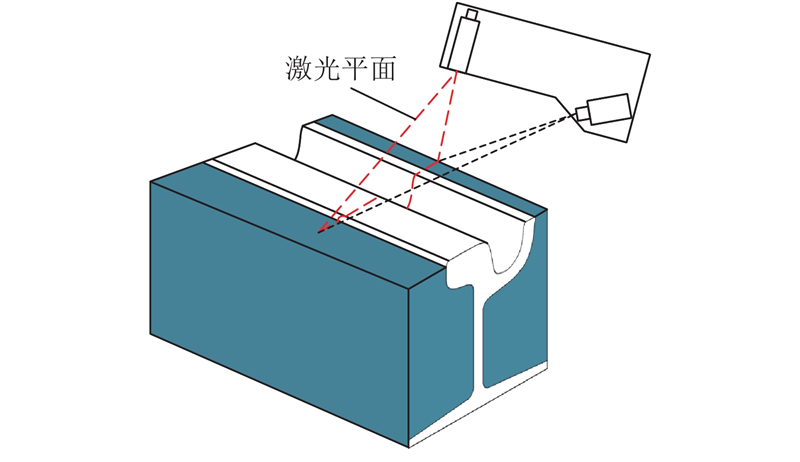
按照激光光源的类型不同可分为点、线性、面阵激光位移传感器. 综合考虑完整轮廓信息的采集要求和系统成本,在轨道轮廓检测中主要采用线性激光位移传感器. 检测时,线结构激光光源发出一道垂直于轨道方向的激光切面,轨道表面将形成一道包含轨道截面信息的激光光条,即为当前钢轨断面轮廓线,检测示意如图2所示. 使用与激光传感器成一定几何关系的CCD传感器采集光条,利用数字图像处理技术和三角测距原理即可得到断面轮廓在激光传感器坐标系中的数据坐标.
图 2
如图3所示,基于激光位移传感器的轨道几何参数检测系统的检测部分,本监测系统由2组激光位移传感器组成. 系统采用的传感器为ELAG公司的OPTIMESS激光位移传感器,传感器的激光Z轴可测范围为300 mm,线性度为量程的±0.1%,X轴方向起始范围130 mm,终止范围240 mm线性度为量程的±0.1%.
图 3
图 3 轨道几何参数检测系统结构简图
Fig.3 Track geometry parameter detection system structure diagram
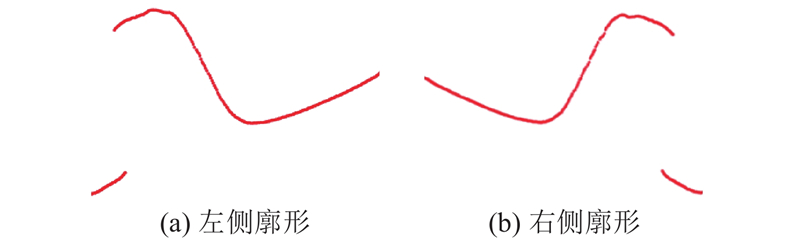
系统采用等距检测的工作方式,在轨检车运行过程中,编码器每隔25 cm触发一次检测系统. 获得的激光图像经过去噪、感兴趣区域分割和光条中心线提取等处理后,形成包含传感器坐标系下真实坐标的轮廓点云数据集,其中每帧轮廓图像可以得到1 280个云数据点,预处理后的实测图像如图4所示.
图 4
实时采集的轮廓点云数据,随检测系统车辆的不规则振动,在传感器坐标系中产生随机的偏移. 此时需要通过匹配算法,将点云坐标从激光传感器坐标系转换到轨道基准坐标系中,并与标准轮廓进行精确匹配,进而精确获取轨道几何参数计算所需要的特征点或者特征区域. 轮廓匹配的精度将直接影响几何参数检测的精度.
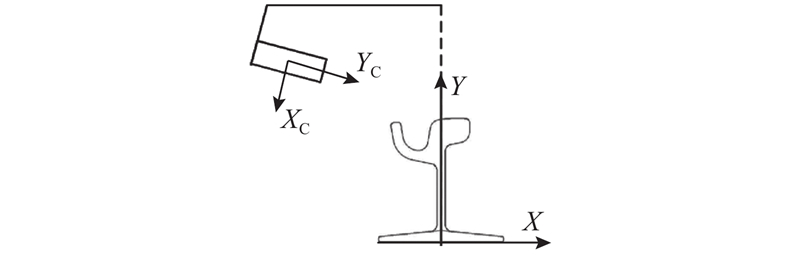
在钢轨断面平面内定义传感器坐标系和轨道基准坐标系,传感器坐标系以传感器水平方向为
图 5
图 5 传感器坐标系与轨道基准坐标系的相对位置
Fig.5 Relative positions of sensor coordinate system and orbital reference coordinate system
2个坐标系的转换通过旋转和平移参数实现. 传感器坐标系相对于基准坐标系的旋转角度为
旋转矩阵为
平移向量为
在静态下,通过系统固有几何参数可计算得到
2. 槽型轨匹配基准的选定
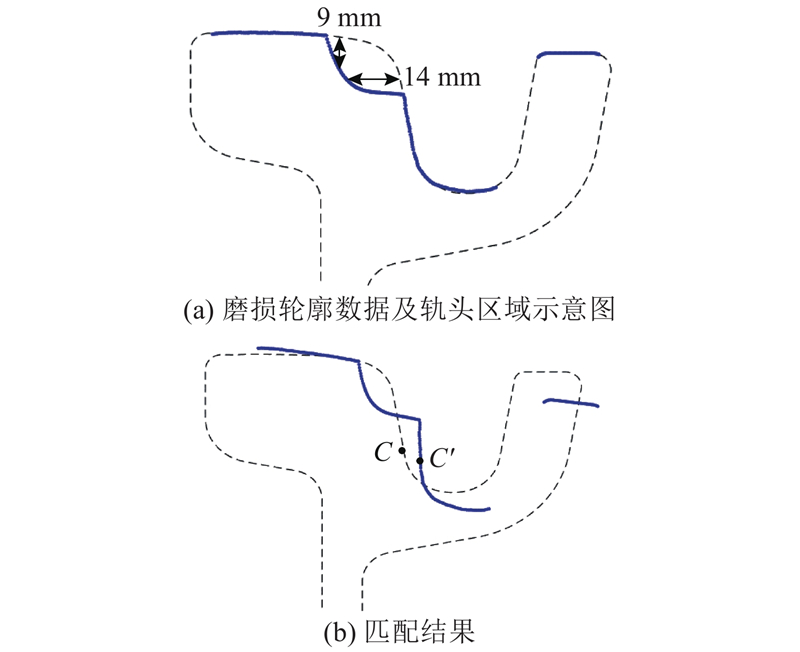
匹配算法通过实测轮廓中没有表面缺陷的区域或特征点同标准轮廓对应部分进行坐标计算,得到整体的旋转平移参数. 其中参与参数计算的实测轮廓部分或特征点称为匹配基准. 匹配基准应具备以下特征:1)在轮轨接触几何关系中,不与车轮直接接触,不易产生表面缺陷;2)区域表面光滑连续,结构不易堆积污渍;3)在实测轮廓中具有明显特征,容易与非匹配基准区域分割.
2.1. 理论分析
图 6
图 6 槽型轨结构及嵌入式安装方式
Fig.6 Structure of groove rail and installation of embedded groove rail
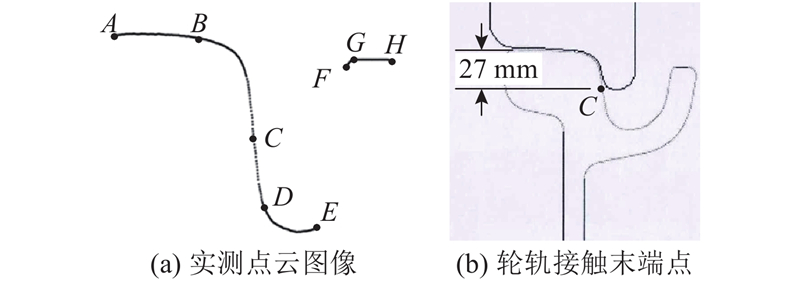
按照结构组成和几何特征可将实测轮廓细分为6段,如图7(a)所示. 图中,
图 7
2.2. 基准区域分割
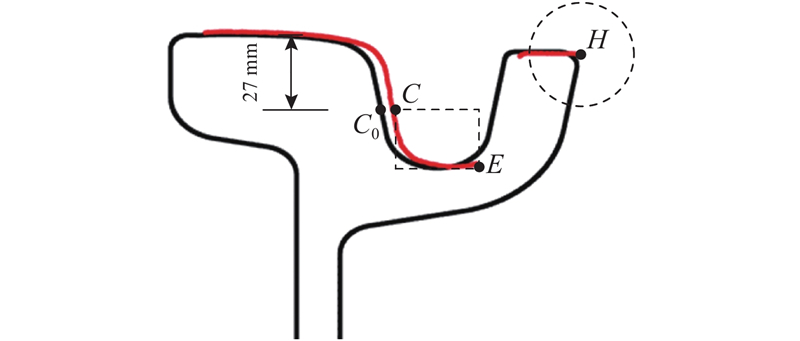
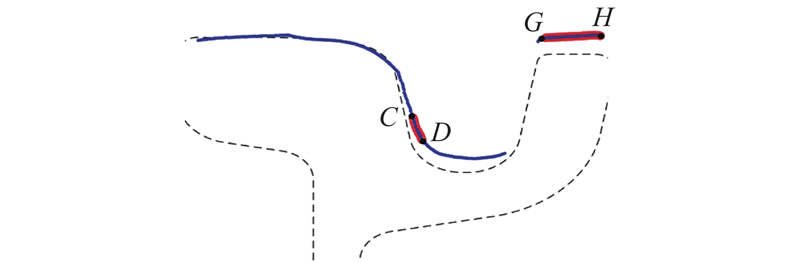
在匹配基准的2个区域中,
图 8
图 8 粗匹配结果及基准区域分割
Fig.8 Rough matching result and segmentation of reference area
如果
式中:
式中:
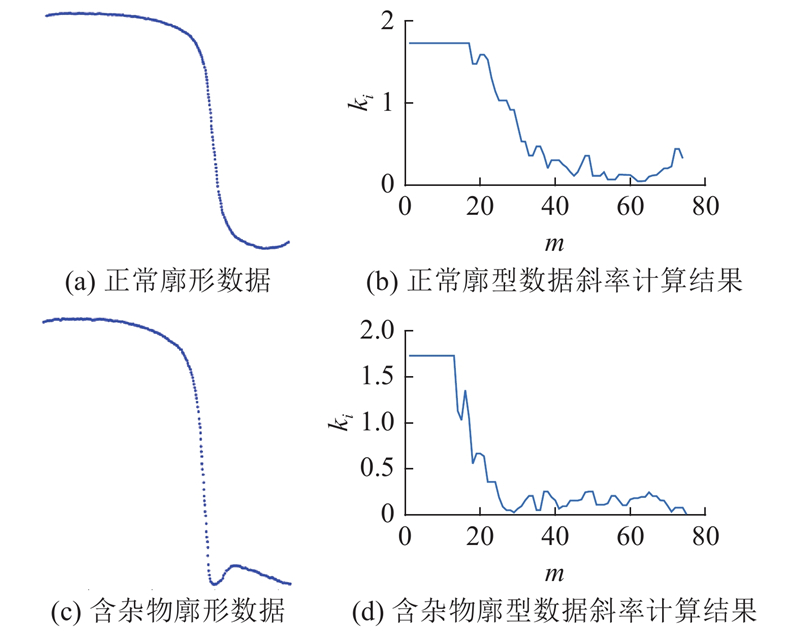
在计算斜率特征值时,考虑到计算速度和斜率可能不存在的问题,设定斜率
图 9
图 9 正常廓形与含杂物廓形的CE斜率曲线对比
Fig.9 Comparison of CE slope curves for normal profile and sundry profile
3. 廓形匹配
采用两段式ICP配准算法,既使用2次ICP算法分别实现粗配准和精配准. 算法思路如下. 1)粗配准:通过容易得到的轨头数据进行初次ICP配准(精度受轨头磨损程度的影响),得到大致匹配的廓形数据. 2)区域分割:对配准后的廓形数据,使用精准区域分割方法得到匹配基准区域. 3)精配准:对匹配基准数据使用改进的加权ICP算法进行精确匹配,得到最终结果.
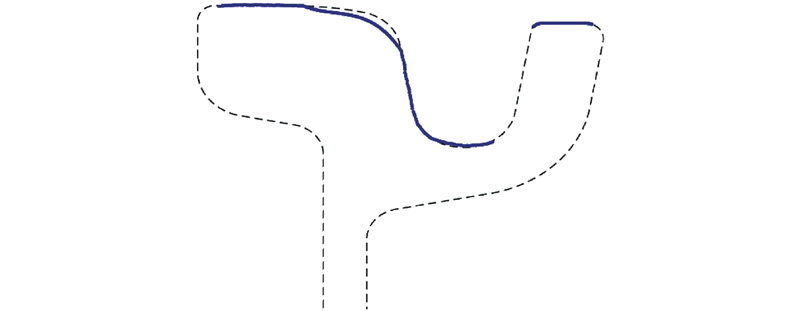
3.1. 粗配准的可行性分析
图 10
3.2. 两段式ICP匹配方法
3.2.1. 粗配准
提取实测轮廓原始数据中轨头数据端点
如果
式中:
式中:
3.2.2. 匹配基准区域分割
通过基准区域分割方法,获取
图 11
3.2.3. 精配准
分割得到的2段数据曲率变化值极小,近似于直线段,而且数据量较小. 改进ICP误差函数,增加以近似曲率特征值为刻度的计算权重,减少采集误差等噪声带来的干扰. 权重函数为
式中:
图 12
将基准区域数据
此时的初始值
图 13
3.3. 旋转平移参数的跟踪和预测
有轨电车运行线路中存在道岔或钢轨表面异物等特殊情况. 当上述情况获取的异常数据用于匹配时,会得到错误的旋转平移矩阵导致匹配错误. 采用卡尔曼滤波算法实现旋转平移参数的跟踪和预测,在不显著增加匹配时间的情况下,解决异常情况的处理问题,增强匹配算法的鲁棒性.
卡尔曼滤波算法的系统状态方程和测量方程可描述为
式中:
式中:
须跟踪和预测的参数为旋转平移参数
设置卡尔曼滤波算法状态向量的初始值为
4. 验 证
匹配算法是轨道检测中用于坐标系转换和特征点及特征区域定位的中间步骤,匹配误差受到多因素的影响,缺乏具体的衡量标准. 目前缺少针对槽型轨的匹配方法研究和可行的对比算法. 本文在匹配算法的基础上,采用文献[9]所述的多传感器坐标系统一标定方法和轨距计算方法计算线路轨距参数. 对建设中未开通运营的新线路进行重复检测,并与使用60R2槽型轨专用轨距仪的人工检测数据进行对比验证,通过验证结果反映匹配算法的性能.
轨道几何参数检测系统安装于检测车前端,安装位置如图14所示. 检测车的运行速度约30 km/h,激光传感器等间距采样,运行中每25 cm采集1次轮廓断面数据. 人工对比检测组在检测范围内选取参照点,使用轨检仪检测轨距数据,并依据公里标标记数据. 轨距动态检测结果如图15所示. 图中,
图 14
图 14 轨道几何参数检测系统安装位置
Fig.14 Installation position of track geometry parameter detection system
图 15
表 1 动态检测与人工检测实验结果对比
Tab.1
| | | | |
| K23+225 | 0.7 | 0.603 7 | −0.096 4 |
| K23+250 | 0.3 | 0.329 6 | 0.029 6 |
| K23+275 | −0.1 | −0.156 4 | −0.056 4 |
| K23+300 | 0.5 | 0.395 5 | −0.104 5 |
| K23+325 | −0.2 | −0.160 3 | 0.039 7 |
| K23+350 | 0.3 | 0.465 5 | 0.165 5 |
| K23+375 | −0.1 | −0.161 4 | −0.061 4 |
| K23+400 | −0.3 | −0.335 5 | −0.035 5 |
| K23+425 | 0.1 | 0.161 3 | 0.061 3 |
| K23+450 | 0.2 | 0.302 2 | 0.102 2 |
综合重复检测和检验对比结果,以本文算法为基础的轨距检测方法的平均误差的绝对值为0.075 2 mm. 相较于目前轨道检测行业中1 mm的精度要求,算法具有良好的精度性能. 考虑有轨电车的平均运行速度和工程应用的精度要求,算法的精度与速度能很好地满足有轨电车轨道动态检测的需要.
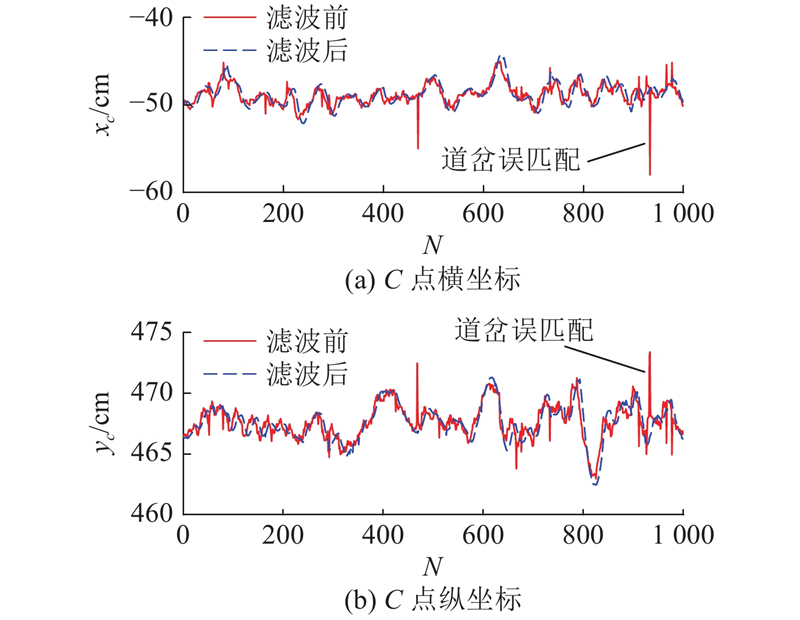
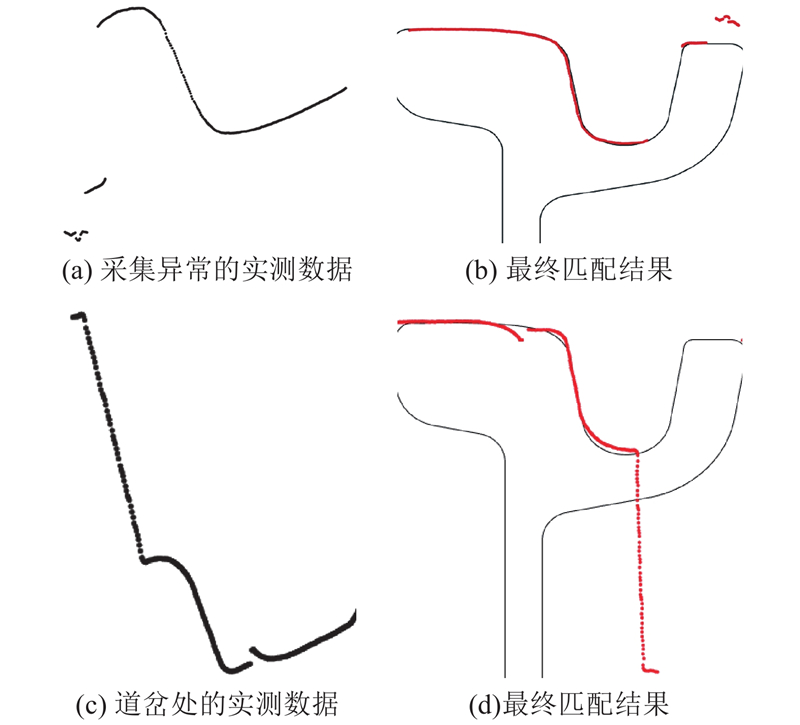
为了验证卡尔曼滤波算法的预测效果,选取实际运营线路中包含道岔部分的1 000帧连续数据用于算法匹配. 由于道岔处轨道形状复杂,检测数据中存在护轨和槽底数据缺失的情况,槽内杂物也将影响槽底数据的采集. 使用该算法不但可以有效避免误匹配的情况发生,还可以减少实测轮廓与标准轮廓的匹配误差.
图 16
图 16 轮轨接触末端点的卡尔曼滤波效果
Fig.16 Kalman filtering effect of wheel-rail contact end points
图 17
图 17 卡尔曼滤波在异常匹配时的修正效果
Fig.17 Correction effect of Kalman filter in abnormal matching
线路实验结果表明本文算法具有快速、高精度和高鲁棒性的特点. 在复杂的工程应用环境下,可靠性高. 当轨道槽内存在少量异物时,通过基于斜率特征值的分割方法动态地区分异物和有效数据. 当护轨区域受遮挡或经过道岔等特殊情况发生但不形成连续多帧异常数据时,通过卡尔曼滤波算法可对旋转平移矩阵进行修正.
当发生轨道槽内杂物过多或护轨区域遮挡过多并连续影响多帧数据的极端情况时,算法可能难以达到理想效果. 获取足够的匹配区域数据是本文算法的关键前提,如果检测时匹配基准区域受到杂物的干扰过大,出现连续多帧的误匹配时,将使基于卡尔曼滤波的修正方法出现较大的预测误差,结果将无法被正确修正.
因此本文方法适用于轨道槽内杂物较少、遮挡物零星分布的情况. 建议在使用本文方法检测前,先对电车轨道进行简单的清理,这样不仅可以保证算法的精度也可以更好地展现轨道的真实状态.
5. 结 论
(1)研究基于激光位移传感器的槽型轨轮廓匹配方法,该方法能有效检测有轨电车槽型轨的轨道几何参数.
(2)受实验硬件条件限制,选用轨距参数作为算法性能验证的对比参数. 轨距检测结果与人工检测数据对比分析显示,基于本文算法的轨距检测方法的平均误差的绝对值为0.075 2 mm,表明算法具有良好的精度性能.
(3)含道岔区域的廓形数据匹配实验验证算法中的卡尔曼滤波器对异常廓形误匹配的修正能力.
(4)本文算法对数据质量要求较高. 如何克服数据采集过程中产生的钢轨廓形数据噪声和缺损将是下一步的研究工作.
参考文献
2018年中国城市轨道交通运营线路统计和分析
[J].
Statistical analysis of urban rail transit lines in 2018 China
[J].
Composite real-time processing for railways track profile measurement
[J].DOI:10.1109/19.850395 [本文引用: 1]
Simple and fast rail wear measurement method based on structured light
[J].DOI:10.1016/j.optlaseng.2011.05.014 [本文引用: 1]
Motion deviation rectifying method of dynamically measuring rail wear based on multi-line structured-light vision
[J].
基于动态参考的钢轨轮廓失真校准方法
[J].DOI:10.3969/j.issn.1001-8360.2018.10.017 [本文引用: 1]
A distortion calibration method of rail profile based on dynamic reference
[J].DOI:10.3969/j.issn.1001-8360.2018.10.017 [本文引用: 1]
The outlier and integrity detection of rail profile based on profile registration
[J].DOI:10.1109/TITS.2019.2901633 [本文引用: 1]
钢轨轮廓全断面检测中的快速高鲁棒性匹配方法研究
[J].DOI:10.3969/j.issn.1001-8360.2019.05.020 [本文引用: 2]
Research on fast and robust matching algorithm in inspection of full cross-section rail profile
[J].DOI:10.3969/j.issn.1001-8360.2019.05.020 [本文引用: 2]
基于动态时间规整的钢轨轨廓匹配方法
[J].
A rail profile matching method based on dynamic time warping
[J].
基于最小二乘法曲线拟合的轨距参数测量方法
[J].DOI:10.3969/j.issn.1001-8360.2019.12.011 [本文引用: 1]
Track gauge measurement method based on least-square curve fitting theory
[J].DOI:10.3969/j.issn.1001-8360.2019.12.011 [本文引用: 1]
基于激光摄像式传感器的轨底坡动态检测方法研究
[J].
Dynamic detection method for rail cants based on laser camera transducers
[J].
现代有轨电车线路轨底坡对槽型轨磨耗的影响
[J].
Effect of rail cant on groove shaped rail wear in modern tram line
[J].
激光三角法综述
[J].
Survey on the Laser tri- angulation
[J].
槽型轨磨耗演变过程数值模拟
[J].DOI:10.3969/j.issn.1672-7029.2016.08.023 [本文引用: 1]
Numerical simulation of groove track wear evolution
[J].DOI:10.3969/j.issn.1672-7029.2016.08.023 [本文引用: 1]
槽型轨与车轮接触几何关系初步研究
[J].DOI:10.3969/j.issn.1002-7602.2006.12.001 [本文引用: 1]
Initial research on the geometrical relation of contact between channel rail and wheels
[J].DOI:10.3969/j.issn.1002-7602.2006.12.001 [本文引用: 1]