浙江大学学报(工学版)

浙江大学学报(工学版), 2021, 55(7): 1339-1350 doi: 10.3785/j.issn.1008-973X.2021.07.013

土木工程、水利工程

基于动态贝叶斯网络的TBM卡机风险预测

颉芳弟,, 翟强, 顾伟红,

兰州交通大学 土木工程学院，甘肃 兰州 730070

Risk prediction of TBM jamming based on dynamic Bayesian network

XIE Fang-di,, ZHAI Qiang, GU Wei-hong,

School of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China

通讯作者: 顾伟红，女，教授. orcid.org/0000-0003-2413-8824. E-maill： lzgwh@163.com

收稿日期: 2020-05-20  

基金资助: 国家自然科学基金资助项目（51668037）

Received: 2020-05-20  

Fund supported: 国家自然科学基金资助项目（51668037）

作者简介 About authors

颉芳弟（1994—），女，硕士生，从事隧道风险管理研究.orcid.org/0000-0002-1506-9700.E-mail：1220530047@qq.com , E-mail：1220530047@qq.com

摘要

为了预测隧道机械施工时隧道掘进机（TBM）卡机风险，基于动态贝叶斯网络（BN）分析卡机概率系统. 通过专家知识以及解释结构模型确定风险因素和风险事件的因果关系，收集国内隧道机械施工地质条件实测数据，根据相关规范、研究成果和云模型云间划分法对风险指标进行区间划分，运用粗糙集分类原理对数据进行离散化，获取风险因素的原始先验概率和风险事件的条件概率. 结合软件GENIE，建立动态BN模型预测卡机风险. 结果表明：在无证据条件下，TBM卡机风险概率为8%；造成TBM卡机的关键风险因素是岩石类型、大量的地下水和断裂破碎带. TBM卡机的关键致因链为岩石类型→掌子面突泥涌沙→卡刀盘→卡机，大量的地下水→掌子面突泥涌沙→卡刀盘→卡机，高地应力→软岩大变形→卡护盾→卡机，围岩坍塌→卡护盾→卡机.

关键词： 隧道掘进机(TBM) ; 卡机风险预测 ; 贝叶斯网络(BN) ; 粗糙集 ; 云模型

Abstract

A probability system of jamming was analyzed based on dynamic Bayesian network(BN), in order to predict the risk of tunnel boring machine (TBM) jamming during tunnel mechanical construction. Through expert knowledge and explanation structure model to determine the causal relationship between risk factors and risk events, collecting the measured data of domestic tunnel mechanical engineering geological conditions. The risk indicators were divided according to the relevant specifications, the research results and the cloud division method of cloud model into internal division. The rough set classification principle was applied to discretization of data to obtain the original prior probability of risk factors and the conditional probability of risk events. Combined GENIE software a dynamic BN model was established to predict the risk of card machines. Results show that the risk probability of TBM jamming is 8% under the condition of no evidence. The key risk factors of TBM jamming are rock type, large amount of groundwater and fracture zone. The key cause chain of TBM clamping machine is as follows: rock type → progradation of mud and sand on palm face → clamping knife plate → clamping machine, a large amount of groundwater → progradation of mud and sand on the palm surface → clamping knife plate → clamping machine, high ground stress → large deformation of soft rock → clamping shield → clamping machine, surrounding rock collapse → clamping shield → clamping machine.

Keywords： tunnel boring machine (TBM) ; risk prediction of jamming machine ; Bayesian network(BN) ; rough set ; cloud model

PDF (3775KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

颉芳弟, 翟强, 顾伟红. 基于动态贝叶斯网络的TBM卡机风险预测. 浙江大学学报(工学版)[J], 2021, 55(7): 1339-1350 doi:10.3785/j.issn.1008-973X.2021.07.013

XIE Fang-di, ZHAI Qiang, GU Wei-hong. Risk prediction of TBM jamming based on dynamic Bayesian network. Journal of Zhejiang University(Engineering Science)[J], 2021, 55(7): 1339-1350 doi:10.3785/j.issn.1008-973X.2021.07.013

近些年，因隧道掘进机（tunnel boring machine，TBM）施工工法在技术上可行，对环境的危害较小，被广泛应用于大型隧道施工中. 然而，TBM在不良地质掘进过程中，选型一旦确定就不便更改. 地质因素对TBM选型的影响更为复杂，从刀盘形式、推力、扭矩、支护系统及其他后配套系统均有较大的影响[1]. 如果在隧道掘进过程中遇到围岩坍塌、大量地下水突涌、涌沙等风险事件，将会造成巨大的经济损失和工期延误. 因此，建立TBM卡机模型防范主要风险，有利于施工企业对风险的控制以及安全管理工作.

Sousa[2]在2010年建立隧道施工可能出现的风险事故数据库.Abdelgawad等[3]结合地铁施工安全提出先验概率风险评估（probabilistic risk assessment, PRA）模型，描述风险事故的出现以及相关风险因素的概率分布，目的是识别关键风险因素和潜在风险事件，帮助项目工程师在施工阶段及时发出预警并采取弥补措施. 2012年，Sousa等[4]提出基于贝叶斯网络（Bayesian network，BN）的地质预测模型，结合TBM的掘进性能数据和BN模型很好地预测了掌子面前方的地质情况. 最传统的方法是故障树分析法（fault tree analysis, FTA）——一种能有效预测风险事件出现频率的概率评估方法[5-6]. 在2004年出版的《隧道风险管理指南》一文中，国际隧道协会（International Tunneling Association，ITA)将FTA高度推荐应用在隧道风险分析与评估中. 2015年，Hyun等[7]利用FTA和层次分析法识别TBM在不良地质情况下最有可能出现的风险事件，并在实际工程中得到较好的应用. 在国内，2013年，周宗青等[8]利用风险评估模型和风险规避方法规避了一次地质灾害. 2015年，佘诗刚等[9]列举TBM在隧道施工中的卡机案例并分析卡机原因和造成的后果，并指出研究TBM地质适应性将是未来的重大课题. 2017年，陈发达等[10]应用BN对盾构隧道施工中刀盘失效进行风险评估. 2018年，顾伟红等[11]采用基于熵权法的模糊综合评估模型分析西秦岭特长铁路隧道TBM施工风险，识别关键风险因素. 2019年，吕擎峰等[12]采用模糊层次和后果当量法评估隧道的塌方风险；同年，黄震等[13]基于模糊−证据理论综合评价盾构施工过程中的风险，解决了盾构隧道风险评价的不确定性，提高了评价结果的置信度. 同时，超前地质预测技术和风险评估方法的结合将会成为隧道风险评估研究的主流方向，但现在技术还不成熟[14].

以上方法依赖于输入风险数据的真实性与有效性，而在实际工程中风险的高度不确定性意味着获得可靠数据的机会很少. 粗糙集能客观地处理随机与冗余不确定性问题，有效地弥补这一缺陷，却不能直观地表达概率变化和反向推理；恰好BN是随机图论和具有反诊断与反推理的模型. 虽然粗糙集和BN方法的互补融合已在医疗决策、电子产品、机械故障处理[15-17]等领域取得良好的效果，但很少应用于隧道施工风险研究领域，同时关于TBM卡机风险分析的研究在国内较少，本文结合粗糙理论和BN建立TBM卡机风险模型，以北疆供水二期工程双三段引水隧洞项目为例验证模型的可靠性. 为TBM施工卡机这一风险不确定性的非线性问题提供有效可行的新解决途径.

1. 研究方法

1.1. BN

BN是基于贝叶斯理论的不确定性知识的概率图推理模型，是目前不确定性知识表达和推理领域最有效的工具之一[18]. BN是一种因果关系的网络图，它能利用在不确定和复杂条件下已获得的知识推论出逻辑结果. BN天生具有分析不确定性信息的能力，可以将数据不完备的系统进行推理和反推理，反映系统中数据间的概率关系. BN分析对数据结果的可能性，进一步量化并将先验结果与数据知识相结合，表示系统中各因素间依赖关系的强弱. BN也可以根据后期提供的数据更新系统中各因素的概率值，推翻之前的结论进一步提高预测精度. BN模型中所有节点都可见，增强了推理的精确性. 这种从不完全、不确定或不精确的系统中得出准确推理的模型，特别适合用于像TBM施工这种高度非线性多控制因素的复杂系统.

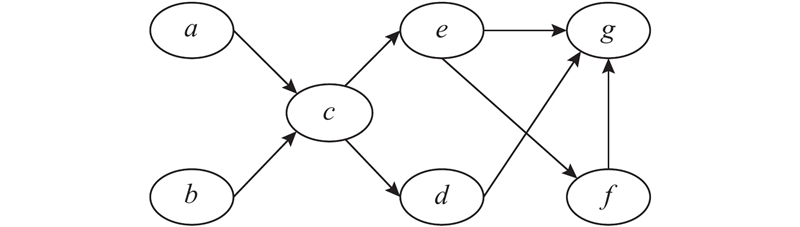
BN图是由几种代表变量的节点组成的有向循环图，并且用有向箭头将节点连接起来表示因果关系. 如图1所示，在BN中，每个变量是有限定和相互独立的，每个节点由一组概率（通常用n×m表格表示）代表当前节点的条件概率. 图中，A节点叫作C节点的父节点（也称为根节点或风险因素），即在A与C的关系中，C是子节点（也称为中间节点或风险事件）；除了A和B没有父节点，其他所有的节点由于与父节点连接而具有条件概率. 图中节点的概率分别表示为p(a)、p(b)、p(c|a,b)、p(d|c)、p(e|c)、p(f |e)和p(g|d,e,f).

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   贝叶斯网络简略图

Fig.1   Brief diagram of Bayesian network


BN评价步骤可分为4步：1）将识别好的风险因素和风险事件根据因果关系转化为BN拓扑图；2）根据专家先验知识或者统计数据获取根事件的先验概率；3）根据专家先验知识或统计数据获取中间事件的条件概率；4）BN模型的概率计算，通常可以借助Matlab、Netic、Genie等软件进行模拟计算.

1.2. 粗糙理论

粗糙集（rough sets）理论是波兰数学家帕拉克提出的关于系统逻辑特性研究的高效解析不精确、不完整信息的数学方法[19]. 其主要理论如下：粗糙集理论用信息系统 $S$表示研究对象， $S = \{U,A, $ $ V,f\}$为四元组. 其中 $U$表示研究对象， $A$是属性集合； $V$是属性的值域， $f$是一种映射，反映对象集合之间的值， $ f{\text{：}}U\times A\to V$称为信息函数，规定了系统中所有样本相应的属性值. 若属性集合 $A$由条件属性集 $C$和决策属性集 $D$组成，且 $A = C \cup D$， $C \cap D = $Ø，则称 $S$为决策表，记为 $S = (U,C \cup D)$. 对于任何一个属性集合 $D$不可分辨关系用IND表示，不可分辨关系就是U上的等价关系，定义为

${\rm{IND}}\left( P \right) = \left\{ {\left( {x,y} \right) \in U \times U:f\left( {x,c} \right) = f\left( {y,c} \right), c \in P} \right\}.$

1.3. 连续型影响因素离散化

粗糙集对不确定性问题的描述及处理是比较客观的，其属性值都是离散数据，为了方便计算使数据统一化，需要将连续数据与离散数据做综合处理，使连续数据转化成离散数据. 常用的离散化方法有替换法、离散相似法、遗传算法以及等区间离散化法等，这类方法实质上将连续的区间划分为小的区间，并将连续的小区间与离散的值关联起来，过程复杂难懂，不适用于大量数据的处理. 云变换可以实现对连续数据的软划分，既能根据某种规律将任意不规则的空间数据分布进行数学变换，又适用于大量数据的处理，因此本文运用云模型划分区间，通过区间离散实现连续属性的离散化.

云模型是李德毅创立的定性与定量相互转换的不确定性模型，用 ${\rm{Ex}}$、 ${\rm{En}}$、 ${\rm{He}}$、y分别表示云模型 ${{C}}({\rm{Ex}},{\rm{En}},{\rm{He}})$的期望、熵、超熵和隶属度[20]. 云模型中仅仅用云的几个数字特征就可以勾画出成千上万的云滴，构成整个云图，云图中将大量的随机性与模糊性语言集成. 对于粗糙集 $S = \{U,A, V,f\}$利用改进峰值云换算法，生成连续属性 ${C_k} \left( {{C_k} \in C} \right)$的初始云模型划分[21]. 将划分好且距离最近的云模型进行合并. 设论域 $U$上的基本云模型为 $ {A}_{1}({\rm{E}}{{\rm{x}}}_{1}, $ $ {\rm{E}}{{\rm{n}}}_{1},{\rm{H}}{{\rm{e}}}_{1})$和 ${{{A}}_2}({\rm{E}}{{\rm{x}}_2},{\rm{E}}{{\rm{n}}_2},{\rm{H}}{{\rm{e}}_2})$，距离为 $d$，可得到 ${A_1}$和 ${A_2}$合并的云模型为 ${{{A}}_3}({\rm{E}}{{\rm{x}}_3},{\rm{E}}{{\rm{n}}_3},{\rm{H}}{{\rm{e}}_3})$.

${{d(}}{{{A}}_{\rm{1}}}{\rm{,}}{{{A}}_{\rm{2}}}{\rm{) = }}\frac{{\left| {{\rm{E}}{{\rm{x}}_{\rm{1}}}{\rm{ - E}}{{\rm{x}}_{\rm{2}}}} \right|}}{{{\rm{E}}{{\rm{n}}_{\rm{1}}}{\rm{ + E}}{{\rm{n}}_{\rm{2}}}}}{\rm{,}}$

${{{A}}_{\rm{3}}}{\rm{ = }}{{{A}}_{\rm{1}}} \cup {{{A}}_{\rm{2}}} \leftrightarrow {\rm{E}}{{\rm{x}}_{\rm{3}}}{\rm{ = }}\frac{{{\rm{E}}{{\rm{x}}_{\rm{1}}}{\rm{ + E}}{{\rm{x}}_{\rm{2}}}}}{{\rm{2}}}{\rm{ + }}\frac{{{\rm{E}}{{\rm{n}}_{\rm{1}}}{\rm{ + E}}{{\rm{n}}_{\rm{2}}}}}{{\rm{4}}}{\rm{,}}$

${\rm{E}}{{\rm{n}}_{\rm{3}}}{\rm{ = }}\frac{{{\rm{E}}{{\rm{x}}_{\rm{2}}}{\rm{ - E}}{{\rm{x}}_{\rm{1}}}}}{{\rm{4}}}{\rm{ + }}\frac{{{\rm{E}}{{\rm{n}}_{\rm{1}}}{\rm{ + E}}{{\rm{n}}_{\rm{2}}}}}{{\rm{4}}}{\rm{,}}$

${\rm{H}}{{\rm{e}}_{\rm{3}}}{\rm{ = max\{H}}{{\rm{e}}_{\rm{1}}}{\rm{,H}}{{\rm{e}}_{\rm{2}}}\}{\rm{.}}$

基本云模型的合并需要考虑决策表的改变程度， ${\mu _{{\rm{u}}}}$和 $\mu _{{\rm{u}}}^\prime $表示 ${A_1}$和 ${A_2}$合并前后属性Ck相对于决策属性分类的不确定性. 属性Ck对决策表S的不确定性为

${\mu _{u}}\left( {{S / {{C_{\rm{k}}}}}} \right) = 1 - \sum\limits_{i = 1}^v {\frac{{\left| {{F_i}} \right|}}{{\left| U \right|}}} {\mu _{{C_{\rm{k}}}}}\left( {{F_i}} \right); i=1,2,\cdots,v.$

式中： $v$为条件属性Ck决定的分类数量， $\left| {{F_i}} \right|$为分类 ${F_i} \in \left\{U\left| {{\rm{IND}}\left( {{C_k}} \right)} \right.\right\}$中实例的数量， $\;{\mu _{{C_{\rm{k}}}}}\left( {{F_i}} \right) = \max $ $ \left\{ {{{\left| {{F_i} \cap {Y_j}} \right|} / {{F_i}}}} \right \}$为分类 ${F_i}$对于决策属性分类的确定程度， ${Y_j} \in \left\{U\left| {{\rm{IND}}\left( D \right)} \right.\right\}$为 $U$上决策属性 $D$决定的分类， $\left| {{F_i} \cap {Y_j}} \right|$为 ${F_i} \cap {Y_j}$中实例的数量.

2. 基于贝叶斯的TBM卡机可能性评价流程

基于贝叶斯理论原理，借助历史资料、专家主观经验和客观数据，构建BN模型求得其概率，结合实际项目进行实例论证. 如图2所示为使用BN模型对TBM卡机风险预测的模型构建路线流程.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   TBM卡机风险评价模型构建流程图

Fig.2   Flow chart of TBM jamming risk assessment model


2.1. TBM卡机风险因素

根据研究对象确定顶事件为TBM卡机，影响TBM卡机（G）的因素复杂众多，结合文献[22]中TBM选型及适应性设计和文献[23]、[24]中掘进性能要求与TBM卡机故障研究，列出可能致使顶事件发生的风险因素清单，请该领域专家进行风险识别和筛选，最终确定本模型由8个地质因素A1~A8、3个设计因素B1~B3、2个施工管理因素C1、C2组成. 结合文献[25]试掘进的施工方案以及历史资料和现场施工情况找出由这些风险因素可能造成致使TBM的风险事件共有7个M1~M7. TBM施工卡机风险指标如表1所示.

表 1   TBM施工卡机风险指标

Tab.1  Risk factors of TBM construction card machine

风险指标 符号 风险指标 符号
岩石类型 A1 刀盘结构的设计 B3
大量的地下水 A2 TBM操作 C1
高地应力 A3 前期地质调查 C2
复合地层 A4 卡刀盘 M1
断裂破碎带 A5 卡护盾 M2
围岩等级 A6 姿态偏差 M3
隧道埋深 A7 围岩坍塌 M4
平曲线半径 A8 岩爆 M5
TBM选型 B1 突泥涌沙 M6
开口率的设计 B2 软岩大变形 M7

新窗口打开| 下载CSV


2.2. 风险指标等级划分

风险指标等级的划分规则：1）根据规范进行划分，2）根据研究文献成果划分，3）根据云模型进行区间软划分. 实际上划分区间越多，越细致，分析结果越准确，但区间越多，会大大增加BN模型的计算量. 用1~5表示具体指标的相关状态，这些状态不表现风险高低. 例如指标姿态偏差M3状态1表示偏差最小，则TBM在该状态下，最适宜掘进，掘进效率最好；指标突泥涌沙M6状态1表示涌水量最大，则TBM在该状态下，掘进效率最差，极可能发生掌子面涌水，迫使停机现象.

以软岩大变形M7为例说明云模型区间划分实现属性离散化的步骤. 根据统计数据得到初始分布的频数折线图，如图3所示. 图中，n表示事件发生频次. 根据n的分布折线图将波峰值定义为云的期望，运用逆向云发生器算出云模型的熵和超熵. 软岩大变形中对应有8个原始峰值. 经改进，得到8个初始云模型，其期望值、熵、超熵以及相邻云间距离如表2所示.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

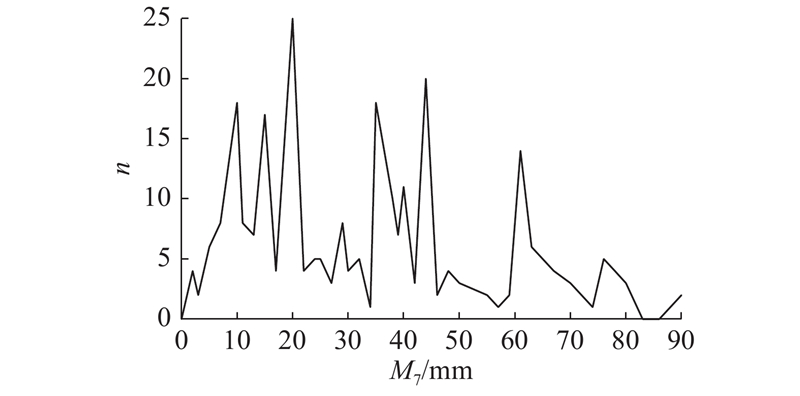
图 3   软岩大变形统计数据的原始分布

Fig.3   Original distribution of statistical data for soft rock large deformation


表 2   软岩大变形的初始云模型数字特征及相邻云间距离

Tab.2  Numerical characteristics of initial cloud model and distance between adjacent clouds for soft rock large deformation

云编号 Ex En He d
1 10 3.241 5 0.402 4 0.764 65
2 15 3.297 4 0.411 4 0.752 67
3 20 3.345 6 0.422 8 1.154 85
4 28 3.581 7 0.432 1 0.971 80
5 35 3.624 4 0.442 2 0.672 89
6 40 3.697 4 0.452 3 0.674 84
7 45 3.711 8 0.462 1 2.675 84
8 65 3.762 5 0.468 9

新窗口打开| 下载CSV


云5和云6间距离最短，为0.672 89，若属性值相对于决策分类的不确定差值小于阈值（ $\alpha {\rm{ = }} $ $ 1\% $），则进行合并，反之重新确定相近的云进行合并. 重复操作最终得到如图4所示的4个云图. 根据合并结果，将软岩大变形的收敛值划分为4个区段，分别为 $\left[ {0,20} \right)$、 $\left[ {20,40} \right)$、 $\left[ {40,55} \right)$和 $\left[ {55, + \infty } \right)$，以此对应4种状态. 同理对其他连续型属性进行离散化，最终等级划分结果见表3和表4. 表3中，k为适宜开口率，根据刀盘的直径和地质条件由专家选取；ha为坍落拱高度，根据 $h_{a}=0.41 \times 1.79^{S}$计算，其中s为围岩等级；围岩强度应力比（ $R_{{\rm{c}}} / P_{0}$）为岩石单轴抗压强度和最大初始地应力的比值；A2、A6和A7根据相关规范分级；A3、A4、A5、A8和B2根据相关研究文献分级；M3、M6、M7和C2采用云模型分级.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   软岩大变形的云模型划分最终结果

Fig.4   Final results of cloud model division for soft rock large deformation


表 3   TBM卡机风险定量评价指标分级标准

Tab.3  Grading standard for quantitative evaluation index of TBM jamming risk index

符号 风险指标 分级依据 分级状态
1 2 3 4 5
M3 姿态偏差 偏移量/mm $\left[ {0,20} \right)$ $\left[ {20,50} \right)$ $\left[ {50,100} \right)$ $\left[ {100, + \infty } \right)$
M6 突泥涌沙 掌子面涌水量/（m3·h−1） $\left[ {400, + \infty } \right)$ $\left[ {200,400} \right)$ $\left[ {100,200} \right)$ $\left[ {0,100} \right)$
M7 软岩大变形 围岩收敛值/mm $\left[ {0,20} \right)$ $\left[ {20,40} \right)$ $\left[ {40,55} \right)$ $\left[ {55, + \infty } \right)$
A2 大量的地下水 单位涌水量/（L·s−1） $\left[ {100, + \infty } \right)$ $\left[ {60,100} \right)$ $\left[ {20,60} \right)$ $\left[ {0,20} \right)$
A3 高地应力 围岩强度应力比 $\left[ {0.45, + \infty } \right)$ $\left[ {0.28,0.45} \right)$ $\left[ {0.2,0.28} \right)$ $\left[ {0.14,0.2} \right)$ $\left[ {0,0.14} \right)$
A4 复合地层 横向地层复合比/% $\left[ {50,60} \right)$ $\left[ {60,70} \right)$ $\left[ {30,50} \right)$ $\left[ {0,30} \right)$ $\left[ {70, + \infty } \right)$
A5 断裂破碎带 破碎带宽度/m $\left[ {30, + \infty } \right)$ $\left[ {10,30} \right)$ $\left[ {5,10} \right)$ $\left[ {1,5} \right)$ $\left[ {0,1} \right)$
A6 围岩等级 纵波波速/（km·s−1） $\left[ {0,1.5} \right)$ $\left[ {1.5,2.5} \right)$ $\left[ {2.5,3.5} \right)$ $\left[ {3.5,4.5} \right)$ $\left[ {4.5, + \infty } \right)$
A7 隧道埋深 埋深/m $\left[ {0,\left( {2 \sim 3} \right){h_a}} \right)$ $\left[ {\left( {2 \sim 3} \right){h_a},500} \right)$ $\left[ {500, + \infty } \right)$
A8 平曲线半径 半径/mm $\left[ {0,350} \right)$ $\left[ {350,500} \right)$ $\left[ {500,600} \right)$ $\left[ {600, + \infty } \right)$
B2 开口率的设计 开口率/% $\left[ {0,k} \right)$ $k$ $\left[ {k,100} \right)$
C2 前期地质调查 勘测结果准确率/% $\left[ {0,55} \right)$ $\left[ {55,70} \right)$ $\left[ {70,80} \right)$ $\left[ {80,95} \right)$ $\left[ {95,100} \right)$

新窗口打开| 下载CSV


表 4   TBM卡机风险定性评价指标分级标准

Tab.4  Grading standard for qualitative evaluation index of TBM jamming risk

符号 风险指标 分级依据 分级状态
1 2 3 4
G 卡机 是否卡机 是 否
M1 卡刀盘 是否卡刀盘 是 否
M2 卡护盾 是否卡护盾 是 否
M4 围岩坍塌 围岩形态 稳定 部分坍塌 严重坍塌
M5 岩爆 岩爆烈级 无岩爆 弱岩爆 中等岩爆 强烈岩爆
A1 岩石类型 风险描述 强可溶岩 中等可溶岩 弱可溶岩 非可溶岩
B1 TBM选型 风险描述 不宜选择TBM施工 TBM型号选择不当 TBM型号选择适当
B3 刀盘设计 风险描述 刀盘直径不合理 刀具设计不合理 刀盘结构形式不合理 刀盘设计合理
C1 TBM操作 风险描述 地质条件复杂，
推进速度控制困难 		地质条件良好，
操作人员操作失误 		合理换步，并选择合理
的施工参数

新窗口打开| 下载CSV


2.3. BN拓扑图的构建

利用解释结构模型（ISM）建立各风险因素与风险事件间的层次关系. 1）根据领域知识和历史资料对风险事件与各风险因素确定相互影响关系，如图5所示. 图（a）为风险因素对风险事件的影响，有影响用1表示，无影响用0表示. 图（b）为各风险事件之间的影响关系. 横排因素影响纵排因素用V表示，纵排因素影响横排因素用A表示，两者互不影响用O表示. 2）将图5转化成邻接矩阵，运用matlab软件算出可达矩阵. 3）根据因果关系，通过有向线段将风险因素和风险事件连接起来得到网络拓扑图，如图6所示.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

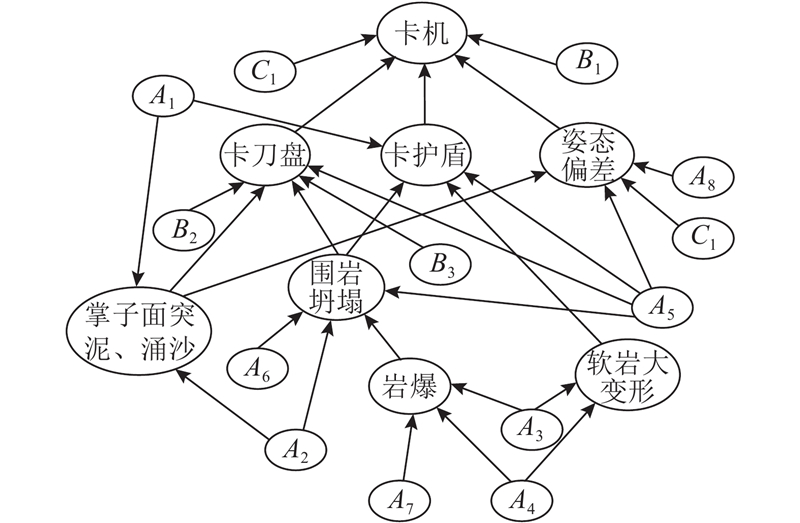
图 5   TBM卡机风险因素和风险事件的相关性

Fig.5   Correlation of risk factors and risk events for TBM jamming


图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6   TBM卡机贝叶斯网络拓扑图

Fig.6   Bayesian network topology on TBM jamming


2.4. 先验概率和条件概率的获取

2.4.1. BN模型参数化

为了减小联合概率分布的计算量，方便计算先验概率和条件概率，须对实测数据进行离散化处理. 实地调查和测量15座敞开式TBM施工隧道，获取大量的实地数据，将部分遗失数据去除，最终确定400组区间数据，根据表3、4的分级标准对数据进行离散化，建立决策系统. 例如：对于指标A2，在区间1组处测得单位涌水量为50 L/s，根据表3该值在状态3的区间范围内，则离散化取值为3；对于指标M4，在区间1组处发现围岩出现部分坍塌，根据表4，该现象属于状态2的风险描述，则离散化取值为2. 据此，可对本文所搜集的400组区间（100 m每个区间组）样本中的所有数据进行离散化处理，最终建立决策系统见表5.

表 5   TBM卡机决策表（部分）

Tab.5  TBM card machine decision table (part)

区间组别 A1 A2 A3 A4 A5 A6 A7 A8 B1 B2 B3 C1 C2 M1 M2 M3 M4 M5 M6 M7 G
1 3 3 3 4 5 3 2 3 3 2 4 3 2 2 2 1 2 2 3 3 2
2 4 4 5 3 5 2 3 3 3 2 4 3 4 2 2 1 2 3 4 2 2
3 2 2 4 4 4 2 2 3 3 2 2 1 5 2 1 2 2 3 4 2 1
4 4 3 3 2 4 3 2 4 3 2 2 2 2 2 2 1 1 1 4 3 2
5 3 2 3 1 3 3 2 4 3 2 4 3 3 2 2 1 1 1 3 3 2
$ \vdots $ $ \vdots $ $ \vdots $ $ \vdots $ $ \vdots $ $ \vdots $ $ \vdots $ $ \vdots $ $ \vdots $ $ \vdots $ $ \vdots $ $ \vdots $ $ \vdots $ $ \vdots $ $ \vdots $ $ \vdots $ $ \vdots $ $ \vdots $ $ \vdots $ $ \vdots $ $ \vdots $ $ \vdots $
400 3 4 3 1 5 4 3 3 3 3 2 3 2 1 2 2 1 2 2 4 1

新窗口打开| 下载CSV


2.4.2. 计算先验概率和条件概率

利用粗糙集分类原理，根据表5计算根节点的先验概率和中间节点的条件概率：

$P\left( {I_1{\rm{ = }}i} \right) = \frac{{m\left( {I_1 = i} \right)}}{n},$

$P\left( {{{{I_3} = i} | {{I_1} = j,{I_2} = k}}} \right) = \frac{{m\left( {{{{I_3} = i} | {{I_1} = j,{I_2} = k}}} \right)}}{n}.$

式中： $P\left( {{I_1} = i} \right)$为当风险指标 ${I_1}$状态为 $i$时的先验概率； $m\left( {{I_1} = i} \right)$为当风险指标 ${I_1}$状态为 $i$时的频数； $P\left( {{{{I_3} = i} | {{I_1} = j,{I_2} = k}}} \right)$为当风险指标 ${I_1}$状态为 $j$，风险指标 ${I_2}$状态为 $k$时，风险指标 ${I_3}$处于状态为 $i$的条件概率； $m\left( {{{{I_3} = i}| {{I_1} = j,{I_2} = k}}} \right)$为当风险指标 ${I_1}$ 状态为 $j$，风险指标 ${I_2}$状态为 $k$时，风险指标 ${I_3}$处于状态为 $i$ 的频数； $n$为总样本数.

以根节点为例，先验概率见表6，以中间节点（M3）为例，条件概率表见表7. 表7的第1行数据表示当节点A5、A8、C1、M6状态都处于1时，节点M3的状态为1、2、3、4的概率分别是0、0、0.138、0.872.

表 6   风险因素的先验概率

Tab.6  Prior probabilities of risk factors

符号 风险因素指标 P
状态1 状态2 状态3 状态4 状态5
A1 岩石类型 0.114 0.354 0.287 0.245
A2 大量地下水 0.050 0.125 0.543 0.282
A3 高地应力 0.342 0.334 0.139 0.103 0.082
A4 复合地层 0.085 0.082 0.124 0.667 0.042
A5 断裂破碎带 0.085 0.124 0.221 0.221 0.349
A6 围岩等级 0.024 0.094 0.187 0.425 0.270
A7 隧道埋深 0.015 0.930 0.055
A8 平曲线半径 0 0.054 0.292 0.654
B1 TBM选型 0.045 0.024 0.931
B2 开口率的设计 0.124 0.721 0.155
B3 刀盘设计 0.097 0.134 0.024 0.745
C1 TBM操作 0.088 0.024 0.888
C2 前期地质调查 0.124 0.115 0.167 0.211 0.383

新窗口打开| 下载CSV


表 7   风险事件M3的条件概率（部分）

Tab.7  Conditional probability of risk events M3 (part)

A5 A8 C1 M6 $P$
状态1 状态2 状态3 状态4
1 1 1 1 0 0 0.138 0.872
1 1 1 2 0 0 0.336 0.674
1 1 1 3 0.104 0.221 0.223 0.452
1 1 1 4 0.110 0.142 0.325 0.423
1 1 2 2 0 0.271 0.274 0.455
$ \vdots $ $ \vdots $ $ \vdots $ $ \vdots $ $ \vdots $ $ \vdots $ $ \vdots $ $ \vdots $
5 4 3 2 0 0.372 0.542 0.086
5 4 3 3 0.212 0.245 0.342 0.201
5 4 3 4 0.844 0.131 0.025 0

新窗口打开| 下载CSV


3. 案例分析

3.1. 工程概况

北疆供水二期工程隧洞穿越的地质条件复杂，具有埋深大，超特长的特点，是世界上已建和在建的最长引水隧洞. 主要是由喀双隧洞、西二隧洞、双三隧洞3部分组成，隧洞占总长度的95.6%以TBM施工为主，钻爆法施工为辅. 其中双三隧洞长92.15 km，采用2台直径为5.53 m的敞开式TBM和3台土压力平衡盾构施工. 主要穿越泥盆系和石炭系凝灰质砂岩、凝灰岩以及华力西晚期侵入的花岗岩地层总长65.34 km；侏罗系和白垩系的泥岩、砂岩地层长13.19 km；新近系的泥岩夹砂岩长11.23 km；第四系碎石土长1.91 km. 双三隧洞地质纵断面，如图7所示. 图中，S为桩号，H为高程. 隧洞Ⅱ、Ⅲ类围岩占总长的68.9%，饱和抗压强度介于30~120 MPa的岩石占比为67.0%，饱和抗压强度小于30 MPa的围岩占比为29.0%，主要为泥岩夹砂岩，在施工中可能存在局部坍塌、大规模突涌水、软岩大变形问题.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7   双三隧洞地质纵断面图

Fig.7   Geological longitudinal section map of Shuangsan tunnel


本文以双三隧道TBM1施工段（21+004.542~21+543.213）、TBM1施工段（40+022.111~41+025.123）、TBM2施工段（50+409.187~51+011.235）为研究对象，对模型的可靠性进行验证.

3.2. 事前风险推理分析

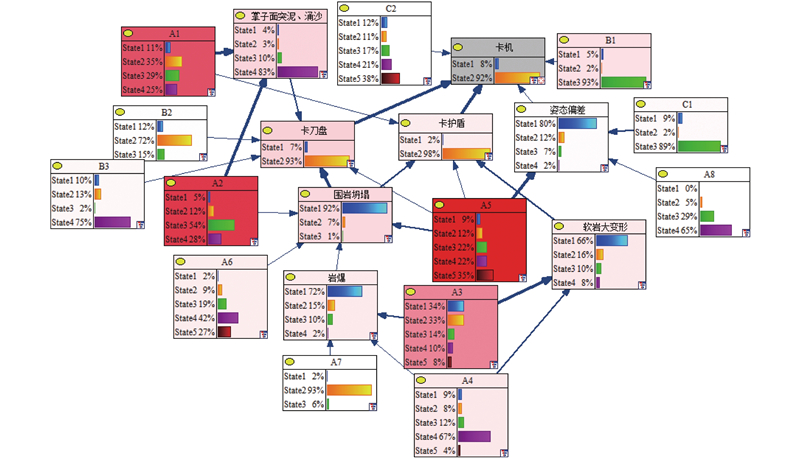
构建卡机BN拓扑图和获取根事件的先验概率和中间事件的条件概率后，即可进行BN模型的推理分析. 将已获得的参数数据输入GENIE 2.0软件，在对决策表中的实测数据进行统计分析得到无证据条件下的TBM卡机风险预测结果，如图8所示.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8   无证据条件下的TBM卡机贝叶斯网络模型

Fig.8   Bayesian network model of TBM jamming without evidence


3.3. 事中风险推理分析

在TBM2施工段，随着TBM施工推进，经过现场调查，掌握证据（A1=2、A2=1、A3=4、A4=3、A5=2、A6=2、A7=2、A8=3、B1=3、B2=2、B3=4、C1=1、C2=4）则可通过更新节点的概率，动态更新BN模型，更新后的BN模型，如图9所示. 由图可以看出，卡机风险概率为47%.

图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9   有证据条件下的TBM卡机贝叶斯网络模型（TBM2施工段）

Fig.9   Bayesian model of TBM jamming with evidence (section TBM2)


3.3.1. 软件敏感度分析和致因链分析

敏感性反映的是根节点对叶节点（卡机）的影响程度，即根节点概率的变化率引起叶节点概率变化的难易程度. 在软件中用颜色的深浅体现根节点的敏感性，颜色越深则敏感性越强，反之，则敏感性越弱. 软件敏感性分析处理可作为故障排查的有效参考指标，结果如图8、9所示. 从图中可以看出风险事件突泥涌沙、卡刀盘对造成卡机现象最为敏感.

致因链分析目的是找出引起事故发生的路径. 在GENIE 2.0软件中用有向箭头的粗细表示致因路线，线条越粗则表示越容易引发顶事件，设定TBM施工卡机为目标事件，得到分析结果如图8、9所示. 图中加粗的有向箭头即为最大致因链，由致因链分析可知，最容易致使顶事件发生的4条路径是：岩石类型→掌子面突泥涌沙→卡刀盘→卡机，大量的地下水→掌子面突泥涌沙→卡刀盘→卡机，高地应力→软岩大变形→卡护盾→卡机，围岩坍塌→卡护盾→卡机.

3.3.2. 软件后验概率计算

后验概率是在先验概率的基础上结合贝叶斯概率公式反推而来的，在本文中指在设定顶事件一定发生的情况下，反推底事件发生的概率分别是多少，并通过底事件的后验概率反应各个底事件的重要程度，以便找出致因因子. 将结果整理成柱状图比较先验概率和后验概率，如图10所示. 由图可看出A1、A2、A5先验概率和后验概率变化幅度较大，其他根节点只有略微变化，故这3个因素为关键因素.

图 10

新窗口打开| 下载原图ZIP| 生成PPT

图 10   无证据条件下先验概率（左）和后验概率（右）柱状图

Fig.10   Bar charts of prior probability (left) and posterior probability (right) without evidence


同理，可对TBM1施工段（21+004.542~21+543.213）、TBM1施工段（40+022.111~41+025.123）进行推理分析，获取TBM卡机概率PJ、敏感性因子F、致因链C ′、关键致因因素F ′，最终推理结果如表8所示.

此处的卡机概率并不是TBM卡机的故障率，而是风险等级概率，为了衡量卡机风险程度的大小，对实际工程施工有参考意义，本文将决策表中400组数据的条件属性（根节点的状态）作为证据，反推出贝叶斯模型卡机概率P0，并与决策属性（现场卡机情况）的卡机概率P1对比，进行数据分析，得出关系如表9所示.

3.4. 讨论分析

在无证据条件下，根据决策表中的数据，进行BN模型推理，TBM卡机概率为8%（极低风险），敏感性风险因素为岩石类型、大量的地下水、断裂破碎带，说明这3类因素是影响TBM施工的最不利因素.

表 8   TBM卡机风险因素统计表

Tab.8  Statistical table of risk factors for TBM jamming

研究区间 条件 PJ/% F C ′ F ′ 现场是否卡机
原始数据 无证据 8 A1、A2、A5 A1→M6→M1→G、
A2→M6→M1→G、
A3→M7→M2→G、
M4→M2→G 		A1、A2、A5
21+004.542~21+543.213 A1=3、A2=2、A3=1、A4=4、A5=4、
A6=2、A7=2、A8=3、B1=3、B2=2、
B3=4、C1=1、C2=4 		0 A5、A6 A1→M6→M1→G、
A2→M6→M1→G、
A3→M7→M2→G、
M4→M2→G 		A1、A2、A5 否
40+022.111~41+025.123 A1=4、A2=2、A3=4、A4=2、A5=3、
A6=4、A7=2、A8=4、B1=3、B2=2、
B3=4、C1=3、C2=3 		53 A5、M4、M2 A1→M6→M1→G、
A2→M6→M1→G、
A3→M7→M2→G、
M4→M2→G 		A1、A2、A5 是
50+409.187~51+011.235 A1=2、A2=1、A3=4、A4=3、A5=2、
A6=2、A7=2、A8=3、B1=3、B2=2、
B3=4、C1=1、C2=4 		47 M6、M1 A1→M6→M1→G、
A2→M6→M1→G、
A3→M7→M2→G、
M4→M2→G 		A1、A2、A5 是

新窗口打开| 下载CSV


表 9   TBM卡机的模型概率和现场概率

Tab.9  Probability of model and field for TBM jamming

风险定义 P0/% P1/%
极高风险 $ \geqslant 40$ $ \geqslant 65$
高风险 $30 \sim 40$ $37 \sim 65$
中等风险 $20 \sim 30$ $18 \sim 38$
低风险 $10 \sim 20$ $2 \sim 18$
极低风险 $ \leqslant 10$ $ \leqslant 2$

新窗口打开| 下载CSV


在有证据条件下，TBM1施工段（21+004.542~21+543.213），由该模型获取TBM卡机概率为0%（极低风险），敏感性风险因素为断裂破碎带、围岩等级，通过实地考察该区间大部分为凝灰质砂岩，整体稳定性较好，无较大断裂破碎带、涌水、软弱围岩等不良地质，施工环境较好. TBM1施工段（40+022.111~41+025.123），该模型计算出卡机概率为53%（极高风险），敏感性风险因素为断裂破碎带，敏感性风险事件为围岩坍塌、卡刀盘，通过实地考察该区间存在约50 m长的断裂破碎带，围岩稳定性和节理较差，当TBM施工至40+424.236~40+867.278处时，多次出现严重的塌方掉块现象，2次塌方致使刀盘楔嵌卡机. 塌方掉块现场照片如图11所示. 在TBM2施工段，经该模型推理计算，TBM卡机概率为47%（极高风险），敏感性风险因素为大量地下水，敏感性风险事件为突泥涌沙、卡刀盘，经实地调查，该区间存在富水地段，节理裂隙发育，为节理密集带，岩体破碎，呈碎石、块状结构；当TBM施工到50+900.456处时，刀盘内出现极大涌水，瞬时流量约400 m3/h，TBM停止掘进，停机堵水30天. 突涌水现场照片如图12所示. 经该模型推理分析，找出4条最容易致使TBM卡机的关键致因链：岩石类型→掌子面突泥涌沙→卡刀盘→卡机；大量的地下水→掌子面突泥涌沙→卡刀盘→卡机；高地应力→软岩大变形→卡护盾→卡机；围岩坍塌→卡护盾→卡机，决策者可以通过阻断关键路径，避免TBM卡机事件的发生. 通过对比分析发现，该模型的推理结果和现场施工情况基本一致，可为TBM卡机风险管理提供一定的理论依据.

图 11

新窗口打开| 下载原图ZIP| 生成PPT

图 11   隧道塌方掉块现场照片

Fig.11   Scene photo of tunnel collapse


图 12

新窗口打开| 下载原图ZIP| 生成PPT

图 12   隧道突涌水现场照片

Fig.12   Scene photo of water inrush


4. 结　论

（1）从地质条件、设计因素和施工管理水平3个方面，筛选造成卡机故障的13个风险因素和7个风险事件，利用解释结构模型解决风险因素和风险事件的因果逻辑关系. 通过相关规范、研究成果和云模型区间划分法对各指标进行区间等级划分，以此建立BN的TBM卡机模型.

（2）通过粗糙集分类原理从实测数据中获取根节点的先验概率和中间节点的条件概率，经过推理计算，在无证据条件下TBM卡机风险等级概率为8%（极低风险），岩石类型、大量地下水和断裂破碎带为最关键风险因素.

（3）运用该模型对双三隧道3个施工区段进行TBM卡机风险预测，推理出风险等级概率，找出敏感性风险因素和风险事件，并和实际工程施工情况做对比，评价结果和实际情况基本吻合，验证了该评价方法的科学性.

（4）基于粗糙集−BN法的TBM卡机模型，通过大量的实测数据可以确定无证据条件下TBM施工过程中造成卡机的关键路径. 该模型可以运用于类似工程，只需掌握相应工程的节点证据，输入相应参数即可动态更新TBM卡机风险等级概率，获得风险等级. 该过程简单易行，操作方便，可作为TBM卡机风险管理的决策工具.

（5）所建模型没有考虑机械故障和人为原因所造成的停机情况；此外，由于对采集的数据均来自敞开式TBM施工项目，仅适应于敞开式TBM，其他类型的TBM施工项目使用该模型，须采集相应类型施工项目的施工数据，进行模型更新.

参考文献

龚秋明. 掘进机隧道掘进概论[M]. 北京: 科学出版社, 2014: 51.

[本文引用: 1]

SOUSA R L

Risk analysis for tunneling project

[J]. Tunnelling and Underground Space Technology incorporating Trenchless Technology Research, 2010, 44 (8): 103- 121

[本文引用: 1]

ABDELGAWAD M, FAYEK A R

Fuzzy reliability analyzer: quantitative assessment of risk events in industry using fuzzy fault-tree analysis

[J]. Journal of Construction Engineering and Management, 2011, 137 (4): 294- 302

DOI:10.1061/(ASCE)CO.1943-7862.0000285      [本文引用: 1]

SOUSA R L, EINSTEIN H H

Risk analysis during tunnel construction using Bayesian Networks: Porto Metro case study

[J]. Tunnelling and Underground Space Technology incorporating Trenchless Technology Research, 2011, 27 (1): 86- 100

URL     [本文引用: 1]

MOLLON G, DIAS D, SOUBRA A H, et al

Extension of CSRSM for the parametric study of the face stability of pressurized tunnels

[J]. Geotechnical Special Publication, 2011, 43 (9): 1149- 1156

URL     [本文引用: 1]

WANG Y, NI X, WANG J, et al

A comprehensive investigation on the fire hazards and environmental risks in a commercial complex based on fault tree analysis and the analytic hierarchy process

[J]. International Journal of Environmental Research and Public Health, 2020, 17 (19): 7347

DOI:10.3390/ijerph17197347      [本文引用: 1]

HYUN K C, MIN S, CHOI H, et al

Risk analysis using fault-tree analysis (FTA) and analytic hierarchy process (AHP) applicable to shield TBM tunnels

[J]. Tunnelling and Underground Space Technology incorporating Trenchless Technology Research, 2015, 49 (6): 121- 129

URL     [本文引用: 1]

周宗青, 李术才, 李利平, 等

浅埋隧道塌方地质灾害成因及风险控制

[J]. 岩土力学, 2013, 34 (5): 1375- 1382

URL     [本文引用: 1]

ZHOU Zong-qing, LI Zhu-cai, LI Li-ping, et al

Causes of geological hazards and risk control of collapse in shallow tunnels

[J]. Rock and Soil Mechanics, 2013, 34 (5): 1375- 1382

URL     [本文引用: 1]

佘诗刚, 林鹏

中国岩石工程若干进展与挑战

[J]. 岩石力学与工程学报, 2014, 33 (3): 433- 457

URL     [本文引用: 1]

SHE Shi-gang, LIN Peng

Some developments and challenging issues in rock engineering field in china

[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33 (3): 433- 457

URL     [本文引用: 1]

陈发达, 吴贤国, 王彦玉, 等

基于贝叶斯网络的土压盾构刀盘失效故障诊断

[J]. 土木工程与管理学报, 2017, 34 (6): 57- 62

DOI:10.3969/j.issn.2095-0985.2017.06.010      [本文引用: 1]

CHEN Fa-da, WU Xian-guo, WANG Yan-yu, et al

Fault diagnosis of cutterhead failure of earth pressure shield based on Bayesian network

[J]. Journal of Civil Engineering and Management, 2017, 34 (6): 57- 62

DOI:10.3969/j.issn.2095-0985.2017.06.010      [本文引用: 1]

顾伟红, 王恩茂, 张文达

铁路隧道TBM施工风险评估

[J]. 安全与环境学报, 2018, 18 (3): 843- 848

URL     [本文引用: 1]

GU Wei-hong, WANG En-mao, ZHANG wen-da

Risk assessment on the TBM construction of railway tunnels

[J]. Journal of Safety and Environment, 2018, 18 (3): 843- 848

URL     [本文引用: 1]

吕擎峰, 霍振升, 赵本海, 等

基于模糊层次和后果当量法的隧道塌方风险评估

[J]. 隧道建设, 2018, 38 (增2): 31- 38

URL     [本文引用: 1]

LU Qing-feng, HUO Zhen-sheng, ZHAO Ben-hai, et al

Risk assessment of tunnel collapse based on fuzzy hierarchy and consequences equivalent method

[J]. Tunnel Construction, 2018, 38 (增2): 31- 38

URL     [本文引用: 1]

黄震, 傅鹤林, 张加兵, 等

基于模糊−证据理论的盾构隧道施工风险综合评价

[J]. 武汉大学学报: 工学版, 2019, 52 (8): 694- 702

URL     [本文引用: 1]

HUANG Zhen, FU He-lin, ZHANG Jia-bing, et al

Comprehensive evaluation of shield tunnel construction risk based on fuzzy-evidence theory

[J]. Engineering Journal of Wuhan University, 2019, 52 (8): 694- 702

URL     [本文引用: 1]

REN T, JIANG D Y, CHEN J, et al

Tunnel surrounding rock classification forecast based on the geological advanced prediction system in seismic area

[J]. Applied Mechanics and Materials, 2012, 226-228: 910- 915

DOI:10.4028/www.scientific.net/AMM.226-228.910      [本文引用: 1]

王效俐, 刘潇, 苏强

邻域粗糙集融合贝叶斯神经网络在医疗决策中的应用研究

[J]. 工业工程与管理, 2016, 21 (5): 141- 147

DOI:10.3969/j.issn.1007-5429.2016.05.022      [本文引用: 1]

WANG Xiao-li, LIU Xiao, SU Qiang

Application in medical decision making based on neighborhood rough set and Bayes neural network

[J]. Industrial Engineering and Management, 2016, 21 (5): 141- 147

DOI:10.3969/j.issn.1007-5429.2016.05.022      [本文引用: 1]

朱敏, 刘卫东

基于粗糙集贝叶斯网络的电子产品设计缺陷评估模型

[J]. 计算机应用研究, 2013, 30 (3): 706- 711

DOI:10.3969/j.issn.1001-3695.2013.03.016     

ZHU Min, LIU Wei-dong

Prediction models of electronic products design defects based on rough set Bayesian network theory

[J]. Application Research of Computers, 2013, 30 (3): 706- 711

DOI:10.3969/j.issn.1001-3695.2013.03.016     

吕启深, 曾辉雄, 姚森敬, 等

基于贝叶斯网络和粗糙集约简的变压器故障诊断

[J]. 中国电力, 2013, 46 (9): 75- 79

DOI:10.3969/j.issn.1004-9649.2013.09.017      [本文引用: 1]

LU Qi-shen, ZENG Hui-xiong, YAO Sen-jing, et al

Transformer fault diagnosis method based on Bayesian network and rough set reduction theory

[J]. Electric Power, 2013, 46 (9): 75- 79

DOI:10.3969/j.issn.1004-9649.2013.09.017      [本文引用: 1]

胡记磊, 唐小微, 裘江南

基于贝叶斯网络的地震液化概率预测分析

[J]. 岩土力学, 2016, 37 (6): 1745- 1752

URL     [本文引用: 1]

HU Ji-lei, TANG Xiao-wei, QIU Jian-gnan

Prediction of probability of seismic-induced liquefaction based on Bayesian network

[J]. Rock and Soil Mechanics, 2016, 37 (6): 1745- 1752

URL     [本文引用: 1]

王晨晖, 袁颖, 周爱红, 等

基于粗糙集优化支持向量机的泥石流危险度预测模型

[J]. 科学技术与工程, 2019, 19 (31): 70- 77

DOI:10.3969/j.issn.1671-1815.2019.31.009      [本文引用: 1]

WANG Chen-hui, YUAN Ying, ZHOU Ai-hong, et al

Prediction model of debris flow danger degree based on support vector machine optimized by rough set

[J]. Science Technology and Engineering, 2019, 19 (31): 70- 77

DOI:10.3969/j.issn.1671-1815.2019.31.009      [本文引用: 1]

王洪利

一种参照模糊集的云模型集合论方法研究

[J]. 智能系统学报, 2020, 15 (3): 507- 513

URL     [本文引用: 1]

WANG Hong-li

A method of cloud model referring to fuzzy sets

[J]. GAAI Transacting on Intelligent Systems, 2020, 15 (3): 507- 513

URL     [本文引用: 1]

李兴生, 李德毅

一种基于云模型的决策表连续属性离散化方方法

[J]. 模式识别与人工智能, 2003, 16 (1): 33- 38

DOI:10.3969/j.issn.1003-6059.2003.01.007      [本文引用: 1]

LI Xing-sheng, LI De-yi

A discretization method for continuous attributes of decision table based on cloud model

[J]. Pattern Recognition and Artificial Intelligence, 2003, 16 (1): 33- 38

DOI:10.3969/j.issn.1003-6059.2003.01.007      [本文引用: 1]

陈馈, 张振川, 李涛. TBM设计与施工[M]. 北京: 人民交通出版社, 2018: 85-101.

[本文引用: 1]

杜彦良, 杜立杰. 全断面岩石隧道掘进机—系统原理与集成设计[M]. 武汉: 华中科技大学出版社, 2010: 20-21.

[本文引用: 1]

廖湘平, 龚国芳, 彭雄斌, 等

基于黏性耦合机理的TBM刀盘脱困特性

[J]. 浙江大学学报: 工学版, 2016, 50 (5): 902- 912

DOI:10.3785/j.issn.1008973X.2016.05.013      [本文引用: 1]

LIAO Xiang-ping, GONG Guo-fang, PENG Xiong-bin, et al

Jam breakout characteristic of tunnel boring machine based on hydro−viscous drive mechanism

[J]. Journal of Zhejiang University: Engineering Science, 2016, 50 (5): 902- 912

DOI:10.3785/j.issn.1008973X.2016.05.013      [本文引用: 1]

邓铭江, 谭忠盛

超特长隧洞TBM集群试掘进阶段适应性分析

[J]. 隧道建设, 2019, 39 (1): 1- 22

URL     [本文引用: 1]

DENG Ming-jiang, TAN Zhong-sheng

Analysis of adaptability of TBM in trial boring stage of super-long tunnel

[J]. Tunnel Construction, 2019, 39 (1): 1- 22

URL     [本文引用: 1]

/

〈 〉