电液伺服系统具有抗负载刚性大、响应快及功重比高等优点，在国防和众多重要工业领域^[1]内得到了广泛应用. 电液伺服系统是一个典型的非线性系统，包含各类参数不确定和时变干扰^[2]，其中时变干扰包括匹配干扰（与控制输入在同一通道的干扰，如未建模摩擦、未建模动态、外干扰等）和不匹配干扰（与控制输入不在同一通道的干扰，如系统压力动态建模误差等）. 这些因素的存在会严重恶化控制器期望的控制性能，使高精度跟踪控制器的设计变得困难.

一般来讲，鲁棒控制^[3-5]能够保证规定的输出跟踪性能，但需要使用很大的反馈增益来保证实际应用中的高控制精度. 自适应鲁棒控制方法^[6]可以通过对系统参数的自适应降低反馈增益，取得很好的瞬态和稳态性能^[7-10]，但由于控制律中采用了饱和函数有界抑制鲁棒控制的思想，导致其不能实现时变干扰下的渐进跟踪控制. Yao等^[11-12]使用扩张状态观测器估计液压系统中的干扰，Kim等^[13]设计扰动观测器来估计电液执行器中的偏置正弦失配扰动，但这2种方法无法处理同时存在的匹配和不匹配干扰. Won等^[14]设计能够同时处理匹配和不匹配干扰的高增益干扰观测器，但使用了未知的压力动态，理论上无法获得准确的干扰估计. Levant等^[15-16]提出有限时间干扰观测器（FTDO），取得了很好的拓展^[17]，但由于实际系统中干扰的随机性，很难实现高精度控制.

滑模控制^[18-19]理论上可以实现渐近跟踪控制，但通常会导致不连续的控制输入和物理系统中的抖动问题. Xian等^[20]提出连续误差符号的鲁棒积分控制器（RISE），能够实现渐近跟踪性能，Makkar等^[21]使用该技术来开发用于电动机的跟踪控制器. 近年来，RISE与自适应控制结合得到了极大的发展^[22-26]. 此外，基于RISE的控制成功应用于各种物理非线性系统^[27-30].

本文提出基于FTDO的渐进鲁棒积分跟踪控制策略. 采用系统参数的名义值，系统中所有的不确定性集中到干扰中，通过FTDO对干扰进行估计，从而实现针对干扰的前馈补偿；结合RISE，实现对实习系统中干扰的完全处理；采用期望补偿，降低噪声对跟踪性能的影响，使系统获得了全局渐进稳定的性能，增强了电液位置伺服系统抵抗干扰的能力.

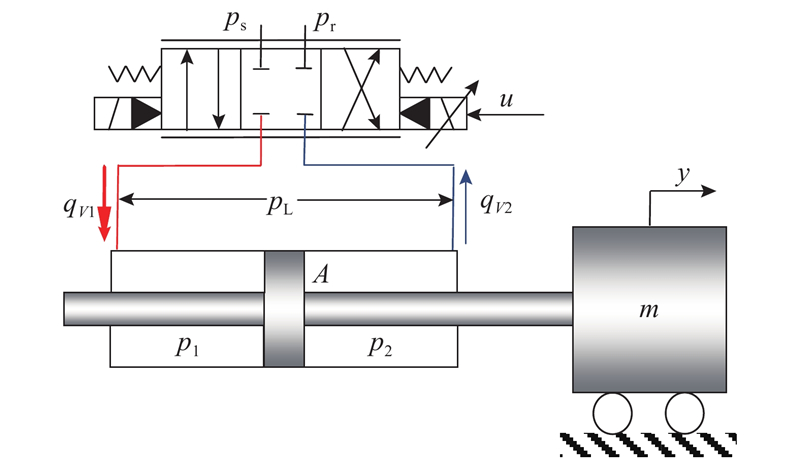
考虑的电液位置伺服系统结构如图1所示，惯性负载运动学方程为

(1) $m\ddot y = {p_{\rm L}}A - B\dot y - f\left( t \right).$

式中：m和y分别为运动部件的惯性负载和负载位移；p_L=p₁−p₂为液压缸负载压差，其中p₁和p₂分别为液压缸左、右两腔的压力；A为液压缸内腔的有效作用面积；B为有效黏性阻尼系数；f(t)为系统其他未建模干扰，包含未建模摩擦、未建模动态、外干扰等，其中t为时间变量.

忽略外部泄露，系统的压力动态方程为

(2) $\frac{{{V_{\rm t}}}}{{4{\beta _{\rm e}}}}{\dot p_{\rm L}} = - A\dot y - {C_{\rm t}}{p_{\rm L}} - q\left( t \right) + {q_{V \rm L}}.$

式中：V_t为系统控制腔总容积；β_e为液压缸有效容积液体弹性模数；C_t为液压缸内的泄露系数；q(t)为系统压力动态建模误差；q_VL=(q_V1+q_V2)/2为伺服阀负载体积流量，其中q_V1和q_V2分别为伺服阀进入/流出液压缸左/右腔的液压体积流量.

忽略阀芯动态，则伺服阀的负载体积流量方程为

(3) ${q_{V{\rm L}}} = {K_{\rm t}}u\sqrt {{p_{\rm s}} - {\rm{sgn}}\left( u \right){p_{\rm L}}} .$

式中：K_t和p_s分别为伺服阀控制流量增益和系统供油压力，u为系统控制输入.

为了方便控制器设计，定义系统状态变量为 $x = {\left[ {{x_1},{x_2},{x_3}} \right]^{\rm T}} = {\left[ {y,\dot y,{p_{\rm L}}A/m} \right]}^{\rm T}$,则整个系统方程可以由如下状态空间形式表示：

(4) $ \left. \begin{array}{l} {{\dot x}_1} = {x_2}, \\ {{\dot x}_2} = {x_3} - {\varphi _1}{x_2} - {d_1} , \\ {{\dot x}_3} = gu - {\varphi _2}{x_2} - {\varphi _3}{x_3} - {d_2}. \\ \end{array} \right\}$

式中：

$g = \frac{{4A{\beta _{\rm e}}{K_{\rm t}}}}{{m{V_{\rm t}}}}\sqrt {{p_{\rm s}} - {\rm{sgn}}\left( u \right)\frac{m}{A}{x_3}} ,$

φ₁=B/m，φ₂=4A²β_e/(mV_t)，φ₃=4β_eC_t/V_t都是系统的名义参数；d₁为系统的不匹配干扰，d₁=f(t)/m；d₂为系统的匹配干扰，d₂=4Aβ_eq(t)/(mV_t).

为了方便系统的设计，作出以下假设.

1）电液位置伺服系统在正常工况下工作，液压缸左、右两腔的压力p₁和p₂须满足如下条件：0<p_r<p₁<p_s，0<p_r<p₂<p_s，其中p_r为系统回油压力.

2）期望位置指令x_1d∈C³且有界.

3）干扰项d_k（k=1，2）是4−k阶可导的.

设计有限时间干扰观测器，估计式（4）中的匹配和不匹配干扰，具体形式如下：

(5) $\left. \begin{array}{*{35}{l}} {{{\dot{\mu }}}_{0}}={{\omega }_{0}}-{{\varphi }_{1}}{{x}_{2}},\;\;{{{\dot{\mu }}}_{1}}={{\omega }_{1}}={{{\dot{\hat{d}}}}_{1}},\;\;{{{\dot{\mu }}}_{2}}={{\omega }_{2}}={{{\dot{\hat{\dot{d}}}}}_{1}}\,, \\ {{\omega }_{0}}=-{{a}_{1}}{{\left| {{\mu }_{0}}-{{x}_{2}} \right|}^{2/3}}\;{\rm{sgn}}\left( {{\mu }_{0}}-{{x}_{2}} \right)+{{\mu }_{1}}\,, \\ {{\omega }_{1}}=-{{a}_{2}}{{\left| {{\mu }_{1}}-{{\omega }_{0}} \right|}^{1/2}}\;{\rm{sgn}}\left( {{\mu }_{1}}-{{\omega }_{0}} \right)+{{\mu }_{2}}\,, \\ {{\omega }_{2}}=-{{a}_{3}}\;{\rm{sgn}}\left( {{\mu }_{2}}-{{\omega }_{1}} \right) , \\ {{{\dot{\mu }}}_{3}}={{\omega }_{3}}+gu-{{\varphi }_{2}}{{x}_{2}}-{{\varphi }_{3}}{{x}_{3}},\;\;{{{\dot{\mu }}}_{4}}={{\omega }_{4}}={{{\dot{\hat{d}}}}_{2}}\, , \\ {{\omega }_{3}}=-{{a}_{4}}{{\left| {{\mu }_{3}}-{{x}_{3}} \right|}^{1/2}}\;{\rm{sgn}}\left( {{\mu }_{3}}-{{x}_{3}} \right)+{{\mu }_{4}}\,, \\ {{\omega }_{4}}=-{{a}_{5}}\;{\rm{sgn}}\left( {{\mu }_{4}}-{{\omega }_{3}} \right)\, . \end{array} \right\}$

式中：a_i>0（i=1，2，3，4，5）为观测器系数；μ₀、μ₃、μ₁、μ₂和μ₄分别为x₂、x₃、d₁、 ${\dot d_1}$和d₂的估计值.

定义估计误差为σ₀=μ₀−x₂，σ₁=μ₁−d₁， ${\sigma _2} = {\mu _2} - {\dot d_1}$，σ₃=μ₃−x₃，σ₄=μ₄−d₂，根据式（4）、（5）可以给出观测器的动态观测误差：

(6) $\left.\begin{array}{l} \left. \begin{array}{l} {{\dot \sigma }_0} = - {a_1}{\left| {{\sigma _0}} \right|^{2/3}}\;{\rm{sgn}}\, {{\sigma _0}} + {\sigma _1} \,, \\ {{\dot \sigma }_1} = - {a_2}{\left| {{\sigma _1} - {{\dot \sigma }_0}} \right|^{1/2}}\;{\rm{sgn}}\, \left( {{\sigma _1} - {{\dot \sigma }_0}} \right) + {\sigma _2} \, , \\ {{\dot \sigma }_2} \in - {a_3}\;{\rm{sgn}}\, \left( {{\sigma _2} - {{\dot \sigma }_1}} \right) + \left[ { - {l_1},{l_1}} \right] \, , \\ \end{array} \right. \\ \left. \begin{array}{l} {{\dot \sigma }_3} = - {a_4}{\left| {{\sigma _3}} \right|^{1/2}}\;{\rm{sgn}}\, {{\sigma _3}} + {\sigma _4}\, , \\ {{\dot \sigma }_4} \in - {a_5}\;{\rm{sgn}} \left( {{\sigma _4} - {{\dot \sigma }_3}} \right) + \left[ { - {l_2},{l_2}} \right] \, . \\ \end{array} \right. \end{array}\right\} $

式中：l_k为d_k^(3−k)（k=1，2）的Lipschitz常数，由文献[16]可知，观测器误差系统（见式（6））是有限时间稳定的，即存在一个有限时间使得σ_i=0.

定义如下误差变量：

(7) $\left.\begin{split} & {e_1} = {x_1} - x{}_{1{\rm d}},\quad{e_2} = {{\dot e}_1} + {k_1}{e_1}\, , \\ & {e_3} = {{\dot e}_2} + {k_2}{e_2},\quad r = {{\dot e}_3} + {k_3}{e_3} \, . \end{split}\right\} $

式中：e₁为系统的跟踪误差；x_1d为系统的期望位置指令信号；k₁、k₂、k₃均为正的反馈增益；r为辅助误差信号，由式（4）、（7）可知，r的扩展形式为

(8) $\begin{split} r =& {{\dot x}_3} - {\varphi _1}{{\dot x}_2} - {{\dot d}_1} - {{\dddot x}_{1{\rm d}}} + {k_1}{{\ddot e}_1} + {k_2}{{\dot e}_2} + {k_3}{e_3}= \\ & gu - {\varphi _2}{x_2} - {\varphi _3}{x_3} - {d_2} - {\varphi _1}\left( {{x_3} - {\varphi _1}{x_2} - {d_1}} \right)- \\ & {{\dot d}_1} - {{\dddot x}_{1{\rm d}}} + {k_1}{{\ddot e}_1} + {k_2}{{\dot e}_2} + {k_3}{e_3} \, . \end{split} $

为了抑制传感器的测量噪声，采用期望指令信号x_1d、x_2d、x_3d分别代替x₁、x₂、x₃进行补偿，在期望情况下，e₁=0，d₁=0，则有

(9) $ \left. \begin{array}{l} {x_1} = {x_{1{\rm d}}} + {e_1} \, ; \\ {x_2} = {x_{2{\rm d}}} + {{\dot e}_1},\;\,{x_{2{\rm d}}} \triangleq {{\dot x}_{1{\rm d}}}\, ; \\ {x_3} = {x_{3{\rm d}}} + {{\ddot e}_1} + {\varphi _1}{{\dot e}_1} + {d_1},\;\,{x_{3{\rm d}}} \triangleq {{\ddot x}_{1{\rm d}}} + {\varphi _1}{{\dot x}_{1{\rm d}}}\, . \end{array} \right\} $

将式（9）代入式（8），可得

(10) $\begin{split} r =& gu - {\varphi _2}{x_{2{\rm d}}} - {\varphi _3}{x_{3{\rm d}}} - {\varphi _3}{d_1} - {d_2} - {{\dot d}_1}- \\ & {\varphi _1}{{\ddot x}_{1{\rm d}}} - {{\dddot x}_{1{\rm d}}} - \left( {{\varphi _1} + {\varphi _3} - {k_1}} \right){{\ddot e}_1} + {k_2}{{\dot e}_2} + \\ & {k_3}{e_3} - \left( {{\varphi _2} + {\varphi _1}{\varphi _3}} \right){{\dot e}_1} \, . \end{split} $

在期望情况下，由e₁恒为0可以推出 ${\dot e_1}$、 ${\ddot e_1}$、 ${\dot e_2}$、e₃均为0，因此期望辅助信号r_d的具体形式为

(11) $\begin{split} {r_{\rm d}} = gu - {\varphi _2}{x_{2{\rm d}}} - {\varphi _3}{x_{3{\rm d}}} - {\varphi _3}{d_1} - {d_2} - {{\dot d}_1} - {\varphi _1}{{\ddot x}_{1{\rm d}}} - {{\dddot x}_{1{\rm d}}} \, . \end{split} $

设计鲁棒控制器如下：

(12) $\left.\begin{aligned} u = & \left( {{u_{\rm a}} + {u_{\rm s}}} \right)/g,\;{u_{\rm s}} = {u_{{\rm s}1}} + {u_{{\rm s}2}},\;{u_{{\rm s}1}} = - {k_3}{e_3}, \\ {u_{{\rm s}2}} =& - \int\limits_0^t {\left[ {{k_{\rm r}}{k_3}{e_3}\left( \upsilon \right) + \beta {\rm{sgn}}\left( {{e_3}\left( \upsilon \right)} \right)} \right]} {\rm d}\upsilon - \\ & {k_{\rm r}}{e_3} + {k_{\rm r}}{e_3}\left( 0 \right) \, . \end{aligned}\right\} $

式中：k₃>0，k_r>0为控制器增益，β>0为鲁棒增益，u_a为基于模型的补偿项，u_s1为线性鲁棒反馈项，u_s2为RISE鲁棒项.

根据式（11）设计模型补偿项u_a为

(13) ${{u}_{\rm a}}={{\varphi }_{2}}{{x}_{2{\rm d}}}+{{\varphi }_{3}}{{x}_{3{\rm d}}}+{{\varphi }_{1}}{{\ddot{x}}_{1{\rm d}}}+{{\dddot x}_{1{\rm d}}} +{{\varphi }_{3}}{{\hat{d}}_{1}}+{{\hat{d}}_{2}}+{{\hat{\dot{d}}}_{1}}\, .$

式中： ${{\hat{d}}_{1}}{\text{、}}{{\hat{d}}_{2}}{\text{、}}{{\hat{\dot{d}}}_{1}}$分别为 ${d_1}{\text{、}}{d_2}{\text{、}}{\dot d_1}$的估计值.

基于该鲁棒控制器，将式（13）代入式（10），可得

(14) $ \begin{split} r= & {{\varphi }_{3}}{{\tilde{d}}_{1}}+{{\tilde{d}}_{2}}+{{\tilde{\dot{d}}}_{1}}+{{u}_{{\rm s}2}}-\left( {{\varphi }_{2}}+{{\varphi }_{1}}{{\varphi }_{3}} \right){{\dot{e}}_{1}}- \\ & \left( {{\varphi }_{1}}+{{\varphi }_{3}}-{{k}_{1}} \right){{\ddot{e}}_{1}}+{{k}_{2}}{{\dot{e}}_{2}} \, . \end{split} $

对式（14）两边求微分，可得

(15) $ \dot r = N - {k_{\rm r}}r - \beta {\rm{sgn}}\left( {{e_3}} \right) - {\lambda _1}{e_1} - {\lambda _2}{e_2} - {\lambda _3}{e_3} - {\lambda _{\rm r}}r\, . $

式中：λ₁=(φ₂+φ₁φ₃)k₁²−(φ₁+φ₃−k₁)k₁³，λ₂= (φ₁+φ₃−k₁)(k₁²+k₁k₂+k₂²)−k₂³−(φ₂+φ₁φ₃)(k₁+k₂)，λ₃=φ₂+φ₁φ₃+k₂²+k₂k₃−(φ₁+φ₃−k₁)(k₁+k₂+k₃)k₁³，λ_r=φ₁+φ₃−k₁−k₂， $N\triangleq {{\varphi }_{3}}{{\dot{\tilde{d}}}_{1}}+{{\dot{\tilde{d}}}_{2}}+{{\dot{\tilde{\dot{d}}}}_{1}}$.

根据式(6)与假设3，可知

(16) $\left| N \right| \leqslant {\delta _1},\;\;\left| {\dot N} \right| \leqslant {\delta _2}.$

式中：δ₁、δ₂为已知正数.

由式（7）、（15）可知，系统的动态误差方程为

(17) $\left.\begin{array}{l} {{\dot e}_1} = {e_2} - {k_1}{e_1}\, , \\ {{\dot e}_2} = {e_3} - {k_2}{e_2}\, , \\ {{\dot e}_3} = r - {k_3}{e_3} \, , \\ \dot r = N - {k_{\rm r}}r - \beta {\rm{sgn}}\left( {{e_3}} \right)- \\ \;\;\;\; {\lambda _1}{e_1} - {\lambda _2}{e_2} - {\lambda _3}{e_3} - {\lambda _{\rm r}}r \, . \end{array} \right\}$

为了方便后续控制器稳定性的证明，给出如下的引理.

引理1　定义变量L(t)及辅助函数P(t)如下：

(18) $\left.\begin{array}{l} L\left( t \right) = r\left[ {N - \beta {\rm{sgn}}\left( {{e_3}} \right)} \right] \, , \\ P\left( t \right) = \beta \left| {{e_3}\left( 0 \right)} \right| - {e_3}\left( 0 \right)N\left( 0 \right) - \int\limits_0^t {L\left( \upsilon \right)} {\rm d}\upsilon \, . \end{array}\right\} $

若鲁棒增益β满足条件：

(19) $\beta > {\delta _1} + {\delta _2}/{k_3}\, ,$

则有P(t)>0恒成立.

证明：见文献[21]、[22].

定理1　给定一个非线性系统，如式（4）所示，若在满足式（19）的条件下，通过调节反馈增益k₁、k₂、k₃、k_r，能够使得如下定义的矩阵Λ为正定矩阵：

(20) $\varLambda = \left[ {\begin{array}{*{20}{c}} {{k_1}}&{ - \displaystyle\frac{1}{2}}&0&{\displaystyle\frac{{{\lambda _1}}}{2}} \\ { - \displaystyle\frac{1}{2}}&{{k_2}}&{ - \displaystyle\frac{1}{2}}&{\displaystyle\frac{{{\lambda _2}}}{2}} \\ 0&{ - \displaystyle\frac{1}{2}}&{{k_3}}&{\displaystyle\frac{{{\lambda _3} - 1}}{2}} \\ {\displaystyle\frac{{{\lambda _1}}}{2}}&{\displaystyle\frac{{{\lambda _2}}}{2}}&{\displaystyle\frac{{{\lambda _3} - 1}}{2}}&{{k_{\rm r}} + {\lambda _{\rm r}}} \end{array}} \right]\, ,$

则提出的控制律（12）能够保证所有的系统信号都是有界的，且当时间趋于无穷大时，系统误差e₁能够渐进收敛到0.

证明：根据控制理论中系统的稳定性分析，选取Lyapunov方程为

(21) $V = \frac{1}{2}\left( {{e_1}^2 + {e_2}^2 + {e_3}^2 + {r^2}} \right) + P\left( t \right).$

由引理1可知，V恒为正.

定义变量e=[e₁，e₂，e₃，r]^T，将式（17）、（21）代入求导后的Lyapunov方程，可得

(22) $\begin{split} \dot V = & {e_1}{{\dot e}_1} + {e_2}{{\dot e}_2} + {e_3}{{\dot e}_3} + r\dot r + \dot P = \\ & - {k_1}{e_1}^2 + {e_1}{e_2} - {k_2}{e_2}^2 + {e_2}{e_3} - {k_3}{e_3}^2 +\\ & \left( {1 - {\lambda _3}} \right){e_3}r - \left( {{k_{\rm r}} + {\lambda _{\rm r}}} \right){r^2} - {\lambda _1}{e_1}r - {\lambda _2}{e_2}r \, . \end{split} $

因此有

(23) $\dot V \leqslant - {\lambda _{\min }}\left( \varLambda \right)\left( {{e_1}^2 + {e_2}^2 + {e_3}^2 + {r^2}} \right) \triangleq - W\, .$

由式（23）可知： $\forall t > 0,V\left( t \right) < V\left( 0 \right)$，由此可知V有界，因此e有界，系统的所有信号都是有界的.

对式（23）积分，可得

(24) $\int_0^t {W\left( \upsilon \right){\rm d}\upsilon } \leqslant - \int_0^t {\dot V\left( \upsilon \right){\rm d}\upsilon } = V\left( 0 \right) - V\left( t \right) \leqslant V\left( 0 \right).$

由式（24）可知， $W \in {L_2}$范数，且根据式（17）可得 $\dot W \in {L_\infty }$范数，因此W是一致连续的. 由Barbalat引理可知：当t→∞时，W→0，即e→0. 当t→∞时，e₁→0，由此证明了系统的渐进稳定性.

为了验证所提的控制策略，采用4种性能指标（最大值、平均值、标准差、归一化的控制输入变化量）评价跟踪的性能，分别定义如下.

1）跟踪误差的最大绝对值为

(25) ${M_{\rm e}} = \mathop {\max }\limits_{i = 1,\cdots,N} \left\{ {\left| {{e_1}(i)} \right|} \right\}.$

式中：N为记录的数字信号的数量.

2）跟踪误差的平均值为

(26) $\mu = \frac{1}{N}\sum\limits_{i = 1}^N {\left| {{e_1}(i)} \right|} .$

3）跟踪误差的标准差为

(27) $\sigma = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left[ {\left| {{e_1}(i)} \right| - \mu } \right]}^2}} } .$

4）归一化的控制输入变化量为

(28) ${L_{\rm c}} = \frac{{\sqrt {\displaystyle\frac{1}{N}\displaystyle\sum\limits_{i = 1}^N {{{\left| {u(i\Delta T) - u((i - 1)\Delta T)} \right|}^2}} } }}{{\sqrt {\displaystyle\frac{1}{N}\displaystyle\sum\limits_{i = 1}^N {{{\left| {u(i)} \right|}^2}} } }}.$

式中：u(i)为控制输入； $\Delta T$为采样时间，取0.5 ms.

电液位置伺服系统实验平台如图2所示. 该平台由如下部分组成：一个包含导轨的工作台；一个由双杆液压缸组成的液压定位系统，高效冲压面积A=904.778 mm²，行程为±44 mm；用于测量位置和速度信息的线性编码器，精度等级为±5 μm，型号为Heidenhain LC483；2个用于测量p₁和p₂的油压传感器，型号为MEAS US175-C00002-200BG，测量精度为1 bar；带宽在120 Hz以上的伺服阀，型号为Moog G761-3003，额定体积流量为19 L/min，压力为7 MPa；一个驱动轴；一个负载质量块，质量m=30 kg；p_s=10 MPa的液压油供应路；测量和控制系统.

测量和控制系统由监控软件和实时控制软件组成，A/D卡型号为Advantech PCI-1716，D/A卡为Advantech PCI-1723，计数卡为Heidenhain IK-220，所有这些卡均为16位. 监控软件使用NI LabWindows/CVI编程，实时控制软件使用Microsoft Visual Studio 2005和Ardence RTX 7.0编译. Ardence RTX 7.0用于为Windows XP操作系统下的实时控制软件提供实时工作环境.

液压系统参数如下：m=30 kg，B=4 000 N/(m·s)，A = 9.05×10⁻⁴ m²，V_t=7.96×10⁻⁵ m³，β_e=700 MPa，C_t=10⁻¹² m³/(s·Pa)，k_t=1.196 9×10⁻⁸ m³/(s·V·Pa^−1/2)，p_s=10 MPa，p_r=0.08 MPa，采样时间为0.5 ms.

为了验证提出控制方案的有效性，选取以下4种控制策略进行对比实验.

1）基于FTDO的鲁棒积分跟踪控制器，记为RF，具体形式为式（12）、（13）.

2）有限时间干扰观测器，记为FTDO，具体形式如下：

(29) $\left. \begin{array}{l} {e_1} = {x_1} - x{}_{1{\rm d}},\;{e_2} = {{\dot e}_1} + {k_1}{e_1}{\rm{ = }}{x_2} - {\alpha _1},\;{\alpha _1} \triangleq {{\dot x}_{1{\rm d}}} - {k_1}{e_1}\, , \\ {e_3} = {{\dot e}_2} + {k_2}{e_2} = {x_3} - {\alpha _2},\;{\alpha _2} = {\varphi _1}{x_2} + {{\dot \alpha }_1} + {{\hat d}_1} - {k_2}{e_2} \, . \end{array}\right\} $

(30) $\begin{split} u = {u_{\rm a}} + {u_{\rm s}},{u_{\rm s}} = - {k_3}{e_3}/g,\; {u_{\rm a}} = \left( {{\varphi _2}{x_2} + {\varphi _3}{x_3}{\rm{ + }}{{\dot \alpha }_2} + {{\hat d}_2}} \right)/g \, . \end{split} $

3）速度前馈PI控制器，记为VFPI，具体形式如下：

(31) $u = {k_{\rm P}}{e_1}(t) + {k_{\rm I}}\int {{e_1}(t)} {\rm d}t + {k_{\rm D}}{\dot e_1}(t) + {k_{\rm F}}{\dot x_{1{\rm d}}}.$

式中：e₁(t)=x₁−x_1d；k_P、k_I、k_D分别为比例常数、积分常数、微分常数；k_F为速度前馈系数，取为0.028 1 V·s/mm.

4）反馈线性化控制器，记为FLC，具体形式如下：

(32) $\left. \begin{array}{l} {e_1} = {x_1} - x{}_{1{\rm d}},\;{e_2} = {{\dot e}_1} + {k_1}{e_1}{\rm{ = }}{x_2} - {\alpha _1},\;{\alpha _1} \triangleq {{\dot x}_{1{\rm d}}} - {k_1}{e_1}\, , \\ {e_3} = {{\dot e}_2} + {k_2}{e_2} = {x_3} - {\alpha _2},\;{\alpha _2} = {\varphi _1}{x_2} + {{\dot \alpha }_1} - {k_2}{e_2} \, . \end{array} \right\} $

(33) $ \left. \begin{split} u = & {u_{\rm a}} + {u_{\rm s}},{u_{\rm s}} = - {k_3}{e_3}/g\, , \\ {u_{\rm a}} =& \left( {{\varphi _2}{x_2} + {\varphi _3}{x_3}{\rm{ + }}{{\dot \alpha }_2}} \right)/g \, . \end{split}\right\} $

各控制策略的参数取值如下.

1）RF参数如下：k₁=1 800，k₂=200，k₃=100，k_r=100，β=500，a₁=30，a₂=25，a₃=40，a₄=6 000，a₅=1 000.

2）FTDO参数如下：k₁=1 800，k₂=200，k₃=100，a₁=30，a₂=25，a₃=40，a₄=6 000，a₅=1 000.

3）VFPI参数：k_P=8 000，k_I=2 000，k_D=0.

4）FLC参数：k₁=1 800，k₂=200，k₃=100.

对于实验测试信号的幅值选取，是依据现有的实验平台物理参数进行选取的. 由于实验平台液压缸活塞的行程是±44 mm，选择一个在该行程之间的测试信号幅值，选为10 mm.

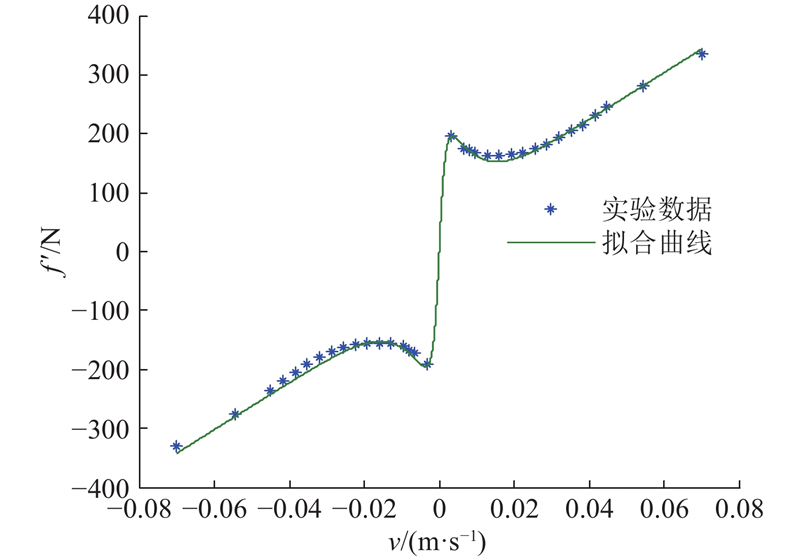
对于测试信号的频率选取，是根据图3所示的实验辨识的摩擦力（系统主要的干扰）曲线进行选取的. 图中，f′为摩擦力，v为速度. 在实际情况下，一般实验工况均为0.5 Hz的中等速度工况，为了考查RF控制器在不同频率下的跟踪性能，选择3种频率进行实验，分别为0.5、0.2、1.0 Hz.

对于测试信号幅值为10 mm，实验工况为0.2 Hz的正弦测试信号，最大速度约等于0.013 m/s，由辨识的摩擦力曲线可知，在该速度范围内运动，系统的摩擦力集中在未建模的Stribeck效应区域，可以用于验证提出的控制算法对于未建模扰动的鲁棒性；对于测试信号幅值为10 mm，实验工况为0.5 Hz的正弦测试信号，最大速度为0.031 4 m/s，属于中等速度区域；对于测试信号幅值为10 mm，实验工况为1 Hz的正弦信号，最大速度为0.062 8 m/s，属于较快速工况.

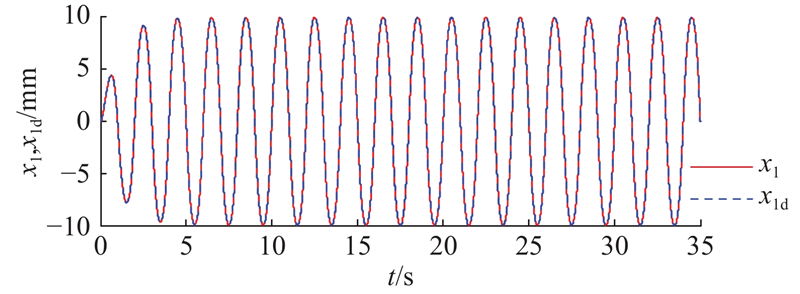
在0.5 Hz的中等速度工况下，选取期望指令信号为x_1d=10arctan (sin(πt))[1−e^-t]/0.785 4 mm.

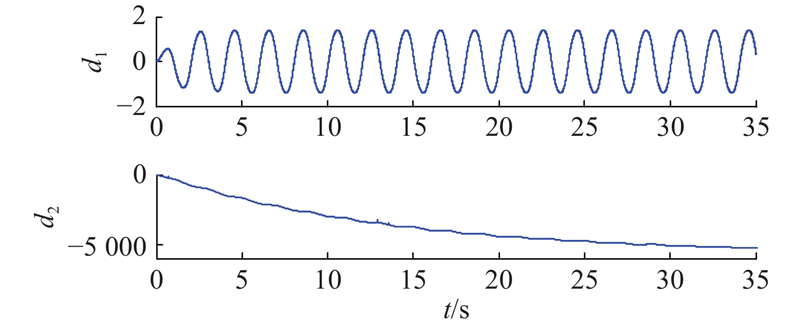
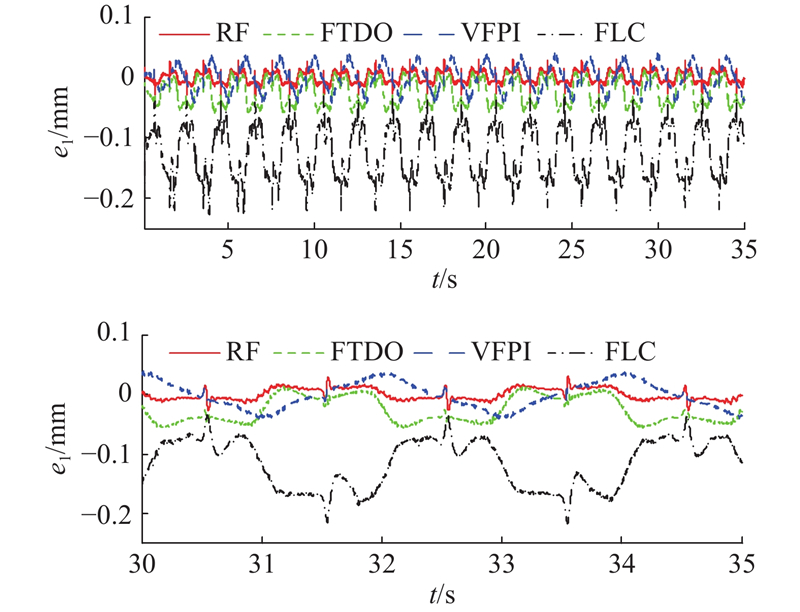
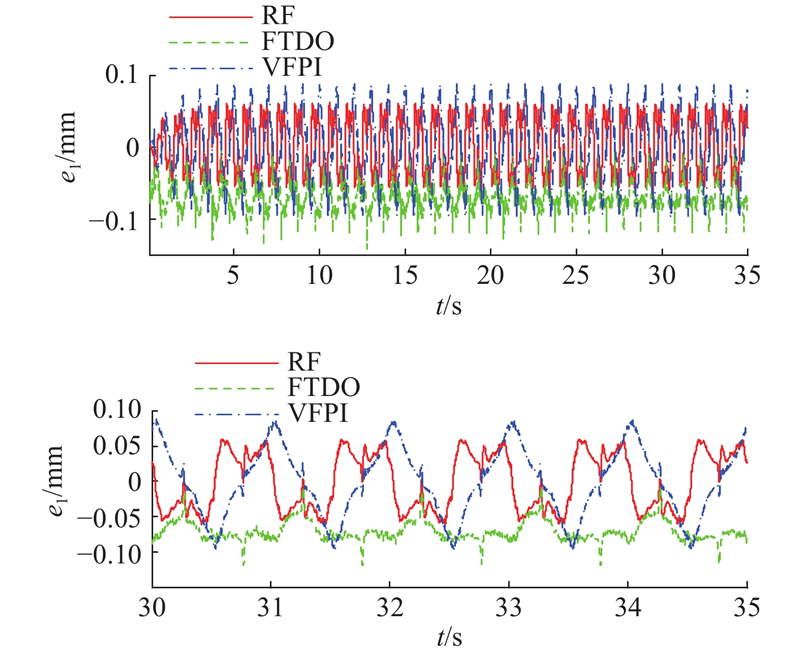
如图4所示为RF控制器作用下的干扰估计. 如图5所示为各控制器作用下系统的跟踪误差对比. 可以看出，FLC作用下得到的跟踪误差效果不太理想；在FLC的基础上添加了FTDO的控制效果得到了极大的提高，不仅系统的跟踪精度明显提高，而且零点漂移问题得到了改善，说明所设计的FTDO观测器在控制性能的改善上发挥了至关重要的作用，验证了所设计FTDO观测器的有效性；RF控制策略是在FTDO的基础上融合了积分鲁棒控制，实验表明，跟踪精度得到了进一步的提升，由此可以推出新加入的积分鲁棒控制策略的有效性. 与FLC相比，RF控制器不仅极大地提高了系统的跟踪精度，而且零点漂移问题得到了改善，由此可以推出RF控制策略有很好的处理干扰，提高系统的跟踪精度.

如图6所示为RF作用下控制输入的变化情况. 如图7、8所示分别为RF控制器作用下系统的位置跟踪曲线和压力变化图. 如表1所示为3个控制器的各项性能指标对比情况. 可以看出，RF控制效果总体上明显优于其他控制器，反映了RF控制器能够很好地抵抗干扰的能力.

由工况1可以看出，FLC的控制效果不太理想，之后的实验工况中只作了前3种控制器的对比实验. 在实验频率为0.2 Hz的慢变工况下，选取期望指令信号x_1d=10arctan (sin(0.4πt))[1−e^-t]/0.785 4 mm作为测试信号.

该工况考查在慢变跟踪下的控制性能. 各控制器作用下系统位置的跟踪误差对比如图9所示. 可以看出，在RF控制器作用下，系统能够达到渐进稳定状态. 如表2所示为各控制器的性能指标对比. 可以看出，RF控制器的控制性能整体上较优于其他控制器，但在跟踪误差的最大绝对值M_e这一指标上相对于VFPI来说优势不明显. 总体来说，RF控制器在0.2 Hz的慢变跟踪工况下能够较好地抵抗干扰对系统的影响.

在实验频率为1 Hz的快变工况下，选取期望指令信号x_1d=10arctan (sin (2πt))[1−e^-t]/0.785 4 mm作为测试信号.

该工况考查在快变跟踪下的控制性能. 各控制器作用下系统位置的跟踪误差对比如图10所示. 可以看出，在RF控制器作用下，系统能够达到渐进稳定状态且跟踪效果优于其他控制器. 如表3所示为各控制器的性能指标对比. 可以看出，RF控制器的性能指标均明显优于其他控制器，反映了RF控制器在1 Hz的快变跟踪工况下能够很好地抵抗干扰对系统的影响.

本文提出基于FTDO的电液位置伺服系统鲁棒积分跟踪控制策略，实现了匹配干扰和不匹配干扰同时在线观测. 通过设计基于误差符号函数（RISE）的FTDO观测器，实现了干扰在线观测，将FTDO融合设计于RISE控制策略中，提高了干扰观测的准确度和系统的稳定性. 结合期望补偿提高了针对干扰的模型补偿精度，增强了电液位置伺服系统抵抗干扰的能力. 通过Lyapunov稳定性理论，证明了闭环系统的全局渐进稳定性. 对比实验结果显示，RF控制器与VFPI相比跟踪精度提高了25%左右，与FTDO相比跟踪精度提高了45%左右，有效解决了干扰对系统稳定性和跟踪精度的影响，提高了电液位置伺服系统在干扰作用下的跟踪性能.

本文对于高频下的指令跟踪问题讨论较浅，在后续的研究工作中，笔者将更加关注电液伺服系统高频非线性控制的研究工作.