在现代工业生产与科学研究中,真空技术的应用非常广泛。罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] 。罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域。理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] 。在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取。李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] 。在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向。罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] 。具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] 。此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度。在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] 。2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限。在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别。显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道。在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性。因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失。上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏。鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型。本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值。
1 罗茨泵转子轮廓构造
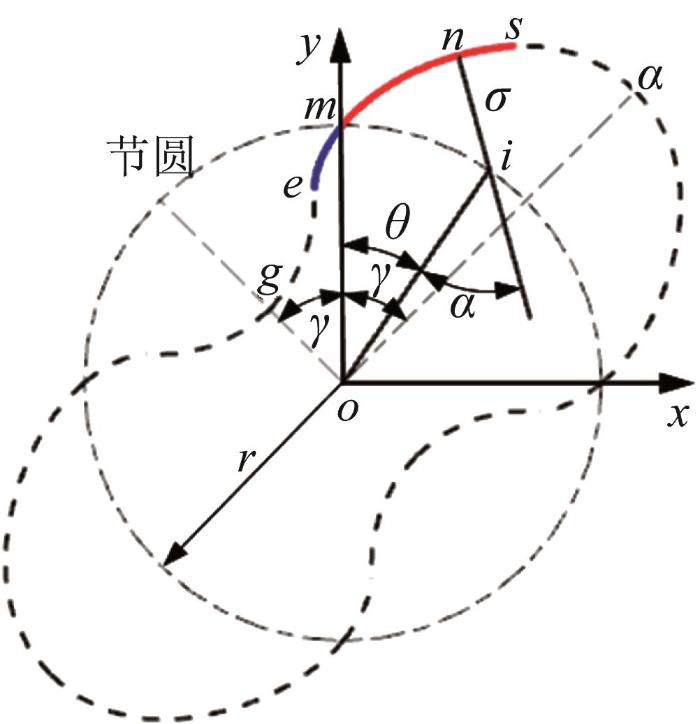
罗茨泵转子轮廓由顶过渡圆弧a s ̑ s m ̑ m e ̑ e g ̑ 图1 所示。其中,a s ̑ e g ̑ oa、og 与节圆的交点。
图1
图1
转子轮廓构造及其坐标系构建
Fig.1
Rotor contour structure and its coordinate system construction
在图1 所示的坐标系xoy 下,由啮合点n (x , y )的参数化坐标,可得啮合轮廓方程:
x ( θ ) = r s i n θ - σ s i n ( α - θ ) y ( θ ) = r c o s θ + σ c o s ( α - θ )
x r 2 + y r 2 = 1 + σ r 2 + 2 σ r c o s α
式中:σ 和α 均为ε 的解析函数。啮合点位于m e ̑ σ 为正,位于m s ̑ σ 为负。
啮合轮廓在不同曲线类型下的解析函数可参见文献[9 ]。其中,渐开线啮合轮廓为:
σ r ( θ , ε ) = ε - 1 γ θ , α ( θ , ε ) = a r c s i n ε - 1 γ
由此构建的转子轮廓具有关于唯一变量ε 的全参数化特征。此外,研究中所有插图均采用UGNX 9.0软件绘制,根据啮合轮廓方程(1),通过“工具”→“表达式”录入、“插入”→“曲线”→“规律曲线”生成,以保证研究结果的准确性与可重复性。
在转子啮合轮廓曲线类型相同的前提下,其形状系数的最大值由转子叶数唯一确定。文献[9 ]和文献[25 ]已针对不同轮廓曲线类型的转子,推导出最大形状系数与转子叶数之间的关系式。基于上述理论基础及本研究的建模前提,本文结论的适用范围如下:其一,在介质类型上,适用于以空气为主要成分的气体或蒸汽介质(本研究的核心推导以空气为介质展开);其二,在设备结构上,适用于二叶转子罗茨泵。
2 罗茨泵理论流量特性分析
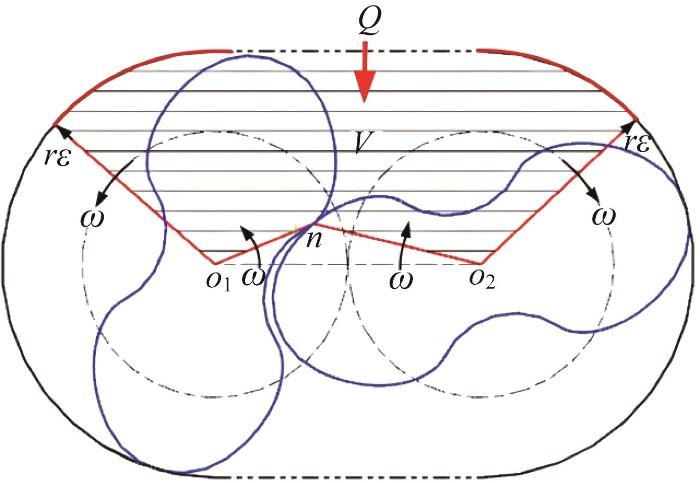
罗茨泵的理论流量通过求解转子副旋转所扫过的面积获得[9 ] ,如图2 所示。其中,画有剖面线的动态封闭容积为V ,2个转子的旋转角速度均为ω 。
图2
图2
罗茨泵理论流量求解方法
Fig.2
Solution method of theoretical flow of Roots pump
d V ( θ , ε ) = 2 × 1 2 b ( r ε ) 2 d θ - 1 2 b r n 1 2 d θ - 1 2 b r n 2 2 d θ = 1 2 b 2 ( r ε ) 2 - r n 1 2 - r n 2 2 ω d t
主动轮上的轮廓点和从动轮上的轮廓点在点n 处啮合,所以两者具有相同的α 和互为正负的σ ,则由式(2),可得:
r n 1 r 2 + r n 2 r 2 = 2 + 2 σ r 2
Q ( θ , ε ) = r 2 b ω ε 2 - 1 - σ r 2
Q m a x ( ε ) = Q ( 0 , ε ) = r 2 b ω × ( ε 2 - 1 ) Q m i n ( ε ) = Q ( γ , ε ) = r 2 b ω × ε 2 - 1 - ( ε - 1 ) 2 Q a v e ( ε ) = 1 γ ∫ 0 γ Q ( θ , ε ) d θ = ( r ε ) 2 b ω λ
ξ ( ε ) = Q m a x - Q m i n Q a v e = ( ε - 1 ) 2 λ ε 2 = ( 1 - 1 / ε ) 2 λ
文献[8 ]给出了不同啮合轮廓曲线类型下的容积利用系数。其中,渐开线啮合轮廓的容积利用系数为:
λ ( ε ) = 1 - 1 ε 2 - 1 3 1 - 1 ε 2
3 罗茨泵内三大泄漏流量计算
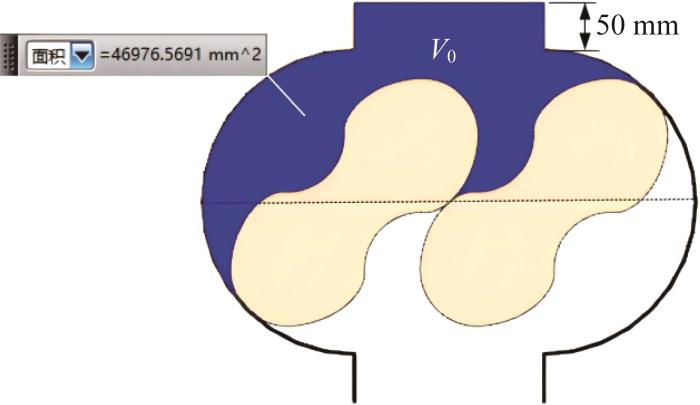
罗茨泵内三大泄漏流量(径漏流量、啮漏流量和端漏流量)的计算和后续CFD仿真均采用表2 所示的参数值。其中,预抽基准容积V 0 如图3 所示。
图3
图3
罗茨泵真空预抽基准容积
Fig.3
Baseline volume of vacuum pre-pumping for Roots pump
V 0 值可通过UGNX软件的“分析”→“测量面”→“面积”×b 来求得,也可直接计算如下:
V 0 ( ε ) = 2 r ( r ε + 50 ) + 0.5 π ( r ε ) 2 - ( 1 - λ ) π ( r ε ) 2 × b = 0.018 8 m 3
径漏的几何特征为非同心圆环缝隙,啮漏的几何特征为凸-凸双曲面缝隙,因此可采用孔口泄漏模型。
由孔口流量计算公式[26 ] 及基准空气压力p 0 折算到进口真空压力p 下的泄漏流量[27 ] ,得到径漏返流流量为:
Q 1 ( p ) = 2 C 1 A 1 p 0 p 2 ( p 0 - p ) ρ 0
Q 2 ( p ) = C 2 A 2 p 0 p 2 ( p 0 - p ) ρ 0
需要说明的是,C ₁、C ₂的取值需优先结合孔口几何形状(其边缘结构为核心考量项)、流动可压缩性(以压力比、马赫数为主要评价指标)等要素确定,且两者的取值精度将直接决定预测模型的计算精度。参考文献[28 ],对于锐缘结构的方形或矩形孔口:当孔口长宽比接近1时,系数取值为0.55~0.60;当孔口为狭长缝隙时,系数取值降至0.50~0.55。由于本文中Q ₁、Q ₂均对应狭长缝隙的返流流量,故C ₁、C ₂均取为0.55。在实际应用时,可通过实验或仿真对该系数进行精准测定与修正,确保模型计算结果的可靠性。
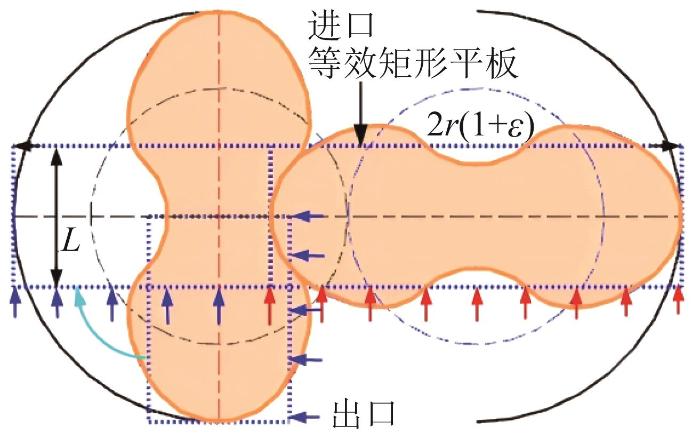
由于传统平行圆盘泄漏模型的计算误差较大[29 ] ,本文提出一种改进方案:采用端漏面积相同的新型等效平行矩形板,如图4 所示。其中:朝上的红色箭头指示对应于从动转子全端面的等效平行矩形板的上端泄漏方向;朝左的蓝色箭头指示对应于主动转子单叶半端面的等效平行矩形板的泄漏方向。需要特别说明的是:在主动转子逆时针旋转之前,在该蓝色箭头所示位置主动转子左侧的工作腔始终与进口腔相通,腔内介质的压力维持在进口压力水平;同时,主动转子的单叶半端面等效平行矩形板顺时针旋转90°后,能够与从转子的全端面等效平行矩形板拼接成一个完整的端漏等效平行矩形板。
图4
图4
相同端漏面积的等效平行矩形板
Fig.4
Equivalent parallel rectangular plate with same end-leakage area
L = ( 1 - λ ) π ( r ε ) 2 2 r ε = 1 2 π r ε ( 1 - λ ) = 110 m m
等效平行矩形板的宽度为2r (1+ε ),可得端漏返流流量为:
Q 3 ( p ) = 2 × 2 r ( 1 + ε ) δ 3 3 12 μ L ( p 0 - p ) = r ( 1 + ε ) δ 3 3 3 μ L ( p 0 - p )
4 罗茨泵极限真空度及其预抽时间分析
Q a v e ( ε ) = Q 1 ( p ) + Q 2 ( p ) + Q 3 ( p )
Q 1 ( p ) + Q 2 ( p ) + Q 3 ( p ) - Q a v e ( ε ) = 0
对于式(16),有2种求解方法:一是通过Excel软件的“数据”菜单进入“模拟分析”,选择“单变量求解”功能;二是通过UG NX软件的“分析”菜单进入“优化和灵敏度”,调用“优化”工具。通过这2种方法,均求得p min =16.533 kPa。结合模型集成性考量,优选后者进行求解。
忽略抽气过程中V 0 的变化,将原有pV 0 气体与p (Q 1 +Q 2 +Q 3 -Q ave )dT 0 的微量气体进行等温混合。
p V 0 + p ( Q 1 + Q 2 + Q 3 - Q a v e ) d T 0 = ( p + d p ) V 0
T 0 = ∫ p m i n p 0 V 0 p ( Q 1 + Q 2 + Q 3 - Q a v e ) d p = 0.1636 s
由将p 0 下的V 0 转换成p min 下的V 0max ,得到极限真空度预抽时间的解析解为:
T 0 = V 0 m a x - V 0 Q a v e = V 0 Q a v e p 0 p m i n - 1 = 0.1598 s
解析解与数值解的误差为2.38%。这里给出数值解旨在验证解析解的正确性。
T = T 0 × V s V 0 = 141.71 m i n
5 CFD 仿真验证
5.1 仿真软件
采用泵用CFD专业软件Pumplinx。该软件集成了通用网格模块与模板网格模块,其中模板网格模块具备高效的间隙网格生成能力——操作时仅需输入间隙的内外半径、偏心距及宽度等参数,即可自动生成高质量的间隙网格。
5.2 仿真模型
仿真中介质参数和边界参数的设置如表3 所示。其中,初始转动300次,待流场趋于稳定后可手动终止计算。
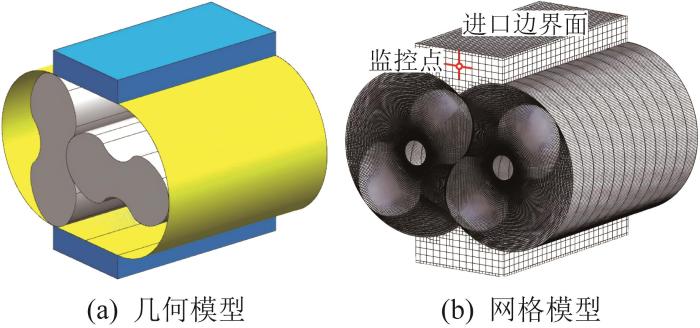
几何模型通过UG NX软件构建,其包含主/从动转子体、主/从动转子壁片体及进/出口实体,如图5 (a)所示。模型关键间隙参数的设置如表2 所示。其中,啮漏间距通过将主/从动转子的啮合面沿面内方向偏置0.15 mm实现。为了提升几何精度,在导出STL格式文件时,将“三角公差”和“相邻公差”由默认的0.08 mm调整为0.01 mm。
图5
图5
仿真模型
Fig.5
Simulation model
在Pumplinx软件中构建网格模型,如图5 (b)所示。构建流程为:1)导入上述STL格式的文件;2)按非联通区域对几何体进行分割,并将单位从“mm”转换为“m”;3)对主/从动转子体生成专用转子网格,采用通用网格模块对进/出口实体生成网格;4)通过多重网格界面(multiple grid interfaces,MGI)连接选定的边界,最终构建一体化连续网格模型。其中,转子网格采用高级生成模式,其核心参数设置:侧漏间距为0.000 3 m,间隙内径为0.024 m,间隙外径为0.016 01 m,转子中心距为0.2 m。
仿真中的核心设置主要包含四部分:仿真模块选择、转子运动参数设置、介质物性参数设置和边界与监控点设置。
5.3 仿真结果与分析
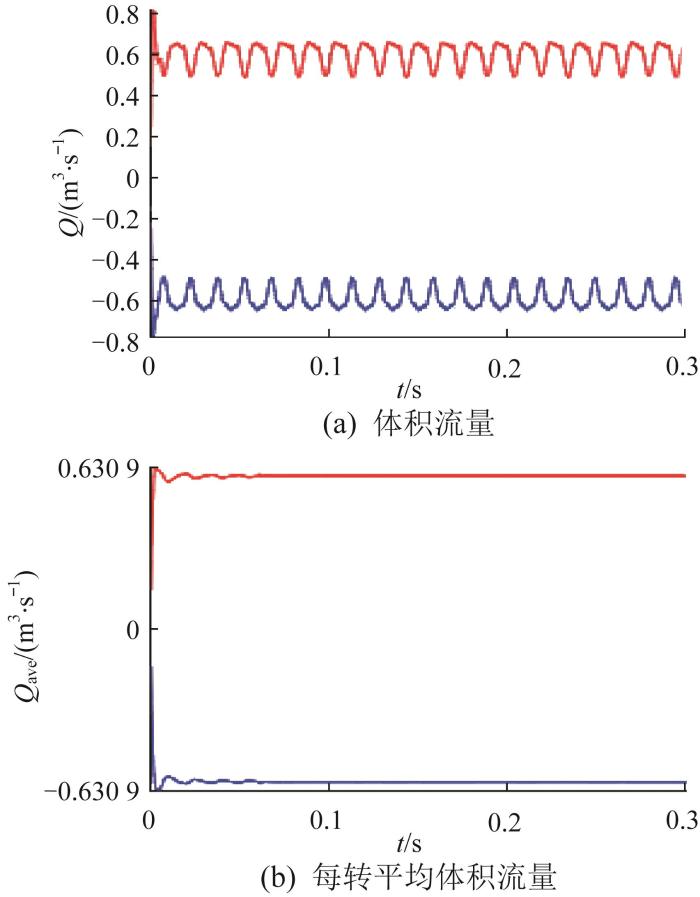
在进出口零压差(无内泄漏)的前提下,项目I中进口边界面的体积流量和每转平均体积流量的仿真结果如图6 所示,仿真值与理论值的相对误差如表5 所示。
图6
图6
项目 I 仿真结果
Fig.6
Simulation results of project I
Q ave 、ξ 的相对误差分别为0.75%、3.84%,验证了式(1)至式(8)理论推导的正确性和仿真方法的可靠性。
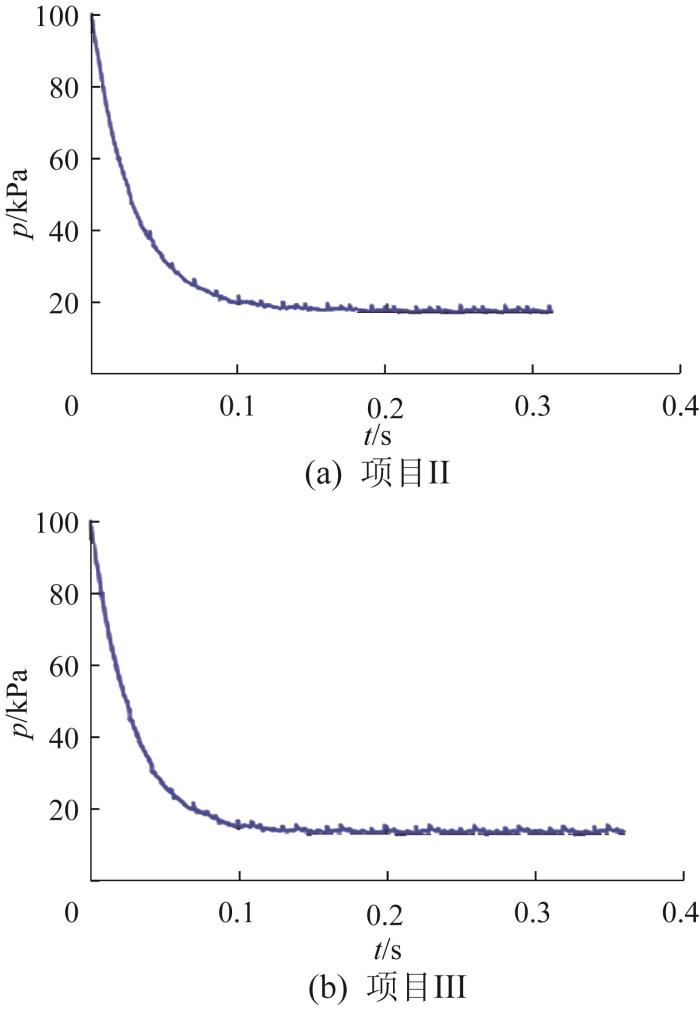
在项目Ⅱ、Ⅲ中监控点处的压力仿真结果如图7 所示,仿真值与理论值的相对误差如表6 所示。
图7
图7
项目II 和项目III 仿真结果
Fig.7
Simulation results of project II and project III
p min (Ⅱ)、p min (Ⅲ)、T 0 (Ⅲ)的相对误差分别为4.72%、4.03%、1.88%差,相互验证了式(9)至式(16)理论推导的正确性、仿真方法的可靠性及极限真空度及其预抽时间预测模型的高精度,同时验证了孔口流量及其进/出口压力的折算、等端漏面积矩形板等效方法的合理性。
预测模型的主要误差来源可归纳为以下三方面:其一为流量系数C ₁和C ₂的取值精度,该参数的准确性直接影响泄漏流量的计算结果,C ₁和C ₂取值越大,流量Q 1 和Q 2 越大,预抽时间T 越长,反之,则T 越短;其二为泵腔内介质分布及压力场的非均匀性,这种非均匀性会导致介质实际流动状态与理论假设存在偏差;其三,端漏计算中采用的等效平行矩形板模型虽然较传统模型提升了计算精度,但受限于模型对真实端漏通道几何形态的简化,仍无法完全消除与实际的偏差。
6 结 论
1)基于形状系数的全参数化转子轮廓模型,为罗茨泵理论流量及泄漏模型的推导奠定了统一的几何基础,显著提升了转子轮廓与性能参数的关联度;利用该模型,可通过UGNX软件快速生成转子实体轮廓,具有良好的可操作性与可重复性。
2)基于全参数化设计方法的理论流量解析方法,可准确计算不同转子轮廓(如渐开线)下的瞬时流量、平均流量及流量脉动系数。其中,渐开线轮廓下流量特性参数理论值与CFD仿真值的最大误差不超过3.84%,验证了该方法在流量特性评估中的有效性。
3)利用非同心圆环缝隙和渐开线凸-凸双曲面缝隙的孔口泄漏模型,尤其是等端漏面积的等效平行矩形板创新模型,可有效解决复杂间隙结构的泄漏流量计算难题。泄漏流量的计算结果与CFD仿真结果的一致性误差在4.72%以内,验证了泄漏模型的合理性和适用性。
4)利用基于理论抽气流量等于泄漏流量的极限真空度模型及基于预抽基准容积等温转化理论的预抽时间模型,可实现极限真空度及其预抽时间的精准预测。其中,极限真空度理论值与仿真值的相对误差为4.03%,预抽时间的相对误差为1.88%,兼顾了计算精度与效率。
5)预测模型经CFD仿真与多维度(流量特性、泄漏流量、极限真空度、预抽时间)验证,其误差均处于工程可接受范围内,且具备参数化设计特性,可直接应用于罗茨泵的性能优化与快速设计,为罗茨泵在中高真空系统的工程应用提供了可靠的理论支撑。
参考文献
View Option
[1]
RAYKOV A BURMISTROV A SALIKEEV S et al Working process of Roots vacuum pumps
[J]. Vakuum in Forschung und Praxis , 2021 , 33 (3 ): 29 -33 .
[本文引用: 1]
[2]
许海虹 RH用机械真空泵抽气过程影响因素研究
[J]. 真空科学与技术学报 , 2019 , 39 (3 ): 214 -225 .
[本文引用: 1]
XU H H Design of fume extraction unit for RH vacuum refining furnace: a simulation study
[J]. Chinese Journal of Vacuum Science and Technology , 2019 , 39 (3 ): 214 -225 .
[本文引用: 1]
[3]
高源 , 林梦竹 氢气循环泵的转子动力学特性分析
[J]. 同济大学学报(自然科学版) , 2025 , 53 (1 ): 107 -114 .
[本文引用: 1]
GAO Y LIN M Z Dynamic characteristics analysis of rotors in hydrogen circulation pump
[J]. Journal of Tongji University (Natural Science) , 2025 , 53 (1 ): 107 -114 .
[本文引用: 1]
[4]
刘振超 , 何雪明 , 黄海楠 NURBS曲线在罗茨泵转子型线设计中的应用
[J]. 食品与机械 , 2019 , 35 (7 ): 110 -116 .
[本文引用: 1]
LIU Z C HE X M HUANG H N Application of NURBS curve in rotor profile design of Roots pump
[J]. Food & Machinery , 2019 , 35 (7 ): 110 -116 .
[本文引用: 1]
[5]
胡冰 真空磁控溅射镀膜设备中罗茨泵的保养与维护
[J]. 玻璃 , 2019 , 46 (8 ): 42 -46 .
[本文引用: 1]
HU B Maintenance of Roots pump in vacuum magnetron sputtering coating equipment
[J]. Glass , 2019 , 46 (8 ): 42 -46 .
[本文引用: 1]
[6]
肖荣和 , 李玉龙 基于罗茨泵平均理论流量的转子容积利用系数反求法
[J]. 机械传动 , 2022 , 46 (6 ): 73 -77 .
[本文引用: 1]
XIAO R H LI Y L Inverse method on volume utilization factors of rotor based on average theoretical flow of Roots pump
[J]. Journal of Mechanical Transmission , 2022 , 46 (6 ): 73 -77 .
[本文引用: 1]
[7]
王建森 , 李文宣 , 司国雷 , 等 航空燃油斜齿轮泵瞬时几何流量的计算方法
[J]. 浙江大学学报(工学版) , 2025 , 59 (5 ): 1040 -1050 .
[本文引用: 1]
WANG J S LI W X SI G L et al Calculation method for instantaneous geometric flow rate of aviation fuel helical gear pump
[J]. Journal of Zhejiang University (Engineering Science) , 2025 , 59 (5 ): 1040 -1050 .
[本文引用: 1]
[8]
李玉龙 , 臧勇 , 赵岩 , 等 转子泵容积利用系数的通用计算模型
[J]. 排灌机械工程学报 , 2021 , 39 (2 ): 116 -121 .
[本文引用: 2]
LI Y L ZANG Y ZHAO Y et al General calculation model of effective volume utilization coefficient for rotor pumps
[J]. Journal of Drainage and Irrigation Machinery Engineering , 2021 , 39 (2 ): 116 -121 .
[本文引用: 2]
[9]
李玉龙 , 孙付春 , 刘萍 泵用凸转子的轮廓设计方法 [M].上海 : 上海交通大学出版社 , 2022 .
[本文引用: 5]
LI Y L SUN F C LIU P Profile design method of convex rotor for pumps [M]. Shanghai : Shanghai Jiaotong University Press , 2022 .
[本文引用: 5]
[10]
陈云鹏 , 张中波 , 陈亭西 齿轮泵内部间隙泄漏的研究综述
[J]. 液压气动与密封 , 2024 , 44 (5 ): 49 -57 .
[本文引用: 1]
CHEN Y P ZHANG Z B CHEN T X Review on internal clearance leakage of gear pump
[J]. Hydraulics Pneumatics & Seals , 2024 , 44 (5 ): 49 -57 .
[本文引用: 1]
[11]
BURMISTROV A RAYKOV A ISAEV A et al Efficiency improvement of Roots vacuum pump working process
[J]. Vakuum in Forschung und Praxis , 2022 , 34 (3 ): 32 -37 .
[本文引用: 1]
[12]
陈长琦 , 王旭迪 罗茨泵径向间隙泄漏量的研究与建模
[J]. 流体机械 , 2002 , 30 (11 ): 29 -31 .
[本文引用: 1]
CHEN C Q WANG X D Research and modeling of the leakage through the radial clearance of the Roots vacuum pump
[J]. Fluid Machinery , 2002 , 30 (11 ): 29 -31 .
[本文引用: 1]
[13]
李琴 , 王慧 , 黄志强 , 等 输油转子泵啮合间隙与转子叶数对泵性能影响规律研究
[J]. 过程工程学报 , 2022 , 22 (12 ): 1666 -1675 .
[本文引用: 1]
LI Q WANG H HUANG Z Q et al Research on influence of meshing clearance and number of rotor blades on pump performance
[J]. The Chinese Journal of Process Engineering , 2022 , 22 (12 ): 1666 -1675 .
[本文引用: 1]
[14]
饶罗 , 钟易成 轴向间隙对摆线转子泵性能影响的数值模拟研究
[J]. 机械制造与自动化 , 2021 , 50 (5 ): 110 -112 .
[本文引用: 1]
RAO L ZHONG Y C Axial clearance effects on performance of gerotor pump using numerial simulation
[J]. Machine Building & Automation , 2021 , 50 (5 ): 110 -112 .
[本文引用: 1]
[15]
李玉龙 , 孙付春 泵用齿轮副困油卸荷的H型侧隙结构研究
[J]. 工程设计学报 , 2019 , 26 (1 ): 15 -19 , 28 .
[本文引用: 1]
LI Y L SUN F C Research on H-shaped backlash structure on gear pairs for relief of trapped-oil in pumps
[J]. Chinese Journal of Engineering Design , 2019 , 26 (1 ): 15 -19 , 28 .
[本文引用: 1]
[16]
邢文帅 , 张帆 , 赵菲菲 , 等 内回流槽结构对罗茨泵内部流动特性的影响
[J]. 排灌机械工程学报 , 2024 , 42 (5 ): 448 -455 .
[本文引用: 1]
XING W S ZHANG F ZHAO F F et al Influence of inner reflux groove structure on flow characteristics of Roots pump
[J]. Journal of Drainage and Irrigation Machinery Engineering , 2024 , 42 (5 ): 448 -455 .
[本文引用: 1]
[17]
杜浩强 , 张永强 , 顾广溪 , 等 齿轮泵泄漏计算、卸荷槽优化和性能测试的实验研究
[J]. 机电工程 , 2024 , 41 (10 ): 1914 -1922 .
[本文引用: 1]
DU H Q ZHANG Y Q GU G X et al Experimentel study on leakage calculation, unloading groove optimization and performance test of gear pump
[J]. Journal of Mechanical & Electrical Engineering , 2024 , 41 (10 ): 1914 -1922 .
[本文引用: 1]
[18]
魏列江 , 刘榕民 , 强彦 , 等 基于CFD的齿轮泵实际最优端面间隙确定方法
[J]. 液压与气动 , 2022 , 46 (10 ): 115 -121 .
[本文引用: 1]
WEI L J LIU R M QIANG Y et al Determination method of actual optimal end clearance of gear pump based on CFD
[J]. Chinese Hydraulics & Pneumatics , 2022 , 46 (10 ): 115 -121 .
[本文引用: 1]
[19]
RAYKOV A SALIKEEV S BURMISTROV A et al Roots multi-lobe vacuum pumps with external compression
[J]. Vakuum in Forschung und Praxis , 2024 , 36 (3 ): 39 -42 .
[本文引用: 1]
[20]
田野 溅射离子泵阴极板溅射过程的模拟分析
[D]. 沈阳 : 东北大学 , 2019 .
[本文引用: 1]
TIAN Y Simulation analysis of sputter ion pump cathode plate's sputtering process
[D]. Shenyang : Northeastern University , 2019 .
[本文引用: 1]
[21]
张世伟 , 高雷鸣 , 李润达 , 等 罗茨真空机组预抽阶段的抽气特性比较研究
[J]. 真空 , 2022 , 59 (1 ): 1 -6 .
[本文引用: 1]
ZHANG S W GAO L M LI R D et al Comparative study on pumping characteristics of the Roots vacuum unit in start-up process
[J]. Vacuum , 2022 , 59 (1 ): 1 -6 .
[本文引用: 1]
[22]
张志宇 航空燃油凸轮泵内部流动特性研究
[D]. 兰州 : 兰州理工大学 , 2023 .
[本文引用: 1]
ZHANG Z Y Study on internal flow characteristics in aviation fuel cam pump
[D]. Lanzhou : Lanzhou University of Technology , 2023 .
[本文引用: 1]
[23]
焦撼宇 , 韩建超 , 杨东升 , 等 罗茨式氢气循环泵型线优化分析研究
[J]. 载人航天 , 2022 , 28 (3 ): 358 -364 .
[本文引用: 1]
JIAO H Y HAN J C YANG D S et al Analysis of profile optimization of Roots hydrogen circulating pump
[J]. Manned Spaceflight , 2022 , 28 (3 ): 358 -364 .
[本文引用: 1]
[24]
秦佳 , 李伟 , 季磊磊 , 等 轴向间隙对罗茨式氢气循环泵性能的影响
[J]. 中南大学学报(自然科学版) , 2025 , 56 (3 ): 1174 -1183 .
[本文引用: 1]
QIN J LI W JI L L et al Effect of axial clearance on performance of Roots-type hydrogen pump
[J]. Journal of Central South University (Science and Technology) , 2025 , 56 (3 ): 1174 -1183 .
[本文引用: 1]
[25]
李玉龙 , 刘萍 , 李秀荣 , 等 泵用转子上限形状系数的统一计算模型
[J]. 流体机械 , 2020 , 48 (11 ): 32 -36 .
[本文引用: 1]
LI Y L LIU P LI X R et al A unified calculation model of maximum shape factor of rotor for pumps
[J]. Fluid Machinery , 2020 , 48 (11 ): 32 -36 .
[本文引用: 1]
[26]
宋陆昊 , 宋安然 , 李玉龙 外啮合齿轮泵困油压力的函数创建及其波动峰值控制研究
[J/OL]. 机电工程 , 2025 : 1 -11 . (2025-06-09 )[2025-07-01 ]. .
URL
[本文引用: 1]
SONG L H SONG A R LI Y L Study on function creation and fluctuation peak control of trapped oil pressure of external gear pump
[J/OL]. China Industrial Economics , 2025 : 1 -11 . (2025-06-09 )[2025-07-01 ]. .
URL
[本文引用: 1]
[27]
翟云飞 , 张世伟 , 韩峰 , 等 三叶转子罗茨真空泵内气体过程的热力学计算
[J]. 真空 , 2019 , 56 (3 ): 10 -15 .
[本文引用: 1]
ZHAI Y F ZHANG S W HAN F et al Thermodynamic calculation for pumping process in the trilobal Roots vacuum pump
[J]. Vacuum , 2019 , 56 (3 ): 10 -15 .
[本文引用: 1]
[28]
达道安 真空设计手册 [M]. 3版 . 北京 : 国防工业出版社 , 2006 .
[本文引用: 1]
DA D A QIU J W Vacuum design manual [M]. 3th ed . Beijing : National Defense Industry Press , 2004 .
[本文引用: 1]
[29]
黄志强 , 刘伯韬 , 王美玲 , 等 散热流道对转子泵密封性能影响的仿真及试验研究
[J]. 润滑与密封 , 2025 , 50 (3 ): 58 -67 .
[本文引用: 1]
HUANG Z Q LIU B T WANG M L et al Simulation and experimental study on the influence of heat dissipation channel on the sealing performance of rotor pump
[J]. Lubrication Engineering , 2025 , 50 (3 ): 58 -67 .
[本文引用: 1]
Working process of Roots vacuum pumps
1
2021
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
RH用机械真空泵抽气过程影响因素研究
1
2019
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
RH用机械真空泵抽气过程影响因素研究
1
2019
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
氢气循环泵的转子动力学特性分析
1
2025
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
氢气循环泵的转子动力学特性分析
1
2025
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
NURBS曲线在罗茨泵转子型线设计中的应用
1
2019
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
NURBS曲线在罗茨泵转子型线设计中的应用
1
2019
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
真空磁控溅射镀膜设备中罗茨泵的保养与维护
1
2019
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
真空磁控溅射镀膜设备中罗茨泵的保养与维护
1
2019
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
基于罗茨泵平均理论流量的转子容积利用系数反求法
1
2022
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
基于罗茨泵平均理论流量的转子容积利用系数反求法
1
2022
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
航空燃油斜齿轮泵瞬时几何流量的计算方法
1
2025
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
航空燃油斜齿轮泵瞬时几何流量的计算方法
1
2025
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
转子泵容积利用系数的通用计算模型
2
2021
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
... 文献[8 ]给出了不同啮合轮廓曲线类型下的容积利用系数.其中,渐开线啮合轮廓的容积利用系数为: ...
转子泵容积利用系数的通用计算模型
2
2021
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
... 文献[8 ]给出了不同啮合轮廓曲线类型下的容积利用系数.其中,渐开线啮合轮廓的容积利用系数为: ...
5
2022
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
... [9 ].在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
... 啮合轮廓在不同曲线类型下的解析函数可参见文献[9 ].其中,渐开线啮合轮廓为: ...
... 在转子啮合轮廓曲线类型相同的前提下,其形状系数的最大值由转子叶数唯一确定.文献[9 ]和文献[25 ]已针对不同轮廓曲线类型的转子,推导出最大形状系数与转子叶数之间的关系式.基于上述理论基础及本研究的建模前提,本文结论的适用范围如下:其一,在介质类型上,适用于以空气为主要成分的气体或蒸汽介质(本研究的核心推导以空气为介质展开);其二,在设备结构上,适用于二叶转子罗茨泵. ...
... 罗茨泵的理论流量通过求解转子副旋转所扫过的面积获得[9 ] ,如图2 所示.其中,画有剖面线的动态封闭容积为V ,2个转子的旋转角速度均为ω . ...
5
2022
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
... [9 ].在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
... 啮合轮廓在不同曲线类型下的解析函数可参见文献[9 ].其中,渐开线啮合轮廓为: ...
... 在转子啮合轮廓曲线类型相同的前提下,其形状系数的最大值由转子叶数唯一确定.文献[9 ]和文献[25 ]已针对不同轮廓曲线类型的转子,推导出最大形状系数与转子叶数之间的关系式.基于上述理论基础及本研究的建模前提,本文结论的适用范围如下:其一,在介质类型上,适用于以空气为主要成分的气体或蒸汽介质(本研究的核心推导以空气为介质展开);其二,在设备结构上,适用于二叶转子罗茨泵. ...
... 罗茨泵的理论流量通过求解转子副旋转所扫过的面积获得[9 ] ,如图2 所示.其中,画有剖面线的动态封闭容积为V ,2个转子的旋转角速度均为ω . ...
齿轮泵内部间隙泄漏的研究综述
1
2024
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
齿轮泵内部间隙泄漏的研究综述
1
2024
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
Efficiency improvement of Roots vacuum pump working process
1
2022
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
罗茨泵径向间隙泄漏量的研究与建模
1
2002
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
罗茨泵径向间隙泄漏量的研究与建模
1
2002
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
输油转子泵啮合间隙与转子叶数对泵性能影响规律研究
1
2022
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
输油转子泵啮合间隙与转子叶数对泵性能影响规律研究
1
2022
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
轴向间隙对摆线转子泵性能影响的数值模拟研究
1
2021
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
轴向间隙对摆线转子泵性能影响的数值模拟研究
1
2021
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
泵用齿轮副困油卸荷的H型侧隙结构研究
1
2019
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
泵用齿轮副困油卸荷的H型侧隙结构研究
1
2019
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
内回流槽结构对罗茨泵内部流动特性的影响
1
2024
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
内回流槽结构对罗茨泵内部流动特性的影响
1
2024
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
齿轮泵泄漏计算、卸荷槽优化和性能测试的实验研究
1
2024
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
齿轮泵泄漏计算、卸荷槽优化和性能测试的实验研究
1
2024
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
基于CFD的齿轮泵实际最优端面间隙确定方法
1
2022
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
基于CFD的齿轮泵实际最优端面间隙确定方法
1
2022
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
Roots multi-lobe vacuum pumps with external compression
1
2024
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
溅射离子泵阴极板溅射过程的模拟分析
1
2019
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
溅射离子泵阴极板溅射过程的模拟分析
1
2019
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
罗茨真空机组预抽阶段的抽气特性比较研究
1
2022
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
罗茨真空机组预抽阶段的抽气特性比较研究
1
2022
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
航空燃油凸轮泵内部流动特性研究
1
2023
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
航空燃油凸轮泵内部流动特性研究
1
2023
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
罗茨式氢气循环泵型线优化分析研究
1
2022
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
罗茨式氢气循环泵型线优化分析研究
1
2022
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
轴向间隙对罗茨式氢气循环泵性能的影响
1
2025
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
轴向间隙对罗茨式氢气循环泵性能的影响
1
2025
... 在现代工业生产与科学研究中,真空技术的应用非常广泛.罗茨(真空)泵作为获取中高真空环境的核心设备,其性能优化及精准评估一直是学术界和工业界的研究热点[1 ] .罗茨泵因在较大压力范围内具备大抽速的特性,及对被抽气体中的灰尘、水蒸气不敏感等显著优势,已被广泛应用于冶金[2 ] 、化工[3 ] 、食品加工[4 ] 、电子镀膜[5 ] 等多个领域.理论流量是评估罗茨泵抽真空性能的核心指标,也用来验证在产品设计阶段罗茨泵的极限真空度、预抽时间等关键参数是否满足实际工况需求[6 ] .在罗茨泵理论流量研究方面,针对齿轮泵、凸轮泵等特定结构的转子,常采用“扫过面积法”推导瞬时流量[7 ] ,其计算难度取决于泵几何参数解析途径的选取.李玉龙等[8 -9 ] 根据啮合理论系统分析了不同轮廓转子的容积利用系数,并以形状系数为独立变量,结合啮合传动角与啮合线长度等中间参数,提出了罗茨泵转子轮廓的系统设计方法[9 ] .在罗茨泵极限真空度研究领域,泵内缝隙泄漏的量化分析是核心方向.罗茨泵内径向泄漏(简称径漏)、啮合泄漏(简称啮漏)和端面泄漏(简称端漏)的计算模型,多基于层流流动理论并结合各自缝隙的几何特征建立[10 -11 ] .具体而言,径漏计算模型常采用同心环形缝隙流动(如齿轮泵径漏)[12 ] 和不同心孔口缝隙流动(如凸转子泵径漏)[13 ] 两类模型,啮漏常采用等效矩形缝隙流动[14 ] 和孔口缝隙流动[15 ] 两类模型,端漏则多采用平行圆盘缝隙流动模型[16 ] .此外,部分研究还结合实验数据对模型进行校准[17 ] ,或通过CFD(computational fluid dynamics,计算流体力学)仿真模拟复杂流场[18 ] ,以进一步优化泄漏流量的计算精度.在罗茨泵极限真空度及其预抽时间的相关研究中,当前主流的计算模型主要分为2类:一类基于泄漏流量与抽气流量平衡原理[19 -20 ] ,另一类基于压缩比理论[21 ] .2类模型的计算精度均高度依赖泄漏流量和抽气流量计算的准确度,而现有研究在这两大核心计算环节均存在明显的局限.在泄漏流量计算方面,尤其是关键的端漏计算,多数研究仍沿用齿轮泵的端漏计算公式[22 ] ,未充分考虑罗茨泵与齿轮泵在核心结构上的本质差异——罗茨泵的叶数远少于齿轮泵的齿数(即“叶大齿小”),这种差异直接导致两者端漏通道的几何形态存在显著区别.显然,适用于齿轮泵的平行圆盘缝隙端漏计算公式无法匹配罗茨泵的端漏特性,而能够精准描述罗茨泵端漏规律的计算公式,目前在公开文献中仍鲜见报道.在抽气流量计算方面,现有方法普遍忽略了气体介质的强可压缩性,该特性会导致气流通过关键孔道时,其孔前与孔后的容积发生剧烈变化,进而影响计算的准确性.因此,当前抽气流量的计算多依赖数值计算方法展开[23 -24 ] ,理论层面的系统性推导与建模存在明显缺失.上述泄漏流量和抽气流量计算的双重局限,导致极限真空度预抽时间精准预测理论模型在现有文献中极为匮乏.鉴于此,本文以高通用性、简洁性、可靠性及高精度为总体要求,依次开展罗茨泵转子轮廓构造、罗茨泵理论流量特性分析、泵内三大泄漏流量计算、极限真空度及其预抽时间分析、CFD仿真验证等研究,旨在构建精度高、解析性好的流量计算模型和极限真空度及其预抽时间预测模型.本研究对于简化罗茨泵性能评估流程,提升泵整体性能及对泵的优化设计、降低能耗及拓展应用范围具有重要的理论与应用价值. ...
泵用转子上限形状系数的统一计算模型
1
2020
... 在转子啮合轮廓曲线类型相同的前提下,其形状系数的最大值由转子叶数唯一确定.文献[9 ]和文献[25 ]已针对不同轮廓曲线类型的转子,推导出最大形状系数与转子叶数之间的关系式.基于上述理论基础及本研究的建模前提,本文结论的适用范围如下:其一,在介质类型上,适用于以空气为主要成分的气体或蒸汽介质(本研究的核心推导以空气为介质展开);其二,在设备结构上,适用于二叶转子罗茨泵. ...
泵用转子上限形状系数的统一计算模型
1
2020
... 在转子啮合轮廓曲线类型相同的前提下,其形状系数的最大值由转子叶数唯一确定.文献[9 ]和文献[25 ]已针对不同轮廓曲线类型的转子,推导出最大形状系数与转子叶数之间的关系式.基于上述理论基础及本研究的建模前提,本文结论的适用范围如下:其一,在介质类型上,适用于以空气为主要成分的气体或蒸汽介质(本研究的核心推导以空气为介质展开);其二,在设备结构上,适用于二叶转子罗茨泵. ...
外啮合齿轮泵困油压力的函数创建及其波动峰值控制研究
1
2025
... 由孔口流量计算公式[26 ] 及基准空气压力p 0 折算到进口真空压力p 下的泄漏流量[27 ] ,得到径漏返流流量为: ...
外啮合齿轮泵困油压力的函数创建及其波动峰值控制研究
1
2025
... 由孔口流量计算公式[26 ] 及基准空气压力p 0 折算到进口真空压力p 下的泄漏流量[27 ] ,得到径漏返流流量为: ...
三叶转子罗茨真空泵内气体过程的热力学计算
1
2019
... 由孔口流量计算公式[26 ] 及基准空气压力p 0 折算到进口真空压力p 下的泄漏流量[27 ] ,得到径漏返流流量为: ...
三叶转子罗茨真空泵内气体过程的热力学计算
1
2019
... 由孔口流量计算公式[26 ] 及基准空气压力p 0 折算到进口真空压力p 下的泄漏流量[27 ] ,得到径漏返流流量为: ...
1
2004
... 需要说明的是,C ₁、C ₂的取值需优先结合孔口几何形状(其边缘结构为核心考量项)、流动可压缩性(以压力比、马赫数为主要评价指标)等要素确定,且两者的取值精度将直接决定预测模型的计算精度.参考文献[28 ],对于锐缘结构的方形或矩形孔口:当孔口长宽比接近1时,系数取值为0.55~0.60;当孔口为狭长缝隙时,系数取值降至0.50~0.55.由于本文中Q ₁、Q ₂均对应狭长缝隙的返流流量,故C ₁、C ₂均取为0.55.在实际应用时,可通过实验或仿真对该系数进行精准测定与修正,确保模型计算结果的可靠性. ...
1
2004
... 需要说明的是,C ₁、C ₂的取值需优先结合孔口几何形状(其边缘结构为核心考量项)、流动可压缩性(以压力比、马赫数为主要评价指标)等要素确定,且两者的取值精度将直接决定预测模型的计算精度.参考文献[28 ],对于锐缘结构的方形或矩形孔口:当孔口长宽比接近1时,系数取值为0.55~0.60;当孔口为狭长缝隙时,系数取值降至0.50~0.55.由于本文中Q ₁、Q ₂均对应狭长缝隙的返流流量,故C ₁、C ₂均取为0.55.在实际应用时,可通过实验或仿真对该系数进行精准测定与修正,确保模型计算结果的可靠性. ...
散热流道对转子泵密封性能影响的仿真及试验研究
1
2025
... 由于传统平行圆盘泄漏模型的计算误差较大[29 ] ,本文提出一种改进方案:采用端漏面积相同的新型等效平行矩形板,如图4 所示.其中:朝上的红色箭头指示对应于从动转子全端面的等效平行矩形板的上端泄漏方向;朝左的蓝色箭头指示对应于主动转子单叶半端面的等效平行矩形板的泄漏方向.需要特别说明的是:在主动转子逆时针旋转之前,在该蓝色箭头所示位置主动转子左侧的工作腔始终与进口腔相通,腔内介质的压力维持在进口压力水平;同时,主动转子的单叶半端面等效平行矩形板顺时针旋转90°后,能够与从转子的全端面等效平行矩形板拼接成一个完整的端漏等效平行矩形板. ...
散热流道对转子泵密封性能影响的仿真及试验研究
1
2025
... 由于传统平行圆盘泄漏模型的计算误差较大[29 ] ,本文提出一种改进方案:采用端漏面积相同的新型等效平行矩形板,如图4 所示.其中:朝上的红色箭头指示对应于从动转子全端面的等效平行矩形板的上端泄漏方向;朝左的蓝色箭头指示对应于主动转子单叶半端面的等效平行矩形板的泄漏方向.需要特别说明的是:在主动转子逆时针旋转之前,在该蓝色箭头所示位置主动转子左侧的工作腔始终与进口腔相通,腔内介质的压力维持在进口压力水平;同时,主动转子的单叶半端面等效平行矩形板顺时针旋转90°后,能够与从转子的全端面等效平行矩形板拼接成一个完整的端漏等效平行矩形板. ...