基于改进SMC与ILC的泳池清洁机器人轨迹跟踪控制

doi:10.3785/j.issn.1006-754X.2025.05.118

基于改进SMC与ILC的泳池清洁机器人轨迹跟踪控制

唐军^,^,, 许海琳, 张少文

江西理工大学机电工程学院，江西赣州 341000

Trajectory tracking control of swimming pool cleaning robot based on improved SMC and ILC

TANG Jun^,^,, XU Hailin, ZHANG Shaowen

School of Mechanical and Electrical Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China

收稿日期: 2025-03-06 修回日期: 2025-04-15

基金资助:

国家自然科学基金资助项目. 52465010
江西省自然科学基金面上项目. 20224BAB204047

Received: 2025-03-06 Revised: 2025-04-15

作者简介 About authors

唐　军（1975—），男，副教授，硕士生导师，硕士，从事水下机器人研究，E-mail:9120060030@jxust.edu.cn，https://orcid.org/0009-0009-4618-3491 , E-mail：9120060030@jxust.edu.cn

摘要

针对泳池清洁机器人在执行任务时因外部干扰和转向滑移而偏离预定轨迹的问题，提出了一种基于改进滑模控制（sliding mode control, SMC）和（iterative learning control, ILC）的轨迹跟踪控制方法，旨在提高机器人在滑移干扰下的轨迹跟踪精度。首先，建立了机器人的运动学模型和动力学模型，并引入滑移参数以表征滑移干扰的影响。然后，结合SMC增强了机器人控制系统的鲁棒性，设计了适应滑移干扰的非线性积分滑模面，并利用ILC进一步提高了轨迹跟踪精度。最后，采用PD（proportional-derivative，比例-微分）型闭环ILC控制律作为反馈，通过理论分析证明了非线性积分SMC-ILC控制器在滑移干扰下的稳定性和收敛性。仿真结果显示，与传统的PID（proportional-integral-derivative，比例-积分-微分）控制相比，非线性积分SMC-ILC在轨迹跟踪精度和鲁棒性上具有显著优势。实验结果验证了所设计的控制器在实际泳池清洁机器人应用中的有效性，其能够在外部干扰和滑移干扰下实现精确的轨迹跟踪，进而提升清洁效率。研究结果为泳池清洁机器人的智能控制提供了新的解决方案，并为相关领域的轨迹跟踪控制提供了理论依据和实践支持。

关键词： 滑模控制 ; 泳池清洁机器人 ; 迭代学习控制 ; 轨迹跟踪

Abstract

Aiming at the problem that the swimming pool cleaning robot deviates from the predetermined trajectory due to external interference and steering slip when performing tasks, a trajectory tracking control method based on improved sliding mode control (SMC) and iterative learning control (ILC) is proposed. It aims to improve the trajectory tracking accuracy of robots under slip interference. Firstly, the kinematics and dynamics models of the robot were established, and slip parameters were introduced to characterize the influence of slip interference. Then, the robustness of the robot control system was enhanced by combining SMC, and a nonlinear integral sliding mode surface adapted to slip interference was designed. Meanwhile, the ILC was used to further improve the trajectory tracking accuracy. Finally, by using the PD (proportional-derivative) type closed-loop ILC control law as the feedback, the stability and convergence of the designed nonlinear integral SMC-ILC controller in the presence of slip interference were proved through theoretical analysis. The simulation results showed that compared with the traditional PID (proportional-integral-derivative) control, the nonlinear integral SMC-ILC had significant advantages in trajectory tracking accuracy and robustness. The experimental results verified the effectiveness of the designed controller in practical swimming pool cleaning robot applications, which could achieve precise trajectory tracking under external interference and slip interference, thereby improving cleaning efficiency. The research results provide a new solution for the intelligent control of swimming pool cleaning robots and offer theoretical basis and practical support for trajectory tracking control in related fields.

Keywords： sliding mode control ; swimming pool cleaning robot ; iterative learning control ; trajectory tracking

PDF (1522KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

唐军, 许海琳, 张少文. 基于改进SMC与ILC的泳池清洁机器人轨迹跟踪控制[J]. 工程设计学报, 2025, 32(6): 803-812 doi:10.3785/j.issn.1006-754X.2025.05.118

TANG Jun, XU Hailin, ZHANG Shaowen. Trajectory tracking control of swimming pool cleaning robot based on improved SMC and ILC[J]. Chinese Journal of Engineering Design, 2025, 32(6): 803-812 doi:10.3785/j.issn.1006-754X.2025.05.118

泳池清洁机器人是一种具备自主运行能力的服务型机器人，主要用于协助清洁人员完成泳池底部与池壁的清洁作业，属于清洁机器人领域的重要分支。这类机器人通常配备水泵与过滤系统，通过水流吸附与杂质过滤相结合的方式，实现对泳池的自动清洁^[1-2]。在实际作业过程中，泳池清洁机器人需要在水下完成频繁的转向与路径调整，其运动行为受到水动力作用以及移动机构与池底接触力等的影响。在多重因素影响下，机器人在转向或加减速过程中易产生滑移现象，导致其实际运动轨迹偏离预定轨迹^[3]，使得部分泳池区域无法得到有效覆盖，进而影响整体清洁效果。因此，对滑移干扰下泳池清洁机器人的运动特性及轨迹跟踪控制进行深入研究，对提高其清洁效率具有重要意义。

泳池清洁机器人通常采用履带式、轮式或混合式等移动机构。其中，履带式移动机构凭借接地面积大、通过性好及地形适应能力强等优点，得到了广泛应用。基于此，本文以履带式泳池清洁机器人作为研究对象。履带式移动机器人运动建模的方法主要分为两类^[4]：一类是将履带式机器人等效简化为轮式机器人进行分析，该类方法的建模过程相对简单，适用于低速、低滑移工况，但由于忽略了履带与地面（或池底）的接触特性，所建模型与实际的误差较大；另一类是基于机器人整体的动力学平衡关系，引入履带与接触面之间的摩擦力与滑移效应，通过建立包含驱动力、阻力及外部干扰项的动力学模型来分析机器人的运动特性。目前，履带式移动机器人的轨迹跟踪控制大多基于理想的运动学模型，而对履带驱动过程中普遍存在的滑移现象及其引起的动力学非线性影响考虑不足，这在一定程度上限制了轨迹跟踪控制方法的精度。为此，本文通过分析履带式泳池清洁机器人的运动受力特点，引入水动力作用并考虑滑移干扰的影响，建立机器人的运动学与动力学模型，以实现其轨迹跟踪的精确控制。

对于泳池清洁机器人的轨迹跟踪控制，早期研究大多采用PID（proportional-integral-derivative，比例-积分-微分）控制策略。PID控制结构简单且参数整定方便，在外部扰动较小的场景下可实现精确控制。然而，当系统受到大量动态变化、非线性因素影响时，传统PID控制难以保证控制精度与系统鲁棒性。而泳池清洁机器人在实际作业过程中的运动轨迹具有显著的重复性特征，且伴有随机扰动与滑移偏差。在此类工况下，仅依赖单次反馈调节的PID控制难以实现机器人的高精度轨迹跟踪。为解决上述问题，一些学者引入了迭代学习控制（iterative learning control, ILC）^[5]。ILC可在多次任务执行过程中利用上一轮任务的跟踪误差对控制输入进行补偿修正，使系统的控制性能随迭代逐步改善，从而有效弥补传统PID控制在重复轨迹跟踪任务中的不足。目前，ILC控制律包括D型、P型、PD型等多种^[6-10]。尽管ILC在重复运动控制中具有显著优势，但其仍面临对初始条件较为敏感、对未知外部扰动和模型不确定性抑制能力有限等问题。基于此，陶洪峰等^[11]提出了一种基于ILC的离散非线性系统轨迹跟踪鲁棒优化算法；Meng等^[12]针对非重复不确定系统的鲁棒ILC策略进行了深入研究。为进一步增强ILC在复杂非线性系统中的鲁棒性，部分学者将ILC与滑模控制（sliding mode control, SMC）相结合^[13-17]。SMC是一种典型的非线性控制方法^[18-19]，通过构造滑模面并设计不连续的控制律，使得系统状态在有限时间内收敛至滑模面附近并沿其运动，从而有效抑制外部扰动和参数不确定性的影响。Goswami等^[20]提出了一种基于SMC的移动机器人轨迹跟踪控制方法，验证了SMC在复杂工况下的有效性。

基于此，本文针对履带式泳池清洁机器人移动时因存在转向滑移而导致轨迹偏离的问题，提出了一种基于改进SMC和ILC的轨迹跟踪控制方法。首先，建立机器人的运动学模型与动力学模型，并推导满足Lyapunov稳定性判据的速度控制律；然后，引入滑移参数以表征滑移干扰对机器人运动的影响，构造非线性积分滑模面，引入SMC以增强系统对外部扰动和模型不确定性的鲁棒性，同时结合PD型闭环ILC策略来提高机器人的轨迹跟踪精度；最后，对所设计的滑模面和PD型闭环ILC控制律进行收敛性证明，并通过仿真模拟和实验来验证所提出控制方法的有效性。

1 泳池清洁机器人运动学与动力学建模

泳池清洁机器人的主要运动方式为沿泳池底部和池壁表面移动，其运动状态受到多个作用力的影响，包括履带的驱动力、履带与池底或池壁接触所产生的法向支承力与摩擦力以及水的阻力等。当泳池清洁机器人需要转向时，其左、右履带所受的力不同，这可能会导致机器人产生姿态偏转、位置偏移等。

1.1　机器人运动学建模

为了简化泳池清洁机器人的运动学模型，作以下假设：

1）二维运动。假设机器人主要在泳池的底部或四周壁面上运动，忽略垂直方向上的运动。

2）独立驱动。履带式移动等效为差速轮式移动，即每条履带的驱动力独立控制，进而实现机器人的转向和前进。

3）阻力均匀。假设泳池中的水对机器人的阻力是均匀的，且与其速度成正比。

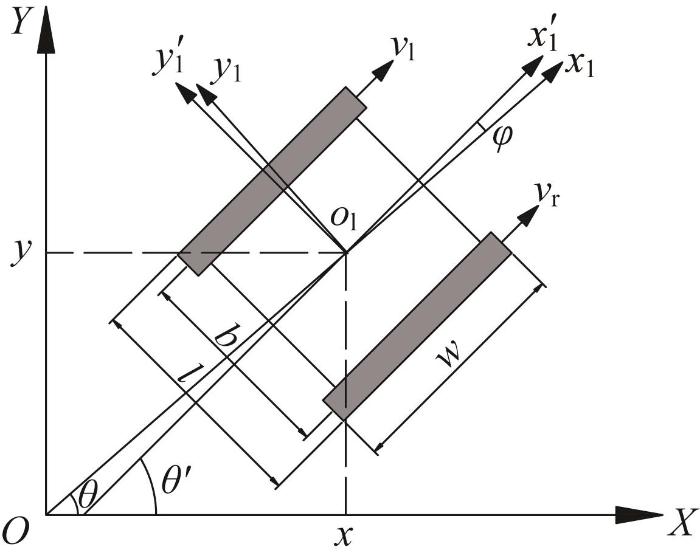
基于上述假设，对泳池清洁机器人的运动情况进行分析。为描述机器人在平面内的运动状态，以泳池底部平面上的某一固定点为原点构建参考坐标系O-XY，如图1所示。当机器人位于泳池底部平面上某一点时，其位姿可用位置(x, y)和航向角θ表示；机器人的速度由左右侧履带的速度控制，设左、右侧履带沿机器人前进方向的线速度分别为v_l、v_r。令机器人的长度为l、宽度为w，左右侧履带的中心距为b，以机器人质心为原点构建运动坐标系o₁-x₁y₁，其中 $x_{1}$ 轴的正方向为机器人的前进方向。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 泳池清洁机器人运动示意

Fig.1 Movement diagram of swimming pool cleaning robot

首先，假设机器人的履带与泳池底部接触时无滑移，则其前进时的运动学模型可表示为：

\{\begin{array}{l} \dot{x} = [(v_{r} + v_{l}) c o s θ] / 2 \\ \dot{y} = [(v_{r} + v_{l}) s i n θ] / 2 \\ \dot{θ} = (v_{r} - v_{l}) / b \end{array}

(1)

其中：

v_{r} = ω_{r} r, v_{l} = ω_{l} r

式中： $\dot{x} 、 \dot{y}$ 分别为机器人质心速度沿X、Y方向的分量， $\dot{θ}$ 为转向角速度， $ω_{l} 、 ω_{r}$ 分别为左、右侧履带驱动轮的角速度， $r$ 为履带驱动轮半径。

随后，考虑机器人的履带与泳池底部接触时存在侧滑的情况，令侧滑角为φ。在参考坐标系中，机器人的速度可表示为 $v = [v_{x} v_{y}]^{Τ}$ ，其中v_x 、v_y 分别为机器人速度沿x₁、y₁轴方向的速度分量；机器人的侧滑角 $φ = a r c t a n (v_{y} / v_{x})$ 。在存在侧滑的情况下，机器人速度的分量v_x 、v_y 及转向角速度 $\dot{θ}$ 可表示为：

\{\begin{array}{l} v_{x} = [v_{r} (1 - i_{l}) + v_{l} (1 - i_{r})] / 2 \\ v_{y} = v_{x} t a n φ \\ \dot{θ} = [v_{r} (1 - i_{r}) - v_{l} (1 - i_{l})] / b \end{array}

(2)

式中：i_l、i_r分别为机器人左、右侧履带与泳池底部接触时的滑移比， $i_{l} = 1 - v_{l}^{'} / v_{l}^{}$ ， $i_{r} = 1 - v_{r}^{'} / v_{r}^{}$ ，其中 $v_{l}^{'} 、 v_{r}^{'}$ 分别为左、右侧履带发生侧移时的相对速度。

在存在侧滑的情况下，机器人在参考坐标系中的运动学模型可表示为：

[\begin{matrix} \dot{x} \\ \dot{y} \\ \dot{θ} \end{matrix}] = [\begin{matrix} c o s θ & - s i n θ & 0 \\ s i n θ & c o s θ & 0 \\ 0 & 0 & 1 \end{matrix}] [\begin{matrix} v_{x} \\ v_{y} \\ \dot{θ} \end{matrix}]

(3)

将式(2)和式(3)代入式(1)，即可得到考虑滑移干扰时机器人的运动学模型：

[\begin{matrix} \dot{x} \\ \dot{y} \\ \dot{θ} \end{matrix}] = [\begin{matrix} \frac{(1 - i_{r}) (c o s θ - t a n φ s i n θ)}{2} \\ \frac{(1 - i_{l}) (s i n θ + t a n φ s i n θ)}{2} \\ \frac{1 - i_{r}}{b} \end{matrix} \begin{matrix} \frac{(1 - i_{r}) (c o s θ - t a n φ s i n θ)}{2} \\ \frac{(1 - i_{l}) (s i n θ + t a n φ s i n θ)}{2} \\ \frac{i_{l} - 1}{b} \end{matrix}] [\begin{matrix} v_{r} \\ v_{l} \end{matrix}]

(4)

1.2　机器人动力学建模

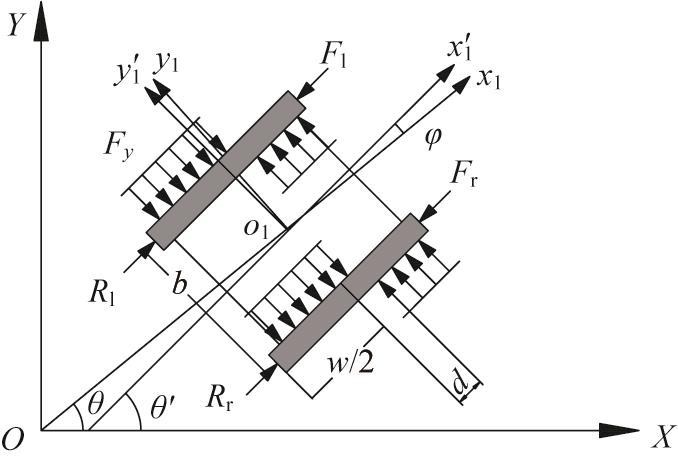
基于上述运动学模型，对泳池清洁机器人转向过程中的受力情况进行分析，建立其动力学模型，如图2所示。图中：F_l、F_r分别为机器人左、右侧履带的牵引力，R_l、R_r分别为机器人左、右侧履带的径向阻力，F_y 为机器人履带的转向阻力，d为机器人转动瞬心与质心在x₁轴方向上的距离。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 泳池清洁机器人受力示意

Fig.2 Force diagram of swimming pool cleaning robot

考虑到泳池清洁机器人在水下运动，在进行动力学建模时须考虑其运动时所受到的水作用力，如水的黏性阻力和水动力学效应。水的黏性阻力分为摩擦阻力与黏压阻力，其源于水与机器人表面之间的黏性作用。其中，摩擦阻力R_f可表示为：

R_{f} = \frac{1}{2} (C_{f} + Δ C_{f}) ρ_{w} v^{2} A

(5)

式中： $C_{f}$ 为摩擦阻力系数， $Δ C_{f}$ 为粗糙度补偿系数，ρ_w为水的密度，v为机器人与水的相对速度， $A$ 为机器人的湿表面积。

黏压阻力R_pv可表示为：

R_{p v} = \frac{1}{2} C_{p v} ρ_{w} v^{2} A

(6)

式中：C_pv为黏压阻力系数。

则水的黏性阻力R_t可表示为：

R_{t} = R_{f} + R_{p v}

(7)

综上，机器人的动力学方程可表示为：

\{\begin{array}{l} m \ddot{x} = F_{l} + F_{r} - R_{l} - R_{r} - R_{t} \\ m \ddot{y} = F_{y} - R_{t} \\ I \ddot{θ} = M_{x} - M_{y} \end{array}

(8)

其中：

R_{l} = R_{r} = μ_{x} (m g + ρ_{w} g h A) / 2

F_{y} = μ_{y} (m g + ρ_{w} g h A) / w

M_{x} = (F_{r} - R_{r}) b / 2 - (F_{l} - R_{l}) b / 2

M_{y} = 2 F_{y} (w^{2} / 4 - d^{2})

式中：m为机器人的质量，I为机器人的转动惯量， $μ_{x}$ 为径向摩擦系数， $μ_{y}$ 为侧向摩擦系数，g为重力加速度，h为机器人质心距离泳池水面的高度，M_x 、M_y 分别为机器人的径向、侧向转弯阻力矩。

联立上述公式，可整理得到机器人的非线性动力学模型：

M (q) \ddot{q} + F_{1} (q, \dot{q}) + F_{2} (q) + R_{t} (q) = D (q) τ

(9)

其中：

\begin{array}{l} M (q) = [\begin{matrix} m & 0 & 0 \\ 0 & m & 0 \\ 0 & 0 & I \end{matrix}], F_{1} (q, \dot{q}) = [\begin{matrix} - F_{y} s i n θ \\ F_{y} c o s θ \\ M_{y} \end{matrix}] \\ F_{2} (q) = [\begin{matrix} (R_{l} + R_{r}) c o s θ \\ (R_{l} + R_{r}) s i n θ \\ (R_{l} - R_{r}) b / 2 \end{matrix}], R_{t} (q) = [\begin{matrix} R_{t} c o s θ \\ R_{t} s i n θ \\ 0 \end{matrix}] \\ D (q) = [\begin{matrix} c o s θ \\ s i n θ \\ - b / 2 \end{matrix} \begin{matrix} c o s θ \\ s i n θ \\ b / 2 \end{matrix}], q = [\begin{matrix} x \\ y \\ θ \end{matrix}], τ = [\begin{matrix} F_{l} \\ F_{r} \end{matrix}] \end{array}

式中： M $(q)$ 为惯性矩阵， $F_{1} (q, \dot{q})$ 为科氏力与离心力项， $F_{2} (q)$ 为阻力项， R_t $(q)$ 为水阻力项， D $(q)$ 为输入矩阵， $q 、 \dot{q} 、 \ddot{q}$ 分别为机器人的广义坐标、广义速度和广义加速度， $τ$ 为控制输入。

在参考坐标系O-XY中，机器人的实际位姿 $q = {[\begin{matrix} x & y & θ \end{matrix}]}^{Τ}$ 与参考位姿 $q_{d} = {[\begin{matrix} x_{d} & y_{d} & θ_{d} \end{matrix}]}^{Τ}$ 的偏差 e 可表示为：

e = [\begin{matrix} x_{e} \\ y_{e} \\ θ_{e} \end{matrix}] = [\begin{matrix} c o s θ & s i n θ & 0 \\ - s i n θ & c o s θ & 0 \\ 0 & 0 & 1 \end{matrix}] [\begin{matrix} x_{d} - x \\ y_{d} - y \\ θ_{d} - θ \end{matrix}]

(10)

式中：x_e、y_e和θ_e为机器人的位置和航向角误差。

对式(10)进行求导，得到对应的微分方程：

\dot{e} = [\begin{matrix} {\dot{x}}_{e} \\ {\dot{y}}_{e} \\ {\dot{θ}}_{e} \end{matrix}] = [\begin{matrix} {\dot{y}}_{e} \dot{θ} - v + v_{d} c o s θ_{e} \\ - x_{e} \dot{θ} + v_{d} s i n θ_{e} \\ {\dot{θ}}_{d} - \dot{θ} \end{matrix}]

(11)

式中： $v_{d}$ 为机器人的参考速度。

结合式(10)，设计如下Lyapunov函数：

v_{1} = x_{e}^{2} / 2 + y_{e}^{2} / 2 + (1 - c o s θ_{e}) / k_{y}

(12)

式中：k_y 为控制参数。

v₁的一阶导数可表示为：

\begin{array}{l} {\dot{v}}_{1} = x_{e} {\dot{x}}_{e} + y_{e} {\dot{y}}_{e} + {\dot{θ}}_{e} s i n θ_{e} / k_{y} = \\ x_{e} (\dot{θ} y_{e} - v - v_{d} c o s θ_{e}) + \\ y_{e} (- \dot{θ} x_{e} + v_{d} s i n θ_{e}) + ({\dot{θ}}_{d} - \dot{θ}) s i n θ_{e} / k_{y} = \\ x_{e} v_{d} c o s θ_{e} - x_{e} v + \\ y_{e} v_{d} s i n θ_{e} + {\dot{θ}}_{d} s i n θ_{e} / k_{y} - \dot{θ} s i n θ_{e} / k_{y} \end{array}

(13)

机器人的控制输入选择如下：

[\begin{matrix} v \\ \dot{θ} \end{matrix}] = [\begin{matrix} v_{d} c o s θ_{e} + k_{x} x_{e} \\ {\dot{θ}}_{d} + k_{y} v_{d} y_{e} + k_{θ} v_{d} s i n θ_{e} \end{matrix}]

(14)

式中：k_x 、k_θ 为控制参数。

将式(14)代入式(13)，可得：

{\dot{v}}_{1} = - k_{x} x_{e}^{2} - k_{θ} v_{d} s i n^{2} θ_{e} / k_{y}

(15)

由式(15)可知，当k_x 、k_y 、k $_{θ}$ 均大于0时， $v_{l}$ 小于等于0，表明式(15)满足Lyapunov理论的稳定性条件，这可确保控制系统在全局中的渐近稳定性^[21]。

2 非线性积分SMC-ILC控制器设计

在泳池清洁机器人执行清洁任务的过程中，不同的行驶路径会导致机器人产生不同的滑移。结合式(4)，可得任意时刻t下机器人的速度 $v (t)$ 、转向角速度 $\dot{θ} (t)$ 与广义速度 $\dot{q}$ 的关系：

\dot{q} (t) = [\begin{matrix} \dot{x} (t) \\ \dot{y} (t) \\ \dot{θ} (t) \end{matrix}] = [\begin{matrix} c o s θ (t) \\ s i n θ (t) \\ 0 \end{matrix} \begin{matrix} 0 \\ 0 \\ 1 \end{matrix}] [\begin{matrix} v (t) \\ \dot{θ} (t) \end{matrix}]

考虑滑移干扰 $η (t)$ （ $η = v_{l}^{'} / v_{l}$ ， $v_{l}^{'} \neq v_{l}$ ， $v_{r}^{'} \neq v_{r}$ ）的影响，机器人左右侧履带驱动电机的实际输入 $u_{l} (t) 、 u_{r} (t)$ 与机器人输出 ${[\begin{matrix} v (t) & \dot{θ} (t) \end{matrix}]}^{Τ}$ 之间满足以下关系：

[\begin{matrix} v (t) \\ \dot{θ} (t) \end{matrix}] = [\begin{matrix} w / (4 η (t)) & w / (4 η (t)) \\ - w / (b η (t)) & w / (b η (t)) \end{matrix}] [\begin{matrix} u_{l} (t) \\ u_{r} (t) \end{matrix}]

由此推导得到滑移干扰下机器人的离散运动学模型，可表示为：

\dot{q} (t) = q (t) + Δ t w [\begin{matrix} c o s \dot{θ} \\ s i n \dot{θ} \\ - 1 / b \end{matrix} \begin{matrix} c o s \dot{θ} \\ s i n \dot{θ} \\ 1 / b \end{matrix}] [\begin{matrix} u_{l} (t) \\ u_{r} (t) \end{matrix}] / 4 η (t)

式中： $Δ t$ 为采样时间。

令机器人控制系统的输入 $u (t) = {[\begin{matrix} u_{l} (t) & u_{r} (t) \end{matrix}]}^{T}$ ，滑移参数 $h (t) = w / (4 η (t))$ ，式(18)可改写为：

\dot{q} (t) = q (t) + h (t) B (q (t), t) u (t)

其中：

B (q (t), t) = Δ t [\begin{matrix} c o s \dot{θ} \\ s i n \dot{θ} \\ - 1 / b \end{matrix} \begin{matrix} c o s \dot{θ} \\ s i n \dot{θ} \\ 1 / b \end{matrix}]

式中： $B (q (t), t)$ 为非线性矩阵函数。

在机器人轨迹跟踪过程中，第 $k$ 次迭代时的系统状态 ${\dot{q}}_{k} (t)$ 与输出 $p_{k} (t)$ 分别表示为：

\{\begin{array}{l} {\dot{q}}_{k} (t) = q_{k} (t) + h_{k} (t) B (q_{k} (t), t) u_{k} (t) + β_{k} (t) \\ p_{k} (t) = c_{1} q_{k} (t) \end{array}

式中： c₁为常数矩阵， $β_{k} (t)$ 为干扰项。

在进行控制器设计前，假定以下条件成立。

假设1：滑移参数、系统输入、系统状态输出和状态干扰均有界，即 $‖h_{k} (t)‖ \leq b_{h}$ ， $‖u_{k} (t)‖ \leq b_{u}$ ， $‖B (q_{k} (t), t)‖ \leq b_{B}$ ， $‖β_{k} (t)‖ \leq b_{β}$ ，其中 $b_{h} 、 b_{u} 、 b_{B} 、$ $b_{β}$ 分别为 $h_{k} (t) 、 u_{k} (t) 、 B (q_{k} (t), t) 、$ $β_{k} (t)$ 的上界，均为正常数。

假设2：每一次跟踪时系统的初始状态均满足 $q_{d} (0) = q_{k} (0)$ ， $q_{d} (t)$ 为期望状态。

假设3：始终满足 $‖B (q_{1} (t), t) - B (q_{2} (t), t)‖ \leq h_{B} ‖q_{1} (t) - q_{2} (t)‖$ ， $h_{B}$ 为 $L i p s c h i t z$ 常数。

假设4：期望输出 $p_{d} (t)$ 、期望输入 $u_{d} (t)$ 与期望状态 $q_{d} (t)$ 满足以下条件。

\{\begin{array}{l} q_{d} (t + 1) = q_{d} (t) + h_{k} (t) B (q_{d} (t), t) u_{d} (t) \\ p_{d} (t) = c_{1} q_{d} (t) \end{array}

基于上述假设，设计滑模控制器，其中非线性滑模面函数可表示为：

S_{k} (t) = α_{1} e_{k} (t) + α_{2} {\dot{e}}_{k} (t)

式中：α₁、α₂为系数， $0 < α_{1} < 1$ ， $0 < α_{2} < 1$ ； $e_{k} (t)$ 为第k次迭代时的轨迹跟踪误差。

对式(22)进行求导，可得：

{\dot{S}}_{k} (t) = α_{1} {\dot{e}}_{k} (t) + α_{2} {\ddot{e}}_{k} (t)

基于 $e_{k} (t) = p_{d} (t) - p_{k} (t)$ ，将式(23)进一步展开，可得：

\begin{array}{l} {\dot{S}}_{k} (t) = α_{1} ({\dot{p}}_{d} (t) - p_{k} (t)) + α_{2} ({\ddot{p}}_{d} (t) - p_{k} (t)) + \\ (p_{d} (t) - q_{k} (t) - h_{k} (t) B (q_{k} (t), t) u_{k} (t) - β_{k} (t)) = \\ \sum_{i = 1}^{2} α_{i} p_{d}^{i} (t) - \sum_{i = 1}^{2} α_{i} p_{k} (t) - \\ q_{k} (t) - h_{k} (t) B (q_{k} (t), t) u_{k} (t) - β_{k} (t) \end{array}

式(24)可用于描述滑模变量的变化规律， $|S (t)| = 0$ 定义了控制系统在滑模面上的运动轨迹。将控制输入信号 $u (t)$ 设计为迭代连续的信号，使得滑模面能够在有限时间内收敛至预定区间。

结合连续二阶滑模概念^[22-23]，第k次迭代时的系统输入设计如下：

u_{k} (t) = h_{k}^{- 1} (t) B^{- 1} (q_{k} (t), t) \cdot (\sum_{i = 1}^{2} α_{i} p_{d}^{i} (t) - \sum_{i = 1}^{2} α_{i} p_{k} (t)) - (q_{k} (t) - V_{k} (t) + β_{1} {|S_{k}|}^{2 / 3} s g n (S_{k}) + β_{2} S_{k} (t))

其中：

{\dot{V}}_{k} (t) = - γ_{1} S_{k}^{} (t) - γ_{2} {|S_{k}|}^{1 / 3} s g n (S_{k})

式中： $β_{1} 、 β_{2}$ 为正常数， $V_{k} (t)$ 为积分项， $γ_{1} 、 γ_{2}$ 为正常数。

为保证矩阵 $B$ 可逆，当 $θ = 90 ° + k π$ 或θ= $k π$ 时，须满足以下条件：

B^{- 1} (q_{k} (t), t) = B^{Τ} (q_{k} (t), t) {(B (q_{k} (t), t) B^{Τ} (q_{k} (t), t))}^{- 1}

式(24)与式(25)定义了二阶连续的SMC-ILC控制律，其中 ${|S_{k}|}^{i / 3} s g n (S_{k})$ （ $i = 1, 2$ ）为连续函数， ${|S_{k}|}^{1 / 3} s g n (S_{k})$ 被积分后，使得 $V_{k} (t)$ 成为一个连续的函数。综上，所设计控制器的输入为连续信号，可实现无抖振的控制动作。

因此，可在滑模动力学方程(24)中插入ILC控制律(25)以进行简化：

\begin{array}{l} {\dot{S}}_{k} (t) = - β_{2} S_{k} (t) + q_{k} (t) + V_{k} (t) - \\ β_{k} (t) - β_{1} {|S_{k}|}^{2 / 3} s g n (S_{k}) \end{array}

在简化后的滑模动力学方程中，使用积分项 $V_{k} (t)$ 来减小未知干扰 $β_{k} (t)$ 的影响。

为评估跟踪误差 $e (t)$ 的收敛性，定义Lyapunov函数 $V_{k} (t) = V_{k}^{2} (t) / 2$ 。首先，推导相邻2次迭代之间的Lyapunov函数差值；随后，评估跟踪误差 $e (t)$ 的收敛性。当 $t = 0$ 时， $V_{k}^{} (0) = 0$ ， $Δ V_{k} (0) = V_{k} (0) - V_{k - 1} (0) = 0$ ；当 $0 < t \leq T$ 时：

\begin{array}{l} Δ V_{k} (t) = (V_{k}^{2} (t) - V_{k - 1}^{2} (t)) / 2 = \\ \int_{0}^{t} V_{k}^{} (τ) {\dot{V}}_{k}^{} (τ) d τ - V_{k - 1}^{2} (t) / 2 \end{array}

将式(26)代入式(28)，可得：

\begin{array}{l} Δ V_{k} (t) = - γ_{1} \int_{0}^{t} V_{k}^{} (τ) S_{k}^{} (τ) d τ - \\ γ_{2} \int_{0}^{t} V_{k}^{} (τ) {|S_{k}|}^{1 / 3} s g n (S_{k}^{}) d τ - V_{k - 1}^{2} (t) / 2 \end{array}

当 $|S_{k} (t)| \neq 0$ ， $t \in [0, T]$ 时， $Δ V_{k} (t)$ 负定，由此可得函数 $V_{k} (t)$ 是收敛的。

考虑到机器人重复执行清洁任务，结合ILC中的PD型闭环控制律，对SMC进行优化：

u_{k + 1} (t) = u_{k} (t) + L_{P} e_{k + 1} (t) + L_{D} {\dot{e}}_{k + 1} (t)

其中：

e_{k + 1} (t) = p_{d} (t) - p_{k + 1} (t) = c_{1} (q_{d} (t) - q_{k + 1} (t))

{\dot{e}}_{k + 1} (t) = c_{2} (q_{d} (t) - q_{k + 1} (t))

L_{P} = k_{P} L (t), L_{D} = k_{D} L (t)

式中：k_P、k_D为迭代学习因子； $L (t)$ 为学习增益矩阵，定义其范数会收敛，且满足 $‖L_{P}‖ \leq b_{P}$ ， $‖L_{D}‖ \leq b_{D}$ ， $b_{P} > 0$ ， $b_{D} > 0$ ； c₂为对 $p_{k} (t)$ 求导后得到的系数矩阵。

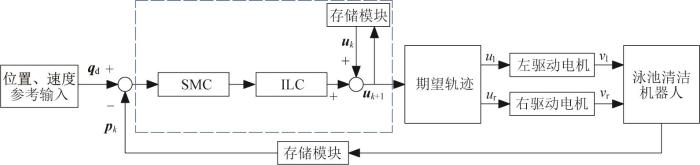
综上，本文所设计的非线性积分SMC-ILC控制器的结构如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 非线性积分SMC-ILC控制器结构

Fig.3 Structure of nonlinear integral SMC-ILC controller

设控制目标为 $\underset{k \to \infty}{l i m} p_{k} (t) = q_{d} (t)$ ，采用Bellman-Gronwall定理与 $λ$ 范数及其性质，对所设计的控制律的收敛性进行证明。

定义1 正实数f的a范数可表示为：

{‖f (\cdot)‖}_{a} = {(1 / a)}^{t} ‖f (t)‖, t \in N, a > 1

其中：a为时间衰减系数，用于控制衰减速度。

定义2 给定期望轨迹 $q_{d} (t)$ ，则在ILC控制律(30)下有：

\{\begin{array}{l} \underset{k \to \infty}{l i m} u_{d} (t) - u_{k} (t) = Δ u_{k} (t) \to 0 \\ \underset{k \to \infty}{l i m} q_{d} (t) - q_{k} (t) = Δ q_{k} (t) \to 0 \\ \underset{k \to \infty}{l i m} p_{d} (t) - p_{k} (t) = Δ p_{k} (t) \to 0 \end{array}

定义3 记 $B (Δ q_{k} (t)) = (B (q_{d} (t), t) - B (q_{k} (t), t))$ 对于任意t、k均满足 $‖B (q_{k} (t), t)‖ \leq b_{B}$ 。

定理1：对于式(20)和式(21)，若系统满足 $‖E - (c_{1} L_{P} + c_{2} L_{D}) h_{k} (t) B (q_{k} (t), t)‖ \leq ρ \leq 1$ （ E 为单位矩阵），则系统输入 $u_{k} (t)$ 与系统状态 $q_{k} (t)$ 在迭代 $k$ 次后趋于期望值。

具体证明过程如下。根据式(30)以及上述定义，可得：

Δ u_{k + 1} (t) = Δ u_{k} (t) - L_{P} e_{k + 1} (t) - L_{D} {\dot{e}}_{k + 1} (t)

根据定义2，对式(20)取范数，可得：

\begin{array}{l} ‖Δ q_{k} (t + 1)‖ = ‖Δ q_{k} (t)‖ + ‖h_{k} (t)‖ ‖B (q_{d} (t), t)‖ ‖u_{d} (t)‖ - \\ ‖h_{k} (t)‖ ‖B (q_{k} (t), t)‖ ‖Δ u_{k} (t)‖ + b_{β} = \\ ‖Δ q_{k} (t)‖ + ‖h_{k} (t)‖ ‖B (q_{d} (t), t) - B (q_{k} (t), t)‖ \\ ‖u_{d} (t)‖ + ‖h_{k} (t)‖ ‖B (q_{k} (t), t)‖ \\ ‖u_{d} (t) - u_{k} (t)‖ + b_{β} = ‖Δ q_{k} (t)‖ + ‖h_{k} (t)‖ \\ ‖B (Δ q_{k} (t), t)‖ ‖u_{d} (t)‖ + ‖h_{k} (t)‖ \\ ‖B (q_{k} (t), t)‖ ‖Δ u_{k} (t)‖ + b_{β} \end{array}

结合式(20)、式(31)与定义2并取相应范数，可得：

\begin{array}{l} ‖Δ u_{k} (t + 1)‖ = ‖Δ u_{k} (t) - L_{P} e_{k + 1} (t) - L_{D} {\dot{e}}_{k + 1} (t)‖ = \\ ‖Δ u_{k} (t) - (c_{1} L_{P} + c_{2} L_{D}) (Δ q_{k} (t))‖ + \\ ‖h_{k} (t) (B (Δ q_{k} (t), t) u_{d} (t) + B (q_{k} (t), t) Δ u_{k} (t))‖ \leq \\ ‖E - (c_{1} L_{P} + c_{2} L_{D}) h_{k} (t) B (q_{k} (t), t)‖ ‖Δ u_{k} (t)‖ + \\ ‖c_{1} L_{P} + c_{2} L_{D}‖ ‖Δ q_{k} (t)‖ + \\ ‖c_{1} L_{P} + c_{2} L_{D}‖ ‖h_{k} (t)‖ ‖B (Δ q_{k} (t), t)‖ ‖u_{d} (t)‖ \end{array}

令 $‖E - (c_{1} L_{P} + c_{2} L_{D}) h_{k} (t) B (q_{k} (t), t)‖ \leq ρ$ ，结合假设3和式(33)，整理可得：

\begin{array}{l} ‖Δ u_{k} (t + 1)‖ \leq ρ ‖Δ u_{k} (t)‖ + ‖c_{1} b_{P} + c_{2} b_{D}‖ \cdot \\ (1 + b_{h} h_{B} b_{u}) ‖Δ q_{k} (t)‖ \end{array}

根据式(32)并结合假设1，可得：

\begin{array}{l} ‖Δ q_{k} (t + 1)‖ \leq ‖Δ q_{k} (t)‖ + \\ b_{h} h_{B} ‖Δ q_{k} (t)‖ ‖u_{d} (t)‖ + b_{h} h_{B} ‖Δ u_{k} (t)‖ \leq \\ (1 + b_{h} h_{B} b_{u}) ‖Δ q_{k} (t)‖ + b_{h} h_{B} ‖Δ u_{k} (t)‖ \end{array}

令 $c_{3} = (1 + b_{h} h_{B} b_{u})$ ，根据假设2以及递推公式(35)，可推导得到：

‖Δ q_{k} (t + 1)‖ \leq \sum_{j = 0}^{t} {c_{3}}^{t - j} (b_{h} h_{B} ‖Δ u_{k} (j)‖)

联立式(34)和式(36)，可得：

‖Δ u_{k + 1} (t)‖ \leq ρ ‖Δ u_{k} (t)‖ + ‖c_{4}‖ \sum_{j = 0}^{t - 1} {c_{3}}^{t - 1 - j} (b_{h} h_{B} ‖Δ u_{k} (j)‖)

其中：

c_{4} = (c_{1} b_{P} + c_{2} b_{D}) (1 + b_{h} h_{B} b_{u})

令 $a \geq c_{3} \geq 1$ ，对式(37)左右同乘 ${(1 / a)}^{t}$ ，可得：

{‖Δ u_{k + 1} (t)‖}_{a} \leq ρ {‖Δ u_{k} (t)‖}_{a} + ‖c_{4}‖ b_{h} h_{B} {‖Δ u_{k} (t)‖}_{a} \cdot c_{3} {[1 - (c_{3} / a)]}^{t - 1} / [a (a - c_{3})]

联立上述公式，整理可得：

{‖Δ u_{k + 1} (t)‖}_{a} \leq {\bar{ρ}}^{k} {‖Δ u_{1} (t)‖}_{a}

其中：

\bar{ρ} = ρ + c_{3} ‖c_{4}‖ {[1 - (c_{3} / a)]}^{t - 1} / [a (a - c_{3})]

当 $a$ 足够大时， $\bar{ρ} \approx ρ < 1$ ，则对式(39)两侧同时取 $k \to \infty$ 时的极限，可得：

\underset{k \to \infty}{l i m} {‖Δ u_{k} (t)‖}_{a} \leq {\bar{ρ}}^{k} \underset{k \to \infty}{l i m} {‖Δ u_{1} (t)‖}_{a} = 0

对式(36)取a范数，可得：

{‖Δ q_{k} (t)‖}_{a} \leq b_{h} h_{B} {‖Δ u_{k} (t)‖}_{a} c_{3} {[1 - (c_{3} / a)]}^{t - 1} / [a (a - c_{3})]

对式(41)两侧同时取 $k \to \infty$ 时的极限，由于右侧为有界项与趋于0项的乘积，则可得：

\underset{k \to \infty}{l i m} {‖Δ q_{k} (t)‖}_{a} = 0

通过上述证明可知，在存在滑移干扰的前提下，系统状态与控制输入能够实现收敛，达到期望值。

3 仿真与实验分析

3.1　仿真分析

为了进一步验证本文所设计的非线性积分SMC-ILC控制器对泳池清洁机器人存在转向滑移和外部扰动时的鲁棒性，在MATLAB R2022a平台上开展轨迹跟踪仿真模拟，并与期望轨迹和基于PID控制的轨迹跟踪结果进行对比。其中：期望轨迹设定为 $x_{d} (t) = c o s (π t / 4)$ ， $y_{d} (t) = s i n (π t / 4)$ ， $θ_{d} (t) = π t / 63$ ；泳池清洁机器人质量m=7.5 kg，长度l=398 mm，宽度w=400 mm，履带中心距b=378 mm，湿表面积 $A = 0.72 m^{2}$ ，移动速度 $v = 0.2 m / s$ ，径向转弯阻力矩 $M_{x} = 2.8 N \cdot m$ ；履带驱动轮半径r=65 mm，履带的径向摩擦系数 $μ_{x} = 0.12$ ，侧向摩擦系数 $μ_{y} = 0.16$ ，摩擦阻力系数 $C_{f} = 0.4 \times 10^{- 3}$ ，黏压阻力系数 $C_{p v} = 1.3 \times 10^{- 2}$ ；水的密度 $ρ_{w} = 1 000 k g / m^{3}$ ，水的黏性阻力 $R_{t} = 2.3 N$ 。在所设计的控制器中，相关控制参数如下： $α_{1} = 0.5$ ， $α_{2} = 0.9$ ， $β_{1} = 0.1$ ， $β_{2} = 0.01$ ， $γ_{1} = 1$ ， $γ_{2} = 0.5$ ， $η (t) = 0.8 t$ ，最大迭代次数k_max=10；其余控制参数如表1所示。

表1 控制参数

Table 1 Control parameters

参数	数值
$k_{x}$	0.1
$k_{y}$	0.05
$k_{θ}$	0.5
$k_{P}$	5
$k_{D}$	15

新窗口打开| 下载CSV

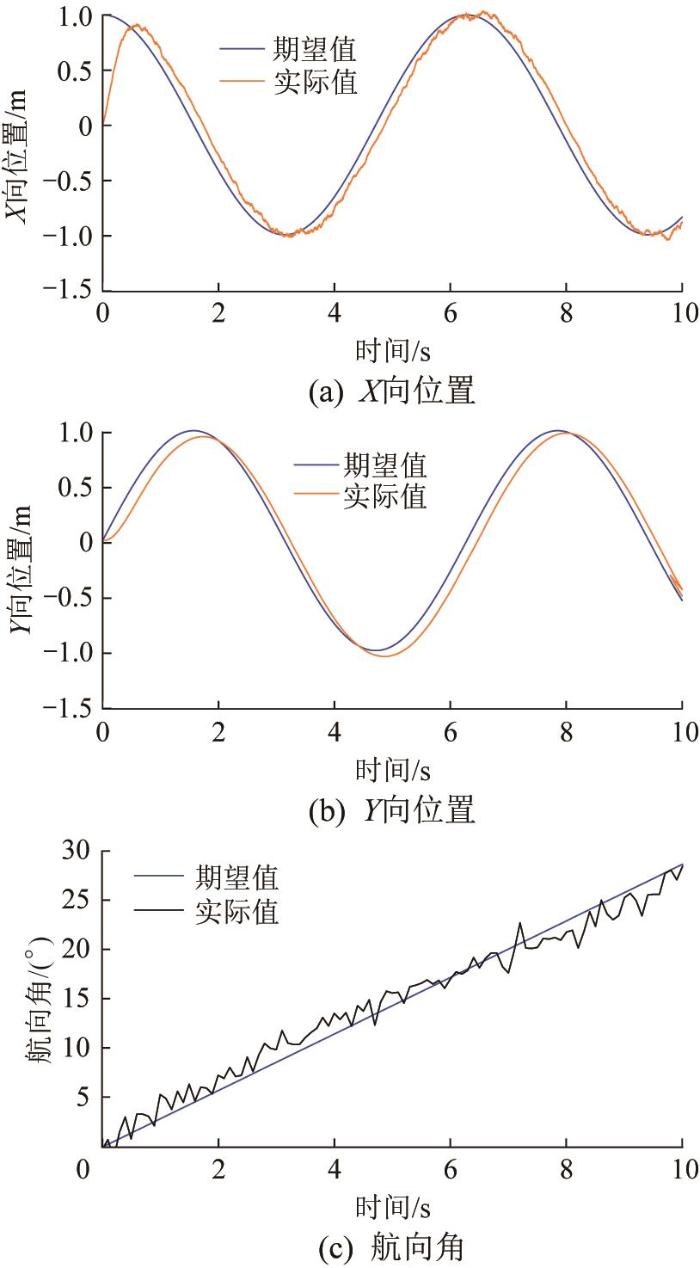
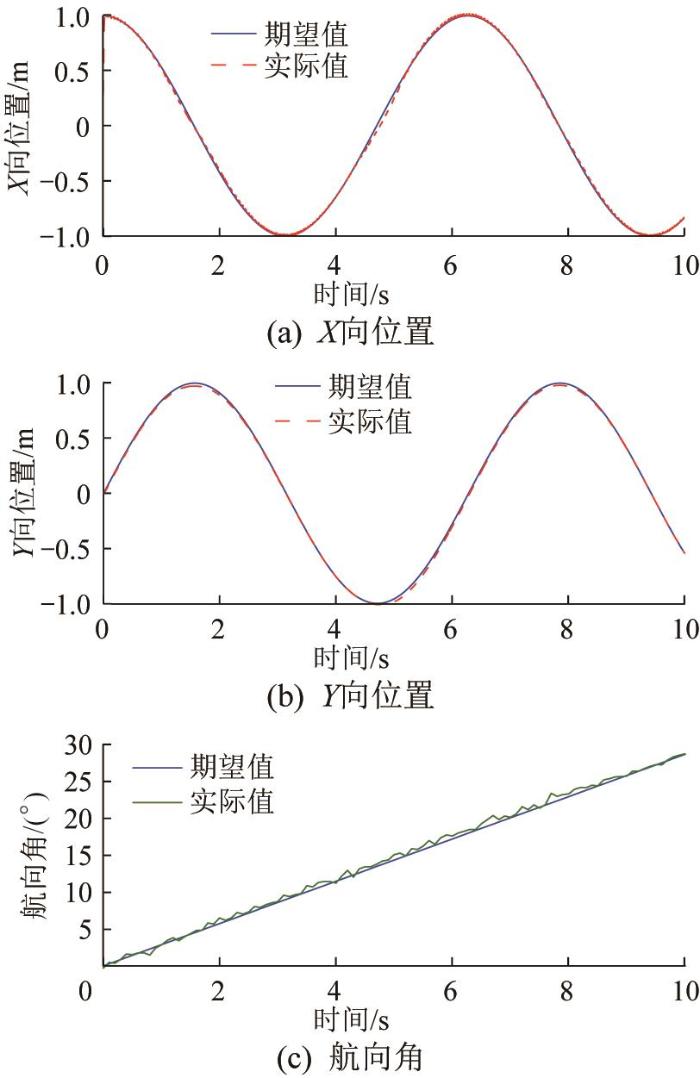
图4和图5分别为基于PID控制和基于非线性积分SMC-ILC的泳池清洁机器人的X、Y向位置和航向角的跟踪曲线。其中：非线性积分SMC-ILC在迭代5次后的跟踪误差达到较低水平，故选择第5次迭代的仿真结果进行对比。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 基于PID控制的机器人轨迹跟踪仿真结果

Fig.4 Simulation results of robot trajectory tracking based on PID control

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 基于非线性积分SMC-ILC的机器人轨迹跟踪仿真结果

Fig.5 Simulation results of robot trajectory tracking based on nonlinear integral SMC-ILC

由图4可以看出，在外部干扰与滑移干扰的影响下，基于PID控制的机器人的位置跟踪误差为0.1 m左右，航向角跟踪误差为2°左右。由图5可以看出，在外部干扰与滑移干扰的影响下，基于非线性积分SMC-ILC的机器人的位置跟踪误差在0.05 m以下，航向角跟踪误差在0.5 °以下。

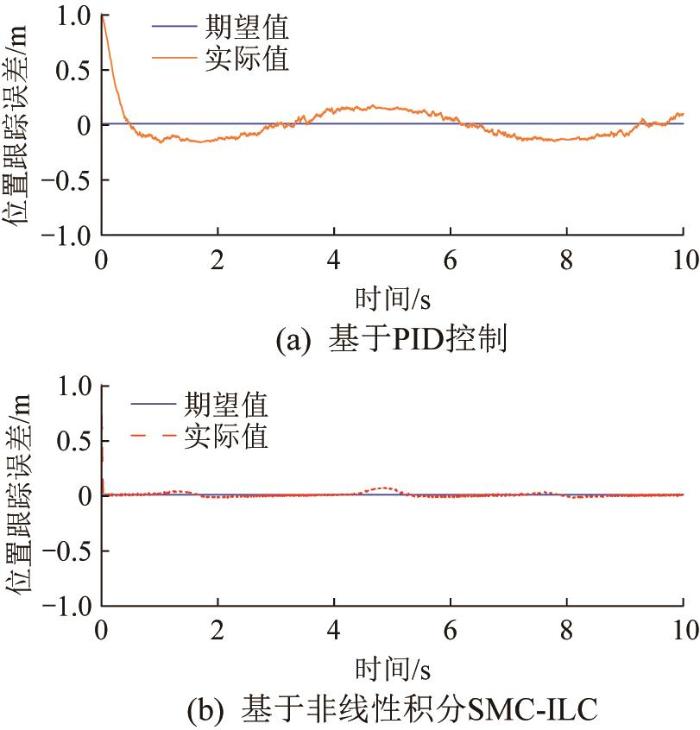
2种控制下机器人的综合位置跟踪误差如图6所示（X、Y方向的位置误差合并处理）。从图6中可以看出，采用非线性积分SMC-ILC后，机器人的实际位置跟踪误差与期望误差几乎完全吻合，说明非线性积分SMC-ILC在轨迹跟踪精度和鲁棒性方面均优于PID控制。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 机器人的综合位置跟踪误差对比

Fig.6 Comparison of comprehensive position tracking error of robot

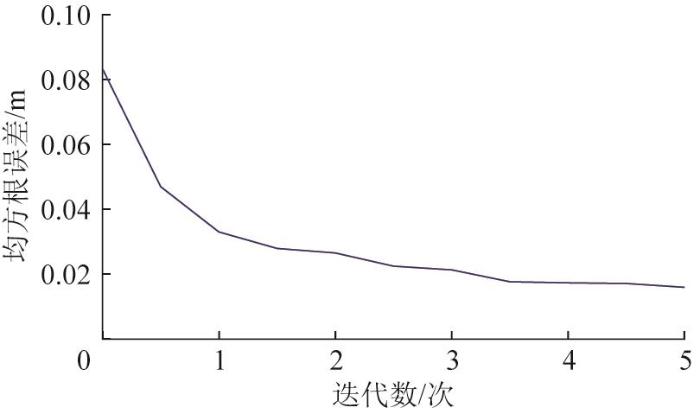
在泳池清洁机器人执行清洁任务的过程中，非线性积分SMC-ILC算法会基于第k次的跟踪误差来修正第k+1次的控制输入。基于图6数据，计算位置跟踪的均方根误差，如图7所示。结果表明，本文所提出的控制算法在机器人的轨迹跟踪中具有优异的收敛性。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 基于非线性积分SMC-ILC的位置跟踪均方根误差

Fig.7 Root mean square error of position tracking based on nonlinear integral SMC-ILC

3.2　实验分析

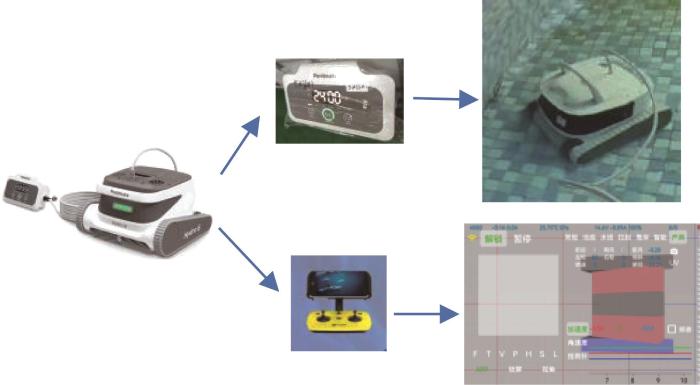
为进一步验证所提出的非线性积分SMC-ILC算法在泳池清洁机器人系统中应用的有效性，以深圳潜行创新科技有限公司研发的“Poolmate Hydro6”系列泳池清洁机器人为对象，对所设计的控制算法进行实验验证。所选用的泳池清洁机器人是一款由2个无刷直流行星齿轮减速电机驱动的三自由度机器人，由32位GD32F303微控制器控制，其控制板上集成了温度传感器、压力传感器、水位检测传感器模块、加速度传感器和陀螺仪等。机器人通过防缠绕浮力线缆与控制盒连接，控制盒连接电源；控制盒集成蓝牙模块，通过蓝牙模块连接手机，使用“Poolmate Bot”App即可控制机器人运动。在机器人运动过程中获得的传感器数据和位置信息可在泳池调试器模块中读取，如图8所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 实验设备与连接系统

Fig.8 Experimental equipment and connection systems

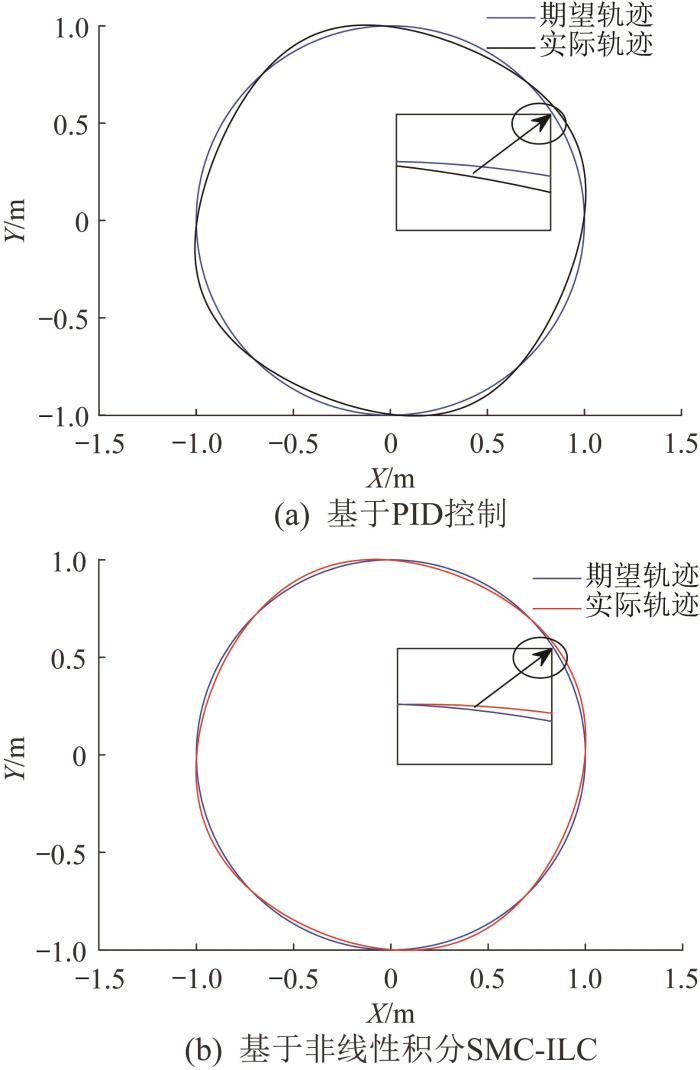
在尺寸为1.5 m×1.5 m×1.5 m的立方水池中开展实验。控制代码在树莓派上编写，在虚拟机平台上运行调试无误后烧录至GD32F303微控制器。将机器人的期望轨迹设为直径为1 m的圆形轨迹，使其作圆周运动，并与另一台由PID控制的机器人进行对比。在实验开始10 s后，即机器人进入圆形轨迹后采集相关的位置数据，并利用MATLAB软件绘制实际轨迹，结果如图9所示。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 基于不同控制算法的机器人轨迹对比

Fig.9 Comparison of robot trajectory based on different control algorithms

由图9可知，当机器人在水池环境下运行时，相比于传统的PID控制算法，非线性积分SMC-ILC算法的轨迹跟踪精度更高，可使机器人沿期望轨迹平稳行驶，位置误差较小。随着迭代次数的增加，机器人的位置跟踪误差可在有限时间内渐进收敛至接近0。实验结果表明，与PID控制相比，非线性积分SMC-ILC具有更高的控制精度。

4 结束语

本文提出了一种基于改进SMC和ILC的泳池清洁机器人轨迹跟踪控制方法，旨在解决机器人工作时因转向滑移而导致的轨迹偏移问题。首先，假设机器人在二维平面上运动，引入滑移参数后建立了机器人的运动学模型；同时，考虑机器人在水下运动时的受力特性，建立了其动力学模型。然后，在机器人控制器设计中引入SMC，设计了适应滑移干扰的非线性积分滑模面，并结合ILC提高了轨迹跟踪精度。通过理论分析，证明了所设计的控制器在滑移干扰下的收敛性。最后，通过仿真与实验验证了非线性积分SMC-ILC在轨迹跟踪精度方面优于PID控制，能够在外部干扰和滑移干扰下实现高精度的轨迹跟踪，表现出良好的鲁棒性。后续研究可聚焦于多台泳池清洁机器人协同工作时的轨迹跟踪控制策略，以实现清洁效率的进一步提升。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

何笑书

泳池清洁机器人的研究与设计

［D］. 杭州：浙江工业大学， 2020： 1-5.