正交簧片型大行程柔性球铰设计及柔度分析

doi:10.3785/j.issn.1006-754X.2023.00.069

正交簧片型大行程柔性球铰设计及柔度分析

谢超^,^,, 陈云壮, 石光楠, 赖磊捷^,^,

上海工程技术大学机械与汽车工程学院，上海 201620

Design and compliance analysis of large stroke flexible ball hinge with orthogonal reeds

XIE Chao^,^,, CHEN Yunzhuang, SHI Guangnan, LAI Leijie^,^,

School of Mechanical and Automotive Engineering, Shanghai University of Engineering Science, Shanghai 201620, China

通讯作者: 赖磊捷（1984—），男，浙江宁波人，副教授，博士，从事微位移驱动控制、微纳制造装备等研究，E-mail: lailj@sues.edu.cn, https://orcid.org/0000-0002-8767-4715

收稿日期: 2023-03-08 修回日期: 2023-04-03

基金资助:

国家自然科学基金资助项目.  51605275
上海市自然科学基金资助项目.  21ZR1426000
机械系统与振动国家重点实验室课题资助项目.  MSV202210

Received: 2023-03-08 Revised: 2023-04-03

作者简介 About authors

谢超（1999—），男，安徽芜湖人，硕士生，从事微纳米定位技术研究，E-mail:silencexc@126.com,https://orcid.org/0009-0006-1363-1188 , E-mail：silencexc@126.com

摘要

传统缺口型柔性球铰的工作行程较小，且存在结构构型及柔度计算复杂、加工工艺要求高等问题，不能应用于需大行程的场合。为此，设计了一种正交簧片型大行程柔性球铰，即将具有较大变形能力的簧片梁通过正交组合形成虎克铰，使其能够实现3个功能轴线方向的运动。该柔性球铰具有结构构型简单、加工制作容易和工作行程较大等优点。根据柔性球铰单个簧片梁的柔度矩阵及连接方式，采用柔度矩阵法和坐标变换方法，对柔性球铰的全局柔度矩阵进行建模和计算，通过有限元仿真和实验测试对所建立的柔度模型进行验证，并分析了柔性球铰几何参数对柔度的影响规律。结果表明：柔度理论计算值与仿真值的相对误差基本在10%以内，与测试值的相对误差在8%以内；几何参数对柔度影响程度从大到小依次是柔性簧片梁2的厚度、宽度、长度。研究结果可以为大行程空间柔顺机构的多样化设计提供参考。

关键词： 簧片 ; 柔性球铰 ; 大行程 ; 有限元分析 ; 柔度

Abstract

The traditional notched flexible ball hinge has smaller working stroke, complex structural configuration and compliance calculation, and high processing requirements, so it can not be applied to the occasions requiring large stroke. Therefore, a large stroke flexible ball hinge with orthogonal reeds was designed, which meant that the reed beam with large deformation capacity could form a Hooke joint through orthogonal combination, enabling it to achieve movement in three functional axis directions. The flexible ball hinge had the advantages of simple structural configuration, easy processing and manufacturing, and large working stroke. Based on the compliance matrix and connection type of a single reed beam of the flexible ball hinge, the global compliance matrix of the flexible ball hinge was modeled and calculated by the compliance matrix method and coordinate transformation method. The established compliance model was verified through finite element simulation and experimental test, and the influence of geometric parameters of the flexible ball hinge on compliance was analyzed. The results showed that the relative error between the theoretical calculating value and the simulated value of compliance was basically within 10%, and the relative error between the calculated value and the test value was within 8%; the influence degree of geometric parameters on compliance was in descending order: thickness, width and length of reed beam 2. The research results can provide reference for the diversified design of large stroke spatial compliant mechanism.

Keywords： reed ; flexible ball hinge ; large stroke ; finite element analysis ; compliance

PDF (4904KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

谢超, 陈云壮, 石光楠, 赖磊捷. 正交簧片型大行程柔性球铰设计及柔度分析. 工程设计学报[J], 2023, 30(5): 626-633 doi:10.3785/j.issn.1006-754X.2023.00.069

XIE Chao, CHEN Yunzhuang, SHI Guangnan, LAI Leijie. Design and compliance analysis of large stroke flexible ball hinge with orthogonal reeds. Chinese Journal of Engineering Design[J], 2023, 30(5): 626-633 doi:10.3785/j.issn.1006-754X.2023.00.069

柔性铰链是一种其薄弱环节在力和力矩的作用下有着较明显弹性变形的弹性机构^[1]，具有无机械摩擦、运动平稳、尺寸小、易加工及装配等优点^[2]，已被广泛应用于诸如微定位工作台、微操作机器人、超精密加工、精密姿态调整、显微镜和芯片制造等精密工程制造领域^[3-7]。

传统的柔性铰链如簧片型和切口型柔性铰链的自由度只有1个，在实际使用时受到了很大限制^[8]。为了使柔性铰链实现如常规球铰般绕三轴在空间旋转的运动功能，其构型设计十分重要。柔性球铰一般指具有3个转动自由度的柔性铰链^[9]，已有许多学者对其进行了研究。如：Lonbontiu等^[10]设计了具有双轴抛物线形切口截面轮廓线的柔性球铰，推导了球铰柔度计算公式；朱仁胜等^[11]、陈应舒等^[12]分别对切口截面轮廓线为圆弧形和椭圆弧形的柔性球铰进行了研究，得到了其柔度计算公式。传统的缺口型柔性球铰利用铰链细颈，能够实现绕3个功能轴转动。此外，将柔性虎克铰与柔性铰链进行组合，形成轴线相交型柔性球铰，也能实现绕3个轴转动^[13-14]。上述各类球铰的工作行程较小，只能在小范围内进行有效的工作，不能应用于需大行程的场合。

针对传统柔性球铰结构构型和柔度计算复杂、加工工艺要求较高以及工作行程较小等问题，作者设计了一种基于正交弹性簧片的轴线相交型大行程柔性球铰，即将具有较大变形能力的簧片梁通过正交组合形成虎克铰，使得该新型柔性球铰能够绕3个功能轴线转动较大的角度，且具有结构构型简洁、易于加工制作及工作行程较大等优点。首先，进行了新型柔性球铰的结构设计和柔度计算；其次，进行了球铰柔性有限元仿真和实验验证；最后，研究了柔性球铰相关几何参数对其柔度的影响。

1 大行程柔性球铰结构设计

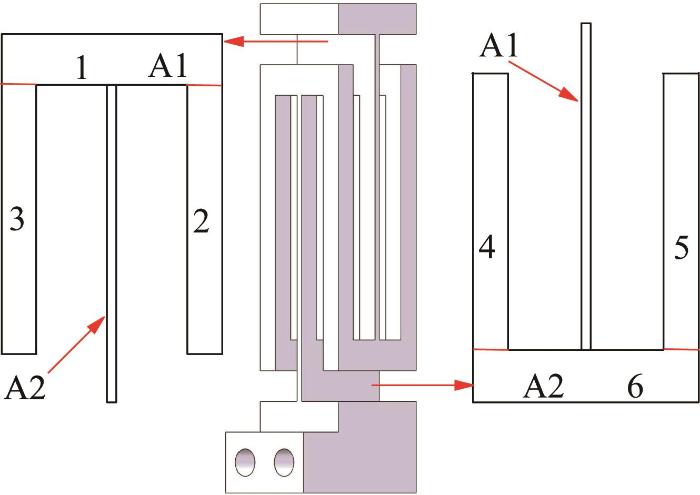
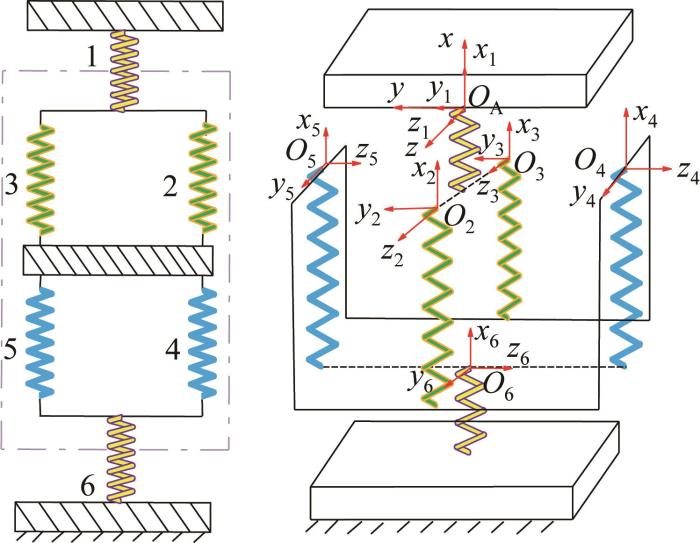
作者设计的大行程柔性球铰的结构如图1所示，其可以采用整体线切割加工工艺制成。柔性球铰结构的主体部分由6个柔性簧片梁组成，簧片梁1，2，3组成一个整体A1，簧片梁4，5，6组成另一个整体A2。簧片梁2与3并联之后串联到簧片梁1上，簧片梁1上端连接机架，簧片梁4，5，6采用相同的方式连接。A1与A2互相垂直并且通过中间连接件正交串联，由此构成柔性球铰的工作部分，球铰的剩余部分为刚件。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 大行程柔性球铰的结构

Fig.1 Structure of large stroke flexible ball hinge

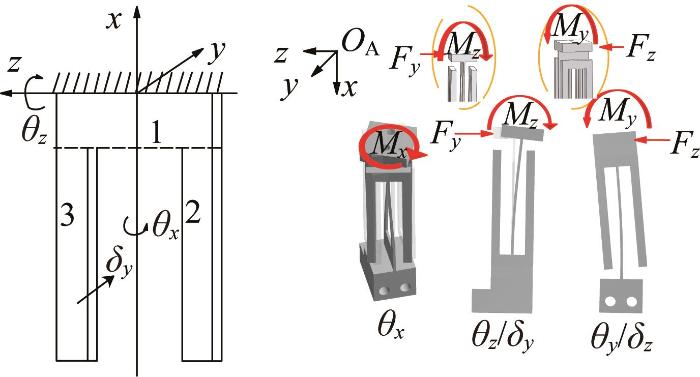
大行程柔性球铰的变形原理如图2所示。在全局坐标系O_A-xyz中，由于柔性机构的弹性形变，整体A1可以产生沿y轴的位移δ_y 以及绕z轴的角位移θ_z。此外，由于簧片梁较小的扭转刚度，A1也能产生绕x轴的有限角位移θ_x，可将其视为绕x轴的转动自由度。因此，A1可以产生3个自由度。同样，A2也可以产生3个自由度。将A1与A2进行正交串联，组成一个新型大行程柔性球铰整体，其除了在竖直方向不能产生位移外，能够产生包含3个轴向运动的五自由度运动。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 大行程柔性球铰变形原理示意

Fig.2 Schematic diagram of deformation principle of large stroke flexible ball hinge

2 大行程柔性球铰柔度计算

2.1　簧片梁柔度矩阵

柔性球铰的运动是由簧片梁的弹性形变导致的，因此，对簧片梁进行柔度建模是柔性球铰整体柔度计算的基础。柔度矩阵法具有建模简单、计算效率高、精度高等优点^[15]，可以精确描述复杂柔性机构所受载荷与位移或转动变形之间的关系。因此，根据柔性球铰的结构形状和特点，采用柔度矩阵法对柔性球铰的柔度计算公式进行推导。

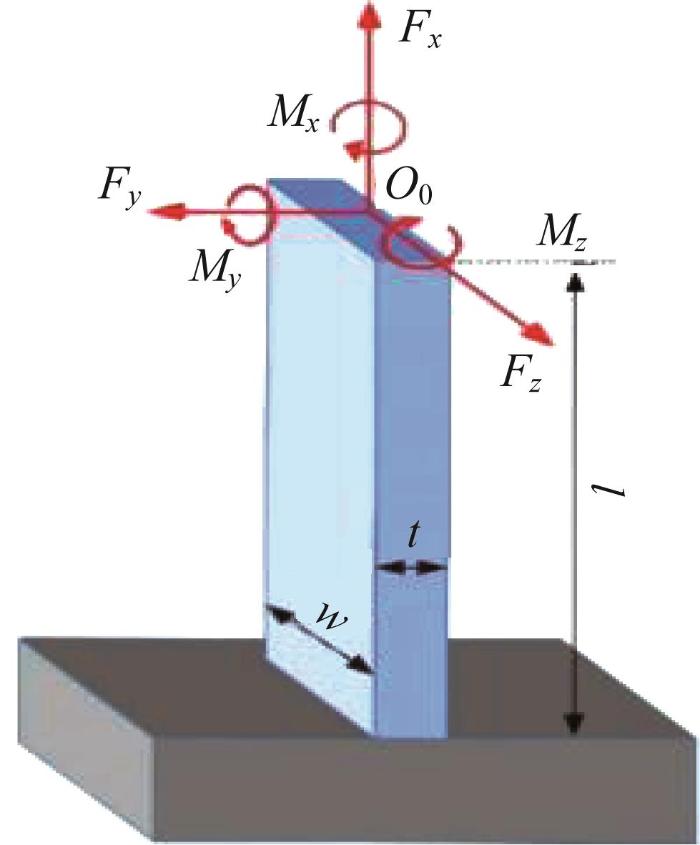
簧片梁如图3所示。为了获得球铰的整体柔度矩阵，首先须获得簧片梁i的柔度矩阵 C_i⁰（i=1, 2, …, 6）。

X = C_{i}^{0} F

(1)

式中： X =[δ_xδ_yδ_zθ_xθ_yθ_z ]^T，为簧片梁自由端在各方向产生的变形； F =[F_xF_yF_zM_xM_yM_z ]^T，为簧片梁自由端所受载荷。

根据材料力学中的欧拉伯努利梁理论^[16]，通过簧片梁在单独力或力矩作用下产生的变形与力之间的关系来推导簧片梁的柔度矩阵，即：

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 簧片梁示意图

Fig.3 Schematic diagram of reed beam

[\begin{matrix} δ_{x} \\ δ_{y} \\ δ_{z} \\ θ_{x} \\ θ_{y} \\ θ_{z} \end{matrix}] = [\begin{matrix} C_{δ_{x} - F_{x}} & 0 & 0 & 0 & 0 & 0 \\ 0 & C_{δ_{y} - F_{y}} & 0 & 0 & 0 & C_{δ_{y} - M_{z}} \\ 0 & 0 & C_{δ_{z} - F_{z}} & 0 & - C_{δ_{z} - M_{y}} & 0 \\ 0 & 0 & 0 & C_{θ_{x} - M_{x}} & 0 & 0 \\ 0 & 0 & - C_{θ_{y} - F_{z}} & 0 & C_{θ_{y} - M_{y}} & 0 \\ 0 & C_{θ_{z} - F_{y}} & 0 & 0 & 0 & C_{θ_{z} - M_{z}} \end{matrix}] [\begin{matrix} F_{x} \\ F_{y} \\ F_{z} \\ M_{x} \\ M_{y} \\ M_{z} \end{matrix}]

(2)

簧片梁柔度矩阵 C_i⁰的参数及其计算公式如表1所示。表中：l、w和t分别为图3所示簧片梁的长度、宽度和厚度；E为弹性模量；G为剪切模量；J为扭转系数。

G = \frac{E}{2 (1 + v)}

(3)

J = \frac{β t^{3} w}{12}

(4)

式中：ν为泊松比；β为与t/w的值有关的因数，

β = 12 \{\frac{1}{3} - 0.21 \frac{t}{w} [1 - \frac{1}{12} {(\frac{t}{w})}^{4}]\}

(5)

表1 簧片梁柔度矩阵的参数及其计算公式

Table 1 Parameters and their calculation formulas of compliance matrix of reed beam

参数	计算公式
$C_{δ_{x} - F_{x}}$	l/(Etw)
$C_{δ_{y} - F_{y}}$	4l³/(Et³w)
$C_{δ_{z} - F_{z}}$	4l³/(Etw³)
$C_{θ_{x} - M_{x}}$	l/(GJ)
$C_{θ_{y} - M_{y}}$	12l/(Etw³)
$C_{θ_{z} - M_{z}}$	12l/(Et³w)
$C_{δ_{y} - M_{z}}$	6l²/(Et³w)
$C_{δ_{z} - M_{y}}$	6l²/(Etw³)
$C_{θ_{y} - F_{z}}$	6l²/(Etw³)
$C_{θ_{z} - F_{y}}$	6l²/(Et³w)

新窗口打开| 下载CSV

2.2　柔性球铰柔度计算公式推导

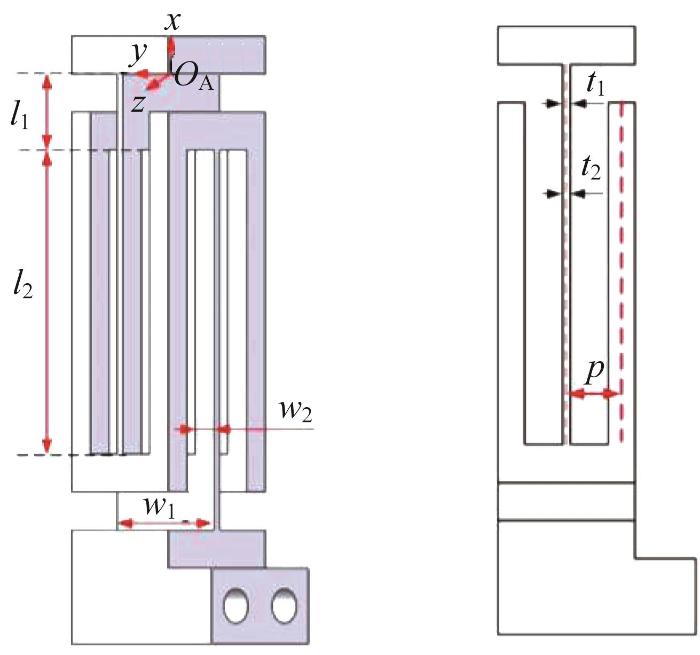
柔性球铰的截面如图4所示。全局坐标系O_A-xyz的原点O_A位于柔性球铰顶部中心。簧片梁1和6的长度、宽度和厚度分别为l₁、w₁和t₁，簧片梁2，3，4，5的长度、宽度和厚度分别为l₂、w₂和t₂，簧片梁2的中心线与簧片梁4宽度方向竖直中心线之间的距离为p，其余部分视为刚性件。所有簧片梁共用同一个全局坐标系O_A-xyz。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 柔性球铰的截面

Fig.4 Section of flexible ball hinge

对柔性球铰进行建模时，将每个簧片梁都视为一个六自由度的簧片（弹簧），得到柔性铰链的弹簧模型，如图5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 柔性铰链的弹簧模型

Fig.5 Spring model of flexible hinge

将簧片i在局部坐标系O_j -x_jy_jz_j （j=1, 2, …, 6）中的柔度矩阵定义为 $C_{i}^{j}$ 。首先将图5中局部坐标系O_j -x_jy_jz_j 中的簧片柔度矩阵 $C_{i}^{j}$ 转换到全局坐标系O_A-xyz中，得到在统一的全局坐标系O_A-xyz中簧片i的柔度矩阵 $C_{i}^{A}$ 。弹簧中任意一点的柔度矩阵可以通过坐标系变换得到，其变换公式^[17]为：

{C_{i}}^{j} = {T_{i}}^{j} C_{i}^{0} {({T_{i}}^{j})}^{Τ}

(6)

其中：

{T_{i}}^{j} = [\begin{matrix} R_{i}^{j} & S (r_{i}^{j}) R_{i}^{j} \\ O & R_{i}^{j} \end{matrix}]

(7)

式中： O 为3×3的零矩阵； $R_{i}^{j}$ 为局部坐标系O_i -x_iy_iz_i 相对于坐标系O_j -x_jy_jz_j 的旋转变换矩阵，为：

\begin{array}{l} R_{i}^{j} = R_{x} (θ) R_{y} (θ) R_{z} (θ) = [\begin{matrix} 1 & 0 & 0 \\ 0 & c o s θ_{x} & - s i n θ_{x} \\ 0 & s i n θ_{x} & c o s θ_{x} \end{matrix}] \cdot \\ [\begin{matrix} c o s θ_{y} & 0 & s i n θ_{y} \\ 0 & 1 & 0 \\ - s i n θ_{y} & 0 & c o s θ_{y} \end{matrix}] \cdot [\begin{matrix} c o s θ_{z} & - s i n θ_{z} & 0 \\ s i n θ_{z} & c o s θ_{z} & 0 \\ 0 & 0 & 1 \end{matrix}] \end{array}

(8)

式中：θ_x、θ_y、θ_z 分别为绕x、y、z轴的旋转角度。

$r_{i}^{j}$ 为O_i 在坐标系O_j -x_jy_jz中的坐标，为：

r_{i}^{j} = (r_{x}, r_{y}, r_{z})

(9)

$S (r_{i}^{j})$ 为反对称算子矩阵，为：

S (r_{i}^{j}) = [\begin{matrix} 0 & - r_{z} & r_{y} \\ r_{z} & 0 & - r_{x} \\ - r_{y} & r_{x} & 0 \end{matrix}]

(10)

将6个簧片的柔度矩阵都转换到坐标系O_A-xyz中，则：

C_{1}^{A} = T_{1}^{A} C_{1}^{0} {(T_{1}^{A})}^{Τ}, R_{1}^{A} = I, r_{1}^{A} = (0, 0, 0)

(11)

C_{2}^{A} = T_{2}^{A} C_{2}^{0} {(T_{2}^{A})}^{Τ}, R_{2}^{A} = I, r_{2}^{A} = (- l_{1}, 0, p)

(12)

C_{3}^{A} = T_{3}^{A} C_{3}^{0} {(T_{3}^{A})}^{Τ}, R_{3}^{A} = I, r_{3}^{A} = (- l_{1}, 0, - p)

(13)

C_{4}^{A} = T_{4}^{A} C_{4}^{0} {(T_{4}^{A})}^{Τ}, R_{4}^{A} = R_{x} (\frac{π}{2}), r_{4}^{A} = (- l_{1}, - p, 0)

(14)

C_{5}^{A} = T_{5}^{A} C_{5}^{0} {(T_{5}^{A})}^{Τ}, R_{4}^{A} = R_{x} (\frac{π}{2}), r_{5}^{A} = (- l_{1}, p, 0)

(15)

C_{6}^{A} = T_{6}^{A} C_{6}^{0} {(T_{6}^{A})}^{Τ}, R_{6}^{A} = R_{x} (\frac{π}{2}), r_{6}^{A} = (- (l_{1} + l_{2}), 0, 0)

(16)

式中： $R_{i}^{A}$ 为局部坐标系O_i -x_iy_iz_i 相对于全局坐标系O_A-xyz的旋转变换矩阵； $r_{i}^{A}$ 为O_i 在坐标系O_A-xyz中的坐标； I 为单位矩阵。

柔性球铰模型中，簧片2与簧片3并联，簧片4与簧片5并联，因此，该4个簧片在坐标系O_A-xyz中的柔度总和 $C_{E}^{A}$ 可以表示为:

C_{E}^{A} = {[{(C_{2}^{A})}^{- 1} + {(C_{3}^{A})}^{- 1}]}^{- 1} + {[{(C_{4}^{A})}^{- 1} + {(C_{5}^{A})}^{- 1}]}^{- 1}

(17)

簧片1和簧片6在坐标系O_A-xyz中的柔度分别为 $C_{1}^{A}$ 与 $C_{6}^{A}$ ，则根据串并联结构的柔度建模方法，柔性球铰在O_A-xyz坐标系中的总柔度 $C_{Z}^{A}$ 为：

C_{Z}^{A} = C_{1}^{A} + C_{E}^{A} + C_{6}^{A}

(18)

3 柔性球铰柔性仿真分析及实验验证

3.1　仿真分析

为了验证柔性球铰柔度计算公式的准确性，设置实际的材料参数和几何参数，利用MATLAB软件进行理论计算，然后利用ANSYS软件进行有限元仿真。

设置柔性球铰的材料为铝合金。其材料参数和几何参数如表2所示。根据公式(18)，利用MATLAB软件计算柔度矩阵。

表2 柔性球铰的材料参数和几何参数

Table 2 Material and geometric parameters of flexible ball hinge

参数	数值	参数	数值
E/GPa	71.70	w₁/mm	18.00
G/GPa	26.69	w₂/mm	3.50
ν	0.33	t₁/mm	1.00
l₁/mm	10.00	t₂/mm	1.00
l₂/mm	40.00	p/mm	7.25

新窗口打开| 下载CSV

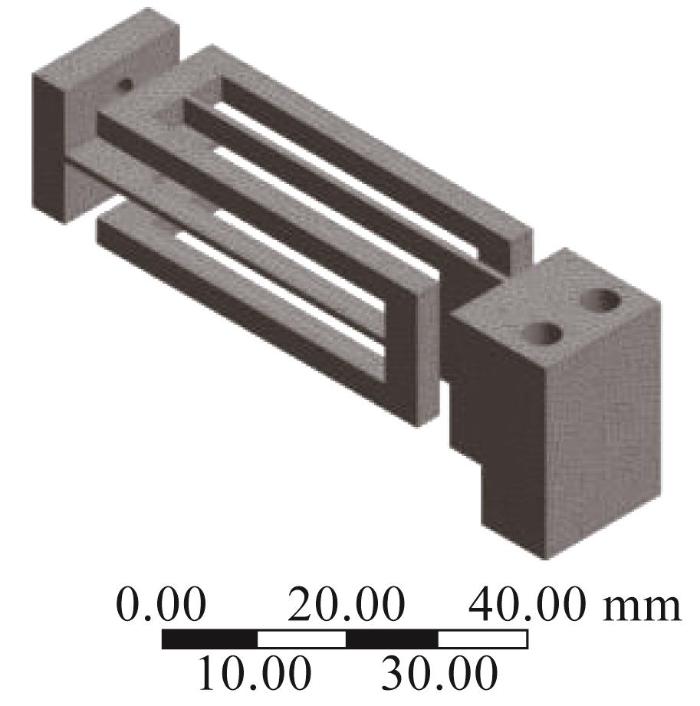
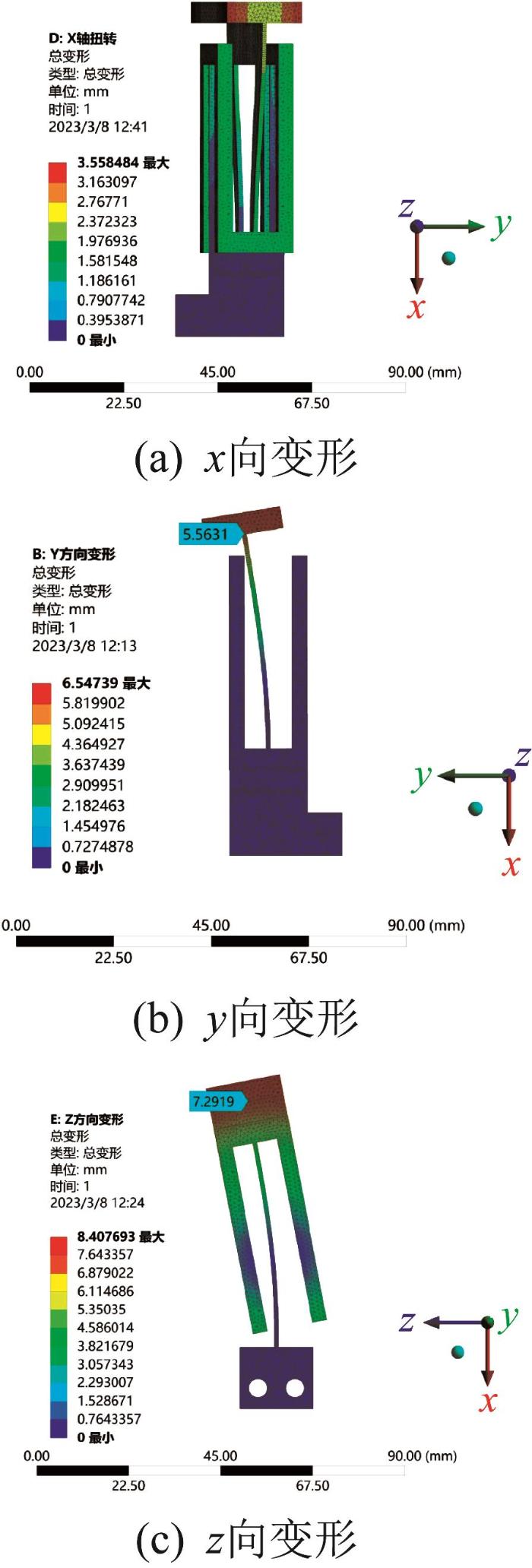
在SolidWorks软件中建立柔性球铰三维模型，并将它导入ANSYS Workbench进行静力学仿真分析。仿真模型的网格划分越精细，模型就越接近真实物理模型，所求得结果的精度就越高。本文采用四面体单元对柔性球铰进行网格划分，尺寸设置为0.5 mm，并进行局部网格细化，以保证仿真的准确性。柔性球铰仿真模型的网格划分如图6所示，其静力学仿真分析结果如图7所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 柔性球铰仿真模型的网格划分

Fig.6 Mesh generation of flexible ball hinge simulation model

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 柔性球铰静力学仿真分析结果

Fig.7 Static simulation analysis results of flexible ball hinge

根据输入载荷和仿真得到的输出位移计算相应的柔度值，并与理论计算值进行对比，结果如表3所示。结果表明，两者的相对误差基本上在10%以内，最大相对误差为10.85%，表明柔度的计算精度较高。

表3 柔性球铰柔度理论计算和仿真分析结果

Table 3 Theoretical calculation and simulation analysis results of compliance of flexible ball hinge

柔度	计算值	仿真值	相对误差/%
$C_{δ_{y} - F_{y}}$ /(mm/N)	1.013 9	1.112 6	8.87
$C_{δ_{z} - F_{z}}$ /(mm/N)	1.300 0	1.458 3	10.85
$C_{θ_{x} - M_{x}}$ /(rad/(N·m))	1.316 3	1.426 0	7.69
$C_{δ_{y} - M_{z}}$ ， $C_{θ_{z} - F_{y}}$ /(rad/N)	0.029 5	0.031 9	7.52
$C_{δ_{z} - M_{y}}$ ， $C_{θ_{y} - F_{z}}$ /(rad/N)	-0.034 2	-0.033 0	3.64
$C_{θ_{y} - M_{y}}, C_{θ_{z} - M_{z}}$ /(rad/(N·m))	1.061 5	1.032 3	2.83

新窗口打开| 下载CSV

3.2　实验验证

为了进一步验证柔性球铰柔度计算公式的准确性，按表2所示的柔性球铰的材料参数和几何参数加工柔性球铰，并进行其柔度测试。柔度测试装置如图8所示。平移方向（y、z向）柔度测试装置包括测力仪、测微仪和固定支架；扭转方向（x向）柔度测试装置包括测微仪、千分表、固定支架和力矩扳手。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 柔性球铰柔度测试装置

Fig.8 Testing device of compliance of flexible ball hinge

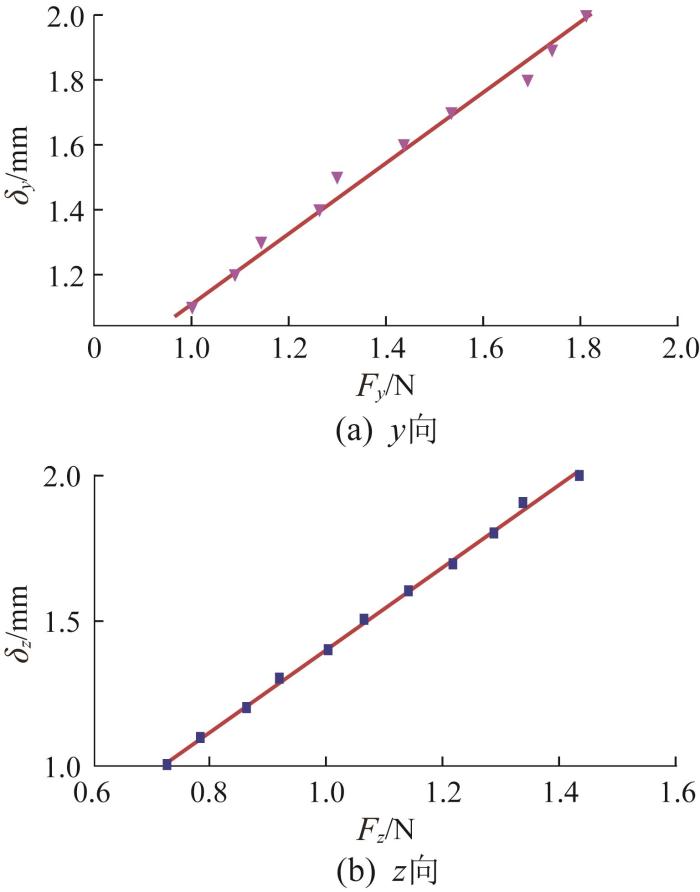
平移方向柔度测试实验：分别施加y、z向的力使柔性球铰产生变形；在球铰变形从1 mm增大到2 mm的过程中，每间隔0.1 mm变形记录其所需的力的大小。以施加的力为横坐标、变形位移为纵坐标，对采集到的数据进行拟合，得到的拟合直线的斜率即为柔度^[18]。柔性球铰y、z向的力—位移曲线如图9所示。由图可知，柔性球铰y向的柔度 $C_{δ_{y} - F_{y}}$ =1.092 mm/N，z向的柔度 $C_{δ_{z} - F_{z}}$ =1.401 2 mm/N。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 柔性球铰y、 z向的力—位移曲线

Fig.9 Force-displacement curve of flexible ball hinge in the y and z directions

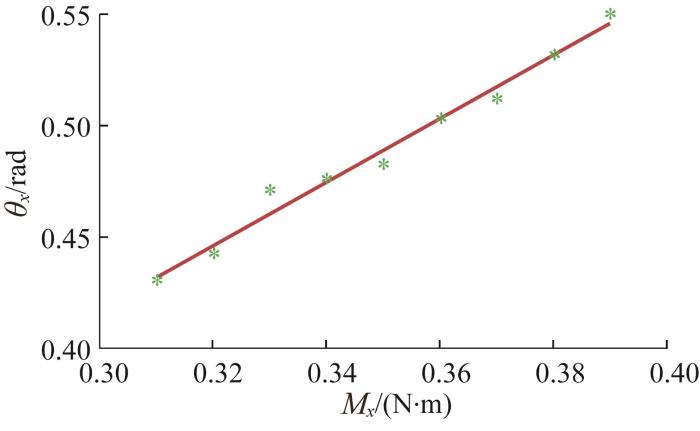
扭转方向柔度测试实验：固定测微仪指针与千分表指针之间的水平距离L=12 mm，用力矩扳手在球铰末端施加x向的扭矩M_x；在扭矩由0.30 N·m增大至0.39 N·m的过程中，每间隔0.01 N·m记录测微仪指针的水平移动距离Δd₁和千分表指针的水平移动距离Δd₂。利用所得的数据计算不同扭矩下球铰的扭转角度θ：

θ = a r c t a n \frac{Δ d_{1} + Δ d_{2}}{L}

(19)

柔性球铰扭矩—扭角曲线如图10所示。由图可知，柔性球铰扭转方向的柔度 $C_{θ_{x} - M_{x}}$ =1.411 7 rad/(N·m)。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 柔性球铰扭矩—扭角曲线

Fig.10 Torque‒angle curve of flexible ball hinge

比较实验结果与计算结果可知，柔性球铰y、z向柔度的相对误差分别为7.70%和7.78%，x向柔度的相对误差为7.25%，验证了柔度计算公式具有较高的准确性。产生误差的原因主要包括三部分：其一，簧片梁的尺寸存在加工误差；其二，在测试过程中存在力和位移的测量误差；其三，最重要的原因是大变形簧片梁存在的几何非线性并不完全符合采用柔度矩阵法进行理论计算时线性小变形的假设，这将在后续研究中进行进一步分析。

4 柔性球铰几何参数对柔度的影响

正交簧片型柔性球铰的结构相比传统的球铰有本质的区别，并且其具有易加工制作和工作行程大等优点。在不同的应用场合，其所需要的行程和负载能力有所不同，因此，有必要分析柔性球铰的几何参数对柔度的影响。

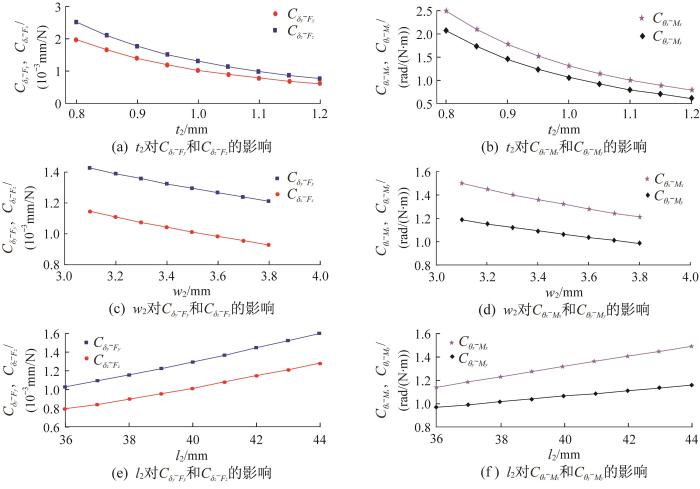
保持柔性球铰的材料参数不变，采用控制变量法，通过改变柔性球铰某一几何参数来分析该参数对柔度的影响^[19]。根据柔性球铰的结构可知，簧片梁1，2的厚度相同，即t₁=t₂。由有限元仿真结果可知，簧片梁1的变形较小，其对柔性球铰的柔度影响较小，故设置l₁=10 mm，w₁=18 mm，分别改变t₂、w₂和l₂来分析簧片梁2的几何参数对柔度的影响，结果如图11所示。由图可知： $C_{δ_{y} - F_{y}}$ 、 $C_{δ_{z} - F_{z}}$ 、 $C_{θ_{x} - M_{x}}$ 、 $C_{θ_{y} - M_{y}}$ 均随t₂和w₂的增大而减小，随l₂的增大而增大，与l₂呈正相关。通过对比可以得出，柔性球铰几何参数对其柔度影响程度从大到小依次为t₂、w₂、l₂。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 簧片梁2的几何参数对柔性球铰柔度的影响

Fig.11 Influence of geometric parameters of reed beam 2 on compliance of flexible ball hinge

5 结论

本文设计了一种正交簧片型大行程柔性球铰，即将具有较大变形能力的簧片梁通过正交组合形成虎克铰，使其实现3个功能轴线方向的运动。采用柔度矩阵法和坐标变换方法对柔性球铰的全局柔度矩阵进行理论建模，通过有限元仿真和实验测试对所建立的柔度理论模型进行分析和验证。结果表明，柔度理论计算值与仿真值的相对误差基本上在10%以内，与测试值的相对误差在8%以内，证明了柔度计算公式具有较高的准确性。通过改变柔性球铰的几何参数来分析其对柔度的影响，得出几何参数对柔度影响程度从大到小依次是柔性簧片梁2的厚度、宽度、长度。作者设计的正交簧片型大行程柔性球铰及其柔度计算和特性分析能够为大行程空间柔顺机构的多样化设计提供参考。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

姜玉涛，张银.

双轴椭圆切口型柔性球铰柔度建模及分析

［J］.自动化与仪器仪表，2022（2）：33-42.