天然气发动机广泛应用于工业设备、农业机械、汽车和船舶. 为了提升经济性和动力性,空燃比(air-fuel ratio,AFR)控制技术受到了广泛的关注. 空燃比控制在天然气发动机中至关重要,直接影响燃烧效率、排放性能和发动机寿命. AFR控制仍面临系统滞后、非最小相位特性、强非线性、外部扰动及模型不确定性等挑战,使精确控制变得困难.
上述滑模控制方法属于传统的有限时间或渐近稳定性控制,收敛时间对初始状态高度敏感. 为了改善该问题,有限时间控制通过设计适当的滑模面与控制律,可以在有限时间内实现稳定,提高系统的响应速度[7–8],但性能受到初始条件的影响. 为了克服这一局限,提出固定时间控制. 杨佳等[9]提出固定时间非奇异终端滑模控制,以应对机械臂中的未知扰动与建模误差. 刘永慧等[10]针对永磁同步电机中的不匹配扰动,提出固定时间滑模跟踪控制. 为了突破固定时间值与控制参数间的精确关联难以获得的难题,学者们研究预定义时间稳定控制方法. 该方法可以在不依赖初始条件的情况下明确给出可调的收敛时间上限[11]. Yan等[12]提出预定义时间控制策略,解决了参数不确定与时变干扰下的空间飞行器轨迹跟踪问题. 刘宜成等[13]提出预定义时间自适应滑模控制,用于柔性空间机器人的轨迹跟踪. 郑力文等[14]提出预定义时间分数阶滑模控制,用于风火打捆外送系统的振荡抑制.
本文提出结合预定义时间滑模控制与改进Smith预估器的空燃比控制策略. 该方法利用预定义时间控制,确保系统在预设时间内收敛,增强了控制性能的确定性与响应速度. 通过改进的Smith预估器补偿系统时滞,有效提升了对时变滞后和模型不确定性的鲁棒性.
1. 空燃比延迟动态分析
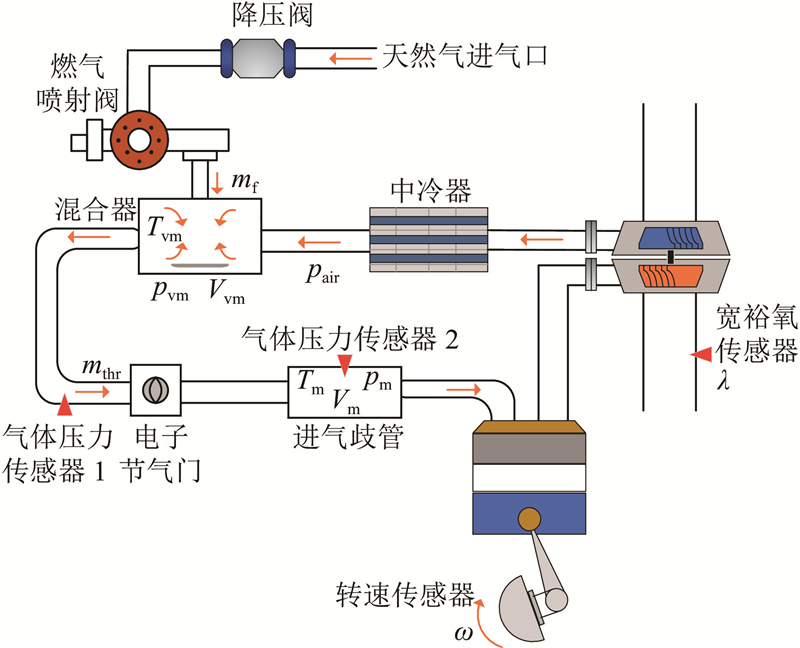
图 1
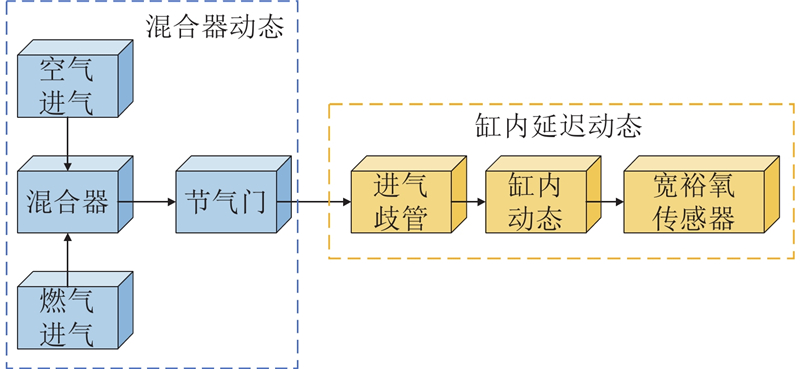
图 2
图 2 天然气发动机空燃比延迟动力学模型的结构
Fig.2 Structure of natural gas engine air-fuel ratio delay dynamic model
氧传感器的测量输出为过量空气系数
基于质量守恒原理和理想气体质量方程对混合器的动态特性进行建模[17],得到混合器处空燃比的动态表达式如下:
式中:
将混合气从流入进气歧管到流出汽缸的过程中产生的传输延迟记为
式中:
氧传感器对过量空气系数的检测可以视为惯性环节,对排气中的惯性特性和传感器的惯性特性进行建模:
式中:
结合式(2)、(4)、(5),可以得到天然气发动机空燃比从燃料喷射到氧传感器检测的动态特性:
式中:
在天然气发动机中,空燃比反馈控制回路中存在较大的延迟,导致空燃比的变化需要经过一段时间才能被氧传感器检测到. 若直接将氧传感器的输出反馈到控制器,则可能引发响应迟缓和输出不稳定的问题. 根据非最小相位系统的控制方法,采用改进的Smith预估器对氧传感器的输出进行补偿,并将补偿后的信号反馈至预定义时间控制器,从而显著提高延迟系统的闭环控制性能.
2. 空燃比精确控制
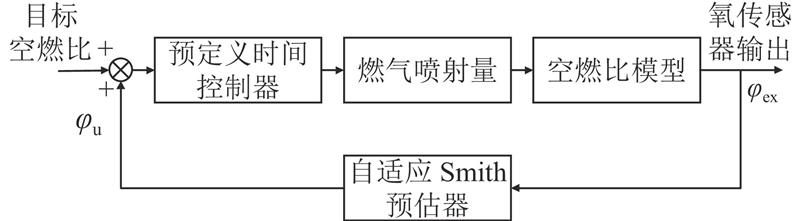
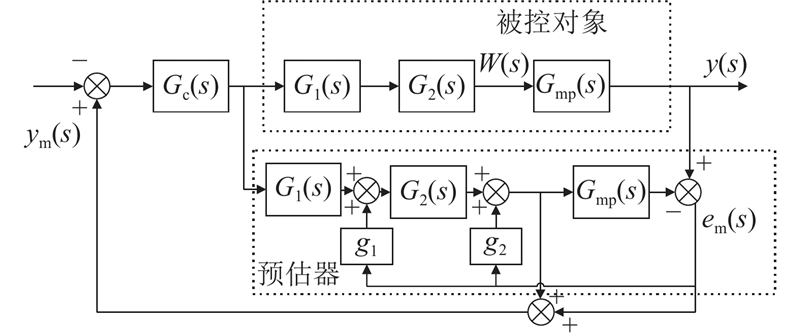
对于空燃比控制,基于改进的Smith预估器对传感器输出进行动态补偿. 基于补偿输出和设定值之间的差异,设计空燃比闭环控制器. 控制策略如图3所示.
图 3
2.1. 改进的Smith预估器设计
将空燃比控制模型写为如下的传递函数形式:
式中:
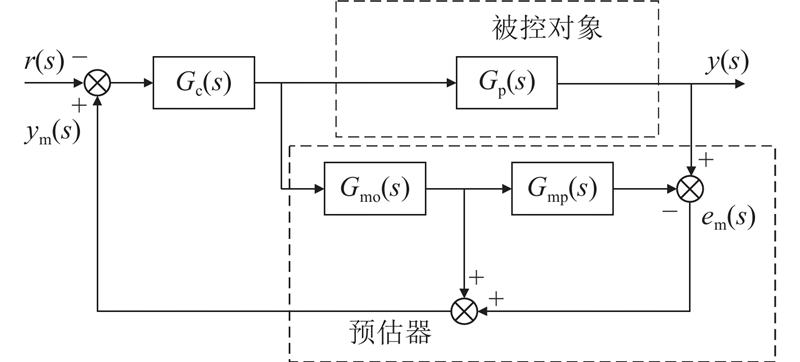
采用Smith预估器对时滞被控对象
图 4
图3中,
式中:
将
当预估器中的模型参数和被控对象的实际参数相等,即
当Smith预估器模型的参数与被控对象的实际参数一致时,可以有效消除延迟项对闭环系统的影响. 在实际系统中,传统的Smith预估器假设过程模型是精确已知的,系统模型往往存在不确定性或未建模动态,从而影响补偿效果,导致预测输出偏离真实输出,影响系统性能.
由于Smith预估器依赖于过程模型的准确性,在不稳定系统或非最小相位系统中,补偿效果可能较差,甚至可能引起不稳定. 当设置的参数与实际系统相差较大时,Smith预估器甚至会损害系统性能. 提出改进的Smith预估器,将系统分成两部分,分别引入补偿系数
式中:
被控对象
被控对象
对于系统
改进的Smith预估器通过引入补偿系数
图 5
传统Smith预估器仅对固定时滞有效,而改进方案能够更好地应对时滞变化,提高系统的适应性和动态响应性能. 该方法在处理不稳定对象、模型不确定性和外部干扰方面,较传统Smith预估器具有显著优势.
2.2. 预定义时间滑模控制器的设计
使用改进的Smith预估器补偿氧传感器的输出,并将补偿后的信号反馈给预定义的时间控制器,可以有效地消除延迟项对闭环系统的影响. 式(6)经过改进的Smith预估器补偿后,改写如下:
设空燃比目标值为
式中:
根据文献[18]可知,非奇异终端滑动面设计为
式中:
式中:
在给定系统(22) 和滑动面(23) 的条件下,若将设计的控制输入(24)应用于系统(22),则所有的系统状态都会在预定义的时间内接近零. 此外,预定义收敛时间为
通过使用PTSMC技术实现非线性系统的预定义时间稳定,需要以下2个步骤. 1)定义的控制输入应确保在预定义的时间滑动运动,即
1)证明:当控制输入(24)作用于系统(22)时,系统轨迹将到达滑动面,即
滑动面的时间导数为
将方程(24)的设计控制输入代入式(26),可得
将式(27)代入式(25),可得
由于
设
通过向系统(22)施加控制输入(24),系统状态到达滑动表面
2)为了获得证明的第2步,有
通过将
因此,所有系统状态在预定义时间内达到零. 此外,预定义稳定时间为
系统(22)在
3. 对比验证
试验验证平台通过在闭环回路中使用实际物理实体替代控制器或控制对象,更真实地再现发动机运行过程中的信号传输干扰,以及电磁元件、执行器可能存在的动态延迟效应. 这种实验方式不仅能够更准确地模拟发动机在不同工况下的工作状态,还可以灵活调整实验参数,以适应复杂多变的运行环境. 该平台具备高度的实时性和可调控性,可以在实验过程中动态调整温度、压力、转速等关键变量,以模拟发动机在不同工况下的真实运行状态. 此外,该平台试验周期短、重复性高、成本低,广泛用于发动机性能验证、控制优化和故障诊断[19].
3.1. 验证平台的搭建
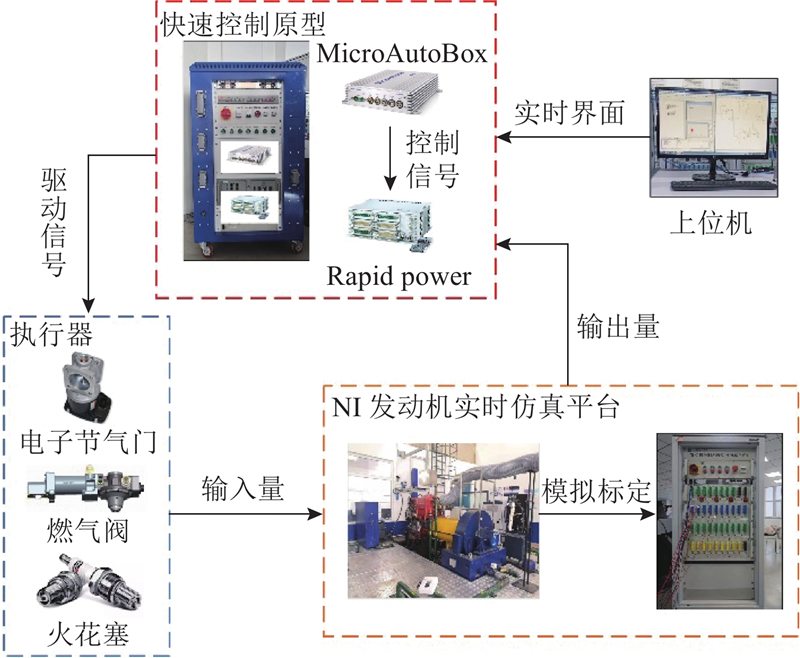
为了验证改进的预定义时间滑模控制器的性能,开展对比验证. 验证平台由实时控制器和实时仿真机组成,如图6 所示.
图 6
实时控制器采用基于dSPACE的快速控制原型系统,而实时仿真机基于 NI 平台构建的实时仿真系统,用于模拟虚拟发动机并进行实验验证. 在基于dSPACE的快速原型试验验证平台中,控制系统由MicroAutoBox和RapidPower组成. MicroAutoBox负责采集电子节气门、燃气阀、火花塞等执行器的位置信号,并执行控制算法计算. RapidPower接收MicroAutoBox发送的控制信号,并驱动相应的执行器执行控制指令. 在基于NI的发动机实时仿真平台中,仿真软件以Veristand为核心. 通过配置硬件板卡及相应的通道参数,提供真实的实验环境支持.
3.2. 不同控制器的对比分析
图 7
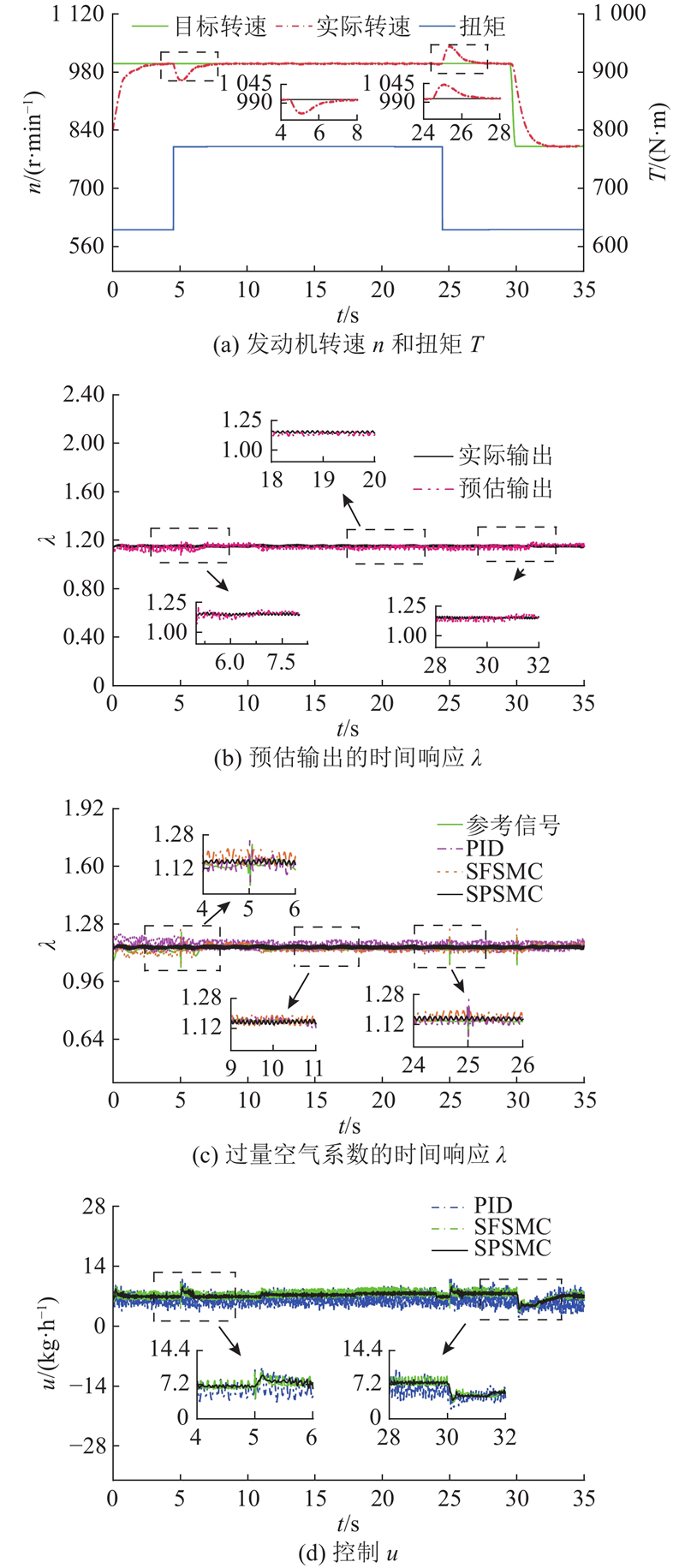
案例1验证了天然气发动机模型在稳态工况下下预定义时间控制器的控制性能,并在恒定速度与扭矩条件下验证其对过量空气系数的跟踪能力. 案例2验证了天然气发动机模型在瞬态工况下预定义时间控制器的控制性能. 它比较了Smith快速收敛滑模控制器(Smith fast convergence sliding mode controller, SFSMC)和PID控制器与改进的Smith预定义时间滑模控制器(Smith pre-defined time sliding mode controller, SPSMC)在速度阶跃变化和负载突变下的过量空气系数.
SFSMC滑模控制器的滑动面设计[22]如下:
SFSMC控制率设计如下:
式中:
案例1:验证预定义时间控制器的稳定性能,参考信号是过量空气系数的阶跃变化. 在发动机转速分别设置为900 r/min、负载扭矩为700 N·m的稳态工况下,使用改进的Smith预估器对过量空气系数进行预估效果的分析,将提出的预定义时间空燃比控制策略与PID控制器和SFSMC控制器进行对比.
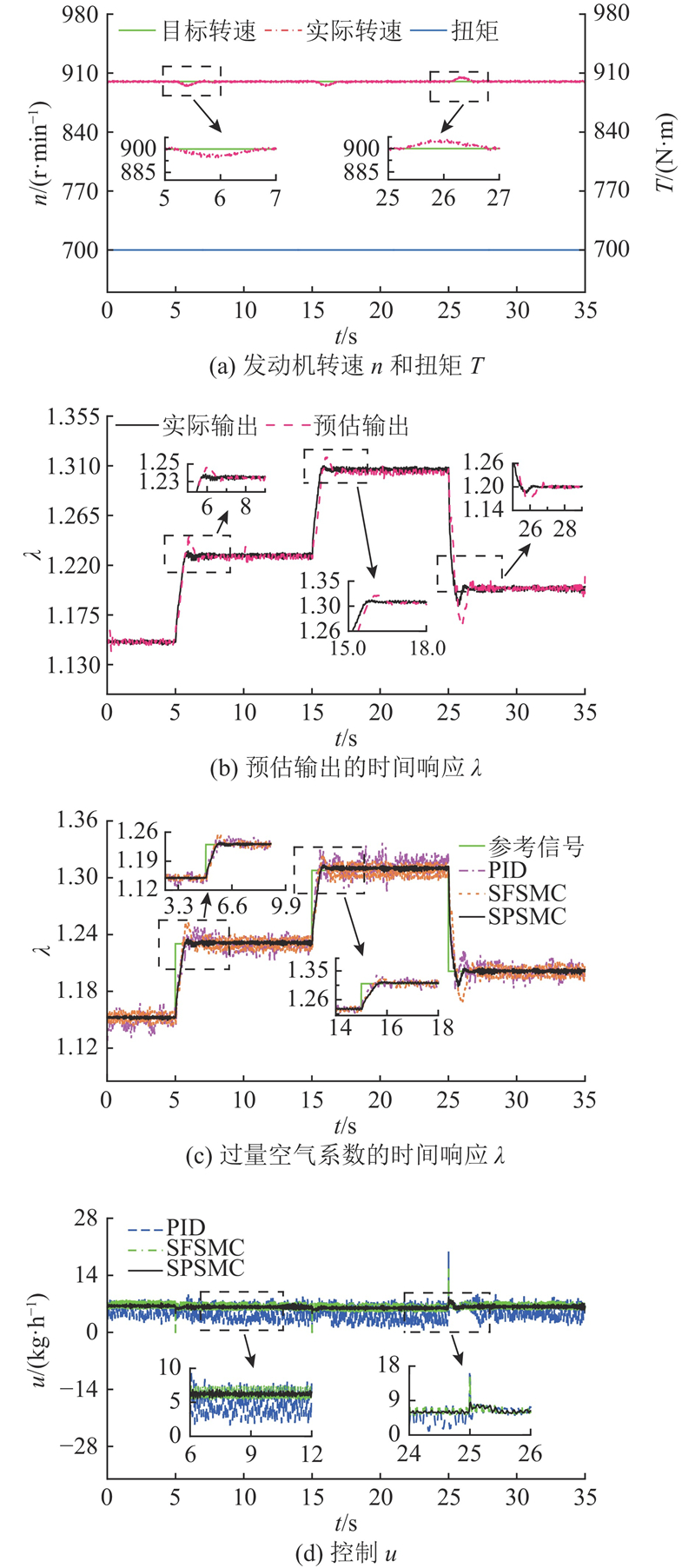
在案例1中,选取900 r/min转速和700 N·m扭矩作为典型稳态工况进行分析. 从图8 (a)可知,当目标过量空气系数发生阶跃变化时,发动机转速出现小幅抖动,波动量小于8 r/min,系统整体保持良好的动态稳定性. 如图8 (b)所示为改进Smith预估器对过量空气系数的估计效果,能够在多个瞬态响应区间(如6~8 s、26~28 s)中实现对实际值的准确预测,最大估计误差小于0.02,验证了该预估器在复杂工况下的高精度与快速响应能力. 如图8 (c)所示为PID、SFSMC与所提SPSMC 3种控制策略下的过量空气系数动态响应性能. 在第6 s阶跃响应的过程中,PID控制器出现明显的超调,峰值误差约为+0.32,SFSMC控制器的峰值误差为+0.21, SPSMC控制器的峰值误差仅为+0.12,降低幅度约为63%和43%. 从稳态误差来看,SPSMC控制下的过量空气系数最终稳定小于0.005,相较于PID控制的0.02与SFSMC控制的0.01,表现出更强的稳态性能与动态跟踪能力. 如图8 (d)所示为控制输入的时间响应曲线. 在外界扰动(如第25 s)作用下,SPSMC控制信号的波动幅度控制为1.5 kg/h,SFSMC控制约为2.2 kg/h,PID控制则达到4 kg/h. 利用SPSMC控制策略,有效降低了控制信号的抖振程度. 在案例1中,选取900 r/min转速和700 N·m扭矩作为典型稳态工况进行分析.
图 8
图 8 定转速定扭矩下的过量空气系数实验效果图
Fig.8 Experimental effect diagram of excess air coefficient under constant speed and constant torque
案例2:将过量空气系数目标值设为定值,分别测试在转速突变及负载突变工况下的过量空气系数变化情况.
在案例2中,采用固定的过量空气系数设定值和负载突变条件作为测试工况,模拟发动机在800与1 000 r/min之间变速的瞬态运行工况. 从图9 (a)可知,在参考转速阶跃变化及负载突变的双重扰动下,发动机转速仍保持在±50 r/min的波动范围内,系统展现出良好的动态稳定性. 如图9 (b)所示为改进Smith预估器在复杂扰动下的估计效果. 可见,在转速和负载发生突变的区间(如5~8 s、28~32 s),预估输出能够稳定贴合实际输出,波动幅度不超过±0.05,验证了预估器对动态变化的快速响应能力与准确性. 如图9 (d)所示为3种控制方法在该工况下的过量空气系数动态响应性能比较. 以第5 s突变点为例,SPSMC的过量空气系数误差小于0.05,SFSMC控制器的误差约为0.09,而PID控制器的误差达到0.13,说明SPSMC能够更有效地解决发动机转速与燃气动态之间的强耦合问题,提升系统的控制精度. 如图9 (d)所示,进一步比较控制输入的响应情况. SPSMC控制器在扰动时刻(如第5 s)的波动幅度小于2.0 kg/h,相比之下,SFSMC控制器的波动幅度为2.5 kg/h,PID控制器甚至达到3.0 kg/h. 该结果表明SPSMC不仅在跟踪精度上表现优异,而且在控制信号抑制与能耗效率方面具备明显的优势.
图 9
图 9 转速扭矩突变下的过量空气系数实验效果图
Fig.9 Experimental effect diagram of excess air coefficient under sudden change in speed and torque
为了验证所提控制器的性能优势,对3种控制器在2个典型工况下进行量化对比分析. 将系统稳态误差的最大值
式中:e1为跟踪误差,N为采样点个数. 具体性能指标如表1所示.
表 1 案例1和案例2的性能指标对比结果
Tab.1
| 案例 | 控制器 | |||
| 案例1 | PID | 0.32 | 0.020 | 0.016 |
| SFSMC | 0.21 | 0.012 | 0.009 | |
| SPSMC | 0.12 | 0.006 | 0.004 | |
| 案例2 | PID | 0.13 | 0.065 | 0.040 |
| SFSMC | 0.09 | 0.045 | 0.030 | |
| SPSMC | 0.05 | 0.025 | 0.014 |
案例1中,SPSMC控制器相较于PID控制器,
4. 结 语
针对天然气发动机空燃比控制中存在的系统时延与强非线性问题,提出结合改进 Smith 预估器与预定义时间滑模控制的 SPSMC 方法,实现了过量空气系数的快速、精确调节,并有效补偿系统时延. 基于李雅普诺夫理论完成了稳定性证明. 仿真结果表明,该方法在2种典型工况下的3项性能指标较传统 PID 和 SFSMC 均有显著改善,表现出更优的动态响应与稳态精度,验证了该方法在复杂工况下的鲁棒性与有效性. 未来工作将结合硬件平台开展实验验证,进一步研究在更广工况范围和实际发动机系统中的应用推广.
参考文献
Optimization of air–fuel ratio control of fuel-powered UAV engine using adaptive fuzzy-PID
[J].DOI:10.1016/j.jfranklin.2018.09.003 [本文引用: 1]
Design of output power control system based on mass flow rate comparison of air-fuel ratio (AFR) on dual fuel generator set by using PID control method
[J].DOI:10.14716/ijtech.v11i3.2710 [本文引用: 1]
Design of a hybrid fault-tolerant control system for air–fuel ratio control of internal combustion engines using genetic algorithm and higher-order sliding mode control
[J].
Second-order sliding mode strategy for air–fuel ratio control of lean-burn SI engines
[J].DOI:10.1109/TCST.2013.2281437 [本文引用: 1]
Hybrid fault-tolerant control for air-fuel ratio control system of internal combustion engine using fuzzy logic and super-twisting sliding mode control techniques
[J].DOI:10.3390/en15197010 [本文引用: 1]
Achievement of MPPT by finite time convergence sliding mode control for photovoltaic pumping system
[J].DOI:10.1016/j.solener.2018.03.026 [本文引用: 1]
Improved sliding mode disturbance observer-based model-free finite-time terminal sliding mode control for IPMSM speed ripple minimization
[J].
机械臂新型固定时间非奇异终端滑模控制
[J].DOI:10.3969/j.issn.1674-8425(z).2025.01.011 [本文引用: 1]
A new fixed time nonsingular terminal sliding mode control for robot arms
[J].DOI:10.3969/j.issn.1674-8425(z).2025.01.011 [本文引用: 1]
不匹配扰动下永磁同步电动机的固定时间滑模跟踪控制
[J].DOI:10.19570/j.cnki.jsspu.2024.04.007 [本文引用: 1]
Fixed time sliding mode tracking control of permanent magnet synchronous motor under mismatched disturbances
[J].DOI:10.19570/j.cnki.jsspu.2024.04.007 [本文引用: 1]
Predefined-time sliding mode attitude control for liquid-filled spacecraft with large amplitude sloshing
[J].DOI:10.1016/j.ejcon.2024.100970 [本文引用: 1]
A non-singular predefined-time sliding mode tracking control for space manipulators
[J].
柔性空间机器人预定义时间自适应滑模控制
[J].DOI:10.3785/j.issn.1008-973X.2025.02.013 [本文引用: 1]
Predefined time adaptive sliding mode control for flexible space robot
[J].DOI:10.3785/j.issn.1008-973X.2025.02.013 [本文引用: 1]
基于预定义时间分数阶滑模控制的风火打捆外送系统振荡抑制策略
[J].DOI:10.16081/j.epae.202412015 [本文引用: 1]
Oscillation suppression strategy of wind-fire bundling delivery system based on predefined time fractional sliding mode control
[J].DOI:10.16081/j.epae.202412015 [本文引用: 1]
基于改进型Smith预估法对航向控制的分析
[J].
Analysis of control of heading based on improved Smith estimation method
[J].
航空发动机大延迟系统Smith预估补偿模糊PID控制算法
[J].
A Smith predict fuzzy PID algorithm for aeroengine system with long time-delay
[J].
A new strongly predefined time sliding mode controller for a class of cascade high-order nonlinear systems
[J].
Evaluation of a semi-physical model to predict NOx and soot emissions of a CI automotive engine under warm-up like conditions
[J].DOI:10.1016/j.applthermaleng.2018.04.005 [本文引用: 1]
Modeling and validation of a lean burn natural gas engine
[J].DOI:10.1115/1.1386790 [本文引用: 1]
Natural gas engine model for speed and air-fuel control
[J].DOI:10.1504/IJMIC.2020.116193 [本文引用: 1]
Ship trajectory tracking control based on adaptive fast non-singular integral terminal sliding mode
[J].DOI:10.1016/j.oceaneng.2024.118975 [本文引用: 1]