随着大数据时代的到来，推荐系统在信息过滤方面扮演着重要角色^[1]. 协同过滤（collaborative filtering, CF）是有效的推荐方法，在假设行为相似的用户对项目具有相似偏好的前提下^[2]，根据用户和项目的历史交互行为进行预测. 例如矩阵分解^[3]可以将用户-项目交互矩阵分解为嵌入向量，根据内积预测用户与项目之间的交互. 近年来，图神经网络（graph neural network, GNN）在协同过滤任务中展示出巨大的潜力^[4-5]. 许多工作利用GNN学习有效的节点表示，然后进行推荐预测，这种方法被称为图协同过滤.

现有的图协同过滤方法虽然性能优异，但推荐系统中的一些经典问题仍会显著削弱模型效率. 1）原始用户-项目交互图难免包含局部噪声. 当GNN在图上迭代聚合时，噪声信息也会在图中传播，影响节点表征学习的质量. 根据文献[6]的结论，交互数据中只有少数对应较大奇异值的组件对推荐性能有贡献，大多数信息都包含噪声. 基于GNN的方法与低秩方法（如奇异值分解）存在密切联系，构建两者的协作关系成为抑制噪声问题的思路. 2）在推荐系统中用户和项目的交互数据通常是稀疏的. GNN的传播机制可以在一定程度上缓解数据稀疏问题，但它依赖于图结构上的显式交互，忽略了用户和项目之间更丰富的关联信息. 原始图的信息不足可能会限制GNN的表征能力，进而降低推荐任务的准确性. 有研究通过对比学习来缓解数据稀疏问题^[7-9]，通过破坏图结构或随机游走构建对比任务. 这种设计能够提升模型性能和鲁棒性，但会扭曲原始图信息. 如何有效利用低秩表示抑制噪声，同时为图协同过滤方法构建更有意义的对比学习任务仍需要进一步探索.

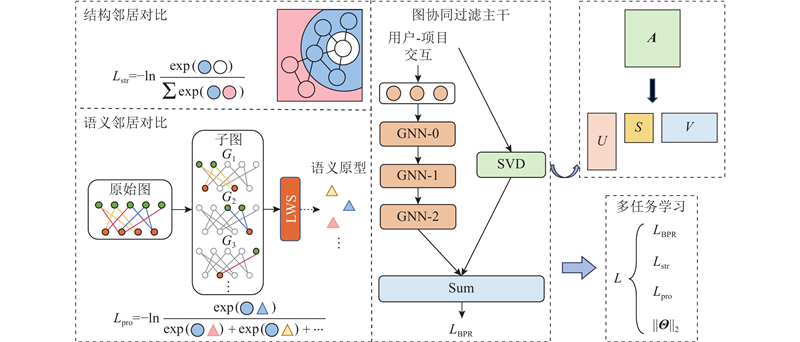
本研究提出融合全局信息和对比学习的图神经网络推荐模型（graph neural network recommendation model integrating global information and contrastive learning, GICL）. 该模型通过奇异值分解（singular value decomposition, SVD）截断邻接矩阵获取低秩表示，从全局角度抑制噪声数据；构建节点级的对比任务，从结构感知和语义相似角度学习代表性嵌入，用以构建正负样本对，挖掘交互图上的潜在关系. 本研究将1）开展原始图的噪声与低秩方法（如SVD）的关系研究，利用SVD改进图协同过滤框架，捕捉全局信息中主要的关联模式. 2)设计基于2种增强邻居的对比学习目标，分别利用图结构上的同质邻居和划分语义子图来构造节点的对比视图，作为辅助任务缓解数据稀疏问题. 3)在4个公开数据集上开展GICL与多个主流推荐模型的性能对比研究.

相较于传统神经网络，GNN在处理非欧式数据时更具优势，其中图卷积网络(graph convolutional network, GCN)^[10]是其中较为流行的变体. 研究者将交互数据建模为用户-项目二部图，利用GCN学习图的拓扑结构和节点表征. GCN通过邻域信息传播机制学习节点嵌入，能够逐层聚合邻域节点的特征. 例如Wang等^[4]提出的神经图协同过滤（neural graph collaborative filtering, NGCF），利用多层图卷积捕捉二部图上的高阶关系，并融合不同层的嵌入获取节点的最终表示. He等^[5]提出LightGCN，证实特征变换和非线性激活对推荐性能贡献甚微，只保留邻域聚合的部分. 这种轻量化设计启发了后续的模型设计，许多研究者在其基础上提出改进. 然而大多数基于图的协同过滤方法主要关注历史交互记录，无法利用潜在的关系和约束（如节点相似性）学习节点表示. 为了捕获用户和项目之间的关联信息，Sun等^[7]提出构建更多的图结构，将同质节点的相似性纳入节点嵌入的学习中，利用交互数据中的潜在信息提高建模的质量.

对比学习作为自监督方法，也能够有效提高信息的利用率. 有研究将对比学习引入图协同过滤中，以提高模型的性能. 数据增强是构造对比学习任务的重要步骤，通过改变原始数据的结构或者添加扰动生成对比视图. 在此基础上，研究者将对比学习作为辅助任务探索交互数据中的潜在关系，并设计了多种构造方案. Wu等^[8]提出的自监督图学习（self-supervised graph learning，SGL）模型，通过丢弃节点和边，以及随机游走策略，对图结构进行增强. 这种构造方式虽然简单，但对比视图可能会丢失关键信息，变成断开的片段，强行拉近片段之间的距离可能会产生负面影响. 对此，Yu等^[9]放弃图结构增强，而是在嵌入空间中添加均匀噪声生成对比视图，使节点表示分布更均匀. 进一步地，Lin等^[11]提出为节点学习代表性嵌入，从节点的结构和语义2个角度构造对比视图，使结合对比学习的推荐模型在对比效率和推荐精度上有所提升. Li等^[12]基于图的局部和全局结构提出多视图的对比学习模块，捕获不同聚合范式下的深层图结构和语义区分特征.

给定用户集合U和项目集合I，将用户交互数据建模为图$ G=(V,E) $. 交互图中的节点集为$ V=U\cup I $，边集为$ E=\{(u,i)|u\in U,i\in I,{R}_{u,i}=1\} $，$ {R}_{u,i}=1 $表示用户u与项目i发生过交互，交互矩阵记作$ \boldsymbol{R}\in {\left\{0,1\right\}}^{|U|\times |I|} $. 如图1所示，GICL以融合SVD的图协同过滤方法为主干，由2种对比策略挖掘节点的潜在关系，进行联合训练.

在GICL中，利用图卷积神经网络对交互图$ G $进行建模，通过多层次的信息传播进行节点表示学习. 交互图对应的邻接矩阵为

(1)$ \boldsymbol{A}=\left[\begin{matrix}\bf{0} & \boldsymbol{R}\\{\boldsymbol{R}}^{\text{T}} & \bf{0}\end{matrix}\right]. $

学习低秩表示在协同过滤中起着重要作用，能够保留数据中最重要的结构信息. 对邻接矩阵A进行奇异值分解，捕捉图中全局性的模式：

(2)$ \boldsymbol{A}=\boldsymbol{U}\mathrm{diag}\;({s}_{m})\boldsymbol{V}_{}^{\text{T}}\approx \sum\limits_{m=1}^{M}{s}_{m}{\boldsymbol{u}}_{m}\boldsymbol{v}_{m}^{\text{T}}. $

式中：$ {\boldsymbol{u}}_{m} $和$ {\boldsymbol{v}}_{m} $分别为左、右奇异向量；$ {s}_{m} $为奇异值，且$ {s}_{1} > {s}_{2} > \cdot \cdot \cdot > {s}_{m}\geqslant 0 $. 由于较大奇异值对应的分量对交互的贡献更大^[6]，本研究仅用前M个最大的奇异值来近似A，令M与节点嵌入维度保持一致. 从SVD截断后的矩阵$ {\boldsymbol{U}}_{M} $和$ {\boldsymbol{V}}_{M} $中获取初始的用户/项目的嵌入矩阵$ {\boldsymbol{Z}}_{Su} $和$ {\boldsymbol{Z}}_{Si} $，作为预训练嵌入参与更新. 根据已有的工作^[5]，本研究在传播中舍弃非线性激活和特征变换，过程如下：

(3)$ \boldsymbol{z}_{u}^{({l}+1)}=\sum\limits_{i\in {N}_{u}}\frac{1}{\sqrt{|{N}_{u}||{N}_{i}|}}\boldsymbol{z}_{i}^{({l})}, $

(4)$ \boldsymbol{z}_{i}^{({l}+1)}=\sum\limits_{u\in {N}_{i}}\frac{1}{\sqrt{|{N}_{i}||{N}_{u}|}}\boldsymbol{z}_{u}^{({l})}. $

式中：$ {N}_{u} $和$ {N}_{i} $分别为用户u和项目i在交互图$ G $中的邻居集合. 在图上进行L层传播之后，采用平均函数作为读出函数，将SVD得到的初始嵌入和各层的嵌入组合起来，得到最终表示：

(5)$ {\boldsymbol{z}}_{u}=\text{MEAN}\left({\boldsymbol{z}}_{Su}+\sum\limits_{{l}=0}^{L}\boldsymbol{z}_{u}^{({l})}\right), $

(6)$ {\boldsymbol{z}}_{i}=\text{MEAN}\left({\boldsymbol{z}}_{Si}+\sum\limits_{{l}=0}^{L}\boldsymbol{z}_{i}^{({l})}\right). $

基于用户u和项目i的最终表示，根据内积预测两者之间的交互概率，预测得分为

(7)$ {\hat{y}}_{u,i}=\boldsymbol{z}_{u}^{\mathrm{T}}{\boldsymbol{z}}_{i}. $

为了捕获交互中的信息，采用贝叶斯个性化排名（Bayesian personalized ranking, BPR）损失^[13]作为判断用户对项目偏好程度的目标函数：

(8)$ {L}_{\text{BPR}}=\sum\limits_{(u,i,j)\in O}-\ln \sigma ({\hat{y}}_{u,i}-{\hat{y}}_{u,j}). $

式中：$ O=\{(u,i,j)|{R}_{u,i}=1,{R}_{u,j}=0\} $为交互数据集合，$ \sigma $为Sigmoid函数.

现有的图协同过滤方法大多依赖于历史交互信息学习节点表示，在数据稀疏的场景下，这些方法的性能会显著降低. 考虑到交互图$ G $是二部图，每个节点的偶数跳结构邻居为同质节点，基于GCN的推荐模型在偶数层的输出中可以获取同质结构邻居的信息. 本研究提出利用对比学习的优势捕获同质节点之间的潜在关系，以缓解数据稀疏问题. 具体地，将用户节点的可学习嵌入和同一节点在GCN偶数层的输出视为正样本对. 基于InfoNCE^[14]，提出结构邻居对比目标最小化正样本对之间的距离：

(9)$ L_{\text{str}}^{U}=\sum\limits_{u\in U}-\ln \frac{\exp \; ((\boldsymbol{z}_{u}^{(k)}\cdot \boldsymbol{z}_{u}^{(\text{0})})/\tau )}{\displaystyle\sum\limits_{v\in U}\exp ((\boldsymbol{z}_{u}^{(k)}\cdot \boldsymbol{z}_{v}^{(\text{0})})/\tau )}. $

式中：$ \boldsymbol{z}_{u}^{(\text{0})} $为用户的初始特征或可学习嵌入；$ \boldsymbol{z}_{u}^{(k)} $为该节点在GCN第k层的归一化输出，且k为偶数；$ \tau $为Softmax的温度超参数. 类似地，项目侧的结构对比损失可表示为

(10)$ L_{\text{str}}^{I}=\sum\limits_{i\in I}-\ln \frac{\exp \; ((\boldsymbol{z}_{i}^{(k)}\cdot \boldsymbol{z}_{i}^{(\text{0})})/\tau )}{\displaystyle\sum\limits_{j\in I}\exp ((\boldsymbol{z}_{i}^{(k)}\cdot \boldsymbol{z}_{j}^{(\text{0})})/\tau )}. $

完整的结构邻居对比目标表达式为

(11)$ {L}_{\text{str}}=L_{\text{str}}^{U}+L_{\text{str}}^{I}. $

结构邻居对比基于二部图上的结构性邻域构造. 这个环节对节点的同质邻居一视同仁，容易被用户的随机交互干扰，将噪声引入对比学习任务. 本研究引入语义邻居对比以减少结构邻居噪声的影响. 语义邻居是指没有显式的图连接，但特征相似（项目）或偏好相近（用户）的节点. 相似的节点在嵌入空间中往往是相邻的，可以通过学习用户和项目节点的潜在原型识别语义邻居，原型是指同质语义邻居的簇中心^[15]. 本研究提出原型对比目标探索潜在的语义邻居，获取用户和项目的原型，具体分为3个步骤：语义子图构建、局部加权平滑和原型对比学习.

采用基于线性投影的无监督方法将用户/项目的节点嵌入聚类到K个子图上，从而构建语义子图. 相比注意力机制，线性投影是稳健且计算高效的映射方式，不容易受局部噪声的干扰. 具体地，通过线性变换将节点嵌入投影到子图空间，过程表达式为

(12)$ {\boldsymbol{H}}_{u}={\boldsymbol{Z}}_{u}{\boldsymbol{W}}_{u}\text+{\boldsymbol{b}}_{u}\text{,}\;\;{\boldsymbol{H}}_{i}={\boldsymbol{Z}}_{i}{\boldsymbol{W}}_{i}\text+{\boldsymbol{b}}_{i}\text{.} $

式中：$ {\boldsymbol{W}}_{u} $、$ {\boldsymbol{W}}_{i} $为权重矩阵，$ {\boldsymbol{b}}_{u} $、$ {\boldsymbol{b}}_{i} $为偏置向量，$ {\boldsymbol{H}}_{u} $、$ {\boldsymbol{H}}_{i} $为用户和项目节点投影后的logits表示. 通过Softmax函数将每个节点映射到K个子图中的概率分布，进而确定节点所属的子图：

(13)$ {g}_{u}=\arg \underset{k}{\max }{P}_{u}(k|u),\quad{g}_{i}=\arg \underset{k}{\max }{P}_{i}(k|i). $

式中：$ {P}_{u} $、$ {P}_{i} $为用户和项目节点在K个子图上的归属概率分布，$ {g}_{u},{g}_{i}\in \{{1, 2,} \cdots {,}K\} $为节点的子图归属标签，子图$ {G}_{k}=({V}_{k},{E}_{k}) $内节点之间的边与原始图$ G $保持一致，即$ {E}_{k}\in E $.

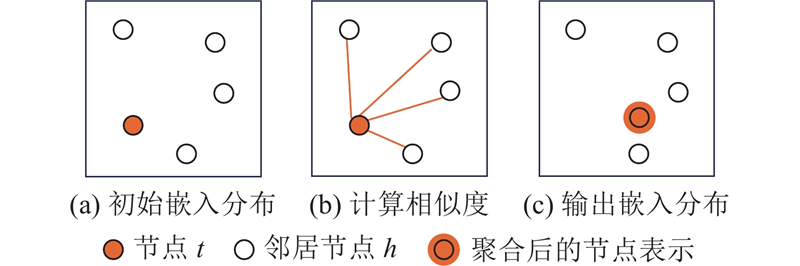
对于获得的语义子图，设计局部加权平滑（local weighted smoothing, LWS）机制，用于聚合子图上节点的直接邻居. 该机制的核心是通过迭代更新节点的表示，使节点在嵌入空间中更接近直接邻居，从而优化子图上的节点嵌入. LWS机制在单次迭代中的核心操作如图2所示. 对于子图$ {G}_{k} $中的节点h，邻居节点集可表示为$ {N}_{K}(h)=\{t|(h,t)\in {E}_{k}\} $. 为了明确不同的邻居对节点h的贡献，计算节点h和t之间的相似度$ \pi (h,t) $，作为局部信息传播中的权重：

(14)$ \pi (h,t)=\boldsymbol{e}_{{h}}^{(0)}\cdot \boldsymbol{e}_{{t}}^{(0)}. $

在邻居节点集$ {N}_{K}(h) $中，节点t越重要，在聚合时传递的局部信息越多. 因此让节点h在嵌入空间中更接近其重要邻居，可以使节点在推荐任务中更具优势. 为了表征$ {G}_{k} $的局部拓扑结构，使用权重$ \pi (h,t) $对邻居节点的嵌入进行加权平滑：

(15)$ \boldsymbol{e}_{{N}_{k}(h)}^{\text{(0)}}=\sum\limits_{{t}\in {N}_{k}(h)}\pi (h,t)\boldsymbol{e}_{t}^{\text{(0)}}. $

将节点h的嵌入与局部加权表示相加来更新节点表示，得到临时表示$ \boldsymbol{u}_{h,k}^{\text{(1)}} $，

(16)$ \boldsymbol{u}_{h,k}^{(1)}=\text{NORM} \; (\boldsymbol{e}_{h}^{(0)}+\boldsymbol{e}_{{N}_{k}(h)}^{(0)}). $

为了防止更新后的向量变大且不可比，对临时表示$ \boldsymbol{u}_{h,k}^{\text{(1)}} $进行归一化：

(17)$ \text{NORM}\;(\boldsymbol{u})=\frac{\boldsymbol{u}}{\parallel \boldsymbol{u}\parallel }\cdot \frac{\parallel \boldsymbol{u}{\parallel }^{\text{2}}}{\parallel \boldsymbol{u}{\parallel }^{\text{2}}+\text{1}}. $

归一化操作能够保持向量的方向和相对大小，使不同的节点嵌入在同一尺度下可比. 至此，节点h的表示更新为$ \boldsymbol{e}_{h}^{(1)}=\boldsymbol{u}_{h,k}^{(1\text{)}} $. 用$ {f}_{\text{LWS}}(\cdot ) $表示将一阶邻居信息合并到节点嵌入中的加权平滑操作：

(18)$ \boldsymbol{e}_{h}^{(\text{1})}={f}_{\text{LWS}}\left(\{(\boldsymbol{e}_{h}^{(\text{0})},\boldsymbol{e}_{t}^{(\text{0})})|t\in {N}_{k}(h)\}\right). $

式中：$ \boldsymbol{e}_{h}^{(\text{1})} $为子图$ {G}_{k} $中节点h的更新表示. 为了整合高阶邻居的信息，进一步堆叠更多的LWS聚合层，递归地定义经过l层聚合后节点h的表示：

(19)$ \boldsymbol{e}_{h}^{(l)}={f}_{\text{LWS}}\left(\{(\boldsymbol{e}_{h}^{(l-\text{1})},\boldsymbol{e}_{t}^{(l-\text{1})})|t\in {N}_{k}(h)\}\right). $

式中：$ \boldsymbol{e}_{h}^{(l)} $为节点h在第l层的嵌入.

在子图上进行l层的LWS操作后，子图内的节点表示更接近语义邻居. 同一子图内的用户节点可视为一组语义邻居，计算其簇中心作为原型表示. 本研究对分布在各个子图上的用户都计算了原型，将用户的节点表示与所属原型作为正样本对，在InfoNCE^[14]的基础上进行原型对比学习，目标是最小化用户目标函数：

(20)$ L_{\text{pro}}^{U}=\sum\limits_{u\in U}-\ln \frac{{\exp }\;(\boldsymbol{e}_{u}^{(l)}\cdot {c}_{u,k}/\tau )}{\displaystyle\sum\limits_{{c}_{j}\in C}{\exp }\;(\boldsymbol{e}_{u}^{(l)}\cdot {c}_{j}/\tau )}. $

式中：$ {c}_{u,k} $为在子图$ {G}_{k} $上进行LWS操作后，算出的用户u的原型；C为包含所有子图上潜在原型的集合. 类似地，项目节点的目标函数为

(21)$ L_{\text{pro}}^{I}=\sum\limits_{i\in I}-\ln \frac{{\exp }\;(\boldsymbol{e}_{i}^{(l)}\cdot {c}_{i,k}/\tau )}{\displaystyle\sum\limits_{{c}_{t}\in C}{\exp }\;(\boldsymbol{e}_{i}^{(l)}\cdot {c}_{t}/\tau )}. $

完整的原型对比学习目标是用户和项目的目标函数之和：

(22)$ {L}_{\text{pro}}=L_{\text{pro}}^{U}+L_{\text{pro}}^{I}. $

协同过滤的主要目标是对用户和项目之间的交互进行建模. 采用以BPR损失为主，对比损失为辅的多任务学习策略，总体训练目标函数为

(23)$ L={L}_{\text{BPR}}+{\lambda }_{1}{L}_{\text{str}}+{\lambda }_{2}{L}_{\text{pro}}+{\lambda }_{3}\parallel {\boldsymbol{\varTheta}} {\parallel }_{2}. $

式中：$ {\lambda }_{1} $、$ {\lambda }_{2} $和$ {\lambda }_{3} $为超参数，用于调节对比任务和正则项的权重；$ \parallel {\boldsymbol{\varTheta}}{\parallel }_{2} $为参数集合的L2范数. GICL的训练过程如算法1所示.

算法1　融合全局信息和对比学习的图神经网络推荐模型训练过程

输入 用户-项目二部图$ G $

输出 项目评分排名列表

预处理 根据交互矩阵R构建邻接矩阵A；

截断SVD获取用户/项目的初始嵌入；

For epoch = 1 to N

1.在交互图$ G $上进行信息传播，根据式(5)和式(6)获取用户和项目的最终表示$ {\boldsymbol{z}}_{u} $和$ {\boldsymbol{z}}_{i} $，计算内积作为预测得分；

2.根据式(8)计算BPR损失$ {L}_{\text{BPR}} $；

3.执行结构邻居对比学习，根据式(9)和式(10)计算结构邻居对比损失$ {L}_{\text{str}} $；

4.执行语义邻居对比学习，根据式(20)和式(21)计算语义邻居对比损失$ {L}_{\text{pro}} $；

5.根据式(23)计算总损失，并更新模型参数；

End for

使用4个数据集：MovieLens-1M(ML-1M)^[16]，Yelp^[17]，Amazon-Books(Books)^[18]，Gowalla^[19]验证GICL的性能. 为了保障数据质量，在预处理阶段过滤掉交互记录少于15条的样本. 对于每个数据集，随机选择80%的交互作为训练数据，10%的交互作为验证数据，其余10%的交互用于性能比较. 数据集的基本信息如表1所示.

为了评估模型的top-N推荐性能，采用召回率Recall@N和归一化折损累计增益NDCG@N作为评测指标，取N=10、20、50. Recall@N表示在模型推荐前N个项目中，用户实际喜欢的项目被推荐比例；该指标用于衡量推荐的命中率. NDCG@N考虑推荐项目的顺序，对排名靠前的项目给予更高的权重；该指标用于衡量推荐项目排序的合理性. 模型整体采用全排序策略，对用户未交互的所有候选项目进行评分.

为了验证GICL的有效性，从图协同过滤基础模型和对比学习增强模型2个角度，选取以下具有代表性的基线方法进行比较.1）NGCF^[4]：利用交互数据构建图结构，通过图神经网络逐层传播，学习用户和项目的节点特征. 2）LightGCN^[5]：简化图卷积操作以减少计算复杂度，保留协同过滤中重要的信息传播机制. 3）SGL^[8]：将自监督学习引入GNN中，利用对比学习提升推荐系统的嵌入质量和预测准确性. 4）SimGCL^[9]：在图结构上引入随机扰动生成对比样本，舍弃图增强操作，降低计算复杂度，缓解长尾推荐偏差问题. 5）NCL^[11]：通过结构近邻和K-means聚类寻找节点的正样本，显式捕获节点之间的关联性. 6）AdaGCL^[20]：采用可训练的视图生成器，包括图生成模型和图去噪模型，以创建自适应的对比视图. 7）GraphAug^[21]：通过可学习的图采样与重参数化，自适应地生成高质量的对比视图，在聚合时利用混合跳跃图编码器缓解过度平滑问题.

实验在Python3.8、Pytorch1.9.0环境下进行，服务器环境为Ubuntu 16.04，显卡为RTX 2080Ti. 所有模型统一使用Adam优化器进行优化，用Xavier分布进行参数初始化，嵌入维度设置为64，批处理大小为4096，学习率设置为0.001. 各个基线模型所特有的超参数均按照对应文献调至最优，确保对比实验的公平性. 设置GICL的对比任务权重$ {\lambda }_{1} $和$ {\lambda }_{2} $的范围为[10⁻⁸,10⁻⁴]，正则化系数$ {\lambda }_{3} $=1.0×10⁻⁴，语义子图数量K和LWS聚合层数$ {L}_{\text{W}} $分别在范围[3,11]和[1,3]进行调整. 为了防止过拟合，采用耐心度为10的早停策略.

GICL和对比模型的性能对比结果如表2所示，其中表现最好的基线模型指标用下划线标注，η为GICL与最佳基线模型相比的性能提升率. 在图协同过滤模型中，LightGCN的优异表现说明舍弃图神经网络中的冗余操作可以更高效地完成推荐任务. SGL和SimGCL利用图增强和添加扰动的方法构建对比视图，性能表现稳定超过LightGCN，这表明对比学习能够有效地提高推荐性能. NCL、AdaGCL和GraphAug采用更新颖的方式构造对比视图，给模型提供额外的高质量训练信号，推荐性能进一步提升. GICL在图协同过滤的基础上，使用SVD处理邻接矩阵，从图的全局信息中提取最显著的关系模式，参与节点表示的学习过程. 设计在该模型中的基于结构邻居和语义邻居的对比辅助任务能够提高节点嵌入学习的质量. 由实验结果可以看出，GICL的性能始终优于基线模型. 特别是在Books数据集上，与最强基线相比，Recall@50和NDCG@50指标分别提升了5.97%和4.84%. 此外，GICL在ML-1M数据集上的性能提升明显低于其他数据集. 经过分析，原因可能是ML-1M的数据相对稠密（见表1），能够提供更多的监督信号，即使不设置增强邻居构建对比任务，模型也能学到较好的节点表示. 在稀疏的数据集中，有效交互的数量不足，充分利用潜在的邻居关系对于推荐任务至关重要，因此GICL性能提升更显著.

分析GICL的时间复杂度，选取先进模型NCL、AdaGCL和GraphAug进行比较，结果如表3所示. 其中d为嵌入维度，L为图卷积层数，B为单个批次中的节点数，S为对比任务中负样本数量，$ \left| E\right| $为二部图中的边数且数值远大于其他参数. 在图卷积环节，GraphAug采用混合跳跃机制^[21]，$ M $为最大跳数. 其余模型采用LightGCN的聚合方案，复杂度为$ O\left(2\left| E\right| Ld\right) $. GraphAug和AdaGCL的对比任务复杂度不突出，但这2个模型采用可学习的图增强策略，导致整体的复杂度较高. GICL中的SVD操作只在预处理阶段执行1次，故不纳入训练的复杂度分析. 该模型中对比任务的时间复杂度为$ O\left(B(S+{K}_{\text{S}}+\overline{N}{L}_{\text{W}})d\right) $，其中$ {K}_{\text{S}} $为划分语义子图得到的原型数量，$ \overline{N} $和$ {L}_{\text{W}} $分别为节点的平均邻居数量和LWS聚合层数. NCL和GICL的时间复杂度相似，但NCL采用K-means聚类获取节点原型^[11]，其定义的原型数量$ {K}_{\text{m}}\in [500,1\;500] $；GICL中的$ {K}_{\text{S}}\in [3,11] $、$ \overline{N}\in [30,80] $、$ {L}_{\text{W}}\in [1,3] $，显然$ {K}_{\text{m}} > {K}_{\text{S}}+\overline{N}{L}_{\text{W}} $；因此GICL的时间复杂度低于NCL，在性能和效率上都更有优势.

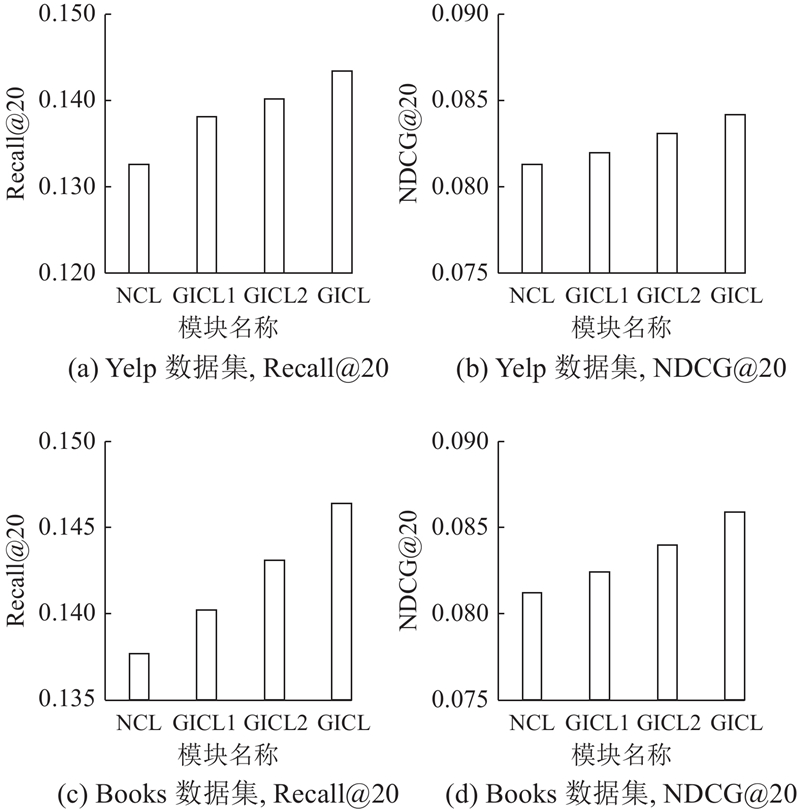
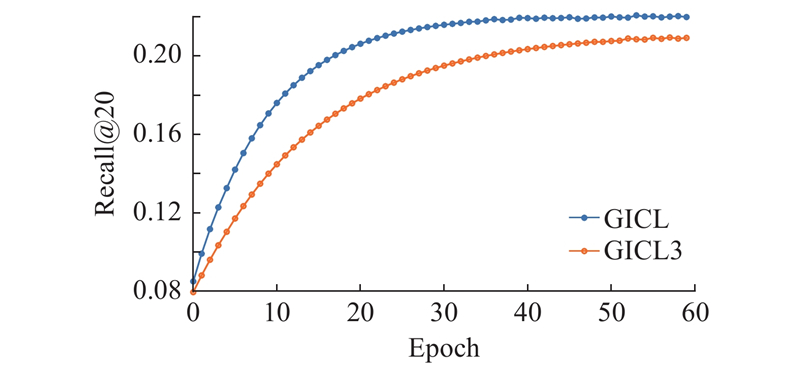
在Yelp和Books数据集上进行模块消融实验，以探索GICL各组件设计对模型的实际影响. 设计以下3个模型变体. 1）GICL1：去除结构邻居对比任务，模型其他部分保持不变. 2）GICL2：对于语义邻居对比任务，使用K-means聚类的方式获取用户和项目的原型，代替模型中的划分子图和LWS操作，模型其他部分保持不变. 3）GICL3：去除图协同过滤主干中SVD截断的部分，只保留LightGCN的设计. 各变体去除或替换对应组件之后，对比任务的权重以及其他超参数均保持不变. 原模型与变体的对比实验结果如图3所示. 可以看出，去除任一设计都会导致模型性能下降，表明这些组件都有助于性能提升. GICL1性能下降最明显，说明结构邻居对比任务能够挖掘同质节点之间的相似性，这些潜在关系对推荐任务意义重大. GICL2使用K-means替换原有组件导致模型性能下滑，证明在子图上进行LWS操作获取用户和项目的原型能够更有效地捕捉节点之间的语义关联. 对于GICL3，绘制以Recall@20为指标的训练曲线，与原模型进行对比，探究SVD在模型中的具体作用，结果如图4所示. 该训练过程在Gowalla数据集上进行，GICL始终拥有更好的性能且收敛速度更快，说明将SVD截断后的向量作为预训练嵌入能够为训练提供更合理的起点，同时将捕获的全局信息融入节点的最终表示能够提升推荐的性能.

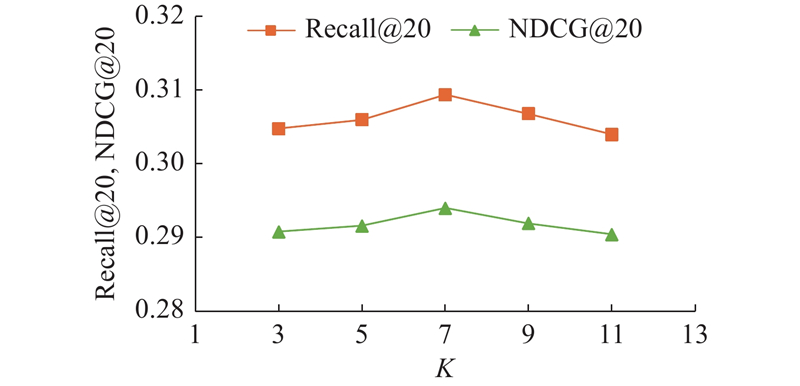
为了探索语义子图数量K对模型性能的影响，在ML-1M数据集上进行实验，实验结果如图5所示. 实验过程中固定模型中的其他参数，测试K变化对实验结果的影响， K的取值范围为{3, 5, 7, 9, 11}. 可以看出，当K从3增加到11，GICL的性能指标曲线呈先升后降的趋势. 分析原因，当K较小时，语义子图数量过少，可能会把一些相似度较低的节点划分到同一子图中，给后续的原型对比学习带来干扰. 当K=7时，推荐性能达到最佳. 如果K再继续变大，将导致子图个数过多，相似的节点嵌入分散在不同的子图上，无法充分利用节点之前的潜在关联.

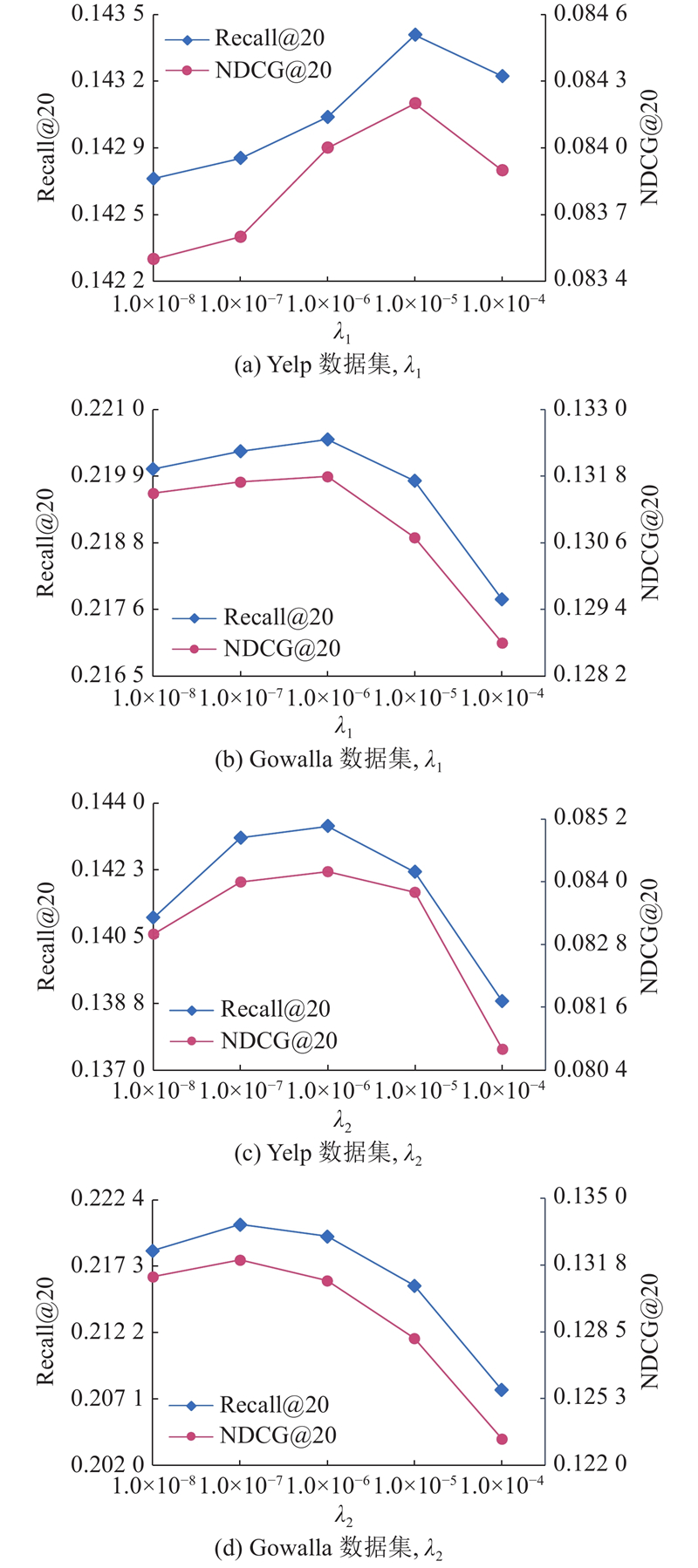
GICL中超参数$ {\lambda }_{1} $和$ {\lambda }_{2} $的调节范围均为[10⁻⁸,10⁻⁴]，先从区间中确认模型性能最佳时$ {\lambda }_{1} $的数值，再固定$ {\lambda }_{1} $，对不同的$ {\lambda }_{2} $进行测试. 实验在Yelp和Gowalla数据集上进行，结果如图6所示. 可以看出，对于Gowalla数据集，在$ {\lambda }_{1} $=1.0×10⁻⁶和$ {\lambda }_{2} $=1.0×10⁻⁷时模型达到最佳性能. 对于Yelp数据集，在$ {\lambda }_{1} $=1.0×10⁻⁵和$ {\lambda }_{2} $=1.0×10⁻⁶时模型达到最佳性能. 最优参数存在差异的原因可能在于数据集的大小和稠密度，Yelp数据集中交互更多且更稠密，因此对比辅助任务需要更大的权重. 此外，超参数较小会限制对比学习目标的发挥，且$ {\lambda }_{1} $比$ {\lambda }_{2} $更明显. 综上所述，$ {\lambda }_{1} $和$ {\lambda }_{2} $对模型的性能都很重要，合理的搭配有助于模型达到最佳性能.

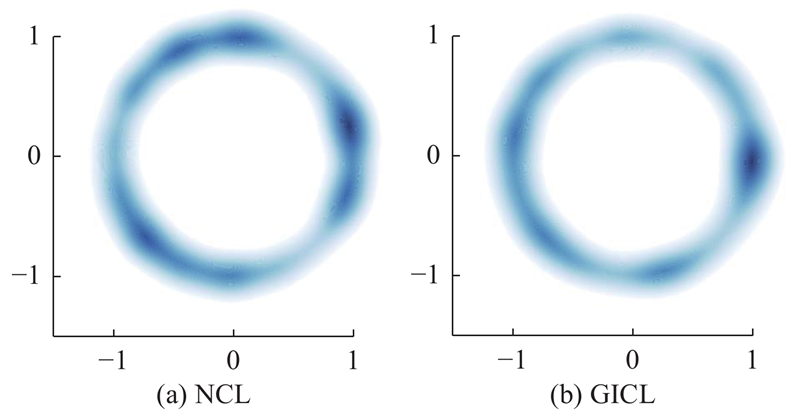
为了进一步探究GICL性能提高的原因，分别将GICL和NCL在ML-1M数据集上学到的项目嵌入进行可视化，如图7所示. 具体地，将项目的嵌入表示映射到二维空间，再使用高斯核密度估计计算项目特征的分布情况. 对比2种模型的分布情况可知，GICL学到的嵌入表现出更均匀的分布，能够更好地建模多样化的用户偏好和项目特征；也表明GICL能够更充分地利用二部图中的潜在信息，提高推荐性能和泛化能力.

本研究针对图协同过滤任务中的噪声和数据稀疏问题，提出融合全局信息和对比学习的图神经网络推荐模型. 该模型利用奇异值分解，在嵌入初始化和最终计算的阶段强调全局结构的降噪；构建对比学习任务，在训练阶段强调局部邻域的节点关联性. 在4个数据集上的模型性能对比实验结果表明，所提模型的性能优于主流推荐方法，且训练效率有所提升. 所提模型只针对用户和物品是否存在交互进行建模，忽略了用户点击、收藏和购买等不同行为之间的差异，难以挖掘深层次的用户意图. 未来计划进一步研究更精细化的图协同过滤模型，对不同的隐式反馈行为进行区分，以提升推荐的准确性和可靠性.