针对上述问题,充分考虑热电联产系统的复杂性,重点分析机组种类多样性、数量及性能劣化等关键因素,对能效、㶲、经济、环境等子问题进行数学建模,综合考虑在1个运行周期内机组启停消耗、爬坡速率、时间及其他约束条件,构建兼顾能效、㶲、经济及环境这些目标的运行规划多目标优化模型. 通过熵权法实现各目标的客观权重分配,将多目标优化模型转化为可以获得唯一最优解的单目标运行规划优化模型,求解得到可直接应用于实践的复杂热电联产系统的运行规划方案.
1. 复杂热电联产系统运行问题分析
复杂热电联产系统是指能够实现热电联合供应的高效能源系统. 其不仅能够满足热、电2种形式的能量需求,而且通常包含多个互联的组成部分,能够实现更高效的能源管理和分配,适用于更广泛的应用场景. 复杂热电联产系统的复杂性主要体现在以下几个方面.
1)机组类型和配置的多样性:复杂热电联产系统包含不同类型的发电和热能生产机组,如背压式机组、纯凝式机组、抽背式机组、抽凝式机组、燃气-蒸汽联合循环机组以及二次调节抽汽式机组等.
2)机组数量的可拓展性:随着用户需求的增长和变化,复杂热电联产系统可以通过增加机组数量来扩展其生产能力,或者通过优化现有机组的配置来提高系统效率.
3)需求的多变性和适应性:复杂热电联产系统能够适应各种不同的能源需求变化,包括季节性变化、日变化以及突发性高峰需求.
4)能源品位的多样性:除电力外,复杂热电联产系统还能够提供不同品位的热能产品,以满足不同用户的能源需求.
5)机组特性的差异性:不同类型的机组,如燃气轮机、背压式机组、抽背式机组、抽凝式机组等,其能源转换效率各不相同;相同机组在经过改造后,其性能也可能与改造前有所偏差.
6)机组工质损失的可调性:根据不同用户需求场景,通过节能降耗来减少机组的能耗,并改进工质损失以满足实际需求.
7)机组出力的可调性:在相同的热电负荷需求下,对于复杂热电联产系统而言,用于生产热电产品的机组组合方式也不固定,须合理调整机组之间的出力情况.
复杂热电联产系统运行规划问题涉及多个层面,是一个需要识别系统特征的多阶段决策过程. 对复杂热电联产的运行特点进行分析,得到具体运行特点如下.
1)阶段性决策. 复杂热电联产系统的运行规划涵盖生产计划、负荷分配、机组调度等多方面,是多阶段决策问题,处理过程分为3个步骤:先根据需求侧的热电负荷需求与热电厂出力能力制定生产计划;再跟据机组性能和预定生产计划制定热电负荷分配方案;最后依照前阶段分配结果开展机组运行调度以确定启停策略. 各阶段决策既取决于之前的系统状态,又影响后续的状态与决策.
2)最优子结构. 复杂热电联产系统的运行规划涉及多层面决策,经阶段性分解,部分子问题有最优解,如运行规划的最优方案包含热电负荷分配子问题的最优解. 若求出各子问题的最优解并与剩余子问题整合,则能够得到该系统的最优运行规划方案.
3)重叠子问题. 在进行复杂热电联产系统的运行规划时,部分子问题在决策中经常重复出现,如运行周期内某些机组频繁启停. 为了避免重复计算,可以采用动态规划算法存储已解子问题的解,以提升解决问题的效率.
4)确定性和复杂性. 由于复杂热电联产系统运行规划问题的确定性与复杂性高,须从众多运行决策路径中寻求最优解. 可以通过提前构建优化目标来选取最优路径,为复杂决策的制定提供有效方案.
5)明确的边界条件和递归关系. 复杂热电联产系统的运行规划问题拥有明确的边界定义和递归关系. 通过定义清晰的边界条件(基案例)和递归关系(状态转移方程),可以准确模拟热电联产系统的运行规划过程.
热电联产系统的运行规划涉及多个连续的时段,不同时段内机组的启停与功率调整天然构成了多阶段决策场景. 动态规划能够将复杂的整体问题拆解成一系列相互关联的子问题,从起始阶段逐步递推至最终阶段,精准找到全过程的最优策略,契合热电联产系统运行规划随时间分步决策的特性.
综上所述,可以将复杂热电联产系统的运行规划问题分解成各子问题,采用动态规划算法进行求解.
2. 数学模型
在求解复杂热电联产系统的运行规划问题时,采取将原问题拆解为若干子问题的策略. 为了实现对最终结果的定量求解,针对每一个子问题构建数学模型,进而建立多目标优化模型. 随后,依据熵权法将多目标优化模型转化为单目标优化模型,同时充分考虑由多种影响因素构成的约束条件,在此基础上运用线性规划法进行求解.
2.1. 子问题划分
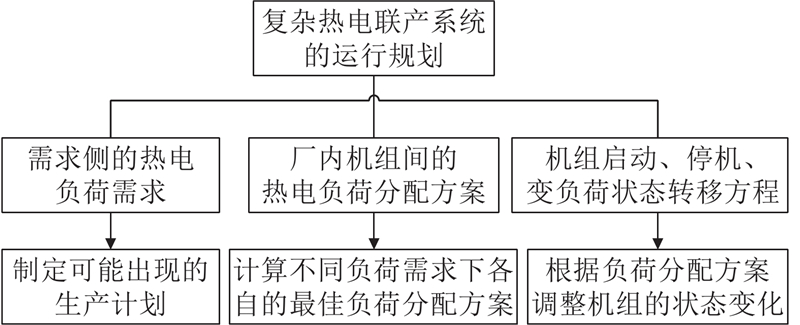
将复杂热电联产系统的运行规划问题分解为若干子问题,可以更系统地解决整体规划问题. 下面详述分解后主要的子问题及其解决步骤,分解示意图如图1所示.
图 1
图 1 复杂热电联产系统运行规划子问题分解图
Fig.1 Diagram of subproblem decomposition in operation planning of complicated combined heat and power systems
子问题1:基于需求侧的热电负荷需求制定生产计划. 先分析热电联产系统中各机组的性能特性与相互作用,明确机组输出范围;再对比、排序需求侧热电负荷特征,找出满足负荷条件的潜在机组组合方案;最后由这些方案构成热电厂多元化生产计划,为热电需求动态变化提供策略与优化路径.
子问题2:计算不同负荷需求下的最佳负荷分配方案. 由于日前热电负荷需求不恒定,机组组合具有多样性,须针对满足需求侧负荷条件的潜在机组组合方案,建立目标函数并求解负荷分配,以得出各方案的最优解.
子问题3:根据最优的负荷分配方案调整机组的状态变化. 当需求侧的热电负荷需求发生变化时,通过对比当前负荷下的机组组合方案(记作状态1)与识别得到的满足需求侧负荷条件的潜在机组组合方案(记作状态2),从而确定从状态1变为状态2时所需的机组状态转移操作. 随后,根据运行规划的目标函数计算得到最优运行规划方案,并按照求解得到的最优运行规划方案更新机组的状态变化.
2.2. 多目标优化模型构建
2.2.1. 基于多E指标的运行规划优化模型
1)能源利用效率
式中:
2)㶲. 通过对复杂热电联产系统中能量的品位变化进行分析,评价机组内关键设备的性能优劣. 㶲效率定义为收益㶲与支付㶲的比值,计算公式为
式中:
3) 经济. 在复杂热电联产系统正常运行的情况下,综合考虑各项费用后总运行成本费用(单位:元/d)的计算公式为
式中:
针对本研究中的复杂热电联产系统,基于2种不同的情况考虑其运行规划目标函数.
(a)在负荷平稳的工况下,机组运行时的经济成本目标函数由负荷分配的经济成本目标函数计算得到,具体计算公式为
式中:
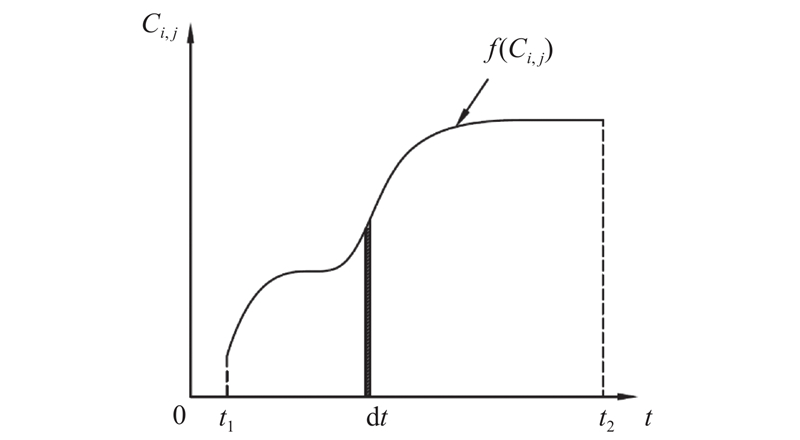
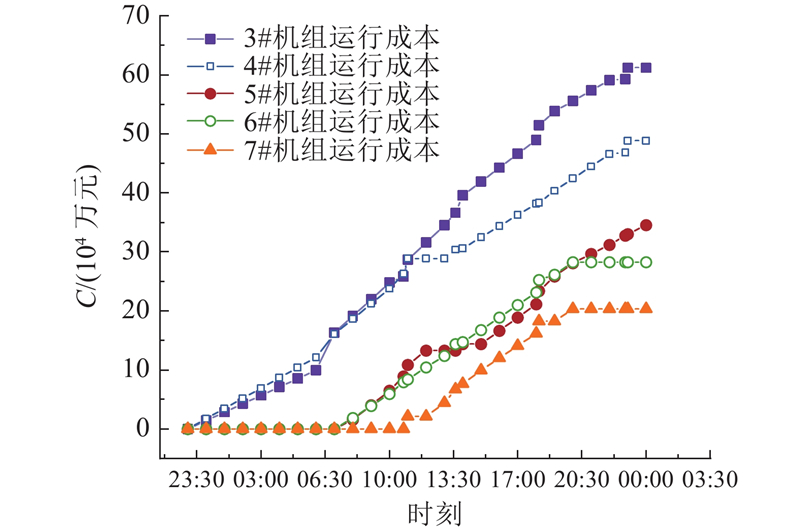
(b)对于负荷不平稳的工况,如机组启动、停机、变负荷以及其他负荷不稳定工况,结合经济成本变化曲线与坐标轴围成的面积的物理意义进行求解,如图2所示. 具体公式如下:
图 2
图 2 负荷不平稳工况下经济成本计算示意图
Fig.2 Schematic diagram of economic cost calculation under unstable load conditions
式中:
4) 环境. 热电联产系统的燃料通过燃烧排放出CO、CO2、SO2、NOx和烟尘等污染物,对环境造成负面影响. 采用排放因子[16]和系统的燃煤消耗总量来计算对应污染物的排放总量,计算公式为
式中:
综上可得复杂热电联产系统运行规划的目标函数:
2.2.2. 单目标优化模型的权重分配
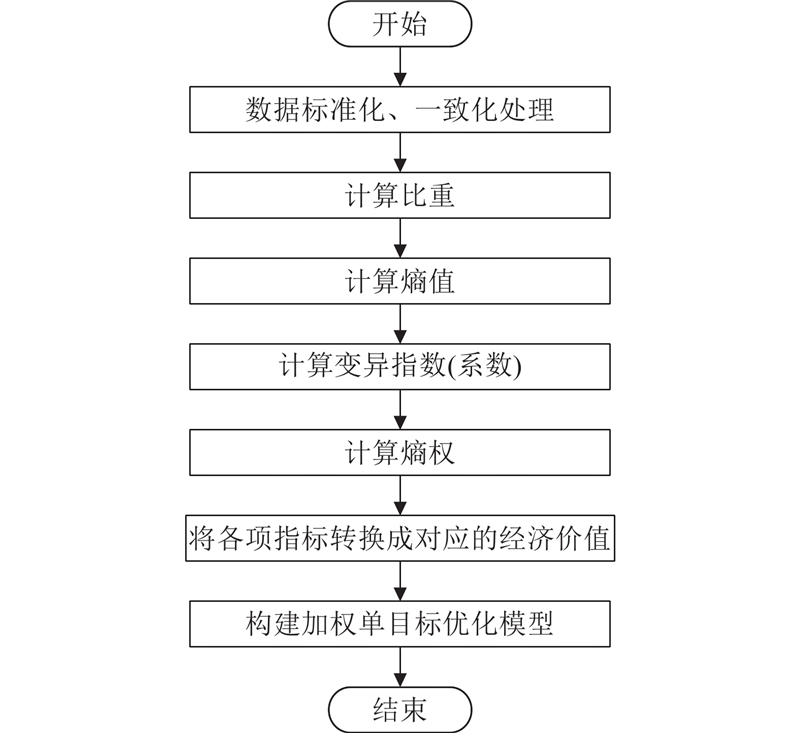
在热电联产系统的运行规划中,考虑能效、㶲、经济、环境等因素,得到2.2.1节中的式(7)作为优化模型. 在对多目标优化模型进行求解的过程中,不同目标之间存在冲突现象,具体表现为在对某一目标进行优化改善时,往往会导致另一个目标的恶化[17]. 由于寻优过程涉及多个决策变量,这一情况致使问题维度增加,进而导致求解难度上升. 而且在获得多目标优化解集后,最终的决策方案需要人为地从解集中挑选,使得方案选择过程受到主观因素的干扰,决策的客观性难以得到有效保障. 因此,运用熵权法对多目标进行客观权重分配,将多目标优化模型转化为单目标优化模型,通过求解得到唯一决策方案,以确保决策的客观性.
图 3
图 3 基于熵权法的加权单目标优化模型的计算流程图
Fig.3 Calculation flowchart of weighted single-objective optimization model based on entropy weight method
1) 数据标准化、一致化处理. 收集相关因素的数据,由于各因素的量纲、数量级不同,须做标准化、一致化处理来消除量纲影响. 评价指标一致化处理针对多目标优化模型中的 “极大值”、“极小值”指标,采用倒数一致化或减法一致化方法. 为了解决不同指标因单位、数量级产生的不可公度性,数据标准化处理采用极差标准化方法,以避免综合评价时指标大小排序不合理的问题.
式中:
式中:
式中:
2) 计算比重,具体计算公式为
式中:
3) 计算熵值. 熵值实际上是对离散程度的度量,计算得到的熵值越低,目标的离散程度越高. 具体计算公式为
式中:
4) 计算变异指数(变异系数),具体计算公式为
5) 计算熵权,具体计算公式为
式中:
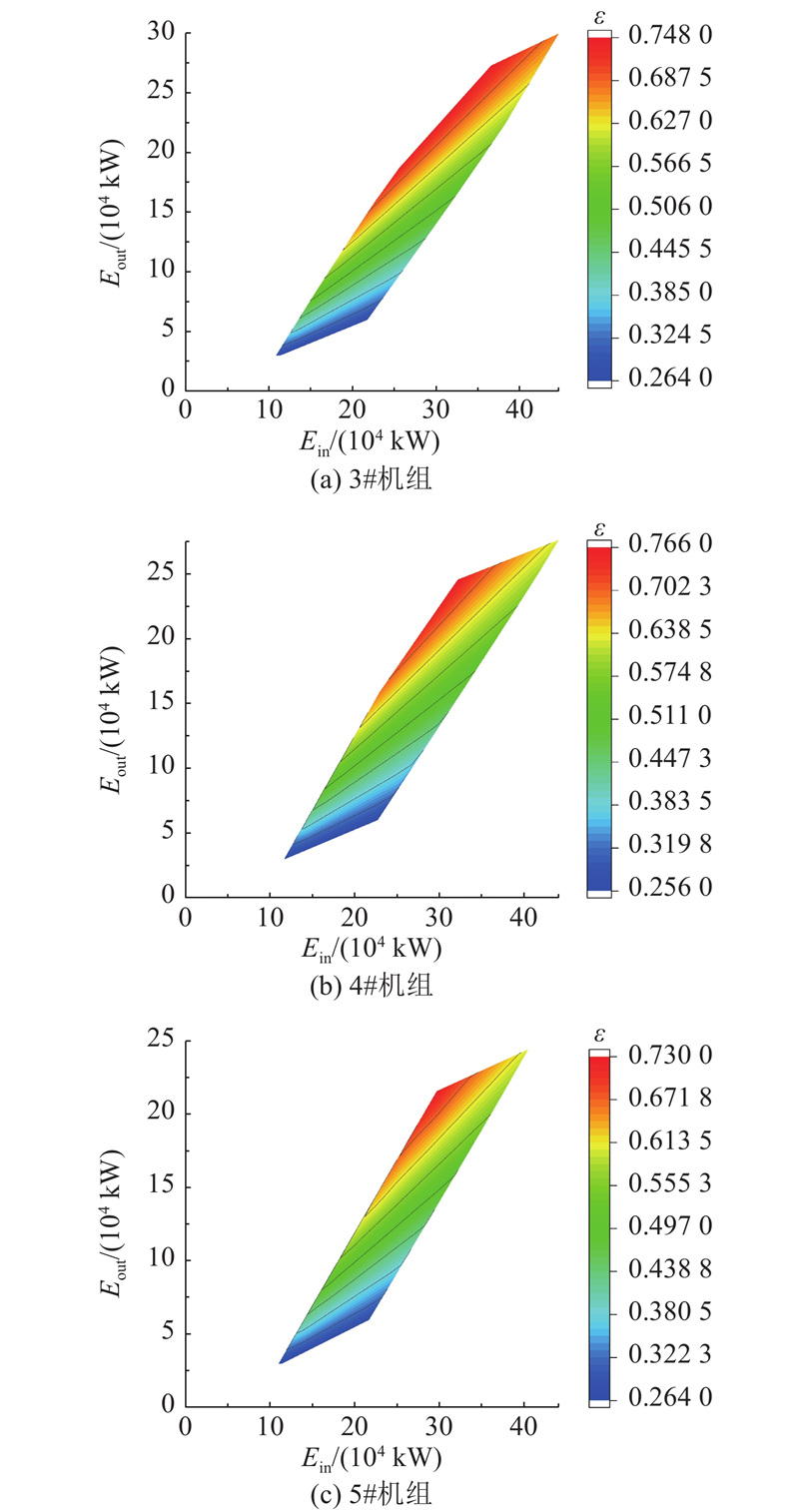
6) 将各项指标转换成对应的经济价值. 通过各项指标对应的经济价值量化方法实现指标与经济价值之间的转换. 将非货币性指标转换为货币性指标,从而在经济分析中进行综合比较. 以能源利用效率为例,其经济价值转换过程阐述如下:首先,根据各机组可行域和工况图绘制得到能源利用效率与能量的总输入
图 4
图 4 不同机组能源利用效率与能量流关系图
Fig.4 Diagram of relationship between energy utilization efficiency and energy flow for different units
7) 将计算得到的熵权结果作为各指标的权重,并利用第6步得到的各项指标的经济价值,将多目标优化模型转为加权后的单目标优化模型,具体的单目标计算公式为
式中:
最后,将系统负荷分配的多目标优化模型转换为以经济成本最小化为目标的单目标优化模型:
式中:
2.3. 约束条件
约束条件对复杂热电联产系统的高效稳定运行至关重要. 其不仅需要涵盖机组热电负荷分配后的稳定运行要求,而且应包括状态转换过程须遵循的额外限制. 在稳定运行阶段,约束条件主要涉及负荷分配过程中的需求侧日前热电负荷约束、供给侧机组性能约束以及供给侧安全边界约束等核心要素. 在此基础上,进一步引入机组状态转换约束,涵盖需求侧热电负荷变化、机组启停及爬坡速率等方面的限制. 通过本节内容的补充,可以确保在运行规划过程中充分考虑系统从稳定运行状态向非稳定运行状态过渡的潜在影响,从而使系统在各阶段保持最佳运行状态.
1) 需求侧热电负荷需求约束.
需求侧热电负荷需求约束是从日前出发,涵盖机组平稳运行和机组状态变化时所需要考虑的热电负荷约束,具体表达式为
式中:
2) 机组启停约束.
在复杂热电联产系统运行规划中,需要考虑机组启动和停机的影响. 机组的状态变化可以表示为
式中:
汽轮机停机方式包括正常停机和故障停机2种,不考虑机组出现故障的情况.
(a) 启动方式确定[24].
汽轮机机组启动方式的选取可以参考表1. 其中,
表 1 汽轮机启动方式
Tab.1
| 启动方式 | ts/d | |
| 冷态额定参数启动 | < 150 | > 7 |
| 温态额定参数启动 | 150~350 | 2~7 |
| 热态额定参数启动 | > 350 | < 2 |
| 滑参数启动 | — | — |
由表可知,在热电联产系统的运行规划研究中,应对机组状态和保持该状态的时长进行判定,随后基于2.1节中构建的目标函数进行计算求解,选择最佳的启动方式.
(b) 停机方式确定.
正常停机过程是指有计划的停机,包括按照预定检修计划停机、热备用停机等方式. 一般情况下,对于短期的正常临时停机,采用额定参数停机;当机组需要进行大修、小修时,或者在需要汽缸快速冷却的情况下,多采用滑参数停机方式.
综上所述,当确定启动和停机方式后,对应的机组启动约束和机组停机约束为
3) 机组爬坡约束.
机组的爬坡速率约束是指机组输出变化速度限制. 本研究只涉及机组并网状态下负荷调整后的负荷约束,不包括并网状态下的爬坡约束. 不同类型的机组的爬坡特性存在差异. 首先,机组升、降负荷时,上升和下降爬坡速率的最大值可能不同;其次,对于有抽汽供热的机组,不同品质的机组的供热爬坡速率也有差异. 具体约束表达式可以依据机组的实际运行特性和要求来制定. 爬坡速率约束的通用表述方法为
式中:
3. 求 解
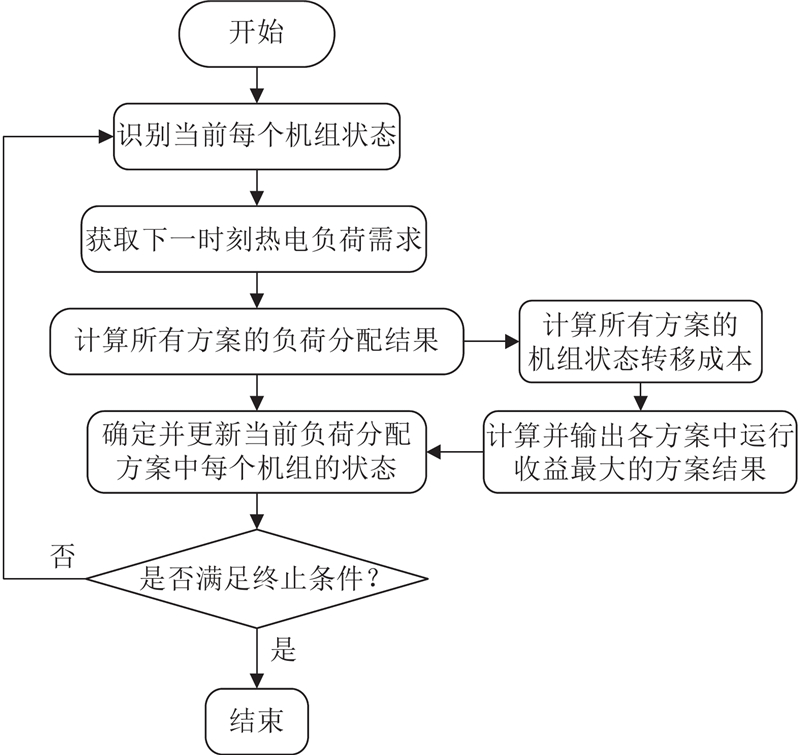
在复杂热电联产系统的运行规划问题的求解过程中,以经济成本最小化为目标构建目标函数及相关约束条件,将整体问题拆解为若干子问题. 通过建立这些子问题间的逻辑和递归关系,实现迭代优化,从而计算出最优的运行规划方案. 具体求解思路如图5所示.
图 5
图 5 复杂热电联产系统运行规划求解流程图
Fig.5 Flowchart of solution process for operation planning of complex CHP systems
将得到的目标函数以及约束条件通过上述运行规划求解思路应用于实际机组模型,采用动态规划算法进行寻优计算,求解得到复杂热电联产系统的运行规划结果.
4. 实例计算及分析
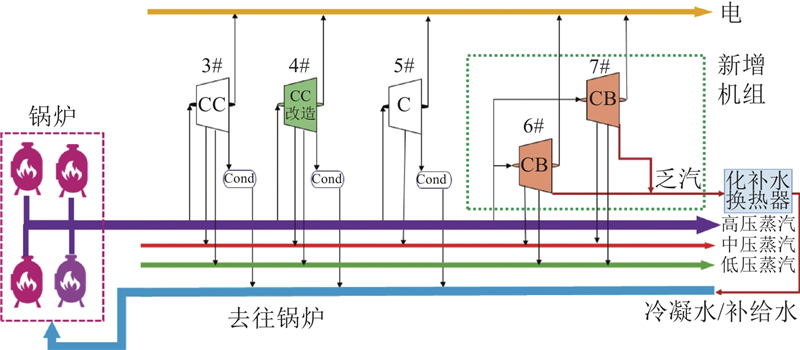
某石化热电厂现配置有3台50 MW汽轮机发电机组(总装机容量达到150 MW),型号分别为CC50-8.83/4.12/1.47/535(简称为3#机组)、CC60-8.83/4.12/1.47/535(简称为4#机组)及C50-8.83/4.12/535(简称为5#机组). 目前投入运行的3台机组中,3#机组出现了一定程度的性能劣化;4#机组根据生产需求经过了改造优化,该机组的性能曲线与原曲线相比也有一定程度的差异. 新增的2套背压式汽轮发电机组被称为6#机组和7#机组,进汽参数为535 ℃、8.83 MPa,工业抽汽压力为4.50 MPa,供热抽汽压力为1.74 MPa,排汽背压为0.15 MPa. 热电厂全厂的系统拓扑结构如图6所示.
图 6
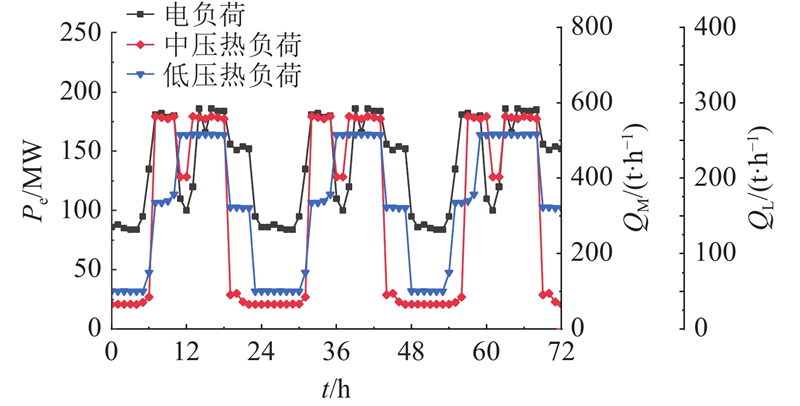
图 7
图 7 热电厂3×24 h热电负荷曲线
Fig.7 Thermoelectric load curves of thermal power plant in 3×24 h
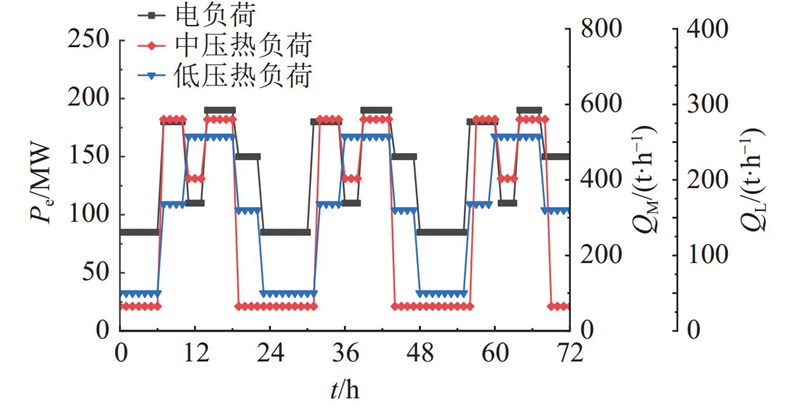
图 8
图 8 简化处理后的热电厂3×24 h热电负荷曲线
Fig.8 Thermoelectric load curves of thermal power plant in 3×24 h after simplification treatment
原方案中,在满足热电负荷需求后,机组3#、4#、5#、6#、7#的运行成本分别为55.30、52.47、30.19、31.56、31.57万元/d,案例热电厂的运行成本为201.09万元/d.
表 2 各方案定量计算结果
Tab.2
| 方案 | f(η)/万元 | f(e)/万元 | f(c)/万元 | F/万元 |
| 原方案 | 355 092 | 27 960 | 234 910 | 92 222 |
| 方案1 | 364 292 | 27 960 | 234 634 | 101 698 |
| 方案2 | 366 277 | 27 960 | 234 405 | 103 912 |
| 方案3 | 361 922 | 27 960 | 237 819 | 96 143 |
| 方案4 | 361 181 | 27 960 | 240 202 | 93 019 |
| 方案5 | 359 581 | 27 960 | 240 133 | 91 488 |
| 方案6 | 364 815 | 27 960 | 238 321 | 98 534 |
| 方案7 | 364 722 | 27 960 | 238 287 | 98 475 |
| 方案8 | 379 824 | 27 960 | 236 782 | 115 082 |
| 方案9 | 363 224 | 27 960 | 236 826 | 98 438 |
图 9
图 9 寻优计算后各机组运行方案成本曲线
Fig.9 Cost curves of operating schemes for each unit after optimization
表2中,f(η)为各方案下生产的蒸汽与电能的金钱价值;f(e)为污染物及温室气体的排放量,本研究中排放量相关计算仅与锅炉燃料消耗量有关,因此各方案的f(e)值相同;f(c)为各方案运行所需的纯成本,不包含电力上网、蒸汽外售等收益;F为运用经济学中的成本收益法计算得到的收益. 在包含能源、环境、经济的多目标情况下,方案8是唯一最优方案.
图 10
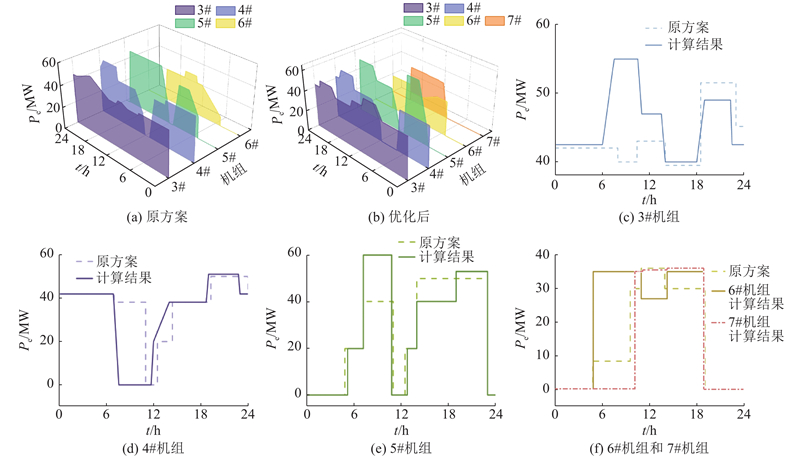
图 10 热电厂各机组在24 h内的功率运行规划曲线
Fig.10 Power operation planning curves for each unit of thermal power plant over a 24-hour period
图 11
图 11 热电厂各机组在24 h内的中压抽汽量运行规划曲线
Fig.11 Operation planning curves of medium-pressure steam extraction volume for each unit of thermal power plant over a 24-hour period
图 12
图 12 热电厂各机组在24 h内的低压抽汽量运行规划曲线
Fig.12 Operation planning curves of low-pressure steam extraction volume for each unit of thermal power plant over a 24-hour period
按照求解得到的运行规划方案,在试运行24 h后,案例热电厂的总运行成本为193.13万元/d,其中3#机组运行成本为61.05万元/d,4#机组运行成本为48.61万元/d,5#机组运行成本为34.56万元/d,6#机组运行成本为28.23万元/d,7#机组运行成本为20.68万元/d. 相比于原设计方案,提出的运行规划方法通过调整汽轮机在不同工况下的出力情况,使案例热电厂的运行成本降低了7.96万元/d.
5. 结 论
围绕复杂热电联产系统的多目标运行规划问题展开研究,聚焦于系统复杂性和多目标优化2个方面,得出以下结论.
(1)综合考虑机组的种类多样性、数量及性能劣化程度等多种因素,系统分析其对复杂热电联产系统运行规划过程中复杂度、稳定性与可靠性的影响. 研究结果表明,该类问题具有阶段性决策、最优子结构、重叠子问题的特点,并存在明确的边界条件和递归关系. 此外,通过归纳热电联产系统复杂性的特征规律,总结运行规划中所须解决的关键性问题,为求解提供了理论参考.
(2)针对复杂热电联产系统运行规划中的多目标优化问题,基于能效、㶲、经济和环境等多维指标构建多目标优化模型. 为了解决多目标优化解集中最终方案的选择容易受到主观因素干扰的问题,采用熵权法对各目标进行客观权重分配,将多目标优化问题转化为单目标优化问题,从而获得唯一的可直接应用于实践的最优决策方案,有效提升了决策的科学性.
(3)以某热电厂的复杂热电联产系统为研究对象,针对随机抽取的24 h热电负荷需求进行运行规划,将优化后的方案与原设计的平均分配方案进行详细对比并可视化表达,表明优化方案充分考虑了不同机组性能差异、启停约束以及出力限制等多方面因素,在分配科学性和合理性上明显优于平均分配方案. 与原方案相比,优化后的运行成本降低了7.96万元/d,验证了所提方法在提升运行经济性与可靠性方面的有效性.
参考文献
多目标粒子群优化算法及其应用研究综述
[J].
Survey of multi-objective particle swarm optimization algorithms and their applications
[J].
Evaluation of the ventilation mode in an ISO class 6 electronic cleanroom by the AHP-entropy weight method
[J].DOI:10.1016/j.energy.2023.128586 [本文引用: 1]
Performance optimization and scheme evaluation of liquid cooling battery thermal management systems based on the entropy weight method
[J].
Data-driven stochastic dynamic economic dispatch for combined heat and power systems using particle swarm optimization
[J].DOI:10.1016/j.egyr.2024.10.032 [本文引用: 1]
Effects of normalization on the entropy-based TOPSIS method
[J].DOI:10.1016/j.eswa.2019.06.035
A novel strategy for real-time optimal scheduling of grid-tied microgrid considering load management and uncertainties
[J].DOI:10.1016/j.energy.2024.131419 [本文引用: 1]
Multi-objective optimization for hydrogen-mixed combined heat and power (CHP) plants considering economic and environmental factors based on MILP
[J].DOI:10.1016/j.jpgr.2023.109442 [本文引用: 1]
Multi-objective optimization of a novel offshore CHP plant based on a 3E analysis
[J].DOI:10.1016/j.energy.2021.120135 [本文引用: 1]
Integrated unit commitment and economic dispatch of combined heat and power system considering heat-power decoupling retrofit of CHP unit
[J].
Two-layer optimal scheduling method for regional integrated energy system considering flexibility characteristics of CHP system
[J].DOI:10.1016/j.energy.2024.132970 [本文引用: 1]
灵活性驱动下的热电联产机组多目标协同控制策略
[J].
Flexibility-driven multi-objective cooperative control strategy for combined heat and power units
[J].
Operation scheduling of a coal-fired CHP station integrated with power-to-heat devices with detail CHP unit models by particle swarm optimization algorithm
[J].DOI:10.1016/j.energy.2020.119022 [本文引用: 1]
基于多目标优化的多区域热电联产最优调度
[J].
Optimal dispatch of multi-region combined heat and power generation based on multi-objective optimization
[J].
含储热的热电联产机组经济性与灵活性多目标优化算法
[J].DOI:10.12158/j.2096-3203.2024.02.026 [本文引用: 1]
Multi-objective optimization algorithm for economy and flexibility of cogeneration unit with heat storage
[J].DOI:10.12158/j.2096-3203.2024.02.026 [本文引用: 1]
Analysis of economy, energy efficiency, environment: a case study of the CHP system with both civil and industrial heat users
[J].DOI:10.1016/j.csite.2022.101768 [本文引用: 1]
计及(火用)效率的电-气-热综合能源系统多目标优化调度方法
[J].
A multi-objective optimal scheduling method for integrated electricity-gas-heat energy system taking into account the exergy efficiency of the integrated energy system
[J].
Revealing the benefits of entropy weights method for multi-objective optimization in machining operations: a critical review
[J].DOI:10.1016/j.jmrt.2020.12.114
Multi-objective optimization of integrated lithium-ion battery thermal management system
[J].DOI:10.1016/j.applthermaleng.2023.119991 [本文引用: 1]