目前,关于建成环境与共享单车使用关系的研究,学者们多采用传统最小二乘回归[3]、多元线性回归[4]方法. 考虑到空间异质性,有学者利用地理加权模型揭示建成环境对单车使用需求的影响. 例如,Wu等[5]使用地理加权回归模型(geographically weighted regression, GWR)检验建成环境对单车使用需求的局部影响,发现人口密度和公共交通可达性对市中心周边地区的单车出行量有正向影响,而在市中心的影响较弱. Sun等[6]采用多尺度地理加权回归模型同样证明了建成环境对共享单车使用量的空间异质性影响. 徐标等[7]构建以骑行距离为约束的多尺度时空地理加权回归模型,研究建成环境对单车停车需求的时空异质性,并发现内环中心区位条件的负向影响呈现较显著的局部异质性.
上述研究表明建成环境对共享单车的使用需求具有明显的空间异质性影响,然而,多数研究仅针对选定的因素和变量开展建模和结果讨论,较明显地受限于模型假设,结果具有一定的局限性. 这主要是因为统计学或空间回归模型预先假定了变量和因子之间的线性关系[8],难以反映建成环境与单车使用之间潜在的更复杂的非线性关系[9-10]. 机器学习技术不预先定义变量之间的关系,可以灵活处理变量之间复杂的非线性关联[11]. 近年来,机器学习方法已被广泛用于分析共享单车出行的影响因素相关研究. 例如,Lv等[12]采用轻量级梯度提升模型探讨影响共享单车竞争力的因素,发现自行车道长度超过一定阈值对单车需求有促进作用,交叉口数量超过一定阈值对单车需求具有抑制作用. Wang等[13]使用随机森林模型探究影响因素对单车骑行量的非线性影响,发现政府机构数量和公交车站距离对单车使用表现出显著的非线性影响,而自行车道长度对骑行量的影响不显著. Zhou等[14]构建梯度提升模型分析多尺度城市建成环境特征对单车使用的影响,发现湿度、人口密度和自行车道密度与单车使用量呈U形的非线性关系. Zhu等[15]精准识别共享单车在综合公共交通系统中的通勤需求,基于极端梯度提升模型(extreme gradient boosting, XGBoost)分析其关键驱动因素,发现骑行缓冲区内自行车密度和地铁客流量两参数超出一定阈值会对单车需求产生促进作用. 上述研究采用不同的机器学习模型揭示了多维因素对共享单车出行需求的非线性影响,但传统的机器学习方法通常假设变量影响在空间上是均匀的,难以反映建成环境的空间异质性影响. 这会影响不同区域的模型解释力,且无法反映不同地理空间的影响机制.
综上所述,传统回归模型受限于线性假设难以捕捉复杂的非线性关系,而现有机器学习方法又无法有效刻画变量影响的空间异质性. 本研究通过引入地理加权改进现有的机器学习模型,采用局部建模刻画建成环境对共享单车出行量的空间异质性影响,构建GW-XGBoost模型解决机器学习建模中忽略的空间异质性问题,进而有效解析空间异质性下建成环境对共享单车出行量的非线性影响.
1. 研究区域及数据描述
1.1. 研究区域概况
深圳位于中国南部海滨,地处广东省南部,是中国经济中心城市,也是中国大陆经济发展最好的城市之一. 深圳市是中国活跃的共享单车市场之一,其共享单车行业得到了快速发展. 根据交通管理部门数据统计,截止至2021年5月底,深圳市互联网租赁自行车运营车辆共37.72万辆,每车日均使用次数为3.71次[16]. 研究所用数据为2021年1月1日—4月15日包含工作日和周末全天0∶00—24∶00共15周的3 825万条共享单车骑行数据. 根据共享单车原始订单数据,对数据进行清洗,筛除掉异常数据,包括查询并删除空值和重复值,并依据计算得到的骑行时长移除小于1 min和大于90 min的数据以及移除掉骑行距离OD小于100 m与大于
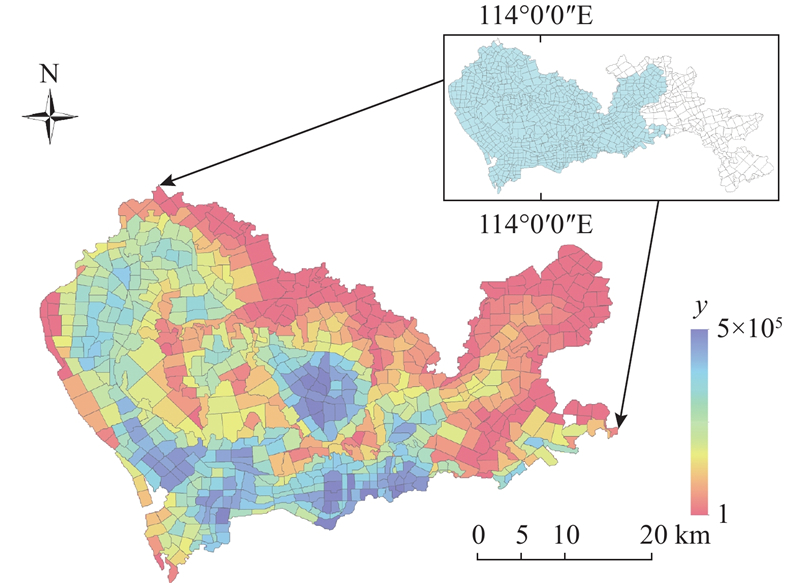
为了保证数据具有代表性,选择共享单车集聚分布的区域作为主要研究范围,涵盖罗湖区、福田区、南山区、宝安区、龙岗区、盐田区和光明区7个主要行政区,面积约为1 535.78 km2. 交通分析小区 (traffic analysis zone, TAZ) 是分析具有相似人口统计和出行特征的一种典型尺度划分方法[17]. 与规则网格划分方法相比,TAZ划分考虑到实际的城市功能区分布和道路网络,能够有效地适应区域间的差异,反映更真实的交通需求,在共享单车及其他相关交通研究中已有广泛应用[18-20]. 本研究根据Yao等[21]的研究考虑地块发展实际格局,沿着主要道路或边界进行有序分裂,将研究区域共划分为741个交通小区作为基本研究单元. 根据数据清洗之后的共享单车订单数据和TAZ数据进行空间匹配,对每个TAZ内的共享单车出行起点进行集计,得到各个区域内的共享单车出行量. 如图1所示展示了研究区域内共享单车出行量y的空间分布情况.
图 1
1.2. 变量描述性统计及检验
基于现有共享单车出行与建成环境关系的研究[22-24],根据Ewing等[25]提出的“5Ds”理论框架,选取反映建成环境特征的变量. “5Ds”维度包括密度、多样性、道路设计、区位条件以及公共交通可达性. 交通网络数据来自Openstreetmap提供的路网数据,人口数据来源于第7次全国人口普查,兴趣点POI数据获取自高德地图. 由于各TAZ单元面积存在差异,直接比较不同区域的共享单车出行量可能产生偏差. 为了保证不同空间单元结果的可比性,将各TAZ的共享单车出行量标准化为每平方千米的出行量作为研究的因变量. 各变量的描述性统计和检验结果如表1所示. 其中,容积率为
表 1 变量描述性统计及检验结果
Tab.1
| 变量类别 | 变量名 | 平均值 | 标准差 | 最小值 | 最大值 | VIF | Moran’s I | z得分 |
| 1)注:*表示p值小于0.05,**表示p值小于0.01. | ||||||||
| 共享单车出行量/万 | 4.756 | 0.815 | 0 | 43.997 | / | 0.785**1) | ||
| 密度 | 容积率 | 0.985 | 0.900 | 0 | 4.676 | 8.517 | 0.589* | 24.273 |
| 人口密度/(人·km−2) | 11 704.798 | 10 131.176 | 0 | 42 209.842 | 5.461 | 0.687** | 28.609 | |
| 多样性 | 土地利用混合度 | 0.751 | 0.527 | 0 | 2.024 | 1.729 | 0.408* | 16.852 |
| 餐饮类POI密度/(个·km−2) | 175.322 | 244.348 | 0 | 1 595.084 | 4.822 | 0.409* | 16.498 | |
| 工作类POI密度/(个·km−2) | 188.802 | 321.093 | 0 | 5 991.526 | 1.901 | 0.378* | 16.442 | |
| 住宅类POI密度/(个·km−2) | 38.120 | 45.066 | 0 | 298.171 | 6.799 | 0.528** | 21.363 | |
| 休闲类POI密度/(个·km−2) | 24.149 | 33.109 | 0 | 229.635 | 3.873 | 0.518* | 21.278 | |
| 道路设计 | 支路密度/(km·km−2) | 3.751 | 3.074 | 0 | 22.794 | 1.525 | 0.313* | 13.042 |
| 自行车道密度/(km·km−2) | 0.553 | 1.289 | 0 | 12.115 | 1.039 | 0.366* | 15.456 | |
| 区位条件 | 到CBD的距离/km | 20.307 | 9.546 | 0.600 | 39.712 | 1.453 | 0.991** | 40.149 |
| 公共交通可达性 | 公交站点密度/(个·km−2) | 4.372 | 3.994 | 0 | 24.147 | 3.416 | 0.424* | 18.036 |
| 地铁站点密度/(个·km−2) | 0.203 | 0.468 | 0 | 2.993 | 1.741 | 0.334* | 14.376 | |
式中:
式中:
2. 研究方法
2.1. XGBoost模型
在定义GW-XGBoost模型之前,引入XGBoost模型[26]的理论方法,有助于进一步讨论GW-XGBoost模型的构建. XGBoost基于梯度提升树,通过构建多个决策树拟合数据,在前向迭代过程中会训练多棵树,样本在模型中的最终预测值是每棵树对样本的预测结果之和,函数定义如下:
式中:
该模型的训练核心是通过优化目标函数进而最小化模型误差,目标函数通常由损失函数和正则化项构成,表达式如下:
式中:
每轮迭代XGBoost通过添加新的函数
式中:
2.2. GW-XGBoost模型
XGBoost模型被广泛应用于非线性的相关研究,该算法假设所有数据点的特征对目标变量的影响是相同的,因而无法揭示空间异质性问题. 因此,本研究对传统XGBoost模型进行改进,充分考虑变量在地理空间上的差异,引入空间加权解决地理空间中的异质性问题,基于TAZ层面构建GW-XGBoost模型. 改进模型的具体实现步骤如下.
1) 明确空间权重矩阵
式中:
2) 构建并训练局部模型GW-XGBoost. 基于每个TAZ及其相邻的加权特征训练模型,相邻的TAZ区域即
式中:
式中:
式中:
3. 模型结果及分析
3.1. 模型性能
采用GWR和XGBoost作为基准模型,与改进的GW-XGBoost模型进行比较. 应用网格搜索法确定模型的最优参数,以及十折交叉验证评估模型的性能,采用决定系数R2、均方误差MSE以及平均绝对误差MAE作为评估模型的性能指标. 最终设定机器学习模型的最佳生成树的数量为600,树的最大深度为3,学习率为0.01,行采样比例为0.8,列采样比例为0.9. 模型性能如表2所示. 其中,
表 2 模型性能比较
Tab.2
| 模型名称 | R2 | MSE | MAE | |
| GWR | 0.582 | 27.108 | 4.216 | |
| XGBoost | 0.674 | 8.758 | 2.230 | |
| GW-XGBoost | 最小值 | 0.611 | 6.904 | 1.244 |
| 最大值 | 0.786 | 8.649 | 2.579 | |
| 平均值 | 0.722 | 7.628 | 1.850 | |
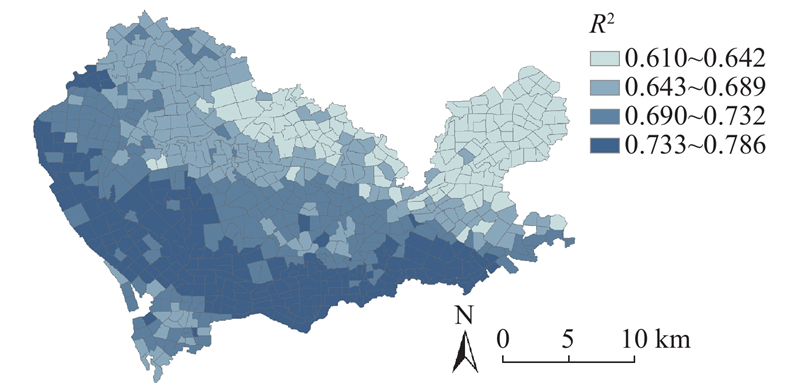
R2的局部空间分布图如图2所示,R2较高的区域集中分布在中南部,而东北部地区的R2相对较低. 这种空间分布特征反映了模型在不同区域对共享单车出行量的解释能力存在差异. 中南部涵盖福田、罗湖、南山区等核心城区,人口密度高且经济活动频繁,从图1可以看出这些区域整体共享单车出行量较大,模型能够更好地捕捉出行需求的空间分布特征,因而拟合效果更优. 相反,东北部区域包含部分山区和城乡结合部,从图1可以看出这些区域共享单车的出行量相对更低. 该区域的共享单车出行可能受基础设施供给和居民出行需求碎片化因素的影响,导致区域内的共享单车数据分布较为稀疏. 此外,由于部分区域距离核心城区较远,居民出行需求更具随机性和多样性,从而增加了模型拟合的难度.
图 2
3.2. 变量影响的空间异质性
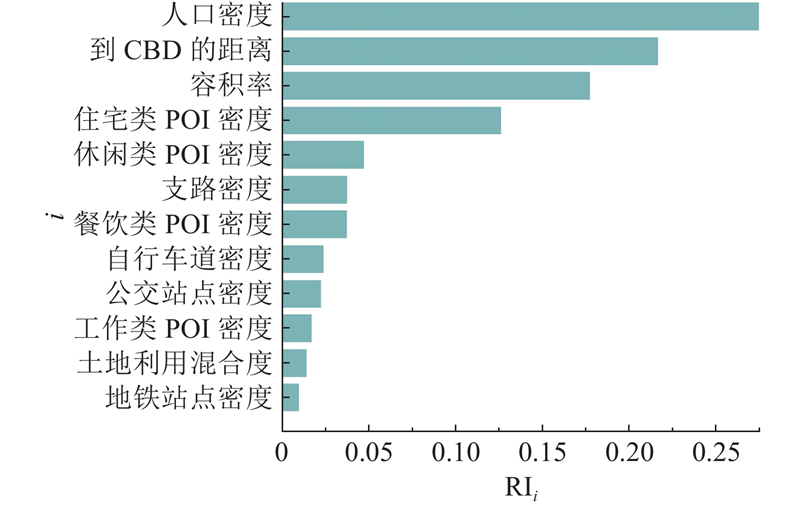
采用SHAP模型解释GW-XGBoost模型的预测结果,评估建成环境的特征重要性. 如图3所示展示了基于SHAP模型计算的全局特征重要性分布,将各变量的平均影响程度转化为百分比形式.可以看出,人口密度、到CBD距离和容积率是对共享单车出行量影响最大的3个建成环境变量,分别占总重要性的27.40%、21.60%和17.68%. 全局特征重要性反映的是变量对共享单车出行量的总体平均贡献.
图 3
表 3 GW-XGBoost模型的局部SHAP
Tab.3
| 变量 | SHAP | |||
| 最小值 | 最大值 | 平均值 | 标准差 | |
| 容积率 | −1.076 | 13.569 | −0.029 | 1.547 |
| 人口密度 | −1.263 | 10.999 | −0.040 | 1.920 |
| 土地利用混合度 | −0.705 | 1.361 | 0.031 | 0.145 |
| 餐饮类POI密度 | −0.726 | 2.793 | −0.050 | 0.304 |
| 工作类POI密度 | −0.414 | 0.760 | 0.028 | 0.137 |
| 住宅类POI密度 | −0.822 | 4.319 | 0.056 | 0.843 |
| 休闲类POI密度 | −0.476 | 1.668 | 0.014 | 0.323 |
| 支路密度 | −0.830 | 0.990 | 0.042 | 0.244 |
| 自行车道密度 | −0.341 | 3.078 | −0.011 | 0.343 |
| 到CBD的距离 | −2.866 | 6.111 | −0.075 | 1.379 |
| 公交站点密度 | −1.141 | 2.413 | 0.015 | 0.215 |
| 地铁站点密度 | −1.226 | 0.682 | −0.006 | 0.133 |
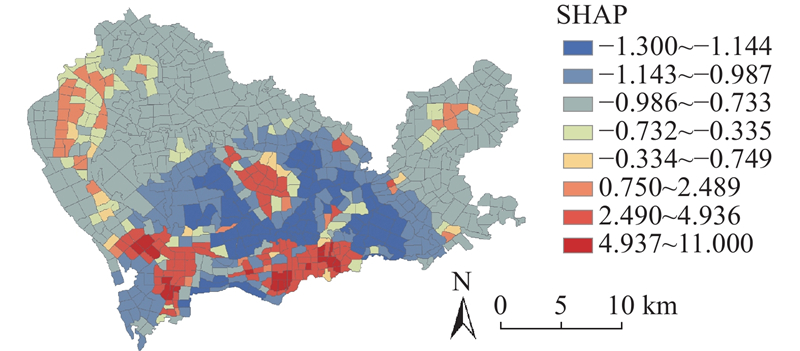
图 4
图 5
图 6
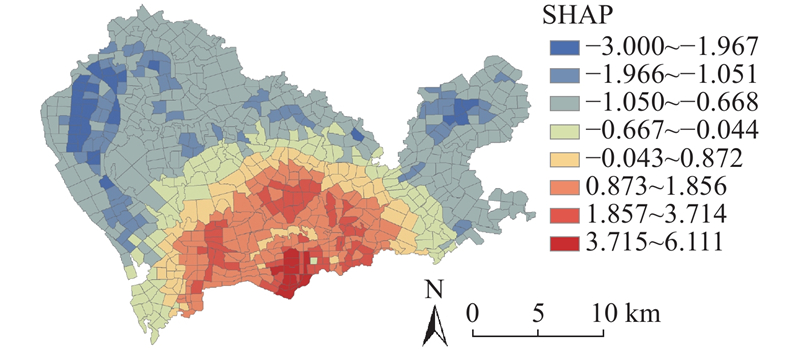
如图4所示展示了人口密度重要度的空间分布. 高SHAP(大于0.7)集中分布在研究区域的中部和南部地区,表明人口密度在这些区域对共享单车出行量具有显著的正向影响. 中部和南部地区人口密集,商业和交通网络发达,居民对共享单车的出行需求较高. 相较之下,低SHAP(小于−0.9)的区域多位于高SHAP区域的外围,表现为负向影响,即人口密度对共享单车出行量产生抑制作用. 这些区域多分布在城市扩展区或新开发区域,人口密度较低、区域功能分散,且居民的出行目的地较远而公共交通系统的覆盖不足,可能导致共享单车出行吸引力较弱. 与Wang等[30]采用的全局回归模型相比,本研究构建的GW-XGBoost模型通过为不同区域构建局部模型,避免整体线性关系或全局非线性关系的限制,揭示了不同区域的人口密度在空间上影响的异质性. 现有研究发现人口密度对共享单车出行需求在整体上具有促进作用,但本研究发现人口密度的影响在不同区域表现出显著的空间差异. 在城市核心区域,人口密度的增加显著促进了共享单车的出行量,而在核心区域的部分外围区域,人口密度对共享单车出行量具有抑制作用.
如图5所示,到CBD距离的影响程度在空间上明显呈现梯度变化,自市中心向城市外围逐渐递减. 城市中心区域的SHAP最高,随着到CBD距离的增加,SHAP逐渐降低. 此外,部分区域即使距离CBD较近,到CBD距离影响因素的SHAP仍然较低,这表明共享单车出行量未受到明显促进. 这些区域的功能可能以居住为主,较完善的小区内部道路和步行环境使短途步行成为更优选择. 且住宅区居民的通勤需求相对固定,出行目的较为分散,居民更倾向于选择其他长距离的交通工具,进一步降低了居民对共享单车的依赖. 该结论反映了到CBD的距离与共享单车出行量之间的负相关性以及空间异质性. 这与Bi等[31]采用机器学习模型XGBoost发现到CBD距离超过一定范围后,共享单车需求量显著增加并趋于稳定的结论不同. 机器学习模型仅揭示全局变化,未能充分考虑到局部区域的异质性. 相比之下,本研究构建的GW-XGBoost模型通过双平方加权核函数构造空间权重矩阵,能够为不同区域赋予空间加权. 这一特点使本研究能够精确捕捉到局部特征与共享单车出行量之间的细微变化. 此外,深圳市的CBD区域集中在南部地区使其核心作用更加集中,高密度的商业、办公区域以及完善的交通和基础设施促使共享单车成为居民出行的主要选择. 而在远离CBD的外围区域,共享单车出行量受其他因素的影响较大.
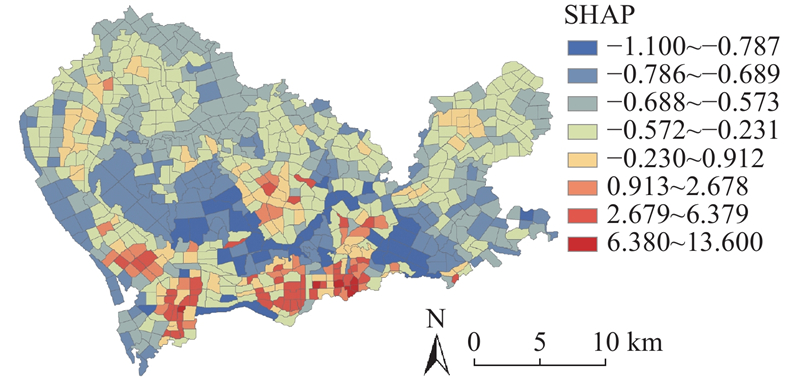
如图6所示显示了容积率对不同地区的共享单车出行量的影响程度. 容积率的SHAP为正且较高的区域分布在深圳市的南部地区,表明这些区域的容积率与共享单车出行量之间呈现较强的正相关性. 高容积率通常伴随较高的土地利用强度,带来更多的职住融合混合功能区域,增加了短距离出行需求,从而促进了共享单车的出行. 相较之下,在中南部交界处的区域SHAP较低且呈现负向影响,表明容积率的提升未能有效促进共享单车的出行量. 这反映了交界区域针对共享单车的基础设施建设不足问题,例如骑行网络不完善或停车点布局欠优化,进而降低了共享单车的使用率. 此外,部分高容积率区域以工业用途为主,职住分离明显,居民通勤需求较远,使得共享单车的适用性较低. Zhou等[14]在不同尺度上研究,发现建筑密度与共享单车出行无显著关联,但其采用的梯度提升决策树方法难以从局部的角度反映影响关系的区域变化. 而 GW-XGBoost 模型能够识别局部区域的特征变化,从而进一步揭示容积率对单车出行量的影响模式.
3.3. 非线性关系
图 7
图 8
图 9
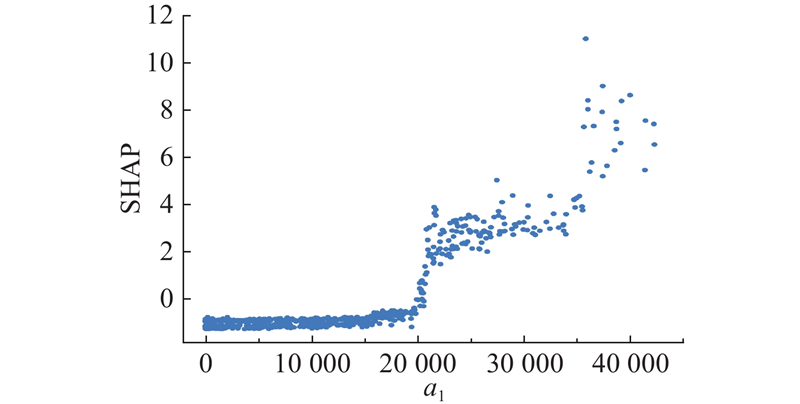
如图7所示展示了人口密度a1对共享单车出行量的影响. 结果显示,人口密度对共享单车出行量的影响呈现出明显的阶段性变化. 当人口密度超过 38 000 人/km2时,SHAP显著增加,表明此时共享单车的出行量受到了较强的正向促进作用. 这一增加由多种因素驱动,包括短途高频出行需求的增加、步行替代效应、公共交通接驳需求的增强等. 当人口密度为20 000~38 000 人/km2时,SHAP由负转正且逐渐趋于平稳,这表明在人口密度达到20 000 人/km2时,对共享单车的出行量的影响开始转为正向促进作用,且此时人口密度对单车出行量的边际影响趋于稳定. 虽然以往研究揭示了人口密度与单车出行量之间的非线性关系,但受限于全局模型建模假设相同的特征在不同区域产生的影响是相同的,所揭示的非线性关系整体呈现正相关性[9,14]. 本研究采用自适应核函数选择带宽使GW-XGBoost模型能够捕捉不同区域的人口密度对单车出行量的局部影响. 从图中还可以看出,在人口密度小于20 000 人/km2的区域,SHAP为负且变化较平稳,这表明人口密度对共享单车出行量产生一定的抑制作用,可能由于低人口密度区的共享单车基础设施不足或居民出行模式更多依赖其他交通方式.
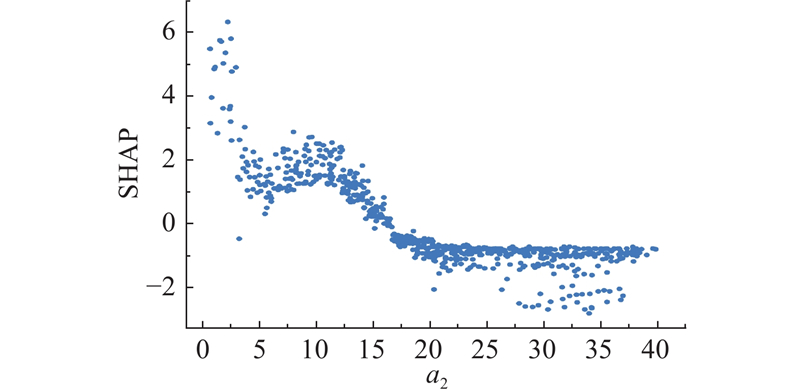
如图8所示描绘了到CBD的距离a2对共享单车出行量的影响,整体表现为随距离增加而逐渐减弱的下降趋势. 这与Yang等[8]基于PDP图对整体趋势分析所得的结论一致. 相比之下,本研究结合SHAP解释方法,构建了GW-XGBoost模型,以更直观的方式展示特征对模型输出的贡献,并揭示变量影响的方向与强度. GW-XGBoost 模型与 SHAP 分析的结合,不仅验证了到CBD的距离对共享单车出行量的空间约束效应,也揭示了过渡区域和远郊区域共享单车出行量的独特模式. 具体而言,距离市中心5 km以内,SHAP显著为正,表明共享单车需求较高. 这与CBD 区域集中分布的办公场所和高人口流动性有关,短途出行需求旺盛. 在距离市中心5~10 km,SHAP表现出轻微的上升趋势,这反映了郊区与中心城区之间存在一定的交通衔接需求,而这一特性在以往PDP方法中往往被忽略. 随着到CBD距离增加至超过15 km,SHAP转为负值并在15~20 km区间呈现下降趋势,这一趋势反映了共享单车对短途出行的适用性以及距离的空间约束效应,离CBD距离超过15 km后共享单车的出行量受到抑制. 在距离CBD超过20 km的区域,SHAP逐渐趋于稳定. 这表明共享单车的出行量在此范围已达到最低点并保持平稳,反映了该区域超出了共享单车的核心服务半径,共享单车出行量受到长距离模式、区域功能特性、基础设施条件等多方面的综合限制.
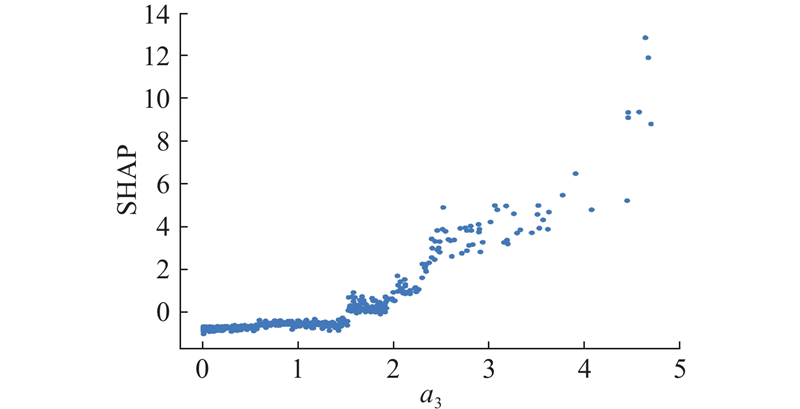
如图9所示展示了容积率a3与共享单车出行量之间的关系. 可以看出,在容积率低于1.8的区间,SHAP为负且变化较平稳. 这反映了在低容积率区域,共享单车出行量受到抑制. 由于低密度区域的居民更倾向于其他交通方式[27]以满足长距离出行需求,且低容积率区域通常人口密度较低、土地混合利用有限以及共享单车基础设施不足,进而抑制了共享单车出行量.当容积率达到1.8时,SHAP从负值跃升为正值,表明此时容积率对共享单车出行量的影响由抑制转为促进作用. 这一变化反映了随容积率增加,人口密度和混合土地利用程度的提高带来更多的短途出行需求和更舒适的骑行环境,此时共享单车出行需求开始被激发. 当容积率超过1.8之后,SHAP呈现持续上升趋势,表明共享单车出行量随容积率增加而不断增长. 可能是因为高容积率区域通常具有更紧凑的城市结构和更完善的自行车道网络,共享单车成为居民短途出行和接驳公共交通的重要方式. 这与严亚磊等[32]发现高容积率地区促进共享单车出行的结论一致,但本研究进一步揭示了容积率对共享单车出行量提升的非线性规律.
4. 结 论
所构建的GW-XGBoost模型,解决了传统机器学习模型忽略的空间异质性问题. 通过融合地理加权和机器学习的优势,在兼顾空间效应和非线性特征的基础上,解析了不同建成环境因素对共享单车出行量的影响. 此外,采用SHAP模型揭示特征重要度以及建成环境因素与共享单车出行量之间的非线性关系. 主要结论如下.
(1) 相比于基准模型GWR和XGBoost,GW-XGBoost模型在平均拟合优度上分别提高了24.05%和7.12%. 地理空间加权机制和自适应带宽的引入使GW-XGBoost模型能够为不同区域分配动态权重,并根据不同区域的数据密度灵活调整最佳权重范围. 不仅能够更准确地捕捉建成环境与共享单车出行量之间的非线性关系,也能够揭示不同地理区域中共享单车出行模式的局部差异.
(2) 建成环境影响因素对共享单车出行量的影响方向和程度从城市中心区域到外围区域呈现显著差异. 其中,人口密度、到CBD的距离和容积率是主要驱动因素,且这些驱动因素在不同区域对共享单车出行量的影响存在梯度变化. 人口密度在市中心区对单车出行量的影响较强且呈现稳定的正向关系,而在低密度区域(人口密度小于20 000人/km2),单车出行受到抑制,当人口密度增加到20 000~
(3) 基于上述结果,建议共享单车运营企业在高人口密度(>20 000 人/km2)、距离CBD在15 km以内和适中容积率(1.8~4.0)区域优先增加共享单车投放量以满足较高的需求. 此外,距离CBD 5~10 km的区域应考虑交通衔接需求,建议结合公共交通站点布局共享单车投放点以提高接驳效率. 城市规划者应进一步完善非机动车道网络,提高骑行可达性. 对于单车出行量受到抑制的区域,建议共享单车运营商避免过度投放,结合需求特征实行差异化投放策略. 此外,为了鼓励绿色出行,城市规划者或政府可适当增加非机动车道完善骑行基础设施建设,以及鼓励办公居住功能混合发展增加短途出行需求,进一步提高绿色出行比例.
(4) 未来研究可以进一步聚焦于城市功能区内部需求特征,构建引入时间维度的模型探讨共享单车出行的动态变化规律. 同时,在考虑可塑性面积单元问题基础上,深入挖掘建成环境因素之间的交互效应,探索多因素交互、时空异质和非线性对共享单车出行的综合作用,为精细化管理策略提供更具针对性的理论支持和实践依据.
参考文献
A review on bike-sharing: the factors affecting bike-sharing demand
[J].DOI:10.1016/j.scs.2019.101882 [本文引用: 1]
Dockless bike-sharing systems: what are the implications?
[J].DOI:10.1080/01441647.2019.1710306 [本文引用: 1]
Modeling bike share station activity: effects of nearby businesses and jobs on trips to and from stations
[J].DOI:10.1061/(ASCE)UP.1943-5444.0000273 [本文引用: 1]
Bike-sharing station usage and the surrounding built environments in major Texas Cities
[J].DOI:10.1177/0739456X19862854 [本文引用: 1]
The effects of built environment spatial variation on bike-sharing usage: a case study of Suzhou, China
[J].DOI:10.1016/j.cities.2020.103063 [本文引用: 1]
How does the urban built environment affect dockless bikesharing-metro integration cycling? Analysis from a nonlinear comprehensive perspective
[J].DOI:10.1016/j.jclepro.2024.141770 [本文引用: 1]
共享单车停车需求的多尺度时空影响因素
[J].
Multi-scale spatiotemporal influencing factors of bike-sharing parking demand
[J].
Time-varying and non-linear associations between metro ridership and the built environment
[J].DOI:10.1016/j.tust.2022.104931 [本文引用: 2]
Synergistic effects of the built environment and commuting programs on commute mode choice
[J].DOI:10.1016/j.tra.2018.08.041 [本文引用: 2]
Non-linear associations between the urban built environment and commuting modal split: a random forest approach and SHAP evaluation
[J].DOI:10.1109/ACCESS.2023.3241627 [本文引用: 1]
Geographically weighted machine learning for modeling spatial heterogeneity in traffic crash frequency and determinants in US
[J].DOI:10.1016/j.aap.2024.107528 [本文引用: 1]
An origin-destination level analysis on the competitiveness of bike-sharing to underground using explainable machine learning
[J].DOI:10.1016/j.jtrangeo.2023.103716 [本文引用: 1]
Nonlinear effects of factors on dockless bike-sharing usage considering grid-based spatiotemporal heterogeneity
[J].DOI:10.1016/j.trd.2022.103194 [本文引用: 1]
Assessing the effects of the built environment and microclimate on cycling volume
[J].DOI:10.1016/j.trd.2023.103936 [本文引用: 3]
Revealing the driving factors and mobility patterns of bike-sharing commuting demands for integrated public transport systems
[J].DOI:10.1016/j.scs.2024.105323 [本文引用: 1]
Urban form breeds neighborhood vibrancy: a case study using a GPS-based activity survey in suburban Beijing
[J].DOI:10.1016/j.cities.2017.11.008 [本文引用: 1]
城中村对深圳市职住空间融合的影响: 基于手机信令数据的研究
[J].
Impact of urban village on job-housing balance in Shenzhen: a study using mobile phone signaling data
[J].
Quantifying the nighttime economy–housing separation from a human activity standpoint: a case study in Shenzhen, China
[J].DOI:10.1016/j.cities.2024.104894
基于MGWR的共享单车空间异质性分析
[J].
Spatial heterogeneity analysis of bikesharing based on MGWR
[J].
Simulating urban land-use changes at a large scale by integrating dynamic land parcel subdivision and vector-based cellular automata
[J].DOI:10.1080/13658816.2017.1360494 [本文引用: 1]
Bike share usage and the built environment: a review
[J].DOI:10.3389/fpubh.2022.848169 [本文引用: 1]
城市建成环境对公共自行车使用的影响机制研究: 以深圳市南山区为例
[J].
How urban built environment affects the use of public bicycles: a case study of Nanshan District of Shenzhen
[J].
建成环境对共享单车与地铁组合出行的影响关系
[J].
Influence of built environment on integrated use of bike sharing and metro
[J].
Travel and the built environment: a synthesis
[J].
Nonlinear and synergistic effects of TOD on urban vibrancy: applying local explanations for gradient boosting decision tree
[J].DOI:10.1016/j.scs.2021.103063 [本文引用: 2]
Environmental factors for outdoor jogging in Beijing: insights from using explainable spatial machine learning and massive trajectory data
[J].DOI:10.1016/j.landurbplan.2023.104969 [本文引用: 1]
基于Leiden算法的共享单车活动社区识别方法: 南京案例分析
[J].
A method for identifying operation zones of free-floating shared bikes based on leiden algorithm: a case study of the city of Nanjing
[J].
Exploring the effect of neighbouring built and demographic environment on station-level bike-sharing trips under COVID-19
[J].
Examining the varying influences of built environment on bike-sharing commuting: empirical evidence from Shanghai
[J].DOI:10.1016/j.tranpol.2022.10.004 [本文引用: 1]