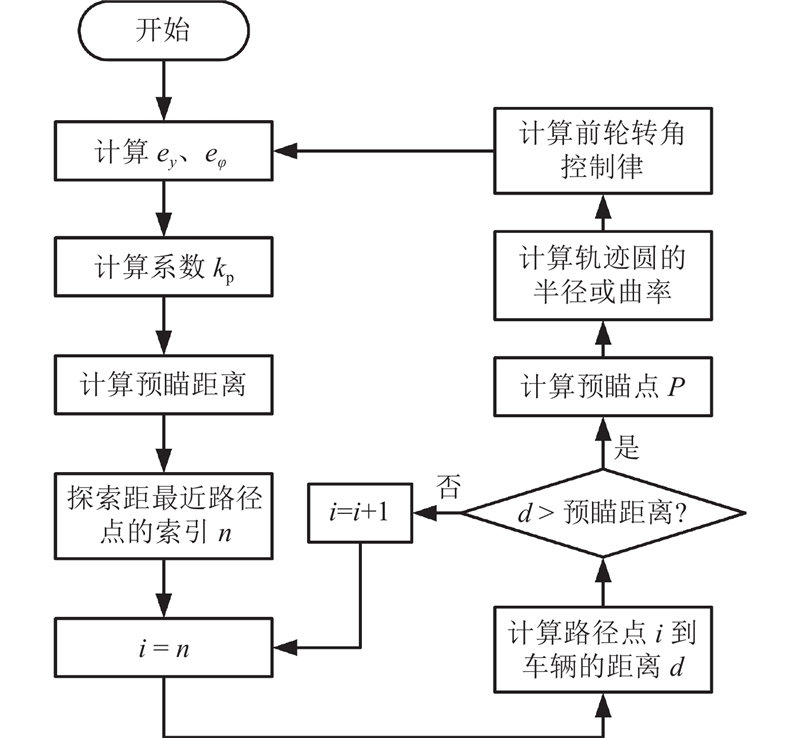
将横向误差e y e φ e y e φ k p 为输出变量.
[1]
ZHOU S, LIU J, WANG Z, et al Research on design optimization and simulation of regenerative braking control strategy for pure electric vehicle based on EMB systems
[J]. Transactions of Famena , 2023 , 47 (4 ): 33 - 49
DOI:10.21278/TOF.474045522
[本文引用: 1]
[2]
XU Z, GERADA C Enhanced estimation of clamping-force for automotive EMB actuators using a switching extended state observer
[J]. IEEE Transactions on Industrial Electronics , 2024 , 71 (3 ): 2220 - 2230
DOI:10.1109/TIE.2023.3265060
[本文引用: 1]
[3]
HOSEINNEZHAD R, BABHADIASHAR A, HARDING P Calibration of resolver sensors in electromechanical braking systems: a modified recursive weighted least-squares approach
[J]. IEEE Transactions on Industrial Electronics , 2007 , 54 (2 ): 1052 - 1060
DOI:10.1109/TIE.2007.893049
[本文引用: 1]
[4]
孙丽琴, 陈欢, 张晓亮, 等 面向线控制动车辆单轮制动失效的稳定性控制
[J]. 重庆理工大学学报: 自然科学 , 2024 , 38 (4 ): 55 - 63
[本文引用: 3]
SUN Liqin, CHEN Huan, ZHANG Xiaoliang, et al Single-wheel brake failure stability control for vehicle equipped with brake-by-wire system
[J]. Journal of Chongqing University of Technology: Natural Science , 2024 , 38 (4 ): 55 - 63
[本文引用: 3]
[5]
ZHENG L, LU Y, WANG J, et al Braking failure anti-rollover control and hardware-in-the-loop verification of wire-controlled heavy vehicles
[J]. Scientific Reports , 2024 , 14 (1 ): 29802
DOI:10.1038/s41598-024-80854-9
[本文引用: 1]
[6]
PARK J I, JEON K, CHOI S. Design of fail-safe controller for brake-by-wire systems using optimal braking force distribution [C]//2013 World Electric Vehicle Symposium and Exhibition . Barcelona: IEEE, 2013: 1-7.
[本文引用: 1]
[7]
ZHOU J, DI Y, MIAO X Single-wheel failure stability control for vehicle equipped with brake-by-wire system
[J]. World Electric Vehicle Journal , 2023 , 14 (7 ): 177
DOI:10.3390/wevj14070177
[本文引用: 1]
[8]
ZHANG L, PANG, Z, WANG, S, et al Electromechanical composite brake control for two in-wheel motors drive electric vehicle with single motor failure
[J]. Proceedings of the Institution of Mechanical Engineers Part D Journal of Automobile Engineering , 2020 , 234 (4 ): 1057 - 1074
DOI:10.1177/0954407019864229
[本文引用: 1]
[9]
TANG X, SHI L, WANG B, et al. EMB-based brake failure stability control strategy for distributed drive electric vehicles [C]//6th CAA International Conference on Vehicular Control and Intelligence . Nanjing: IEEE, 2022: 1-6.
[本文引用: 1]
[10]
陈佳瑶, 彭晓燕 线控制动车辆弯道制动力优化分配控制策略
[J]. 机械设计 , 2020 , 37 (2 ): 1 - 9
[本文引用: 1]
CHEN Jiayao, PENG Xiaoyan Strategy for optimal braking-force allocation of vehicles with the brake-by-wire system during a braking-in-turn maneuver
[J]. Journal of Machine Design , 2020 , 37 (2 ): 1 - 9
[本文引用: 1]
[11]
ITO A, AZUMA S I Autonomous distributed braking and driving force control architecture based on broadcast control for vehicles with in-wheel motors on four wheels
[J]. Advanced Robotics , 2024 , 38 (9/10 ): 672 - 683
DOI:10.1080/01691864.2024.2349919
[本文引用: 1]
[12]
刘炎. 线控制动系统制动失效工况下整车稳定性控制策略研究[D]. 长沙: 湖南大学, 2018.
[本文引用: 4]
LIU Yan. Research on vehicle stability control strategy of the brake-by-wire system brake failure [D]. Changsha: Hunan University, 2018.
[本文引用: 4]
[13]
PENG Z, NING G. 2 Dof lateral dynamic model with force input of skid steering wheeled vehicle [C]//IEEE Transportation Electrification Conference and Expo, Asia-Pacific . [S. l.]: IEEE, 2014: 1-5.
[本文引用: 1]
[14]
WU D, ZHANG Q, DU C, et al. Path tracking and stability control of 4WID electric vehicles based on variable prediction horizon MPC [J]. International Journal of Vehicle Design , 2024, 95(3/4): 291−319.
[本文引用: 1]
[15]
DING S, WANG J, ZHENG W X Second-order sliding mode control for nonlinear uncertain systems bounded by positive functions
[J]. IEEE Transactions on Industrial Electronics , 2015 , 62 (9 ): 5899 - 5909
DOI:10.1109/TIE.2015.2448064
[16]
SHAN W, LI K SMC-fuzzy joint vector control of built-in permanent magnet synchronous motorized spindle
[J]. Journal of Mechanical Engineering , 2022 , 58 (3 ): 177
DOI:10.3901/JME.2022.03.177
[17]
GOKUL K S, SURESH K P, NASSAR M N, et al Real-time experimental evaluation and analysis of PID and MPC controllers using HIL setup for robust steering system of autonomous vehicles
[J]. IEEE Access , 2024 , 12 : 74711 - 74723
DOI:10.1109/ACCESS.2024.3406219
[18]
邓斌, 李维汉, 吴迪, 等 基于KFESO的四轮主动转向积分滑模控制[J]. 汽车工程, 2024, 46(1): 100-108.
[本文引用: 1]
DENG Bin, LI Weihan, WU Di, et al. Integral sliding mode control for four-wheel active steering based on Kalman filter extended state observer [J]. Automotive Engineering , 2024, 46(1): 100-108.
[本文引用: 1]
[19]
胡杰, 张志凌, 钟杰锋, 等 考虑复杂扰动的轻型商用车路径跟踪混合控制方法
[J]. 汽车工程 , 2024 , 46 (9 ): 1576 - 1586
[本文引用: 1]
HU Jie, ZHANG Zhiling, ZHONG Jiefeng, et al A hybrid control strategy for light commercial vehicle path tracking considering complex disturbances
[J]. Automotive Engineering , 2024 , 46 (9 ): 1576 - 1586
[本文引用: 1]
[20]
丁海涛, 郭孔辉, 陈虹 汽车稳定性控制中横摆力矩决策的LQR方法
[J]. 吉林大学学报: 工学版 , 2010 , 40 (3 ): 597 - 601
[本文引用: 1]
DING Haitao, GUO Konghui, CHEN Hong LQR method for vehicle yaw moment decision in vehicle stability control
[J]. Journal of Jilin University: Engineering and Technology Edition , 2010 , 40 (3 ): 597 - 601
[本文引用: 1]
[21]
ESKANDARIPOUR M, GOLMOHAMMADI M H, SOLTANINIA S Optimization of low-impact development facilities in urban areas using slime mould algorithm
[J]. Sustainable Cities and Society , 2023 , 93 : 104508
DOI:10.1016/j.scs.2023.104508
[本文引用: 1]
[22]
LIU J, FU Y, LI Y, et al An effective theoretical and experimental analysis method for the improved slime mould algorithm
[J]. Expert Systems with Applications , 2024 , 247 : 123299
DOI:10.1016/j.eswa.2024.123299
[本文引用: 1]
[23]
LUO Q, YIN S, ZHOU G, et al Multi-objective equilibrium optimizer slime mould algorithm and its application in solving engineering problems
[J]. Structural and Multidisciplinary Optimization , 2023 , 66 (5 ): 114
DOI:10.1007/s00158-023-03568-y
[本文引用: 1]
[24]
吴桐, 荣劲, 王军年, 等 面向转向制动工况的制动力动态分配策略
[J]. 汽车工程 , 2024 , 46 (10 ): 1755 - 1765
[本文引用: 1]
WU Tong, RONG Jing, WANG Junnian, et al Dynamic braking allocation strategy for turning-braking maneuver
[J]. Automotive Engineering , 2024 , 46 (10 ): 1755 - 1765
[本文引用: 1]
[25]
刘英杰, 赵又群, 许健雄, 等 基于Gauss伪谱法的紧急避让汽车操纵逆动力学
[J]. 机械工程学报 , 2012 , 48 (22 ): 127 - 132
DOI:10.3901/JME.2012.22.127
[本文引用: 1]
LIU Yingjie, ZHAO Youqun, XU Jianxiong, et al Vehicle handling inverse dynamics based on gauss pseudospectral method while encountering emergency collision avoidance
[J]. Journal of Mechanical Engineering , 2012 , 48 (22 ): 127 - 132
DOI:10.3901/JME.2012.22.127
[本文引用: 1]
[26]
KIM S, LEE J, HAN K, et al Vehicle path tracking control using pure pursuit with MPC-based look-ahead distance optimization
[J]. IEEE Transactions on Vehicular Technology , 2024 , 73 (1 ): 53 - 66
DOI:10.1109/TVT.2023.3304427
[本文引用: 1]
[27]
HU C, RU Y, LI X, et al Path tracking control for brake-steering tracked vehicles based on an improved pure pursuit algorithm
[J]. Biosystems Engineering , 2024 , 242 : 1 - 15
DOI:10.1016/j.biosystemseng.2024.04.006
[本文引用: 1]
[28]
GUAN Y, LI N, CHEN P, et al Research on path tracking control based on optimal look-ahead points
[J]. International Journal of Automotive Technology , 2024 , 25 (6 ): 1355 - 1374
DOI:10.1007/s12239-024-00117-4
[本文引用: 1]
[29]
YU L, YAN X, KUANG Z, et al Driverless bus path tracking based on fuzzy pure pursuit control with a front axle reference
[J]. Applied Sciences , 2019 , 10 (1 ): 230
DOI:10.3390/app10010230
[本文引用: 1]
Research on design optimization and simulation of regenerative braking control strategy for pure electric vehicle based on EMB systems
1
2023
... 近年来,纯电动汽车的快速发展推动了汽车制动系统技术的革新. 相较于传统的液压制动系统,线控制动系统,特别是电子机械制动(electromechanical brake, EMB)系统,凭借结构紧凑、响应迅速的优势,逐渐成为研究热点[1 -2 ] . 与传统的液压制动相比,EMB通过电机直接驱动卡钳,实现了对每个车轮的独立、精确控制[3 ] ,提高了车辆的稳定性、操控性和安全性. EMB系统的全电控特性使其对故障更敏感. 相较于传统液压制动系统冗余的液压备份,EMB故障可能导致制动性能严重下降[4 -5 ] . 提升EMB系统的容错性,是保障车辆行驶安全的重要课题,也是当前研究的热点之一. 针对单轮制动失效,Park等[6 ] 提出基于Karush-Kuhn-Tucker 条件优化设计方法和拉格朗日乘子进行制动力重构的方法. Zhou等[7 ] 引入故障因子衡量制动失效程度并对制动力进行重构,使用滑模控制器控制车辆横摆力矩. Zhang等[8 ] 提出内层基于模型预测控制,外层基于模糊控制的双层控制器. Tang等[9 ] 设计基于规则的扭矩重建控制器和基于高增益反馈鲁棒控制算法的前轮转角控制器,分别控制车辆纵向和横向的加速度. 基于弯道失效工况,陈佳瑶等[10 ] 使用滑模控制器计算车辆所需的横摆力矩,基于弯道制动时的动力学特征使用序列二次规划法分配制动力. 孙丽琴等[4 ] 通过滑模控制器计算维持车辆稳定所需的前轮转角,通过规则对制动力进行重构. Ito等[11 ] 通过广播控制,将架构从常规集中控制转变为自主分布式控制制动力和驱动力,当出现单轮或双轮失效时,车辆通过其他车轮的自主分布式行为来保持性能. ...
Enhanced estimation of clamping-force for automotive EMB actuators using a switching extended state observer
1
2024
... 近年来,纯电动汽车的快速发展推动了汽车制动系统技术的革新. 相较于传统的液压制动系统,线控制动系统,特别是电子机械制动(electromechanical brake, EMB)系统,凭借结构紧凑、响应迅速的优势,逐渐成为研究热点[1 -2 ] . 与传统的液压制动相比,EMB通过电机直接驱动卡钳,实现了对每个车轮的独立、精确控制[3 ] ,提高了车辆的稳定性、操控性和安全性. EMB系统的全电控特性使其对故障更敏感. 相较于传统液压制动系统冗余的液压备份,EMB故障可能导致制动性能严重下降[4 -5 ] . 提升EMB系统的容错性,是保障车辆行驶安全的重要课题,也是当前研究的热点之一. 针对单轮制动失效,Park等[6 ] 提出基于Karush-Kuhn-Tucker 条件优化设计方法和拉格朗日乘子进行制动力重构的方法. Zhou等[7 ] 引入故障因子衡量制动失效程度并对制动力进行重构,使用滑模控制器控制车辆横摆力矩. Zhang等[8 ] 提出内层基于模型预测控制,外层基于模糊控制的双层控制器. Tang等[9 ] 设计基于规则的扭矩重建控制器和基于高增益反馈鲁棒控制算法的前轮转角控制器,分别控制车辆纵向和横向的加速度. 基于弯道失效工况,陈佳瑶等[10 ] 使用滑模控制器计算车辆所需的横摆力矩,基于弯道制动时的动力学特征使用序列二次规划法分配制动力. 孙丽琴等[4 ] 通过滑模控制器计算维持车辆稳定所需的前轮转角,通过规则对制动力进行重构. Ito等[11 ] 通过广播控制,将架构从常规集中控制转变为自主分布式控制制动力和驱动力,当出现单轮或双轮失效时,车辆通过其他车轮的自主分布式行为来保持性能. ...
Calibration of resolver sensors in electromechanical braking systems: a modified recursive weighted least-squares approach
1
2007
... 近年来,纯电动汽车的快速发展推动了汽车制动系统技术的革新. 相较于传统的液压制动系统,线控制动系统,特别是电子机械制动(electromechanical brake, EMB)系统,凭借结构紧凑、响应迅速的优势,逐渐成为研究热点[1 -2 ] . 与传统的液压制动相比,EMB通过电机直接驱动卡钳,实现了对每个车轮的独立、精确控制[3 ] ,提高了车辆的稳定性、操控性和安全性. EMB系统的全电控特性使其对故障更敏感. 相较于传统液压制动系统冗余的液压备份,EMB故障可能导致制动性能严重下降[4 -5 ] . 提升EMB系统的容错性,是保障车辆行驶安全的重要课题,也是当前研究的热点之一. 针对单轮制动失效,Park等[6 ] 提出基于Karush-Kuhn-Tucker 条件优化设计方法和拉格朗日乘子进行制动力重构的方法. Zhou等[7 ] 引入故障因子衡量制动失效程度并对制动力进行重构,使用滑模控制器控制车辆横摆力矩. Zhang等[8 ] 提出内层基于模型预测控制,外层基于模糊控制的双层控制器. Tang等[9 ] 设计基于规则的扭矩重建控制器和基于高增益反馈鲁棒控制算法的前轮转角控制器,分别控制车辆纵向和横向的加速度. 基于弯道失效工况,陈佳瑶等[10 ] 使用滑模控制器计算车辆所需的横摆力矩,基于弯道制动时的动力学特征使用序列二次规划法分配制动力. 孙丽琴等[4 ] 通过滑模控制器计算维持车辆稳定所需的前轮转角,通过规则对制动力进行重构. Ito等[11 ] 通过广播控制,将架构从常规集中控制转变为自主分布式控制制动力和驱动力,当出现单轮或双轮失效时,车辆通过其他车轮的自主分布式行为来保持性能. ...
面向线控制动车辆单轮制动失效的稳定性控制
3
2024
... 近年来,纯电动汽车的快速发展推动了汽车制动系统技术的革新. 相较于传统的液压制动系统,线控制动系统,特别是电子机械制动(electromechanical brake, EMB)系统,凭借结构紧凑、响应迅速的优势,逐渐成为研究热点[1 -2 ] . 与传统的液压制动相比,EMB通过电机直接驱动卡钳,实现了对每个车轮的独立、精确控制[3 ] ,提高了车辆的稳定性、操控性和安全性. EMB系统的全电控特性使其对故障更敏感. 相较于传统液压制动系统冗余的液压备份,EMB故障可能导致制动性能严重下降[4 -5 ] . 提升EMB系统的容错性,是保障车辆行驶安全的重要课题,也是当前研究的热点之一. 针对单轮制动失效,Park等[6 ] 提出基于Karush-Kuhn-Tucker 条件优化设计方法和拉格朗日乘子进行制动力重构的方法. Zhou等[7 ] 引入故障因子衡量制动失效程度并对制动力进行重构,使用滑模控制器控制车辆横摆力矩. Zhang等[8 ] 提出内层基于模型预测控制,外层基于模糊控制的双层控制器. Tang等[9 ] 设计基于规则的扭矩重建控制器和基于高增益反馈鲁棒控制算法的前轮转角控制器,分别控制车辆纵向和横向的加速度. 基于弯道失效工况,陈佳瑶等[10 ] 使用滑模控制器计算车辆所需的横摆力矩,基于弯道制动时的动力学特征使用序列二次规划法分配制动力. 孙丽琴等[4 ] 通过滑模控制器计算维持车辆稳定所需的前轮转角,通过规则对制动力进行重构. Ito等[11 ] 通过广播控制,将架构从常规集中控制转变为自主分布式控制制动力和驱动力,当出现单轮或双轮失效时,车辆通过其他车轮的自主分布式行为来保持性能. ...
... [4 ]通过滑模控制器计算维持车辆稳定所需的前轮转角,通过规则对制动力进行重构. Ito等[11 ] 通过广播控制,将架构从常规集中控制转变为自主分布式控制制动力和驱动力,当出现单轮或双轮失效时,车辆通过其他车轮的自主分布式行为来保持性能. ...
... 使用序列二次规划(SQP)法优化求解该目标函数[25 ] ,得到重构后的剩余三轮制动力. 从图4 可知,若其他条件相同,则同侧的单轮制动失效造成的转动大致相同,且由于轴荷转移,前轴制动失效的危险性更大;异侧单轮制动失效间的区别更多集中在横摆力矩方向上[4 ,12 ] ,因此当其他车轮发生随机制动失效时,可以采用相同的方法计算横摆力矩. 仅在制动力分配环节调整k x i 图6 所示. ...
面向线控制动车辆单轮制动失效的稳定性控制
3
2024
... 近年来,纯电动汽车的快速发展推动了汽车制动系统技术的革新. 相较于传统的液压制动系统,线控制动系统,特别是电子机械制动(electromechanical brake, EMB)系统,凭借结构紧凑、响应迅速的优势,逐渐成为研究热点[1 -2 ] . 与传统的液压制动相比,EMB通过电机直接驱动卡钳,实现了对每个车轮的独立、精确控制[3 ] ,提高了车辆的稳定性、操控性和安全性. EMB系统的全电控特性使其对故障更敏感. 相较于传统液压制动系统冗余的液压备份,EMB故障可能导致制动性能严重下降[4 -5 ] . 提升EMB系统的容错性,是保障车辆行驶安全的重要课题,也是当前研究的热点之一. 针对单轮制动失效,Park等[6 ] 提出基于Karush-Kuhn-Tucker 条件优化设计方法和拉格朗日乘子进行制动力重构的方法. Zhou等[7 ] 引入故障因子衡量制动失效程度并对制动力进行重构,使用滑模控制器控制车辆横摆力矩. Zhang等[8 ] 提出内层基于模型预测控制,外层基于模糊控制的双层控制器. Tang等[9 ] 设计基于规则的扭矩重建控制器和基于高增益反馈鲁棒控制算法的前轮转角控制器,分别控制车辆纵向和横向的加速度. 基于弯道失效工况,陈佳瑶等[10 ] 使用滑模控制器计算车辆所需的横摆力矩,基于弯道制动时的动力学特征使用序列二次规划法分配制动力. 孙丽琴等[4 ] 通过滑模控制器计算维持车辆稳定所需的前轮转角,通过规则对制动力进行重构. Ito等[11 ] 通过广播控制,将架构从常规集中控制转变为自主分布式控制制动力和驱动力,当出现单轮或双轮失效时,车辆通过其他车轮的自主分布式行为来保持性能. ...
... [4 ]通过滑模控制器计算维持车辆稳定所需的前轮转角,通过规则对制动力进行重构. Ito等[11 ] 通过广播控制,将架构从常规集中控制转变为自主分布式控制制动力和驱动力,当出现单轮或双轮失效时,车辆通过其他车轮的自主分布式行为来保持性能. ...
... 使用序列二次规划(SQP)法优化求解该目标函数[25 ] ,得到重构后的剩余三轮制动力. 从图4 可知,若其他条件相同,则同侧的单轮制动失效造成的转动大致相同,且由于轴荷转移,前轴制动失效的危险性更大;异侧单轮制动失效间的区别更多集中在横摆力矩方向上[4 ,12 ] ,因此当其他车轮发生随机制动失效时,可以采用相同的方法计算横摆力矩. 仅在制动力分配环节调整k x i 图6 所示. ...
Braking failure anti-rollover control and hardware-in-the-loop verification of wire-controlled heavy vehicles
1
2024
... 近年来,纯电动汽车的快速发展推动了汽车制动系统技术的革新. 相较于传统的液压制动系统,线控制动系统,特别是电子机械制动(electromechanical brake, EMB)系统,凭借结构紧凑、响应迅速的优势,逐渐成为研究热点[1 -2 ] . 与传统的液压制动相比,EMB通过电机直接驱动卡钳,实现了对每个车轮的独立、精确控制[3 ] ,提高了车辆的稳定性、操控性和安全性. EMB系统的全电控特性使其对故障更敏感. 相较于传统液压制动系统冗余的液压备份,EMB故障可能导致制动性能严重下降[4 -5 ] . 提升EMB系统的容错性,是保障车辆行驶安全的重要课题,也是当前研究的热点之一. 针对单轮制动失效,Park等[6 ] 提出基于Karush-Kuhn-Tucker 条件优化设计方法和拉格朗日乘子进行制动力重构的方法. Zhou等[7 ] 引入故障因子衡量制动失效程度并对制动力进行重构,使用滑模控制器控制车辆横摆力矩. Zhang等[8 ] 提出内层基于模型预测控制,外层基于模糊控制的双层控制器. Tang等[9 ] 设计基于规则的扭矩重建控制器和基于高增益反馈鲁棒控制算法的前轮转角控制器,分别控制车辆纵向和横向的加速度. 基于弯道失效工况,陈佳瑶等[10 ] 使用滑模控制器计算车辆所需的横摆力矩,基于弯道制动时的动力学特征使用序列二次规划法分配制动力. 孙丽琴等[4 ] 通过滑模控制器计算维持车辆稳定所需的前轮转角,通过规则对制动力进行重构. Ito等[11 ] 通过广播控制,将架构从常规集中控制转变为自主分布式控制制动力和驱动力,当出现单轮或双轮失效时,车辆通过其他车轮的自主分布式行为来保持性能. ...
1
... 近年来,纯电动汽车的快速发展推动了汽车制动系统技术的革新. 相较于传统的液压制动系统,线控制动系统,特别是电子机械制动(electromechanical brake, EMB)系统,凭借结构紧凑、响应迅速的优势,逐渐成为研究热点[1 -2 ] . 与传统的液压制动相比,EMB通过电机直接驱动卡钳,实现了对每个车轮的独立、精确控制[3 ] ,提高了车辆的稳定性、操控性和安全性. EMB系统的全电控特性使其对故障更敏感. 相较于传统液压制动系统冗余的液压备份,EMB故障可能导致制动性能严重下降[4 -5 ] . 提升EMB系统的容错性,是保障车辆行驶安全的重要课题,也是当前研究的热点之一. 针对单轮制动失效,Park等[6 ] 提出基于Karush-Kuhn-Tucker 条件优化设计方法和拉格朗日乘子进行制动力重构的方法. Zhou等[7 ] 引入故障因子衡量制动失效程度并对制动力进行重构,使用滑模控制器控制车辆横摆力矩. Zhang等[8 ] 提出内层基于模型预测控制,外层基于模糊控制的双层控制器. Tang等[9 ] 设计基于规则的扭矩重建控制器和基于高增益反馈鲁棒控制算法的前轮转角控制器,分别控制车辆纵向和横向的加速度. 基于弯道失效工况,陈佳瑶等[10 ] 使用滑模控制器计算车辆所需的横摆力矩,基于弯道制动时的动力学特征使用序列二次规划法分配制动力. 孙丽琴等[4 ] 通过滑模控制器计算维持车辆稳定所需的前轮转角,通过规则对制动力进行重构. Ito等[11 ] 通过广播控制,将架构从常规集中控制转变为自主分布式控制制动力和驱动力,当出现单轮或双轮失效时,车辆通过其他车轮的自主分布式行为来保持性能. ...
Single-wheel failure stability control for vehicle equipped with brake-by-wire system
1
2023
... 近年来,纯电动汽车的快速发展推动了汽车制动系统技术的革新. 相较于传统的液压制动系统,线控制动系统,特别是电子机械制动(electromechanical brake, EMB)系统,凭借结构紧凑、响应迅速的优势,逐渐成为研究热点[1 -2 ] . 与传统的液压制动相比,EMB通过电机直接驱动卡钳,实现了对每个车轮的独立、精确控制[3 ] ,提高了车辆的稳定性、操控性和安全性. EMB系统的全电控特性使其对故障更敏感. 相较于传统液压制动系统冗余的液压备份,EMB故障可能导致制动性能严重下降[4 -5 ] . 提升EMB系统的容错性,是保障车辆行驶安全的重要课题,也是当前研究的热点之一. 针对单轮制动失效,Park等[6 ] 提出基于Karush-Kuhn-Tucker 条件优化设计方法和拉格朗日乘子进行制动力重构的方法. Zhou等[7 ] 引入故障因子衡量制动失效程度并对制动力进行重构,使用滑模控制器控制车辆横摆力矩. Zhang等[8 ] 提出内层基于模型预测控制,外层基于模糊控制的双层控制器. Tang等[9 ] 设计基于规则的扭矩重建控制器和基于高增益反馈鲁棒控制算法的前轮转角控制器,分别控制车辆纵向和横向的加速度. 基于弯道失效工况,陈佳瑶等[10 ] 使用滑模控制器计算车辆所需的横摆力矩,基于弯道制动时的动力学特征使用序列二次规划法分配制动力. 孙丽琴等[4 ] 通过滑模控制器计算维持车辆稳定所需的前轮转角,通过规则对制动力进行重构. Ito等[11 ] 通过广播控制,将架构从常规集中控制转变为自主分布式控制制动力和驱动力,当出现单轮或双轮失效时,车辆通过其他车轮的自主分布式行为来保持性能. ...
Electromechanical composite brake control for two in-wheel motors drive electric vehicle with single motor failure
1
2020
... 近年来,纯电动汽车的快速发展推动了汽车制动系统技术的革新. 相较于传统的液压制动系统,线控制动系统,特别是电子机械制动(electromechanical brake, EMB)系统,凭借结构紧凑、响应迅速的优势,逐渐成为研究热点[1 -2 ] . 与传统的液压制动相比,EMB通过电机直接驱动卡钳,实现了对每个车轮的独立、精确控制[3 ] ,提高了车辆的稳定性、操控性和安全性. EMB系统的全电控特性使其对故障更敏感. 相较于传统液压制动系统冗余的液压备份,EMB故障可能导致制动性能严重下降[4 -5 ] . 提升EMB系统的容错性,是保障车辆行驶安全的重要课题,也是当前研究的热点之一. 针对单轮制动失效,Park等[6 ] 提出基于Karush-Kuhn-Tucker 条件优化设计方法和拉格朗日乘子进行制动力重构的方法. Zhou等[7 ] 引入故障因子衡量制动失效程度并对制动力进行重构,使用滑模控制器控制车辆横摆力矩. Zhang等[8 ] 提出内层基于模型预测控制,外层基于模糊控制的双层控制器. Tang等[9 ] 设计基于规则的扭矩重建控制器和基于高增益反馈鲁棒控制算法的前轮转角控制器,分别控制车辆纵向和横向的加速度. 基于弯道失效工况,陈佳瑶等[10 ] 使用滑模控制器计算车辆所需的横摆力矩,基于弯道制动时的动力学特征使用序列二次规划法分配制动力. 孙丽琴等[4 ] 通过滑模控制器计算维持车辆稳定所需的前轮转角,通过规则对制动力进行重构. Ito等[11 ] 通过广播控制,将架构从常规集中控制转变为自主分布式控制制动力和驱动力,当出现单轮或双轮失效时,车辆通过其他车轮的自主分布式行为来保持性能. ...
1
... 近年来,纯电动汽车的快速发展推动了汽车制动系统技术的革新. 相较于传统的液压制动系统,线控制动系统,特别是电子机械制动(electromechanical brake, EMB)系统,凭借结构紧凑、响应迅速的优势,逐渐成为研究热点[1 -2 ] . 与传统的液压制动相比,EMB通过电机直接驱动卡钳,实现了对每个车轮的独立、精确控制[3 ] ,提高了车辆的稳定性、操控性和安全性. EMB系统的全电控特性使其对故障更敏感. 相较于传统液压制动系统冗余的液压备份,EMB故障可能导致制动性能严重下降[4 -5 ] . 提升EMB系统的容错性,是保障车辆行驶安全的重要课题,也是当前研究的热点之一. 针对单轮制动失效,Park等[6 ] 提出基于Karush-Kuhn-Tucker 条件优化设计方法和拉格朗日乘子进行制动力重构的方法. Zhou等[7 ] 引入故障因子衡量制动失效程度并对制动力进行重构,使用滑模控制器控制车辆横摆力矩. Zhang等[8 ] 提出内层基于模型预测控制,外层基于模糊控制的双层控制器. Tang等[9 ] 设计基于规则的扭矩重建控制器和基于高增益反馈鲁棒控制算法的前轮转角控制器,分别控制车辆纵向和横向的加速度. 基于弯道失效工况,陈佳瑶等[10 ] 使用滑模控制器计算车辆所需的横摆力矩,基于弯道制动时的动力学特征使用序列二次规划法分配制动力. 孙丽琴等[4 ] 通过滑模控制器计算维持车辆稳定所需的前轮转角,通过规则对制动力进行重构. Ito等[11 ] 通过广播控制,将架构从常规集中控制转变为自主分布式控制制动力和驱动力,当出现单轮或双轮失效时,车辆通过其他车轮的自主分布式行为来保持性能. ...
线控制动车辆弯道制动力优化分配控制策略
1
2020
... 近年来,纯电动汽车的快速发展推动了汽车制动系统技术的革新. 相较于传统的液压制动系统,线控制动系统,特别是电子机械制动(electromechanical brake, EMB)系统,凭借结构紧凑、响应迅速的优势,逐渐成为研究热点[1 -2 ] . 与传统的液压制动相比,EMB通过电机直接驱动卡钳,实现了对每个车轮的独立、精确控制[3 ] ,提高了车辆的稳定性、操控性和安全性. EMB系统的全电控特性使其对故障更敏感. 相较于传统液压制动系统冗余的液压备份,EMB故障可能导致制动性能严重下降[4 -5 ] . 提升EMB系统的容错性,是保障车辆行驶安全的重要课题,也是当前研究的热点之一. 针对单轮制动失效,Park等[6 ] 提出基于Karush-Kuhn-Tucker 条件优化设计方法和拉格朗日乘子进行制动力重构的方法. Zhou等[7 ] 引入故障因子衡量制动失效程度并对制动力进行重构,使用滑模控制器控制车辆横摆力矩. Zhang等[8 ] 提出内层基于模型预测控制,外层基于模糊控制的双层控制器. Tang等[9 ] 设计基于规则的扭矩重建控制器和基于高增益反馈鲁棒控制算法的前轮转角控制器,分别控制车辆纵向和横向的加速度. 基于弯道失效工况,陈佳瑶等[10 ] 使用滑模控制器计算车辆所需的横摆力矩,基于弯道制动时的动力学特征使用序列二次规划法分配制动力. 孙丽琴等[4 ] 通过滑模控制器计算维持车辆稳定所需的前轮转角,通过规则对制动力进行重构. Ito等[11 ] 通过广播控制,将架构从常规集中控制转变为自主分布式控制制动力和驱动力,当出现单轮或双轮失效时,车辆通过其他车轮的自主分布式行为来保持性能. ...
线控制动车辆弯道制动力优化分配控制策略
1
2020
... 近年来,纯电动汽车的快速发展推动了汽车制动系统技术的革新. 相较于传统的液压制动系统,线控制动系统,特别是电子机械制动(electromechanical brake, EMB)系统,凭借结构紧凑、响应迅速的优势,逐渐成为研究热点[1 -2 ] . 与传统的液压制动相比,EMB通过电机直接驱动卡钳,实现了对每个车轮的独立、精确控制[3 ] ,提高了车辆的稳定性、操控性和安全性. EMB系统的全电控特性使其对故障更敏感. 相较于传统液压制动系统冗余的液压备份,EMB故障可能导致制动性能严重下降[4 -5 ] . 提升EMB系统的容错性,是保障车辆行驶安全的重要课题,也是当前研究的热点之一. 针对单轮制动失效,Park等[6 ] 提出基于Karush-Kuhn-Tucker 条件优化设计方法和拉格朗日乘子进行制动力重构的方法. Zhou等[7 ] 引入故障因子衡量制动失效程度并对制动力进行重构,使用滑模控制器控制车辆横摆力矩. Zhang等[8 ] 提出内层基于模型预测控制,外层基于模糊控制的双层控制器. Tang等[9 ] 设计基于规则的扭矩重建控制器和基于高增益反馈鲁棒控制算法的前轮转角控制器,分别控制车辆纵向和横向的加速度. 基于弯道失效工况,陈佳瑶等[10 ] 使用滑模控制器计算车辆所需的横摆力矩,基于弯道制动时的动力学特征使用序列二次规划法分配制动力. 孙丽琴等[4 ] 通过滑模控制器计算维持车辆稳定所需的前轮转角,通过规则对制动力进行重构. Ito等[11 ] 通过广播控制,将架构从常规集中控制转变为自主分布式控制制动力和驱动力,当出现单轮或双轮失效时,车辆通过其他车轮的自主分布式行为来保持性能. ...
Autonomous distributed braking and driving force control architecture based on broadcast control for vehicles with in-wheel motors on four wheels
1
2024
... 近年来,纯电动汽车的快速发展推动了汽车制动系统技术的革新. 相较于传统的液压制动系统,线控制动系统,特别是电子机械制动(electromechanical brake, EMB)系统,凭借结构紧凑、响应迅速的优势,逐渐成为研究热点[1 -2 ] . 与传统的液压制动相比,EMB通过电机直接驱动卡钳,实现了对每个车轮的独立、精确控制[3 ] ,提高了车辆的稳定性、操控性和安全性. EMB系统的全电控特性使其对故障更敏感. 相较于传统液压制动系统冗余的液压备份,EMB故障可能导致制动性能严重下降[4 -5 ] . 提升EMB系统的容错性,是保障车辆行驶安全的重要课题,也是当前研究的热点之一. 针对单轮制动失效,Park等[6 ] 提出基于Karush-Kuhn-Tucker 条件优化设计方法和拉格朗日乘子进行制动力重构的方法. Zhou等[7 ] 引入故障因子衡量制动失效程度并对制动力进行重构,使用滑模控制器控制车辆横摆力矩. Zhang等[8 ] 提出内层基于模型预测控制,外层基于模糊控制的双层控制器. Tang等[9 ] 设计基于规则的扭矩重建控制器和基于高增益反馈鲁棒控制算法的前轮转角控制器,分别控制车辆纵向和横向的加速度. 基于弯道失效工况,陈佳瑶等[10 ] 使用滑模控制器计算车辆所需的横摆力矩,基于弯道制动时的动力学特征使用序列二次规划法分配制动力. 孙丽琴等[4 ] 通过滑模控制器计算维持车辆稳定所需的前轮转角,通过规则对制动力进行重构. Ito等[11 ] 通过广播控制,将架构从常规集中控制转变为自主分布式控制制动力和驱动力,当出现单轮或双轮失效时,车辆通过其他车轮的自主分布式行为来保持性能. ...
4
... 以上研究大多考虑直线制动下的单轮失效工况,未考虑路面状况对制动的影响. 在多轮失效的情况下,完全通过直接横摆力矩控制前轮转角难以满足系统的实时性. 由于3个及3个以上车轮发生制动失效的概率很小,且当车辆只有一个车轮正常制动时,制动力几乎完全损失,研究3个或者3个以上车轮制动失效的意义不大[12 ] . 本文提出针对EMB系统失效的弯道制动车辆稳定性控制策略,主要内容如下. ...
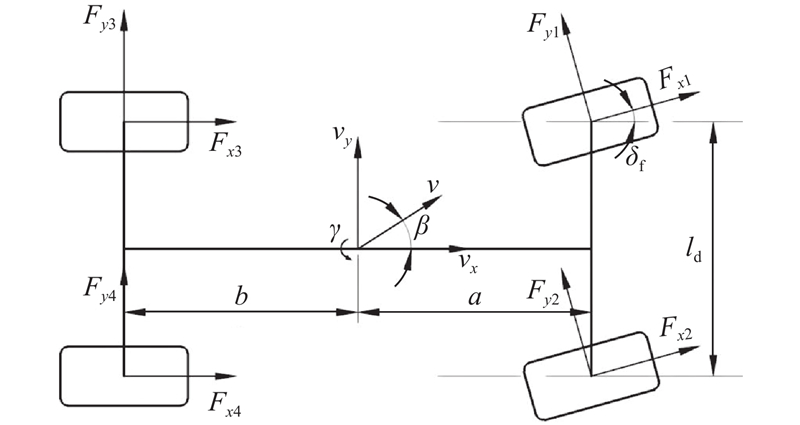
... 以左转中的左前轮制动失效为例,如图4 所示,由于失去了F x 1[12 ] ,为了维持车辆稳定,须对车辆产生的横摆力矩进行抑制. 设计相应的控制器对车轮进行控制. ...
... 使用序列二次规划(SQP)法优化求解该目标函数[25 ] ,得到重构后的剩余三轮制动力. 从图4 可知,若其他条件相同,则同侧的单轮制动失效造成的转动大致相同,且由于轴荷转移,前轴制动失效的危险性更大;异侧单轮制动失效间的区别更多集中在横摆力矩方向上[4 ,12 ] ,因此当其他车轮发生随机制动失效时,可以采用相同的方法计算横摆力矩. 仅在制动力分配环节调整k x i 图6 所示. ...
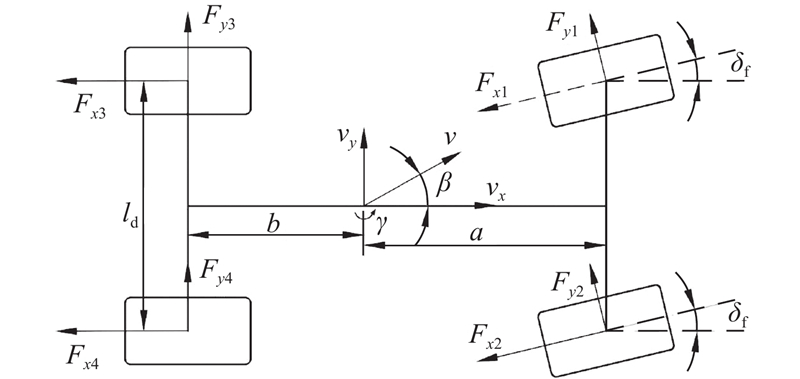
... EMB系统出现双轮制动失效共有3种情况:同轴轮失效,对角轮失效和同侧轮失效. 前两者对整车稳定性的影响小于同侧轮失效的情况. 由于本文进行了适当的简化,在相同的制动条件下,左、右两侧的制动失效,横摆力矩的方向相反[12 ] ,以左转中左侧双轮制动失效为例. 此时车辆将发生严重转向不足,且无法通过差动制动的方法抑制横摆. 设计基于模糊控制的纯跟踪算法(pure pursuit algorithm)进行路径跟踪. ...
4
... 以上研究大多考虑直线制动下的单轮失效工况,未考虑路面状况对制动的影响. 在多轮失效的情况下,完全通过直接横摆力矩控制前轮转角难以满足系统的实时性. 由于3个及3个以上车轮发生制动失效的概率很小,且当车辆只有一个车轮正常制动时,制动力几乎完全损失,研究3个或者3个以上车轮制动失效的意义不大[12 ] . 本文提出针对EMB系统失效的弯道制动车辆稳定性控制策略,主要内容如下. ...
... 以左转中的左前轮制动失效为例,如图4 所示,由于失去了F x 1[12 ] ,为了维持车辆稳定,须对车辆产生的横摆力矩进行抑制. 设计相应的控制器对车轮进行控制. ...
... 使用序列二次规划(SQP)法优化求解该目标函数[25 ] ,得到重构后的剩余三轮制动力. 从图4 可知,若其他条件相同,则同侧的单轮制动失效造成的转动大致相同,且由于轴荷转移,前轴制动失效的危险性更大;异侧单轮制动失效间的区别更多集中在横摆力矩方向上[4 ,12 ] ,因此当其他车轮发生随机制动失效时,可以采用相同的方法计算横摆力矩. 仅在制动力分配环节调整k x i 图6 所示. ...
... EMB系统出现双轮制动失效共有3种情况:同轴轮失效,对角轮失效和同侧轮失效. 前两者对整车稳定性的影响小于同侧轮失效的情况. 由于本文进行了适当的简化,在相同的制动条件下,左、右两侧的制动失效,横摆力矩的方向相反[12 ] ,以左转中左侧双轮制动失效为例. 此时车辆将发生严重转向不足,且无法通过差动制动的方法抑制横摆. 设计基于模糊控制的纯跟踪算法(pure pursuit algorithm)进行路径跟踪. ...
1
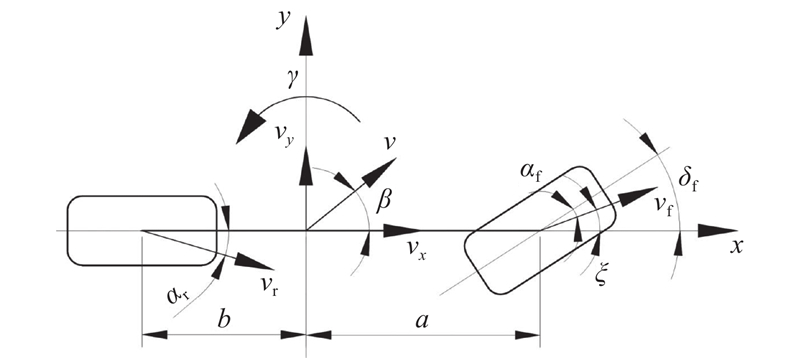
... 当车辆进行稳态转向时,车辆的操纵特性可以用线性二自由度车辆模型来近似描述[13 ] . 选取经典的线性二自由度单轨车辆模型作为参考模型,如图1 所示. ...
1
... 在上层结构的横摆力矩计算中,PID控制、滑模控制、线性二次调节器(linear quadratic regulator, LQR)和模型预测控制较常用. PID控制过于依赖经验,滑模控制的抖振会破坏系统稳定且难以抑制,模型预测控制虽然较准确但运算量过大,会对系统的时效性造成影响[14 –18 ] . 选择LQR作为计算车辆附加横摆力矩的方法. ...
Second-order sliding mode control for nonlinear uncertain systems bounded by positive functions
0
2015
SMC-fuzzy joint vector control of built-in permanent magnet synchronous motorized spindle
0
2022
Real-time experimental evaluation and analysis of PID and MPC controllers using HIL setup for robust steering system of autonomous vehicles
0
2024
1
... 在上层结构的横摆力矩计算中,PID控制、滑模控制、线性二次调节器(linear quadratic regulator, LQR)和模型预测控制较常用. PID控制过于依赖经验,滑模控制的抖振会破坏系统稳定且难以抑制,模型预测控制虽然较准确但运算量过大,会对系统的时效性造成影响[14 –18 ] . 选择LQR作为计算车辆附加横摆力矩的方法. ...
1
... 在上层结构的横摆力矩计算中,PID控制、滑模控制、线性二次调节器(linear quadratic regulator, LQR)和模型预测控制较常用. PID控制过于依赖经验,滑模控制的抖振会破坏系统稳定且难以抑制,模型预测控制虽然较准确但运算量过大,会对系统的时效性造成影响[14 –18 ] . 选择LQR作为计算车辆附加横摆力矩的方法. ...
考虑复杂扰动的轻型商用车路径跟踪混合控制方法
1
2024
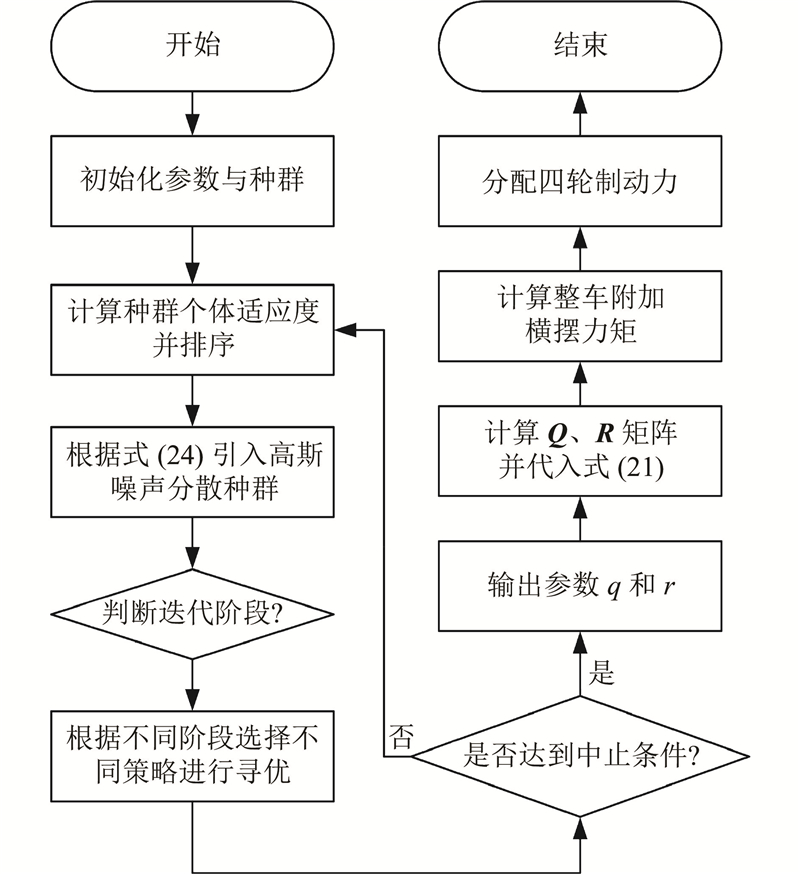
... 式中:Q R Q R $\Delta \beta $ $\Delta \gamma $ . 系统的控制量为车辆稳定横摆力矩$\Delta M$ . 在传统的LQR方法中,Q R [19 ] . 针对这一问题,制定基于改进黏菌算法的权重优化策略. ...
考虑复杂扰动的轻型商用车路径跟踪混合控制方法
1
2024
... 式中:Q R Q R $\Delta \beta $ $\Delta \gamma $ . 系统的控制量为车辆稳定横摆力矩$\Delta M$ . 在传统的LQR方法中,Q R [19 ] . 针对这一问题,制定基于改进黏菌算法的权重优化策略. ...
汽车稳定性控制中横摆力矩决策的LQR方法
1
2010
... 考虑到车辆稳定性控制的物理意义,将Q q 1 、q 2 ;R R r ]. 引入系数$ {w}_{\beta }\left(0\leqslant {w}_{\beta}\leqslant 1.0\right) $ [20 ] . ...
汽车稳定性控制中横摆力矩决策的LQR方法
1
2010
... 考虑到车辆稳定性控制的物理意义,将Q q 1 、q 2 ;R R r ]. 引入系数$ {w}_{\beta }\left(0\leqslant {w}_{\beta}\leqslant 1.0\right) $ [20 ] . ...
Optimization of low-impact development facilities in urban areas using slime mould algorithm
1
2023
... 黏菌优化算法(SMA)基于黏菌觅食的行为. 黏菌主要依靠生物振荡器产生的传播波来改变静脉内的细胞质流动,使其倾向于处于较好的食物富集位置,从而达到寻优效果. 相较于其他群体智能优化算法具有参数少、收敛速度快的特点[21 ] ,但黏菌优化算法的结果依赖于初始解且容易陷入局部最优,容易造成SMA的求解精度下降[22 -23 ] . 为了解决以上问题,提出如下改进. ...
An effective theoretical and experimental analysis method for the improved slime mould algorithm
1
2024
... 黏菌优化算法(SMA)基于黏菌觅食的行为. 黏菌主要依靠生物振荡器产生的传播波来改变静脉内的细胞质流动,使其倾向于处于较好的食物富集位置,从而达到寻优效果. 相较于其他群体智能优化算法具有参数少、收敛速度快的特点[21 ] ,但黏菌优化算法的结果依赖于初始解且容易陷入局部最优,容易造成SMA的求解精度下降[22 -23 ] . 为了解决以上问题,提出如下改进. ...
Multi-objective equilibrium optimizer slime mould algorithm and its application in solving engineering problems
1
2023
... 黏菌优化算法(SMA)基于黏菌觅食的行为. 黏菌主要依靠生物振荡器产生的传播波来改变静脉内的细胞质流动,使其倾向于处于较好的食物富集位置,从而达到寻优效果. 相较于其他群体智能优化算法具有参数少、收敛速度快的特点[21 ] ,但黏菌优化算法的结果依赖于初始解且容易陷入局部最优,容易造成SMA的求解精度下降[22 -23 ] . 为了解决以上问题,提出如下改进. ...
面向转向制动工况的制动力动态分配策略
1
2024
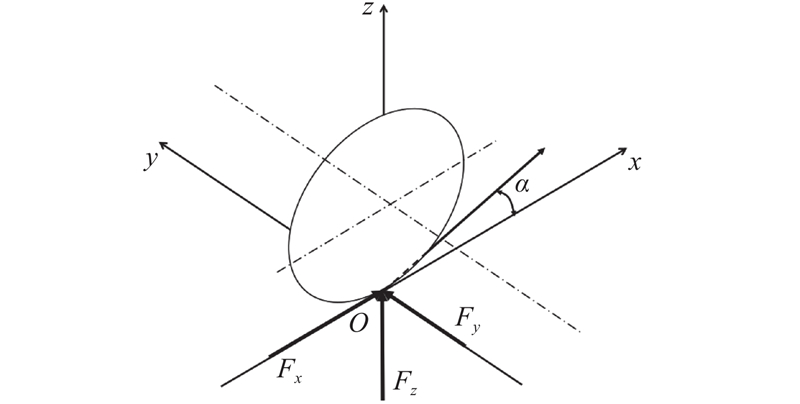
... 为了提高车辆的稳定性,使车轮产生的制动力和横摆力矩达到最大,考虑轮胎的附着椭圆[24 ] 与路面状况,建立弯道单轮制动失效时的目标函数如下: ...
面向转向制动工况的制动力动态分配策略
1
2024
... 为了提高车辆的稳定性,使车轮产生的制动力和横摆力矩达到最大,考虑轮胎的附着椭圆[24 ] 与路面状况,建立弯道单轮制动失效时的目标函数如下: ...
基于Gauss伪谱法的紧急避让汽车操纵逆动力学
1
2012
... 使用序列二次规划(SQP)法优化求解该目标函数[25 ] ,得到重构后的剩余三轮制动力. 从图4 可知,若其他条件相同,则同侧的单轮制动失效造成的转动大致相同,且由于轴荷转移,前轴制动失效的危险性更大;异侧单轮制动失效间的区别更多集中在横摆力矩方向上[4 ,12 ] ,因此当其他车轮发生随机制动失效时,可以采用相同的方法计算横摆力矩. 仅在制动力分配环节调整k x i 图6 所示. ...
基于Gauss伪谱法的紧急避让汽车操纵逆动力学
1
2012
... 使用序列二次规划(SQP)法优化求解该目标函数[25 ] ,得到重构后的剩余三轮制动力. 从图4 可知,若其他条件相同,则同侧的单轮制动失效造成的转动大致相同,且由于轴荷转移,前轴制动失效的危险性更大;异侧单轮制动失效间的区别更多集中在横摆力矩方向上[4 ,12 ] ,因此当其他车轮发生随机制动失效时,可以采用相同的方法计算横摆力矩. 仅在制动力分配环节调整k x i 图6 所示. ...
Vehicle path tracking control using pure pursuit with MPC-based look-ahead distance optimization
1
2024
... 纯跟踪算法是基于几何关系的路径跟踪控制算法. 该算法通过在参考路径上选取一个预瞄点,利用车辆当前位置与该预瞄点之间的几何关系,计算出车辆所需的转向角,从而使车辆渐进逼近并跟踪预设路径[26 -27 ] . 由于假设车辆在路面上进行稳态转向,预设路径可以通过失效前的方向盘转角获得. ...
Path tracking control for brake-steering tracked vehicles based on an improved pure pursuit algorithm
1
2024
... 纯跟踪算法是基于几何关系的路径跟踪控制算法. 该算法通过在参考路径上选取一个预瞄点,利用车辆当前位置与该预瞄点之间的几何关系,计算出车辆所需的转向角,从而使车辆渐进逼近并跟踪预设路径[26 -27 ] . 由于假设车辆在路面上进行稳态转向,预设路径可以通过失效前的方向盘转角获得. ...
Research on path tracking control based on optimal look-ahead points
1
2024
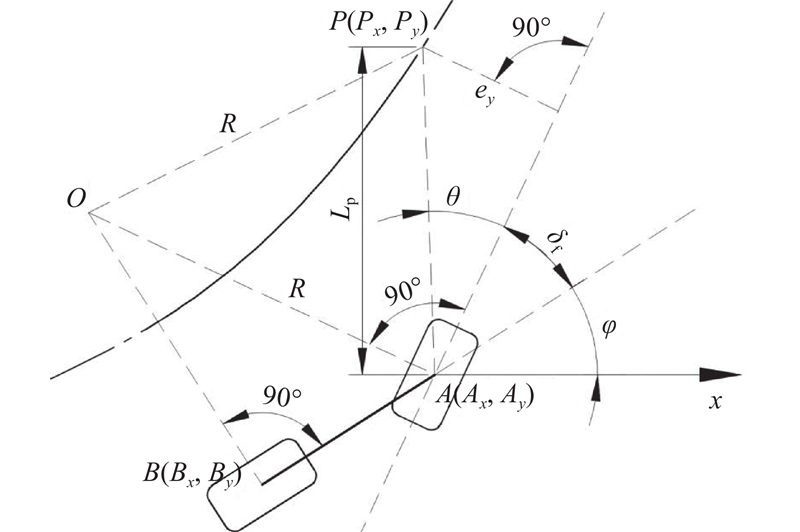
... 式中:$ \varPhi = \arctan\; [({{{P_{{y}}} - {A_{{y}}}}})/({{{P_{{x}}} - {A_{{x}}}}})] - \varphi $ Ax 、Ay 分别为前轮的x 、y 坐标,Px 、Py 分别为预瞄点的x 、y 坐标;预瞄距离$ {L_{\text{p}}} = {k_{\text{p}}} v+{L_{{\text{fc}}}} $ k p 为预瞄距离系数,L fc 为预设距离,根据文献[28 ]确定为3 m. ...
Driverless bus path tracking based on fuzzy pure pursuit control with a front axle reference
1
2019
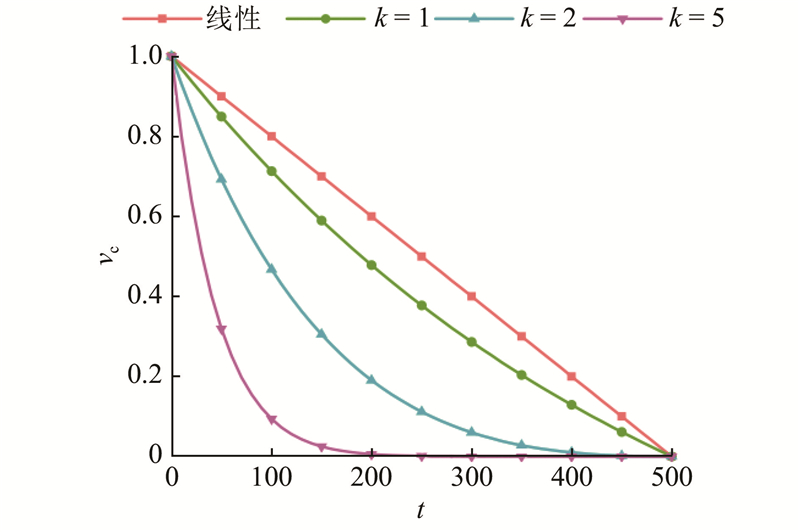
... 式(32)中的L p 仅考虑了车速的影响,忽略了横向误差ey 和航向误差e φ [29 ] . 为了便于实现,采用解析式的形式,对该模糊控制器进行描述: ...