目前,对于混合交通流特性的研究主要集中在CAV跟驰特性研究及混合交通流队列分析2个方面. 在CAV跟驰特性的研究方面,PATH实验室提出恒定车间距的协同自适应巡航控制(cooperative adaptive cruise control,CACC)模型,该模型得到了广泛应用. 秦严严等[3]基于CACC模型,提出非线性动态期望车头间距策略的跟驰模型. 宋成举[4]通过分析车头间距与速度的关系,给出期望车头间距的一般函数形式. Li等[5]考虑不同车辆对突发扰动的反应时延,分析反应时间对基本图的影响. 宋慧等[6]研究CAV与其他车辆的差异对跟驰特性的影响. 孙启鹏等[7]提出基于驾驶员行为预测的自动驾驶车辆行为决策模型. Wang 等[8]提出新的考虑多前方车辆最优速度影响的跟驰模型,但只考虑了车辆的速度. Xie等[9]考虑到多前车对主体车的影响程度主要取决于高级驾驶员辅助系统(ADAS)对驾驶员的影响. Zong等[10]考虑通过前方车辆在交通流队列中的位置来表达对主体车的影响权重,未充分考虑车辆在运行过程中由于距离变化而导致的权重变化.
上述文献在CAV的跟驰模型中多考虑紧邻前车对驾驶行为的影响,而 CAV能够通过智能网联技术收到多前车的信息反馈[15]. 本文在CACC模型的基础上,考虑CAV将行驶前方多辆CAV的速度、加速度及位置信息纳入自身的加速度优化中,构建考虑多前车信息反馈的交互协同自适应巡航控制(interactive-cooperative adaptive cruise control,I-CACC)跟驰模型. 基于该模型,分析不同渗透率及不同队列下的队列稳定性与基本图特性.
1. 车辆跟驰模型
当CAV车辆前方紧邻HV车辆时,由于HV车辆缺乏车车通信设备,CAV 将自动实现功能退化,退化为自动驾驶(automatic vehicle,AV)车辆. 该AV车辆仍然保留车车通信系统,与该CAV队列中其后的 CAV车辆实现车车通信[16].
在常态化的混合交通流条件下,假定该混合交 通流仅存在3种类型车辆:能够接收多信息反馈的CAV车辆、人工驾驶车辆HV及CAV退化后的AV车辆.
1.1. CAV跟驰模型
在美国加州大学PATH实验室提出的基于恒定车间距的CACC跟驰模型中,CAV作为跟驰车辆,其加速度主要取决于3部分:紧邻前车的加速度、主体车与前车的速度差以及实际车头间距与期望车头间距之间的误差项. 可以看出,该模型主要考虑CAV紧邻前车的运动状态,通过实时获取前车的行驶参数,结合自身的速度、加速度及位置信息,优化自身的驾驶行为[17].
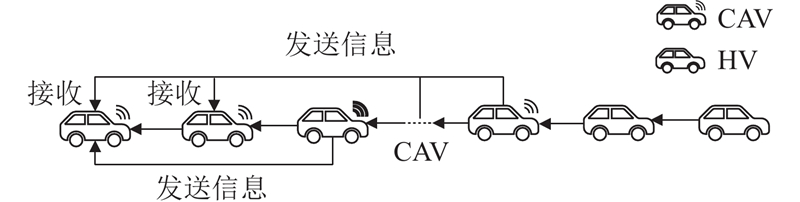
PATH实验室提出的CACC模型是目前常用的CAV跟驰模型. 随着智能网联设备的引入,CAV能够通过V2V技术实时获取多前车的运动状态. 为了更准确地描述智能网联环境下CAV车辆的驾驶行为,在该CACC模型的基础上,构建考虑多前车信息反馈的I-CACC跟驰模型,通过实时获取多前车(CAV)的速度、加速度及距离等信息,纳入自身的加速度模型中,优化自身的驾驶行为. 该模型的示意图如图1所示.
图 1
图 1 I-CACC模型信息传递过程的示意图
Fig.1 Schematic diagram of information transfer process of I-CACC model
如图1所示,CAV接收多前车信息的数量取决于其在该CAV队列中的位置.
基于CACC模型,构建考虑多前车信息反馈的CAV跟驰模型. 主体车辆n(CAV)的加速度由紧邻前车n−1以及行驶前方的CAV车队共同作用决定,使用前车与主体车的间距来判别对主体CAV的影响程度. 改进后的模型如下.
式中:
使用多前车与主体车之间的车头间距差值为判别影响程度的指标,不仅能够直接表示不同车辆之间的空间关系,而且能够反映车辆相对速度的动态变化. 当车辆速度发生变化时,间距差会随之调整,表现车辆之间的相对运动趋势.
1.2. HV跟驰模型和AV跟驰模型
利用智能驾驶员模型(intelligent drive model,IDM)[18] ,能够更准确地反映交通流从自由流到拥堵流不同状况下的驾驶员跟驰行为. 该模型具有参数少、易标定的特点. 采用IDM模型表示混合交通流中HV的驾驶行为. 该模型的结构如下:
式中:
加州大学 PATH 实验室采用实测数据标定ACC(adaptive cruise control)跟驰模型. 该模型能够很好地描述CAV车辆退化为AV车辆的驾驶行为. 该模型的公式为
式中:
2. 队列排列模型及特性计算方法
2.1. 队列排列
混合交通流中不同类型车辆的空间分布会对其各项特性产生不同的影响,特别是当CAV的渗透率增大到一定程度时. 为了更好地表述该空间的分布形式,Ghiasi等[11]使用马尔科夫链模型来表示混合交通流中不同类型车辆的空间排列. 其中转换矩阵的定义如下 :
式中:
式中:
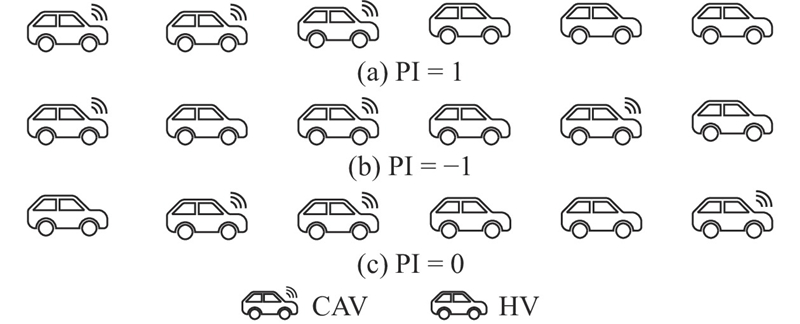
为了能够更准确地描述不同类型车辆排队队列对交通流特性的影响,引入排队强度(platoon intensity,PI)的概念[11]来描述混合交通流中CAV的聚集特性,取值为
当CAV渗透率为0.5时,不同排队强度下的混合交通流车辆排列如图2所示.
图 2
图 2 不同排队强度下队列排列的示意图
Fig.2 Schematic of queue arrangement under different queuing intensity
1)当
2)当
3)当
2.2. 混合交通流队列的稳定性模型
混合交通流队列的稳定性研究主要考虑不同类型车辆驾驶方式的不同,Ward[19]提出的在常规驾驶环境下的由“大车-小车”组成的混合交通流稳定性解析模型如下所示:
式中:
在该模型的基础上,Ngoduy[20]利用特征方程的方法,将该方法推广到智能网联环境下由自动驾驶车辆和人工驾驶车辆组成的混合交通流中,改进后的混合交通流稳定性判定模型得到了广泛应用. 本文的混合交通流中存在3种跟驰行为,由式(12)可知,混合交通流的稳定性仅与交通流组成及各单一驾驶行为所构成的交通流相关参数有关,因此得到混合交通流稳定性计量值的计算方法,如下所示:
式中:F为混合交通流稳定性的计量值,当F < 0时交通流处于不稳定状态,当F > 0时交通流处于稳定状态;
根据I-CACC模型,可以求得CAV的各项偏微分表达式如下.
式中:N为混合交通流队列中所有CAV的数量,
由于不同位置的车辆具有不同的偏导数,使用所有CAV车辆的受影响程度的平均值
同理,可以求得IDM模型与ACC跟驰模型的各项偏微分表达式如下所示.
2.3. 混合交通流基本图的计算方法
当混合交通流处于平衡状态时开展基本图分析,通过求取平衡状态下混合交通流中所有车辆的平均车头间距,可以得到交通流的密度.
对于建立的I-CACC跟驰模型、IDM模型及ACC模型,可以求得不同类型车辆的平衡态车间距,如下所示.
式中:
混合交通流中CAV、AV、HV的渗透率分别为
式中:
在流量-密度关系中,随着交通密度的增加,流量初期稳步上升,通行能力逐渐增强. 达到最佳密度
3. 队列稳定性的分析
交通流稳定性能够反映受扰动后恢复平衡状态的能力. 若扰动沿上游传播过程中逐步衰减,最终回归平衡,则交通流稳定;若扰动在传播过程中持续放大,则交通流不稳定.
3.1. 渗透率的影响
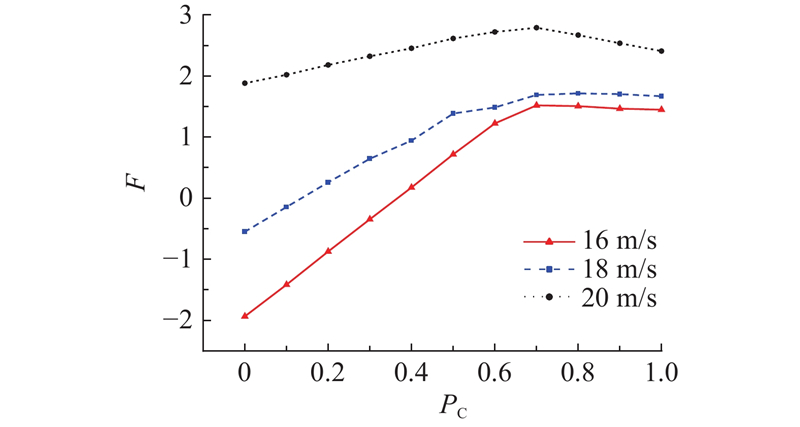
从F的计算方法可以看出,当交通流平衡态速度较小时,混合交通流处于不稳定状态;当速度较大时,混合交通流处于稳定状态. 取混合交通流的平衡态速度为16、18及20 m/s,当排队强度固定为0时,通过计算CAV渗透率为0~1.0情况下的F,得到混合交通流稳定性的变化情况,如图3所示.
图 3
图 3 不同CAV渗透率下的F变化
Fig.3 Change in F-value under different CAV permeability levels
从图3可以看出,速度越大,交通流稳定性越强. 在3种速度下计算得到的F呈现相同的变化趋势,即当CAV的渗透率为0~0.7时,混合交通流的队列稳定性逐渐增强,且增长速度逐渐减小.
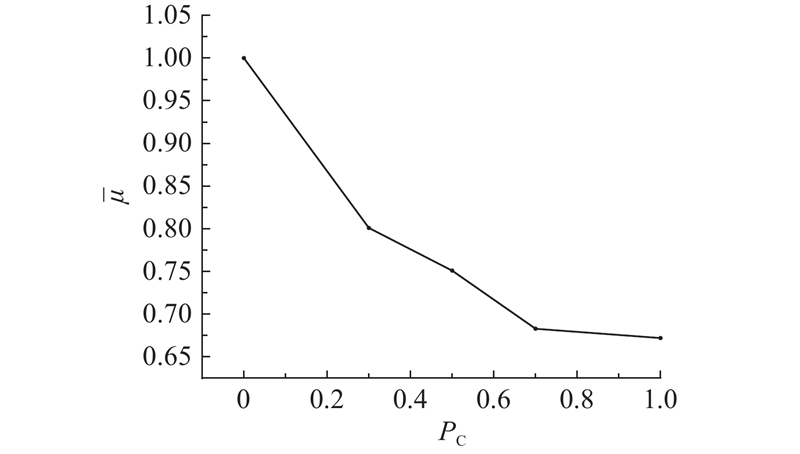
从图4可以看出,随着渗透率的增大,连接成一个队列的CAV数量越来越多,因此队列中能够接收信息反馈的CAV数量越来越多,
图 4
图 4
不同渗透率下的
Fig.4
Changes in
3.2. 排队强度的影响
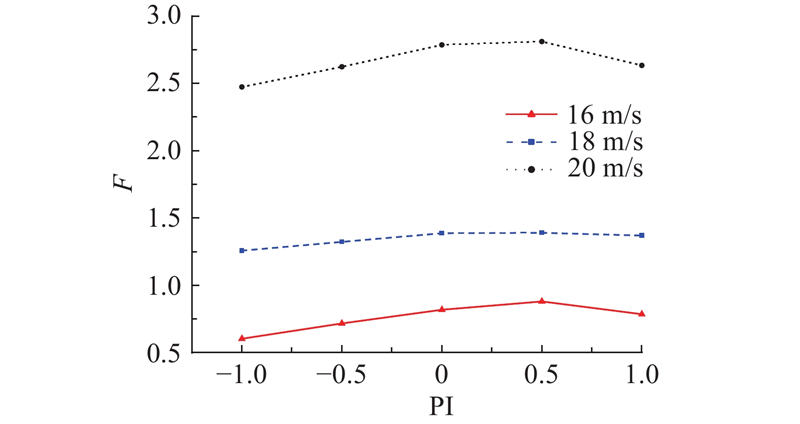
为了分析队列排列特性对混合交通流稳定性的影响,平衡态速度取16、18及20 m/s,在渗透率为0.5的情况下,分析排队强度分别为−1、−0.5、0、0.5及1这5种情况下的稳定性,如图5所示.
图 5
图 6
图 6
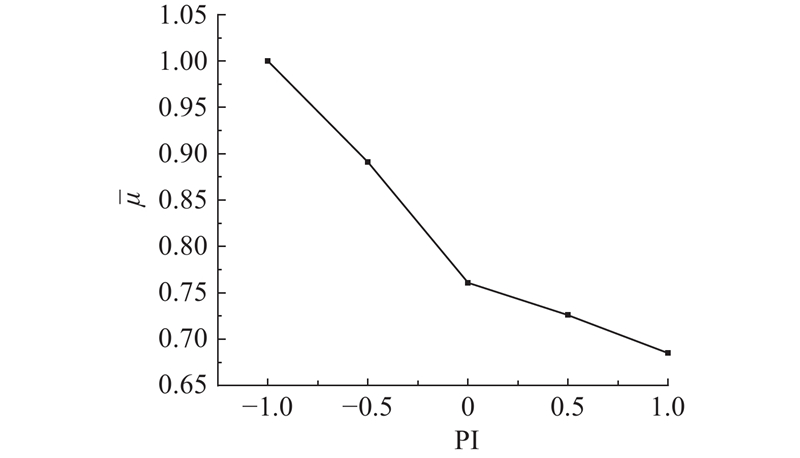
不同排队强度下的
Fig.6
Change in
随着排队强度继续增大到1,所有的CAV聚集为一个车队,尽管只有一辆CAV退化为AV,但紧邻前车的影响程度均值
3.3. 多因素的影响
从上述混合交通流稳定性分析可以看出,混合交通流的稳定性与CAV渗透率和排队强度2个因素相关. 在实际的交通运行过程中,2种因素通常都维持动态变化,有必要进一步研究两因素共同作用下混合交通流整体稳定性的变化趋势.
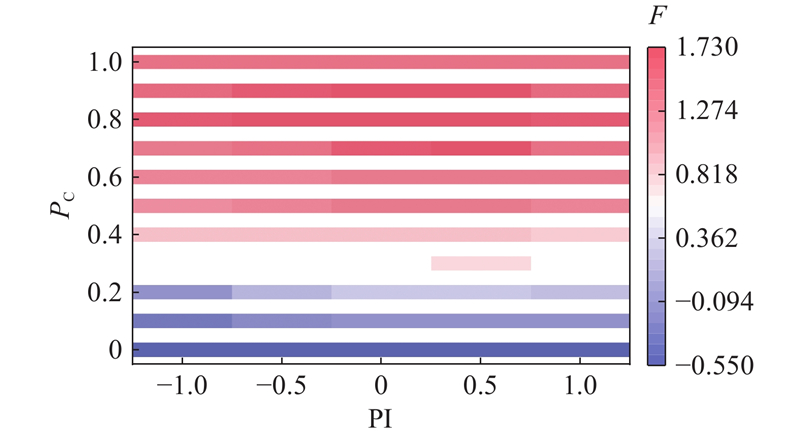
在速度设置为18 m/s的情况下,分析在渗透率和排队强度共同作用下混合交通流稳定性判别值的变化过程,如图7所示.
图 7
从图7可以得出与上述相同的结论:在渗透率与排队强度增大到一定程度后,混合交通流的稳定性出现降低的情况.
4. 基本图特性的分析
交通流基本图用于量化反映交通流处于平衡态时交通流流量、密度及速度三者之间的关系.
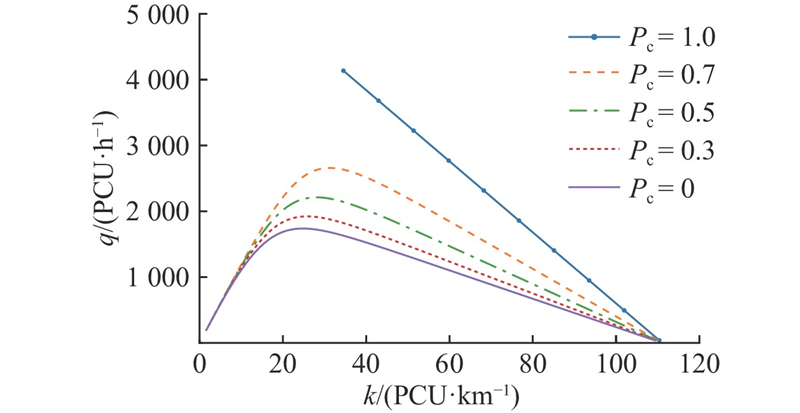
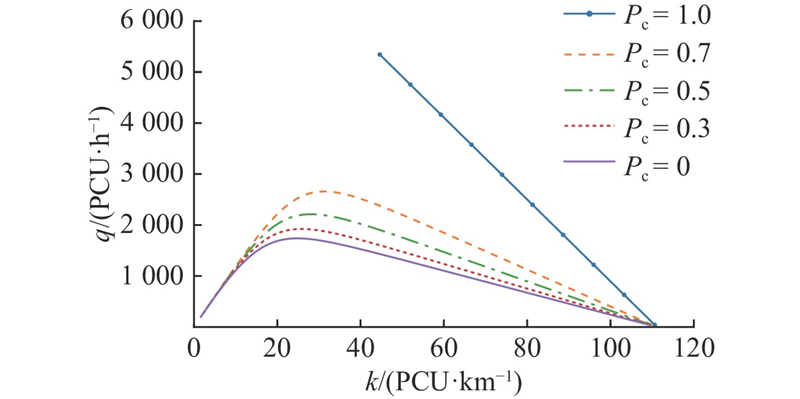
4.1. 渗透率的影响
图 8
图 9
为了更好地分析这一变化趋势的交通流运行机理,计算CAV分别采用CACC模型及I-CACC模型2种情况下,不同渗透率下的道路通行能力以及临界速度与最佳密度,如表1所示.
表 1
不同
Tab.1
| PC | (km·h−1) | |||||
| I-CACC | CACC | I-CACC | CACC | |||
| 0 | 24.79 | 24.79 | 70.128 | |||
| 0.3 | 25.83 | 25.67 | 1 923 | 1 911 | 74.448 | |
| 0.5 | 28.09 | 27.33 | 80.476 | |||
| 0.7 | 31.27 | 29.23 | 84.996 | |||
| 1.0 | 42.66 | 37.14 | 120 | |||
从表1可知,采用CACC模型的CAV车辆在渗透率为1的情况下,交通流通行能力约为纯HV交通流通行能力的2.36倍. 采用考虑多前车信息反馈的I-CACC跟驰模型的CAV车辆在渗透率为1的纯CAV交通流下,通行能力约为纯HV交通流通行能力的3.09倍. 随着CAV比例的增加,交通流的最佳密度逐渐增大,相应的交通流临界速度增大.
当CAV采用I-CACC模型时,混合交通流中CAV车辆受紧邻前车的平均影响程度
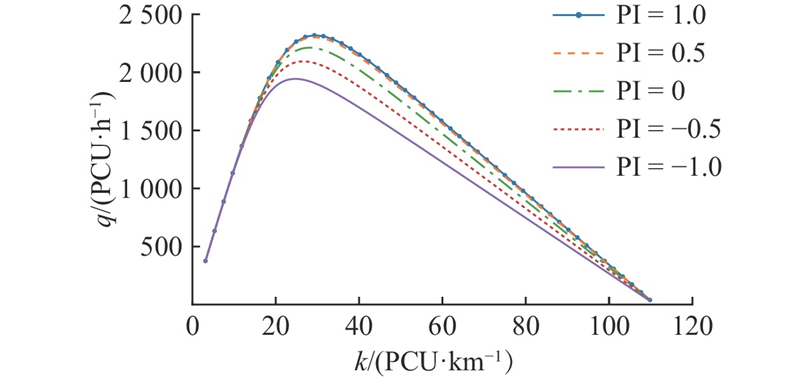
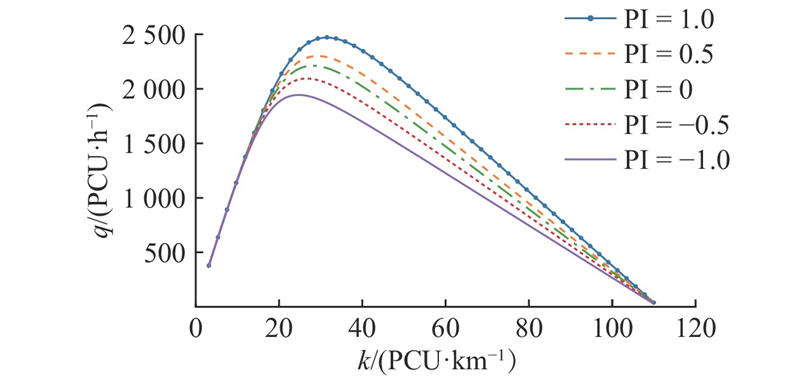
4.2. 排队强度的影响
图 10
图 11
根据表2可知,混合交通流中CAV渗透率为0.5的情况下,采用CACC模型的CAV车辆在排队强度为1时,通行能力约为排队强度为0时的1.19倍. 采用I-CACC模型的CAV交通流在同样的条件下,通行能力约为排队强度为0时的1.27倍.
表 2 不同PI下混合交通流的基本图特性
Tab.2
| PI | |||||
| I-CACC | CACC | I-CACC | CACC | ||
| −1.0 | 24.68 | 24.68 | |||
| −0.5 | 26.59 | 26.39 | |||
| 0 | 28.09 | 27.33 | |||
| 0.5 | 29.21 | 28.09 | |||
| 1.0 | 31.39 | 29.45 | |||
当CAV渗透率为 0~1.0时,在CAV应用了考虑多前车信息反馈的I-CACC跟驰模型后,随着排队强度的增大,形成队列的CAV数量增多,
5. 结 论
(1)在CAV采用多前车信息反馈的跟驰模型后,混合交通流的队列稳定性不是随着渗透率与排队强度的增大而逐渐增大的线性关系. 混合交通流的队列稳定性分别在渗透率为0.7及排队强度为0.5时达到最大值. 当渗透率及排队强度继续增大时,稳定性呈现下降趋势. 需要确定最合适的前车通讯数量,根据不同的智能网联车辆的渗透率制定相应的排队策略,优化混合交通流的队列稳定性.
(2)在CAV多前车信息反馈跟驰的策略下,CAV车辆能够以较高的交通流密度行驶,显著地提升道路通行能力. 与采用CACC模型的混合交通流相比,纯 CAV 车辆的交通流的通行能力可以达到由HV组成的交通流的2.36倍,引入多前车信息反馈后,通行能力进一步提高到了3.09倍. 随着CAV渗透率与排队强度的增大,混合交通流中紧邻前车对CAV的平均影响程度下降,CAV可以与前车保持更小的车头间距,混合交通流的最佳密度与通行能力的增长速度逐渐加快.
(3)混合交通流的队列稳定性与基本图特性受到CAV渗透率、排队强度及速度等多重因素的影响. 在实际的交通流运行过程中,车辆的队列排列、速度及渗透率等因素共同处于动态变化的状态,因此有必要进一步探究渗透率、速度与排队强度共同作用下混合交通流特性的变化趋势.
参考文献
Forecasting Americans’ long-term adoption of connected and autonomous vehicle technologies
[J].DOI:10.1016/j.tra.2016.10.013 [本文引用: 1]
基于MFD的快速路新型混合交通流特性分析
[J].
Characteristic analysis on MFD-based new mixed traffic flow on expressways
[J].
CACC 车辆跟驰建模及混合交通流分析
[J].
Vehicle following modeling and mixed traffic flow analysis with CACC
[J].
协同自适应巡航控制车辆跟驰模型优化及仿真分析
[J].
Optimization and simulation analysis of vehicle following model for collaborative adaptive cruise control
[J].
Fundamental diagram of mixed traffic flow considering time lags, platooning intensity, and the degradation of connected automated vehicles
[J].DOI:10.1016/j.physa.2023.129130 [本文引用: 1]
考虑多车响应的网联混行车流跟驰模型及稳态分析
[J].
Connected mixed traffic flow car-following model and stability analysis considering multiple vehicles response
[J].
基于风险预测的自动驾驶车辆行为决策模型
[J].
Decision-making model of autonomous vehicle behavior based on risk prediction
[J].
MVCM car-following model for connected vehicles and simulation-based traffic analysis in mixed traffic flow
[J].
Heterogeneous traffic mixing regular and connected vehicles: modeling and stabilization
[J].DOI:10.1109/TITS.2018.2857465 [本文引用: 1]
An improved intelligent driver model considering the information of multiple front and rear vehicles
[J].DOI:10.1109/ACCESS.2021.3072058 [本文引用: 1]
A mixed traffic capacity analysis and lane management model for connected automated vehicles: a Markov chain method
[J].DOI:10.1016/j.trb.2017.09.022 [本文引用: 3]
Analysis of the impact of maximum platoon size of CAVs on mixed traffic flow: an analytical and simulation method
[J].DOI:10.1016/j.trc.2022.103989 [本文引用: 1]
Analytical analysis of the effect of maximum platoon size of connected and automated vehicles
[J].DOI:10.1016/j.trc.2020.102882 [本文引用: 1]
Influence of CAVs platoon characteristics on fundamental diagram of mixed traffic flow
[J].DOI:10.1016/j.physa.2023.128906 [本文引用: 1]
智能网联车和人驾车辆混合交通流排队长度估计模型
[J].
Queue length estimation model for mixed traffic flow of intelligent connected vehicles and human-driven vehicles
[J].
Graceful degradation of cooperative adaptive cruise control
[J].DOI:10.1109/TITS.2014.2349498 [本文引用: 1]
A prediction model with wavelet neural network optimized by the chicken swarm optimization for on-ramps metering of the urban expressway
[J].DOI:10.1080/15472450.2021.1890070 [本文引用: 1]
Congested traffic states in empirical observations and microscopic simulations
[J].DOI:10.1103/PhysRevE.62.1805 [本文引用: 1]
Analytical studies on the instabilities of heterogeneous intelligent traffic flow
[J].DOI:10.1016/j.cnsns.2013.02.018 [本文引用: 1]