在供电计划的制定和实现电网电量的供需平衡方面，负荷预测发挥着越来越重要的作用^[1-2]. 短期负荷预测主要关注未来几小时、1天至几天的电力需求，对于未来电力系统的规划、运行、控制及调度具有至关重要的意义^[3].

常见的负荷预测方法包括多元线性回归^[4]、指数平滑^[5]、朴素贝叶斯^[6]和隐马尔可夫模型^[7]等. 近年来，深度学习因其出色的多元映射效应，被国内外学者广泛应用于负荷预测领域^[8]. Tang等^[9]使用双向循环神经网络（recurrent neural network，RNN)预测短期负荷，精度高，但容易遇到梯度消失和爆炸的问题. 陆继翔等^[10]通过卷积神经网络(CNN)提取非线性耦合关系，建立增强型的循环神经网络（CNN-LSTM），避免了梯度消失的问题. 黄炜等^[11]通过添加分解层和误差修正层，将采集到的特征输入到叠式双向门控循环单元(SBiGRU)中，减小预测结果中的误差，取得了较好的结果.

在短期负荷预测的实践中，负荷数据的随机性、波动性较大，预测结果不理想. 为了解决该问题，李文武等^[12]基于信号分解的组合预测模型. 在负荷预测领域，分解算法主要分为以下2类. 1）分别将分解所得的本征模态函数 (intrinsic mode function，IMF)输入预测模型，将预测模型的结果进行加和，求得最终的负荷预测值^[13]. 某些分量的波动性较高，直接进行预测的误差较大，得到的结果可信度不高. 2）利用熵值方式评估各个IMF的复杂性，对每个分量进行分类和重新构建，随后输入适当的模型并将结果整合重构，得到最终的预测值^[14]. 熵值计算常用的方法有排列熵、近似熵和样本熵. 常雨芳等^[15]结合自适应噪声的完全集合经验模态分解(complete ensemble empirical mode decompositions with adaptive noise，CEEMDAN)和排列熵来评估IMF的复杂水平，使用小波包分解进一步分割和预测复杂信号，显著增强了预测准确性. 双重分解产生了大量分量，增加了计算负担与计算时间，降低了训练效率. 陈锦鹏等^[16]结合CEEMDAN与近似熵，判断平稳与非平稳分量，将非平稳分量通过变分模态分解(variational mode decomposition，VMD)进一步分解，使用主成分分析降维后，输入不同模型进行预测，减少了计算量，但近似熵依赖于数据的长度，当数据的长度超过某个阈值时，容易导致模型的预测性能下降.

综上分析，本文提出基于重组二次分解及LSTNet-Atten的短期负荷预测方法. 基于CEEMDAN、SE以及VMD的自适应二次分解框架，将原始负荷自适应地分解-重组-分解，降低原始数据的波动性和随机性. 通过皮尔逊、斯皮尔曼、最大信息系数方法，评估输入影响因素与负荷数据之间的相关性. 采用证据优化组合理论计算相关系数，优化输入数据的特征维度. 将高相关性特征与IMF分量构成特征矩阵，输入重新设计的LSTNet预测模型中，通过重构得到最终的预测结果. 采用西班牙瓦伦西亚区域数据集进行实例验证，通过对比实验表明，利用该模型可以有效地提高负荷序列的预测精度. 通过消融模型研究，证明了各模块的必要性和有效性.

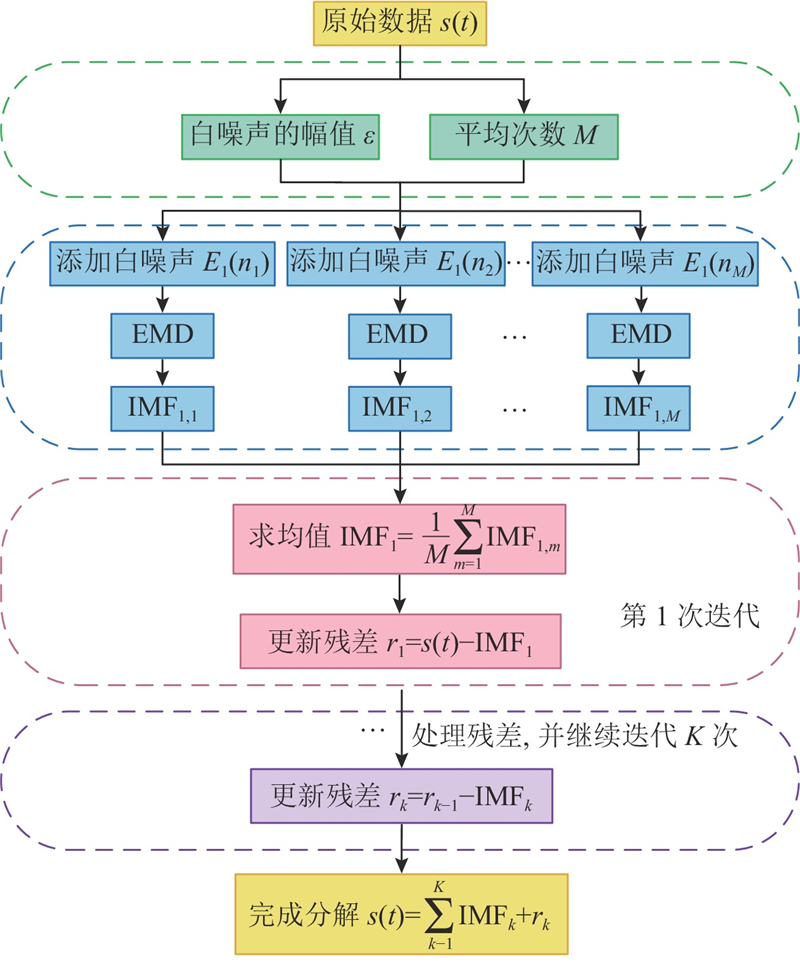
CEEMDAN可以将复杂的原始负荷数据分解成不同频率的本征模态函数(IMF)，IMF根据频率的不同表示不同尺度的特征，利用该方法可以有效地降低预测的难度. CEEMDAN分解过程如图1所示. 图中，${\mathrm{IMF}}_{k, M}$中$k$表示EMD算法的分解次数，$M$表示第$M$个固有模态函数分量.

CEEMDAN在EMD的基础上进行改进，结合EEMD算法，通过添加多组符号相反的白噪声，解决了模态混叠、重构误差大的问题.

VMD是自适应、非递归的模态分解方法，在求解过程中寻找模态分量的集合及各自的中心频率，每个模态在解调成基带之后是平滑的. 对于采样和噪声，该方法更具有鲁棒性.

VMD的分解过程可以理解为对变分问题的构造和求解的过程，相应转化为变分问题的构造和求解. 假设$X\left( t \right)$为原始序列，构建变分最优问题如下：

(1)$ \left.\begin{array}{l}\min \limits_{\left\{\boldsymbol{u}_k\right\},\left\{\boldsymbol{w}_k\right\}}\left\{\displaystyle\sum\limits_{k=1}^K\left\|\partial_t\left[ \left(\delta(t) + \frac{{\mathrm{j}}}{{\text{π}} t}\right) * \boldsymbol{u}_k(t)\right] \exp{(-{\mathrm{j}} \boldsymbol{\omega}_k t)}\right\|_2^2\right\} ; \\\text { s.t. } \displaystyle\sum\limits_{k=1}^K \boldsymbol{u}_k(t)=\boldsymbol{X}(t) .\end{array}\right\} $

式中：$ {{{\boldsymbol{u}}_k}} $和$ {{{\boldsymbol{\omega }}_k}} $为对应的分量和中心频率， $\delta \left( t \right)$为Dirac分布，∗为卷积运算符，$K$为分解得到的模态数. 在式(1)中引入二次惩罚因子$\alpha $和Lagrange乘子$\lambda $，利用交替方向乘子法（alternate direction method of multipliers，ADMM）寻优，不断更新${{\boldsymbol{u}}_k}$、${{\boldsymbol{\omega}}_k}$，获得指定分解个数的IMF分量.

D-S理论的核心思想为辨识框架和信任函数. D-S理论的目标是通过融合多种评价指标，对历史负荷数据与天气、日期等多重因素之间的相关性进行综合评估，可以显著减少不同评价体系带来的不确定性，而不是单单以某一种评价指标作为筛选特征的方法.

皮尔逊相关性指数反映了变量间的线性相关程度. 斯皮尔曼相关性指数是非参数的度量，用于评估2个变量之间的单调相关性. 最大信息系数用来探索变量之间的间接、非线性的内部深层联系. 3种评价指标都能够衡量负荷数据与影响特征的相关性，但是每一种相关性评价指标的侧重点不同，使用单一特征筛选方法可能会忽略关键信息，容易造成选取误差，所以采用D-S证据理论对不同的评价指标进行双重组合. 具体步骤如下.

1) 为了消除量纲不同带来的影响，需要将特征数据与负荷进行归一化处理，归一化公式为

(2)$ {y^*} = \frac{{y - {y_{\min }}}}{{{y_{\max }} - {y_{\min }}}}. $

式中：$y$为原始数据，${y^*}$为归一化之后的数据，${y_{\max }}$和${y_{\min }}$分别为原始数据的最大值和最小值.

2) 计算不同评价体系下每一个影响因素与负荷序列的关联程度.

3) 选择并删除每一种评价指标下关联程度最低的特征，避免无关特征对模型预测精度的影响.

4) 将3）删除后留下的特征确定为模型输入特征，计算剩余输入特征在每一种评价指标系数中所占的比重，计算公式为

(3)$ {W}_{ {{\mathrm{fea}} }}^{{i}}=\frac{{w}_j^i}{\displaystyle{\sum}_{i=1}^n {w}_j^i};\; j=1,2,3 . $

式中：$ {W}_{{\mathrm{fea}}}^i $为相同评价标准下每个特征数据的权重，$ \displaystyle\sum\nolimits_{i = 1}^n {{W}_{{\mathrm{fea}}}^i} = 1 $.

5) 根据式(3)得到的权重占比进行双重指标的优化组合，得到最终的组合信任度$\lambda $.

6) 引入累计贡献率$\gamma $的概念^[17]，将$\lambda $从大到小排序，选取$\gamma \geqslant 90\text{%} $的特征数据，实现敏感特征因子的筛选.

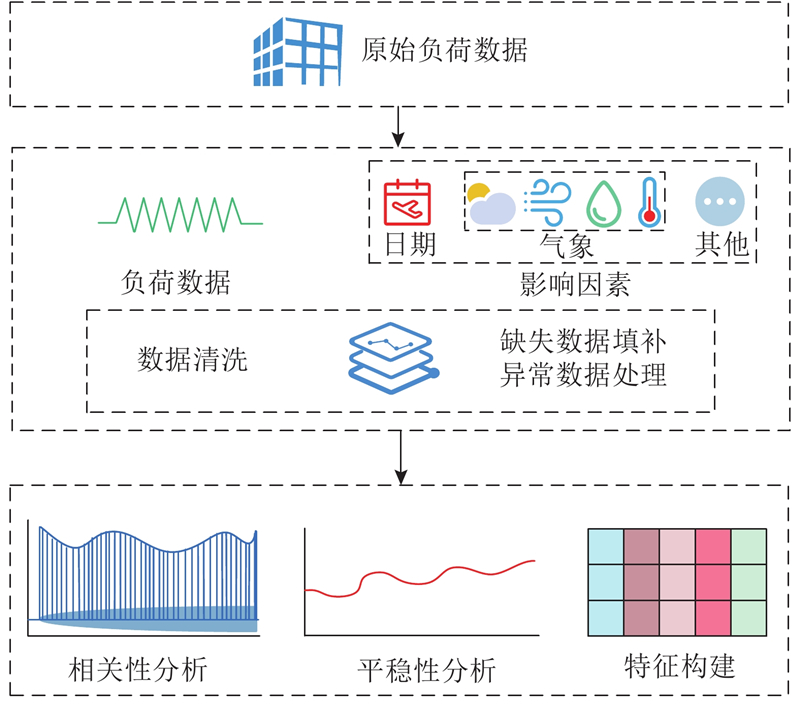
本研究方法初期旨在处理和提取负荷数据特征，具体过程见图2.

该阶段的主要任务如下.

1) 通过计算机进行数据的初步清理，为后面特征的选择奠定基础. 具体措施包括缺失值的填充、重复值的删除和异常值的替换等，以减小数据噪声，提升数据可靠性.

2) 数据的分析描述：相关性分析、平稳性分析. 使用ACF函数(autocorrelation function) 检验负荷时间序列是否具有短期和长期重复模式，对于时间序列预测的研究，这种重复特性是必须考虑的. 使用ADF检验(augmented dickey-fuller test)、DF-GLS检验(Dickey-Fuller Test with GLS Detrending)和KPSS检验(Kwiatkowski-Phillips-Schmidt-Shin test)进行平稳性检验. 在预测过程中，时间序列的波动性越低，预测结果越有效可靠.

3) 特征工程. 在数据集中，负荷时间序列及其相关影响因素构成了特征. 面对多种特征，通过多种分析方法分别计算特征与负荷时间序列的相关性，采用D-S证据优化组合理论选取特征数据，使用$3\sigma $原则检测离群点，这些离群点的存在会影响预测模型的性能. 使用线性插值法替换检测到的异常值.

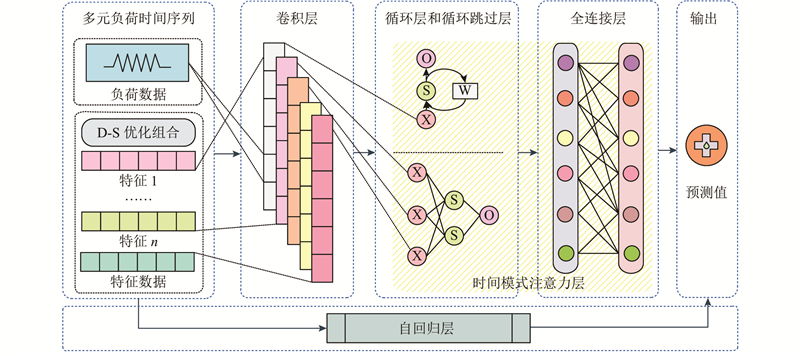
提出LSTNet-Atten预测模型，通过卷积层、循环层和循环跳过层构成的非线性部分提取数据中的短期和长期依赖关系. 利用时间模式注意力机制重点关注关键序列，剔除干扰因素. 由自回归模型提取序列线性特征，将非线性部分与线性部分的结果进行叠加得到预测结果，结构如图3所示.

该模块为不包含池化层的卷积神经网络(convolutional neural network, CNN)，作用是提取预处理后的时序数据的短期局部特性和变量间的依赖关系，传入循环和循环跳过模块. 第$k$个滤波器对矩阵$ {{\boldsymbol{X}}_t} $进行卷积操作的公式如下所示：

(4)$ {{\boldsymbol{h}}_k} = R\left( {{{\boldsymbol{W}}_{{k}}} * {{\boldsymbol{X}}_t}+{{\boldsymbol{b}}_k}} \right). $

式中：${{\boldsymbol{h}}_k}$为输出的特征向量，$R$为ReLU激活函数，${{\boldsymbol{W}}_k}$为连接到第$k$个特征图的卷积核的权重矩阵，$ {{\boldsymbol{X}}_t} $为卷积层的输入向量，${{\boldsymbol{b}}_k}$为该特征图的偏置向量.

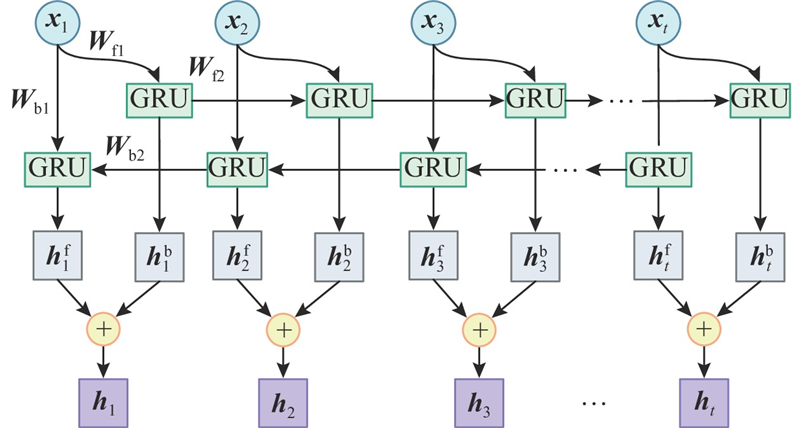
卷积模块输出的特征向量将同时输入循环模块和循环跳跃模块. BiGRU模型由2层输出相同但信息传递方向相反的GRU组成，在任何时刻都可以接收来自正向和反向2个方向的信息，克服了传统GRU单向信息传递的不足，能够充分挖掘负荷数据的时序特征，提高数据利用率和模型预测精度. 选择BiGRU组成循环模块和循环跳过模块. BiGRU模型的基本结构如图4所示.

在时刻$t$时，循环模块的隐藏状态计算如下：

(5)$ \boldsymbol{h}_t^{\mathrm{f}}=\delta\left(\boldsymbol{W}_{{\mathrm{f}} 1} \boldsymbol{x}_t+\boldsymbol{W}_{{\mathrm{f}} 2} \boldsymbol{h}_{t-1}^{\mathrm{f}}\right), $

(6)$ \boldsymbol{h}_t^{\mathrm{b}}=\delta\left(\boldsymbol{W}_{{\mathrm{b}} 1} \boldsymbol{x}_t+\boldsymbol{W}_{{\mathrm{b}} 2} \boldsymbol{h}_{t+1}^{\mathrm{b}}\right), $

(7)$ \boldsymbol{h}_t=\delta\left(\boldsymbol{W}_1 \boldsymbol{h}_t^{\mathrm{f}}+\boldsymbol{W}_2 \boldsymbol{h}_t^{\mathrm{b}}\right) . $

式中：${{{\boldsymbol{x}}}_t}$为$t$时刻的输入，$\delta $为sigmoid激活函数，${{\boldsymbol{h}}}_t^{\mathrm{f}}$与${{\boldsymbol{h}}}_t^{\mathrm{b}}$分别为$t$时刻正序GRU和负序隐藏层的输出，${{\boldsymbol{W}}_{{\mathrm{f}}1}}$与${{\boldsymbol{W}}_{{\mathrm{f}}2}}$分别为正序GRU隐藏层的权重向量和$t - 1$时刻隐藏层的权重向量，${{\boldsymbol{W}}_{{\mathrm{b}}1}}$与${{\boldsymbol{W}}_{{\mathrm{b}}2}}$分别为负序GRU模型的隐藏层权重向量和$t+1$时刻的隐藏层权重向量，${{\boldsymbol{W}}_1}$与${{\boldsymbol{W}}_2}$分别为正序GRU模型和负序GRU模型的隐藏层权重向量.

通过BiGRU的双向循环结构，可以捕捉数据间的长期时序关系. 对于超长期的依赖关系，BiGRU无法提取到有效特征. 为了解决该问题，引入循环跳过模块. 循环跳过模块的计算过程如下：

(8)$ \boldsymbol{h}_t^{\mathrm{f}}=\delta\left(\boldsymbol{W}_{{\mathrm{f}} 1} \boldsymbol{x}_t+\boldsymbol{W}_{{\mathrm{f}} 2} \boldsymbol{h}_{t-p}^{\mathrm{f}}\right), $

(9)$ \boldsymbol{h}_t^{\mathrm{b}}=\delta\left(\boldsymbol{W}_{{\mathrm{b}} 1} \boldsymbol{x}_t+\boldsymbol{W}_{{\mathrm{b}} 2} \boldsymbol{h}_{t+p}^{\mathrm{b}}\right), $

(10)$ {{{\boldsymbol{h}}}_t} = \delta \left( {{{\boldsymbol{W}}_1}{{\boldsymbol{h}}}_t^{\mathrm{f}}+{{\boldsymbol{W}}_2}{{\boldsymbol{h}}}_t^{\mathrm{b}}} \right). $

式中：$p$为隐藏层中要跳过的单元格数量，取值由负荷序列本身的周期性规律决定.

在$t$时刻循环模块的输出为${{\boldsymbol{h}}}_t^{\mathrm{R}}$，在$t - p+1$到$t$时刻循环跳过模块的输出为${{\boldsymbol{h}}}_t^{\mathrm{S}}$，经由全连接网络(Dense)将循环和循环跳过模块的输出进行组合，将最终结果作为非线性部分的预测结果.

Dense层的计算公式为

(11)$ \boldsymbol{h}_t^{\mathrm{D}}=\boldsymbol{W}^{\mathrm{R}} \boldsymbol{h}_t^{\mathrm{R}}+\sum_{i=0}^{p-1} \boldsymbol{W}_i^{\mathrm{S}} \boldsymbol{h}_{t-i}^{\mathrm{S}}+{\boldsymbol{b}} . $

式中：${\boldsymbol{h}}_t^{\mathrm{D}}$为$t$时刻非线性部分的输出.

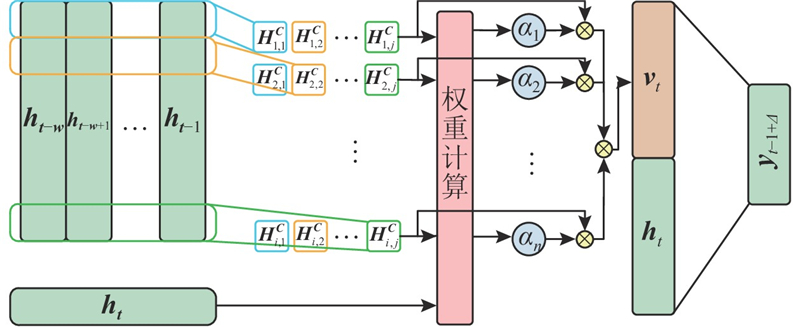
为了避免忽略时间序列中重要维度信息的特征，注意力机制被提出并被广泛应用于模型预测过程中. 经典的注意力机制是基于单个时间步骤的关联度计算，很难识别跨越多个时间步长的时间周期信息. 时间模式注意力机制(temporal pattern attention, TPA)通过一维卷积神经网络从隐层状态矩阵抽取特征，实现了时间序列与不同特征之间内在联系的提取. TPA算法的结构如图5所示.

采用BiGRU对输入序列进行处理，得到时间序列的隐藏特征${{\boldsymbol{h}}_{t - w}} - {{\boldsymbol{h}}_t}$，$w$为时间序列长度. 定义${\boldsymbol{H}} = \left\{ {{{\boldsymbol{h}}_{t - w}},{{\boldsymbol{h}}_{t - w+1}}, \cdot \cdot \cdot ,{{\boldsymbol{h}}_{t - 1}}} \right\}$为隐藏特征，${{\boldsymbol{H}}^{\boldsymbol{C}}}$为利用一维卷积提取的时间模式矩阵，${\boldsymbol{C}}$为过滤器. TPA算法的计算和映射过程如下：

(12)$ \boldsymbol{H}_{i, j}^{\boldsymbol{C}}=\sum_{l=1}^w \boldsymbol{H}_{i,(t-w+l)} * \boldsymbol{C}_{j, T-w+l}, $

(13)$ f\left( {{\boldsymbol{H}}_i^{\boldsymbol{C}},{{\boldsymbol{h}}_t}} \right) = {\left( {{\boldsymbol{H}}_i^{\boldsymbol{C}}} \right)^{\mathrm{T}}}{{\boldsymbol{W}}_a}{{\boldsymbol{h}}_t}, $

(14)$ {{{\boldsymbol{\alpha}} }_i} = \sigma \left( {f\left( {{\boldsymbol{H}}_i^{\boldsymbol{C}},{{\boldsymbol{h}}_t}} \right)} \right), $

(15)$ {{{\boldsymbol{v}}}_t} = \sum\limits_{i = 1}^m {{{\alpha }_i}{\boldsymbol{H}}_i^{\boldsymbol{C}}} , $

(16)$ {{{\boldsymbol{y}}}_{t - 1+\varDelta }} = {{\boldsymbol{W}}_{{h^{'}}}}\left( {{{\boldsymbol{W}}_h}{{\boldsymbol{W}}_t}+{{\boldsymbol{W}}_v}{{\boldsymbol{v}}_t}} \right). $

式中：$ {\boldsymbol{H}}_{i,j}^{\boldsymbol{C}} $为第$i$行向量通过${{\boldsymbol{C}}_j}$中第$j$个长度为T的过滤器提取的特征值；$T$为过滤器提取的权重最大长度；$f$为评估函数；${{{\boldsymbol{\alpha}} }_i}$为注意力权重；$\sigma $为Sigmoid函数；${{{\boldsymbol{v}}}_t}$为注意力向量；${{\boldsymbol{y}}_{t - 1+ \varDelta}}$为最终的预测值，其中$\varDelta $为预测时间步长；${{\boldsymbol{W}}_\alpha }$、${{\boldsymbol{W}}_{{h^{'}}}}$、${{\boldsymbol{W}}_h}$和${{\boldsymbol{W}}_v}$为对应变量的不同权重矩阵.

由于卷积模块和循环模块的非线性特性，会影响预测模型对以非周期方式不断变化的输入数据的预测准确性，采用自回归(autoregressive，AR)模型作为负荷序列中线性数据的预测模型. 预测结果为

(17)$ {{\boldsymbol{h}}}_t^{\mathrm{L}} = \sum\limits_{k = 0}^{{q^{{\mathrm{ar}}}} - 1} {{\boldsymbol{W}}_k^{{\mathrm{ar}}}{{\boldsymbol{y}}_{t - k}}+{{\boldsymbol{b}}^{{\mathrm{ar}}}}} . $

式中：${\boldsymbol{W}}_k^{{\mathrm{ar}}}$和${{\boldsymbol{b}}^{{\mathrm{ar}}}}$为模型的系数，${q^{{\mathrm{ar}}}}$为输入矩阵的大小，${{\boldsymbol{h}}}_t^{\mathrm{L}}$为线性部分的预测结果.

最终的预测结果由线性部分输出结果${{\boldsymbol{h}}}_t^{\mathrm{L}}$和非线性部分输出结果${{\boldsymbol{h}}}_t^{\mathrm{D}}$加权构成：

(18)$ {{\hat {\boldsymbol{Y}}}_t} = {{\boldsymbol{h}}}_t^{\mathrm{D}}+{{\boldsymbol{h}}}_t^{\mathrm{L}}. $

式中：${{\hat {\boldsymbol{Y}}}_t}$为在$t$时刻的最终预测结果.

由于受到天气、季节、用户行为及社会事件等多重因素的影响，负荷时间序列常常伴随着显著非线性和波动性，模型预测精度会受到影响. 为了克服这一难题，采用信号分解的方式降低序列中的波动性与复杂度，采集序列的变化规律，可以有效提升模型的预测性能.

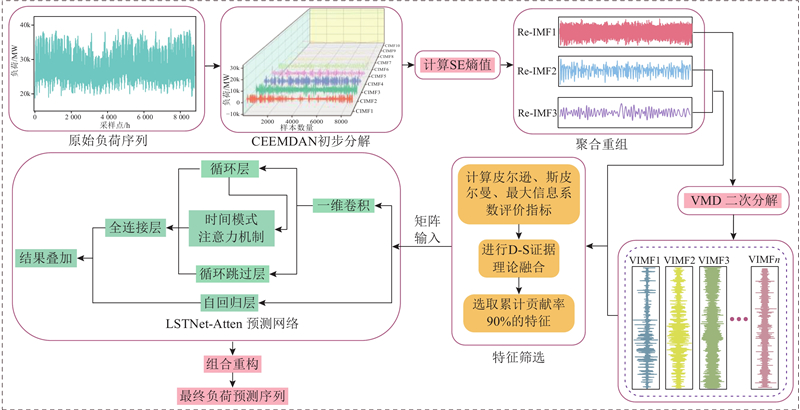
采用CEEMADN方法对经过预处理的负荷序列进行初步分解，以简化负荷时序数据的复杂性. 为了减少后续模型训练时的计算量，使用样本熵方法评估分解后得到的各CIMF复杂程度，对具有相似复杂程度的分量组合重构. 为了进一步降低高频分量中的残留噪声，提高分解效果，采用VMD方法对重构后的高频分量Re-IMF1进行二次分解，得到最终的IMF集合. 使用D-S优化组合算法选取对模态分量贡献度高的特征，采用LSTNet-Atten模型预测分解后得到的各个分量，将IMF预测结果叠加，得到最终的预测结果. 预测的整体框架如图6所示.

采用Jupyter 集成开发环境，使用Pytorch和TensorFlow深度学习框架. 计算机系统为Win11，CPU为Intel Core i9-11900，16 GB 内存；GPU为 NVIDIA Geforce RTX 3060.

对LSTNet-Atten预测模型的超参数采取遍历搜索最佳参数组合，使得模型的性能达到最佳. 最终的模型预测参数如表1所示.

为了全面、客观地展示不同模型的预测结果，采用以下评价指标：平均绝对误差(mean absolute error, MAE)、平均绝对百分比误差(mean absolute percentage error, MAPE)、均方根误差(root mean square error, RMSE)及拟合系数R². 计算公式如下.

(19)$ {\mathrm{MAE}}=(1 / n) {\sum}_{i=1}^n\left|\hat{\boldsymbol{y}}_i-\boldsymbol{y}_i\right|, $

(20)$ {\mathrm{MAPE}} = \left[(1{\boldsymbol{/}}n)\sum\nolimits_{i = 1}^n {|({{{\hat {\boldsymbol{y}}}}_i} - {{{\boldsymbol{y}}}_i})/{{{\boldsymbol{y}}}_i}|} \right] \times 100{\text{%}} , $

(21)$ {\mathrm{RMSE}}=\sqrt{(1 / n) {\sum}_{i=1}^n\left(\hat{{\boldsymbol{y}}}_i-{\boldsymbol{y}}_i\right)^2}, $

(22)$ {R^2} = 1 - \left[\sum\nolimits_{i = 1}^n {{{({{{\hat {\boldsymbol{y}}}}_i} - {{{\boldsymbol{y}}}_i})}^2}} /\sum\nolimits_{i = 1}^n {{{({\bar {\boldsymbol{y}}} - {{{\boldsymbol{y}}}_i})}^2}} \right]. $

式中：$ {{\hat {\boldsymbol{y}}}_i} $、$ {{{\boldsymbol{y}}}_i} $和${\bar {\boldsymbol{y}}}$分别为时刻$i$的预测值、实际值和实际值的平均值，$n$为样本的总体数量. 其中，MAE可以衡量预测值与真实值的平均偏差，MAPE能够反映预测值和实际值之间的误差程度，RMSE可以表示预测值与实际值之间的离散程度. MAE、MAPE和RMSE越小，表示模型的预测准确度越高. R²表示预测值对实际值拟合的接近程度，R²越接近1，说明模型的拟合程度越好.

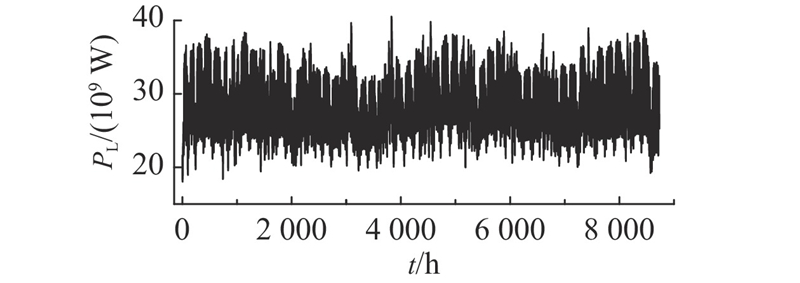
本文的实验数据来自于西班牙瓦伦西亚区域的负荷及气象数据，其中电力负荷数据来自于公共服务运营商（public service operators，PSO）的监督控制和数据采集系统（SCADA）中收集的公共用电数据. 天气数据来自于Kaggle开源数据，在瓦伦西亚开放气象API中获取. 实验数据的时间跨度为2016年1月1日到2016年12月31日，以8︰1︰1的比例划分为训练集、验证集和测试集. 时间分辨率为1 h. 预测方式为单步预测.

为了评估研究对象的长短期重复模式并确定输入数据合适的步长，在负荷中随机选择一部分数据绘制自相关图和负荷数据图，如图7、8所示. 图中，N_a为负荷自相关系数，P_L为负荷.

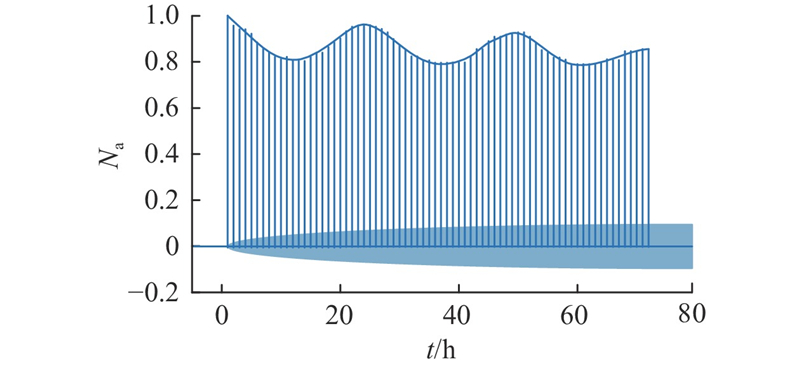
从图7可知，某一时刻的负荷不仅与相近时间步的负荷有关，而且与前一天甚至几天同一时刻的负荷有关，这表明研究对象具有长短期重复模式.

从图8可知，负荷序列存在以星期为周期的超长期重复模式，因此将输入和输出的序列长度分别设定为 168 和 1，输入为预测时刻前一周的负荷数据. 将前一周的数据用于学习超长期特征，前一天的数据用于学习长期特征.

为了检验负荷时间序列的平稳性，采用如下评估方法：ADF、DF-GLS和KPSS单位根检验. 具体结果见表2. 表中，1%、5%、10%为单位根检验的临界值. 从表2可以看出，ADF和DF-GLS单位根检验的P-value都小于0.05，且Test statistic小于1%的临界值，拒绝原假设，故负荷时间序列是平稳的. KPSS单位根检验的结果Test statistic值11.863 1大于1%的临界值0.739 0，证明了负荷时间序列的平稳性.

采集到的原始数据中共有8个特征因素，考虑到时间戳中隐藏的日期和时段因素的不同对电力负荷的需求有所不同，将这些隐藏的时间因素加入特征因素中，以便进行更准确地预测. 具体情况如表3所示.

由于原始负荷序列分解后的IMF分量中含有不同的信息量，各分量与影响因素之间的相关性会改变，使用D-S证据理论方法对分量与影响因素进行特征筛选，以提高信息可靠性. 选取结果如图9所示. 图中，Re-IMF2和Re-IMF3表示原始序列通过CEEMDAN+SE方法重组后的模态分量，VIMF1~VIMF6表示Re-IMF1通过VMD方法再次分解后的各个IMF分量.

从图9可以看出，在影响模态分量的特征数据中，电价和温度、湿度等气候特征占有较大的权重，日期特征（小时和节假日）起到了一定的作用.

为了保证输入数据不会对模型造成额外的干扰，需要对数据中缺失、重复和异常值进行预处理，采用$3\sigma $原则对筛选后的特征进行异常值分析，使用线性插值法对异常值进行处理. 此外，为了避免模型对于量纲大、数量级大的数据的依赖性，对输入数据进行Min-Max归一化^[18]处理. 如图10所示为预处理后的负荷数据. 可以看出，数据中含有大量的高频非平稳信息，如果不进行信号分解处理，那么会增加模型特征提取的难度.

为了验证D-S优化组合算法和异常值处理对特征筛选处理的有效性，采用LSTNet-Atten预测模型，将其与D-S优化组合算法、皮尔逊相关系数、斯皮尔曼相关系数、最大信息系数和未处理的特征集进行对比. 此时，不同特征筛选方法的输入特征个数不同，继续使用拟合系数R²会降低预测结果的可信性，因此采用根据特征个数调整后的拟合系数${{{\hat R}}^{\text{2}}}$，如下所示：

(23)$ {\hat R^2} = 1 - \frac{{n - 1}}{{n - b - 1}}(1 - {R^2}). $

式中：$b$为模型中解释变量的数量. 具体的对比结果见表4. 结果表明，本文所提特征筛选方法和异常值处理方法的预测误差最小. 利用D-S优化组合算法，可以挑选出与负荷序列相关性最高的特征数据. 利用异常值处理方法，可以尽量减少异常值对预测结果的干扰.

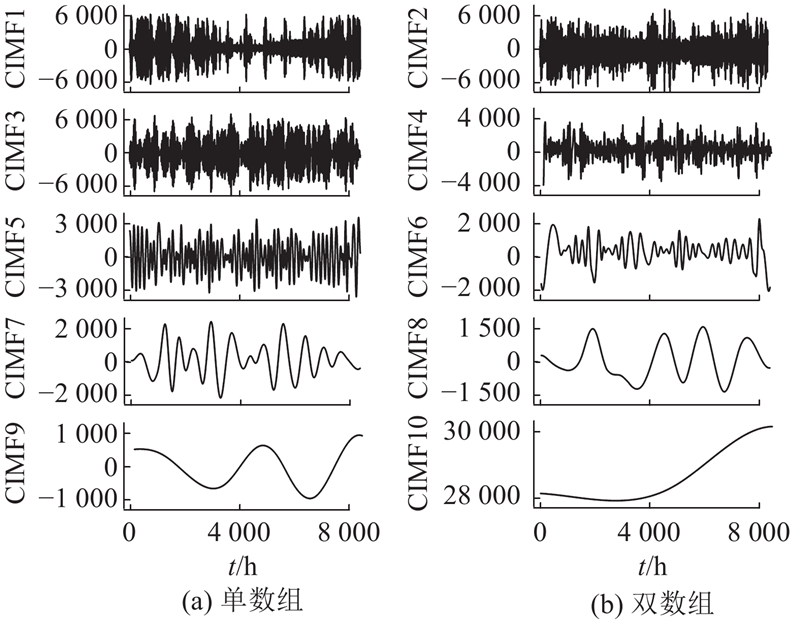
如图11所示为10组本征模态函数（IMF）的分解结果. 可以看出，时间序列数据的频率随分解过程由高到低变化，使得整体的负荷变化趋势更加清晰.

为了降低预测模型的复杂度，提高模型训练的效率. 使用样本熵对初次分解得到的模态分量进行复杂度评估，样本熵与序列的复杂程度成正比关系，样本熵越大，序列越复杂；反之亦然^[19]. 分量评估结果如表5所示. 其中计算得到的阈值是0.878 6，阈值计算式为

(24)$ \begin{split} \hat {{S}} =&0.5\max \left\{ {{{{\bar {{S}}}}_i}|i = 1,2, \cdots ,N} \right\} - \\&0.5\min \left\{ {{{{\bar {{S}}}}_i}|i = 1,2, \cdots,N} \right\}. \end{split}$

式中：$ \left\{ {{{\bar{{S}}}_i}|i = 1,2, \cdots , N} \right\} $为第$i$个IMF分量的样本熵值，$N$为分解序列数量. 将阈值$\hat {{S}}$作为高频、低频和趋势分量划分的依据. 样本熵值高于阈值的分量具有较高的复杂度，当熵小于0.1时，分量蕴含的信息量较少，故将IMF₁~IMF₃序列合并，定义为高频序列Re-IMF1；将IMF₄、IMF₅序列合并，定义为低频序列Re-IMF2；将IMF₆~IMF₁₀序列合并，定义为趋势序列Re-IMF3.

经过样本熵重构所得的负荷强非平稳分量Re-IMF1包含较多的残留噪声，会使预测误差增大. 由于EMD、EEMD、CEEMD和CEEMDAN等经验模态分解都是基于EMD的改进，用它们继续分解高频序列Re-IMF1不能得到很好的结果. VMD可以通过迭代搜索变分模型的最优解来确定每个IMF的频率中心和带宽，从而自适应地实现信号和IMF的频域分割. 对重组分量Re-IMF1使用VMD方法进一步分解，以提高预测精度.

使用VMD分解方法，须提前设定分解模态数K_m，K_m过大或过小都会影响预测精度^[20]. 从表6可以看出，当 K_m =7时，模态5和模态6的中心频率$\omega $相近，根据中心频率法可以确定VMD分解个数为6.

为了验证基于重组二次分解及LSTNet-Atten预测模型的性能优势，将本文所提的预测模型与传统的单一预测模型和混合预测模型进行对比研究. 传统的单一预测模型为LSTM、GRU、CNN、TCN、BPNN、XGboost及SVM模型. 混合预测算法为LSTGru-Atten、LSTNet-Attention 、CNN-LSTM、CNN-GRU、TCN-LSTM、TCN-GRU和LSTM-MLR模型^[21-22]，其中LSTGru-Atten模型是指循环和循环跳过模块使用GRU神经网络单元，LSTNet-Attention模型是指注意力机制模块使用传统的注意力机制.

每个对比模型使用相同的训练集、验证集和测试集作为提出模型的输入. 此外，对输入数据进行相同的预处理和特征筛选方法，以确保模型的一致性和可比性. 为了避免参数造成的性能影响，所提模型的相同部分均具有相同的参数设置，如CNN-LSTM模型、LSTM-MLR模型和LSTM模型中LSTM算法采用同一最优参数，其余的单独模型均采用最优参数. 单一模型、混合模型与本文模型的预测结果对比分别见表7、8.

从表7、8可以看出，提出的模型在所有预测模型中具有最佳性能，比LSTM、GRU、SVM、TCN-GRU和LSTM-MLR等更准确，即该方法的预测结果更接近实际值.

对比表7、8可知，通过采用多种预测方法的组合，混合预测模型能够更准确地预测负荷情况，预测效果优于传统的单一预测模型，证明了混合预测方法在短期负荷预测中的潜力和应用价值.

本文模型和LSTGru-Atten模型相比，MAE提升了12.54%，MAPE提升了12.65%，RMSE提升了11.60%，这是得益于双向GRU利用了电力负荷的时间相关性.

对比本文模型和LSTNet-Attention模型可知，与传统注意力机制相结合的LSTNet模型性能比本文模型差. 其中，MAPE指标提升了约15.31%；从R²指标来看，本文的预测结果能够达到99.41%的拟合效果，这表明TPA机制使得模型能够更好地捕捉时间序列数据的动态特性和长期依赖关系，提升了模型在时间序列任务中的性能.

为了进一步验证本文方法的预测效果及泛化能力，在不同季节的数据上进行预测对比实验. 模型预测效果的对比如表9所示. 表中，t_p为预测步长. 对比4个季节的预测结果可知，各种方法在春季的各项评价指标上表现最好，在秋季的预测效果较差，这可能与瓦伦西亚春季气候较平稳而秋季气候波动性较大有关. 与其他4种方法相比，本文方法在4个季节均有最优的预测效果，且随着步长的增加，本文模型的MAPE变化范围不大，这体现了该模型在预测尺度变化方面具有一定的鲁棒性，能够合理地预测短期变化趋势.

为了验证本文所提模态分解方法的优势，以不进行分解、EMD分解、EEMD分解、CEEMDAN分解、CEEMDAN+SE分解与本文所提出的分解方式作为对比负荷分解方法. 不同模态分解方法与提出模型的预测结果对比如表10所示.

利用EMD方法分解，会导致不同模态之间的混叠现象，负荷变化特征的提取效果受到限制. 利用EEMD方法分解，存在重构误差大的问题，影响了预测的精度. 从表10可以看出，EMD方法在负荷预测中的评价指标均比不进行负荷分解和使用EEMD方法差.

在EMD方法的基础上，结合EEMD方法，通过引入自适应噪声控制和多次迭代的方式，避免了EMD方法中的模态混叠和EEMD方法中的重构误差大的问题. 与不进行分解相比，CEEMDAN方法对应的预测性能更好. CEEMDAN和SE相结合，使得模型性能有所提升，说明SE方法促进了信号特征的提取，降低了数据波动性. 以评价指标MAPE和RMSE为例，与不进行模态分解、EMD分解、EEMD分解、CEEMDAN分解和CEEMDAN+SE分解相比，本文方法的MAPE分别降低了22.38%、32.63%、21.25%、18.69%、16.12%，RMSE分别降低了24.62%、41.32%、22.40%、21.62%、19.24%，表明基于CEEMDAN+SE+VMD分解算法的LSTNet-Atten预测模型性能最优，验证了所提负荷分解方法的有效性.

为了验证所提出LSTNet-Atten预测模型中各个模块对模型结构的影响，采用经过相同预处理的输入数据进行精细化的消融研究，即通过逐步移除预测模型的各个模块，评估它们对预测性能的具体贡献. 消融实验的设置分别如下：原模型（Origin）、去掉卷积模块（De-CNN）、去掉循环跳过模块（De-Skip）、去掉注意力模块（De-Attn）、去掉自回归模块（De-AR）. 此外，保持模型相同部分的参数不变，以消除参数引起的性能影响.

各模型的预测结果如表11所示，可得如下结论.

1）预测效果最好的模型是包含全部模块的LSTNet-Atten模型，该模型的各项指标都优于其他模型.

2）分别消除卷积模块、循环跳过模块及注意力机制模块后，模型误差都有所增大.

3）消除AR模块后，预测模型的预测精度明显下降，这说明在捕捉数据线性特征方面，AR模型起着重要的作用，有效降低了预测的误差.

经过消融实验证明，LSTNet-Atten预测模型中的每个模块都展现出了独特的优势，这使得该模型展现了优越的性能.

（1）本文针对短期负荷预测中负荷数据复杂度高、具有周期性和波动性的问题，使用CEEMDAN+SE方法进行数据重组，削减分量噪声并显著增强负荷序列的可分析性. 对重组产生的高频强非平稳IMF分量进行VMD分解，可以获得更加稳定的子序列，从而提高预测的准确性.

（2）通过将LSTNet-Atten预测模型分为线性和非线性两部分，考虑了负荷数据所具有的长期和超长期重复模式，与传统的短期负荷预测模型相比，本文方法具有更强的鲁棒性和更高的预测精度.

（3）通过采用D-S证据理论对不同评价指标的特征选取差异进行优化组合，与不进行或使用单一特征筛选方法相比，预测的结果更好. 通过消融实验，证明了本文模型中各模块的必要性与有效性，提升了负荷预测的精度.

（4）在未来的负荷预测研究中，可以在本文的基础上考虑母线节点、微电网、单一用户、用户集群等不同场景对模型的不同要求，提升模型预测的泛化能力，增强负荷预测的现实作用.