[1]
JABOVEDOFF M, OPPIKOFER T, ABELLÁN A, et al Use of LIDAR in landslide investigations: a review
[J]. Natural Hazards , 2012 , 61 (1 ): 5 - 28
DOI:10.1007/s11069-010-9634-2
[本文引用: 2]
[2]
RUSU R B, MARTON Z C, BLODOW N, et al Towards 3D point cloud based object maps for household environments
[J]. Robotics and Autonomous Systems , 2008 , 56 (11 ): 927 - 941
DOI:10.1016/j.robot.2008.08.005
[本文引用: 1]
[3]
QI C R, LIU W, WU C, et al. Frustum pointnets for 3d object detection from rgb-d data [C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition . Salt Lake City: IEEE, 2018: 918-927.
[本文引用: 1]
[4]
FAN H, SU H, GUIBAS L J. A point set generation network for 3d object reconstruction from a single image [C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition . Honolulu: IEEE, 2017: 605-613.
[本文引用: 3]
[5]
SU H, MAJI S, KALOGERAKIS E, et al. Multi-view convolutional neural networks for 3d shape recognition [C]// Proceedings of the IEEE International Conference on Computer Vision . Santiago: IEEE, 2015: 945-953.
[本文引用: 3]
[6]
LI Y, PIRK S, SU H, et al Fpnn: field probing neural networks for 3d data
[J]. Advances in Neural Information Processing Systems , 2016 , 29 : 307 - 315
[本文引用: 1]
[7]
QI C R, SU H, MO K, et al. Pointnet: deep learning on point sets for 3d classification and segmentation [C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition . Honolulu: IEEE, 2017: 652-660.
[本文引用: 9]
[8]
QI C R, YI L, SU H, et al. PointNet++: deep hierarchical feature learning on point sets in a metric space [C] // Proceedings of the 30th International Conference on Neural Information Processing Systems. Cambridge: MIT Press, 2017: 5099-5108.
[本文引用: 7]
[9]
LIU Y C, FAN B, XIANG S M, et al. Relation-shape convolutional neural network for point cloud analysis [C] // Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019: 8895–8904.
[本文引用: 1]
[10]
HU Q Y, YANG B, XIE L H, et al. Randla-net: efficient semantic segmentation of large-scale point clouds [C] // Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition . Seattle: IEEE, 2020: 11108–11117.
[11]
YAN X, ZHENG C, LI Z, et al. Pointasnl: robust point clouds processing using nonlocal neural networks with adaptive sampling [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Seattle: IEEE, 2020: 5589-5598.
[本文引用: 3]
[12]
ZHAO H, JIANG L, FU C W, et al. Pointweb: enhancing local neighborhood features for point cloud processing [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Long Beach: IEEE, 2019: 5565-5573.
[本文引用: 2]
[13]
WANG Y, SUN Y, LIU Z, et al Dynamic graph CNN for learning on point clouds
[J]. ACM Transactions on Graphics , 2019 , 38 (5 ): 1 - 12
[本文引用: 12]
[14]
SIMONOVSKY M, KOMODAKIS N. Dynamic edge-conditioned filters in convolutional neural networks on graphs [C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition . Honolulu: IEEE, 2017: 3693-3702.
[15]
LIU Z, ZHOU S, SUO C, et al. Lpd-net: 3d point cloud learning for large-scale place recognition and environment analysis [C]// Proceedings of the IEEE/CVF International Conference on Computer Vision . Seoul: IEEE, 2019: 2831-2840.
[本文引用: 3]
[16]
LAI X, LIU J, JIANG L, et al. Stratified transformer for 3d point cloud segmentation [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . New Orleans: IEEE, 2022: 8500-8509.
[本文引用: 5]
[17]
WU W, QI Z, FUXIN L. Pointconv: deep convolutional networks on 3d point clouds [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Long Beach: IEEE, 2019: 9621-9630.
[本文引用: 2]
[18]
THOMAS H, QI C R, DESCHAUD J E, et al. Kpconv: flexible and deformable convolution for point clouds [C]// Proceedings of the IEEE/CVF International Conference on Computer Vision. Seoul: IEEE, 2019: 6411-6420.
[本文引用: 5]
[19]
XU M, DING R, ZHAO H, et al. Paconv: position adaptive convolution with dynamic kernel assembling on point clouds [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Nashville: IEEE, 2021: 3173-3182.
[本文引用: 3]
[20]
QIU S, ANWAR S, BARNES N Geometric back-projection network for point cloud classification
[J]. IEEE Transactions on Multimedia , 2021 , 24 : 1943 - 1955
[本文引用: 4]
[21]
RAN H, LIU J, WANG C. Surface representation for point clouds [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. New Orleans: IEEE, 2022: 18942-18952.
[本文引用: 4]
[22]
ZHANG R, WANG L, WANG Y, et al. Starting from non-parametric networks for 3D point cloud analysis [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Vancouver: IEEE, 2023: 5344-5353.
[本文引用: 1]
[23]
CHEN B, XIA Y, ZANG Y, et al. Decoupled local aggregation for point cloud learning [EB/OL]. (2023-08-31). https://doi.org/10.48550/arXiv.2308.16532.
[本文引用: 1]
[24]
DEFFERRARD M, BRESSON X, VANDERGHEYNST P Convolutional neural networks on graphs with fast localized spectral filtering
[J]. Advances in Neural Information Processing Systems , 2016 , 29 : 3844 - 3852
[本文引用: 1]
[25]
LI G, MULLER M, THABET A, et al. Deepgcns: can gcns go as deep as cnns? [C]// Proceedings of the IEEE/CVF International Conference on Computer Vision. Seoul: IEEE 2019: 9267-9276.
[本文引用: 2]
[26]
LIN Z H, HUANG S Y, WANG Y C F. Convolution in the cloud: learning deformable kernels in 3d graph convolution networks for point cloud analysis [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Seattle: IEEE, 2020: 1800-1809.
[本文引用: 1]
[27]
XU M, ZHOU Z, QIAO Y. Geometry sharing network for 3d point cloud classification and segmentation [C]// Proceedings of the AAAI Conference on Artificial Intelligence . Palo Alto: AAAI Press, 2020, 34(7): 12500-12507.
[本文引用: 1]
[28]
ZHOU H, FENG Y, FANG M, et al. Adaptive graph convolution for point cloud analysis [C]// Proceedings of the IEEE/CVF International Conference on Computer Vision . Montreal: IEEE, 2021: 4965-4974.
[本文引用: 2]
[29]
VASWANI A, SHAZEER N, PARMAR N, et al. Attention is all you need [C]// Proceedings of the 31st International Conference on Neural Information Processing Systems . Long Beach: Curran Associates Inc., 2017: 6000-6010.
[本文引用: 1]
[31]
ZHAO H, JIANG L, JIA J, et al. Point transformer [C]// Proceedings of the IEEE/CVF International Conference on Computer Vision. Montreal: IEEE, 2021: 16259-16268.
[本文引用: 5]
[32]
PARK J, LEE S, KIM S, et al. Self-positioning point-based transformer for point cloud understanding [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Vancouver: IEEE, 2023: 21814-21823.
[本文引用: 3]
[33]
RAN H, ZHUO W, LIU J, et al. Learning inner-group relations on point clouds [C]// Proceedings of the IEEE/CVF International Conference on Computer Vision . Montreal: IEEE, 2021: 15477-15487.
[34]
WU X Y, JIANG L, WANG P S, et al. Point Transformer V3: simpler, faster, stronger [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2024: 4840-4851.
[本文引用: 3]
[35]
WU Z, SONG S, KHOSLA A, et al. 3d shapenets: a deep representation for volumetric shapes [C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Los Alamitos: IEEE, 2015: 1912-1920.
[本文引用: 2]
[36]
UY M A, PHAM Q H, HUA B S, et al. Revisiting point cloud classification: a new benchmark dataset and classification model on real-world data [C]// Proceedings of the IEEE/CVF International Conference on Computer Vision. Seoul: IEEE, 2019: 1588-1597.
[本文引用: 1]
[37]
YI L, KIM V G, CEYLAN D, et al A scalable active framework for region annotation in 3d shape collections
[J]. ACM Transactions on Graphics , 2016 , 35 (6 ): 1 - 12
[本文引用: 1]
[38]
DAI A, CHANG A X, SAVVA M, et al. ScanNet: richly-annotated 3D reconstructions of indoor scenes [C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017: 2432-2443.
[本文引用: 1]
[39]
ARMENI I, SENER O, ZAMIR A R, et al. 3d semantic parsing of large-scale indoor spaces [C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016: 1534-1543.
[本文引用: 1]
[40]
CHOE J, PARK C, RAMEAU F, et al. Pointmixer: Mlp-mixer for point cloud understanding [C]// European Conference on Computer Vision. Cham: Springer, 2022: 620-640.
[本文引用: 2]
[41]
MUZAHID A A M, WAN W, SOHEL F, et al CurveNet: curvature-based multitask learning deep networks for 3D object recognition
[J]. IEEE/CAA Journal of Automatica Sinica , 2020 , 8 (6 ): 1177 - 1187
[本文引用: 3]
[42]
QIAN G, LI Y, PENG H, et al. Pointnext: revisiting pointnet++ with improved training and scaling strategies [J]. Advances in Neural Information Processing Systems , 2022: 23192-23204.
[本文引用: 3]
[43]
MONTANARO A, VALSESIA D, MAGLI E Rethinking the compositionality of point clouds through regularization in the hyperbolic space
[J]. Advances in Neural Information Processing Systems , 2022 , 35 : 33741 - 33753
[本文引用: 2]
[44]
LIU Y, TIAN B, LV Y, et al Point cloud classification using content-based transformer via clustering in feature space
[J]. IEEE/CAA Journal of Automatica Sinica , 2023 , 11 : 231 - 239
[本文引用: 2]
[45]
WOO S, LEE D, HWANG S, et al MKConv: multidimensional feature representation for point cloud analysis
[J]. Pattern Recognition , 2023 , 143 : 109800
DOI:10.1016/j.patcog.2023.109800
[本文引用: 3]
[46]
MA X, QIN C, YOU H X, et al. Rethinking network design and local geometry in point cloud: a simple residual MLP framework [EB/OL]. (2022-02-15). https://doi.org/10.48550/arXiv.2202.07123.
[本文引用: 3]
[47]
ZEID K A, SCHULT J, HERMANS A, et al. Point2Vec for self-supervised representation learning on point clouds [C]// DAGM German Conference on Pattern Recognition . Cham: Springer, 2023: 131-146.
[本文引用: 1]
[48]
ROBERT D, RAGUET H, LANDRIEU L. Efficient 3D semantic segmentation with superpoint Transformer [C]// IEEE/CVF International Conference on Computer Vision. Paris: IEEE, 2023: 17149-17158.
[本文引用: 1]
Use of LIDAR in landslide investigations: a review
2
2012
... 点云是描述三维物体的重要表示形式,它主要通过激光雷达[1 ] 、深度相机、结构光等设备采集而得. 这种数据能够包含物体丰富的几何、形状和空间信息,为复杂场景的理解提供了更多的可能性. 目前,点云数据已被广泛应用到机器人[2 ] 、虚拟和增强现实[3 ] 、三维重建[4 ] 等多个领域. 由于点云具有无序、不规则性,难以直接应用传统二维卷积方法. 点云的稀疏性和噪声问题进一步制约了传统二维卷积方法应用于点云数据处理时的性能表现. ...
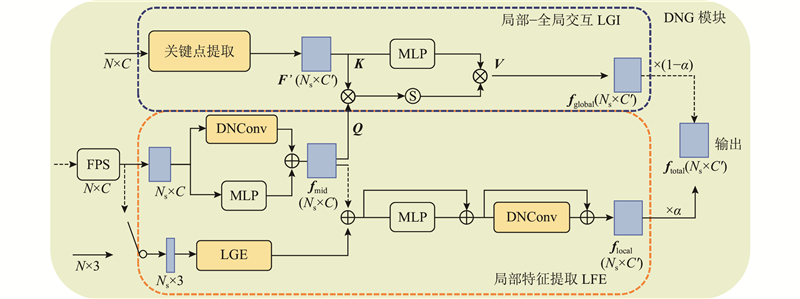
... 通过堆叠DNG模块,构建编码器. 对于形状分类任务(见图4 ),编码器有以下3个阶段. 在第1阶段中,仅嵌入局部分支的下半部分对点云特征进行学习(见图3 的实线数据流),初始特征嵌入为3维原始点云坐标信息,$\alpha $ $ m $ 1 、4 、4 . 将通道维度设置为96、192、384. 特征通过最大池化聚合,经过线性投影层得到分类分数. ...
Towards 3D point cloud based object maps for household environments
1
2008
... 点云是描述三维物体的重要表示形式,它主要通过激光雷达[1 ] 、深度相机、结构光等设备采集而得. 这种数据能够包含物体丰富的几何、形状和空间信息,为复杂场景的理解提供了更多的可能性. 目前,点云数据已被广泛应用到机器人[2 ] 、虚拟和增强现实[3 ] 、三维重建[4 ] 等多个领域. 由于点云具有无序、不规则性,难以直接应用传统二维卷积方法. 点云的稀疏性和噪声问题进一步制约了传统二维卷积方法应用于点云数据处理时的性能表现. ...
1
... 点云是描述三维物体的重要表示形式,它主要通过激光雷达[1 ] 、深度相机、结构光等设备采集而得. 这种数据能够包含物体丰富的几何、形状和空间信息,为复杂场景的理解提供了更多的可能性. 目前,点云数据已被广泛应用到机器人[2 ] 、虚拟和增强现实[3 ] 、三维重建[4 ] 等多个领域. 由于点云具有无序、不规则性,难以直接应用传统二维卷积方法. 点云的稀疏性和噪声问题进一步制约了传统二维卷积方法应用于点云数据处理时的性能表现. ...
3
... 点云是描述三维物体的重要表示形式,它主要通过激光雷达[1 ] 、深度相机、结构光等设备采集而得. 这种数据能够包含物体丰富的几何、形状和空间信息,为复杂场景的理解提供了更多的可能性. 目前,点云数据已被广泛应用到机器人[2 ] 、虚拟和增强现实[3 ] 、三维重建[4 ] 等多个领域. 由于点云具有无序、不规则性,难以直接应用传统二维卷积方法. 点云的稀疏性和噪声问题进一步制约了传统二维卷积方法应用于点云数据处理时的性能表现. ...
... 通过堆叠DNG模块,构建编码器. 对于形状分类任务(见图4 ),编码器有以下3个阶段. 在第1阶段中,仅嵌入局部分支的下半部分对点云特征进行学习(见图3 的实线数据流),初始特征嵌入为3维原始点云坐标信息,$\alpha $ $ m $ 1 、4 、4 . 将通道维度设置为96、192、384. 特征通过最大池化聚合,经过线性投影层得到分类分数. ...
... 、4 . 将通道维度设置为96、192、384. 特征通过最大池化聚合,经过线性投影层得到分类分数. ...
3
... 近年来,深度学习方法在处理点云数据方面[5 -7 ] 取得了显著进展,基于点直接进行处理,以简单、高效的方式应对点云的无序性. PointNet[7 ] 为该类方法的开创性工作,通过多层感知机逐点进行特征提取,但忽略了局部结构信息. Qi等[8 ] 对此进行改进,引入层次结构和多尺度特征提取,但损失了过多的局部细节. 此后,一系列方法[9 -12 ] 针对局部特征进行研究,在欧氏或特征空间中构建点间的相互关系. 目前,利用图状结构进行特征提取[13 -15 ] ,成为点云理解中的流行范式. 利用图结构,能够自然地捕获点云的局部几何结构,以DGCNN[13 ] 为代表的图卷积通过边缘向量构建有向图,捕获局部特征. ...
... 由于点云固有的无序性、不规则性及稀疏性, 难以直接应用传统二维卷积方法. 近年来,深度学习方法在处理点云数据方面[5 -7 ] 进展显著,部分工作间接地对点云进行处理,将点云转换为规则的体素[6 ] 或多视图图像[5 ] . 尽管如此,这些方法通常存在计算复杂度高或几何信息丢失的情况. 相比而言,直接将原始点云作为输入是目前最简单高效的手段. PointNet是直接处理点云的开创性工作,逐点采用多层感知机,通过最大池化聚合高维特征,但忽略了点间关系[7 ] . 为此,PointNet++通过层次结构和局部分组进行改进,但对于局部特征的表示不足[8 ] . 此后,更多方法关注于局部特征学习的研究[12 ,17 -19 ] ,PointConv[17 ] 、KPConv[18 ] 和 PAConv[19 ] 等方法设计适合点云形状的卷积算子来获取相关特征. GBNet在局域内构建几何描述符,为网络提供低级的几何线索[20 ] . RepSurf通过重建三角形和伞面特征,显式地描述拓扑结构[21 ] . 此外,PointNN[22 ] 、DeLA[23 ] 均从轻量化角度进行改进,旨在降低计算复杂度,提升网络效率. ...
... [5 ]. 尽管如此,这些方法通常存在计算复杂度高或几何信息丢失的情况. 相比而言,直接将原始点云作为输入是目前最简单高效的手段. PointNet是直接处理点云的开创性工作,逐点采用多层感知机,通过最大池化聚合高维特征,但忽略了点间关系[7 ] . 为此,PointNet++通过层次结构和局部分组进行改进,但对于局部特征的表示不足[8 ] . 此后,更多方法关注于局部特征学习的研究[12 ,17 -19 ] ,PointConv[17 ] 、KPConv[18 ] 和 PAConv[19 ] 等方法设计适合点云形状的卷积算子来获取相关特征. GBNet在局域内构建几何描述符,为网络提供低级的几何线索[20 ] . RepSurf通过重建三角形和伞面特征,显式地描述拓扑结构[21 ] . 此外,PointNN[22 ] 、DeLA[23 ] 均从轻量化角度进行改进,旨在降低计算复杂度,提升网络效率. ...
Fpnn: field probing neural networks for 3d data
1
2016
... 由于点云固有的无序性、不规则性及稀疏性, 难以直接应用传统二维卷积方法. 近年来,深度学习方法在处理点云数据方面[5 -7 ] 进展显著,部分工作间接地对点云进行处理,将点云转换为规则的体素[6 ] 或多视图图像[5 ] . 尽管如此,这些方法通常存在计算复杂度高或几何信息丢失的情况. 相比而言,直接将原始点云作为输入是目前最简单高效的手段. PointNet是直接处理点云的开创性工作,逐点采用多层感知机,通过最大池化聚合高维特征,但忽略了点间关系[7 ] . 为此,PointNet++通过层次结构和局部分组进行改进,但对于局部特征的表示不足[8 ] . 此后,更多方法关注于局部特征学习的研究[12 ,17 -19 ] ,PointConv[17 ] 、KPConv[18 ] 和 PAConv[19 ] 等方法设计适合点云形状的卷积算子来获取相关特征. GBNet在局域内构建几何描述符,为网络提供低级的几何线索[20 ] . RepSurf通过重建三角形和伞面特征,显式地描述拓扑结构[21 ] . 此外,PointNN[22 ] 、DeLA[23 ] 均从轻量化角度进行改进,旨在降低计算复杂度,提升网络效率. ...
9
... 近年来,深度学习方法在处理点云数据方面[5 -7 ] 取得了显著进展,基于点直接进行处理,以简单、高效的方式应对点云的无序性. PointNet[7 ] 为该类方法的开创性工作,通过多层感知机逐点进行特征提取,但忽略了局部结构信息. Qi等[8 ] 对此进行改进,引入层次结构和多尺度特征提取,但损失了过多的局部细节. 此后,一系列方法[9 -12 ] 针对局部特征进行研究,在欧氏或特征空间中构建点间的相互关系. 目前,利用图状结构进行特征提取[13 -15 ] ,成为点云理解中的流行范式. 利用图结构,能够自然地捕获点云的局部几何结构,以DGCNN[13 ] 为代表的图卷积通过边缘向量构建有向图,捕获局部特征. ...
... [7 ]为该类方法的开创性工作,通过多层感知机逐点进行特征提取,但忽略了局部结构信息. Qi等[8 ] 对此进行改进,引入层次结构和多尺度特征提取,但损失了过多的局部细节. 此后,一系列方法[9 -12 ] 针对局部特征进行研究,在欧氏或特征空间中构建点间的相互关系. 目前,利用图状结构进行特征提取[13 -15 ] ,成为点云理解中的流行范式. 利用图结构,能够自然地捕获点云的局部几何结构,以DGCNN[13 ] 为代表的图卷积通过边缘向量构建有向图,捕获局部特征. ...
... 由于点云固有的无序性、不规则性及稀疏性, 难以直接应用传统二维卷积方法. 近年来,深度学习方法在处理点云数据方面[5 -7 ] 进展显著,部分工作间接地对点云进行处理,将点云转换为规则的体素[6 ] 或多视图图像[5 ] . 尽管如此,这些方法通常存在计算复杂度高或几何信息丢失的情况. 相比而言,直接将原始点云作为输入是目前最简单高效的手段. PointNet是直接处理点云的开创性工作,逐点采用多层感知机,通过最大池化聚合高维特征,但忽略了点间关系[7 ] . 为此,PointNet++通过层次结构和局部分组进行改进,但对于局部特征的表示不足[8 ] . 此后,更多方法关注于局部特征学习的研究[12 ,17 -19 ] ,PointConv[17 ] 、KPConv[18 ] 和 PAConv[19 ] 等方法设计适合点云形状的卷积算子来获取相关特征. GBNet在局域内构建几何描述符,为网络提供低级的几何线索[20 ] . RepSurf通过重建三角形和伞面特征,显式地描述拓扑结构[21 ] . 此外,PointNN[22 ] 、DeLA[23 ] 均从轻量化角度进行改进,旨在降低计算复杂度,提升网络效率. ...
... [7 ]. 为此,PointNet++通过层次结构和局部分组进行改进,但对于局部特征的表示不足[8 ] . 此后,更多方法关注于局部特征学习的研究[12 ,17 -19 ] ,PointConv[17 ] 、KPConv[18 ] 和 PAConv[19 ] 等方法设计适合点云形状的卷积算子来获取相关特征. GBNet在局域内构建几何描述符,为网络提供低级的几何线索[20 ] . RepSurf通过重建三角形和伞面特征,显式地描述拓扑结构[21 ] . 此外,PointNN[22 ] 、DeLA[23 ] 均从轻量化角度进行改进,旨在降低计算复杂度,提升网络效率. ...
... Classification result on ModelNet40 benchmark
Tab.1 方法 年份 mAcc/% OA/% PointNet[7 ] 2017 86.2 89.2 PointNet++[8 ] 2017 — 91.9 KPConv[18 ] 2019 — 92.9 DGCNN[13 ] 2019 90.2 92.9 PointASNL[11 ] 2020 — 92.9 PointTransformer[31 ] 2020 90.6 93.7 PointMixer[40 ] 2021 91.4 93.6 CurveNet[41 ] 2021 — 93.8 PointNeXT[42 ] 2022 91.1 94.0 DGCNN+HyCoRe[43 ] 2022 91.0 93.7 PointConT[44 ] 2023 — 93.5 MKConv[45 ] 2023 — 93.7 DNG-Net(本文方法) 2024 91.3 94.1
ModelNet40被视为点云分析的经典基准,但它不足以应对实际场景中的复杂情况. 在具有挑战性的ScanObjectNN基准测试上进行实验. ...
... Classification result on ScanObjectNN benchmark
Tab.2 方法 年份 mAcc/% OA/% PointNet[7 ] 2017 63.4 68.2 PointNet++[8 ] 2017 75.4 77.9 DGCNN[13 ] 2019 73.6 78.1 GBNet[20 ] 2021 77.8 80.5 PointMLP[46 ] 2022 84.4 85.7 RepSurf-U[21 ] 2022 83.1 86.0 PointMLP+HyCoRe[43 ] 2022 85.9 87.2 PointNeXT[42 ] 2022 86.8 88.2 PointConT[44 ] 2023 86.0 88.0 SPoTr[32 ] 2023 86.8 88.6 DNG-Net(本文方法) 2024 88.3 89.6
3.3. 部件分割任务 在ShapeNetPart上进行部件分割实验,遵循文献[7 ]的设置,随机选择2 048个点作为输入,进行公平的比较. 对于评估指标,采用类别平均交并比mIoUcls 和实例平均交并比mIoUins . ...
... 在ShapeNetPart上进行部件分割实验,遵循文献[7 ]的设置,随机选择2 048个点作为输入,进行公平的比较. 对于评估指标,采用类别平均交并比mIoUcls 和实例平均交并比mIoUins . ...
... Segmentation result on ShapeNetPart benchmark
Tab.3 方法 年份 mIoUcls /% mIoUins /% PointNet[7 ] 2017 80.4 83.7 PointNet++[8 ] 2017 81.9 85.1 KPConv[18 ] 2019 85.0 86.2 DGCNN[13 ] 2019 82.3 85.2 PointASNL[11 ] 2020 — 86.1 PAConv[19 ] 2021 84.6 86.1 CurveNet[41 ] 2021 — 86.6 PointTransformer[31 ] 2020 83.7 86.6 StratifiedFormer[16 ] 2022 85.1 86.6 PointMLP[46 ] 2022 84.6 86.1 Point2vec[47 ] 2023 84.6 86.3 MKConv[45 ] 2023 — 86.5 DNG-Net(本文方法) 2024 84.7 86.7
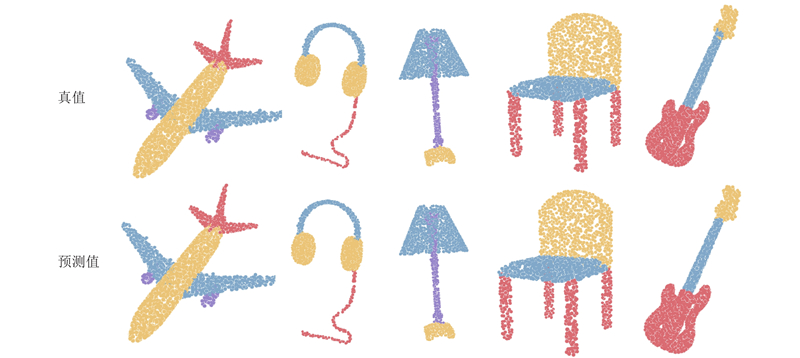
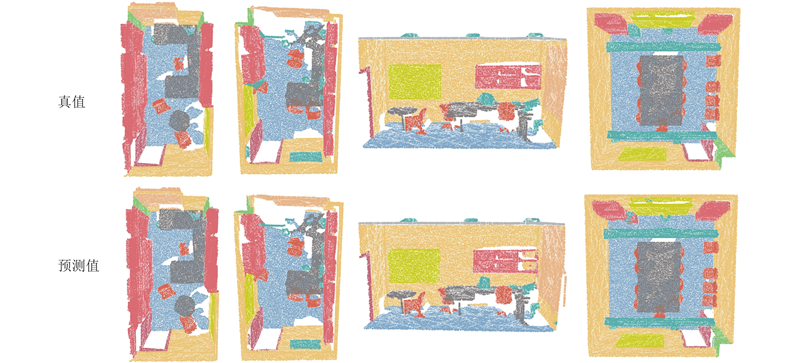
如图5 所示为DNG-Net在部件分割上预测值与真值的可视化对比. 可以看出,本文方法非常接近于真值,即使在部件边界部分也分割得较清晰. ...
... Complexity analysis on ModelNet40
Tab.11 模型 FLOPs/109 P /106 OA/% PointNet[7 ] 0.5 3.5 89.2 PointNet++[8 ] 4.1 1.8 91.9 DGCNN[13 ] 3.0 2.6 92.9 PointTransformer[31 ] 18.4 9.6 93.7 CurveNet[41 ] 0.3 2.1 93.8 PointMixer[40 ] — 6.5 93.6 PointNeXT[42 ] 6.5 4.5 94.0 PointMLP[46 ] 15.7 13.2 94.1 DNG-Net(本文方法) 1.92 4.9 94.1
实验结果表明,DNG-Net在可接受的计算成本内显著优于其他方法. 另外,PointMLP和DNG-Net在总体精度上表现均为最优,但DNG-Net在FLOPs和参数量方面均显著优于PointMLP,FLOPs降低了约8.3倍,参数量降低了约2.7倍. 可见,本文所提出的方法在精度和复杂度之间取得了更好的平衡. ...
7
... 近年来,深度学习方法在处理点云数据方面[5 -7 ] 取得了显著进展,基于点直接进行处理,以简单、高效的方式应对点云的无序性. PointNet[7 ] 为该类方法的开创性工作,通过多层感知机逐点进行特征提取,但忽略了局部结构信息. Qi等[8 ] 对此进行改进,引入层次结构和多尺度特征提取,但损失了过多的局部细节. 此后,一系列方法[9 -12 ] 针对局部特征进行研究,在欧氏或特征空间中构建点间的相互关系. 目前,利用图状结构进行特征提取[13 -15 ] ,成为点云理解中的流行范式. 利用图结构,能够自然地捕获点云的局部几何结构,以DGCNN[13 ] 为代表的图卷积通过边缘向量构建有向图,捕获局部特征. ...
... 由于点云固有的无序性、不规则性及稀疏性, 难以直接应用传统二维卷积方法. 近年来,深度学习方法在处理点云数据方面[5 -7 ] 进展显著,部分工作间接地对点云进行处理,将点云转换为规则的体素[6 ] 或多视图图像[5 ] . 尽管如此,这些方法通常存在计算复杂度高或几何信息丢失的情况. 相比而言,直接将原始点云作为输入是目前最简单高效的手段. PointNet是直接处理点云的开创性工作,逐点采用多层感知机,通过最大池化聚合高维特征,但忽略了点间关系[7 ] . 为此,PointNet++通过层次结构和局部分组进行改进,但对于局部特征的表示不足[8 ] . 此后,更多方法关注于局部特征学习的研究[12 ,17 -19 ] ,PointConv[17 ] 、KPConv[18 ] 和 PAConv[19 ] 等方法设计适合点云形状的卷积算子来获取相关特征. GBNet在局域内构建几何描述符,为网络提供低级的几何线索[20 ] . RepSurf通过重建三角形和伞面特征,显式地描述拓扑结构[21 ] . 此外,PointNN[22 ] 、DeLA[23 ] 均从轻量化角度进行改进,旨在降低计算复杂度,提升网络效率. ...
... Classification result on ModelNet40 benchmark
Tab.1 方法 年份 mAcc/% OA/% PointNet[7 ] 2017 86.2 89.2 PointNet++[8 ] 2017 — 91.9 KPConv[18 ] 2019 — 92.9 DGCNN[13 ] 2019 90.2 92.9 PointASNL[11 ] 2020 — 92.9 PointTransformer[31 ] 2020 90.6 93.7 PointMixer[40 ] 2021 91.4 93.6 CurveNet[41 ] 2021 — 93.8 PointNeXT[42 ] 2022 91.1 94.0 DGCNN+HyCoRe[43 ] 2022 91.0 93.7 PointConT[44 ] 2023 — 93.5 MKConv[45 ] 2023 — 93.7 DNG-Net(本文方法) 2024 91.3 94.1
ModelNet40被视为点云分析的经典基准,但它不足以应对实际场景中的复杂情况. 在具有挑战性的ScanObjectNN基准测试上进行实验. ...
... Classification result on ScanObjectNN benchmark
Tab.2 方法 年份 mAcc/% OA/% PointNet[7 ] 2017 63.4 68.2 PointNet++[8 ] 2017 75.4 77.9 DGCNN[13 ] 2019 73.6 78.1 GBNet[20 ] 2021 77.8 80.5 PointMLP[46 ] 2022 84.4 85.7 RepSurf-U[21 ] 2022 83.1 86.0 PointMLP+HyCoRe[43 ] 2022 85.9 87.2 PointNeXT[42 ] 2022 86.8 88.2 PointConT[44 ] 2023 86.0 88.0 SPoTr[32 ] 2023 86.8 88.6 DNG-Net(本文方法) 2024 88.3 89.6
3.3. 部件分割任务 在ShapeNetPart上进行部件分割实验,遵循文献[7 ]的设置,随机选择2 048个点作为输入,进行公平的比较. 对于评估指标,采用类别平均交并比mIoUcls 和实例平均交并比mIoUins . ...
... Segmentation result on ShapeNetPart benchmark
Tab.3 方法 年份 mIoUcls /% mIoUins /% PointNet[7 ] 2017 80.4 83.7 PointNet++[8 ] 2017 81.9 85.1 KPConv[18 ] 2019 85.0 86.2 DGCNN[13 ] 2019 82.3 85.2 PointASNL[11 ] 2020 — 86.1 PAConv[19 ] 2021 84.6 86.1 CurveNet[41 ] 2021 — 86.6 PointTransformer[31 ] 2020 83.7 86.6 StratifiedFormer[16 ] 2022 85.1 86.6 PointMLP[46 ] 2022 84.6 86.1 Point2vec[47 ] 2023 84.6 86.3 MKConv[45 ] 2023 — 86.5 DNG-Net(本文方法) 2024 84.7 86.7
如图5 所示为DNG-Net在部件分割上预测值与真值的可视化对比. 可以看出,本文方法非常接近于真值,即使在部件边界部分也分割得较清晰. ...
... Segmentation result on ScanNetV2 benchmark
Tab.4 方法 年份 P /106 mIOUval /% mIOUtest /% PointNet++[8 ] 2017 — 53.5 55.7 KPConv[18 ] 2019 — 69.2 68.6 PointTransformer[31 ] 2021 7.8 70.6 — StratifiedFormer[16 ] 2022 18.8 74.3 73.7 PTv3[34 ] 2023 46.2 77.5 77.9 DNG-Net(本文方法) 2024 9.2 75.6 74.9
如表5 所示为S3DIS Area5数据集上DNG-Net的分割性能. 使用类似文献[21 ]的方法,通过网格采样对数据进行预处理. ...
... Complexity analysis on ModelNet40
Tab.11 模型 FLOPs/109 P /106 OA/% PointNet[7 ] 0.5 3.5 89.2 PointNet++[8 ] 4.1 1.8 91.9 DGCNN[13 ] 3.0 2.6 92.9 PointTransformer[31 ] 18.4 9.6 93.7 CurveNet[41 ] 0.3 2.1 93.8 PointMixer[40 ] — 6.5 93.6 PointNeXT[42 ] 6.5 4.5 94.0 PointMLP[46 ] 15.7 13.2 94.1 DNG-Net(本文方法) 1.92 4.9 94.1
实验结果表明,DNG-Net在可接受的计算成本内显著优于其他方法. 另外,PointMLP和DNG-Net在总体精度上表现均为最优,但DNG-Net在FLOPs和参数量方面均显著优于PointMLP,FLOPs降低了约8.3倍,参数量降低了约2.7倍. 可见,本文所提出的方法在精度和复杂度之间取得了更好的平衡. ...
1
... 近年来,深度学习方法在处理点云数据方面[5 -7 ] 取得了显著进展,基于点直接进行处理,以简单、高效的方式应对点云的无序性. PointNet[7 ] 为该类方法的开创性工作,通过多层感知机逐点进行特征提取,但忽略了局部结构信息. Qi等[8 ] 对此进行改进,引入层次结构和多尺度特征提取,但损失了过多的局部细节. 此后,一系列方法[9 -12 ] 针对局部特征进行研究,在欧氏或特征空间中构建点间的相互关系. 目前,利用图状结构进行特征提取[13 -15 ] ,成为点云理解中的流行范式. 利用图结构,能够自然地捕获点云的局部几何结构,以DGCNN[13 ] 为代表的图卷积通过边缘向量构建有向图,捕获局部特征. ...
3
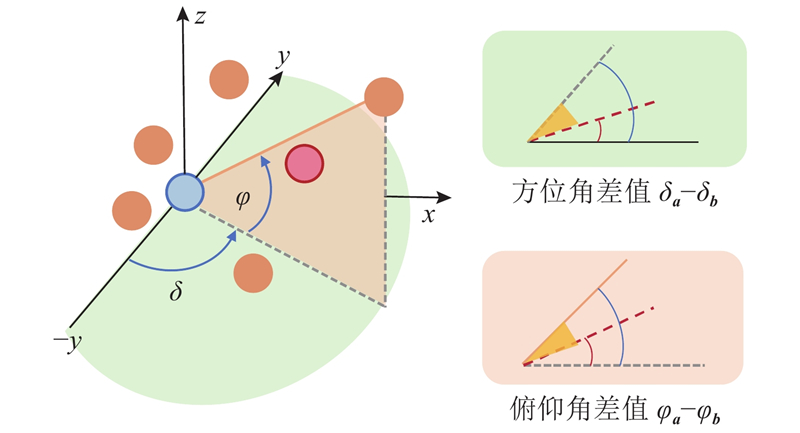
... 随着网络的加深,局域中的逐层传播和信息聚合虽然能够扩大节点的感受野,但有效感受野的效用是边际递减的. 网络难以充分捕捉到较远距离上的依赖关系,对于整体形态的感知不足. 受PointASNL[11 ] 的启发,设计基于内容的局部-全局信息交互模块(local-global interaction, LGI). 该模块主要由提取关键点和特征交互2部分组成. ...
... Classification result on ModelNet40 benchmark
Tab.1 方法 年份 mAcc/% OA/% PointNet[7 ] 2017 86.2 89.2 PointNet++[8 ] 2017 — 91.9 KPConv[18 ] 2019 — 92.9 DGCNN[13 ] 2019 90.2 92.9 PointASNL[11 ] 2020 — 92.9 PointTransformer[31 ] 2020 90.6 93.7 PointMixer[40 ] 2021 91.4 93.6 CurveNet[41 ] 2021 — 93.8 PointNeXT[42 ] 2022 91.1 94.0 DGCNN+HyCoRe[43 ] 2022 91.0 93.7 PointConT[44 ] 2023 — 93.5 MKConv[45 ] 2023 — 93.7 DNG-Net(本文方法) 2024 91.3 94.1
ModelNet40被视为点云分析的经典基准,但它不足以应对实际场景中的复杂情况. 在具有挑战性的ScanObjectNN基准测试上进行实验. ...
... Segmentation result on ShapeNetPart benchmark
Tab.3 方法 年份 mIoUcls /% mIoUins /% PointNet[7 ] 2017 80.4 83.7 PointNet++[8 ] 2017 81.9 85.1 KPConv[18 ] 2019 85.0 86.2 DGCNN[13 ] 2019 82.3 85.2 PointASNL[11 ] 2020 — 86.1 PAConv[19 ] 2021 84.6 86.1 CurveNet[41 ] 2021 — 86.6 PointTransformer[31 ] 2020 83.7 86.6 StratifiedFormer[16 ] 2022 85.1 86.6 PointMLP[46 ] 2022 84.6 86.1 Point2vec[47 ] 2023 84.6 86.3 MKConv[45 ] 2023 — 86.5 DNG-Net(本文方法) 2024 84.7 86.7
如图5 所示为DNG-Net在部件分割上预测值与真值的可视化对比. 可以看出,本文方法非常接近于真值,即使在部件边界部分也分割得较清晰. ...
2
... 近年来,深度学习方法在处理点云数据方面[5 -7 ] 取得了显著进展,基于点直接进行处理,以简单、高效的方式应对点云的无序性. PointNet[7 ] 为该类方法的开创性工作,通过多层感知机逐点进行特征提取,但忽略了局部结构信息. Qi等[8 ] 对此进行改进,引入层次结构和多尺度特征提取,但损失了过多的局部细节. 此后,一系列方法[9 -12 ] 针对局部特征进行研究,在欧氏或特征空间中构建点间的相互关系. 目前,利用图状结构进行特征提取[13 -15 ] ,成为点云理解中的流行范式. 利用图结构,能够自然地捕获点云的局部几何结构,以DGCNN[13 ] 为代表的图卷积通过边缘向量构建有向图,捕获局部特征. ...
... 由于点云固有的无序性、不规则性及稀疏性, 难以直接应用传统二维卷积方法. 近年来,深度学习方法在处理点云数据方面[5 -7 ] 进展显著,部分工作间接地对点云进行处理,将点云转换为规则的体素[6 ] 或多视图图像[5 ] . 尽管如此,这些方法通常存在计算复杂度高或几何信息丢失的情况. 相比而言,直接将原始点云作为输入是目前最简单高效的手段. PointNet是直接处理点云的开创性工作,逐点采用多层感知机,通过最大池化聚合高维特征,但忽略了点间关系[7 ] . 为此,PointNet++通过层次结构和局部分组进行改进,但对于局部特征的表示不足[8 ] . 此后,更多方法关注于局部特征学习的研究[12 ,17 -19 ] ,PointConv[17 ] 、KPConv[18 ] 和 PAConv[19 ] 等方法设计适合点云形状的卷积算子来获取相关特征. GBNet在局域内构建几何描述符,为网络提供低级的几何线索[20 ] . RepSurf通过重建三角形和伞面特征,显式地描述拓扑结构[21 ] . 此外,PointNN[22 ] 、DeLA[23 ] 均从轻量化角度进行改进,旨在降低计算复杂度,提升网络效率. ...
Dynamic graph CNN for learning on point clouds
12
2019
... 近年来,深度学习方法在处理点云数据方面[5 -7 ] 取得了显著进展,基于点直接进行处理,以简单、高效的方式应对点云的无序性. PointNet[7 ] 为该类方法的开创性工作,通过多层感知机逐点进行特征提取,但忽略了局部结构信息. Qi等[8 ] 对此进行改进,引入层次结构和多尺度特征提取,但损失了过多的局部细节. 此后,一系列方法[9 -12 ] 针对局部特征进行研究,在欧氏或特征空间中构建点间的相互关系. 目前,利用图状结构进行特征提取[13 -15 ] ,成为点云理解中的流行范式. 利用图结构,能够自然地捕获点云的局部几何结构,以DGCNN[13 ] 为代表的图卷积通过边缘向量构建有向图,捕获局部特征. ...
... [13 ]为代表的图卷积通过边缘向量构建有向图,捕获局部特征. ...
... 图结构是用来建模点云局部几何结构的自然表示,将点云当作图的节点,依据点之间的空间邻近性和特征相似性来构建边缘向量. GCN的概念源自文献[24 ],为了降低计算复杂度,采用Chebyshev多项式来近似特征分解的过程. 最近关于点云上的图卷积的研究验证了GCN[13 ,15 ,25 -28 ] 的有效性. DGCNN提出EdgeConv,采用动态图编码中心点与其特征空间邻居之间的关系,对后续的工作产生了深远的影响[13 ] . DeepGCN通过堆叠多个图卷积层,采用残差连接,增加了模型深度,解决了图节点过平滑的问题[25 ] . 3D-GCN开发可变形的3D核,在训练期间更新核的形状和权重[26 ] . GSNet[27 ] 扩展了DGCNN[13 ] 的工作,在欧几里德空间和特征值空间中进行邻域聚合.LPD-Net[15 ] 在空间邻居和特征邻居上扩展DGCNN[13 ] ,进行聚合. AdaptConv根据动态学习的特征,为点生成自适应核[28 ] . ...
... [13 ]. DeepGCN通过堆叠多个图卷积层,采用残差连接,增加了模型深度,解决了图节点过平滑的问题[25 ] . 3D-GCN开发可变形的3D核,在训练期间更新核的形状和权重[26 ] . GSNet[27 ] 扩展了DGCNN[13 ] 的工作,在欧几里德空间和特征值空间中进行邻域聚合.LPD-Net[15 ] 在空间邻居和特征邻居上扩展DGCNN[13 ] ,进行聚合. AdaptConv根据动态学习的特征,为点生成自适应核[28 ] . ...
... [13 ]的工作,在欧几里德空间和特征值空间中进行邻域聚合.LPD-Net[15 ] 在空间邻居和特征邻居上扩展DGCNN[13 ] ,进行聚合. AdaptConv根据动态学习的特征,为点生成自适应核[28 ] . ...
... [13 ],进行聚合. AdaptConv根据动态学习的特征,为点生成自适应核[28 ] . ...
... 大多数工作都是针对关系函数$R( \cdot )$ [13 ] 提出边卷积算子EdgeConv, 通过动态构建包含自环连接的有向图结构,实现局部特征聚合. 对于每个中心点, 在特征空间中选取其K近邻(包括自身), 建立具有方向性的边连接, 形成局部感知域. 关系函数的形式如下: ...
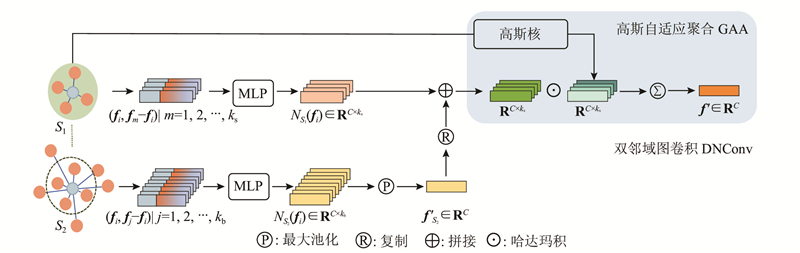
... 受DGCNN[13 ] 的启发,提出新的图卷积算子(dual-neighborhood graph convolution,DNConv). 具体如图2 所示,该算子采用双邻域互补的机制,在扩大感受野的同时,有效提取大尺度局部图的边缘显著特征,尽可能多地保留原始邻域内的细节信息. ...
... Classification result on ModelNet40 benchmark
Tab.1 方法 年份 mAcc/% OA/% PointNet[7 ] 2017 86.2 89.2 PointNet++[8 ] 2017 — 91.9 KPConv[18 ] 2019 — 92.9 DGCNN[13 ] 2019 90.2 92.9 PointASNL[11 ] 2020 — 92.9 PointTransformer[31 ] 2020 90.6 93.7 PointMixer[40 ] 2021 91.4 93.6 CurveNet[41 ] 2021 — 93.8 PointNeXT[42 ] 2022 91.1 94.0 DGCNN+HyCoRe[43 ] 2022 91.0 93.7 PointConT[44 ] 2023 — 93.5 MKConv[45 ] 2023 — 93.7 DNG-Net(本文方法) 2024 91.3 94.1
ModelNet40被视为点云分析的经典基准,但它不足以应对实际场景中的复杂情况. 在具有挑战性的ScanObjectNN基准测试上进行实验. ...
... Classification result on ScanObjectNN benchmark
Tab.2 方法 年份 mAcc/% OA/% PointNet[7 ] 2017 63.4 68.2 PointNet++[8 ] 2017 75.4 77.9 DGCNN[13 ] 2019 73.6 78.1 GBNet[20 ] 2021 77.8 80.5 PointMLP[46 ] 2022 84.4 85.7 RepSurf-U[21 ] 2022 83.1 86.0 PointMLP+HyCoRe[43 ] 2022 85.9 87.2 PointNeXT[42 ] 2022 86.8 88.2 PointConT[44 ] 2023 86.0 88.0 SPoTr[32 ] 2023 86.8 88.6 DNG-Net(本文方法) 2024 88.3 89.6
3.3. 部件分割任务 在ShapeNetPart上进行部件分割实验,遵循文献[7 ]的设置,随机选择2 048个点作为输入,进行公平的比较. 对于评估指标,采用类别平均交并比mIoUcls 和实例平均交并比mIoUins . ...
... Segmentation result on ShapeNetPart benchmark
Tab.3 方法 年份 mIoUcls /% mIoUins /% PointNet[7 ] 2017 80.4 83.7 PointNet++[8 ] 2017 81.9 85.1 KPConv[18 ] 2019 85.0 86.2 DGCNN[13 ] 2019 82.3 85.2 PointASNL[11 ] 2020 — 86.1 PAConv[19 ] 2021 84.6 86.1 CurveNet[41 ] 2021 — 86.6 PointTransformer[31 ] 2020 83.7 86.6 StratifiedFormer[16 ] 2022 85.1 86.6 PointMLP[46 ] 2022 84.6 86.1 Point2vec[47 ] 2023 84.6 86.3 MKConv[45 ] 2023 — 86.5 DNG-Net(本文方法) 2024 84.7 86.7
如图5 所示为DNG-Net在部件分割上预测值与真值的可视化对比. 可以看出,本文方法非常接近于真值,即使在部件边界部分也分割得较清晰. ...
... Complexity analysis on ModelNet40
Tab.11 模型 FLOPs/109 P /106 OA/% PointNet[7 ] 0.5 3.5 89.2 PointNet++[8 ] 4.1 1.8 91.9 DGCNN[13 ] 3.0 2.6 92.9 PointTransformer[31 ] 18.4 9.6 93.7 CurveNet[41 ] 0.3 2.1 93.8 PointMixer[40 ] — 6.5 93.6 PointNeXT[42 ] 6.5 4.5 94.0 PointMLP[46 ] 15.7 13.2 94.1 DNG-Net(本文方法) 1.92 4.9 94.1
实验结果表明,DNG-Net在可接受的计算成本内显著优于其他方法. 另外,PointMLP和DNG-Net在总体精度上表现均为最优,但DNG-Net在FLOPs和参数量方面均显著优于PointMLP,FLOPs降低了约8.3倍,参数量降低了约2.7倍. 可见,本文所提出的方法在精度和复杂度之间取得了更好的平衡. ...
3
... 近年来,深度学习方法在处理点云数据方面[5 -7 ] 取得了显著进展,基于点直接进行处理,以简单、高效的方式应对点云的无序性. PointNet[7 ] 为该类方法的开创性工作,通过多层感知机逐点进行特征提取,但忽略了局部结构信息. Qi等[8 ] 对此进行改进,引入层次结构和多尺度特征提取,但损失了过多的局部细节. 此后,一系列方法[9 -12 ] 针对局部特征进行研究,在欧氏或特征空间中构建点间的相互关系. 目前,利用图状结构进行特征提取[13 -15 ] ,成为点云理解中的流行范式. 利用图结构,能够自然地捕获点云的局部几何结构,以DGCNN[13 ] 为代表的图卷积通过边缘向量构建有向图,捕获局部特征. ...
... 图结构是用来建模点云局部几何结构的自然表示,将点云当作图的节点,依据点之间的空间邻近性和特征相似性来构建边缘向量. GCN的概念源自文献[24 ],为了降低计算复杂度,采用Chebyshev多项式来近似特征分解的过程. 最近关于点云上的图卷积的研究验证了GCN[13 ,15 ,25 -28 ] 的有效性. DGCNN提出EdgeConv,采用动态图编码中心点与其特征空间邻居之间的关系,对后续的工作产生了深远的影响[13 ] . DeepGCN通过堆叠多个图卷积层,采用残差连接,增加了模型深度,解决了图节点过平滑的问题[25 ] . 3D-GCN开发可变形的3D核,在训练期间更新核的形状和权重[26 ] . GSNet[27 ] 扩展了DGCNN[13 ] 的工作,在欧几里德空间和特征值空间中进行邻域聚合.LPD-Net[15 ] 在空间邻居和特征邻居上扩展DGCNN[13 ] ,进行聚合. AdaptConv根据动态学习的特征,为点生成自适应核[28 ] . ...
... [15 ]在空间邻居和特征邻居上扩展DGCNN[13 ] ,进行聚合. AdaptConv根据动态学习的特征,为点生成自适应核[28 ] . ...
5
... 此外,现有方法大多利用局部特征的逐层传播和信息聚合来扩大节点的感受野,这种方式的效用是边际递减的. 随着网络层数的加深,节点特征逐渐被稀释,仅依靠局部特征学习无法充分捕捉到远距离依赖关系,对于点云整体结构的感知不足. StratifiedFormer通过体素化将点云分割为不同分辨率的窗口,在每个窗口中利用局部注意力操作进行扩展,但感受野很局限,难以覆盖全局范围[16 ] . ...
... Attention机制[29 ] 作为Transformer中的核心操作,具有捕获远程依赖关系的能力,目前被广泛应用到自然语言处理和二维图像任务中. 由于Attention机制本身不受输入顺序的影响,具有置换不变性,在本质上适用于点云分析. 近年来,Lai等[16 ,20 ,30 -34 ] 在点云分析中采用了注意力操作. Zhao等[31 ] 将注意力机制引入点云,提出向量自注意算子,构建减法关系生成注意权值,但缺乏直接捕获远程依赖的能力,对各种扰动的鲁棒性不足. GBNet提出通道亲和注意力,改进上下文信息建模[20 ] . SPoTr采用解纠缠注意力聚集自定位点特征,提高了模型的可扩展性[32 ] . PTv3采用序列化点云的特定模式替代了普通邻域搜寻操作,显著提高了效率[34 ] . StratifiedFormer通过体素化将点云分割为不同分辨率的窗口,在每个窗口中利用局部注意力操作进行扩展,但感受野很局限[16 ] . 本文利用注意力采样得到更具代表性的全局关键点,借鉴交叉注意力的思想,将全局关键点信息与局部特征进行充分交互. 这种交互使得短程和远程依赖相互融合,显著增大了局部点的空间跨度,提升了特征的表示能力,使特征更有判别性. ...
... [16 ]. 本文利用注意力采样得到更具代表性的全局关键点,借鉴交叉注意力的思想,将全局关键点信息与局部特征进行充分交互. 这种交互使得短程和远程依赖相互融合,显著增大了局部点的空间跨度,提升了特征的表示能力,使特征更有判别性. ...
... Segmentation result on ShapeNetPart benchmark
Tab.3 方法 年份 mIoUcls /% mIoUins /% PointNet[7 ] 2017 80.4 83.7 PointNet++[8 ] 2017 81.9 85.1 KPConv[18 ] 2019 85.0 86.2 DGCNN[13 ] 2019 82.3 85.2 PointASNL[11 ] 2020 — 86.1 PAConv[19 ] 2021 84.6 86.1 CurveNet[41 ] 2021 — 86.6 PointTransformer[31 ] 2020 83.7 86.6 StratifiedFormer[16 ] 2022 85.1 86.6 PointMLP[46 ] 2022 84.6 86.1 Point2vec[47 ] 2023 84.6 86.3 MKConv[45 ] 2023 — 86.5 DNG-Net(本文方法) 2024 84.7 86.7
如图5 所示为DNG-Net在部件分割上预测值与真值的可视化对比. 可以看出,本文方法非常接近于真值,即使在部件边界部分也分割得较清晰. ...
... Segmentation result on ScanNetV2 benchmark
Tab.4 方法 年份 P /106 mIOUval /% mIOUtest /% PointNet++[8 ] 2017 — 53.5 55.7 KPConv[18 ] 2019 — 69.2 68.6 PointTransformer[31 ] 2021 7.8 70.6 — StratifiedFormer[16 ] 2022 18.8 74.3 73.7 PTv3[34 ] 2023 46.2 77.5 77.9 DNG-Net(本文方法) 2024 9.2 75.6 74.9
如表5 所示为S3DIS Area5数据集上DNG-Net的分割性能. 使用类似文献[21 ]的方法,通过网格采样对数据进行预处理. ...
2
... 由于点云固有的无序性、不规则性及稀疏性, 难以直接应用传统二维卷积方法. 近年来,深度学习方法在处理点云数据方面[5 -7 ] 进展显著,部分工作间接地对点云进行处理,将点云转换为规则的体素[6 ] 或多视图图像[5 ] . 尽管如此,这些方法通常存在计算复杂度高或几何信息丢失的情况. 相比而言,直接将原始点云作为输入是目前最简单高效的手段. PointNet是直接处理点云的开创性工作,逐点采用多层感知机,通过最大池化聚合高维特征,但忽略了点间关系[7 ] . 为此,PointNet++通过层次结构和局部分组进行改进,但对于局部特征的表示不足[8 ] . 此后,更多方法关注于局部特征学习的研究[12 ,17 -19 ] ,PointConv[17 ] 、KPConv[18 ] 和 PAConv[19 ] 等方法设计适合点云形状的卷积算子来获取相关特征. GBNet在局域内构建几何描述符,为网络提供低级的几何线索[20 ] . RepSurf通过重建三角形和伞面特征,显式地描述拓扑结构[21 ] . 此外,PointNN[22 ] 、DeLA[23 ] 均从轻量化角度进行改进,旨在降低计算复杂度,提升网络效率. ...
... [17 ]、KPConv[18 ] 和 PAConv[19 ] 等方法设计适合点云形状的卷积算子来获取相关特征. GBNet在局域内构建几何描述符,为网络提供低级的几何线索[20 ] . RepSurf通过重建三角形和伞面特征,显式地描述拓扑结构[21 ] . 此外,PointNN[22 ] 、DeLA[23 ] 均从轻量化角度进行改进,旨在降低计算复杂度,提升网络效率. ...
5
... 由于点云固有的无序性、不规则性及稀疏性, 难以直接应用传统二维卷积方法. 近年来,深度学习方法在处理点云数据方面[5 -7 ] 进展显著,部分工作间接地对点云进行处理,将点云转换为规则的体素[6 ] 或多视图图像[5 ] . 尽管如此,这些方法通常存在计算复杂度高或几何信息丢失的情况. 相比而言,直接将原始点云作为输入是目前最简单高效的手段. PointNet是直接处理点云的开创性工作,逐点采用多层感知机,通过最大池化聚合高维特征,但忽略了点间关系[7 ] . 为此,PointNet++通过层次结构和局部分组进行改进,但对于局部特征的表示不足[8 ] . 此后,更多方法关注于局部特征学习的研究[12 ,17 -19 ] ,PointConv[17 ] 、KPConv[18 ] 和 PAConv[19 ] 等方法设计适合点云形状的卷积算子来获取相关特征. GBNet在局域内构建几何描述符,为网络提供低级的几何线索[20 ] . RepSurf通过重建三角形和伞面特征,显式地描述拓扑结构[21 ] . 此外,PointNN[22 ] 、DeLA[23 ] 均从轻量化角度进行改进,旨在降低计算复杂度,提升网络效率. ...
... Classification result on ModelNet40 benchmark
Tab.1 方法 年份 mAcc/% OA/% PointNet[7 ] 2017 86.2 89.2 PointNet++[8 ] 2017 — 91.9 KPConv[18 ] 2019 — 92.9 DGCNN[13 ] 2019 90.2 92.9 PointASNL[11 ] 2020 — 92.9 PointTransformer[31 ] 2020 90.6 93.7 PointMixer[40 ] 2021 91.4 93.6 CurveNet[41 ] 2021 — 93.8 PointNeXT[42 ] 2022 91.1 94.0 DGCNN+HyCoRe[43 ] 2022 91.0 93.7 PointConT[44 ] 2023 — 93.5 MKConv[45 ] 2023 — 93.7 DNG-Net(本文方法) 2024 91.3 94.1
ModelNet40被视为点云分析的经典基准,但它不足以应对实际场景中的复杂情况. 在具有挑战性的ScanObjectNN基准测试上进行实验. ...
... Segmentation result on ShapeNetPart benchmark
Tab.3 方法 年份 mIoUcls /% mIoUins /% PointNet[7 ] 2017 80.4 83.7 PointNet++[8 ] 2017 81.9 85.1 KPConv[18 ] 2019 85.0 86.2 DGCNN[13 ] 2019 82.3 85.2 PointASNL[11 ] 2020 — 86.1 PAConv[19 ] 2021 84.6 86.1 CurveNet[41 ] 2021 — 86.6 PointTransformer[31 ] 2020 83.7 86.6 StratifiedFormer[16 ] 2022 85.1 86.6 PointMLP[46 ] 2022 84.6 86.1 Point2vec[47 ] 2023 84.6 86.3 MKConv[45 ] 2023 — 86.5 DNG-Net(本文方法) 2024 84.7 86.7
如图5 所示为DNG-Net在部件分割上预测值与真值的可视化对比. 可以看出,本文方法非常接近于真值,即使在部件边界部分也分割得较清晰. ...
... Segmentation result on ScanNetV2 benchmark
Tab.4 方法 年份 P /106 mIOUval /% mIOUtest /% PointNet++[8 ] 2017 — 53.5 55.7 KPConv[18 ] 2019 — 69.2 68.6 PointTransformer[31 ] 2021 7.8 70.6 — StratifiedFormer[16 ] 2022 18.8 74.3 73.7 PTv3[34 ] 2023 46.2 77.5 77.9 DNG-Net(本文方法) 2024 9.2 75.6 74.9
如表5 所示为S3DIS Area5数据集上DNG-Net的分割性能. 使用类似文献[21 ]的方法,通过网格采样对数据进行预处理. ...
... Segmentation result on S3DIS Area5 benchmark
Tab.5 方法 年份 mAcc/% OA/% mIOU/% KPConv[18 ] 2019 72.8 — 67.1 MKConv[45 ] 2023 75.1 89.6 67.7 RepSurf-U[21 ] 2022 76.0 90.2 68.9 SPoTr[32 ] 2023 76.4 90.7 70.8 DNG-Net(本文方法) 2024 76.4 91.0 69.8
DNG-Net在OA、mAcc和mIoU 3个评价指标上表现出了优秀的结果, 该方法在保持与SPoTr相当的mAcc(76.4%)的同时,实现了最高的OA(91.0%). 如图6 所示为对语义分割的部分结果进行的可视化,在一些实例,如椅子、书柜上有着良好的分割效果. ...
3
... 由于点云固有的无序性、不规则性及稀疏性, 难以直接应用传统二维卷积方法. 近年来,深度学习方法在处理点云数据方面[5 -7 ] 进展显著,部分工作间接地对点云进行处理,将点云转换为规则的体素[6 ] 或多视图图像[5 ] . 尽管如此,这些方法通常存在计算复杂度高或几何信息丢失的情况. 相比而言,直接将原始点云作为输入是目前最简单高效的手段. PointNet是直接处理点云的开创性工作,逐点采用多层感知机,通过最大池化聚合高维特征,但忽略了点间关系[7 ] . 为此,PointNet++通过层次结构和局部分组进行改进,但对于局部特征的表示不足[8 ] . 此后,更多方法关注于局部特征学习的研究[12 ,17 -19 ] ,PointConv[17 ] 、KPConv[18 ] 和 PAConv[19 ] 等方法设计适合点云形状的卷积算子来获取相关特征. GBNet在局域内构建几何描述符,为网络提供低级的几何线索[20 ] . RepSurf通过重建三角形和伞面特征,显式地描述拓扑结构[21 ] . 此外,PointNN[22 ] 、DeLA[23 ] 均从轻量化角度进行改进,旨在降低计算复杂度,提升网络效率. ...
... [19 ]等方法设计适合点云形状的卷积算子来获取相关特征. GBNet在局域内构建几何描述符,为网络提供低级的几何线索[20 ] . RepSurf通过重建三角形和伞面特征,显式地描述拓扑结构[21 ] . 此外,PointNN[22 ] 、DeLA[23 ] 均从轻量化角度进行改进,旨在降低计算复杂度,提升网络效率. ...
... Segmentation result on ShapeNetPart benchmark
Tab.3 方法 年份 mIoUcls /% mIoUins /% PointNet[7 ] 2017 80.4 83.7 PointNet++[8 ] 2017 81.9 85.1 KPConv[18 ] 2019 85.0 86.2 DGCNN[13 ] 2019 82.3 85.2 PointASNL[11 ] 2020 — 86.1 PAConv[19 ] 2021 84.6 86.1 CurveNet[41 ] 2021 — 86.6 PointTransformer[31 ] 2020 83.7 86.6 StratifiedFormer[16 ] 2022 85.1 86.6 PointMLP[46 ] 2022 84.6 86.1 Point2vec[47 ] 2023 84.6 86.3 MKConv[45 ] 2023 — 86.5 DNG-Net(本文方法) 2024 84.7 86.7
如图5 所示为DNG-Net在部件分割上预测值与真值的可视化对比. 可以看出,本文方法非常接近于真值,即使在部件边界部分也分割得较清晰. ...
Geometric back-projection network for point cloud classification
4
2021
... 由于点云固有的无序性、不规则性及稀疏性, 难以直接应用传统二维卷积方法. 近年来,深度学习方法在处理点云数据方面[5 -7 ] 进展显著,部分工作间接地对点云进行处理,将点云转换为规则的体素[6 ] 或多视图图像[5 ] . 尽管如此,这些方法通常存在计算复杂度高或几何信息丢失的情况. 相比而言,直接将原始点云作为输入是目前最简单高效的手段. PointNet是直接处理点云的开创性工作,逐点采用多层感知机,通过最大池化聚合高维特征,但忽略了点间关系[7 ] . 为此,PointNet++通过层次结构和局部分组进行改进,但对于局部特征的表示不足[8 ] . 此后,更多方法关注于局部特征学习的研究[12 ,17 -19 ] ,PointConv[17 ] 、KPConv[18 ] 和 PAConv[19 ] 等方法设计适合点云形状的卷积算子来获取相关特征. GBNet在局域内构建几何描述符,为网络提供低级的几何线索[20 ] . RepSurf通过重建三角形和伞面特征,显式地描述拓扑结构[21 ] . 此外,PointNN[22 ] 、DeLA[23 ] 均从轻量化角度进行改进,旨在降低计算复杂度,提升网络效率. ...
... Attention机制[29 ] 作为Transformer中的核心操作,具有捕获远程依赖关系的能力,目前被广泛应用到自然语言处理和二维图像任务中. 由于Attention机制本身不受输入顺序的影响,具有置换不变性,在本质上适用于点云分析. 近年来,Lai等[16 ,20 ,30 -34 ] 在点云分析中采用了注意力操作. Zhao等[31 ] 将注意力机制引入点云,提出向量自注意算子,构建减法关系生成注意权值,但缺乏直接捕获远程依赖的能力,对各种扰动的鲁棒性不足. GBNet提出通道亲和注意力,改进上下文信息建模[20 ] . SPoTr采用解纠缠注意力聚集自定位点特征,提高了模型的可扩展性[32 ] . PTv3采用序列化点云的特定模式替代了普通邻域搜寻操作,显著提高了效率[34 ] . StratifiedFormer通过体素化将点云分割为不同分辨率的窗口,在每个窗口中利用局部注意力操作进行扩展,但感受野很局限[16 ] . 本文利用注意力采样得到更具代表性的全局关键点,借鉴交叉注意力的思想,将全局关键点信息与局部特征进行充分交互. 这种交互使得短程和远程依赖相互融合,显著增大了局部点的空间跨度,提升了特征的表示能力,使特征更有判别性. ...
... [20 ]. SPoTr采用解纠缠注意力聚集自定位点特征,提高了模型的可扩展性[32 ] . PTv3采用序列化点云的特定模式替代了普通邻域搜寻操作,显著提高了效率[34 ] . StratifiedFormer通过体素化将点云分割为不同分辨率的窗口,在每个窗口中利用局部注意力操作进行扩展,但感受野很局限[16 ] . 本文利用注意力采样得到更具代表性的全局关键点,借鉴交叉注意力的思想,将全局关键点信息与局部特征进行充分交互. 这种交互使得短程和远程依赖相互融合,显著增大了局部点的空间跨度,提升了特征的表示能力,使特征更有判别性. ...
... Classification result on ScanObjectNN benchmark
Tab.2 方法 年份 mAcc/% OA/% PointNet[7 ] 2017 63.4 68.2 PointNet++[8 ] 2017 75.4 77.9 DGCNN[13 ] 2019 73.6 78.1 GBNet[20 ] 2021 77.8 80.5 PointMLP[46 ] 2022 84.4 85.7 RepSurf-U[21 ] 2022 83.1 86.0 PointMLP+HyCoRe[43 ] 2022 85.9 87.2 PointNeXT[42 ] 2022 86.8 88.2 PointConT[44 ] 2023 86.0 88.0 SPoTr[32 ] 2023 86.8 88.6 DNG-Net(本文方法) 2024 88.3 89.6
3.3. 部件分割任务 在ShapeNetPart上进行部件分割实验,遵循文献[7 ]的设置,随机选择2 048个点作为输入,进行公平的比较. 对于评估指标,采用类别平均交并比mIoUcls 和实例平均交并比mIoUins . ...
4
... 由于点云固有的无序性、不规则性及稀疏性, 难以直接应用传统二维卷积方法. 近年来,深度学习方法在处理点云数据方面[5 -7 ] 进展显著,部分工作间接地对点云进行处理,将点云转换为规则的体素[6 ] 或多视图图像[5 ] . 尽管如此,这些方法通常存在计算复杂度高或几何信息丢失的情况. 相比而言,直接将原始点云作为输入是目前最简单高效的手段. PointNet是直接处理点云的开创性工作,逐点采用多层感知机,通过最大池化聚合高维特征,但忽略了点间关系[7 ] . 为此,PointNet++通过层次结构和局部分组进行改进,但对于局部特征的表示不足[8 ] . 此后,更多方法关注于局部特征学习的研究[12 ,17 -19 ] ,PointConv[17 ] 、KPConv[18 ] 和 PAConv[19 ] 等方法设计适合点云形状的卷积算子来获取相关特征. GBNet在局域内构建几何描述符,为网络提供低级的几何线索[20 ] . RepSurf通过重建三角形和伞面特征,显式地描述拓扑结构[21 ] . 此外,PointNN[22 ] 、DeLA[23 ] 均从轻量化角度进行改进,旨在降低计算复杂度,提升网络效率. ...
... Classification result on ScanObjectNN benchmark
Tab.2 方法 年份 mAcc/% OA/% PointNet[7 ] 2017 63.4 68.2 PointNet++[8 ] 2017 75.4 77.9 DGCNN[13 ] 2019 73.6 78.1 GBNet[20 ] 2021 77.8 80.5 PointMLP[46 ] 2022 84.4 85.7 RepSurf-U[21 ] 2022 83.1 86.0 PointMLP+HyCoRe[43 ] 2022 85.9 87.2 PointNeXT[42 ] 2022 86.8 88.2 PointConT[44 ] 2023 86.0 88.0 SPoTr[32 ] 2023 86.8 88.6 DNG-Net(本文方法) 2024 88.3 89.6
3.3. 部件分割任务 在ShapeNetPart上进行部件分割实验,遵循文献[7 ]的设置,随机选择2 048个点作为输入,进行公平的比较. 对于评估指标,采用类别平均交并比mIoUcls 和实例平均交并比mIoUins . ...
... 如表5 所示为S3DIS Area5数据集上DNG-Net的分割性能. 使用类似文献[21 ]的方法,通过网格采样对数据进行预处理. ...
... Segmentation result on S3DIS Area5 benchmark
Tab.5 方法 年份 mAcc/% OA/% mIOU/% KPConv[18 ] 2019 72.8 — 67.1 MKConv[45 ] 2023 75.1 89.6 67.7 RepSurf-U[21 ] 2022 76.0 90.2 68.9 SPoTr[32 ] 2023 76.4 90.7 70.8 DNG-Net(本文方法) 2024 76.4 91.0 69.8
DNG-Net在OA、mAcc和mIoU 3个评价指标上表现出了优秀的结果, 该方法在保持与SPoTr相当的mAcc(76.4%)的同时,实现了最高的OA(91.0%). 如图6 所示为对语义分割的部分结果进行的可视化,在一些实例,如椅子、书柜上有着良好的分割效果. ...
1
... 由于点云固有的无序性、不规则性及稀疏性, 难以直接应用传统二维卷积方法. 近年来,深度学习方法在处理点云数据方面[5 -7 ] 进展显著,部分工作间接地对点云进行处理,将点云转换为规则的体素[6 ] 或多视图图像[5 ] . 尽管如此,这些方法通常存在计算复杂度高或几何信息丢失的情况. 相比而言,直接将原始点云作为输入是目前最简单高效的手段. PointNet是直接处理点云的开创性工作,逐点采用多层感知机,通过最大池化聚合高维特征,但忽略了点间关系[7 ] . 为此,PointNet++通过层次结构和局部分组进行改进,但对于局部特征的表示不足[8 ] . 此后,更多方法关注于局部特征学习的研究[12 ,17 -19 ] ,PointConv[17 ] 、KPConv[18 ] 和 PAConv[19 ] 等方法设计适合点云形状的卷积算子来获取相关特征. GBNet在局域内构建几何描述符,为网络提供低级的几何线索[20 ] . RepSurf通过重建三角形和伞面特征,显式地描述拓扑结构[21 ] . 此外,PointNN[22 ] 、DeLA[23 ] 均从轻量化角度进行改进,旨在降低计算复杂度,提升网络效率. ...
1
... 由于点云固有的无序性、不规则性及稀疏性, 难以直接应用传统二维卷积方法. 近年来,深度学习方法在处理点云数据方面[5 -7 ] 进展显著,部分工作间接地对点云进行处理,将点云转换为规则的体素[6 ] 或多视图图像[5 ] . 尽管如此,这些方法通常存在计算复杂度高或几何信息丢失的情况. 相比而言,直接将原始点云作为输入是目前最简单高效的手段. PointNet是直接处理点云的开创性工作,逐点采用多层感知机,通过最大池化聚合高维特征,但忽略了点间关系[7 ] . 为此,PointNet++通过层次结构和局部分组进行改进,但对于局部特征的表示不足[8 ] . 此后,更多方法关注于局部特征学习的研究[12 ,17 -19 ] ,PointConv[17 ] 、KPConv[18 ] 和 PAConv[19 ] 等方法设计适合点云形状的卷积算子来获取相关特征. GBNet在局域内构建几何描述符,为网络提供低级的几何线索[20 ] . RepSurf通过重建三角形和伞面特征,显式地描述拓扑结构[21 ] . 此外,PointNN[22 ] 、DeLA[23 ] 均从轻量化角度进行改进,旨在降低计算复杂度,提升网络效率. ...
Convolutional neural networks on graphs with fast localized spectral filtering
1
2016
... 图结构是用来建模点云局部几何结构的自然表示,将点云当作图的节点,依据点之间的空间邻近性和特征相似性来构建边缘向量. GCN的概念源自文献[24 ],为了降低计算复杂度,采用Chebyshev多项式来近似特征分解的过程. 最近关于点云上的图卷积的研究验证了GCN[13 ,15 ,25 -28 ] 的有效性. DGCNN提出EdgeConv,采用动态图编码中心点与其特征空间邻居之间的关系,对后续的工作产生了深远的影响[13 ] . DeepGCN通过堆叠多个图卷积层,采用残差连接,增加了模型深度,解决了图节点过平滑的问题[25 ] . 3D-GCN开发可变形的3D核,在训练期间更新核的形状和权重[26 ] . GSNet[27 ] 扩展了DGCNN[13 ] 的工作,在欧几里德空间和特征值空间中进行邻域聚合.LPD-Net[15 ] 在空间邻居和特征邻居上扩展DGCNN[13 ] ,进行聚合. AdaptConv根据动态学习的特征,为点生成自适应核[28 ] . ...
2
... 图结构是用来建模点云局部几何结构的自然表示,将点云当作图的节点,依据点之间的空间邻近性和特征相似性来构建边缘向量. GCN的概念源自文献[24 ],为了降低计算复杂度,采用Chebyshev多项式来近似特征分解的过程. 最近关于点云上的图卷积的研究验证了GCN[13 ,15 ,25 -28 ] 的有效性. DGCNN提出EdgeConv,采用动态图编码中心点与其特征空间邻居之间的关系,对后续的工作产生了深远的影响[13 ] . DeepGCN通过堆叠多个图卷积层,采用残差连接,增加了模型深度,解决了图节点过平滑的问题[25 ] . 3D-GCN开发可变形的3D核,在训练期间更新核的形状和权重[26 ] . GSNet[27 ] 扩展了DGCNN[13 ] 的工作,在欧几里德空间和特征值空间中进行邻域聚合.LPD-Net[15 ] 在空间邻居和特征邻居上扩展DGCNN[13 ] ,进行聚合. AdaptConv根据动态学习的特征,为点生成自适应核[28 ] . ...
... [25 ]. 3D-GCN开发可变形的3D核,在训练期间更新核的形状和权重[26 ] . GSNet[27 ] 扩展了DGCNN[13 ] 的工作,在欧几里德空间和特征值空间中进行邻域聚合.LPD-Net[15 ] 在空间邻居和特征邻居上扩展DGCNN[13 ] ,进行聚合. AdaptConv根据动态学习的特征,为点生成自适应核[28 ] . ...
1
... 图结构是用来建模点云局部几何结构的自然表示,将点云当作图的节点,依据点之间的空间邻近性和特征相似性来构建边缘向量. GCN的概念源自文献[24 ],为了降低计算复杂度,采用Chebyshev多项式来近似特征分解的过程. 最近关于点云上的图卷积的研究验证了GCN[13 ,15 ,25 -28 ] 的有效性. DGCNN提出EdgeConv,采用动态图编码中心点与其特征空间邻居之间的关系,对后续的工作产生了深远的影响[13 ] . DeepGCN通过堆叠多个图卷积层,采用残差连接,增加了模型深度,解决了图节点过平滑的问题[25 ] . 3D-GCN开发可变形的3D核,在训练期间更新核的形状和权重[26 ] . GSNet[27 ] 扩展了DGCNN[13 ] 的工作,在欧几里德空间和特征值空间中进行邻域聚合.LPD-Net[15 ] 在空间邻居和特征邻居上扩展DGCNN[13 ] ,进行聚合. AdaptConv根据动态学习的特征,为点生成自适应核[28 ] . ...
1
... 图结构是用来建模点云局部几何结构的自然表示,将点云当作图的节点,依据点之间的空间邻近性和特征相似性来构建边缘向量. GCN的概念源自文献[24 ],为了降低计算复杂度,采用Chebyshev多项式来近似特征分解的过程. 最近关于点云上的图卷积的研究验证了GCN[13 ,15 ,25 -28 ] 的有效性. DGCNN提出EdgeConv,采用动态图编码中心点与其特征空间邻居之间的关系,对后续的工作产生了深远的影响[13 ] . DeepGCN通过堆叠多个图卷积层,采用残差连接,增加了模型深度,解决了图节点过平滑的问题[25 ] . 3D-GCN开发可变形的3D核,在训练期间更新核的形状和权重[26 ] . GSNet[27 ] 扩展了DGCNN[13 ] 的工作,在欧几里德空间和特征值空间中进行邻域聚合.LPD-Net[15 ] 在空间邻居和特征邻居上扩展DGCNN[13 ] ,进行聚合. AdaptConv根据动态学习的特征,为点生成自适应核[28 ] . ...
2
... 图结构是用来建模点云局部几何结构的自然表示,将点云当作图的节点,依据点之间的空间邻近性和特征相似性来构建边缘向量. GCN的概念源自文献[24 ],为了降低计算复杂度,采用Chebyshev多项式来近似特征分解的过程. 最近关于点云上的图卷积的研究验证了GCN[13 ,15 ,25 -28 ] 的有效性. DGCNN提出EdgeConv,采用动态图编码中心点与其特征空间邻居之间的关系,对后续的工作产生了深远的影响[13 ] . DeepGCN通过堆叠多个图卷积层,采用残差连接,增加了模型深度,解决了图节点过平滑的问题[25 ] . 3D-GCN开发可变形的3D核,在训练期间更新核的形状和权重[26 ] . GSNet[27 ] 扩展了DGCNN[13 ] 的工作,在欧几里德空间和特征值空间中进行邻域聚合.LPD-Net[15 ] 在空间邻居和特征邻居上扩展DGCNN[13 ] ,进行聚合. AdaptConv根据动态学习的特征,为点生成自适应核[28 ] . ...
... [28 ]. ...
1
... Attention机制[29 ] 作为Transformer中的核心操作,具有捕获远程依赖关系的能力,目前被广泛应用到自然语言处理和二维图像任务中. 由于Attention机制本身不受输入顺序的影响,具有置换不变性,在本质上适用于点云分析. 近年来,Lai等[16 ,20 ,30 -34 ] 在点云分析中采用了注意力操作. Zhao等[31 ] 将注意力机制引入点云,提出向量自注意算子,构建减法关系生成注意权值,但缺乏直接捕获远程依赖的能力,对各种扰动的鲁棒性不足. GBNet提出通道亲和注意力,改进上下文信息建模[20 ] . SPoTr采用解纠缠注意力聚集自定位点特征,提高了模型的可扩展性[32 ] . PTv3采用序列化点云的特定模式替代了普通邻域搜寻操作,显著提高了效率[34 ] . StratifiedFormer通过体素化将点云分割为不同分辨率的窗口,在每个窗口中利用局部注意力操作进行扩展,但感受野很局限[16 ] . 本文利用注意力采样得到更具代表性的全局关键点,借鉴交叉注意力的思想,将全局关键点信息与局部特征进行充分交互. 这种交互使得短程和远程依赖相互融合,显著增大了局部点的空间跨度,提升了特征的表示能力,使特征更有判别性. ...
Pct: Point cloud transformer
1
2021
... Attention机制[29 ] 作为Transformer中的核心操作,具有捕获远程依赖关系的能力,目前被广泛应用到自然语言处理和二维图像任务中. 由于Attention机制本身不受输入顺序的影响,具有置换不变性,在本质上适用于点云分析. 近年来,Lai等[16 ,20 ,30 -34 ] 在点云分析中采用了注意力操作. Zhao等[31 ] 将注意力机制引入点云,提出向量自注意算子,构建减法关系生成注意权值,但缺乏直接捕获远程依赖的能力,对各种扰动的鲁棒性不足. GBNet提出通道亲和注意力,改进上下文信息建模[20 ] . SPoTr采用解纠缠注意力聚集自定位点特征,提高了模型的可扩展性[32 ] . PTv3采用序列化点云的特定模式替代了普通邻域搜寻操作,显著提高了效率[34 ] . StratifiedFormer通过体素化将点云分割为不同分辨率的窗口,在每个窗口中利用局部注意力操作进行扩展,但感受野很局限[16 ] . 本文利用注意力采样得到更具代表性的全局关键点,借鉴交叉注意力的思想,将全局关键点信息与局部特征进行充分交互. 这种交互使得短程和远程依赖相互融合,显著增大了局部点的空间跨度,提升了特征的表示能力,使特征更有判别性. ...
5
... Attention机制[29 ] 作为Transformer中的核心操作,具有捕获远程依赖关系的能力,目前被广泛应用到自然语言处理和二维图像任务中. 由于Attention机制本身不受输入顺序的影响,具有置换不变性,在本质上适用于点云分析. 近年来,Lai等[16 ,20 ,30 -34 ] 在点云分析中采用了注意力操作. Zhao等[31 ] 将注意力机制引入点云,提出向量自注意算子,构建减法关系生成注意权值,但缺乏直接捕获远程依赖的能力,对各种扰动的鲁棒性不足. GBNet提出通道亲和注意力,改进上下文信息建模[20 ] . SPoTr采用解纠缠注意力聚集自定位点特征,提高了模型的可扩展性[32 ] . PTv3采用序列化点云的特定模式替代了普通邻域搜寻操作,显著提高了效率[34 ] . StratifiedFormer通过体素化将点云分割为不同分辨率的窗口,在每个窗口中利用局部注意力操作进行扩展,但感受野很局限[16 ] . 本文利用注意力采样得到更具代表性的全局关键点,借鉴交叉注意力的思想,将全局关键点信息与局部特征进行充分交互. 这种交互使得短程和远程依赖相互融合,显著增大了局部点的空间跨度,提升了特征的表示能力,使特征更有判别性. ...
... Classification result on ModelNet40 benchmark
Tab.1 方法 年份 mAcc/% OA/% PointNet[7 ] 2017 86.2 89.2 PointNet++[8 ] 2017 — 91.9 KPConv[18 ] 2019 — 92.9 DGCNN[13 ] 2019 90.2 92.9 PointASNL[11 ] 2020 — 92.9 PointTransformer[31 ] 2020 90.6 93.7 PointMixer[40 ] 2021 91.4 93.6 CurveNet[41 ] 2021 — 93.8 PointNeXT[42 ] 2022 91.1 94.0 DGCNN+HyCoRe[43 ] 2022 91.0 93.7 PointConT[44 ] 2023 — 93.5 MKConv[45 ] 2023 — 93.7 DNG-Net(本文方法) 2024 91.3 94.1
ModelNet40被视为点云分析的经典基准,但它不足以应对实际场景中的复杂情况. 在具有挑战性的ScanObjectNN基准测试上进行实验. ...
... Segmentation result on ShapeNetPart benchmark
Tab.3 方法 年份 mIoUcls /% mIoUins /% PointNet[7 ] 2017 80.4 83.7 PointNet++[8 ] 2017 81.9 85.1 KPConv[18 ] 2019 85.0 86.2 DGCNN[13 ] 2019 82.3 85.2 PointASNL[11 ] 2020 — 86.1 PAConv[19 ] 2021 84.6 86.1 CurveNet[41 ] 2021 — 86.6 PointTransformer[31 ] 2020 83.7 86.6 StratifiedFormer[16 ] 2022 85.1 86.6 PointMLP[46 ] 2022 84.6 86.1 Point2vec[47 ] 2023 84.6 86.3 MKConv[45 ] 2023 — 86.5 DNG-Net(本文方法) 2024 84.7 86.7
如图5 所示为DNG-Net在部件分割上预测值与真值的可视化对比. 可以看出,本文方法非常接近于真值,即使在部件边界部分也分割得较清晰. ...
... Segmentation result on ScanNetV2 benchmark
Tab.4 方法 年份 P /106 mIOUval /% mIOUtest /% PointNet++[8 ] 2017 — 53.5 55.7 KPConv[18 ] 2019 — 69.2 68.6 PointTransformer[31 ] 2021 7.8 70.6 — StratifiedFormer[16 ] 2022 18.8 74.3 73.7 PTv3[34 ] 2023 46.2 77.5 77.9 DNG-Net(本文方法) 2024 9.2 75.6 74.9
如表5 所示为S3DIS Area5数据集上DNG-Net的分割性能. 使用类似文献[21 ]的方法,通过网格采样对数据进行预处理. ...
... Complexity analysis on ModelNet40
Tab.11 模型 FLOPs/109 P /106 OA/% PointNet[7 ] 0.5 3.5 89.2 PointNet++[8 ] 4.1 1.8 91.9 DGCNN[13 ] 3.0 2.6 92.9 PointTransformer[31 ] 18.4 9.6 93.7 CurveNet[41 ] 0.3 2.1 93.8 PointMixer[40 ] — 6.5 93.6 PointNeXT[42 ] 6.5 4.5 94.0 PointMLP[46 ] 15.7 13.2 94.1 DNG-Net(本文方法) 1.92 4.9 94.1
实验结果表明,DNG-Net在可接受的计算成本内显著优于其他方法. 另外,PointMLP和DNG-Net在总体精度上表现均为最优,但DNG-Net在FLOPs和参数量方面均显著优于PointMLP,FLOPs降低了约8.3倍,参数量降低了约2.7倍. 可见,本文所提出的方法在精度和复杂度之间取得了更好的平衡. ...
3
... Attention机制[29 ] 作为Transformer中的核心操作,具有捕获远程依赖关系的能力,目前被广泛应用到自然语言处理和二维图像任务中. 由于Attention机制本身不受输入顺序的影响,具有置换不变性,在本质上适用于点云分析. 近年来,Lai等[16 ,20 ,30 -34 ] 在点云分析中采用了注意力操作. Zhao等[31 ] 将注意力机制引入点云,提出向量自注意算子,构建减法关系生成注意权值,但缺乏直接捕获远程依赖的能力,对各种扰动的鲁棒性不足. GBNet提出通道亲和注意力,改进上下文信息建模[20 ] . SPoTr采用解纠缠注意力聚集自定位点特征,提高了模型的可扩展性[32 ] . PTv3采用序列化点云的特定模式替代了普通邻域搜寻操作,显著提高了效率[34 ] . StratifiedFormer通过体素化将点云分割为不同分辨率的窗口,在每个窗口中利用局部注意力操作进行扩展,但感受野很局限[16 ] . 本文利用注意力采样得到更具代表性的全局关键点,借鉴交叉注意力的思想,将全局关键点信息与局部特征进行充分交互. 这种交互使得短程和远程依赖相互融合,显著增大了局部点的空间跨度,提升了特征的表示能力,使特征更有判别性. ...
... Classification result on ScanObjectNN benchmark
Tab.2 方法 年份 mAcc/% OA/% PointNet[7 ] 2017 63.4 68.2 PointNet++[8 ] 2017 75.4 77.9 DGCNN[13 ] 2019 73.6 78.1 GBNet[20 ] 2021 77.8 80.5 PointMLP[46 ] 2022 84.4 85.7 RepSurf-U[21 ] 2022 83.1 86.0 PointMLP+HyCoRe[43 ] 2022 85.9 87.2 PointNeXT[42 ] 2022 86.8 88.2 PointConT[44 ] 2023 86.0 88.0 SPoTr[32 ] 2023 86.8 88.6 DNG-Net(本文方法) 2024 88.3 89.6
3.3. 部件分割任务 在ShapeNetPart上进行部件分割实验,遵循文献[7 ]的设置,随机选择2 048个点作为输入,进行公平的比较. 对于评估指标,采用类别平均交并比mIoUcls 和实例平均交并比mIoUins . ...
... Segmentation result on S3DIS Area5 benchmark
Tab.5 方法 年份 mAcc/% OA/% mIOU/% KPConv[18 ] 2019 72.8 — 67.1 MKConv[45 ] 2023 75.1 89.6 67.7 RepSurf-U[21 ] 2022 76.0 90.2 68.9 SPoTr[32 ] 2023 76.4 90.7 70.8 DNG-Net(本文方法) 2024 76.4 91.0 69.8
DNG-Net在OA、mAcc和mIoU 3个评价指标上表现出了优秀的结果, 该方法在保持与SPoTr相当的mAcc(76.4%)的同时,实现了最高的OA(91.0%). 如图6 所示为对语义分割的部分结果进行的可视化,在一些实例,如椅子、书柜上有着良好的分割效果. ...
3
... Attention机制[29 ] 作为Transformer中的核心操作,具有捕获远程依赖关系的能力,目前被广泛应用到自然语言处理和二维图像任务中. 由于Attention机制本身不受输入顺序的影响,具有置换不变性,在本质上适用于点云分析. 近年来,Lai等[16 ,20 ,30 -34 ] 在点云分析中采用了注意力操作. Zhao等[31 ] 将注意力机制引入点云,提出向量自注意算子,构建减法关系生成注意权值,但缺乏直接捕获远程依赖的能力,对各种扰动的鲁棒性不足. GBNet提出通道亲和注意力,改进上下文信息建模[20 ] . SPoTr采用解纠缠注意力聚集自定位点特征,提高了模型的可扩展性[32 ] . PTv3采用序列化点云的特定模式替代了普通邻域搜寻操作,显著提高了效率[34 ] . StratifiedFormer通过体素化将点云分割为不同分辨率的窗口,在每个窗口中利用局部注意力操作进行扩展,但感受野很局限[16 ] . 本文利用注意力采样得到更具代表性的全局关键点,借鉴交叉注意力的思想,将全局关键点信息与局部特征进行充分交互. 这种交互使得短程和远程依赖相互融合,显著增大了局部点的空间跨度,提升了特征的表示能力,使特征更有判别性. ...
... [34 ]. StratifiedFormer通过体素化将点云分割为不同分辨率的窗口,在每个窗口中利用局部注意力操作进行扩展,但感受野很局限[16 ] . 本文利用注意力采样得到更具代表性的全局关键点,借鉴交叉注意力的思想,将全局关键点信息与局部特征进行充分交互. 这种交互使得短程和远程依赖相互融合,显著增大了局部点的空间跨度,提升了特征的表示能力,使特征更有判别性. ...
... Segmentation result on ScanNetV2 benchmark
Tab.4 方法 年份 P /106 mIOUval /% mIOUtest /% PointNet++[8 ] 2017 — 53.5 55.7 KPConv[18 ] 2019 — 69.2 68.6 PointTransformer[31 ] 2021 7.8 70.6 — StratifiedFormer[16 ] 2022 18.8 74.3 73.7 PTv3[34 ] 2023 46.2 77.5 77.9 DNG-Net(本文方法) 2024 9.2 75.6 74.9
如表5 所示为S3DIS Area5数据集上DNG-Net的分割性能. 使用类似文献[21 ]的方法,通过网格采样对数据进行预处理. ...
2
... ModelNet40[35 ] :由12 311个CAD模型组成,共分为40个类别,其中含有9 843个训练样本和2 468个测试样本. ...
... 在ModelNet40[35 ] 数据集上进行实验,从每个样本中随机采样1024 个点作为实验输入. 对于评估指标,使用类平均精度mAcc和总体精度OA. ...
1
... ScanObjectNN[36 ] :由从真实世界室内扫描中提取的遮挡对象组成,具有挑战性,包括15个类别的2902 个三维物体. ...
A scalable active framework for region annotation in 3d shape collections
1
2016
... ShapeNetPart[37 ] :由来自16个类别的16 881个CAD模型组成,部件共有50种,每个类别分别用2~5个部分标签进行注释. ...
1
... ScanNetv2[38 ] :该数据集相对较大,包含1 513个场景、20个语义类别,用于训练和评估. ...
1
... S3DIS[39 ] :室内场景的大型数据集,包含13个类别. 点云数据采集自6个大尺度区域,271个房间,超过2.15亿个点. ...
2
... Classification result on ModelNet40 benchmark
Tab.1 方法 年份 mAcc/% OA/% PointNet[7 ] 2017 86.2 89.2 PointNet++[8 ] 2017 — 91.9 KPConv[18 ] 2019 — 92.9 DGCNN[13 ] 2019 90.2 92.9 PointASNL[11 ] 2020 — 92.9 PointTransformer[31 ] 2020 90.6 93.7 PointMixer[40 ] 2021 91.4 93.6 CurveNet[41 ] 2021 — 93.8 PointNeXT[42 ] 2022 91.1 94.0 DGCNN+HyCoRe[43 ] 2022 91.0 93.7 PointConT[44 ] 2023 — 93.5 MKConv[45 ] 2023 — 93.7 DNG-Net(本文方法) 2024 91.3 94.1
ModelNet40被视为点云分析的经典基准,但它不足以应对实际场景中的复杂情况. 在具有挑战性的ScanObjectNN基准测试上进行实验. ...
... Complexity analysis on ModelNet40
Tab.11 模型 FLOPs/109 P /106 OA/% PointNet[7 ] 0.5 3.5 89.2 PointNet++[8 ] 4.1 1.8 91.9 DGCNN[13 ] 3.0 2.6 92.9 PointTransformer[31 ] 18.4 9.6 93.7 CurveNet[41 ] 0.3 2.1 93.8 PointMixer[40 ] — 6.5 93.6 PointNeXT[42 ] 6.5 4.5 94.0 PointMLP[46 ] 15.7 13.2 94.1 DNG-Net(本文方法) 1.92 4.9 94.1
实验结果表明,DNG-Net在可接受的计算成本内显著优于其他方法. 另外,PointMLP和DNG-Net在总体精度上表现均为最优,但DNG-Net在FLOPs和参数量方面均显著优于PointMLP,FLOPs降低了约8.3倍,参数量降低了约2.7倍. 可见,本文所提出的方法在精度和复杂度之间取得了更好的平衡. ...
CurveNet: curvature-based multitask learning deep networks for 3D object recognition
3
2020
... Classification result on ModelNet40 benchmark
Tab.1 方法 年份 mAcc/% OA/% PointNet[7 ] 2017 86.2 89.2 PointNet++[8 ] 2017 — 91.9 KPConv[18 ] 2019 — 92.9 DGCNN[13 ] 2019 90.2 92.9 PointASNL[11 ] 2020 — 92.9 PointTransformer[31 ] 2020 90.6 93.7 PointMixer[40 ] 2021 91.4 93.6 CurveNet[41 ] 2021 — 93.8 PointNeXT[42 ] 2022 91.1 94.0 DGCNN+HyCoRe[43 ] 2022 91.0 93.7 PointConT[44 ] 2023 — 93.5 MKConv[45 ] 2023 — 93.7 DNG-Net(本文方法) 2024 91.3 94.1
ModelNet40被视为点云分析的经典基准,但它不足以应对实际场景中的复杂情况. 在具有挑战性的ScanObjectNN基准测试上进行实验. ...
... Segmentation result on ShapeNetPart benchmark
Tab.3 方法 年份 mIoUcls /% mIoUins /% PointNet[7 ] 2017 80.4 83.7 PointNet++[8 ] 2017 81.9 85.1 KPConv[18 ] 2019 85.0 86.2 DGCNN[13 ] 2019 82.3 85.2 PointASNL[11 ] 2020 — 86.1 PAConv[19 ] 2021 84.6 86.1 CurveNet[41 ] 2021 — 86.6 PointTransformer[31 ] 2020 83.7 86.6 StratifiedFormer[16 ] 2022 85.1 86.6 PointMLP[46 ] 2022 84.6 86.1 Point2vec[47 ] 2023 84.6 86.3 MKConv[45 ] 2023 — 86.5 DNG-Net(本文方法) 2024 84.7 86.7
如图5 所示为DNG-Net在部件分割上预测值与真值的可视化对比. 可以看出,本文方法非常接近于真值,即使在部件边界部分也分割得较清晰. ...
... Complexity analysis on ModelNet40
Tab.11 模型 FLOPs/109 P /106 OA/% PointNet[7 ] 0.5 3.5 89.2 PointNet++[8 ] 4.1 1.8 91.9 DGCNN[13 ] 3.0 2.6 92.9 PointTransformer[31 ] 18.4 9.6 93.7 CurveNet[41 ] 0.3 2.1 93.8 PointMixer[40 ] — 6.5 93.6 PointNeXT[42 ] 6.5 4.5 94.0 PointMLP[46 ] 15.7 13.2 94.1 DNG-Net(本文方法) 1.92 4.9 94.1
实验结果表明,DNG-Net在可接受的计算成本内显著优于其他方法. 另外,PointMLP和DNG-Net在总体精度上表现均为最优,但DNG-Net在FLOPs和参数量方面均显著优于PointMLP,FLOPs降低了约8.3倍,参数量降低了约2.7倍. 可见,本文所提出的方法在精度和复杂度之间取得了更好的平衡. ...
3
... Classification result on ModelNet40 benchmark
Tab.1 方法 年份 mAcc/% OA/% PointNet[7 ] 2017 86.2 89.2 PointNet++[8 ] 2017 — 91.9 KPConv[18 ] 2019 — 92.9 DGCNN[13 ] 2019 90.2 92.9 PointASNL[11 ] 2020 — 92.9 PointTransformer[31 ] 2020 90.6 93.7 PointMixer[40 ] 2021 91.4 93.6 CurveNet[41 ] 2021 — 93.8 PointNeXT[42 ] 2022 91.1 94.0 DGCNN+HyCoRe[43 ] 2022 91.0 93.7 PointConT[44 ] 2023 — 93.5 MKConv[45 ] 2023 — 93.7 DNG-Net(本文方法) 2024 91.3 94.1
ModelNet40被视为点云分析的经典基准,但它不足以应对实际场景中的复杂情况. 在具有挑战性的ScanObjectNN基准测试上进行实验. ...
... Classification result on ScanObjectNN benchmark
Tab.2 方法 年份 mAcc/% OA/% PointNet[7 ] 2017 63.4 68.2 PointNet++[8 ] 2017 75.4 77.9 DGCNN[13 ] 2019 73.6 78.1 GBNet[20 ] 2021 77.8 80.5 PointMLP[46 ] 2022 84.4 85.7 RepSurf-U[21 ] 2022 83.1 86.0 PointMLP+HyCoRe[43 ] 2022 85.9 87.2 PointNeXT[42 ] 2022 86.8 88.2 PointConT[44 ] 2023 86.0 88.0 SPoTr[32 ] 2023 86.8 88.6 DNG-Net(本文方法) 2024 88.3 89.6
3.3. 部件分割任务 在ShapeNetPart上进行部件分割实验,遵循文献[7 ]的设置,随机选择2 048个点作为输入,进行公平的比较. 对于评估指标,采用类别平均交并比mIoUcls 和实例平均交并比mIoUins . ...
... Complexity analysis on ModelNet40
Tab.11 模型 FLOPs/109 P /106 OA/% PointNet[7 ] 0.5 3.5 89.2 PointNet++[8 ] 4.1 1.8 91.9 DGCNN[13 ] 3.0 2.6 92.9 PointTransformer[31 ] 18.4 9.6 93.7 CurveNet[41 ] 0.3 2.1 93.8 PointMixer[40 ] — 6.5 93.6 PointNeXT[42 ] 6.5 4.5 94.0 PointMLP[46 ] 15.7 13.2 94.1 DNG-Net(本文方法) 1.92 4.9 94.1
实验结果表明,DNG-Net在可接受的计算成本内显著优于其他方法. 另外,PointMLP和DNG-Net在总体精度上表现均为最优,但DNG-Net在FLOPs和参数量方面均显著优于PointMLP,FLOPs降低了约8.3倍,参数量降低了约2.7倍. 可见,本文所提出的方法在精度和复杂度之间取得了更好的平衡. ...
Rethinking the compositionality of point clouds through regularization in the hyperbolic space
2
2022
... Classification result on ModelNet40 benchmark
Tab.1 方法 年份 mAcc/% OA/% PointNet[7 ] 2017 86.2 89.2 PointNet++[8 ] 2017 — 91.9 KPConv[18 ] 2019 — 92.9 DGCNN[13 ] 2019 90.2 92.9 PointASNL[11 ] 2020 — 92.9 PointTransformer[31 ] 2020 90.6 93.7 PointMixer[40 ] 2021 91.4 93.6 CurveNet[41 ] 2021 — 93.8 PointNeXT[42 ] 2022 91.1 94.0 DGCNN+HyCoRe[43 ] 2022 91.0 93.7 PointConT[44 ] 2023 — 93.5 MKConv[45 ] 2023 — 93.7 DNG-Net(本文方法) 2024 91.3 94.1
ModelNet40被视为点云分析的经典基准,但它不足以应对实际场景中的复杂情况. 在具有挑战性的ScanObjectNN基准测试上进行实验. ...
... Classification result on ScanObjectNN benchmark
Tab.2 方法 年份 mAcc/% OA/% PointNet[7 ] 2017 63.4 68.2 PointNet++[8 ] 2017 75.4 77.9 DGCNN[13 ] 2019 73.6 78.1 GBNet[20 ] 2021 77.8 80.5 PointMLP[46 ] 2022 84.4 85.7 RepSurf-U[21 ] 2022 83.1 86.0 PointMLP+HyCoRe[43 ] 2022 85.9 87.2 PointNeXT[42 ] 2022 86.8 88.2 PointConT[44 ] 2023 86.0 88.0 SPoTr[32 ] 2023 86.8 88.6 DNG-Net(本文方法) 2024 88.3 89.6
3.3. 部件分割任务 在ShapeNetPart上进行部件分割实验,遵循文献[7 ]的设置,随机选择2 048个点作为输入,进行公平的比较. 对于评估指标,采用类别平均交并比mIoUcls 和实例平均交并比mIoUins . ...
Point cloud classification using content-based transformer via clustering in feature space
2
2023
... Classification result on ModelNet40 benchmark
Tab.1 方法 年份 mAcc/% OA/% PointNet[7 ] 2017 86.2 89.2 PointNet++[8 ] 2017 — 91.9 KPConv[18 ] 2019 — 92.9 DGCNN[13 ] 2019 90.2 92.9 PointASNL[11 ] 2020 — 92.9 PointTransformer[31 ] 2020 90.6 93.7 PointMixer[40 ] 2021 91.4 93.6 CurveNet[41 ] 2021 — 93.8 PointNeXT[42 ] 2022 91.1 94.0 DGCNN+HyCoRe[43 ] 2022 91.0 93.7 PointConT[44 ] 2023 — 93.5 MKConv[45 ] 2023 — 93.7 DNG-Net(本文方法) 2024 91.3 94.1
ModelNet40被视为点云分析的经典基准,但它不足以应对实际场景中的复杂情况. 在具有挑战性的ScanObjectNN基准测试上进行实验. ...
... Classification result on ScanObjectNN benchmark
Tab.2 方法 年份 mAcc/% OA/% PointNet[7 ] 2017 63.4 68.2 PointNet++[8 ] 2017 75.4 77.9 DGCNN[13 ] 2019 73.6 78.1 GBNet[20 ] 2021 77.8 80.5 PointMLP[46 ] 2022 84.4 85.7 RepSurf-U[21 ] 2022 83.1 86.0 PointMLP+HyCoRe[43 ] 2022 85.9 87.2 PointNeXT[42 ] 2022 86.8 88.2 PointConT[44 ] 2023 86.0 88.0 SPoTr[32 ] 2023 86.8 88.6 DNG-Net(本文方法) 2024 88.3 89.6
3.3. 部件分割任务 在ShapeNetPart上进行部件分割实验,遵循文献[7 ]的设置,随机选择2 048个点作为输入,进行公平的比较. 对于评估指标,采用类别平均交并比mIoUcls 和实例平均交并比mIoUins . ...
MKConv: multidimensional feature representation for point cloud analysis
3
2023
... Classification result on ModelNet40 benchmark
Tab.1 方法 年份 mAcc/% OA/% PointNet[7 ] 2017 86.2 89.2 PointNet++[8 ] 2017 — 91.9 KPConv[18 ] 2019 — 92.9 DGCNN[13 ] 2019 90.2 92.9 PointASNL[11 ] 2020 — 92.9 PointTransformer[31 ] 2020 90.6 93.7 PointMixer[40 ] 2021 91.4 93.6 CurveNet[41 ] 2021 — 93.8 PointNeXT[42 ] 2022 91.1 94.0 DGCNN+HyCoRe[43 ] 2022 91.0 93.7 PointConT[44 ] 2023 — 93.5 MKConv[45 ] 2023 — 93.7 DNG-Net(本文方法) 2024 91.3 94.1
ModelNet40被视为点云分析的经典基准,但它不足以应对实际场景中的复杂情况. 在具有挑战性的ScanObjectNN基准测试上进行实验. ...
... Segmentation result on ShapeNetPart benchmark
Tab.3 方法 年份 mIoUcls /% mIoUins /% PointNet[7 ] 2017 80.4 83.7 PointNet++[8 ] 2017 81.9 85.1 KPConv[18 ] 2019 85.0 86.2 DGCNN[13 ] 2019 82.3 85.2 PointASNL[11 ] 2020 — 86.1 PAConv[19 ] 2021 84.6 86.1 CurveNet[41 ] 2021 — 86.6 PointTransformer[31 ] 2020 83.7 86.6 StratifiedFormer[16 ] 2022 85.1 86.6 PointMLP[46 ] 2022 84.6 86.1 Point2vec[47 ] 2023 84.6 86.3 MKConv[45 ] 2023 — 86.5 DNG-Net(本文方法) 2024 84.7 86.7
如图5 所示为DNG-Net在部件分割上预测值与真值的可视化对比. 可以看出,本文方法非常接近于真值,即使在部件边界部分也分割得较清晰. ...
... Segmentation result on S3DIS Area5 benchmark
Tab.5 方法 年份 mAcc/% OA/% mIOU/% KPConv[18 ] 2019 72.8 — 67.1 MKConv[45 ] 2023 75.1 89.6 67.7 RepSurf-U[21 ] 2022 76.0 90.2 68.9 SPoTr[32 ] 2023 76.4 90.7 70.8 DNG-Net(本文方法) 2024 76.4 91.0 69.8
DNG-Net在OA、mAcc和mIoU 3个评价指标上表现出了优秀的结果, 该方法在保持与SPoTr相当的mAcc(76.4%)的同时,实现了最高的OA(91.0%). 如图6 所示为对语义分割的部分结果进行的可视化,在一些实例,如椅子、书柜上有着良好的分割效果. ...
3
... Classification result on ScanObjectNN benchmark
Tab.2 方法 年份 mAcc/% OA/% PointNet[7 ] 2017 63.4 68.2 PointNet++[8 ] 2017 75.4 77.9 DGCNN[13 ] 2019 73.6 78.1 GBNet[20 ] 2021 77.8 80.5 PointMLP[46 ] 2022 84.4 85.7 RepSurf-U[21 ] 2022 83.1 86.0 PointMLP+HyCoRe[43 ] 2022 85.9 87.2 PointNeXT[42 ] 2022 86.8 88.2 PointConT[44 ] 2023 86.0 88.0 SPoTr[32 ] 2023 86.8 88.6 DNG-Net(本文方法) 2024 88.3 89.6
3.3. 部件分割任务 在ShapeNetPart上进行部件分割实验,遵循文献[7 ]的设置,随机选择2 048个点作为输入,进行公平的比较. 对于评估指标,采用类别平均交并比mIoUcls 和实例平均交并比mIoUins . ...
... Segmentation result on ShapeNetPart benchmark
Tab.3 方法 年份 mIoUcls /% mIoUins /% PointNet[7 ] 2017 80.4 83.7 PointNet++[8 ] 2017 81.9 85.1 KPConv[18 ] 2019 85.0 86.2 DGCNN[13 ] 2019 82.3 85.2 PointASNL[11 ] 2020 — 86.1 PAConv[19 ] 2021 84.6 86.1 CurveNet[41 ] 2021 — 86.6 PointTransformer[31 ] 2020 83.7 86.6 StratifiedFormer[16 ] 2022 85.1 86.6 PointMLP[46 ] 2022 84.6 86.1 Point2vec[47 ] 2023 84.6 86.3 MKConv[45 ] 2023 — 86.5 DNG-Net(本文方法) 2024 84.7 86.7
如图5 所示为DNG-Net在部件分割上预测值与真值的可视化对比. 可以看出,本文方法非常接近于真值,即使在部件边界部分也分割得较清晰. ...
... Complexity analysis on ModelNet40
Tab.11 模型 FLOPs/109 P /106 OA/% PointNet[7 ] 0.5 3.5 89.2 PointNet++[8 ] 4.1 1.8 91.9 DGCNN[13 ] 3.0 2.6 92.9 PointTransformer[31 ] 18.4 9.6 93.7 CurveNet[41 ] 0.3 2.1 93.8 PointMixer[40 ] — 6.5 93.6 PointNeXT[42 ] 6.5 4.5 94.0 PointMLP[46 ] 15.7 13.2 94.1 DNG-Net(本文方法) 1.92 4.9 94.1
实验结果表明,DNG-Net在可接受的计算成本内显著优于其他方法. 另外,PointMLP和DNG-Net在总体精度上表现均为最优,但DNG-Net在FLOPs和参数量方面均显著优于PointMLP,FLOPs降低了约8.3倍,参数量降低了约2.7倍. 可见,本文所提出的方法在精度和复杂度之间取得了更好的平衡. ...
1
... Segmentation result on ShapeNetPart benchmark
Tab.3 方法 年份 mIoUcls /% mIoUins /% PointNet[7 ] 2017 80.4 83.7 PointNet++[8 ] 2017 81.9 85.1 KPConv[18 ] 2019 85.0 86.2 DGCNN[13 ] 2019 82.3 85.2 PointASNL[11 ] 2020 — 86.1 PAConv[19 ] 2021 84.6 86.1 CurveNet[41 ] 2021 — 86.6 PointTransformer[31 ] 2020 83.7 86.6 StratifiedFormer[16 ] 2022 85.1 86.6 PointMLP[46 ] 2022 84.6 86.1 Point2vec[47 ] 2023 84.6 86.3 MKConv[45 ] 2023 — 86.5 DNG-Net(本文方法) 2024 84.7 86.7
如图5 所示为DNG-Net在部件分割上预测值与真值的可视化对比. 可以看出,本文方法非常接近于真值,即使在部件边界部分也分割得较清晰. ...
1
... 通过实验发现,仅使用位置信息,实验性能不是很好(见模型A、B),模型D加入了点间距离$ l $ [48 ] 在局部采用的线性、平面性、散射等特征进行替换,但总体精度不理想. 这种局部几何特征无法与本文现有的网络层或其他组件良好地集成,导致特征表示可能不准确. ...