机器学习(machine learning, ML)凭借其建立数据与识别结果之间复杂映射关系的优秀性能,在轮轨损伤检测领域得到广泛应用[6-8]. 基于ML的车轮扁疤识别方法,不仅可以实现定性识别,分辨车轮是否存在扁疤故障,还可以实现定量识别,精确到车轮扁疤的尺寸. 根据处理原始数据的不同方式,ML可以分为一维和二维信号模式. Chen等[9]基于一维轴箱振动加速度时域数据,通过车轮半径差间接实现车轮扁疤识别以及故障程度预测. Ye等[10]提取一维轴箱振动数据的平均峰值,利用粒子群-克里金代理模型构建车轮扁疤长度、车辆速度和轴箱垂向振动信号之间存在的非线性映射关系,准确估计了车轮扁疤长度. 由于时域特征下的轴箱振动加速度包含信息有限,一些时频分析结果被用于基于ML的车轮扁疤识别的输入. 赵蓉等[11]通过高阶谱分析提取基于钢轨振动信号的二维等高线图的纹理特征,结合车速输入粒子群-支持向量机模型中,有效确定了车轮扁疤故障等级.
虽然ML能构建样本集与车轮扁疤尺寸之间的复杂非线性映射关系,但以何种输入形式或者输入组合能取得较好识别性能,可参考的文献报道较少. 此外,大部分车轮扁疤定量识别研究集中于识别车轮扁疤的单一尺寸. 在车辆实际服役过程中,车轮扁疤长度和深度的映射关系并非单一固定,仅针对单一尺寸车轮扁疤进行定量识别,无法满足全面且高效的车轮扁疤状态监测需求. 本研究从基于机器学习的车轮扁疤定量识别角度出发,提出基于多结构数据驱动的车轮扁疤定量识别研究方法. 通过构建地铁车辆−轨道刚柔耦合动力学模型,获取各种扁疤激励下的轴箱振动信号,并将该信号转化为一维/二维样本集,融合速度信息输入多输入卷积神经网络(multi-input convolutional neural network, MCNN)模型,对比分析不同输入结构形式下模型的识别性能,探寻最优输入样本组合,实现高效的车轮扁疤智能定量识别.
1. 多输入卷积神经网络基本理论
MCNN模型主要分为2个部分:特征提取和回归预测.
1.1. 特征提取
该部分由交替排列的卷积层、最大池化层、激活层和全局最大池化层共同组成. 卷积层包含多个滤波器,负责提取输入的特征并编码为特征图. 滤波器内神经元与输入点直接连接,并共享权重参数,有效减少网络的优化复杂度,加速训练过程. 卷积层数学模型表达式[12]为
式中:i、j分别为输入与输出数据的位置索引,
式中:x为输入至非线性激活层运算的特征信息. 池化层通常紧随激活层,起特征降维的作用. 采用最大池化算子进行下采样,有效减少模型参数数量,运算式为
式中:
式中:
1.2. 回归预测
该部分由信息融合层、全连接层和输出层组成. 信息融合层将经过MCNN提取后的特征信息与车速信号融合输入至全连接层. 全连接层具有非线性变换和特征交互能力,增加模型的特征提取和应用泛化性能:
式中:k为网络层的序号,Yk为输出,Xk−1为展开的一维特征向量,Wk为权重系数,Bk为偏置项.
2. 所提方法的车轮扁疤定量识别流程
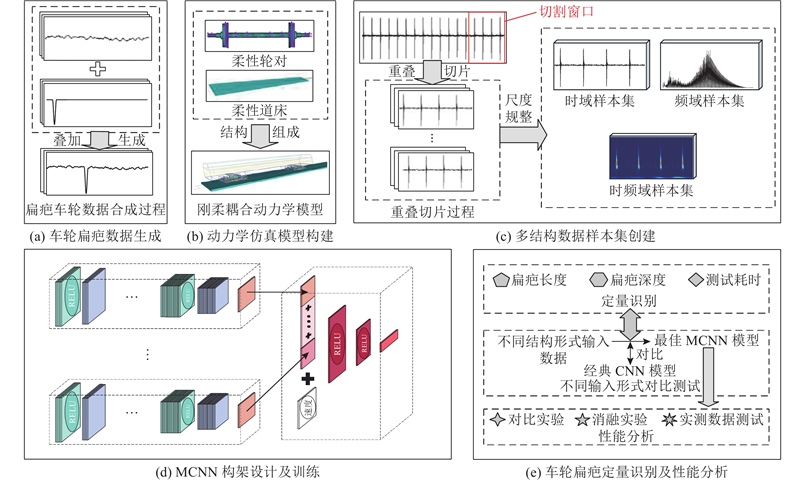
建立地铁车辆−轨道刚柔耦合动力学模型,获取不同工况下轴箱振动响应,制作不同数据结构表达形式的轴箱振动信号样本集,通过构建MCNN模型来映射车轮扁疤与轴箱加速度信号之间的相关关系,讨论分析不同数据结构输入下MCNN模型的识别性能,实现多结构数据驱动的车轮扁疤定量智能识别. 如图1所示,识别流程分为车轮扁疤数据生成,刚柔耦合动力学仿真模型构建,多结构数据样本集创建,MCNN构架设计及训练,车轮扁疤定量识别及性能分析.
图 1
图 1 所提方法的车轮扁疤定量识别流程图
Fig.1 Flowchart of proposed method for quantitative identification of wheel flats
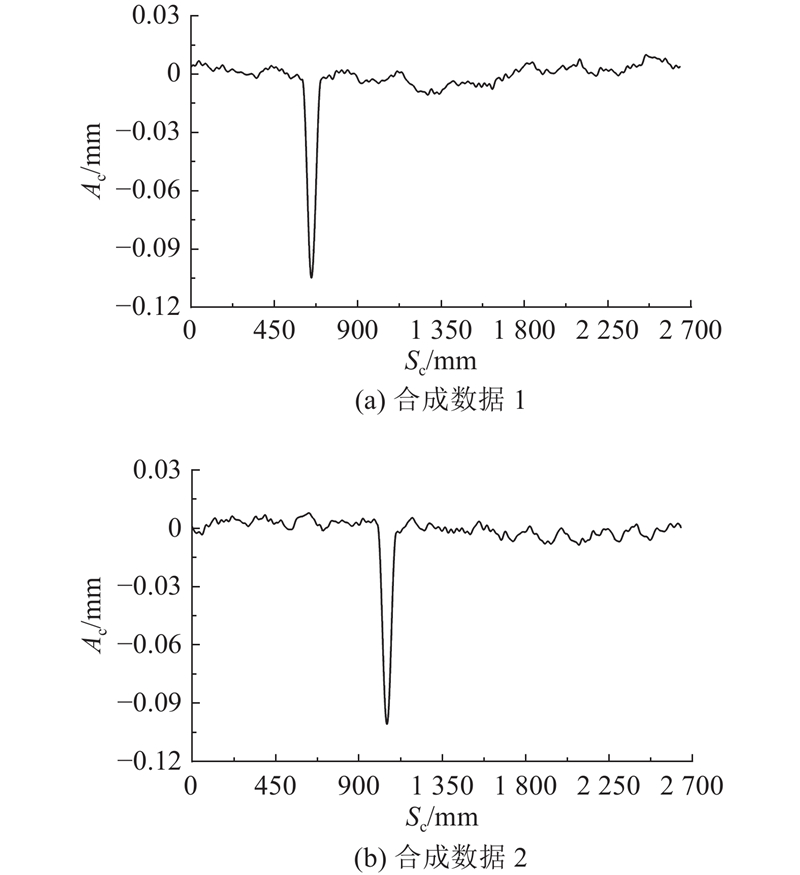
2.1. 车轮扁疤数据生成
式中:
表 1 仿真车轮扁疤尺寸
Tab.1
| Lf/mm | Df/mm | Lf/mm | Df/mm | |
| 30 | 0.1 | 70 | 0.1~0.7 | |
| 40 | 0.1~0.2 | 80 | 0.1~0.9 | |
| 50 | 0.1~0.3 | 90 | 0.1~1.0 | |
| 60 | 0.1~0.5 | 100 | 0.1~1.0 |
图 2
2.2. 刚柔耦合动力学仿真模型构建
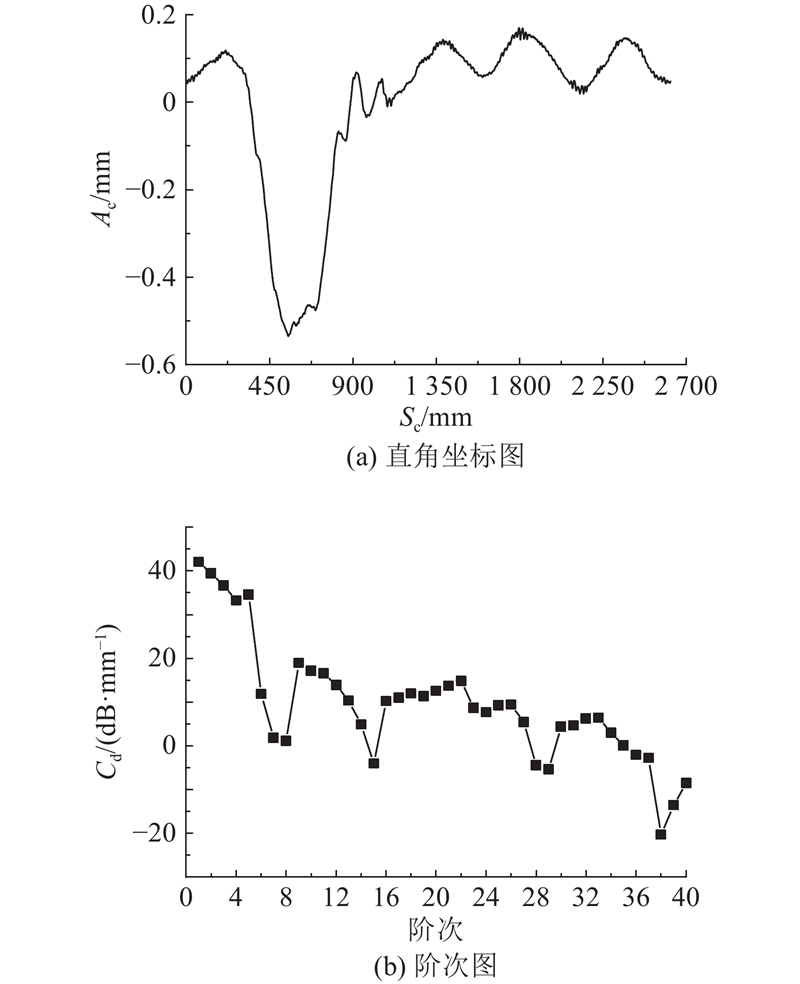
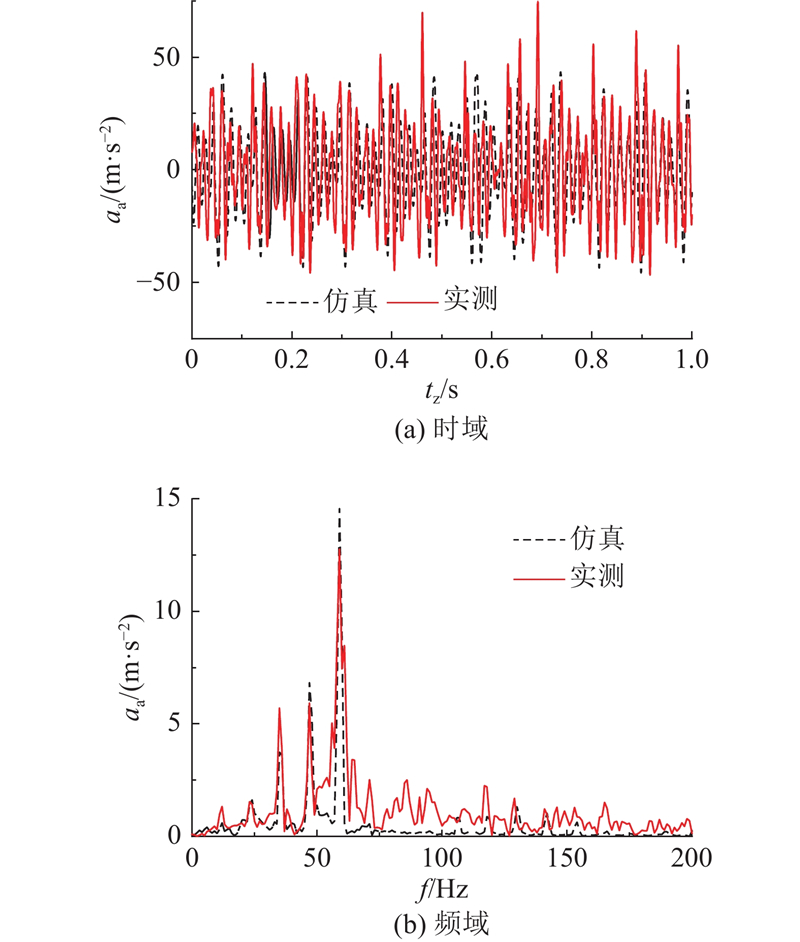
实测车轮扁疤激励下的轴箱振动加速度数据存在样本数量少、种类丰富度低的问题,建立动力学仿真模型以获取多种工况下的轴箱动态响应. 由于纯刚体模型无法有效模拟车轮扁疤引起的轮轨高频相互作用,联合Ansys和Simpack构建刚柔耦合动力学仿真模型[20-21]. 轮对、钢轨和道床均考虑为柔性体,建立轮对有限元模型并对该模型进行模态分析和子结构分析. 利用有限元法建立道床有限元模型,钢轨采用铁木辛柯梁模拟,通过模态叠加法在动力学模型中实现钢轨和道床的弹性化处理,相较纯刚体动力学仿真模型,实现更真实的刚柔耦合动力学仿真地铁车辆−轨道刚柔耦合动力学模型的主要结构参数如表2所示. 为了验证该动力学模型可靠性,将如图3所示的实测车轮不圆度输入动力学仿真模型. 图中,Cd为粗糙度水平. 如图4所示为实测与仿真轴箱振动加速度数据对比结果. 图中,aa为轴箱振动加速度,tz为时间,f为频率. 由图可知,仿真信号在时域、频域都与实测数据具有较高的一致性,表明建立的仿真模型具有较高的准确度.
表 2 仿真模型的主要结构参数
Tab.2
| 参数 | 数值 | 参数 | 数值 | |
| 车体质量/ t | 36.565 | 一系垂向悬挂刚度/(MN·m−1) | 0.326 | |
| 构架质量/ t | 2.533 | 二系垂向悬挂刚度/(MN·m−1) | 0.356 | |
| 轮对质量/ t | 1.349 | 扣件垂向刚度/(MN·m−1) | 55 | |
| 轴箱质量/ t | 0.109 | 扣件垂向阻尼/(kN·s·m−1) | 9.8 | |
| 车体转动惯量I/(t⋅m2) | 1 589.63 | 地基垂向刚度/(MN·m−1) | 170 | |
| 构架转动惯量/(t⋅m2) | 0.583 | 地基垂向阻尼/(kN·s·m−1) | 31 | |
| 轮对转动惯量/(t⋅m2) | 0.116 | — | — |
图 3
图 4
2.3. 不同形式输入样本集创建
将合成的扁疤车轮数据作为地铁车辆−轨道刚柔耦合动力学模型的车轮不平顺激励,轨道不平顺激励采用美国五级谱[22],设置车辆运行速度v=40~120 km/h,间隔为10 km/h,采样频率为5 000 Hz,以获取不同工况下的轴箱振动响应. 为了确保数据片段的数量与质量,以车轮旋转圈数为基准,对模型输出的轴箱振动响应数据进行切片采样. 切片单位选择是关键因素,过小的单位可能受到其他激励源的干扰,在某些情况下,车轮扁疤特征可能不明显;过大的单位可能导致样本不足,增加过拟合风险. 基于大量实验和文献[23]建议,以车轮旋转4圈为单位进行切片重采样,设置重叠量为车轮旋转1周的尺度,确保每段数据都包含相同数量的故障信息. 在不同速度工况下,数据片段的长度不一致,为此对仿真信号分别进行时域、频域和时频域处理,即三次样条曲线插值(cubic spline interpolation,CSI)、快速傅里叶变换(fast Fourier transform,FFT)和连续小波变换(continuous wavelet transform,CWT),以统一样本尺度并探究不同数据结构形式对车轮扁疤识别结果的影响.
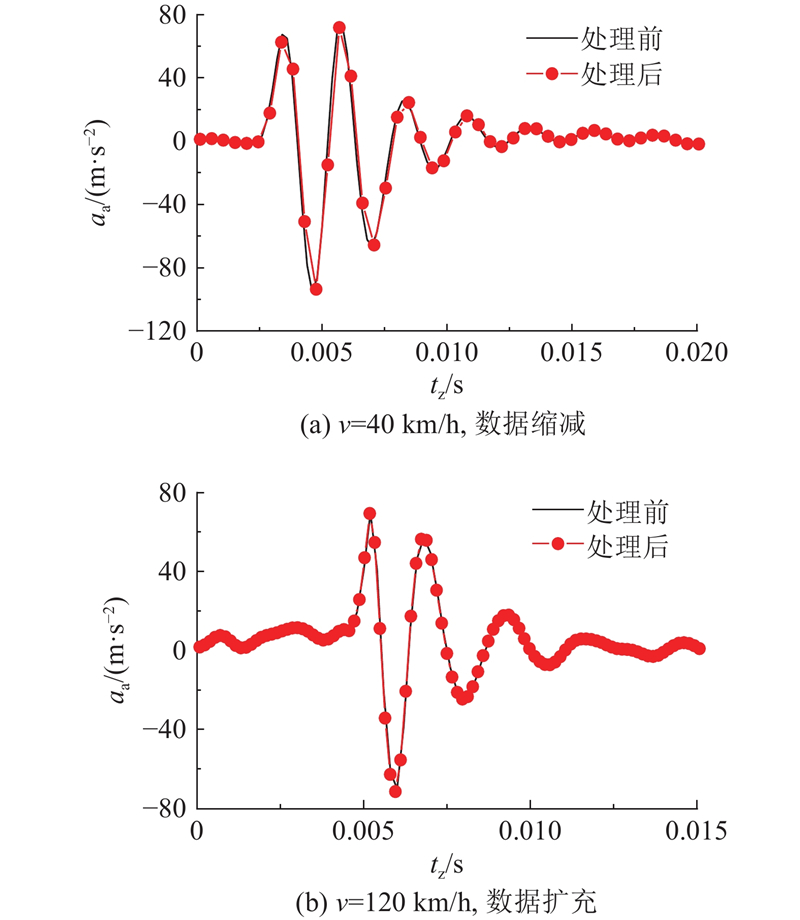
在时域处理过程中,将不同速度下的数据片段通过CSI对数据点进行缩减或扩充,每段数据统一规整为2 048个数据点. 为了清晰地展示数据片段缩减或扩充前后时域波形的差异,以长度为30 mm,深度为0.1 mm的扁疤轴箱振动加速度激励为例(后续样本数据展示均以该工况为例). 如图5所示为轴箱振动响应在2种速度工况下(最低速度为40 km/h,最高速度为120 km/h)车轮旋转1周的时域波形. 由图可知,经过CSI处理后的数据仍能较好地反映原始信号的时域特征.
图 5
图 5 轴箱在2种工况下的振动加速度(时域样本)
Fig.5 Vibration acceleration of axle box at two cases (time domain samples)
在频域处理过程中,重叠切片会导致每段数据的时间尺度不一致,经过FFT处理后的最小频率分辨率也会不同. 频率分辨率
采用设定最大截止频率的数据规整方法会导致每段样本尺度不一致[24]. 此外,受限于数据切片尺度,最小频域分辨率无法统一设置为1. 本研究提出特定频域数据规整方法,即在每个频域样本最小分辨率不同的情况下,固定取前
式中:
图 6
图 6 轴箱在2种工况下的振动加速度(频域样本)
Fig.6 Vibration acceleration of axle box at two cases (frequency domain samples)
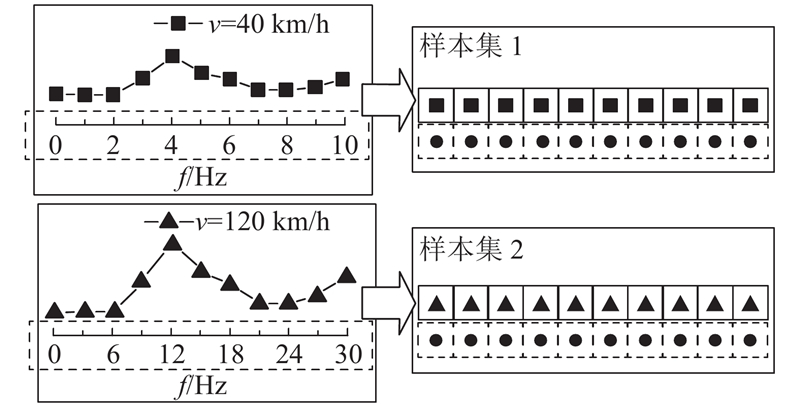
虽然该频域数据规整方法可统一频域样本集尺寸,但各样本集对应速度不同,每个点代表的频域含义不同. 如图7所示,在2种车辆运行速度工况下,样本集中前10个数据点代表的频率范围分别约为0~9 Hz和0~29 Hz. 这些数据点代表的频率信息存在差异,当它们被输入MCNN模型时,每个数据点会被按照顺序对应,导致相应频域信息丢失. 为此,在每个样本的通道维度上,将每个数据点与对应的频率信息(图中虚线框)结合,构建具有双通道的频域样本数据集.
图 7
图 8
图 8 轴箱在2种工况下的振动加速度(频域样本)
Fig.8 Vibration acceleration of axle box at two cases (time-frequency domain samples)
通过上述处理将经过重叠切片的车轮扁疤轴箱动态响应数据片段制作为时域、频域以及时频域3种不同结构形式的样本集. 在每种数据结构形式中,不同速度和尺寸的车轮扁疤样本集数量均匀分布,各扁疤尺寸对应的样本集数量均为711,具体尺寸如表1所示,总计33 417. 将样本集总数的80%作为训练集,剩下的20%作为测试集.
2.4. 模型结构设计及训练
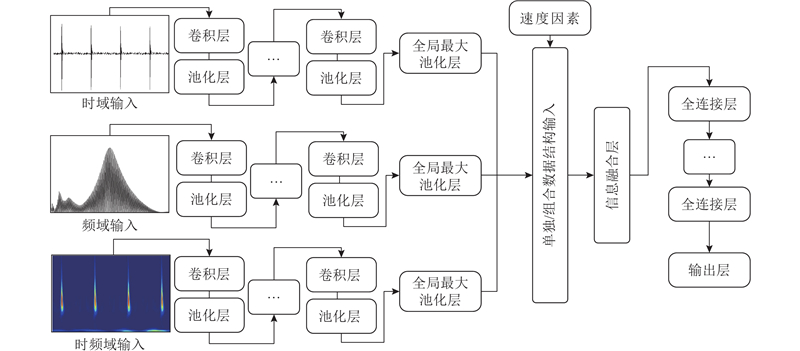
为了探究不同数据结构形式及其组合对车轮扁疤识别效果的影响,设计7种不同数据结构输入的MCNN模型,如图9所示. 图中,单独/组合数据结构输入的7种组合形式如下:组合1为时域,组合2为频域,组合3为时频域,组合4为时域、频域,组合5为时域、时频域,组合6为频域、时频域,组合7为时域、频域、时频域. 不同结构形式对应的特征提取部分采用相同神经网络结构参数,通过全局最大池化层将每个通道压缩为单一的数值,降低网络的计算复杂性[23]. 考虑到时域、频域和时频域信号往往缺失速度信息,在信息融合层额外引入速度信号作为模型的复合特征以提高MCNN模型对车轮扁疤的定量检测能力. 通过多层全连接层增加模型的非线性表达能力和一层输出层,实现车轮扁疤长度与深度的定量识别. 经过大量调参实验,确定MCNN模型的结构参数如表3所示. 采用补零技术维持特征图尺寸,通过设定50轮的早停机制来防止模型过拟合. 在训练过程中,采用128批次大小的批处理样本、Adam优化器和0.001的学习率. 均方误差MSE作为损失函数,计算式为
图 9
图 9 多输入卷积神经网络模型结构示意图
Fig.9 Schematic structure of multi-input convolutional neural network model
式中:n为样本数量,yi为第i个样本的真实值,
表 3 多输入卷积神经网络模型结构参数
Tab.3
| 类型 | K1D,K2D | NN | L1D,L2D | NK |
| 卷积层1 | 8×1,8×8 | — | 2×1,2×2 | 4 |
| 池化层1 | 2×1,2×2 | — | 2×1,2×2 | 4 |
| 卷积层2 | 4×1,4×4 | — | 2×1,2×2 | 8 |
| 池化层2 | 2×1,2×2 | — | 2×1,2×2 | 8 |
| 卷积层3 | 2×1,2×2 | — | 2×1,2×2 | 16 |
| 池化层3 | 2×1,2×2 | — | 2×1,2×2 | 16 |
| 全连接层1 | — | 16 | — | 1 |
| 全连接层2 | — | 8 | — | 1 |
| 输出层 | — | 2 | — | 1 |
2.5. 车轮扁疤定量识别及性能分析
采用平均绝对百分比误差MAPE与拟合度R2为评价指标综合评价模型性能,表达式分别为
式中:
3. 结果分析与讨论
3.1. 多输入卷积神经网络模型识别性能对比
在模型训练时,样本集不同的划分方法、模型不同的初始化权重等因素均可能对最后的识别结果产生影响. 为了消除随机项带来的干扰,采用十折交叉验证方法观察模型性能. 如表4所示为不同数据结构形式及组合输入至MCNN网络后,十折交叉验证的平均识别性能指标. 表中,ts为单个样本的平均处理时间. 由表可知,多组合输入结构形式相较于单一输入结构形式的识别性能更优秀. 这一优势伴随着ts增长,特别是当输入结构形式含有二维数据时,相对于其他组合其耗时增加较多. 在多输入结构形式中,组合7的识别性能达到最佳, 该组合的单个样本平均处理时间略高于其他输入形式,但仍满足车轮扁疤在线监测的时效性需求. 综上,当输入结构形式组合为时域、频域和时频域时,MCNN模型的整体识别性能最佳,下文将该组合形式的MCNN模型表示为TFTF-MCNN,其中T代表时域,F代表频域.
表 4 不同输入形式的识别性能对比
Tab.4
| 组合形式 | MAPE/% | R2 | ts/ms |
| 1 | 7.171 | ||
| 2 | 4.340 | ||
| 3 | 6.330 | ||
| 4 | 3.487 | ||
| 5 | 3.274 | ||
| 6 | 2.851 | ||
| 7 | 1.947 |
3.2. 卷积神经网络模型性能对比
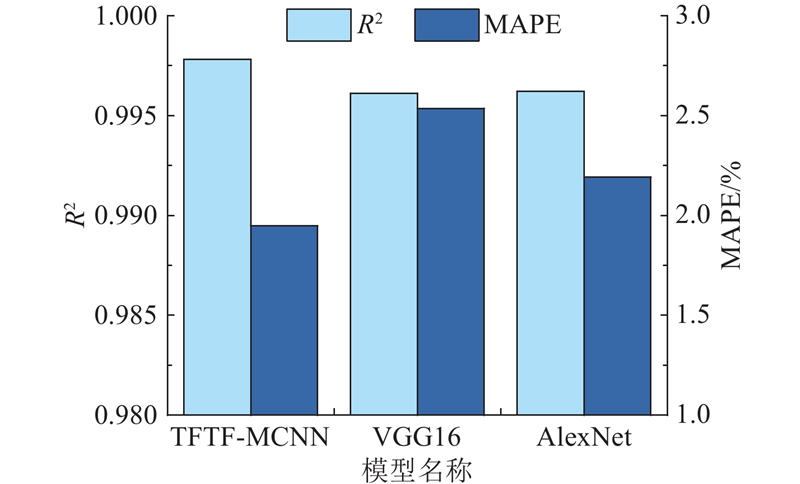
将经典CNN模型:VGG16和AlexNet作为对比模型,评估TFTF–MCNN的识别性能. 考虑到对比模型最初用于分类任务,对其网络进行适当修改以适应本研究的应用场景,其余结构参数保留原有设置. 具体而言,将对比模型原始输出层中softmax激活函数移除,替换为输出维度为2的线性层,以输出连续值. 为了确保各模型在相同条件下进行比较,将对比模型设置统一修改为与TFTF–MCNN相同配置,将其输入结构同样调整为3种不同的数据结构及速度信息组合输入(在原模型全连接层之前添加融合层),以合理地评估和对比各模型性能差异. 如图10所示以为各模型十折交叉验证后的平均识别性能指标. 相比于VGG16和AlexNet,TFTF-MCNN的识别性能均表现优越. 在单个样本的测试样本处理时间上,TFTF-MCNN的ts远低于VGG16(ts=1.253 1 ms)和AlexNet的(ts=0.512 4 ms). 评估结果表明,TFTF-MCNN在处理速度和性能方面优于对比模型.
图 10
图 10 不同模型的识别性能对比
Fig.10 Comparison of recognition performance of different models
3.3. 随机噪声与速度因素影响
对于车轮扁疤激励而言,消除或考虑速度信息的影响,有助于提高模型的自适应性能[23]. 本研究将速度作为关键特征融合到MCNN模型结构中. 为了证明该速度信息约束策略的有效性,将无速度信息作为约束条件的TFTF–MCNN作为消融实验的对比参照,样本集的尺度规整方法和该模型其余结构参数及相关设置均不变. 如图11所示为TFTF–MCNN有无速度信息的实验结果. 为了最小化随机因素对识别结果的影响,图中数据均为十折交叉验证后的平均值. 结果表明,即使在水平噪声为−4 dB的影响下,伴有速度约束信息的TFTF-MCNN的R2依然超过0.96,且MAPE不超过8%,表明TFTF-MCNN在高噪声环境下仍具备较好的识别性能及特征提取能力. 在所有实验工况下,与未融合速度信息的TFTF-MCNN相比,伴有速度约束信息的TFTF-MCNN在既定信噪比
图 11
图 11 有无速度信息的模型识别性能对比
Fig.11 Comparison of model recognition performance with or without speed information
3.4. 实测数据测试
图 12
图 13
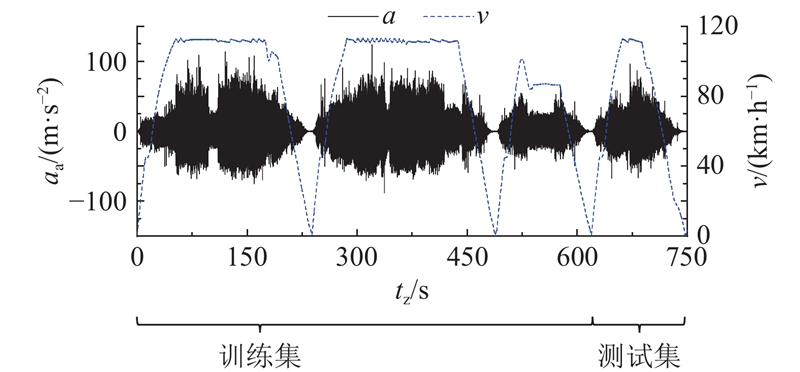
采用实测车轮局部缺陷数据以及对应的轴箱振动响应进一步验证TFTF-MCNN的实际工程应用潜力. 考虑到实测车轮局部缺陷的尺寸较大,远远超出TFTF-MCNN原本训练范围,并且种类较少,采用迁移学习策略,在已通过仿真数据训练模型(采用3.1节中的TFTF-MCNN)的基础上,冻结该模型的一部分网络结构(第一层卷积池化层),保留TFTF-MCNN在仿真数据中学习到的识别机制;解锁模型剩余网络结构,允许这些部分针对实测轴箱振动数据进行再训练[27]. 采用如图13中所示训练集和测试集分割策略,选取速度v=40~120 km/h的实测数据以同2.3节所示的数据处理方法分别进行数据规整后,每类训练集样本数为1 135,测试集样本数为218. 将规整好的3类数据结构形式的样本集输入部分权重冻结后的TFTF-MCNN中进行再训练,在耗费更少计算资源的基础上,更好地识别实测数据中独特的特征模式. 经过迁移学习再训练后,TFTF-MCNN的R2≈0.963 2,MAPE≈11.194%. 相较于仿真样本集训练结果,该模型识别性能有所下降. 如图14所示为在v=80~100、100~120 km/h下(实测样本分布相对较多),每类实测局部缺陷样本的识别结果. 各样本集中MAPE变化幅度较小,均不超过13%. 这表明TFTF-MCNN在实测噪声环境的干扰下,依旧保持较好的故障特征提取能力.
图 14
4. 结 语
开展基于不同结构数据驱动的车轮扁疤定量识别研究,1)多种结构形式组合识别性能对比分析结果表明,输入的数据结构种类越丰富,模型识别性能越高,但样本处理时间会有所增加,其中二维时频图像输入对处理时间有较大影响. 2)实验表明,速度信息可有效提升TFTF-MCNN的各项识别性能. 3)通过迁移学习策略可使得TFTF-MCNN从特定故障识别任务(车轮扁疤识别)迁移到另一种相似识别任务中,有效实现实测车轮局部缺陷的识别. 提出的定量识别方法仅基于单个车轮存在扁疤的情况进行研究,未涉及同一车轮存在多个扁疤或多个车轮存在扁疤等复杂工况. 后续计划扩展样本集,将包含更多车轮扁疤故障工况纳入研究,进一步提升模型在实际应用中的适用性和可靠性.
参考文献
Rail corrugation recognition based on particle probabilistic neural network algorithm
[J].
High-speed railway wheel polygon detection framework using improved frequency domain integration
[J].DOI:10.1080/00423114.2023.2235032
An unsupervised learning approach for wayside train wheel flat detection
[J].DOI:10.3390/s23041910 [本文引用: 1]
Wheel fault diagnosis model based on multichannel attention and supervised contrastive learning
[J].
A data-driven method for estimating wheel flat length
[J].DOI:10.1080/00423114.2019.1620956 [本文引用: 1]
基于高阶谱特征提取的高速列车车轮擦伤识别算法研究
[J].DOI:10.3901/JME.2017.06.102 [本文引用: 2]
Research on wheel-flat recognition algorithm for high-speed train based on high-order spectrum feature extraction
[J].DOI:10.3901/JME.2017.06.102 [本文引用: 2]
A novel method based on nonlinear auto-regression neural network and convolutional neural network for imbalanced fault diagnosis of rotating machinery
[J].DOI:10.1016/j.measurement.2020.107880 [本文引用: 1]
A data-driven convolutional regression scheme for on-board and quantitative detection of rail corrugation roughness
[J].
车轮扁疤伤损对高速列车轮对动力学性能影响
[J].DOI:10.11860/j.issn.1673-0291.2018.03.014 [本文引用: 1]
Influence of wheel flat on dynamic performance of high-speed train wheelset
[J].DOI:10.11860/j.issn.1673-0291.2018.03.014 [本文引用: 1]
Investigation on impact response feature of railway vehicles with wheel flat fault under variable speed conditions
[J].DOI:10.1115/1.4046126 [本文引用: 1]
车轮扁疤所引起的车辆系统振动特性分析
[J].DOI:10.3901/JME.2020.08.182 [本文引用: 1]
Vibration characteristic analysis of vehicle systems due to wheel flat
[J].DOI:10.3901/JME.2020.08.182 [本文引用: 1]
Wheel flat can cause or exacerbate wheel polygonization
[J].DOI:10.1080/00423114.2019.1636098 [本文引用: 1]
Reinvestigation into railway wheel-track interaction and suspension damage
[J].
Impact vibration behavior of railway vehicles: a state-of-the-art overview
[J].DOI:10.1007/s10409-021-01140-9 [本文引用: 1]
铁道车辆车轮扁疤故障检测技术综述
[J].
Review on detection technologies of railway vehicle wheel flat fault
[J].
车轮踏面擦伤识别方法
[J].DOI:10.3969/j.issn.1000-3835.2013.22.004 [本文引用: 1]
Identification method of wheel tread flat
[J].DOI:10.3969/j.issn.1000-3835.2013.22.004 [本文引用: 1]
An approach for wheel flat detection of railway train wheels using envelope spectrum analysis
[J].DOI:10.1080/15732479.2020.1832536 [本文引用: 1]
中高频激励下轮轨不同建模方法对轮轨动态相互作用的影响
[J].
Influence of wheelset and track modelling approaches on wheel-rail dynamic interaction under the excitation of medium-high frequency
[J].
Flexible-rigid wheelset introduced dynamic effects due to wheel tread flat
[J].DOI:10.1155/2021/5537286 [本文引用: 1]
防滑控制策略对机车车轮的损伤影响研究
[J].DOI:10.3901/JME.2023.22.369 [本文引用: 1]
Effect of anti-slip control strategy on locomotive wheel tread damage
[J].DOI:10.3901/JME.2023.22.369 [本文引用: 1]
Shock detection of rotating machinery based on activated time-domain images and deep learning: an application to railway wheel flat detection
[J].DOI:10.1016/j.ymssp.2022.109856 [本文引用: 3]
Rail corrugation detection using one-dimensional convolution neural network and data-driven method
[J].DOI:10.1016/j.measurement.2022.111624 [本文引用: 1]
基于KPCA-LSTM的旋转机械剩余使用寿命预测
[J].
Remaining useful life prediction of rotating machinery based on KPCA-LSTM
[J].
基于小波时频图和卷积神经网络的断路器故障诊断分析
[J].
Fault diagnosis and analysis of circuit breaker based on wavelet time-frequency representations and convolution neural network
[J].
Intelligent diagnosis for railway wheel flat using frequency-domain Gramian angular field and transfer learning network
[J].DOI:10.1109/ACCESS.2020.3000068 [本文引用: 1]