人口老龄化不可逆且加剧^[1]，导致全球养老压力增大. 我国护工行业存在专业性差、待遇低、压力大等问题，引发“养老护工荒”. 随着机器人技术的发展，养老服务机器人被广泛应用于养老机构^[2-3]，减轻了护工压力，但功能单一，仍需人机协作. 在养老情境下，多护工-多机器人协作的多任务分配，兼顾护工感受与老人满意度，成为重要科学问题.

Lujak等^[4]对多机器人生产计划的分布式协调方法进行研究，在生产需求随时间不断变化且资源有限的情况下，对多机器人进行任务的协调分配. Sarkar等^[5]研究不同约束条件下的最小化成本的动态任务分配. Johnson等^[6-7]讨论了不同组织结构的动态任务分配方法. Lerman等^[8-11]对多机器人系统的动态任务分配方法进行建模分析，将任务分配问题以数学的形式进行表达. 已有研究多关注多智能体动态任务分配，如遗传算法^[12]、蚁群算法^[13]、博弈论算法^[14-15]等，但较少涉及人的因素. 针对医疗看护场景，Das等^[16]提出基于多机器人系统的分布式任务分配方案，或开发多智能体系统用于监测^[17]，其服务对象为人，但未考虑人的主观感受. Ramdani等^[18-20]的研究虽然涉及的服务对象为人，但未处理机器人无法完成的任务，也未考虑服务对象的感受. 笔者等^[21]提出智能体Petri网融合框架，考虑满意度和被服务对象的感受，但未涉及服务人员的感受.

综上，在养老情境下，许多任务须人机团队共同完成，现有研究未结合人机团队中“人”和服务对象“人”的因素进行任务协调分配. 本文提出养老情境下多护工-多机器人协作的多任务分配框架（multi-caregiver-multi-robot cooperative task allocation framework, McmrTAF），考虑护工的主观感受，建立护工疲劳度模型. 结合满意度模型建立多目标优化模型，采用多目标进化算法求解，兼顾护工疲劳度和老人满意度.

本文的创新点主要如下.

1）为了考虑养老情境下多任务分配时护工的主观感受，建立护工疲劳度的变化模型，体现护工在完成一个时间窗口下任务的疲劳度变化量.

2）根据养老情境中老人提出的任务的特点，提出二维双约束编码及其合理初始化和更新方法.

3）提出多任务分配框架. 对护工疲劳度和老人满意度进行双目标优化，求解得到Pareto最优解集. 基于min-max与max-min方法，在解集中确认最终任务的分配方案.

与其他多智能体多任务分配情境不同，养老情境下的任务分配具有以下特点. 1）被服务对象是老人，须考虑老人的主观感受. 2）任务类型固定且为并发，同一时间会出现多个常见的任务同时出现的情况. 3）完成任务的智能体包括多异构服务机器人和多位不同职能的护工，须考虑护工服务老人过程中双方的主观感受. 为此，提出任务分配框架McmrTAF，详细描述如下.

1）任务分解. 设定固定时长的时间窗口. 每个时间窗口中央智能体AGC收集老人提出的任务，第$ i $个任务表示为$ {T_i} $，将每一个任务分解为执行智能体AG可完成的子任务，即将$ {T_i} $分解为$ {T_{i,1}} $~$ {T_{i,{r_{{T_i}}}}} $，第$ j $步子任务为$ {T_{i,j}} $，$ {r_{{T_i}}} $为第$ {{i}} $个任务的子任务数量. 将所有子任务发布给AG，第p类AG中的第q个AG表示为$ {\mathrm{A}}{{\mathrm{G}}_{p,q}} $.

2）功能对齐与状态共享. AG中的机器人智能体和护工智能体分别根据自己的功能或职能，匹配自己可执行的子任务T_i,j，形成任务分配向量组（task allocation vector group, TAV），如图1所示. McmrTAF中，AGC生成当前时间窗口的子任务序列$ {{\boldsymbol{S}}_{{\text{ST}}}} $，该$ {{\boldsymbol{S}}_{{\text{ST}}}} $一定有等长功能（或职能）匹配的AG序列$ {{\boldsymbol{S}}_{{\mathrm{AG}}}} $与之对应. AG将自己的状态信息$ {{\mathrm{info}}} \_{\mathrm{AG}} $（如位置、当前任务的剩余执行时间、已匹配的子任务等）共享给其他$ {\text{AG}} $及AGC.

3）任务分配. AGC基于TAV随机生成一定数量的任务执行方案，每个方案用提出的二维双约束编码（two-dimensional double-constrained coding，TDDCC）表示. AGC根据TDDCC，结合$ {{\mathrm{info}}} \_{\mathrm{AG}} $，计算每个执行方案的目标函数（护工疲劳度变化量、老人满意度），利用非支配排序遗传算法求解得到Pareto最优解集. 根据老人满意度min-max原则或护工疲劳度增加量max-min原则，选择Pareto最优解集中的各位老人满意度的最小值最大的执行方案或护工疲劳度增加量最大值最小的执行方案，作为该时间窗口的任务执行方案. 该部分细节将在2章进行阐述.

McmrTAF下要考虑养老护工和老人这两方面的“人”的主观感受：护工疲劳度和老人满意度. McmrTAF的多任务分配多目标优化模型如下所示：

(1)$ \left.\begin{gathered}\min {{F}} \left({\boldsymbol{ x}} \right) = \left[\left. {{f_{\mathrm{f}}}\left( {\boldsymbol{x}} \right),{{{f}}_{\mathrm{s}}}\left( {\boldsymbol{x}} \right)} \right] \right. ; \\ {\mathrm{s.t.}}\; {\mathrm{Subtask\_{{timing\_seq \;\;constraints}}}}, \\ {\mathrm{Subtask\_{{Agent\_skill \;\;constraints}}}} .\end{gathered} \right\}$

式中：决策变量x为多护工-多机器人团队多任务分配方案，f_f（x）、f_s（x）分别为护工疲劳度的目标函数和老人满意度的目标函数，Subtask_timing_seq constraints为时序约束条件，Subtask_Agent_skill constraints为子任务和智能体间的功能约束条件.

养老情境中老人更希望护工为他们提供服务，若一味按照老人意愿，则护工可能会过于劳累. 为了避免这种情况的发生，对护工智能体疲劳度进行建模，将这一影响因素加入优化模型中. 经过对养老机构的调研可知，在阶段性地完成任务后，养老护工的疲劳度变化主要与执行任务前的休息时间、任务困难程度、老人的身体条件、老人和护工之间的好感度以及当前任务的执行时间这些因素有关. 执行任务前的休息时间越短、任务越困难、老人和护工之间的好感度越差、老人的身体条件越差，都会造成护工疲劳度增大. 考虑到这些因素，对护工完成一个时间窗口内的任务的疲劳度变化进行建模，如下式所示：

(2)$ \left. \begin{gathered} {\text{Fat}}{{\text{i}}_{T_{{k}}^{(0)}}} = {\mathrm{Fati}}_{{{T_{K - 1}}}} - {\beta _0}{T_{(K - 1)\_{\mathrm{relax}}}}{{\mathrm{exp}}\left({{\beta _0}{T_{({{K}} - 1){{\_}}{\mathrm{relax}}}}}\right)} , \\ {t_{{T_k}}} = {t_{T_k^{{\mathrm{avg}}}}}+{\beta _1}\ln \left( {\frac{{{{{\mathrm{Fat}}}}{{\rm{i}}_{T_{{k}}^{(0)}}} \times {\mathrm{Trouble}}_{{{T_k}}} \times {\mathrm{PhyCondi}}_{X}}}{{{\mathrm{Favor}}_{{k,X}}}}} \right) , \\ {{{\mathrm{Fat}}}}{{\rm{i}}_{{T_k}}} = {{{\mathrm{Fat}}}}{{\rm{i}}_{T_{{k}}^{(0)}}}+{\beta _2}\frac{{{\mathrm{Trouble}}_{{{T_k}}} \times {\mathrm{PhyCondi}}_{X}}}{{{\mathrm{Favor}}_{k,X}}}{{\mathrm{exp}}\left({{\beta _3}{t_{{T_k}}}}\right)}. \\ \end{gathered} \right\} $

式中：$ {\mathrm{Fati}}_{{{T_{k - 1}}}} $为护工完成第k−1件子任务时的疲劳度，$ {T_{(k - 1)\_{\mathrm{relax}}}} $为完成第k−1件子任务后的休息时间，$ F{\text{at}}{{\text{i}}_{T_{{k}}^{(0)}}} $为开始第k件任务时的疲劳度，$ {\mathrm{Trouble}}_{{{T_k}}} $∈{1, 2, 3, 4, 5}为第k件任务的完成难度，$ {\mathrm{PhyCond{i}}_X} $∈ {1, 2, 3, 4, 5}为老人X的身体状况，$ {\mathrm{Favo{r}}_{k,X}} $∈ {0.1, 0.2, 0.3, 0.4, 0.5, 0.6}为老人和护工之间的好感度，$ {t_{T_k^{{\mathrm{avg}}}}} $为根据养老机构的实际情况计算得到的完成当前任务的平均时间，$ {t_{{T_k}}} $为接受第k件子任务的护工预计完成时间，$ {\mathrm{Fat}}{{\mathrm{i}}_{{T_k}}} $为护工完成第k件子任务的疲劳度，$ {\beta _0} $、$ {\beta _1} $、$ {\beta _2} $、$ {\beta _3} $为可调参数.

护工疲劳度的目标函数$ {f_{\mathrm{f}}}(x) $如下：

(3)$ \left. \begin{gathered} {f_{\mathrm{f}}}\left( {\boldsymbol{x}} \right) = \sum\limits_{k = 1}^{{l}} {\Delta {f_{{T_k}}}}, \\ \Delta {f_{{T_k}}} = {\mathrm{Fati}}_{{T_k}} - {\mathrm{Fati}}_{T_k^{\left( 0 \right)}}. \\ \end{gathered} \right\} $

式中：$ {f_{\mathrm{f}}}({\boldsymbol{x}}) $为一个时间窗口内的多任务执行方案编码中护工总体满意度的变化量，$ \Delta {f_{{T_k}}} $为该时间窗口内各个护工的疲劳度变化量，$ l $为多任务执行方案编码中护工智能体执行的子任务数. 其中，护工疲劳度的增加量越大，疲劳度目标函数值越大.

在养老情境下，将老人的主观感受作为目标函数，引用笔者等^[21]提出的满意度模型：

(4)$ \begin{split}&{\mathrm{Satf}}_{X,k} = {\alpha _0}{\mathrm{Prior}}_{k} - \\&{\alpha _1}{\mathrm{Impat}}{_X} \cdot {{\mathrm{exp}}\left({{\alpha _2}t_{{\mathrm{wait}},X,K}^{}}\right)} - {\alpha _3}{{\mathrm{exp}}\left({{\alpha _4}({v_{X,K}} - v_X^ * )}\right)}. \end{split}$

老人满意度的目标函数如下所示：

(5)$ \left. \begin{aligned} &{f_{\mathrm{s}}}\left( {\boldsymbol{x}} \right) = {{\mathrm{exp}}\left({ - \lambda \left| {\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {{\mathrm{Satf}}_{X,i,j}} } } \right|}\right)}, \\ &{\mathrm{Satf}}_{X,i,j} = {\alpha _0}{\mathrm{Prior}}_i - {\alpha _1}{\mathrm{Impat}}_X \cdot {{\mathrm{exp}}\left({{\alpha _2}t_{{\mathrm{wait}},X,i,j}}\right)} - \\ & \qquad \qquad \;{\alpha _3}{{\mathrm{exp}}\left({{\alpha _4}({v_{X,i,j}} - v_X^{*} )}\right)} , \\ &t_{{\mathrm{wait}},X,i,j} = {t_{{\mathrm{fl}},i,j}}+{t_{{{\mathrm{nl}},i,j}}} .\end{aligned} \right\} $

式中：m为执行方案中的任务数，n为某一任务分解后的子任务数，Satf_X,i,j为完成子任务T_i,j的第X个老人满意度，$ {\mathrm{Prior}} _i$表示事件i的优先级，$ {\mathrm{Impat }}_X$为第X个老人的性格急躁系数，$t_{{\mathrm{wait}},X,i,j} $为第X个老人从提出第i个任务中第j个子任务的需求开始直至机器人到达老人所在位置之间的总等待时间, $v_{X,i,j} $为机器人为第X个老人提供第i个任务中第j个子任务服务的速度, $v_X^ * $为第X个老人被服务的舒适运载速度，$t_{{\mathrm{fl}},i,j} $为对第i个任务中第j个子任务的期望等待时间. $t_{_{{\mathrm{nl}},i,j}} $为对第i个任务中第j个子任务的已经等待时间. 为了方便老人满意度和护工疲劳度的多目标优化，根据笔者等^[21]提出的满意度模型变体得出的满意度目标函数与老人满意度的关系为反比关系，即老人满意度越大，满意度目标函数值越小.

为了更直观地描述任务执行过程中的约束以及计算护工和老人的目标函数，提出新的编码形式，即TDDCC，养老院某一时间窗口3个任务的TDDCC如下：

(6)$ \begin{split} {\mathrm{TDDC}}{{\mathrm{C}}_i} =& {\left[ {{{\boldsymbol{S}}_{{\mathrm{ST}}}}^{\mathrm{T}},{{\boldsymbol{S}}_{{\mathrm{AG}}}}^{\mathrm{T}},{{\boldsymbol{S}}_{{\mathrm{EL}}}}^{\mathrm{T}}} \right]^{\mathrm{T}}} =\\&\left[ {\begin{array}{*{20}{c}} {{T_{2,1}}}&{{T_{3,1}}}&{{T_{1,1}}}&{{T_{3,2}}}&{{T_{2,2}}}&{{T_{1,2}}}&{{T_{1,3}}}&{{T_{2,3}}}&{{T_{2,4}}}&{{T_{2,5}}}&{{T_{1,4}}} \\ {{{\mathrm{A{G}}}}_{1,2}}&{{\mathrm{A{G}}_{1,2}}}&{{\mathrm{A{G}}_{1,3}}}&{{\mathrm{A{G}}_{4,1}}}&{{\mathrm{A{G}}_{3,2}}}&{{\mathrm{A{G}}_{2,2}}}&{{\mathrm{A{G}}_{1,2}}}&{{\mathrm{A{G}}_{1,1}}}&{{\mathrm{A{G}}_{2,2}}}&{{\mathrm{A{G}}_{1,3}}}&{{\mathrm{A}}{{\mathrm{G}}_{4,1}}} \\ {{\mathrm{E{L}}_5}}&{{\mathrm{E{L}}_8}}&{{\mathrm{E{L}}_1}}&{{\mathrm{E{L}}_8}}&{{\mathrm{E{L}}_5}}&{{\mathrm{E{L}}_1}}&{{\mathrm{E{L}}_1}}&{{\mathrm{E{L}}_5}}&{{\mathrm{E{L}}_5}}&{{\mathrm{E{L}}_5}}&{{\mathrm{E{L}}_1}} \end{array}} \right]\end{split}. $

式中：${{T_{i,j}}} $为第i个任务中的第j个子任务，${{{\mathrm{A{G}}}}_{i,j}} $为具有第i个功能的第j个智能体，${{\mathrm{E{L}}_i}} $表示第i位老人.

该编码描述一个时间窗口的任务分配方案.

多护工-多机器人协作任务分配方案有以下2个约束条件：老人提出的任务需求分解的S_ST必须符合时序约束(TDDCC的行)，执行子任务的智能体符合功能约束（TDDCC的列）. 在执行方案的寻优过程中，父代编码迭代生成的子代编码的S_ST必须符合上述约束条件，以保证编码迭代寻优和最终执行方案的合理性. 可以看出，TDDCC的行和列分别描述一个约束条件，即二维双约束.

AGC基于TAV在符合功能约束条件的基础上，生成符合时序约束条件的任务分配向量. 此外，不同的子任务有相对应的提出任务需求的老人，形成老人序列S_EL，$ {\mathrm{E{L}}_X} $表示第X位老人. TDDCC可以描述具有多维度强约束对应关系的任务执行方案，结合本研究提出的TDDCC合理初始化、更新方法，完成多任务分配.

为了保证多目标优化过程中决策变量更新的合理性，要保证初始化变量的合理性. TDDCC合理初始化的过程如下.

1）根据任务分解结果，获取一个时间窗口下的任务个数u及第i个任务T_i的子任务个数$ r_{T_i} $.

2）对于每一个T_i复制生成$ r_{{T}_{i}} $个T_i，将所有复制生成的结果以随机的顺序放到一起，组成长度为$ {\displaystyle \sum}_{i=1}^{u} r_{T_{i}} $的序列. 当$ {r_{{T_1}}} $=4，$ {r_{{T_2}}} $=5，$ {r_{{T_3}}} $=2时，分解后的结果为：T_2, T_3, T_1, T_3, T_2, T_1, T_1, T_2, T_2, T_2, T₁ .

3）将序列中第j个T_i作为子任务T_i,j，生成符合时序约束的S_ST.

4）根据TAV生成方法，为S_ST中T_i,j所需功能对应地分配相应功能或职能的AG，这在另一维度生成了符合功能约束的S_AG.

5）与提出对应任务T_i的老人EL_i相对应，构成序列S_EL.

TDDCC随机初始化生成后，在其更新过程中生成的子代编码需要保证其合理性，以保证“多护工-多机器人”多任务执行方案的合理性. 以3个任务（11个子任务）为例，TDDCC的更新过程如图2所示，编码中的S_ST、S_AG、S_EL是一一对应的. 为了保证迭代生成的子代编码的合理性和可执行性，采用打包交叉的方式生成新的编码. 如图2所示，分别将任意2个父代编码中子任务下标第一个维度i相同的子任务所在列打包起来，依次按顺序交换2个矩阵中的打包列，以保证生成的子代的可执行性.

按上述方法生成TDDCC后，编码中的子任务和AG团队对应起来. 养老情境下一个时间窗口中的AG当前位置都是随机的，若老人提出任务后，直接按TDDCC开始任务的执行，可能会出现同一任务的子任务之间无法交接的情况. 例如，在某AG完成任务的前件子任务后，编码中的后件子任务所分配的AG还未到达；或者前件子任务分配的AG还没到达，后件子任务分配的AG已经到达并要开始服务. 当出现上述情况时，按照TDDCC中的执行方案是无法正常执行任务的，即随机生成的TDDCC编码在进行时间同步之前大概率是无法执行的. 针对TDDCC编码的特殊性，为了保证AG的顺利交接，须解决AG和子任务的时间同步问题，处理流程如图3所示. 图中，$t_{\mathrm{s}} (T_{i, j} )$为TDDCC中子任务$T_{i, j} $的开始时刻； $t_{\mathrm{e}}( T_{i, j} )$为子任务$T_{i, j} $的完成时刻；$t_{\mathrm{s}} (T_{i, j+1}) $为执行T_i,j 的后件子任务$T_{i, j+1} $的AG实际到达时刻，即子任务$T_{i, j+1} $的开始时刻. 按该流程处理时间同步后，将每个子任务$T_{i, j} $在TDDCC中的原始等待时间整合成任务$T_{i} $的总体等待时间. 子任务$T_{i, j} $的等待时间为子任务之间的交接时间.

养老情境下老人和护工的主观感受为对立关系，呈现此消彼长的态势. 很难人为地找出最优的执行方案，故基于TDDCC，采用非支配排序遗传算法（NSGAⅡ）对建立的多任务多目标优化模型进行求解，在完成多人机协作任务分配的同时，对老人满意度和护工疲劳度2个目标进行优化，得到任务执行方案的Pareto最优解集. 优化模型的目标函数之一是老人整体满意度，即一个时间窗口中所有子任务对应的老人满意度的和. 为了避免解集中出现某位老人的满意度极小但整体满意度较大的情况，根据min-max原则，从Pareto最优解集中，选择老人个体满意度，将式（4）的最小值最大的解作为McmrTAF的最终任务执行方案. 此外，另一个目标函数是护工疲劳度的增加量，当选择方案时可以根据护工疲劳度函数，结合max-min原则，选择护工个体疲劳度增加量的最大值最小的解作为McmrTAF的最终任务执行方案.

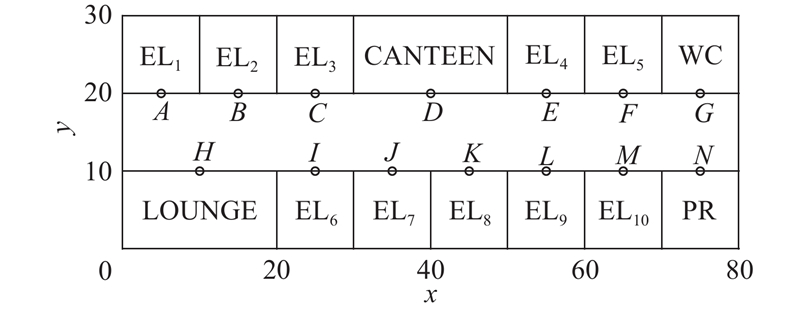
如图4所示为虚拟养老情境下各个房间及其坐标信息. 图中，EL₁~EL₁₀为在该房间的老人，CANTEEN为食堂，WC为卫生间，其中休息室LOUNGE为机器人的停放位置及护工智能体的休息区，PR为老人的娱乐室（康复训练室）. A（5，20），B（15，20），C（25，20），D（40，20），E（55，20），F（65，20），G（75，20），H（10，10），I（25，10），J（35，10），K（45，10），L（55，10），M（65，10），N（75，10），这些信息均储存在智能体信息中. 为了方便计算，将这些固定点的坐标作为这些房间的位置，在不考虑AG碰撞的情况下，将护工智能体和机器人智能体均视为质点. 评价任务分配方案的过程如下：一个TDDCC对应一个任务执行方案，基于式（3）、（5）可以计算老人满意度和护工疲劳度目标函数值，用于评价该TDDCC（即任务分配方案）的优劣.

为了研究算法的优越性，利用TDDCC的非支配排序多目标遗传算法解决“8个机器人-2个护工-40个子任务”的问题. 以养老机构中一天的某一随机时刻为初始状态，该情境下共10位老人，共提出10个任务需求，分解为40个子任务. 在养老情境中的某一时间窗口下，McmrTAF系统接收到上述10位老人提出的任务需求，进行任务分配.

为了量化分配效果，令sol_gene为进化过程中第gene代中可行解的数量占种群规模的百分比，未采用TDDCC编码，只基于TAV随机初始化种群，进行进化求解时sol_gene随gene变大而减小，在求解过程中出现了大量违背时序约束和功能约束条件的不可行解（例如老人还未被从床上拉起，运送任务便已经开始执行）. 以初始种群规模为100为例，迭代到第10代时sol₁₀ = 73%，迭代到第20代时sol₂₀ = 47%，迭代到第30代时sol₃₀ = 22%，迭代到第80代时sol₈₀ = 0%，种群中无可行解. 可以看出，当未采用TDDCC时，多人机协作任务分配系统在寻优过程中的可行解会越来越少，导致进化求解过程无法完成. 加入TDDCC后，在求解过程中sol_gene一直为100%，完成分配后得到的满意度和疲劳度如图5所示. 在如图4所示的虚拟养老情境下的一个时间窗口内，McmrTAF的任务执行方案的Pareto解集如图5所示，根据老人满意度min-max原则确定最终的任务执行方案如下：

$ \left( {\begin{array}{*{20}{c}} {{T_{8,1}}} & {{T_{9,1}}} & {{T_{7,1}}} & \cdots \\ {{\mathrm{A{G}}_{1,2}}} & {{\mathrm{A{G}}_{1,1}}} & {{\mathrm{A{G}}_{1,3}}} & \cdots \\ {{\mathrm{E{L}}_2}} & {{\mathrm{E{L}}_6}} & {{\mathrm{E{L}}_3}} & \cdots\end{array}} \right. \left. {\begin{array}{*{20}{c}} {{T_{10,2}}} & {{T_{3,2}}} & {{T_{1,4}}} \\ {{\mathrm{A{G}}_{4,2}}} & {{\mathrm{A{G}}_{4,1}}} & {{\mathrm{A{G}}_{4,1}}} \\ {{\mathrm{E{L}}_{10}}} & {{\mathrm{E{L}}_8}} & {{\mathrm{E{L}}_1}} \end{array}} \right) .$

以图4中的时刻老人提出的需求为例进行仿真，多护工-多异构机器人系统在收到老人提出的需求后，当不使用McmrTAF时，将这些需求按照任务库分解为异构机器人可以执行的子任务，将这些子任务随机分配给护工和异构服务机器人.

在该多人机协作分配方案下的老人总体满意度为0.03126，护工总体疲劳度增加量为77.43. 与图5中的Pareto前沿解对比可以看出，按照随机分配方法得到的任务执行方案对应的护工疲劳度和老人满意度都远不及本文方法的结果.

在日常的养老情境中，仅由护工为老人服务时，无法做到让护工按照优先级为老人排序，他们会按照先到先得的方式安排老人的先后服务顺序，这样的服务模式能够让老人认同. 按照这种任务分配方法进行仿真，与提出的基于TDDCC编码的多人机协作任务分配方法进行对比. 以图4所示情景中的养老需求为例，将这些需求按智能体任务库分解为子任务后，根据先到先得的方法，将这些子任务分配给多护工-多异构机器人团队.

在图4的场景下，利用该分配方法进行多人机协作任务分配，老人总体满意度为0.026 33，护工总体疲劳度为55.53. 对比图5的任务分配执行方案Pareto前沿解可以看出，先到先得分配方法下的老人满意度和护工疲劳度情况远没有达到Pareto前沿.

基于TDDCCC，利用多目标优化算法可以计算得到多人机协作任务执行方案的Pareto最优解集，分别基于$ \Delta {f}_{{T}_{k}} $的max-min原则或Satf_X,i,j的min-max原则确定最终的任务执行方案. 将基于TDDCC的多人机协作任务分配方法、随机任务分配方法及先到先得任务分配方法所得到的最终任务执行方案中的老人满意度和护工疲劳度进行对比.

如图6~8所示为对比结果. 可以看出，采用随机分配方法和先到先得任务分配方法得到的多人机协作任务执行方案远没有达到任务执行方案的Pareto前沿. 从图6可以看出，当采用随机分配方法进行多护工-多机器人团队任务分配时，老人满意度很小，但护工疲劳度的增加量非常大，不符合本研究的完成多护工-多机器人团队多任务分配的同时兼顾护工疲劳度和老人满意度这一宗旨. 与随机分配方法相比，先到先得多任务分配方法对应的护工疲劳度情况更逼近Pareto前沿. 该方法的老人满意度比随机分配方法稍高的同时，护工疲劳度增加量较少. 这论证了先到先得的方法更能被老人认同这一观点. 虽然先到先得的多任务分配方法较随机分配方法能够得到较优的护工疲劳度和老人满意度情况，但没有达到Pareto前沿解，可以看出提出的基于TDDCC编码的多人机协作任务分配多目标优化方法的优越性.

此外，基于总体-个体护工疲劳度选择的最终任务执行方案和基于总体-个体老人满意度选择的最终任务执行方案会出现如图6~8所示的3种情况. 图6中，2种方案的老人满意度和护工疲劳度情况相差较大，基于老人满意度的min-max原则选择的任务执行方案与基于护工疲劳度max-min原则的任务执行方案相比，老人满意度更高，护工疲劳度增加量越大. 图7中，2种方案重合，这种情况下2种最终任务执行方案选择方法得到的护工疲劳度增加量和老人满意度相同. 图8中，2种方案相差较小，这种情况下，基于老人满意度的min-max原则选择的任务执行方案老人满意度较大，护工疲劳度增加量较小. 经过多次实验对比可知，这3种情况是随机出现的. 在实际应用中，所提方法可以经过多次计算，得到基于护工疲劳度max-min原则或老人满意度min-max原则的最终任务执行方案，养老机构的管理者可以根据实际情况，设置先验偏好，完成McmrTAF下的多人机协作任务分配.

本文针对养老情境下多护工-多异构服务机器人的任务分配问题，提出 “多护工-多机器人”协作的多任务分配框架. 为了解决养老护工工作过于疲惫的问题，建立护工疲劳度变化的模型，以该模型为基础提出护工疲劳度函数计算方法. 基于老人满意度模型建立老人满意度函数的计算公式，在完成多护工-多机器人团队任务分配的同时，兼顾护工疲劳度和老人满意度. 为了完成多人机协作任务分配并得到多任务执行方案的Pareto最优解，提出多护工-多机器人多任务分配方案的二维双约束编码及其合理的初始化和更新方法. 为了兼顾护工整体和个体的疲劳度以及老人整体和个体的满意度并确定最终的任务执行方案，提出基于min-max与max-min原则的任务方案决策方法. 仿真结果表明，提出的养老情境下“多护工-多机器人”协作的多任务分配框架在完成多护工-多机器人团队多任务分配的同时，能够得到兼顾护工疲劳度和老人满意度的Pareto最优执行方案，所确定的最终任务执行方案能够兼顾老人总体和个体的满意度情况或护工总体和个体的疲劳度情况.