[1]
AHOPELTO S, VAHALA R Cost-benefit analysis of leakage reduction methods in water supply networks
[J]. Water, 2020 , 12 (1 ): 195
DOI:10.3390/w12010195
[本文引用: 1]
[2]
SARKAMARYAN S, HAGHIGHI A, ADIB A Leakage detection and calibration of pipe networks by the inverse transient analysis modified by Gaussian functions for leakage simulation
[J]. Journal of Water Supply: Research and Technology-Aqua, 2018 , 67 (4 ): 404 - 413
DOI:10.2166/aqua.2018.176
[本文引用: 1]
[4]
ZHU L J, WANG D M, YUE J K, et al Leakage detection method of natural gas pipeline combining improved variational mode decomposition and Lempel-Ziv complexity analysis
[J]. Transactions of the Institute of Measurement and Control, 2022 , 44 (15 ): 2865 - 2876
DOI:10.1177/01423312221088080
[本文引用: 1]
[5]
XIE J, ZHANG Y B, HE Z Y, et al Automated leakage detection method of pipeline networks under complicated backgrounds by combining infrared thermography and Faster R-CNN technique
[J]. Process Safety and Environmental Protection, 2023 , 174 : 39 - 52
DOI:10.1016/j.psep.2023.04.006
[6]
AMRAN T S T, ISMAIL M P, AHMAD M R, et al. Detection of underground water distribution piping system and leakages using ground penetrating radar (GPR) [C]// Advancing Nuclear Science and Engineering for Sustainable Nuclear Energy Knowledge . [S. l.]: AIP Publishing, 2017, 1799: 030004.
[7]
GONG W J, SURESH M A, SMITH L, et al Mobile sensor networks for optimal leak and back flow detection and localization in municipal water networks
[J]. Environmental Modelling and Software, 2016 , 80 : 306 - 321
DOI:10.1016/j.envsoft.2016.02.001
[8]
QI Z X, ZHENG F F, GUO D L, et al Better understanding of the capacity of pressure sensor systems to detect pipe burst within water distribution networks
[J]. Journal of Water Resources Planning and Management, 2018 , 144 (7 ): 04018035
DOI:10.1061/(ASCE)WR.1943-5452.0000957
[本文引用: 1]
[9]
GAO Y, LIU Y Y Theoretical and experimental investigation into structural and fluid motions at low frequencies in water distribution pipes
[J]. Mechanical Systems and Signal Processing, 2017 , 90 : 126 - 140
DOI:10.1016/j.ymssp.2016.12.018
[本文引用: 1]
[10]
ADEDEJI K B, HAMAM Y, ABE B T, et al Towards achieving a reliable leakage detection and localization algorithm for application in water piping networks: an overview
[J]. IEEE Access, 2017 , 5 (10 ): 20272 - 20285
[本文引用: 1]
[11]
LU H F, LSELEY T, BEHBAHANI S, et al Leakage detection techniques for oil and gas pipelines: state-of-the-art
[J]. Tunnelling and Underground Space Technology, 2020 , 98 : 103249
DOI:10.1016/j.tust.2019.103249
[本文引用: 1]
[12]
ZHOU M F, XU Y Z, CUI B H, et al Pipeline leakage detection and localization using a reliable pipeline-mechanism model incorporating a Bayesian model updating approach
[J]. Water, 2022 , 14 (8 ): 1255
DOI:10.3390/w14081255
[本文引用: 1]
[13]
EI-ZAHAB S, ASAAD A, ABDELKADER E M, et al Collective thinking approach improving leak detection systems
[J]. Smart Water, 2016 , 2 : 3
DOI:10.1186/s40713-017-0007-9
[本文引用: 1]
[14]
KANG J, PARK Y J, LEE J, et al Novel leakage detection by ensemble CNN-SVM and graph-based localization in water distribution systems
[J]. IEEE Transactions on Industrial Electronics, 2018 , 65 (5 ): 4279 - 4289
DOI:10.1109/TIE.2017.2764861
[本文引用: 1]
[15]
XU Z H, MA W, LIN P, et al Deep learning of rock images for intelligent lithology identification
[J]. Computers and Geosciences, 2021 , 154 : 104799
DOI:10.1016/j.cageo.2021.104799
[本文引用: 1]
[16]
朱丹宸, 张永祥, 潘洋洋, 等 基于多传感器信号和卷积神经网络的滚动轴承故障诊断
[J]. 振动与冲击, 2020 , 39 (4 ): 172 - 178
[本文引用: 1]
ZHU Danchen, ZHANG Yongxiang, PAN Yangang, et al Fault diagnosis for rolling element bearings based on multi-sensor signals and CNN
[J]. Journal of Vibration and Shock, 2020 , 39 (4 ): 172 - 178
[本文引用: 1]
[17]
GUO G C, YU X P, LIU S M, et al Leakage detection in water distribution systems based on time-frequency convolutional neural network
[J]. Journal of Water Resources Planning and Management, 2021 , 147 (2 ): 04020101
DOI:10.1061/(ASCE)WR.1943-5452.0001317
[本文引用: 4]
[18]
IOFFE S, SZEGEDY C. Batch normalization: accelerating deep network training by reducing internal covariate shift [C]// International Conference on Machine Learning . San Diego: MIT Press, 2015, 37: 448–456.
[本文引用: 2]
[19]
KAMALAKKANNAN R, ROOPKUMAR R, ZAYED A Short time coupled fractional fourier transform and the uncertainty principle
[J]. Fractional Calculus and Applied Analysis, 2021 , 24 : 667 - 688
DOI:10.1515/fca-2021-0029
[本文引用: 1]
[20]
ZHOU X, TANG Z H, XU W R, et al. Deep learning identifies accurate burst locations in water distribution networks [J]. Water Research , 2019, 166: 115058.
[本文引用: 1]
[21]
赵林硕, 叶郭煊, 申永刚, 等 基于时频卷积神经网络的供水管道漏损检测
[J]. 中国给水排水, 2023 , 39 (17 ): 53 - 58
[本文引用: 1]
ZHAO Linshuo, YE Guoxuan, SHEN Yonggang, et al Leakage detection of water supply pipeline based on time-frequency convolutional neural network
[J]. China Water and Wastewater, 2023 , 39 (17 ): 53 - 58
[本文引用: 1]
[22]
BUTTERFIELD J D, KRYNKIN A, COLLINS R P, et al Experimental investigation into vibro-acoustic emission signal processing techniques to quantify leak flow rate in plastic water distribution pipes
[J]. Applied Acoustics, 2017 , 199 : 146 - 155
[本文引用: 1]
[23]
JALIL M, BUTT F A, MALIK A. Short-time energy, magnitude, zero crossing rate and autocorrelation measurement for discriminating voiced and unvoiced segments of speech signals [C]// 2013 IEEE International Conference on Technological Advances in Electrical, Electronics and Computer Engineering . Konya: IEEE, 2013: 208–212.
[24]
CHUANG W Y, TSAI Y L, WANG L H. Leak detection in water distribution pipes based on CNN with Mel-frequency cepstral coefficients [C]// The 3rd International Conference on Innovation in Artificial Intelligence . Suzhou: [s.n.], 2019: 83–86.
[25]
SUN J D, XIAO Q Y, WEN J T, et al Natural gas pipeline leak aperture identification and location based on local mean decomposition analysis
[J]. Measure, 2016 , 79 : 147 - 157
[本文引用: 1]
Cost-benefit analysis of leakage reduction methods in water supply networks
1
2020
... 由于施工安装、环境腐蚀、管道老化等因素影响[1 ] ,公共供水管网漏损形势严峻. 供水管道漏损的检测研究对防治管网漏损带来的资源浪费、水质污染、地面沉降等危害[2 -3 ] 具有重大意义. Zhu等[4 -8 ] 提出利用外部设备(如气体示踪、探地雷达、光纤传感等)和内部设备(如水力模型、压力或流量传感器等)的先进管道检漏方法. 基于漏损声信号的声学检测法的成本低且易于实施,在水务行业中被广泛使用[9 ] . 听音法是主流的传统声学检测方法,该方法依赖操作人员的听音经验,易受环境随机噪声的影响,因此人员培养成本高,工作强度大[10 ] . 利用声信号的检漏方法主要分为信号处理法和数据驱动法. 基于信号处理的方法依赖泄漏信号先验知识,且受噪声影响大[11 ] ;数据驱动方法应用了机器学习方法[12 -13 ] ,漏损识别效果较好,但方法准确率取决于人为选择的漏损特征. 卷积神经网络(convolutional neural network, CNN)通过卷积计算自动学习图像的层次特征,利用数据增强技术扩充数据集[14 ] ,在图像识别中的应用效果显著且稳定,在岩土结构的裂缝识别以及轴承的故障识别中也有良好的应用效果[15 -16 ] . ...
Leakage detection and calibration of pipe networks by the inverse transient analysis modified by Gaussian functions for leakage simulation
1
2018
... 由于施工安装、环境腐蚀、管道老化等因素影响[1 ] ,公共供水管网漏损形势严峻. 供水管道漏损的检测研究对防治管网漏损带来的资源浪费、水质污染、地面沉降等危害[2 -3 ] 具有重大意义. Zhu等[4 -8 ] 提出利用外部设备(如气体示踪、探地雷达、光纤传感等)和内部设备(如水力模型、压力或流量传感器等)的先进管道检漏方法. 基于漏损声信号的声学检测法的成本低且易于实施,在水务行业中被广泛使用[9 ] . 听音法是主流的传统声学检测方法,该方法依赖操作人员的听音经验,易受环境随机噪声的影响,因此人员培养成本高,工作强度大[10 ] . 利用声信号的检漏方法主要分为信号处理法和数据驱动法. 基于信号处理的方法依赖泄漏信号先验知识,且受噪声影响大[11 ] ;数据驱动方法应用了机器学习方法[12 -13 ] ,漏损识别效果较好,但方法准确率取决于人为选择的漏损特征. 卷积神经网络(convolutional neural network, CNN)通过卷积计算自动学习图像的层次特征,利用数据增强技术扩充数据集[14 ] ,在图像识别中的应用效果显著且稳定,在岩土结构的裂缝识别以及轴承的故障识别中也有良好的应用效果[15 -16 ] . ...
Energy and costs of leaky pipes: towards comprehensive picture
1
2002
... 由于施工安装、环境腐蚀、管道老化等因素影响[1 ] ,公共供水管网漏损形势严峻. 供水管道漏损的检测研究对防治管网漏损带来的资源浪费、水质污染、地面沉降等危害[2 -3 ] 具有重大意义. Zhu等[4 -8 ] 提出利用外部设备(如气体示踪、探地雷达、光纤传感等)和内部设备(如水力模型、压力或流量传感器等)的先进管道检漏方法. 基于漏损声信号的声学检测法的成本低且易于实施,在水务行业中被广泛使用[9 ] . 听音法是主流的传统声学检测方法,该方法依赖操作人员的听音经验,易受环境随机噪声的影响,因此人员培养成本高,工作强度大[10 ] . 利用声信号的检漏方法主要分为信号处理法和数据驱动法. 基于信号处理的方法依赖泄漏信号先验知识,且受噪声影响大[11 ] ;数据驱动方法应用了机器学习方法[12 -13 ] ,漏损识别效果较好,但方法准确率取决于人为选择的漏损特征. 卷积神经网络(convolutional neural network, CNN)通过卷积计算自动学习图像的层次特征,利用数据增强技术扩充数据集[14 ] ,在图像识别中的应用效果显著且稳定,在岩土结构的裂缝识别以及轴承的故障识别中也有良好的应用效果[15 -16 ] . ...
Leakage detection method of natural gas pipeline combining improved variational mode decomposition and Lempel-Ziv complexity analysis
1
2022
... 由于施工安装、环境腐蚀、管道老化等因素影响[1 ] ,公共供水管网漏损形势严峻. 供水管道漏损的检测研究对防治管网漏损带来的资源浪费、水质污染、地面沉降等危害[2 -3 ] 具有重大意义. Zhu等[4 -8 ] 提出利用外部设备(如气体示踪、探地雷达、光纤传感等)和内部设备(如水力模型、压力或流量传感器等)的先进管道检漏方法. 基于漏损声信号的声学检测法的成本低且易于实施,在水务行业中被广泛使用[9 ] . 听音法是主流的传统声学检测方法,该方法依赖操作人员的听音经验,易受环境随机噪声的影响,因此人员培养成本高,工作强度大[10 ] . 利用声信号的检漏方法主要分为信号处理法和数据驱动法. 基于信号处理的方法依赖泄漏信号先验知识,且受噪声影响大[11 ] ;数据驱动方法应用了机器学习方法[12 -13 ] ,漏损识别效果较好,但方法准确率取决于人为选择的漏损特征. 卷积神经网络(convolutional neural network, CNN)通过卷积计算自动学习图像的层次特征,利用数据增强技术扩充数据集[14 ] ,在图像识别中的应用效果显著且稳定,在岩土结构的裂缝识别以及轴承的故障识别中也有良好的应用效果[15 -16 ] . ...
Automated leakage detection method of pipeline networks under complicated backgrounds by combining infrared thermography and Faster R-CNN technique
0
2023
Mobile sensor networks for optimal leak and back flow detection and localization in municipal water networks
0
2016
Better understanding of the capacity of pressure sensor systems to detect pipe burst within water distribution networks
1
2018
... 由于施工安装、环境腐蚀、管道老化等因素影响[1 ] ,公共供水管网漏损形势严峻. 供水管道漏损的检测研究对防治管网漏损带来的资源浪费、水质污染、地面沉降等危害[2 -3 ] 具有重大意义. Zhu等[4 -8 ] 提出利用外部设备(如气体示踪、探地雷达、光纤传感等)和内部设备(如水力模型、压力或流量传感器等)的先进管道检漏方法. 基于漏损声信号的声学检测法的成本低且易于实施,在水务行业中被广泛使用[9 ] . 听音法是主流的传统声学检测方法,该方法依赖操作人员的听音经验,易受环境随机噪声的影响,因此人员培养成本高,工作强度大[10 ] . 利用声信号的检漏方法主要分为信号处理法和数据驱动法. 基于信号处理的方法依赖泄漏信号先验知识,且受噪声影响大[11 ] ;数据驱动方法应用了机器学习方法[12 -13 ] ,漏损识别效果较好,但方法准确率取决于人为选择的漏损特征. 卷积神经网络(convolutional neural network, CNN)通过卷积计算自动学习图像的层次特征,利用数据增强技术扩充数据集[14 ] ,在图像识别中的应用效果显著且稳定,在岩土结构的裂缝识别以及轴承的故障识别中也有良好的应用效果[15 -16 ] . ...
Theoretical and experimental investigation into structural and fluid motions at low frequencies in water distribution pipes
1
2017
... 由于施工安装、环境腐蚀、管道老化等因素影响[1 ] ,公共供水管网漏损形势严峻. 供水管道漏损的检测研究对防治管网漏损带来的资源浪费、水质污染、地面沉降等危害[2 -3 ] 具有重大意义. Zhu等[4 -8 ] 提出利用外部设备(如气体示踪、探地雷达、光纤传感等)和内部设备(如水力模型、压力或流量传感器等)的先进管道检漏方法. 基于漏损声信号的声学检测法的成本低且易于实施,在水务行业中被广泛使用[9 ] . 听音法是主流的传统声学检测方法,该方法依赖操作人员的听音经验,易受环境随机噪声的影响,因此人员培养成本高,工作强度大[10 ] . 利用声信号的检漏方法主要分为信号处理法和数据驱动法. 基于信号处理的方法依赖泄漏信号先验知识,且受噪声影响大[11 ] ;数据驱动方法应用了机器学习方法[12 -13 ] ,漏损识别效果较好,但方法准确率取决于人为选择的漏损特征. 卷积神经网络(convolutional neural network, CNN)通过卷积计算自动学习图像的层次特征,利用数据增强技术扩充数据集[14 ] ,在图像识别中的应用效果显著且稳定,在岩土结构的裂缝识别以及轴承的故障识别中也有良好的应用效果[15 -16 ] . ...
Towards achieving a reliable leakage detection and localization algorithm for application in water piping networks: an overview
1
2017
... 由于施工安装、环境腐蚀、管道老化等因素影响[1 ] ,公共供水管网漏损形势严峻. 供水管道漏损的检测研究对防治管网漏损带来的资源浪费、水质污染、地面沉降等危害[2 -3 ] 具有重大意义. Zhu等[4 -8 ] 提出利用外部设备(如气体示踪、探地雷达、光纤传感等)和内部设备(如水力模型、压力或流量传感器等)的先进管道检漏方法. 基于漏损声信号的声学检测法的成本低且易于实施,在水务行业中被广泛使用[9 ] . 听音法是主流的传统声学检测方法,该方法依赖操作人员的听音经验,易受环境随机噪声的影响,因此人员培养成本高,工作强度大[10 ] . 利用声信号的检漏方法主要分为信号处理法和数据驱动法. 基于信号处理的方法依赖泄漏信号先验知识,且受噪声影响大[11 ] ;数据驱动方法应用了机器学习方法[12 -13 ] ,漏损识别效果较好,但方法准确率取决于人为选择的漏损特征. 卷积神经网络(convolutional neural network, CNN)通过卷积计算自动学习图像的层次特征,利用数据增强技术扩充数据集[14 ] ,在图像识别中的应用效果显著且稳定,在岩土结构的裂缝识别以及轴承的故障识别中也有良好的应用效果[15 -16 ] . ...
Leakage detection techniques for oil and gas pipelines: state-of-the-art
1
2020
... 由于施工安装、环境腐蚀、管道老化等因素影响[1 ] ,公共供水管网漏损形势严峻. 供水管道漏损的检测研究对防治管网漏损带来的资源浪费、水质污染、地面沉降等危害[2 -3 ] 具有重大意义. Zhu等[4 -8 ] 提出利用外部设备(如气体示踪、探地雷达、光纤传感等)和内部设备(如水力模型、压力或流量传感器等)的先进管道检漏方法. 基于漏损声信号的声学检测法的成本低且易于实施,在水务行业中被广泛使用[9 ] . 听音法是主流的传统声学检测方法,该方法依赖操作人员的听音经验,易受环境随机噪声的影响,因此人员培养成本高,工作强度大[10 ] . 利用声信号的检漏方法主要分为信号处理法和数据驱动法. 基于信号处理的方法依赖泄漏信号先验知识,且受噪声影响大[11 ] ;数据驱动方法应用了机器学习方法[12 -13 ] ,漏损识别效果较好,但方法准确率取决于人为选择的漏损特征. 卷积神经网络(convolutional neural network, CNN)通过卷积计算自动学习图像的层次特征,利用数据增强技术扩充数据集[14 ] ,在图像识别中的应用效果显著且稳定,在岩土结构的裂缝识别以及轴承的故障识别中也有良好的应用效果[15 -16 ] . ...
Pipeline leakage detection and localization using a reliable pipeline-mechanism model incorporating a Bayesian model updating approach
1
2022
... 由于施工安装、环境腐蚀、管道老化等因素影响[1 ] ,公共供水管网漏损形势严峻. 供水管道漏损的检测研究对防治管网漏损带来的资源浪费、水质污染、地面沉降等危害[2 -3 ] 具有重大意义. Zhu等[4 -8 ] 提出利用外部设备(如气体示踪、探地雷达、光纤传感等)和内部设备(如水力模型、压力或流量传感器等)的先进管道检漏方法. 基于漏损声信号的声学检测法的成本低且易于实施,在水务行业中被广泛使用[9 ] . 听音法是主流的传统声学检测方法,该方法依赖操作人员的听音经验,易受环境随机噪声的影响,因此人员培养成本高,工作强度大[10 ] . 利用声信号的检漏方法主要分为信号处理法和数据驱动法. 基于信号处理的方法依赖泄漏信号先验知识,且受噪声影响大[11 ] ;数据驱动方法应用了机器学习方法[12 -13 ] ,漏损识别效果较好,但方法准确率取决于人为选择的漏损特征. 卷积神经网络(convolutional neural network, CNN)通过卷积计算自动学习图像的层次特征,利用数据增强技术扩充数据集[14 ] ,在图像识别中的应用效果显著且稳定,在岩土结构的裂缝识别以及轴承的故障识别中也有良好的应用效果[15 -16 ] . ...
Collective thinking approach improving leak detection systems
1
2016
... 由于施工安装、环境腐蚀、管道老化等因素影响[1 ] ,公共供水管网漏损形势严峻. 供水管道漏损的检测研究对防治管网漏损带来的资源浪费、水质污染、地面沉降等危害[2 -3 ] 具有重大意义. Zhu等[4 -8 ] 提出利用外部设备(如气体示踪、探地雷达、光纤传感等)和内部设备(如水力模型、压力或流量传感器等)的先进管道检漏方法. 基于漏损声信号的声学检测法的成本低且易于实施,在水务行业中被广泛使用[9 ] . 听音法是主流的传统声学检测方法,该方法依赖操作人员的听音经验,易受环境随机噪声的影响,因此人员培养成本高,工作强度大[10 ] . 利用声信号的检漏方法主要分为信号处理法和数据驱动法. 基于信号处理的方法依赖泄漏信号先验知识,且受噪声影响大[11 ] ;数据驱动方法应用了机器学习方法[12 -13 ] ,漏损识别效果较好,但方法准确率取决于人为选择的漏损特征. 卷积神经网络(convolutional neural network, CNN)通过卷积计算自动学习图像的层次特征,利用数据增强技术扩充数据集[14 ] ,在图像识别中的应用效果显著且稳定,在岩土结构的裂缝识别以及轴承的故障识别中也有良好的应用效果[15 -16 ] . ...
Novel leakage detection by ensemble CNN-SVM and graph-based localization in water distribution systems
1
2018
... 由于施工安装、环境腐蚀、管道老化等因素影响[1 ] ,公共供水管网漏损形势严峻. 供水管道漏损的检测研究对防治管网漏损带来的资源浪费、水质污染、地面沉降等危害[2 -3 ] 具有重大意义. Zhu等[4 -8 ] 提出利用外部设备(如气体示踪、探地雷达、光纤传感等)和内部设备(如水力模型、压力或流量传感器等)的先进管道检漏方法. 基于漏损声信号的声学检测法的成本低且易于实施,在水务行业中被广泛使用[9 ] . 听音法是主流的传统声学检测方法,该方法依赖操作人员的听音经验,易受环境随机噪声的影响,因此人员培养成本高,工作强度大[10 ] . 利用声信号的检漏方法主要分为信号处理法和数据驱动法. 基于信号处理的方法依赖泄漏信号先验知识,且受噪声影响大[11 ] ;数据驱动方法应用了机器学习方法[12 -13 ] ,漏损识别效果较好,但方法准确率取决于人为选择的漏损特征. 卷积神经网络(convolutional neural network, CNN)通过卷积计算自动学习图像的层次特征,利用数据增强技术扩充数据集[14 ] ,在图像识别中的应用效果显著且稳定,在岩土结构的裂缝识别以及轴承的故障识别中也有良好的应用效果[15 -16 ] . ...
Deep learning of rock images for intelligent lithology identification
1
2021
... 由于施工安装、环境腐蚀、管道老化等因素影响[1 ] ,公共供水管网漏损形势严峻. 供水管道漏损的检测研究对防治管网漏损带来的资源浪费、水质污染、地面沉降等危害[2 -3 ] 具有重大意义. Zhu等[4 -8 ] 提出利用外部设备(如气体示踪、探地雷达、光纤传感等)和内部设备(如水力模型、压力或流量传感器等)的先进管道检漏方法. 基于漏损声信号的声学检测法的成本低且易于实施,在水务行业中被广泛使用[9 ] . 听音法是主流的传统声学检测方法,该方法依赖操作人员的听音经验,易受环境随机噪声的影响,因此人员培养成本高,工作强度大[10 ] . 利用声信号的检漏方法主要分为信号处理法和数据驱动法. 基于信号处理的方法依赖泄漏信号先验知识,且受噪声影响大[11 ] ;数据驱动方法应用了机器学习方法[12 -13 ] ,漏损识别效果较好,但方法准确率取决于人为选择的漏损特征. 卷积神经网络(convolutional neural network, CNN)通过卷积计算自动学习图像的层次特征,利用数据增强技术扩充数据集[14 ] ,在图像识别中的应用效果显著且稳定,在岩土结构的裂缝识别以及轴承的故障识别中也有良好的应用效果[15 -16 ] . ...
基于多传感器信号和卷积神经网络的滚动轴承故障诊断
1
2020
... 由于施工安装、环境腐蚀、管道老化等因素影响[1 ] ,公共供水管网漏损形势严峻. 供水管道漏损的检测研究对防治管网漏损带来的资源浪费、水质污染、地面沉降等危害[2 -3 ] 具有重大意义. Zhu等[4 -8 ] 提出利用外部设备(如气体示踪、探地雷达、光纤传感等)和内部设备(如水力模型、压力或流量传感器等)的先进管道检漏方法. 基于漏损声信号的声学检测法的成本低且易于实施,在水务行业中被广泛使用[9 ] . 听音法是主流的传统声学检测方法,该方法依赖操作人员的听音经验,易受环境随机噪声的影响,因此人员培养成本高,工作强度大[10 ] . 利用声信号的检漏方法主要分为信号处理法和数据驱动法. 基于信号处理的方法依赖泄漏信号先验知识,且受噪声影响大[11 ] ;数据驱动方法应用了机器学习方法[12 -13 ] ,漏损识别效果较好,但方法准确率取决于人为选择的漏损特征. 卷积神经网络(convolutional neural network, CNN)通过卷积计算自动学习图像的层次特征,利用数据增强技术扩充数据集[14 ] ,在图像识别中的应用效果显著且稳定,在岩土结构的裂缝识别以及轴承的故障识别中也有良好的应用效果[15 -16 ] . ...
基于多传感器信号和卷积神经网络的滚动轴承故障诊断
1
2020
... 由于施工安装、环境腐蚀、管道老化等因素影响[1 ] ,公共供水管网漏损形势严峻. 供水管道漏损的检测研究对防治管网漏损带来的资源浪费、水质污染、地面沉降等危害[2 -3 ] 具有重大意义. Zhu等[4 -8 ] 提出利用外部设备(如气体示踪、探地雷达、光纤传感等)和内部设备(如水力模型、压力或流量传感器等)的先进管道检漏方法. 基于漏损声信号的声学检测法的成本低且易于实施,在水务行业中被广泛使用[9 ] . 听音法是主流的传统声学检测方法,该方法依赖操作人员的听音经验,易受环境随机噪声的影响,因此人员培养成本高,工作强度大[10 ] . 利用声信号的检漏方法主要分为信号处理法和数据驱动法. 基于信号处理的方法依赖泄漏信号先验知识,且受噪声影响大[11 ] ;数据驱动方法应用了机器学习方法[12 -13 ] ,漏损识别效果较好,但方法准确率取决于人为选择的漏损特征. 卷积神经网络(convolutional neural network, CNN)通过卷积计算自动学习图像的层次特征,利用数据增强技术扩充数据集[14 ] ,在图像识别中的应用效果显著且稳定,在岩土结构的裂缝识别以及轴承的故障识别中也有良好的应用效果[15 -16 ] . ...
Leakage detection in water distribution systems based on time-frequency convolutional neural network
4
2021
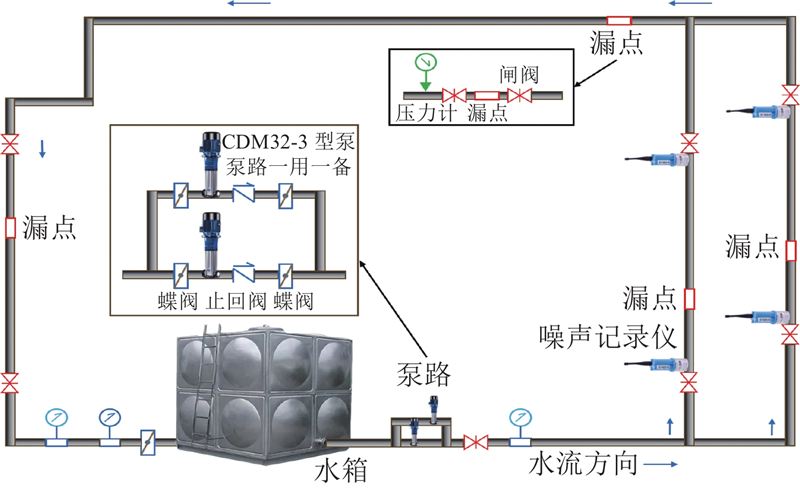
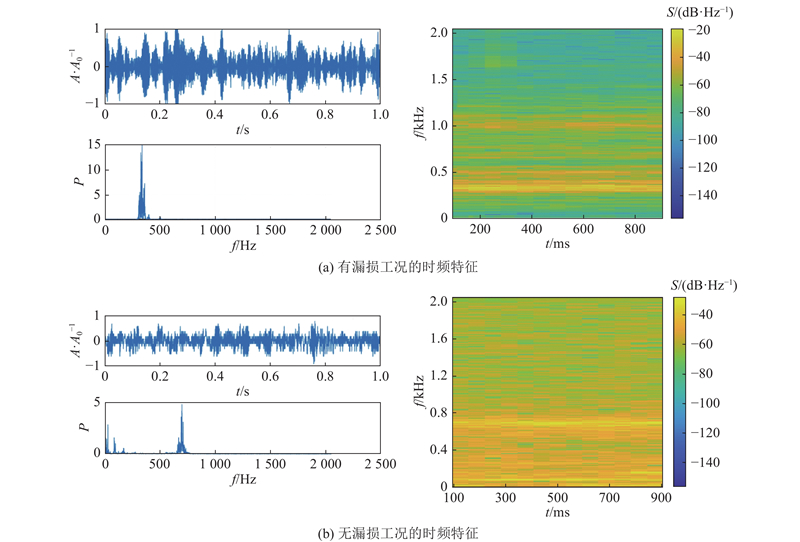
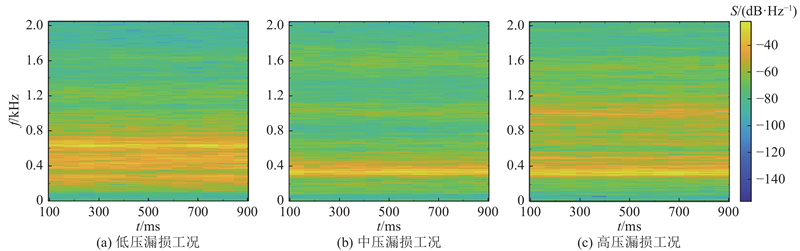
... 对管道漏损声信号进行时频分析,可以同时保留时域和频域特征,充分反映漏损信号的特点. Guo等[17 ] 将多分辨率的短时傅里叶变换(short-time Fourier transform, STFT)谱图作为CNN的输入,获得了良好的管道漏损识别效果,但作者没有对漏损压力判断展开研究. 在实际检修中,相同漏口面积、不同压力漏损工况的管道声信号存在差异,水务公司对此缺乏了解. 为了研究漏损压力对声信号的影响,本研究提出基于STFT和CNN的供水管道漏损压力识别模型( STFT-CNN),通过中试实验平台采集不同压力条件下的管道声信号,提取时频谱图作为分类对象,在判断供水管道是否漏损的基础上,进一步识别漏损工况的压力条件. ...
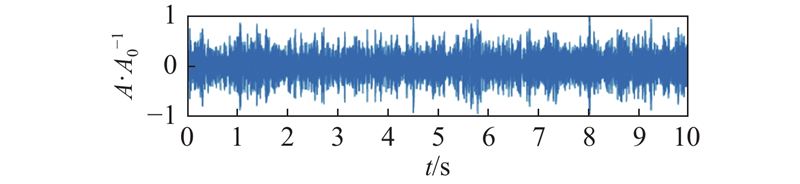
... 管道声信号的数据预处理主要依赖漏损信号的先验知识,通过消除趋势项、直流分量和100~2 000 Hz的带通滤波器处理,可以提高谱估计的准确性[17 ] . 在实际工程中,用水行为具有不确定性,此外漏损与正常信号的频带在不同的管网和环境中也不相同,为此将信号切割为1 s的短信号后,向原始信号中添加不同信噪比(signal to noise ratio, SNR)的高斯白噪声(white Gaussian noise, WGN)以提高模型的鲁棒性[20 ] . SNR的计算式为 ...
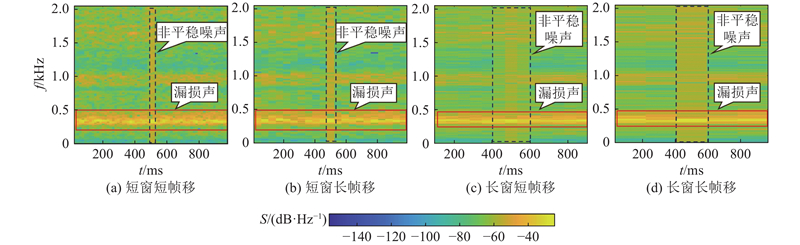
... 常用的窗函数包括矩形窗、汉宁窗、海明窗等,本研究时频谱图窗函数采用汉宁窗. 汉宁窗主瓣较窄,可获得较高的频率分辨率,旁瓣衰减较大,可减少分析失真 [17 ] . FFT长度通常为2的幂,窗长取FFT长度,帧移通常为1/4帧长度的倍数. 为了研究不同时频谱图的窗参数组合对STFT-CNN准确率的影响,设置3种FFT长度和3种帧移,共9种窗参数组合[17 ] ,形成不同的时频谱图输入模型进行训练,取10次随机训练测试集准确率的平均值作为该时频谱图的准确率,各组参数和模型准确率如表2 所示. 表中,$ L $ $ N $ $ {\mathrm{Ip}} $ $ {\mathrm{Acc}} $ [18 ] . 如图5 所示为同一段信号在不同窗长下得到的时频谱图. 管道漏损声信号所在频域在时域上持续稳定,干扰噪声在时域上持续时间短,长窗和短帧移组合可以同时淡化噪声在时域和频域上的分布,避免模型将非平稳噪声识别为关键漏损特征,并且能够更好识别代表漏损和漏损压力的时频特征,第7组窗参数的模型准确率较第3组的模型准确率提高了6.8个百分点. STFT的窗参数最终采用长窗和短帧移的窗参数组合,即第7组. ...
... [17 ],形成不同的时频谱图输入模型进行训练,取10次随机训练测试集准确率的平均值作为该时频谱图的准确率,各组参数和模型准确率如表2 所示. 表中,$ L $ $ N $ $ {\mathrm{Ip}} $ $ {\mathrm{Acc}} $ [18 ] . 如图5 所示为同一段信号在不同窗长下得到的时频谱图. 管道漏损声信号所在频域在时域上持续稳定,干扰噪声在时域上持续时间短,长窗和短帧移组合可以同时淡化噪声在时域和频域上的分布,避免模型将非平稳噪声识别为关键漏损特征,并且能够更好识别代表漏损和漏损压力的时频特征,第7组窗参数的模型准确率较第3组的模型准确率提高了6.8个百分点. STFT的窗参数最终采用长窗和短帧移的窗参数组合,即第7组. ...
2
... 式中:$ C\times H\times W $ $ k、{k}_{h}、{k}_{w} $ $ p $ $ s $ [18 ] . 池化层汇集卷积层提取的特征,可以降低卷积层的位置敏感性和对空间降采样的敏感性,减少模型参数,缩短训练时间,池化计算通常有最大池化(maximum pooling)和平均池化(average pooling)2种方式. 激活函数在卷积计算中可以为网络增强非线性拟合能力,常用的激活函数有ReLU、Sigmoid和Tanh. 全连接层将输入从低维的分布式特征线性映射至高维的样本空间,对特征进行加权和分类. ...
... 常用的窗函数包括矩形窗、汉宁窗、海明窗等,本研究时频谱图窗函数采用汉宁窗. 汉宁窗主瓣较窄,可获得较高的频率分辨率,旁瓣衰减较大,可减少分析失真 [17 ] . FFT长度通常为2的幂,窗长取FFT长度,帧移通常为1/4帧长度的倍数. 为了研究不同时频谱图的窗参数组合对STFT-CNN准确率的影响,设置3种FFT长度和3种帧移,共9种窗参数组合[17 ] ,形成不同的时频谱图输入模型进行训练,取10次随机训练测试集准确率的平均值作为该时频谱图的准确率,各组参数和模型准确率如表2 所示. 表中,$ L $ $ N $ $ {\mathrm{Ip}} $ $ {\mathrm{Acc}} $ [18 ] . 如图5 所示为同一段信号在不同窗长下得到的时频谱图. 管道漏损声信号所在频域在时域上持续稳定,干扰噪声在时域上持续时间短,长窗和短帧移组合可以同时淡化噪声在时域和频域上的分布,避免模型将非平稳噪声识别为关键漏损特征,并且能够更好识别代表漏损和漏损压力的时频特征,第7组窗参数的模型准确率较第3组的模型准确率提高了6.8个百分点. STFT的窗参数最终采用长窗和短帧移的窗参数组合,即第7组. ...
Short time coupled fractional fourier transform and the uncertainty principle
1
2021
... 由STFT得到的时频谱图待定参数包括窗函数、快速傅立叶变换(fast Fourier transform, FFT)长度、窗长、帧移. STFT的窗大小决定时频分辨率:窗长越长,时间分辨率越低,频率分辨率越高;窗长越短,时间分辨率越高,频率分辨率越低[19 ] . 对于漏损和漏损压力识别问题,须通过优化窗参数,选择最佳组合以提高模型的准确率. 声信号通过STFT时频分析得到时频谱图,将所得时频谱图数据矩阵作为特征输入CNN进行分类识别. ...
1
... 管道声信号的数据预处理主要依赖漏损信号的先验知识,通过消除趋势项、直流分量和100~2 000 Hz的带通滤波器处理,可以提高谱估计的准确性[17 ] . 在实际工程中,用水行为具有不确定性,此外漏损与正常信号的频带在不同的管网和环境中也不相同,为此将信号切割为1 s的短信号后,向原始信号中添加不同信噪比(signal to noise ratio, SNR)的高斯白噪声(white Gaussian noise, WGN)以提高模型的鲁棒性[20 ] . SNR的计算式为 ...
基于时频卷积神经网络的供水管道漏损检测
1
2023
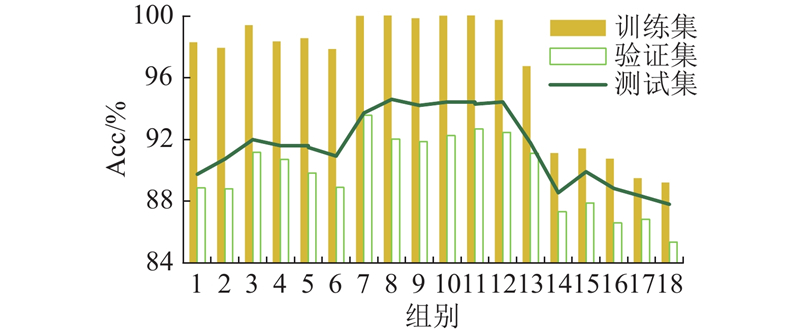
... CNN须优化的超参数为学习率LR和最小批量尺寸MB,设计3种学习率和6种最小批量尺寸的组合来研究超参数对模型训练准确率的影响,采用十折交叉验证方法,取训练测试集准确率的平均值作为该参数组的准确率,如表4 所示. 各学习率和最小批量尺寸的超参数组合试验结果如图7 所示. 随着模型学习率从0.01下降至0.0001 ,模型分类效果先上升后下降. 分析原因:当学习率过大时,模型学习容易越过最优解;当学习率较小时,模型更新速度较慢,在局部极值点就收敛. 最小批量尺寸对模型分类效果影响较小,可能是受到计算机性能的限制,未算出更精确的梯度下降[21 ] . 更大的最小批量尺寸能够提升数据处理和模型收敛速度,减少训练时间,因此模型最终采用第12组超参数组合. ...
基于时频卷积神经网络的供水管道漏损检测
1
2023
... CNN须优化的超参数为学习率LR和最小批量尺寸MB,设计3种学习率和6种最小批量尺寸的组合来研究超参数对模型训练准确率的影响,采用十折交叉验证方法,取训练测试集准确率的平均值作为该参数组的准确率,如表4 所示. 各学习率和最小批量尺寸的超参数组合试验结果如图7 所示. 随着模型学习率从0.01下降至0.0001 ,模型分类效果先上升后下降. 分析原因:当学习率过大时,模型学习容易越过最优解;当学习率较小时,模型更新速度较慢,在局部极值点就收敛. 最小批量尺寸对模型分类效果影响较小,可能是受到计算机性能的限制,未算出更精确的梯度下降[21 ] . 更大的最小批量尺寸能够提升数据处理和模型收敛速度,减少训练时间,因此模型最终采用第12组超参数组合. ...
Experimental investigation into vibro-acoustic emission signal processing techniques to quantify leak flow rate in plastic water distribution pipes
1
2017
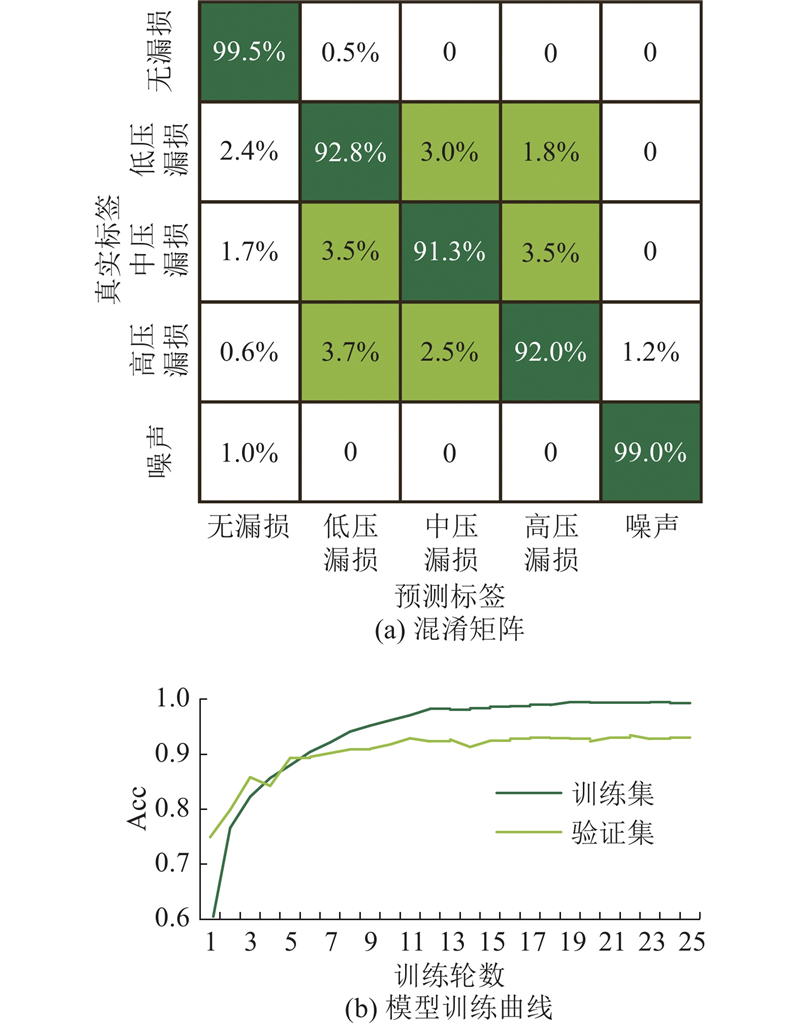
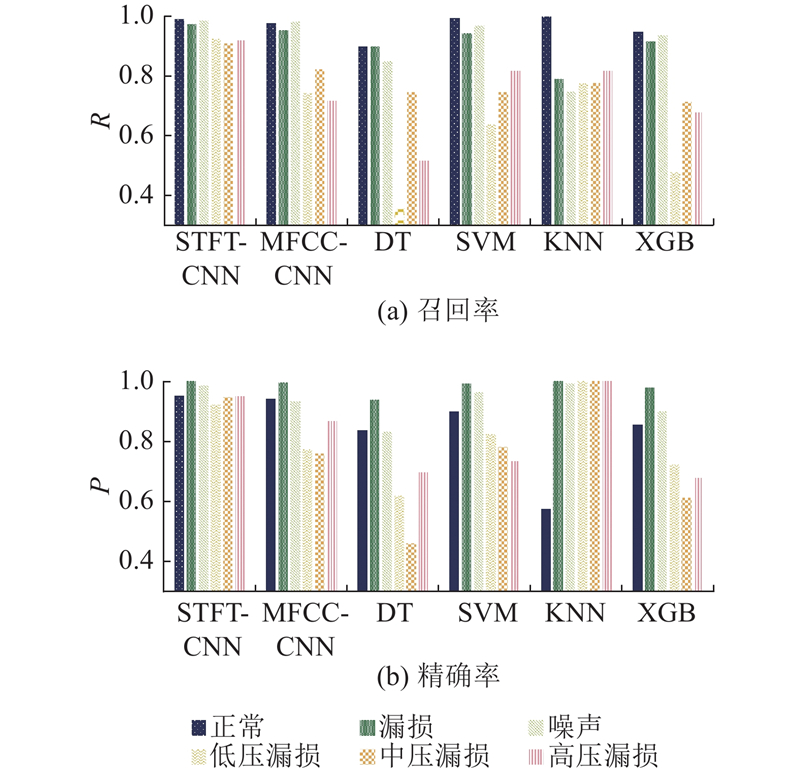
... 为了评估本模型识别漏损和漏损压力的性能,将STFT-CNN与已用于供水管网漏损识别的机器学习方法进行对比,并将梅尔频率倒谱系数MFCC输入CNN进行识别,对比非时频特征的分类效果. 采用相同的数据集提取其他分类模型所需的漏损声信号特征,包括信号的标准差STD、均方根RMS、近似熵ApEn、短时过零率ZCR、MFCC、功率谱密度的平均分贝(PSD)、经验模态分解前三个分量的均方根(IMF)[22 -25 ] . ...
Natural gas pipeline leak aperture identification and location based on local mean decomposition analysis
1
2016
... 为了评估本模型识别漏损和漏损压力的性能,将STFT-CNN与已用于供水管网漏损识别的机器学习方法进行对比,并将梅尔频率倒谱系数MFCC输入CNN进行识别,对比非时频特征的分类效果. 采用相同的数据集提取其他分类模型所需的漏损声信号特征,包括信号的标准差STD、均方根RMS、近似熵ApEn、短时过零率ZCR、MFCC、功率谱密度的平均分贝(PSD)、经验模态分解前三个分量的均方根(IMF)[22 -25 ] . ...