基于多元统计分析的故障诊断方法包括2类,即贡献图法和故障重构法,其中贡献图法通过计算过程变量对统计量的贡献程度,进而定位故障变量[5-6]. Westerhuis等[7]研究贡献图的涂抹效应,并引入贡献的控制限;Li等[8]提出基于全潜结构投影的贡献图方法,用统一的方式描述所有变量对监测统计量的贡献;Alcala等[9-10]相继提出基于重构贡献和相对贡献的故障诊断方法. 相较于贡献图法,故障重构是一种监督的故障诊断方法,通过对历史故障数据的分析,提取故障子空间,其包含了故障的特征[5]. Dunia等[11]利用故障方向信息通过重构进行故障识别;Li等[12]提出与输出相关的故障子空间提取方法和约简故障子空间提取方法,有效降低了故障子空间的维数;冯晓伟等[13]采用广义主成分分析方法剔除正常建模数据和故障建模数据之间的公共信息,构造更精确的故障子空间.
由于物料、能量及信息间的传递和反馈控制作用的存在,过程变量高度耦合[14]. 故障子空间之间存在相似性,一个故障子空间可以重构多个类型的故障,造成故障子空间与故障类型之间存在一对多的问题. 在现有研究中,故障子空间提取高度依赖故障样本,往往假设各故障模式下都具有足够的理想标签样本;然而在实际生产过程中,故障样本往往难以获取,由于不同类型的故障发生概率不同,不同模式的故障样本之间存在严重不平衡[15-17]. 此外,大多现有方法致力于提高故障子空间的高效性,而忽略了故障子空间之间的可分辨性. 这使得故障子空间的故障表征能力和分辨能力严重下降. 因此开展基于数据增强的故障分类研究成为工程实践中的迫切需要.
目前,基于数据增强的虚拟样本生成方法已经被广泛应用到图像分类领域,如生成对抗网络(generative adversarial nets, GAN)[18-19]、自编码器(variational autoencoder, VAE)[20-21],但这些方法难以有效捕获数据在时间上的相关关系及其动态特性. Arjovsky等[22]使用Wasserstein距离代替JS散度来衡量真实样本和生成样本之间的分布距离,提出Wasserstein距离生成对抗网络(Wasserstein GAN, WGAN). 随后,Gulrajani等[23]增加了梯度惩罚项,提出基于梯度惩罚的WGAN(gradient penalty WGAN, WGAN-GP). 此外,合成少数过采样技术(synthetic minority oversampling technique, SMOTE)作为一种重采样方法,利用随机线性插值在一个少数类样本和它最近的邻居样本之间产生新的样本[24]. 这2种数据增强方法被广泛应用到故障诊断领域以解决故障样本不平衡问题. 时间序列生成对抗网络(time-series generative adversarial networks, TimeGAN)是专门用于时间序列数据增强的生成模型,能够有效捕获时间序列数据中的时间相关性[25-27]. 因此,本研究提出基于TimeGAN数据增强的非线性复杂过程故障分类方法,主要创新包括以下4点:1)采用TimeGAN网络对历史故障数据进行数据增强,克服故障样本少、不平衡的问题;2)采用马氏距离对生成虚拟样本进行质量评估,并剔除不可信样本,避免其对模型训练产生负面影响;3)在核空间而非原始数据空间提取故障子空间,提高子空间故障表征能力和分辨能力;4)设计基于故障重构的故障分类策略以实现在线故障样本分类,形成完整的基于数据增强的故障分类方案.
1. 基于TimeGAN的虚拟故障样本生成
时间序列数据的时间特征对传统的数据增强方法提出了严峻的挑战. 时间序列数据的数据增强不仅要处理一个时间点内的特征,而且要捕捉这些特征在时间范围内的复杂属性.
1.1. TimeGAN模型原理
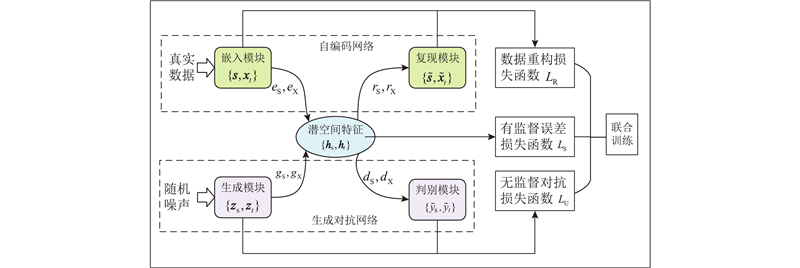
图 1
自编码器网络降低了输入数据的维度,利用嵌入模块将原始特征空间映射到包含静态特征和时态特征的潜空间,映射过程如下:
式中:
式中:
为了提高自编码器中嵌入模块和复现模块对输入数据分布的学习能力,使用数据重构损失函数
表中:T为时间序列的长度,p为数据的分布.
生成对抗网络是为了实现生成器和判别器之间的平衡. 生成器捕获实时序列的潜在分布并生成新的合成序列. 判别器在真实序列和合成序列之间提供正确的分类. 其生成函数可以定义为
式中:
判别器模块采用双向递归神经网络(recurrent neural network, RNN)区分真实样本和合成样本,判别模型如下:
式中:
式中:
1.2. 基于马氏距离的虚拟样本质量评估
尽管TimeGAN的目标是生成与真实数据分布相似的样本,但生成的虚拟样本可能仍存在与真实数据分布不完全一致的问题,或者生成的虚拟样本存在噪声或不可信,这些样本会对模型训练产生负面影响进而影响故障子空间的故障表征能力. 因此,采用合理的方法对生成的虚拟样本进行过滤筛选是必要的,可以保证虚拟样本质量. 在评估虚拟样本质量时,常见的距离准则包括马氏距离、欧式距离及三角隶属度函数法[28]等. 马氏距离考虑了特征之间的相关性和协方差矩阵,因此适用于高维数据和具有相关性的数据[16]. 欧氏距离简单、直观、易于理解和实现,对于线性关系较强的数据有较好效果,但不考虑特征之间的相关性和尺度差异,可能受到特征尺度影响. 三角隶属度函数法具有较高的灵活性,可以根据实际情况调整隶属度函数的形状和参数,适应不同的数据分布和异常情况,但隶属度函数的选择和参数的确定需要一定的经验,可能存在主观性和不确定性,且计算复杂度较高. 在具体应用中,须根据实际数据的特点选择合适的距离准则. 考虑到工业过程数据往往呈现非线性、多维度、高度相关等特点,选择马氏距离来评估虚拟样本质量.
假设系统共有
式中:
式中:
式中:
假设第
算法1 基于马氏距离的虚拟数据筛选
输入:
1 for
2 定义第
3 对
4 按照式(9)对
5 按照式(11)分别计算每个样本
6 求各样本与
7 对虚拟故障数据集
8 for
9 按照式(11)求得样本
10 if
11 将样本
12 else
13 舍弃样本
14 endif
15 endfor
16 求得经数据增强后的
17 从
18 endfor
输出:
2. 基于故障重构的故障分类方法
2.1. 基于核独立成分分析的故障检测原理
核独立成分分析(kernel independent component analysis, KICA)[29]作为独立成分分析的非线性扩展,已经成功地应用于非线性非高斯过程的故障检测中,其故障检测原理如下. 设有非线性系统包含
通常采用径向基作为核函数,即
式中:
式中:
假设存在单位正交矩阵
式中:
一般情况下,KICA模型采用
为了方便后续表述,将式(17)、(18)统一表示为
由于复杂系统的变量分布形式未知,难以确保过程数据遵循特定的分布假设. 为了解决这个问题,核密度估计(kernel density estimation, KDE)通常被用来确定控制限,KDE是一种非参数经验密度估计技术,其不依赖于任何特定的分布假设,适合于估计过程数据的概率密度函数[30-31]. 因此,本研究采用KDE获取控制限
2.2. 故障重构和故障子空间提取
假设主子空间中故障方向为
式中:
对其进行奇异值分解:
式中:
将
同理,假设残差子空间中故障方向为
式中:
对式(24)进行奇异值分解:
将
至此可得故障在主子空间和残差子空间的故障方向(即故障子空间)
2.3. 故障分类策略
对于已知故障方向
式中:
为了使修正后的样本回到正常状态,则将估计故障方向转化为如下优化问题:
这是一个无约束最小二乘问题,其解析解为
式中:
上述为针对某一特定故障方向对故障样本进行重构,进而求得对应故障幅度的过程. 在实际应用中,分别对每类故障提取故障子空间
将其代入式(17)得到修正后的
如此可得故障样本
算法2 故障子空间提取及在线故障分类
输入:正常工况数据
1) 故障子空间提取
(a) 对
(b) for
(c) 对
(d) 按照式(23)对核矩阵的主子空间分量进行奇异值分解,求得
(e) for
(f) 令
(g) 按照式(30)~(32)对
(h) if
(i) break;
(j) endif
(k) endfor
(l) 同理,类似于步骤(d)~(k),求得第
(m) endfor
2) 在线故障分类
(a) 在线样本
(b) if
(c) 分别以
(d) 对比统计量
(e) else if
(f) 类似于步骤(c)~(g),在残差空间判断故障类型;
(g) else
(h)
(i) endif
输出:故障库
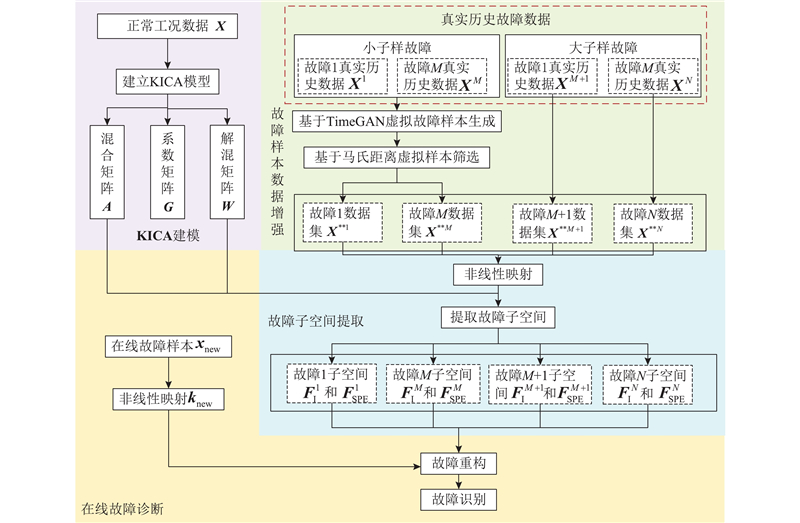
综上所述,本研究所提基于数据增强的复杂过程故障分类方法主要包括KICA模型建立、故障样本数据增强、故障子空间提取及在线故障分类几个部分,算法整体流程如图2所示.
图 2
图 2 基于数据增强的故障分类方法流程图
Fig.2 Flow chart of fault classification method based on data enhancement
3. 实验与分析
3.1. 数据集介绍
为了验证所提故障分类方法的性能,采用田纳西伊士曼过程 (Tennessee Eastman process, TEP)[32]进行实验验证. TEP仿真平台包括正常工况和21种故障工况,正常工况共包括
选取故障1、 2、 6、 7、 12、 14作为已知故障,52个变量作为观测建模变量,具体实验数据设置如表1所示. 其中,故障1作为大子样故障,不对其进行数据增强,其他故障均视作小子样故障进行数据增强. 表中,N1、N2分别为历史故障数据中故障样本数量和增强后故障样本数量. 以此验证所提算法的数据增强性能,并讨论多模式故障分类问题.
表 1 故障样本数据设置
Tab.1
| 故障 类型 | 历史故障数据 | N2 | 验证故障 数据 | |
| 来源 | N1 | |||
| 1 | d01中随机选择 | 400 | 400 | d01_te |
| 2 | d02中随机选择 | 40 | 400 | d02_te |
| 6 | d06中随机选择 | 20 | 400 | d06_te |
| 7 | d07中随机选择 | 200 | 400 | d07_te |
| 12 | d12中随机选择 | 60 | 400 | d12_te |
| 14 | d14中随机选择 | 20 | 400 | d14_te |
3.2. 故障分类性能评价指标
在通常情况下,一个性能良好的故障分类算法应该具备以下几点:1)故障子空间能够精确表征故障属性;2)模型对正样本具有较高的识别能力,对负样本具有较强的区分能力. 具体表现为:如果在线样本属于某一特定故障类型时,只有用该故障类型对应的故障子空间进行故障重构,才可以将统计量恢复到控制限以下;相反,如果使用其他故障类型对应的故障子空间进行故障重构,则无法将统计量恢复到控制限以下. 因此,分别采用精确率P、召回率R和F1得分3个指标来定量评价故障分类性能,其中精确率用于衡量模型对负样本的区分能力,精确率越高,则区分能力越高;召回率用于衡量模型对正样本的识别能力,召回率越高,识别能力越强;F1得分则为精确率和召回率的调和平均值,体现模型的稳健性. 此外,本研究定义重构恢复率(reconstruction recovery rate, R3)指标以衡量故障子空间表征故障属性的能力. 各性能指标具体定义如下:
式中:TP、FN分别表示正样本被诊断为正样本、负样本的样本数,FP、TN分别表示负样本被诊断为正样本、负样本的样本数,
3.3. 数据增强及生成样本质量评估
分别将小子样故障2、 6、 7、 12、 14的历史故障数据作为TimeGAN网络的输入进行模型训练,迭代10 000次后,生成虚拟故障样本,TimeGAN网络的部分参数设置如表2所示.
表 2 TimeGAN网络参数设置表
Tab.2
| 自编码网络参数 | 数值 | 生成对抗网络参数 | 数值 | |
| 采样时间步长 | 18 | 生成器噪声层数 | 32 | |
| 特征维数 | 52 | GAN隐藏层数 | 24 | |
| 隐藏层层数 | 1 | 判别器真实损失 | 1 | |
| 学习率 | 5×10−4 | — | — |
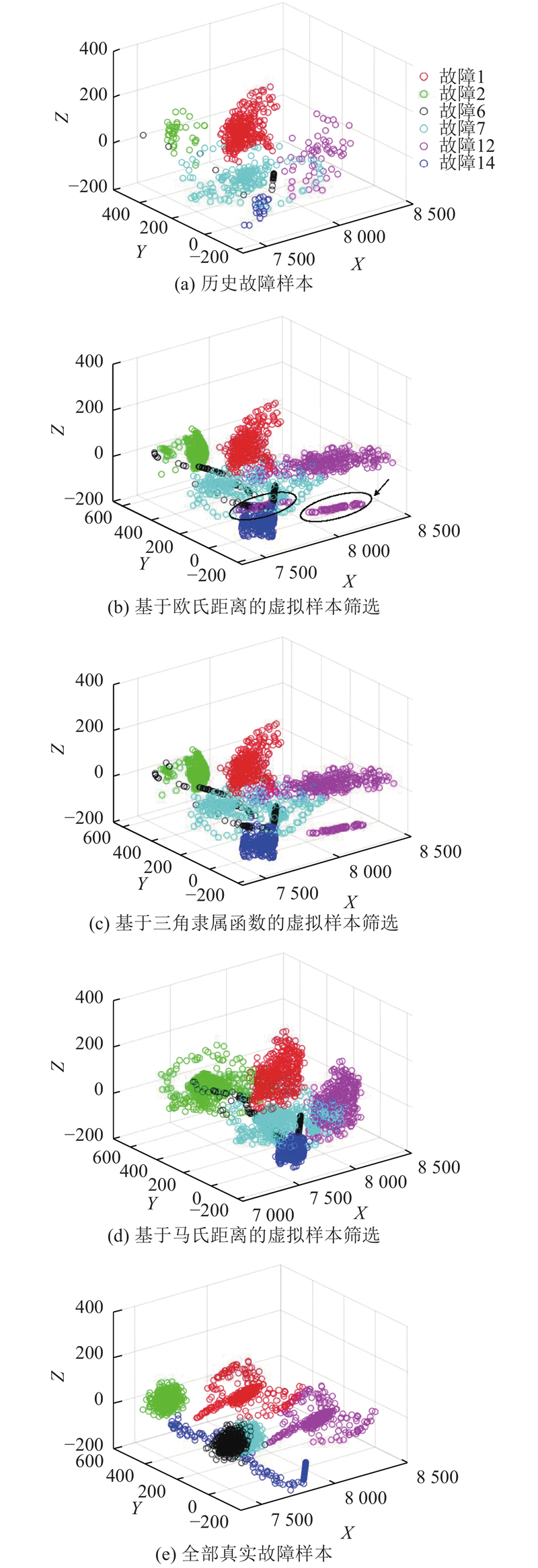
图 3
图 3 不同故障模式下的故障样本三维空间分布
Fig.3 Three-dimensional distribution of fault samples under different fault modes
3.4. 多模式故障分类
3.4.1. 故障样本不平衡下的故障分类
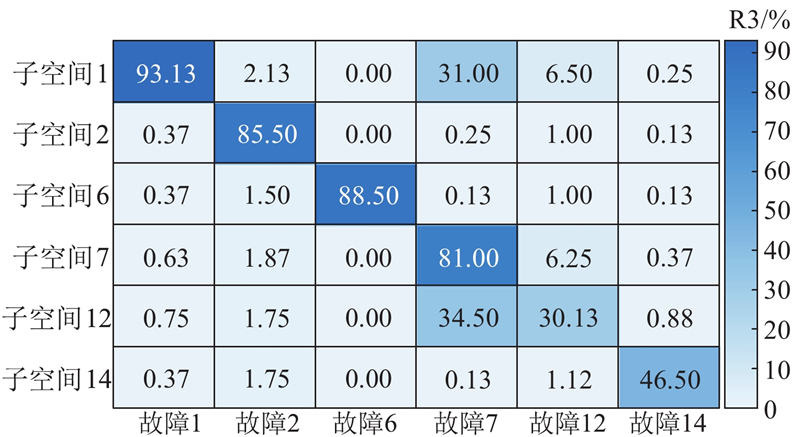
按照3.1节所示故障数据设置情况,大子样故障1的历史故障样本为400个,而小子样故障的历史故障样本甚至低至20个. 在不进行数据增强的情况下直接提取故障子空间
图 4
图 4 故障样本不平衡条件下的重构恢复率混淆矩阵
Fig.4 Confusion matrix of reconstruction recovery rate under unbalanced fault samples
由图4可知,在故障样本不平衡条件下进行故障分类主要存在以下2个问题.
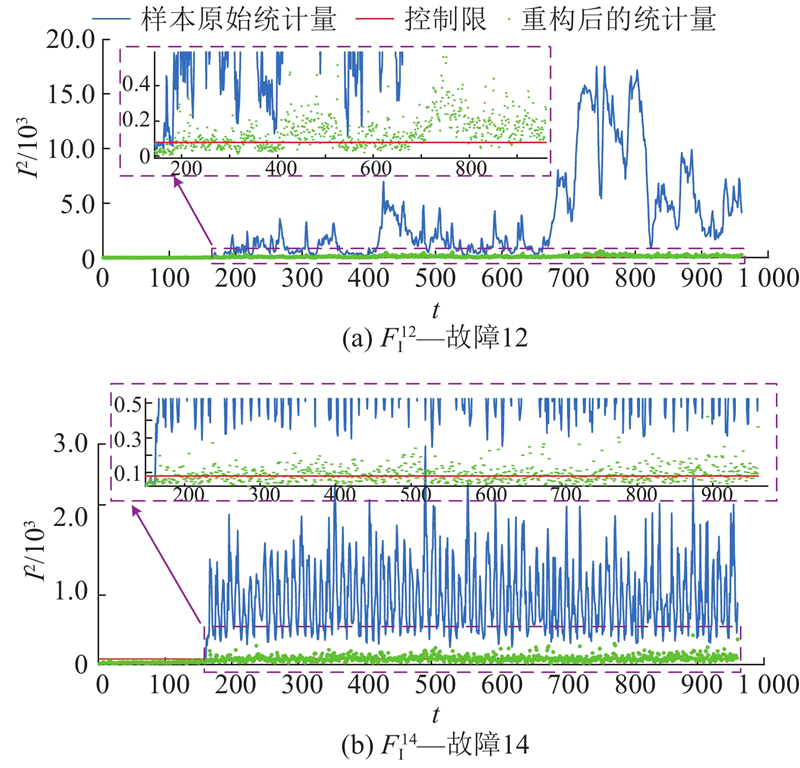
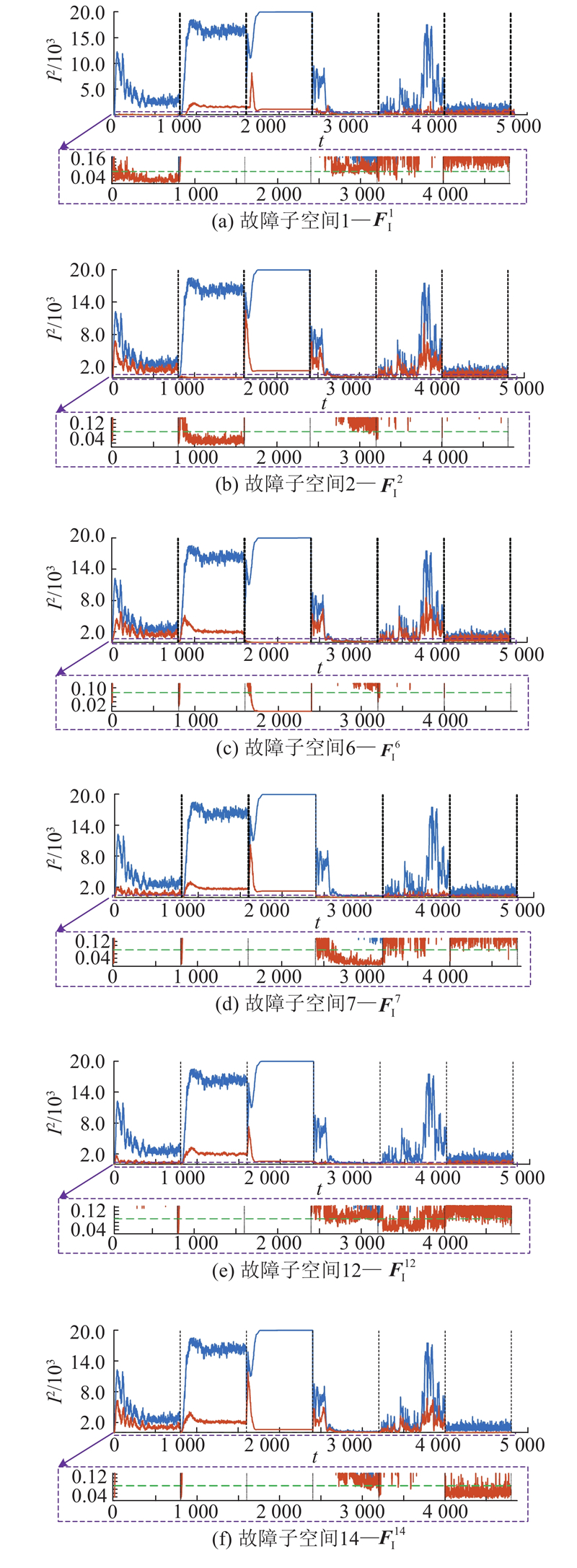
1)在部分故障模式下,用自身的子空间重构故障样本,重构恢复率较低. 例如故障12和故障14的重构恢复率仅为30.13%和46.50%,具体重构情况如图5所示. 图中,蓝色线条代表样本原始统计量,红色粗线条代表相应的控制限,绿色点代表重构后的统计量. 为了清晰展示故障样本(即样本161~960)经重构后的统计量与控制限之间的关系,对图中局部细节进行放大,用紫色虚线框表示. 可以看出,重构后依旧有大量样本的统计量高于控制限. 这说明该故障子空间对正样本的识别能力较弱,即故障子空间表征系统属性的能力有限,本质原因为真实历史故障样本较少,难以表示故障的全部特性.
图 5
图 5 故障样本不平衡情况下的故障重构情况
Fig.5 Fault reconstruction with unbalanced fault samples
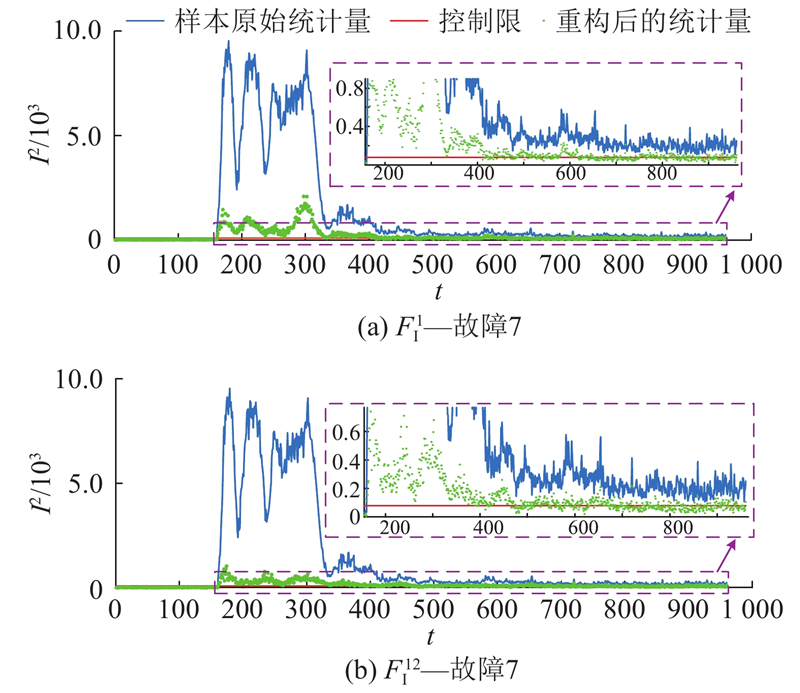
图 6
图 6 用不同故障子空间重构故障7
Fig.6 Reconstruction of fault 7 with different fault subspaces
3.4.2. 数据增强后的故障分类
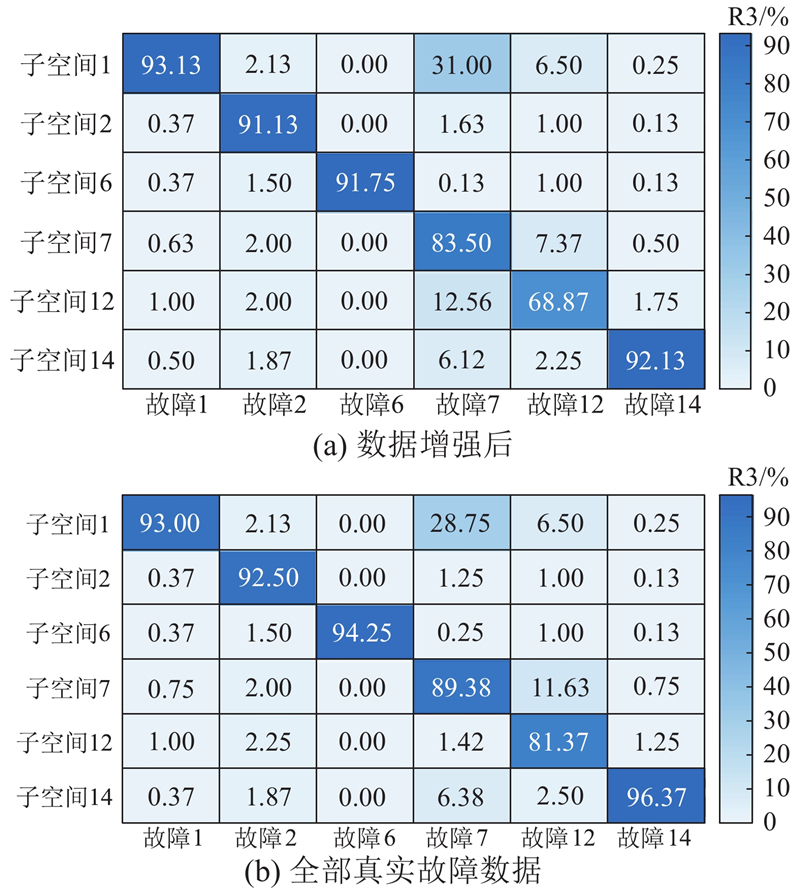
为了克服不平衡故障数据对故障分类性能的影响,采用TimeGAN对小子样故障数据进行数据增强,将所有故障样本增至400个,分别在400个故障样本中提取故障子空间
图 7
图 7 数据增强后的重构恢复率混淆矩阵
Fig.7 Confusion matrix of reconstruction recovery rate after data enhancement
图 8
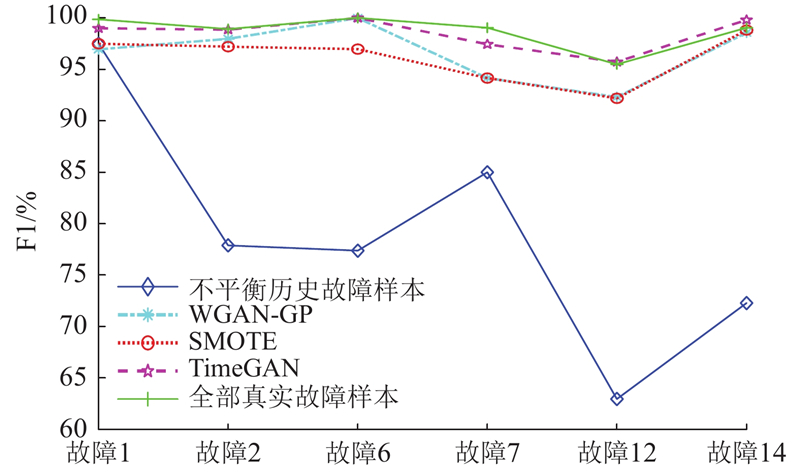
为了验证本研究所提TimeGAN数据增强方法的有效性,采用WGAN-GP、SMOTE作为对比算法,对表1的历史故障样本进行数据增强,然后用故障重构方法进行故障分类,并将分类结果与采用不平衡历史故障样本和全部真实故障样本提取子空间的分类结果进行对比. 分别计算6种故障模式下的精确率、召回率和F1,结果如表3所示. 可以看出,相比直接采用不平衡历史故障样本提取子空间方法,使用数据增强方法可以有效提升故障分类性能. 在3种数据增强方法中,TimeGAN方法在大多数故障模式下可以获得优于其他2种数据增强方法的故障分类性能,尤其在故障7、12和14中,其精确率、召回率和F1得分均高于其他数据增强方法的. 在使用TimeGAN进行数据增强后,故障样本的故障分类性能指标与使用全部真实故障样本的基本相似,只有部分故障的诊断性能略逊于使用全部真实故障样本的,如故障7的召回率和F1得分. 但总体而言,各性能指标之间的差异较小,均低于4个百分点. 为了展示各算法的分类性能,鉴于F1得分能够综合体现模型对正负样本的识别能力和区分能力,将各算法在不同故障模式下的F1得分绘制如图9所示.
表 3 不同故障模式下的故障分类性能评价指标
Tab.3
| 提取子空间 所用数据 | P/% | R/% | F1/% | ||||||||||||||||||
| 故障1 | 故障2 | 故障6 | 故障7 | 故障12 | 故障14 | 故障1 | 故障2 | 故障6 | 故障7 | 故障12 | 故障14 | 故障1 | 故障2 | 故障6 | 故障7 | 故障12 | 故障14 | ||||
| 不平衡故障样本 | 95.56 | 76.35 | 78.26 | 85.37 | 61.70 | 73.21 | 99.50 | 79.50 | 76.50 | 84.62 | 64.25 | 71.37 | 97.49 | 77.89 | 77.37 | 85.00 | 62.95 | 72.28 | |||
| 数据增 强后故 障样本 | WGAN-GP | 98.70 | 99.48 | 100.00 | 99.03 | 87.04 | 98.26 | 95.25 | 96.50 | 100.00 | 89.75 | 98.25 | 98.88 | 96.95 | 97.97 | 100.00 | 94.16 | 92.31 | 98.57 | ||
| SMOTE | 95.56 | 98.71 | 95.85 | 99.03 | 86.93 | 98.51 | 99.50 | 95.75 | 98.12 | 89.75 | 98.12 | 99.12 | 97.49 | 97.21 | 96.97 | 94.16 | 92.19 | 98.82 | |||
| TimeGAN | 99.12 | 100.00 | 100.00 | 99.87 | 92.33 | 100.00 | 98.88 | 97.75 | 100.00 | 95.13 | 99.38 | 99.62 | 99.00 | 98.86 | 100.00 | 97.44 | 95.73 | 99.81 | |||
| 全部真实故障样本 | 99.87 | 100.00 | 100.00 | 99.87 | 91.58 | 100.00 | 99.88 | 97.88 | 100.00 | 98.25 | 99.75 | 98.12 | 99.87 | 98.93 | 100.00 | 99.05 | 95.49 | 99.05 | |||
图 9
图 10
图 11
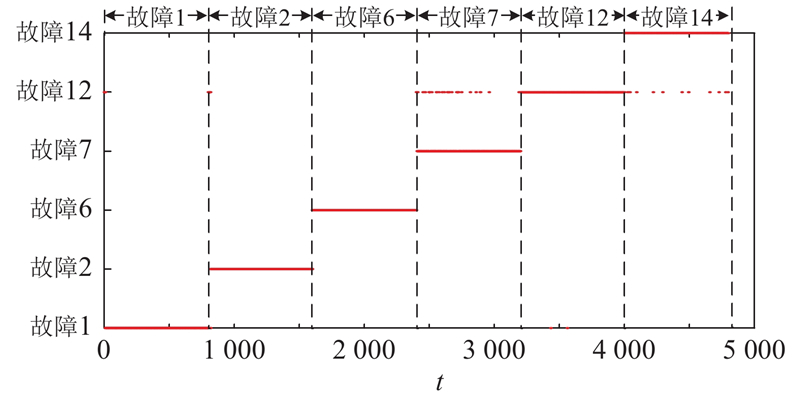
由图10可知,对于所有故障类型,使用该故障对应子空间进行重构后的统计量达到最小. 为了清晰表示,对图中局部进行放大显示. 例如对故障1(即样本1~800),最上方的蓝色点状线表示原始统计量,而红色实线表示用不同故障子空间重构后的统计量,可以看出只有用子空间1进行故障重构可以将大多数样本的统计量恢复至控制限以下,结果与图7(a)所示一致. 故障样本的在线分类结果如图11所示. 图中,
4. 结 语
针对实际工业过程中普遍存在的故障样本稀缺、样本不平衡问题,提出基于TimeGAN数据增强的非线性复杂过程故障分类方法. 研究结果显示,相较于直接使用不平衡数据进行故障重构,采用TimeGAN网络数据增强方法能显著提高诊断准确性. 与WGAN-GP和SMOTE数据增强方法相比,TimeGAN方法在提升诊断精度方面表现出色. 此外,将原始数据映射到核空间后,在核空间提取的故障子空间具有更强的故障特征表征和分辨能力.
由于故障重构是基于多元统计分析的故障诊断方法,诊断精度依赖于故障监测模型的泛化能力. 本研究重点关注非线性非高斯过程的故障诊断,然而实际工业过程通常具有混合特性. 因此,建立更具泛化能力的故障诊断模型是下一步的研究计划.
参考文献
Monitoring and processing signal applied in machining processes: a review
[J].DOI:10.1016/j.measurement.2014.08.035 [本文引用: 1]
基于数据驱动的故障诊断方法综述
[J].
Survey on data driven fault diagnosis methods
[J].
注意力卷积GRU自编码器及其在工业过程监控的应用
[J].
Attention convolutional GRU-based autoencoder and its application in industrial process monitoring
[J].
Joint monitoring of multiple quality-related indicators in nonlinear processes based on multi-task learning
[J].
Data-driven supervised fault diagnosis methods based on latent variable models: a comparative study
[J].DOI:10.1016/j.chemolab.2019.02.006 [本文引用: 2]
基于累计T2贡献值的乙烯裂解炉故障诊断分析
[J].
Fault diagnosis analysis of ethylene cracking furnace based on accumulated T2 contribution value
[J].
Generalized contribution plots in multivariate statistical process monitoring
[J].DOI:10.1016/S0169-7439(00)00062-9 [本文引用: 1]
Total PLS based contribution plots for fault diagnosis
[J].
Reconstruction-based contribution for process monitoring
[J].DOI:10.1016/j.automatica.2009.02.027 [本文引用: 1]
Analysis and generalization of fault diagnosis methods for process monitoring
[J].DOI:10.1016/j.jprocont.2010.10.005 [本文引用: 1]
Subspace approach to multidimensional fault identification and reconstruction
[J].DOI:10.1002/aic.690440812 [本文引用: 1]
Output relevant fault reconstruction and fault subspace extraction in total projection to latent structures models
[J].DOI:10.1021/ie901939n [本文引用: 1]
动态广义主成分分析及其在故障子空间建模中的应用
[J].DOI:10.11959/j.issn.1000-436x.2022091 [本文引用: 1]
Dynamic generalized principal component analysis with applications to fault subspace modeling
[J].DOI:10.11959/j.issn.1000-436x.2022091 [本文引用: 1]
复杂工业过程质量相关的故障检测与诊断技术综述
[J].
Review of quality-related fault detection and diagnosis techniques for complex industrial process
[J].
非均衡小样本条件下基于SAE-ACGANs的复杂供输机构故障诊断方法
[J].
Fault diagnosis method for complex feeding and ramming mechanisms based on SAE-ACGANs with unbalanced limited training data
[J].
Data augmentation classifier for imbalanced fault classification
[J].DOI:10.1109/TASE.2020.2998467 [本文引用: 1]
Imbalanced classification based on minority clustering synthetic minority oversampling technique with wind turbine fault detection application
[J].DOI:10.1109/TII.2020.3046566 [本文引用: 1]
Integrated generative networks embedded with ensemble classifiers for fault detection and diagnosis under small and imbalanced data of building air condition system
[J].DOI:10.1016/j.enbuild.2022.112207 [本文引用: 1]
Auxiliary information-guided industrial data augmentation for any-shot fault learning and diagnosis
[J].DOI:10.1109/TII.2021.3053106 [本文引用: 1]
Spatial-contextual variational autoencoder with attention correction for anomaly detection in retinal OCT images
[J].DOI:10.1016/j.compbiomed.2022.106328 [本文引用: 1]
Variational gated autoencoder-based feature extraction model for inferring disease-miRNA associations based on multiview features
[J].DOI:10.1016/j.neunet.2023.05.052 [本文引用: 1]
SMOTE: synthetic minority over-sampling technique
[J].
Train wheel degradation generation and prediction based on the time series generation adversarial network
[J].DOI:10.1016/j.ress.2022.108816
一种基于TimeGAN和OCSVM的多元退化设备小子样数据增广方法
[J].DOI:10.12263/DZXB.20220079 [本文引用: 1]
A small sample data augmentation method for multivariate degradation equipment based on TimeGAN and OCSVM
[J].DOI:10.12263/DZXB.20220079 [本文引用: 1]
Novel manifold learning based virtual sample generation for optimizing soft sensor with small data
[J].DOI:10.1016/j.isatra.2020.10.006 [本文引用: 1]
Fault detection of non-linear processes using kernel independent component analysis
[J].DOI:10.1002/cjce.5450850414 [本文引用: 2]
Probability density estimation and Bayesian causal analysis based fault detection and root identification
[J].DOI:10.1021/acs.iecr.8b03009 [本文引用: 1]
Hybrid independent component analysis (H-ICA) with simultaneous analysis of high-order and second-order statistics for industrial process monitoring
[J].DOI:10.1016/j.chemolab.2018.12.014 [本文引用: 1]
A plant-wide industrial process control problem
[J].DOI:10.1016/0098-1354(93)80018-I [本文引用: 1]