智能交通系统(intelligent transportation system, ITS )[1]是智慧城市建设的重要组成部分,而交通流量预测技术在ITS中至关重要. 准确预测城市道路交通流量可以缓解拥堵、提高出行效率. 交通流量预测利用历史交通数据来预测未来一段时间内的交通流量状况,这些数据具有时间和空间相关性[2-3]. 时间相关性主要表现在每周工作日的早晚高峰与节假日的出行高峰时间相似,空间相关性表现在交通状况受道路卡口监测点上游、下游和相邻道路历史交通的影响. 有效提取数据的时间和空间相关性是交通流量预测的关键,提取的效果直接影响模型性能. 交通流量不仅受交通时空信息的影响,还受外部因素的干扰,如天气状况、假期和兴趣点(point of interest, POI )分布等[4],这些因素对交通流量预测的准确性有显著影响. 已有研究如Wang等[5-6]往往简单地引入外部因素,忽略了这些因素与交通信息之间的相互关系,导致外部因素对交通流量预测性能提升的贡献不高.
本研究1)结合道路交通信息和外部因素设计静态和动态城市交通知识图谱,使用关系演化图卷积神经网络(recurrent evolution network based on graph convolution network, RE-GCN)[7]对知识图谱进行知识嵌入,提出将车流量数据分别与知识图谱动态和静态信息融合的知识融合方法. 2)在构建路网拓扑图过程中,挖掘交通信息和外部因素的语义关系,将拓扑图重构为静态和动态路网拓扑图. 3)提出融合静态和动态知识图谱的时空多图卷积交通流量预测模型(spatial-temporal multi-graph convolution traffic flow prediction model by integrating static and dynamic knowledge graphs, STMGCN-SDKG)用于交通流量预测任务,在真实的交通流量数据集上评估STMGCN-SDKG的性能;通过消融实验证明引进静态和动态知识图谱、静态和动态路网拓扑图以及知识融合模块在车流量预测中的有效性;在原始的交通流量数据中分别加入高斯噪声(Gaussian noise)和泊松噪声(Poisson noise)进行模型的鲁棒性实验,验证STMGCN-SDKG的抗干扰能力.
1. 相关工作
在时间序列分析中,统计分析方法主要包括历史平均值模型(historical average,HA)、自回归积分移动平均模型(autoregressive integrated moving average,ARIMA)和卡尔曼滤波模型(Kalman filtering model). Pan等[11]将数据内在行为纳入时间序列,使用HA建模;Hamed等[12]采用ARIMA对城市主干道交通流进行简易建模,实现准确预测;Okutani等[13]利用卡尔曼滤波理论预测短期交通量的模型. 线性统计分析方法以时间序列数据平稳的假设为前提,当交通流变化较大时,模型的预测效果较差,且很难处理高维和与时空相关的序列数据.
与统计分析方法相比,机器学习的智能预测模型更具优势. Cai等[14]通过使用改进后的k近邻模型(k-nearest neighbor, KNN)进行交通预测,提高了预测精度. 王博文等[15]将ARIMA和支持向量机模型(support vector regression, SVR)组合. 得到残差优化组合预测模型,该模型能够基本满足不同样本时间间隔的预测需要. Kumar等[16]利用人工神经网络(artificial neural networks, ANN)将各类车辆的速度单独考虑为输入变量,该方法的短时交通流量预测性能良好. 虽然机器学习方法的性能表现优于线性统计分析方法,但是机器学习方法依赖人工设计的特征,当预测任务涉及复杂的规则和因素时,特征设计困难. 此外,机器学习方法往往不能有效捕捉路网层面车流量的时空特征.
研究人员将注意力转向深度学习方法,考虑到交通流量数据具有较强的时间相关性,循环神经网络(recurrent neural network, RNN)及其变体长短记忆网络(long short-term memory networks, LSTM)和门控循环单元(gated recurrent unit, GRU)被广泛应用. Yang等[17]基于LSTM构建交通流量预测模型,并运用注意力机制进行较长序列交通流量的时间特征提取. Hussain等[18]通过GRU构建交通流量预测模型,并提出超参数调整和滑动窗口步骤优化的算法,使得预测效果提升. 虽然基于RNN的模型能有效提取时间特征,但是交通流量还受路网的空间特征影响,而RNN往往难以捕捉这些空间特征. 为了进一步提取路网的空间特征,基于卷积神经网络(convolutional neural network, CNN)的深度学习模型被优先应用. 例如,Ma等[19]通过二维时空矩阵来描述交通流时空关系的图像,搭建出基于CNN的交通流预测模型;Guo等[20]构建的基于三维卷积的端到端深度学习模型能够自动捕获交通数据时空相关性. 此外,为了充分考虑交通流的时间和空间特征,研究者经常将CNN和RNN模型结合,例如,Zheng等[21]将CNN与LSTM结合,并引入注意力机制来提取交通流量的时空特征. 虽然卷积神经网络在交通预测上得到了一定的应用,但是基于CNN的方法只适用于网格结构数据,不适用于复杂的道路网络拓扑结构[22].
为了克服CNN的局限性,研究人员倾向于使用基于图卷积神经网络(graph convolutional network, GCN)的深度学习方法来处理具有拓扑结构的问题. 在交通预测领域,研究者们应用GCN模型来探索路网的空间特征[23]. GCN捕捉时间特征的能力有限,常须结合具有提取时间特征能力的模型(如LSTM或GRU),才能实现对时间特征的有效提取. Zhao等[24]提出时间图卷积网络(temporal graph convolutional network, T-GCN),由GCN提取拓扑结构的空间特征,GRU学习时间相关性. Bai等[25]在T-GCN的基础上加入注意力机制,提出注意力时间图卷积网络(attention temporal graph convolutional network, A3T-GCN),通过注意机制来调整不同时间点的重要性,组装全局时间信息,以提高预测精度. 上述方法没有考虑外部因素或者考虑不够充分,Lv等[26]提出时间多图卷积网络(temporal multi-graph convolutional network, TMGCN),根据道路和其他信息的非欧空间相关性和异构语义相关性编码多个图,并融合时空相关性和外部全局特征,真实数据评估结果显示,TMGCN的性能提升了3%~6%. Zhu等[27]提出基于知识驱动的时空图卷积网络(knowledge-driven spatial-temporal graph convolutional network, KST-GCN),通过构建交通预测知识图谱来挖掘外部因素的相关性对交通的影响. 该研究考虑了知识图谱中的静态和动态因素,但是使用的是较为传统的知识表示方法,不能对知识图谱进行充分表示.
本研究综合考虑交通信息的时空特征和外部因素,通过深入挖掘这些关系的语义,将原始的邻接拓扑图重构为多种语义结构图;应用交通信息和外部因素构建动态和静态城市交通知识图谱;通过知识提取网络进行知识表示,利用提出的知识融合单元将交通流量数据与知识嵌入相融合,形成融合知识的交通流量数据,将这些数据通过时空多图卷积网络提取时间和空间特征,最终经过全连接层输出车流量的预测值.
2. 模型设计
2.1. 问题描述
将交通路网拓扑结构表示为加权图
SDKG表示城市交通动态知识图谱(dynamic knowledge graph, DKG)和城市交通静态知识图谱 (static knowledge graph, SKG). 动态知识图谱
将在
式中:
2.2. 模型整体框架
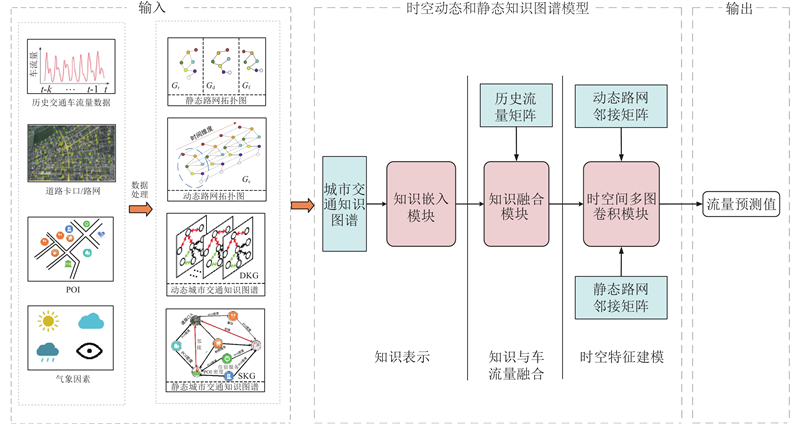
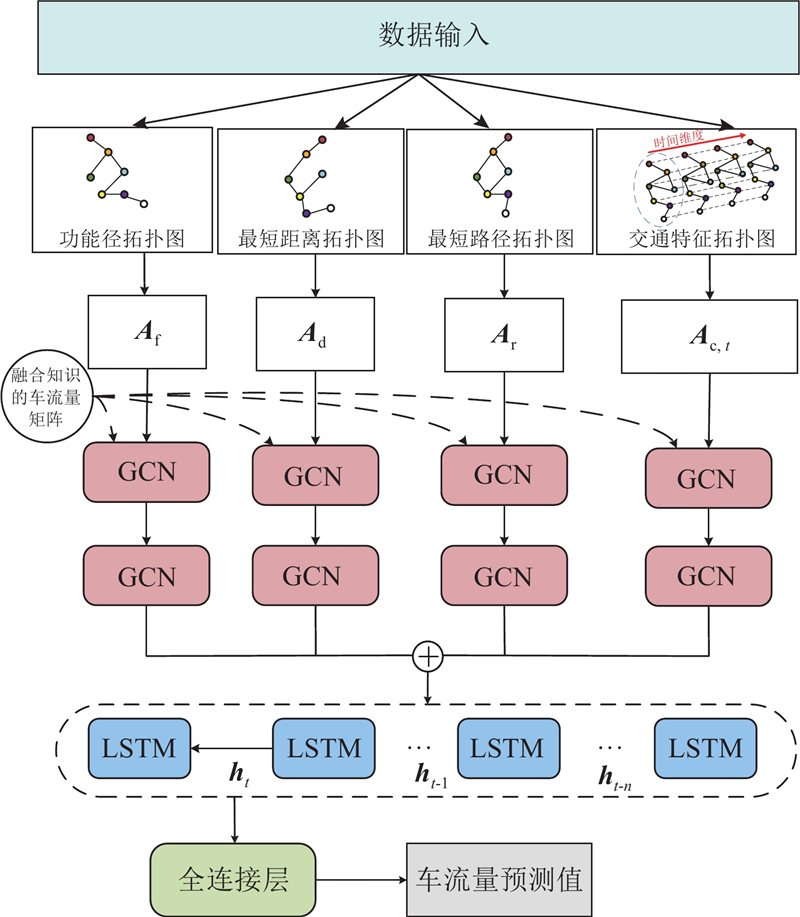
如图1所示为STMGCN-SDKG的框架,由输入、时空动态和静态知识图谱模型(spatiotemporal dynamic and static knowledge graph model, ST-SDKG)及输出3个部分组成. 输入历史交通车流量数据、道路卡口、POI和气象因素,经过数据处理得到静态路网拓扑图
图 1
图 1 所提交通流量预测模型的整体框架图
Fig.1 Overall framework of proposed traffic flow prediction model
2.3. 静态和动态交通知识图谱嵌入模块
2.3.1. 知识图谱
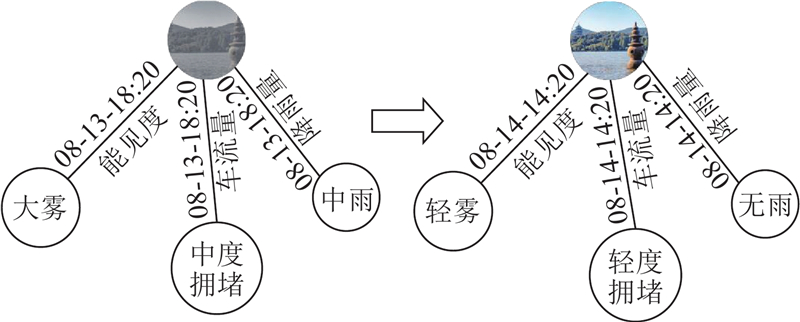
静态知识图谱不随时间变化,其本质为语义网络,由节点、边和属性组成,每个节点表示现实世界中的实体,每条边表示实体间的关系,实体和关系可能包含属性,如“车流量拥堵情况”为实体“道路口”的属性. 静态知识图谱常用三元组的形式来描述各个节点之间的联系. 如图2所示为静态知识图谱示例,其中三元组(道路口A,邻接,道路口B)表示道路口A与道路口B邻接.
图 2
动态知识图谱是反映现实世界中实体及其关系随时间变化的信息表示方式. 与静态知识图谱不同,动态知识图谱不仅考虑实体之间的关系,还考虑这些关系如何随时间演变,这使得动态知识图谱能够更准确地捕捉事物之间的时空关联. 以道路口、车流量和拥堵程度来表示动态知识图谱中的某个关系,以道路卡口作为实体,车流量作为属性关系,拥堵程度作为属性值,时间作为第四维度,如图3所示为动态知识图谱中的示例. 可以看到,随着时间的变化,知识图谱的内容发生变化,记录为(西湖某个道路口,车流量,中度拥堵,2023-08-13-18:20),这个拥堵的情况仅在2023年8月13日的18:20有效.
图 3
2.3.2. 静态和动态交通知识图谱嵌入
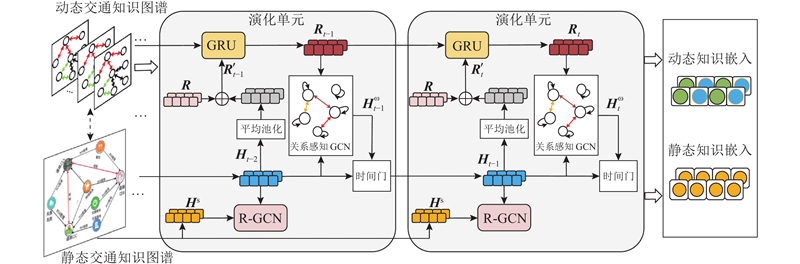
知识图谱嵌入(knowledge graph embedding)是指将由组成知识的实体和关系在低维度连续向量空间中表征的过程. 如图4所示为本研究的知识图谱嵌入过程,使用RE-GCN的演化单元来获得动态交通知识图谱的知识嵌入
图 4
图 4 静态和动态交通知识图谱知识嵌入流程图
Fig.4 Knowledge embedding flow chart of static and dynamic transportation knowledge graph
式中:
式中:
式中:
式中:
式中:
式中:ReLU
2.4. 知识融合模块
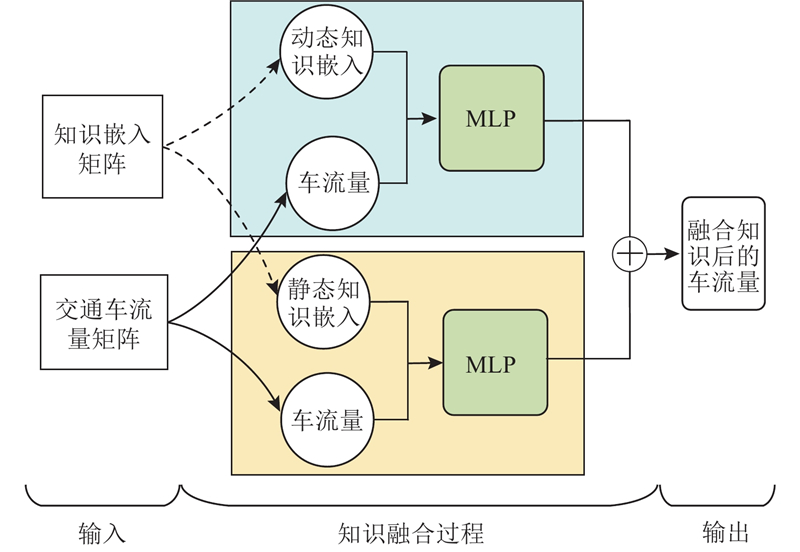
为了将交通知识图谱的知识与车流量信息融合,采用知识融合单元处理相关信息,具体流程如图5所示. 知识嵌入矩阵
图 5
2.5. 时空多图卷积模块
如图6所示为时空多图卷积模块的网络结构,该模块是STMGCN-SDKG的骨干,作用是提取多种网络拓扑图和融合知识后的车流量的时间和空间结构的特征.
图 6
图 6 时空多图卷积模块结构图
Fig.6 Structure of spatial-temporal multi-graph convolution module
2.5.1. 空间相关性
模型的输入数据为历史交通车流量信息、交通路网信息和POI信息,利用3种数据之间的语义信息构图. 图的构建是GCN的关键,如果构建的拓扑图不能有效地表达道路之间的信息,不但无助于模型的学习,还可能降低模型的性能. 在构建多种拓扑图时,参考Lv等[26]构建多种拓扑图的方法重构部分语义图.
静态最短路径拓扑图
静态最短距离拓扑图
式中:
静态功能拓扑图
式中:
功能拓扑图
动态交通特征路网拓扑
在获得4种拓扑图后,对于动态拓扑图,在时刻
式中:
式中:
2.5.2. 时间相关性
使用LSTM获取序列的时间相关性,该算法能够有效解决RNN的梯度消失问题和梯度爆炸问题,且在处理长期依赖问题时,LSTM可以有效传递和表达长时间序列中的信息,不会导致长时间前的有用信息被遗忘,使LSTM能够更好地学习数据中的长短期的时间相关性. 将已获得的特征矩阵输入LSTM进行时间特征的提取,计算式为
式中:Wi、Wf、Wo、Wc均为权重矩阵,
2.6. 损失函数
损失函数是机器学习和深度学习中的重要概念,用于衡量模型预测值和真实值的差异,即模型的预测误差. 损失函数是模型优化的基础,通过观察损失函数可以判断模型优化情况,帮助研究者选择模型框架和参数. 损失函数的表达式为
式中:
3. 实验与结果分析
3.1. 实验数据
多数已公开的交通流数据集缺少对交通流量预测有重要影响的POI数据和天气数据,原因是这些数据不易收集,且有保密性. 本研究基于杭州市某个区的交通数据集,实验具有通用性,可以应用于其他城市. 数据集包含2019年1月1日到12月31日道路卡口的车流量数据、交通路网数据、天气数据和POI数据. 其中可用的道路卡口400个,每个卡口每10 min记录一次车流量数据;按车流大小将车流量划分为不拥堵、轻度拥堵、中度拥堵、严重拥堵4个等级;14种POI数据包含餐饮美食、公司企业、购物消费、交通设施、金融机构、酒店住宿、科教文化、旅游景点、汽车相关、商务住宅、生活服务、休闲娱乐、医疗保健和运动健身;天气数据包含降雨量数据和能见度数据,其中降雨量划分为无雨、小雨、中雨、大雨、暴雨、大暴雨和特大暴雨7个等级,能见度划分为浓雾、重雾、大雾、轻雾和近似无雾5个等级. 将数据进行清洗处理后,构造训练集和测试集,划分比例为4∶1. 实验将进行未来10、30、60 min的交通车流量预测.
根据动态和静态2种情况分别构建知识图谱. 静态知识图谱以三元组的形式表示,例如将道路卡口和其周边POI数量的关系构建属性三元组为(道路卡口A,当前POI的密度等级,POI类型),对于道路与道路之间的关系,构建实体三元组为(道路卡口A,邻接/不邻接,道路卡口B);三元组的总数为172 000. 动态知识图谱是以静态知识图谱为背景,在静态知识图谱的基础上增加时间信息,在描述静态知识图谱的三元组基础上增加时间维度,道路卡口与天气的关系表示为(道路卡口A,降雨量,将雨量等级,时间),道路卡口与POI表示为(道路卡口,POI的密度等级,POI类型,时间);四元组的总数为17 176 800.
3.2. 评价指标及参数设置
为了直观地评估STMGCN-SDKG的预测性能,实验采用4种主流的评价指标来评估模型的车流量预测值和真实交通车流量值之间的差距,分别为均方根误差RMSE、平均绝对误差MAE、准确度Acc和可决系数R2,计算式分别为
RMSE和MAE表示预测值与真实值的误差,值越小,表示预测误差越小,模型的性能越好;
3.3. 基线模型
为了验证STMGCN-SDKG的性能,选取传统的和当前较为先进的交通流量预测模型进行对比实验. 1)历史平均法HA[11]将历史交通车流量数据输入模型,预测未来的交通流量. 2)LSTM[17]为由遗忘门、记忆门和输出门组成的RNN变体模型,引进了注意力机制,输入历史车流量数据进行预测. 3)基于时空图卷积网络的分层交通流预测方法ST-GCN[22]利用图卷积得到空间相关性,GRU网络引入3个周期特征的结构,更新当前状态得到时空相关性,再经过融合层将外部因素和时空相关性进行融合,输出交通车流量预测值. 4)时间多图卷积网络TMGCN[26]利用单层GCN获取空间相关性,通过GRU捕获时间相关性,由全连接神经网络融合外部全局特征,输出交通车流量预测值. 5)基于知识驱动的时空图卷积网络KST-GCN[27]先构建交通预测知识图谱,通过KR-EAR知识表示方法得到知识表示,再用知识融合单元将车流量和知识嵌入进行融合并输入时空图卷积骨干网络中训练,输出车流量预测值.
3.4. 模型对比实验分析
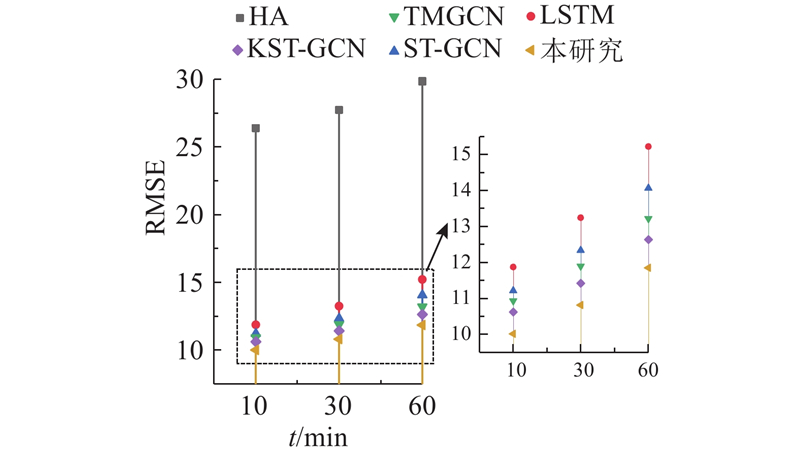
在杭州交通数据集上进行预测模型的对比分析. 不同模型在未来3个时段的交通预测性能指标如表1所示. 可以看出,STMGCN-SDKG在所有模型中预测性能最好,表明该模型能够有效完成时空交通预测任务. 从预测精度角度分析,比较STMGCN-SDKG与基线方法预测未来10 min车流量性能. STMGCN-SDKG在RMSE上比传统方法HA低62.07%,原因是传统的方法模型难以处理复杂的非平稳时间序列数据. STMGCN-SDKG在RMSE和Acc上分别比LSTM低15.67%和高4.68%,原因是LSTM只考虑了交通流的时间特征,未考虑交通流的空间特征. STMGCN-SDKG在RMSE上比ST-GCN低10.71%;ST-GCN考虑了时空间相关性,且通过分层的结构增强时间相关性的提取,引入的外部因素仅以数字代号表示,通过归一化输入网络,这样的处理不能很好体现外部因素对交通流量预测的影响. STMGCN-SDKG与TMGCN和KST-GCN相比,RMSE分别低8.45%和5.76%,Acc分别高3.69%和2.71%;TMGCN只在最后的全连接层将外部因素作为全局变量与时空特征融合,不能充分反映交通信息与外部因素的关系,导致预测的性能不高;KST-GCN考虑外部因素之间以及与交通情况的关系对交通预测的影响,构建知识图谱,但只使用传统的知识表示方法,导致预测效果不佳. 对比其他评估指标,STMGCN-SDKG均优于基线模型,表明所提模型具有较好的时间和空间特征提取的能力,能够有效使用外部因素. 从长期预测角度分析,如图7所示为STMGCN-SDKG与基线模型性能对比的垂线图. 可以看出,随着预测的时间增长,模型的预测效果均有所下降,STMGCN-SDKG优于基线模型,且STMGCN-SDKG的RMSE变化幅度相对平稳,证明该模型可以用于短期预测任务,也可以用于长期预测任务.
表 1 不同交通流量预测模型对未来3个时段的交通状况预测结果
Tab.1
| 模型 | t=10 min | t=30 min | t=60 min | |||||||||||
| RMSE | MAE | Acc | R2 | RMSE | MAE | Acc | R2 | RMSE | MAE | Acc | R2 | |||
| HA | 26.403 | 13.513 | 0.669 | 0.843 | 27.741 | 14.166 | 0.652 | 0.826 | 29.863 | 15.174 | 0.627 | 0.800 | ||
| LSTM | 11.874 | 6.709 | 0.833 | 0.966 | 13.243 | 7.433 | 0.815 | 0.954 | 15.218 | 8.454 | 0.796 | 0.935 | ||
| ST-GCN | 11.214 | 6.445 | 0.838 | 0.972 | 12.338 | 7.129 | 0.833 | 0.964 | 14.062 | 7.998 | 0.824 | 0.951 | ||
| TMGCN | 10.937 | 5.822 | 0.841 | 0.969 | 11.897 | 6.284 | 0.836 | 0.965 | 13.221 | 6.932 | 0.829 | 0.956 | ||
| KST-GCN | 10.625 | 5.673 | 0.849 | 0.971 | 11.421 | 5.962 | 0.843 | 0.966 | 12.637 | 6.371 | 0.834 | 0.959 | ||
| 本研究 | 10.013 | 5.226 | 0.872 | 0.978 | 10.816 | 5.536 | 0.864 | 0.972 | 11.853 | 5.953 | 0.853 | 0.963 | ||
图 7
图 7 不同交通流量预测模型的性能对比垂线图
Fig.7 Vertical diagram of performance comparison for different traffic flow prediction models
3.5. 消融实验分析
为了体现STMGCN-SDKG中各模块对模型性能的影响,进行消融实验,设计STMGCN-SDKG的7种变体,同时与基线TMGCN进行对比. 1)STMGCN-SDKG-no Gc:移除动态交通特征路网拓扑图,保留其余3种路网拓扑图. 2)STMGCN-SDKG-no Gr:移除最短路径拓扑图,保留其余3种路网拓扑图. 3)STMGCN-SDKG-no Gd:移除最短距离路网拓扑图,保留其余3种路网拓扑图. 4)STMGCN-SDKG-no Gf:移除功能拓扑图,保留其余3种路网拓扑图. 5)STMGCN-SDKG-no MLP:移除知识融合模块的MLP,使用一元一次函数代替进行知识融合. 6)STMGCN-SDKG-no SKG:移除静态知识图谱,保留动态知识谱图. 7)STMGCN-SDKG-no DKG:移除动态知识图谱,保留静态知识图谱. 预测未来10 min车流量的消融实验结果如表2所示. 可以看出,STMGCN-SDKG-no Gc在RMSE上比STMGCN-SDKG高4.7%,Acc低2.18%;分别去除最短路径拓扑、最短距离路网拓扑和功能拓扑的模型在RMSE上比STMGCN-SDKG分别高2.91%、3.05%和3.89%. 当用一元一次函数替代知识融合模块中的MLP时,与STMGCN-SDKG相比,模型的RMSE高3.14%;移除静态知识图谱的模型在RMSE上比STMGCN-SDKG高4.40%,预测精度低了2.18%;STMGCN-SDKG-no DKG相对于原模型指标RMSE高了5.89%,预测精度低了2.64%. 实验结果表明,每个模块对模型的性能提升都有贡献,其中引入动态交通特征路网拓扑图对模型性能的影响较其他3种路网拓扑图的影响大;使用MLP能够让知识嵌入和车流量融合更好,经过多层隐藏层提取两者特征进行融合,效果比一元函数更好;引入静态知识图谱,模型性能提升较为明显,引进动态知识图谱对模型提升性能的效果最明显,说明动态知识图谱表达的外部因素与交通信息之间的关系对交通情况的影响更大,当静态和动态知识图谱都引入时,效果达到最优,说明两者具有互补性.
表 2 所提交通流量预测模型的消融实验结果
Tab.2
| 模型 | RMSE | MAE | Acc | R2 |
| TMGCN | 10.937 | 5.822 | 0.841 | 0.969 |
| STMGCN-SDKG-no Gc | 10.484 | 5.536 | 0.853 | 0.970 |
| STMGCN-SDKG-no Gr | 10.304 | 5.309 | 0.865 | 0.974 |
| STMGCN-SDKG-no Gd | 10.318 | 5.423 | 0.863 | 0.973 |
| STMGCN-SDKG-no Gf | 10.403 | 5.451 | 0.856 | 0.971 |
| STMGCN-SDKG-no MLP | 10.327 | 5.347 | 0.856 | 0.973 |
| STMGCN-SDKG-no SKG | 10.454 | 5.446 | 0.853 | 0.971 |
| STMGCN-SDKG-no DKG | 10.603 | 5.687 | 0.849 | 0.969 |
| STMGCN-SDKG | 10.013 | 5.226 | 0.872 | 0.978 |
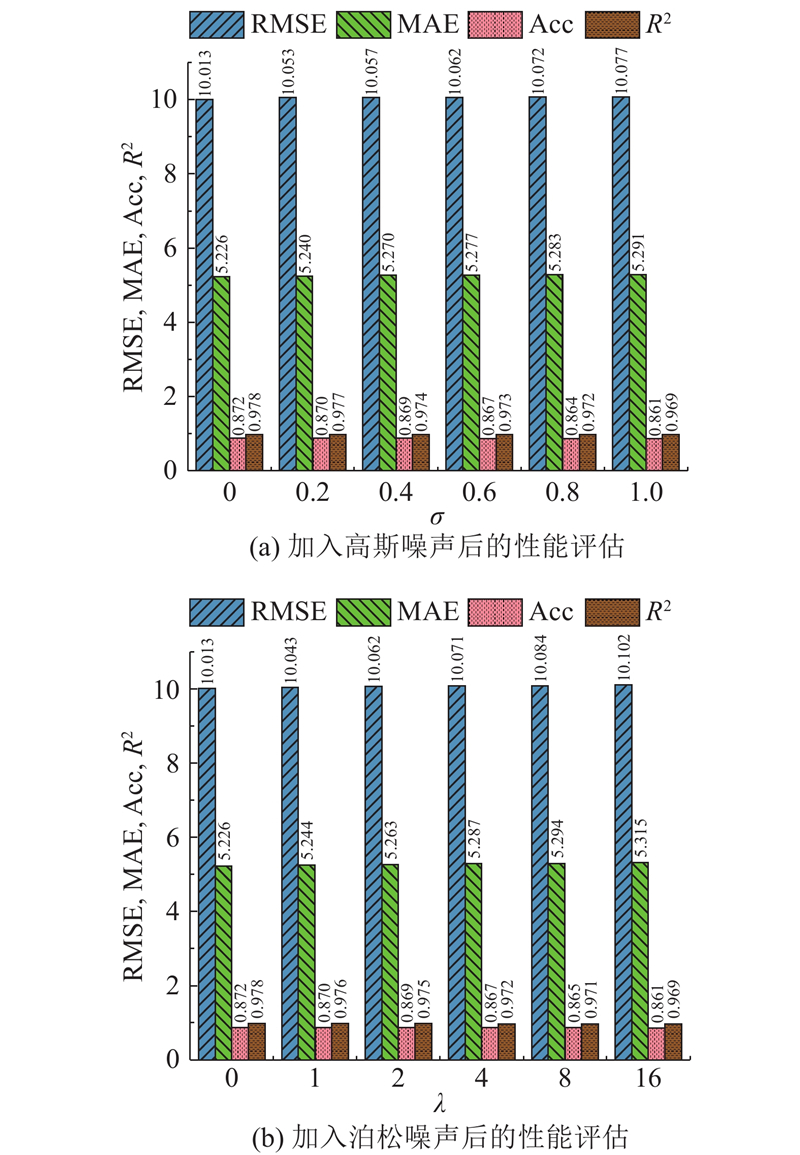
3.6. 鲁棒性实验
数据收集过程中不可避免地存在噪声,在数据预处理过程的噪声过滤难以完全去除噪声,因此模型的抗噪声能力显得尤为重要. 为了检验模型的抗噪能力,开展扰动分析实验,检验模型的鲁棒性. 在实验中,将2种常见的随机噪声分别加入历史交通车流量数据,随机噪声服从高斯分布
图 8
图 8 所提交通流量预测模型的鲁棒性实验结果
Fig.8 Robustness experimental results of proposed traffic flow prediction model
4. 结 语
针对道路卡口交通流量预测问题,本研究提出融合静态和动态知识图谱的时空多图卷积交通流量预测模型. 该模型引入静态和动态知识图谱,由RE-GCN实现知识嵌入,有效表达外部因素与交通信息的关系. 进行多种语义拓扑图重构,将拓扑图与融合知识的车流量信息输入时空多图卷积模块以有效提取时空特征,提升了所提模型的预测性能. 在真实的杭州交通数据集上,所提模型的性能基线模型. 消融实验结果表明,引入知识图谱方法和构建多种路网拓扑图有效;鲁棒性实验证明,模型具有抗干扰能力. 本研究的路网拓扑方法基于开源地图信息且须进行人工筛查,信息或操作的错漏可能导致路网错误而影响模型性能;此外,考虑POI、天气信息、车流量和道路卡口的数据信息表达能力有限,限制了模型的性能. 未来计划优化路网拓扑的构建和城市交通知识图谱的挖掘,研究突发异常情况对交通流量预测的影响,探索如何合理利用突发异常情况与交通状况的相关性.
参考文献
城市智能交通系统的发展现状与趋势
[J].DOI:10.3724/SP.J.1224.2014.00006 [本文引用: 1]
Developing trend of ITS and strategy suggestions
[J].DOI:10.3724/SP.J.1224.2014.00006 [本文引用: 1]
Survey on traffic prediction in smart cities
[J].DOI:10.1016/j.pmcj.2018.07.004 [本文引用: 1]
图神经网络驱动的交通预测技术: 探索与挑战
[J].DOI:10.11959/j.issn.2096-3750.2021.00235 [本文引用: 1]
Graph neural network driven traffic prediction technology: review and challenge
[J].DOI:10.11959/j.issn.2096-3750.2021.00235 [本文引用: 1]
Road traffic forecasting: recent advances and new challenges
[J].DOI:10.1109/MITS.2018.2806634 [本文引用: 1]
An effective dynamic spatiotemporal framework with external features information for traffic prediction
[J].DOI:10.1007/s10489-020-02043-1 [本文引用: 1]
Combining weather condition data to predict traffic flow: a GRU‐based deep learning approach
[J].DOI:10.1049/iet-its.2017.0313 [本文引用: 1]
基于BP神经网络人群流量预测的实现
[J].
Implementation of crowd flow prediction based on BP neural network
[J].
Short-term traffic flow prediction method for urban road sections based on space–time analysis and GRU
[J].DOI:10.1109/ACCESS.2019.2941280 [本文引用: 1]
Short-term prediction of traffic volume in urban arterials
[J].DOI:10.1061/(ASCE)0733-947X(1995)121:3(249) [本文引用: 1]
Dynamic prediction of traffic volume through Kalman filtering theory
[J].DOI:10.1016/0191-2615(84)90002-X [本文引用: 1]
A spatiotemporal correlative k-nearest neighbor model for short-term traffic multistep forecasting
[J].DOI:10.1016/j.trc.2015.11.002 [本文引用: 1]
基于ARMA-SVR的短时交通流量预测模型研究
[J].
Study on short-term traffic volume prediction model based on ARMA-SVR
[J].
Short term traffic flow prediction for a non urban highway using artificial neural network
[J].DOI:10.1016/j.sbspro.2013.11.170 [本文引用: 1]
Traffic flow prediction using LSTM with feature enhancement
[J].DOI:10.1016/j.neucom.2018.12.016 [本文引用: 2]
Intelligent traffic flow prediction using optimized GRU model
[J].DOI:10.1109/ACCESS.2021.3097141 [本文引用: 1]
Learning traffic as images: a deep convolutional neural network for large-scale transportation network speed prediction
[J].DOI:10.3390/s17040818 [本文引用: 1]
Deep spatial–temporal 3D convolutional neural networks for traffic data forecasting
[J].DOI:10.1109/TITS.2019.2906365 [本文引用: 1]
A hybrid deep learning model with attention-based conv-LSTM networks for short-term traffic flow prediction
[J].DOI:10.1109/TITS.2020.2997352 [本文引用: 1]
Hierarchical traffic flow prediction based on spatial-temporal graph convolutional network
[J].DOI:10.1109/TITS.2022.3148105 [本文引用: 2]
Deep learning on traffic prediction: methods, analysis, and future directions
[J].
T-GCN: a temporal graph convolutional network for traffic prediction
[J].DOI:10.1109/TITS.2019.2935152 [本文引用: 1]
A3T-GCN: attention temporal graph convolutional network for traffic forecasting
[J].DOI:10.3390/ijgi10070485 [本文引用: 1]
Temporal multi-graph convolutional network for traffic flow prediction
[J].DOI:10.1109/TITS.2020.2983763 [本文引用: 4]
KST-GCN: a knowledge-driven spatial-temporal graph convolutional network for traffic forecasting
[J].DOI:10.1109/TITS.2021.3136287 [本文引用: 2]
Multilayer perceptron for GEFCom2014 probabilistic electricity price forecasting
[J].DOI:10.1016/j.ijforecast.2015.11.009 [本文引用: 1]
An information-theoretic perspective of tf–idf measures
[J].DOI:10.1016/S0306-4573(02)00021-3 [本文引用: 1]