半球谐振陀螺(hemispherical resonator gyro, HRG)是高精度的振动陀螺仪,其敏感器件全部用熔融石英加工而成,包括半球振子、激励罩和读出基座3个元件. 当HRG的敏感轴绕惯性空间转动时,HRG的谐振子在绕中心轴旋转时有哥氏效应产生,在哥氏效应下谐振子振型在环向相对壳体进动[1]. HRG的输出会随着环境温度变化而变化, 进行温度建模补偿分析对提升HRG的输出精度意义重大. 周小刚等[2]采用独立成分分析方法建立陀螺的温度误差补偿模型,并对与温度有关的确定性漂移进行补偿,同时使用Allan方差对不确定性漂移进行分析补偿. 周强等[3]认为HRG谐振子频率随温度变化导致的输出变化是线性的,进而设计新的温度补偿电路,精准测试HRG的输出温度特性,将漂移由0.05°/h提高到0.03°/h. 吴宗收等[4]提出将改进的粒子群优化(particle swarm optimization, PSO)算法和自回归滑动平均(auto-regressive moving average, ARMA)建模方法结合起来,经过HRG升温实验检验,参数寻优能力相比传统方法提高了一倍. 李广胜等[5]将自回归(auto-regressive, AR)多变量模型引入HRG温度漂移模型的时间序列,借助系统辨识的相关理论,建立并分析了漂移和温度的多变量自回归模型. Li等[6]提出基于多元回归的HRG温度误差补偿方法,建立了补偿温度误差的多元回归模型,并通过升温和降温实验验证了该模型的补偿效果. 虽然补偿效果明显,但多元回归模型对原始数据要求较高,需要数据具有较好的可重复性.
HRG的输出数据具有非线性和非平稳性,传统的时间序列分析模型只能捕捉线性关系,不适合HRG预测分析. 核主成分分析法(kernel principal component analysis, KPCA)和数据处理组合方法(group method of data handing, GMDH)是处理非线性数据的常用方法. 汪国新等[7]将KPCA引入火力发电设备状态诊断与分析,提出多元时序分割算法. 实验结果表明,该算法能有效分析模型并准确提取非线性特征,可用于解决火力发电设备的状态诊断问题. 黄泽丰等[8]为了提升光场成像的空间分辨率,通过多尺度潜在低秩分解图像,并引入KPCA对各层特征系数进行融合,使得基础层和显著层的特征信息更加明显,所生成的图像具有更高的分辨率和更好的视觉效果. 高运广等[9]将KPCA模型引入非线性微惯性测量单元传感器故障诊断,在缩短参数选择时间和减少工作量的同时,使故障检测的准确率提高了18.44%. 段伟等[10]将GMDH神经网络引入地震液化场地分析,建立侧向变形的预测模型,该模型的准确度和可靠性都明显高于其他神经网络. 凯立德·艾尔巴兹[11]以盾构机为研究对象,提出集成GMDH神经网络和遗传算法的智能方法,预测了盾构机滚刀寿命;相比经验模型,该智能方法能够提供更高的准确度. Ahmadi等[12]针对一类逆变器,提出攻击弹性模型预测自适应控制器,借助GMDH网络估计系统的不确定性使系统免受脉冲、缩放和随机攻击的影响. Xie等[13]将GMDH神经网络应用于离群值检测模型,在有效消除离群值的同时,提高了训练后分类模型的分类精度. 针对光伏/燃料/电池系统的电压和功率调节问题,Band等[14]设计了基于GMDH神经网络的控制系统, 考虑了可变未知动态、未知温度和辐照以及输出负荷突然变化等运行条件,该系统在几种场景的仿真中相比其他方法表现出较好的性能.
针对HRG温度建模与补偿问题,本研究1)提出基于KPCA-GMDH神经网络的建模补偿方法,分析HRG全寿命数据的大数据特征,初步选取输入特征向量;2)基于KPCA去除初选特征向量之间的冗余性3)将筛选后特征向量代入GMDH网络建立模型;4)进行单一样本和多样本的训练和预测,对比不同模型的预测效果以验证所提方法的性能.
1. 半球谐振陀螺测试大数据分析
1.1. 半球谐振陀螺温度影响分析
在输入角速度为零时,陀螺的输出叫做零偏. 区别于传统机械陀螺,HRG的核心部件半球谐振子通过径向振动产生驻波,再由驻波的进动敏感输入角速度. HRG在工作时,环境温度的变化以及陀螺内部产热会影响谐振子的密度、半径、弹性模量和泊松比等参数,使得谐振子的固有频率发生变化,表现为陀螺的输出产生温度漂移,因此温度是引起陀螺漂移的重要因素之一. 零偏的温度漂移严重制约陀螺的精度,有必要对零偏的温度漂移进行抑制或补偿.
半球谐振子四波腹振动的谐振频率约为
式中:h为半球谐振子的厚度,r为半球谐振子的半径,E为弹性模量,μ为谐振子材料的泊松比,ρ为谐振子的材料密度. 上述变量中弹性模量受温度影响较大,该参数随温度变化的表达式为
式中:E0为取常温时谐振子的弹性模量,kE为弹性模量随温度变化的系数,量级约为10−5. 式(2)是线性关系式,且E(T)与E0非常接近,将式(2)带入式(1)后在E0处进行泰勒展开即可获得较好的线性近似关系:
kE数值很小,保留一阶项即可获得理想的精度:
当保留一阶项时,谐振子谐振频率f与温度T为线性关系,因此,可以选取谐振频率作为HRG的温度漂移补偿模型的自变量特征. 式(4)中,温度T表示谐振子材料的实时温度,而非真实的环境温度. 谐振子从环境吸热的过程类似于热工过程,传递函数用典型一阶惯性环节近似表示为
式(5)表明,谐振子谐振频率与环境温度存在非线性关系,在建立HRG温度漂移补偿模型时应当考虑;惯性环节表明谐振频率的导数项(离散变量为差分项或前一周期采样值)应当作为自变量特征.
1.2. 半球谐振陀螺测试大数据
工业大数据是以互联网大数据为基础,结合工业过程背景提出的新概念. 通过在时间上不断存储、积累过程运行数据,在空间上扩展、采集、运输数据,工业过程中遍布着不同尺度的时空间数据,以及散落于各级工业部门的不同来源、不同类别的数据. 工业大数据的主要特性是数据规模大,数据总类多,数据要求处理速度快,数据价值密度低,数据真实性低[15]. 为了处理工业过程中的大数据,解决复杂的控制、优化和故障评估等问题,大数据建模成为热门的研究方向. 王晓军[16]建立基于大数据的风洞试验段马赫数预测模型,提出特征子集集成方法、子模型学习算法和集成修建算法,有效提高了马赫数的预测速度及精度. 王龙晖[17]以调节阀为研究对象,提出基于大数据驱动的调节阀故障诊断方法、调节阀阀后压力预测方法,有效提升了调节阀的智能化水平. 杨小佳[18]将腐蚀大数据技术应用于低合金结构钢,并结合深度学习模型挖掘低合金结构钢内在腐蚀规律,验证了该技术的可靠性.
通过数据管理、分析和挖掘体系,可以得到HRG全寿命全周期测试的数据[19]. HRG测试数据数量巨大,符合“数据规模大”的特性;数据的采集和建模须进行实时处理,符合“数据要求处理速度快”的特性;每组数据中均包含冗余数据且数据价值实现程度低,符合“数据价值密度低”的特性;数据里通常包含有噪声数据,符合“数据真实性低”特性. 因此,可以认定HRG测试数据为工业大数据.
2. 核主成分分析和数据处理组合方法神经网络模型
2.1. 初选特征向量
在神经网络中,特征选择的好坏直接影响预测效果. 根据特征和因变量的相关程度,特征分为无关、弱相关和强相关3种,特征之间可能存在关系的相互重叠,根据特征间的相关程度,分为冗余和非冗余特征. 特征选择的作用是,消除原有集合中嘈杂、冗余和不相关的特征,优化训练模型,提高算法搜索效率,提高分类精度[20].
设定测试采集的
2.2. 基于核主成分分析的特征向量选择
初选的非线性特征向量之间存在相关性,不利于后续计算,为此,基于KPCA进一步筛选特征向量. 通过非线性映射
式中:
组合式(7)和式(8),KPCA优化变为
式中:
典型的核函数是高斯核
当
式中:
式中:
2.3. 数据处理组合方法网络
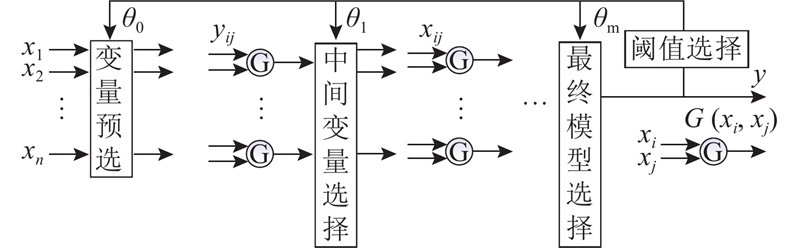
GMDH网络是以KPCA-GMDH多项式为基础的复杂非线性系统辨识方法[23]. 假设非线性系统以
函数
被广泛用于非线性模型的完全描述. 当
图 1
将
2.4. 完整网络模型
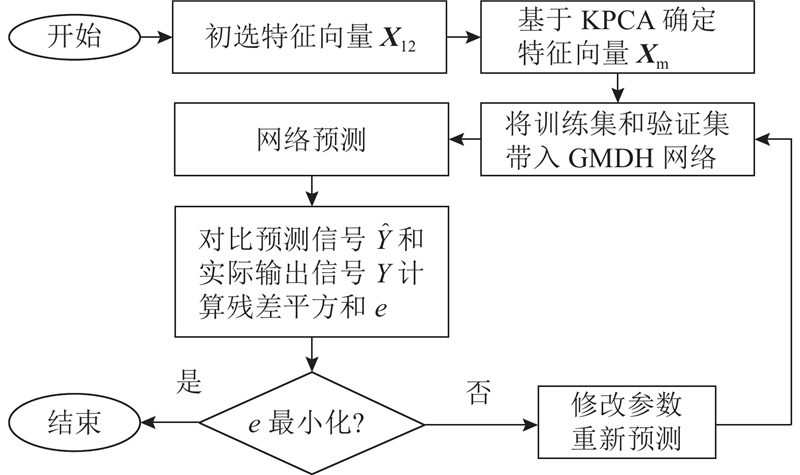
如图2所示为基于KPCA-GMDH神经网络模型的建模补偿方法的基本步骤. 1)分析HRG数据的大数据特征,初步考虑以
图 2
图 2 主成分分析和数据处理组合方法神经网络模型
Fig.2 Network model of kernel principal component analysis and grouped method of data handling neural network
3. 模型预测分析
3.1. 实验条件设置
以HRG的多次输出数据为分析对象. 数据采集方案:将HRG安装在平台单轴回路中,测量地纬度为
图 3
3.2. 实验数据预处理
3.2.1. 原始数据
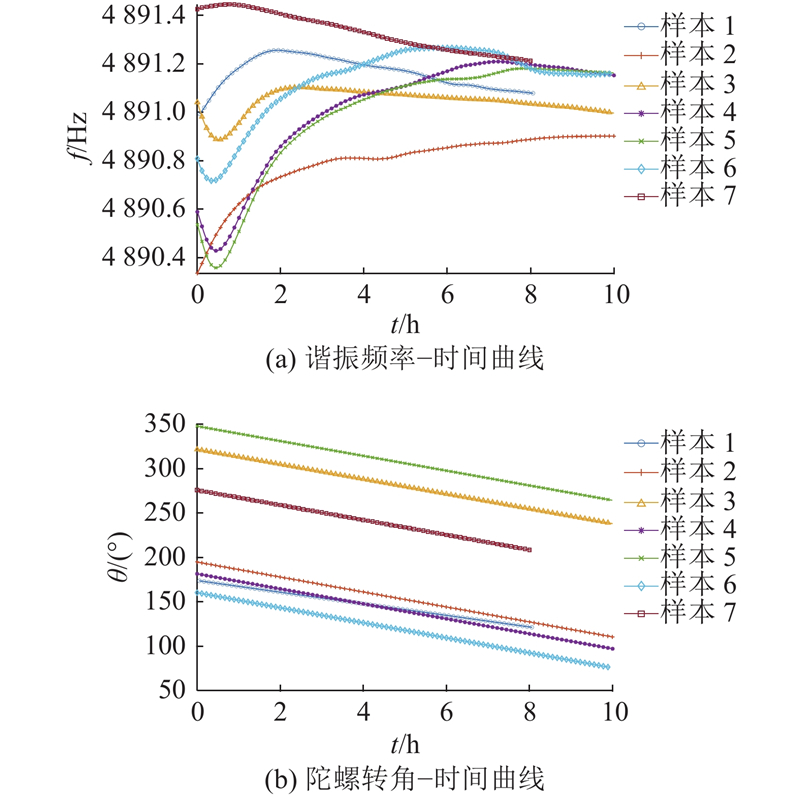
实验共测得7组数据,以时间
图 4
图 4 半球谐振陀螺的参数变化曲线
Fig.4 Parameter variation curves of hemispherical resonator gyro
3.2.2. 扣除转台运动
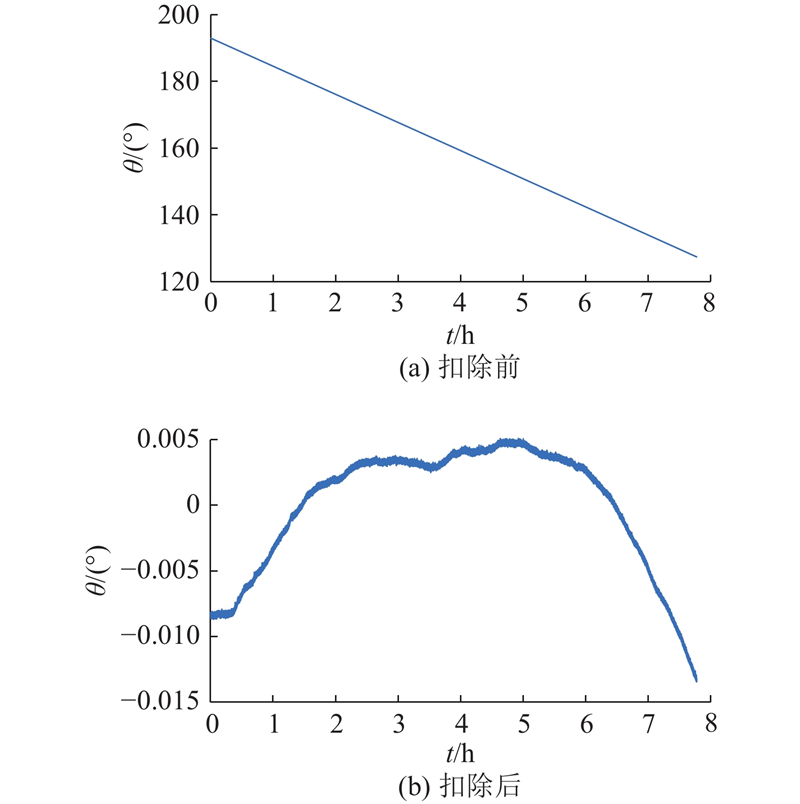
在测试过程中,陀螺仪静止置于稳定平台上,因此将转台运动从实际测量输出中扣除. 考虑到转台近似以匀角速度转动,以一阶线性模型对输出值进行拟合,再由陀螺输出值减去拟合值获得实际输出值,扣除转台运动前、后HRG输出如图5所示.
图 5
图 5 扣除转台运动前后半球谐振陀螺转动角度
Fig.5 Hemispherical resonator gyro rotation angle before and after deducting turntable movement
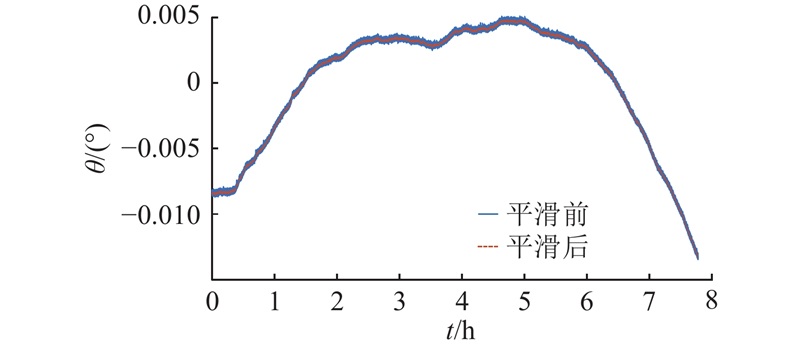
3.2.3. 平滑曲线
图 6
图 6 平滑前后半球谐振陀螺转动角度
Fig.6 Hemispherical resonator gyro rotation angle before and after smoothing
3.2.4. 去除异常样本
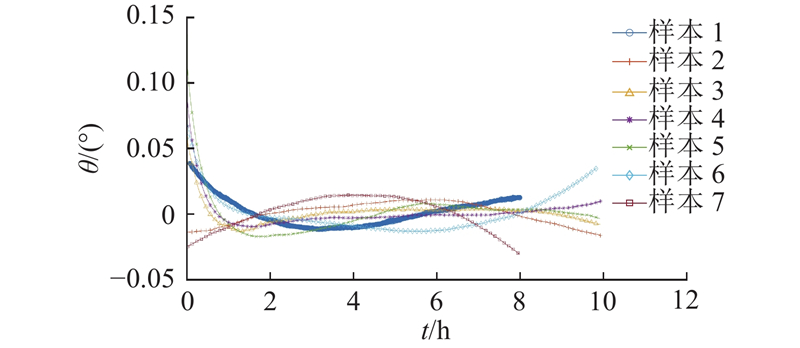
扣除转台运动后,将7次陀螺样本输出值依次解析. 查看原始数据发现,样本1存在500 s的未启动状态,其余样本存在40±3 s的未启动状态. 将未启动状态截除后,所有样本的输出统一按0起始时刻依次画出,如图7所示. 此时样本1不仅在输出时长上与其余样本不同,用于分析的初始段数据丢失较多,且整体输出值也明显异于其余样本,存在大量粗糙数据. 为了提高整体数据的处理精度,综合考虑后剔除样本1.
图 7
图 7 去除未启动状态数据后的半球谐振陀螺转动角度
Fig.7 Hemispherical resonator gyro rotation angle after removing data from inactive state
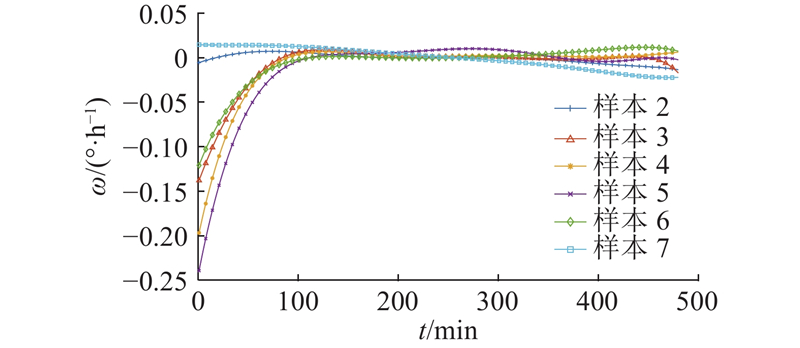
3.2.5. 数据重采样
分析陀螺的角速度
图 8
图 8 重采样后的半球谐振陀螺转动角速度
Fig.8 Hemispherical resonator gyro angular velocity after resampling
3.3. 实验数据分析
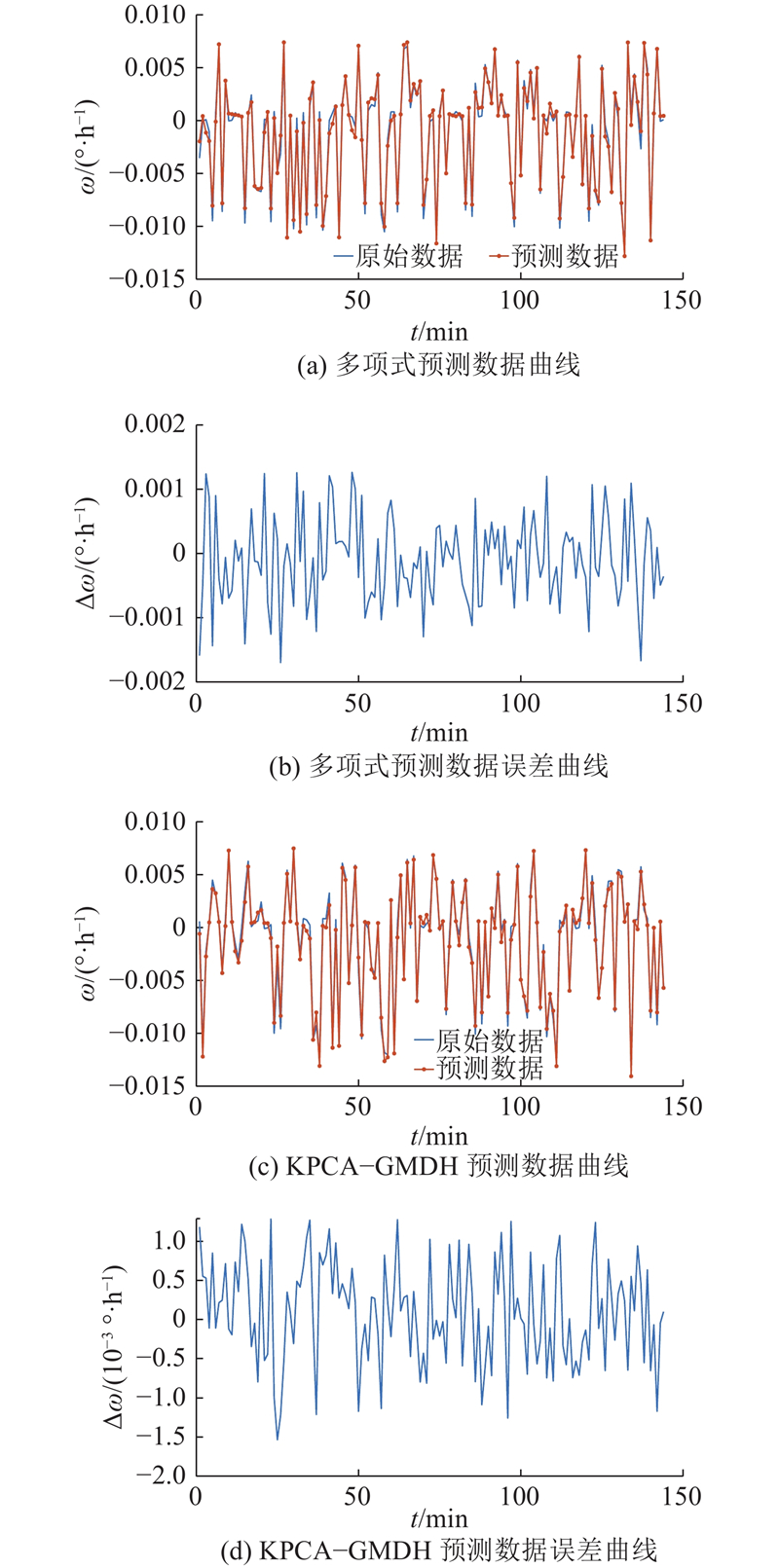
3.3.1. 单一样本预测
表 1 样本初选特征向量的统计特性
Tab.1
| 特征 | 最大值 | 最小值 | 平均值 |
| 69.9349 | 69.9309 | 69.9340 | |
| 4890.8881 | 4890.3364 | 4890.7693 | |
| 2.319 2×107 | 2.391 5×107 | 2.392 0×107 | |
| 0.0042 | −0.0005 | 0.0008 | |
| 0.2950 | −0.0329 | 0.0540 | |
| 20.6294 | −2.3008 | 3.7751 | |
| 1.008 9×105 | −1.125 3×104 | 1.846 3×104 | |
| 1.7795×10−5 | 0 | 1.6851×10−6 | |
| 0.0012 | 0 | 1.1785×10−4 | |
| 0.0870 | 0 | 0.0082 | |
| 425.5719 | 0 | 40.3035 |
表 2 样本经核主成分分析筛选后的特征向量统计特性
Tab.2
| 特征 | 最大值 | 最小值 | 平均值 |
| 18.6932 | −95.1230 | 2.600 9×10−14 | |
| 9.5840 | −14.0542 | −7.9554×10−13 | |
| 6.1600 | −10.3414 | −1.988 5×10−13 |
表 3 样本转动角速度的统计特性
Tab.3
| 特征 | 最大值 | 最小值 | 平均值 |
| 18.6932 | −95.1230 | 2.600 9×10−14 |
GMDH网络训练集的输入为
式中:
GMDH网络验证集的输出为
预测效果的评价指标选择均方根误差RMSE,计算式为
图 9
表 4 不同样本预测结果的均方根误差
Tab.4
| 样本 | RMSE | |
| 多项式预测 | KPCA-GMDH | |
| 2 | 0.00068 | 0.00064 |
| 3 | 0.00380 | 0.00300 |
| 4 | 0.00440 | 0.00290 |
| 5 | 0.00490 | 0.00470 |
| 6 | 0.00410 | 0.00370 |
| 7 | 0.00060 | 0.00050 |
3.3.2. 多样本预测
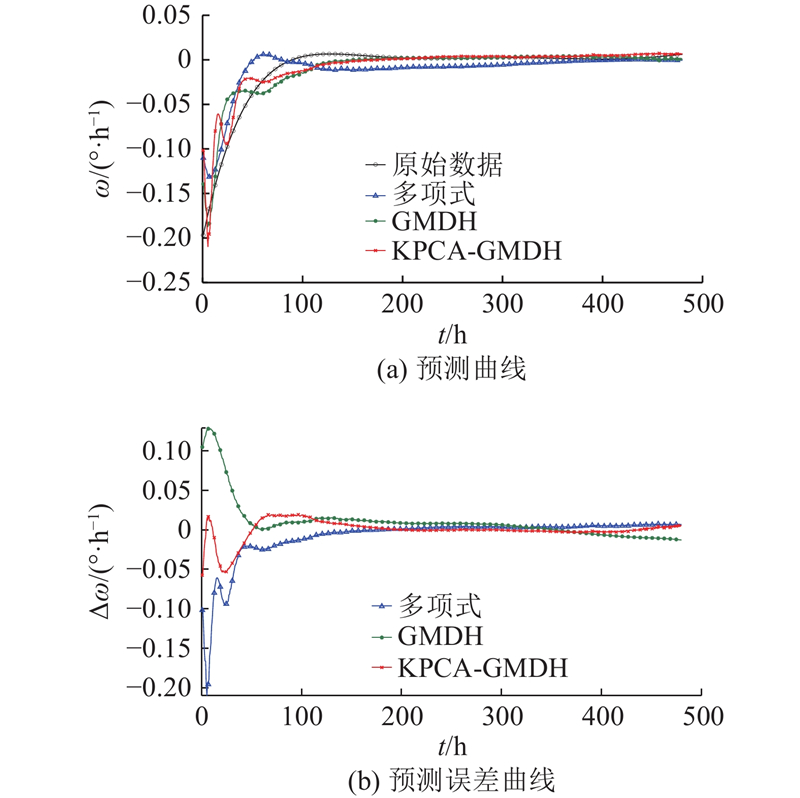
进一步验证KPCA-GMDH神经网络的鲁棒性,将多样本进行融合,其中样本A由原始样本2、3、5、6、7融合而成,样本B由原始样本3、5、6、7融合而成,样本C由原始样本2、5、6、7融合而成,样本D由原始样本3、5、6融合而成. 从实验数据预处理结果来看,样本2和样本7数据趋势较其余4个样本不同,因此推断,去掉样本2和样本7可以提升网络精度. 分别就融合样本A、B、C和D参与训练的4种情况进行实验,考虑到样本4在样本2、3、4、5、6和7中最为稳定,将样本4作为测试组,将KPCA-GMDH神经网络与多项式、GMDH网络进行对比,评价指标为误差标准差:
图 10
图 10 融合样本A拟合样本4的预测曲线及误差曲线
Fig.10 Prediction curve and error curve for fused sample A fitting sample four
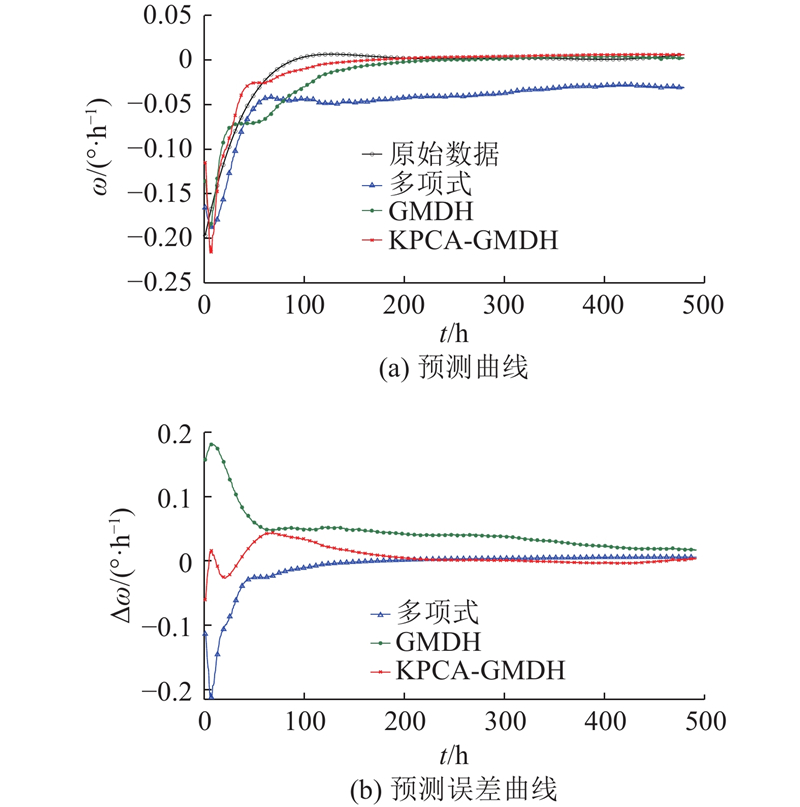
图 11
图 11 融合样本B拟合样本4的预测曲线及误差曲线
Fig.11 Prediction curve and error curve for fused sample B fitting sample four
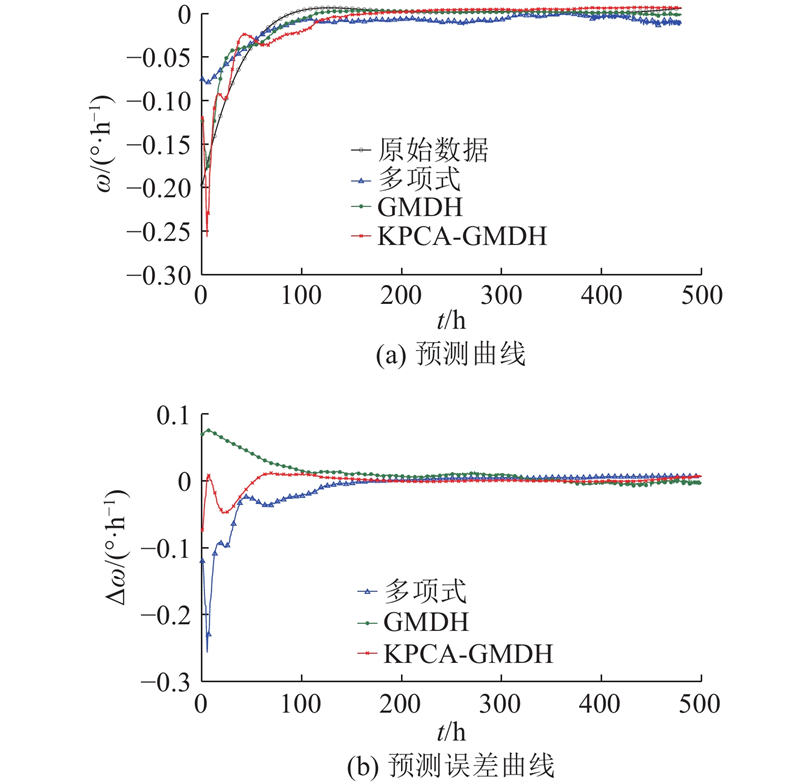
图 12
图 12 融合样本C拟合样本4的预测曲线及误差曲线
Fig.12 Prediction curve and error curve for fused sample C fitting sample four
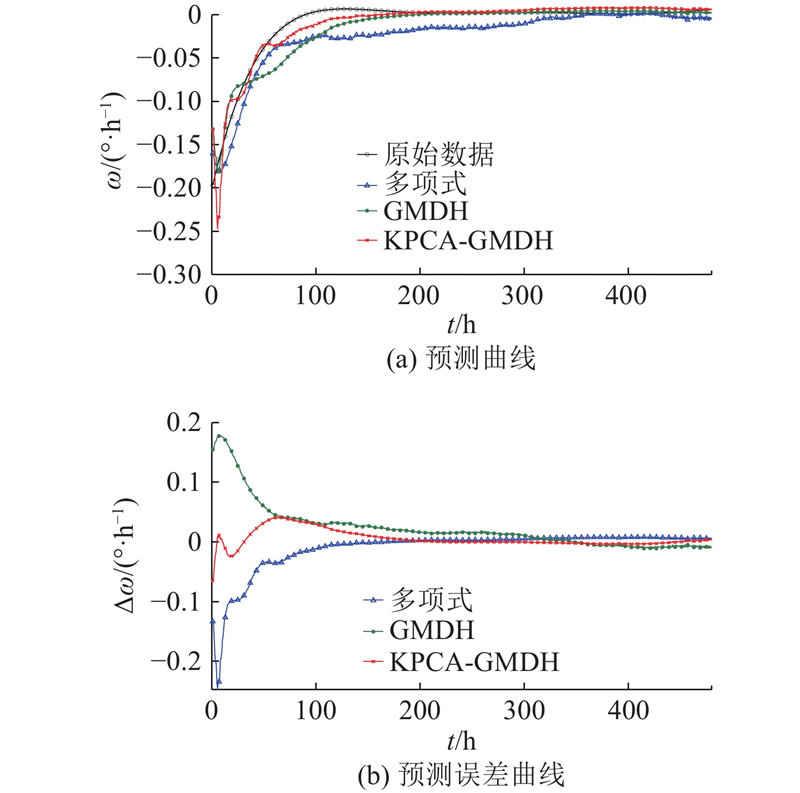
图 13
图 13 融合样本D拟合样本4的预测曲线及误差曲线
Fig.13 Prediction curve and error curve for fused sample D fitting sample four
表 5 不同建模方法的误差标准差对比
Tab.5
| 融合样本 | |||
| 多项式 | GMDH | KPCA-GMDH | |
| A | 0.0258 | 0.0138 | 0.0133 |
| B | 0.0324 | 0.0157 | 0.0149 |
| C | 0.0293 | 0.0133 | 0.0128 |
| D | 0.0395 | 0.0137 | 0.0125 |
4. 结 语
以HRG大数据为研究对象,本研究提出基于KPCA-GMDH神经网络的建模补偿方法,实验并分析不同样本不同条件下HRG的输出精度,验证模型的有效性. 基于HRG大样本数据建立KPCA-GMDH神经网络模型. 实验表明,单一样本预测时,所提方法的预测效果明显好于传统多项式;在多样本预测时,所提方法的预测精度相比多项式模型分别提升了48.5%,54.0%,56.3%,68.4%;相比GMDH模型分别提升了3.6%、5.1%、3.8%、8.8%,说明所建模型适用于HRG建模补偿,且降噪效果良好. KPCA-GMDH神经网络模型会受训练样本的输入自变量(频率)的范围影响,测试样本的频率在训练样本的频率范围内就能够预测出较好的结果. 当新输入的测试数据不在训练集的频率范围内时,预测结果会出现较大的偏差,在后续工作中,计划通过补充实验扩大样本的方式,尽可能扩大训练样本的频率范围. 无论在何种训练模式下,KPCA-GMDH神经网络模型预测的HRG数据的标准差均在千分之一量级,基本满足零偏稳定性和快速启动性的要求.
参考文献
半球谐振陀螺温度补偿与实验研究
[J].
HRG temperature compensation and experiment research
[J].
半球谐振陀螺温度特性及补偿分析
[J].
The temperature characteristic and compensating analysis of HRG
[J].
一种改进PSO-ARMA半球谐振陀螺温度误差建模方法
[J].
An improved PSO-ARMA method for temperature error modeling of hemispherical resonator gyroscope
[J].
基于AR多变量模型的半球谐振陀螺温度漂移建模
[J].
Modeling temperature drift of HRG based on AR multi-variable model
[J].
A multiple regression based method for indirect compensation of hemispherical resonator gyro temperature error
[J].DOI:10.1038/s41598-023-31868-2 [本文引用: 1]
基于KPCA-GG的火力发电设备状态诊断方法
[J].
Condition diagnosis method for thermal power generation equipment based on KPCA-GG
[J].
基于MDLatLRR和KPCA的光场图像全聚焦融合
[J].DOI:10.3788/gzxb20235204.0410004 [本文引用: 1]
Light field all-in-focus image fusion based on MDLatLRR and KPCA
[J].DOI:10.3788/gzxb20235204.0410004 [本文引用: 1]
基于模糊AGA-KPCA的MIMU传感器故障诊断方法
[J].
Fault diagnosis method for MIMU sensors based on fuzzy AGA-KPCA
[J].
基于GMDH的地震液化场地侧向变形预测模型
[J].
Prediction model for liquefaction-induced lateral spread displacement based on GHDH
[J].
Resilient model predictive adaptive control of networked Z-source inverters using GMDH
[J].DOI:10.1109/TSG.2022.3174250 [本文引用: 1]
GMDH-based outlier detection model in classification problems
[J].DOI:10.1007/s11424-020-9002-6 [本文引用: 1]
Voltage regulation for photovoltaics-battery-fuel systems using adaptive group method of data handling neural networks (GMDH-NN)
[J].DOI:10.1109/ACCESS.2020.3037134 [本文引用: 1]
过程工业大数据建模研究展望
[J].
Perspectives on big data modeling of process industries
[J].
大数据理论在高精度惯性导航系统测试技术中的应用
[J].
Application of big data technology on test technology of high accuracy inertial navigation system
[J].
Deep principal component analysis based on layerwise feature extraction and its application to nonlinear process monitoring
[J].DOI:10.1109/TCST.2018.2865413 [本文引用: 1]
偏最小二乘线性模型及其非线性动态扩展模型综述
[J].
Review of partial least squares linear models and their nonlinear dynamic expansion models
[J].
改进的GMDH方法及其在参数预报中的应用
[J].
Improved GMDH algorithm and its application in parameter prediction
[J].
基于平滑样条曲线结合离散状态转移算法的拉曼光谱基线校正方法
[J].DOI:10.3788/CJL202249.1811001 [本文引用: 1]
Baseline correction for raman spectroscopy using cubic spline smoothing combined with discrete state transformation algorithm
[J].DOI:10.3788/CJL202249.1811001 [本文引用: 1]