元启发式算法发展至今大致可以分为4类:群体智能优化算法、进化算法、基于物理的算法以及基于人类的算法. 群体智能优化算法是受动物的社会行为启发的算法,例如粒子群算法(particle swarm algorithm, PSO)[6]、麻雀搜索算法(sparrow search algorithm, SSA)[7]. 进化算法是通过模拟生物的进化行为提出的,著名的进化算法有:遗传算法(genetic algorithm, GA)[8]、差分进化算法(differential evolution, DE)[9]. 基于物理的算法受物理规律的启发,例如亨利气体溶解度算法(Henry gas solubility optimization, HGSO)[10]、流向算法(flow direction algorithm, FDA)[11]. 还有一些算法来源于人类的自然行为和社会关系,例如教学优化算法(teaching learning based optimization, TLBO)[12]、社会进化学习优化算法(social evolutionary learning optimization algorithm, SELO)[13].
虽然上述这些元启发式算法的来源不同,但其都有一些标准的特征,例如优化过程一般都有探索和开发2个阶段. 在第1个阶段,优化算法生成随机算子在搜索空间内进行全局探索;在第2个阶段,优化算法试图从搜索空间中找到最优解. 有效的元启发式优化算法必须平衡探索和开发这2个阶段的探索倾向,避免算法早熟,陷入局部最优. 为了提高算法的性能,研究人员通过一些改进手段,在探索和开发机制之间保持适当的平衡,增强算法的适应性. Mohammad等[14]在灰狼优化算法(GWO)中加入基于维度学习的狩猎搜索策略,该策略以每个个体为中心生成一个半径为R的邻域,在该邻域内信息可以相互传递,这不仅增强了局部开发和全局探索之间的平衡,还保持了种群的多样性. 邓志诚等[15]针对粒子群算法(PSO)探索时间长、易陷入局部最优值的缺点,提出方波触发勘探与开发的粒子群算法,该方法将方波作为一种控制手段,在方波的前半个周期内使用标准粒子群算法进行全局探索,在后半个周期内使用改进的粒子群进行局部开发,提高了算法的精度和收敛速度,但在高维情况下会陷入局部最优.
虽然这些改进手段都不同程度地提升了算法性能,但没有改变算法本身的局限性,所建立的模型在特定的期限内具有良好的效果,期限范围的扩大或缩小会导致“叠加误差”. 部分学者融合2种或多种优化算法,扩大模型的适用范围,以增强模型的抗干扰能力. Amirteimoori等[16]在PSO迭代产生新一代后,采用选择、交叉、变异等遗传算子,将当前种群替换为更好的种群. 这种在粒子群(PSO)算法中嵌入遗传算子的操作克服了标准粒子群算法收敛速度慢和频繁收敛到局部最优值的缺点. 与单一算法相比,这种混合优化算法具有更高的精度和搜索效率.
天鹰优化算法(AO)是Abualigah等[17]提出的新的元启发式优化算法. 该算法通过模拟天鹰对不同猎物的不同捕获方法建立数学模型,具有收敛速度快、全局搜索能力强的优点,但该算法存在易陷入局部最优、受最优个体位置影响较大、种群信息利用率低等缺点.
针对上述问题,提出多策略改进的天鹰优化算法. 结合广义正态分布优化算法与天鹰优化算法,扩大天鹰优化算法的搜索空间,提升全局搜索效率和种群质量. 对于大多数的元启发式算法来讲,它们对控制参数的调整表现出微妙的敏感性,这可能是造成算法出现过早收敛,陷入局部最优解的原因之一. 针对天鹰优化算法的第2阶段存在较多控制参数的情况,引入相量算子使第2阶段变为自适应的非参数优化,进一步平衡算法的探索和开发过程. 在天鹰算法的第3阶段引入流向算子,使每个个体间的信息可以相互交流,提高了迭代后期种群的多样性,增强算法的开发性能,加快收敛速度.
1. 天鹰优化算法
和众多元启发式算法一样,天鹰优化算法的目标是在搜索空间内找到全局最优解. 通过模拟天鹰4种不同的捕食策略建立数学模型,根据搜索空间内解的不同特性,灵活应用不同的搜索策略. 这4个阶段的介绍如下(天鹰优化算法的所有公式均来自于文献[17]).
1.1. 扩展探索阶段(第1阶段)
在第1个阶段,天鹰通过垂直俯身的高空翱翔搜索猎物并选择搜索区域. 这一阶段的数学描述如下所示.
式中:
1.2. 缩小探索阶段(第2阶段)
在该阶段,通过模拟天鹰短滑翔攻击行为建立数学模型. 这一阶段的数学描述如下所示.
式中:
1.3. 扩大开发阶段(第3阶段)
这一阶段模拟天鹰的低空慢降攻击,这种行为在数学上的表现如下所示:
式中:
1.4. 缩小开发阶段(第4阶段)
这一阶段模拟天鹰行走及狩猎地面上移速较慢的生物,这种行为在数学上的表现如下所示.
式中:
2. 多策略改进的天鹰优化算法
2.1. 广义正态分布优化算法
广义正态分布优化算法(generalized normal distribution optimization,GNDO)受正态分布模型的启发,每个个体使用广义正态分布曲线来更新自己的位置. 与大多数优化算法不同,该算法只需要基本的种群大小和终端条件就可以解决优化问题. 该算法包括局部开发和全局探索2部分,这2种学习策略的具体介绍如下.
2.1.1. 局部开发策略
根据种群中个体的分布和正态分布的关系,建立的广义正态分布优化模型如下所示:
式中:
式中:
式(16)中包含了最优位置和平均位置的相关信息,减小了算法对最优值的依赖,增加了跳出局部最优解的能力.
2.1.2. 全局探索策略
广义正态分布优化算法的全局探索是基于3个随机选择的个体,具体表述公式如下:
式中:
式中:
在广义正态分布优化算法中,每次迭代都会选择局部开发和全局探索这2种策略的其中一种进行计算,这2种策略被选择的概率相等,但存在某个个体可能无法通过局部开发策略或全局探索策略找到更好的解的情况. 为了使下一次的迭代可以找到更好的解,设计了筛选机制,如下所示:
将广义正态分布优化算法得到的值与天鹰优化算法扩大探索阶段(第1阶段)得到的值进行比较,选出适应度最小的值作为天鹰优化算法扩大探索阶段的最终结果,数学描述如下所示:
2.2. 相量算子
相量算子[18]来源于数学中的相量理论,通过周期三角函数
利用三角函数的间歇特性,通过相位角
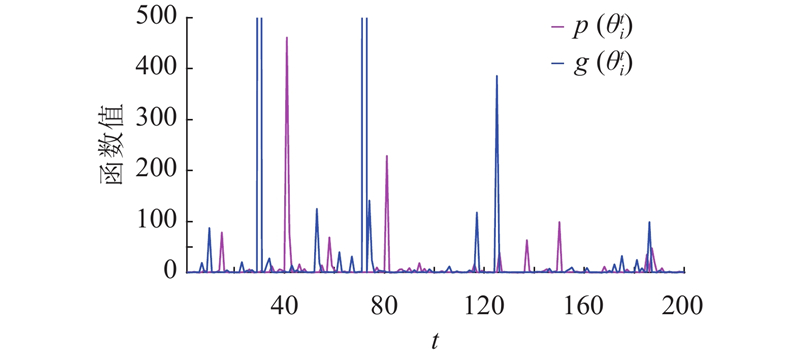
如图1所示为
图 1
图 1
Fig.1
Function behavior of
从图1可以看出,在某些区间内这2个函数同时增加或减少,而在另一些区间内它们的变化是相反的,除此之外,这2个函数的数值在随机变化,这些不同的函数姿态产生自适应的搜索特征. 传统天鹰优化算法的第2阶段是通过自定义的控制参数产生的,但在相量算子的控制下,仅通过个体的相位角产生. 这些斜率不一的起伏可以有效地防止算法早熟,避免过早收敛到局部最优解. 利用相量算子,对天鹰优化算法的第2阶段进行改进,改进公式如下所示:
2.3. 流向算子
流向算子来源于Hojat[12]提出的流向算法,这是基于物理的算法,流向算法(flow direction algorithm, FDA)模拟了径流的运动状态和形成过程. 水流会向目标函数的最优值,即最低点及其周围移动. 流向算法假设在每个水流周围都存在
式中:
式中:
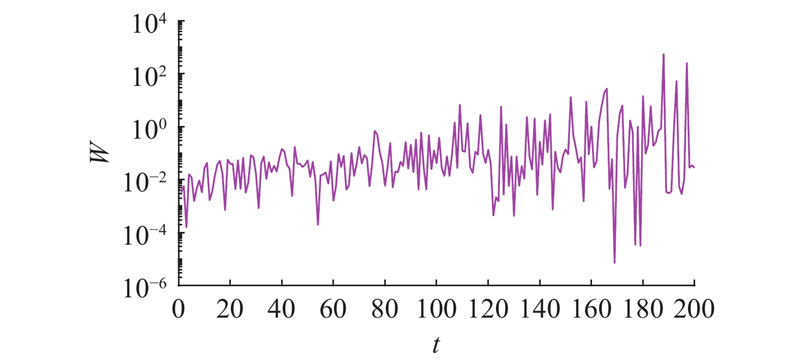
如图2所示为
图 2
在FDA算法中,径流流向相邻区域的流速与斜率直接相关,因此利用下式确定流速矢量:
式中:
式中:
使用的流向算子定义如下:
天鹰优化算法在迭代后期存在种群多样性减少、易陷入局部最优的缺点,因此,引入流向算子改进天鹰优化算法的第3阶段. 流向算法使得个体间的信息可以相互传递,提高信息的利用率. 非线性权重
与传统的天鹰优化算法相比,本文提出的混合多策略改进的天鹰优化算法的收敛速度更快,抗干扰能力更强,收敛精度有显著的提高.
2.4. 时间复杂度的分析
根据文献[19],计算得到AO算法的时间复杂度为
2.5. 多策略改进的天鹰优化算法步骤
融合多策略改进的天鹰优化算法,伪代码如下所示.
算法1 MIAO算法的运行框架
输出:最佳位置、最佳适应度.
随机初始化种群,在搜索空间内生成N个个体,计算个体的适应度,记录最优个体的初始位置.
根据式(24)更新第1阶段的输出结果;
根据式(27)更新第2阶段的输出结果;
根据式(34)更新第3阶段的输出结果;
根据式(11)更新第4阶段的输出结果;
将最终输出结果存储到
end while
Return 最优解
3. 仿真实验与结果分析
3.1. 实验设计与测试函数
为了验证所提算法的有效性,对该算法与海鸥优化算法(SOA)、粒子群优化算法(PSO)、麻雀搜索算法(SSA)、广义正态分布优化算法(GNDO)、相量算子优化的粒子群算法(PPSO)、流向优化算法(FDA)及传统天鹰优化算法(AO)进行性能测试. 所有算法统一设置N = 30,T = 500. MIAO及其对比算法的其他相关参数设置如表1所示.
表 1 MIAO及其对比算法的参数设置
Tab.1
| 算法 | 参数 | 参数值 | 算法 | 参数 | 参数值 | |
| SOA | 2 | PPSO | — | — | ||
| U | 1 | |||||
| V | 1 | |||||
| PSO | C1 | 1.494 45 | FDA | 流数量 | 1 | |
| C2 | 1.494 45 | |||||
| SSA | R2 | [0, 1.0] | AO | S | 0.01 | |
| ST | 0.8 | U | 0.005 65 | |||
| — | — | 1.5 | ||||
| — | — | 0.005 | ||||
| GNDO | — | — | MIAO | S | 0.01 |
为了保证实验结果的科学合理,选取16个测试函数,对这些算法的性能进行测试. 实验平台为MATLAB2016b,每次实验都独立运行30次,所选的测试函数如表2所示.
表 2 测试函数
Tab.2
| 编号 | 函数 | 维数 | 范围 | 最优值 |
| Schwefel2.21 | 30,100 | [−100,100] | 0 | |
| Quartic | 30,100 | [−1.28,1.28] | 0 | |
| Bohachevsky | 30,100 | [−100,100] | 0 | |
| Sum-Squares | 30,100 | [−5.12,5.12] | 0 | |
| Sum-Power | 30,100 | [−1,1] | 0 | |
| Rastrigin | 30,100 | [−5.12,5.12] | 0 | |
| Ackley | 30,100 | [−32,32] | 0 | |
| Griewank | 30,100 | [−600,600] | 0 | |
| Drop-Wave | 30,100 | [−5.12,5.12] | −1 | |
| Eggholder | 30,100 | [−512,512] | −959.6407 | |
| Shekel’s Foxholes | 2 | [−65,65] | 1 | |
| Kowalik | 4 | [−5,5] | 0.0003 | |
| Shekel | 4 | [0,10] | −10.1532 | |
| Hartman | 6 | [0,1] | −3.32 | |
| Composition Function 2 | 30,100 | [−100,100] | 2200 | |
| Composition Function 3 | 30,100 | [−100,100] | 2300 |
表2中,
3.2. 寻优精度分析
表 3
测试函数的结果 (dim=30,
Tab.3
| 函数 | 算法 | 最优值 | 平均值 | 标准差 | 函数 | 算法 | 最优值 | 平均值 | 标准差 | |
| SOA | 0.5803 | 3.4819 | 2.6799 | SOA | 3.462 7×10−7 | 5.348 9×10−6 | 1.334 1×10−7 | |||
| PSO | 0.0053 | 1.4305 | 1.4963 | PSO | 1.153 5×10−8 | 9.214 3×10−5 | 3.662 5×10−6 | |||
| SSA | 7.048 8×10−87 | 9.411 5×10−60 | 8.995 4×10−60 | SSA | 5.913 0×10−88 | 6.441 5×10−72 | 7.014 5×10−72 | |||
| GNDO | 23.0881 | 29.3154 | 16.5622 | GNDO | 1.458 1×10−9 | 3.578 9×10−7 | 2.665 4×10−7 | |||
| PPSO | 0.3126 | 0.3943 | 0.0023 | PPSO | 1.088 2×10−8 | 1.920 6×10−8 | 2.546 1×10−9 | |||
| FDA | 53.4756 | 60.2558 | 11.5469 | FDA | 7.905 2×10−119 | 1.481 4×10−113 | 6.541 1×10−113 | |||
| AO | 2.297 2×10−75 | 2.445 1×10−59 | 1.223 6×10−60 | AO | 1.251 1×10−104 | 1.546 6×10−88 | 3.145 2×10−88 | |||
| MIAO | 1.093 0×10−160 | 2.364 1×10−138 | 9.363 7×10−139 | MIAO | 2.546 4×10−193 | 4.025 7×10−160 | 2.541 9×10−160 | |||
| SOA | 0.1120 | 2.3334 | 3.1452 | SOA | 2.8017 | 15.8255 | 20.9482 | |||
| PSO | 0.0011 | 0.0016 | 6.114 6×10−4 | PSO | 3.9936 | 8.9826 | 2.5335 | |||
| SSA | 2.561 3×10−4 | 0.0020 | 0.0014 | SSA | 0 | 0 | 0 | |||
| GNDO | 6.7915 | 7.2235 | 3.6525 | GNDO | 320.12 | 411.52 | 168.3251 | |||
| PPSO | 0.0348 | 0.0502 | 0.5233 | PPSO | 20.3554 | 39.8408 | 38.4450 | |||
| FDA | 5.206 9×10−4 | 2.314 4×10−3 | 6.447 0×10−3 | FDA | 0 | 0 | 0 | |||
| AO | 9.429 6×10−5 | 1.234 5×10−4 | 2.333 1×10−6 | AO | 0 | 0 | 0 | |||
| MIAO | 1.346×10−7 | 6.321 4×10−7 | 2.655 3×10−8 | MIAO | 0 | 0 | 0 | |||
| SOA | 0.4502 | 2.2234 | 3.5562 | SOA | 0.0043 | 0.2709 | 0.3008 | |||
| PSO | 9.175 8×10−8 | 4.172 4×10−6 | 3.012 5×10−6 | PSO | 0.0066 | 0.4557 | 0.5398 | |||
| SSA | 0 | 2.125 5×10−281 | 1.222 0×10−281 | SSA | 8.881 8×10−16 | 8.881 8×10−16 | 0 | |||
| GNDO | 5.5511×10−17 | 5.5511×10−17 | 1.235 4×10−19 | GNDO | 11.2048 | 14.7193 | 6.9952 | |||
| PPSO | 0 | 0 | 0 | PPSO | 0.0655 | 0.9796 | 0.8023 | |||
| FDA | 4.996 0×10−16 | 1.247 0×10−11 | 3.288 4×10−11 | FDA | 4.440 9×10−15 | 4.440 9×10−15 | 0 | |||
| AO | 0 | 0 | 0 | AO | 8.881 8×10−16 | 8.881 8×10−16 | 0 | |||
| MIAO | 0 | 0 | 0 | MIAO | 8.881 8×10−16 | 8.881 8×10−16 | 0 | |||
| SOA | 0.094 | 3.4513 | 5.2102 | SOA | 1.144 5×10−6 | 1.5935 | 1.4952 | |||
| PSO | 0.1634 | 1.2247 | 2.8542 | PSO | 1.063 9×10−5 | 3.023 4×10−3 | 6.214 2×10−3 | |||
| SSA | 3.420 5×10−163 | 4.562 2×10−144 | 6.213 8×10−145 | SSA | 0 | 0 | 0 | |||
| GNDO | 887.38 | 902.58 | 72.5569 | GNDO | 42.6630 | 48.5482 | 9.3354 | |||
| PPSO | 102.59 | 244.58 | 325.11 | PPSO | 0.0011 | 0.0057 | 3.521 4×10−2 | |||
| FDA | 1.063 7×10−82 | 2.640 5×10−79 | 3.021 1×10−79 | FDA | 0 | 0 | 0 | |||
| AO | 3.044 1×10−152 | 3.205 6×10−139 | 6.112 0×10−143 | AO | 0 | 0 | 0 | |||
| MIAO | 0 | 0 | 0 | MIAO | 0 | 0 | 0 |
表 4
测试函数的结果 (dim=30,
Tab.4
| 函数 | 算法 | 最优值 | 平均值 | 标准差 | 函数 | 算法 | 最优值 | 平均值 | 标准差 | |
| SOA | −0.9750 | −0.8620 | 0.6335 | SOA | 2.300×103 | 2.300 4×103 | 0.6635 | |||
| PSO | −1 | −0.9808 | 0.0235 | PSO | 2.300×103 | 2.300×103 | 0 | |||
| SSA | −1 | −1 | 0 | SSA | 2.300×103 | 2.300×103 | 0 | |||
| GNDO | −1 | −0.9362 | 0.4655 | GNDO | 2.300×103 | 2.300×103 | 2.523 1×10−4 | |||
| PPSO | −1 | −0.9362 | 0.0536 | PPSO | 2.300×103 | 2.300×103 | 0 | |||
| FDA | −1 | −0.9363 | 0.0016 | FDA | 2.300×103 | 2.300×103 | 11.3250 | |||
| AO | −1 | −1 | 0 | AO | 2.300×103 | 2.300×103 | 0 | |||
| MIAO | −1 | −1 | 0 | MIAO | 2.300×103 | 2.300×103 | 0 | |||
| SOA | −954.6222 | −932.0502 | 32.1507 | SOA | 2.450 0×103 | 2.455 5×103 | 23.2264 | |||
| PSO | −66.8437 | −66.8437 | 0 | PSO | 2.450 0×103 | 2.450 0×103 | 10.3210 | |||
| SSA | −959.6407 | −956.6214 | 5.6316 | SSA | 2.450 0×103 | 2.450 0×103 | 8.1243 | |||
| GNDO | −959.6406 | −959.6406 | 2.547 6×10−5 | GNDO | 2.450 0×103 | 2.450 0×103 | 11.2356 | |||
| PPSO | −64.3969 | −61.6541 | 5.3991 | PPSO | 2.450 0×103 | 2.450 0×103 | 6.8401 | |||
| FDA | −959.6407 | −959.6407 | 0 | FDA | 2.433 5×103 | 2.433 5×103 | 16.3205 | |||
| AO | −959.6405 | −954.2410 | 10.2659 | AO | 2.450 0×103 | 2.450 0×103 | 6.0213 | |||
| MIAO | −959.6407 | −959.6407 | 0 | MIAO | 2.433 3×103 | 2.433 3×103 | 6.1089 |
表 5 固定维测试函数
Tab.5
| 函数 | 算法 | 最优值 | 平均值 | 标准差 | 函数 | 算法 | 最优值 | 平均值 | 标准差 | |
| SOA | 2.1994 | 5.8792 | 5.1739 | SOA | −9.8922 | −9.3907 | 0.4532 | |||
| PSO | 12.6705 | 12.6705 | 0 | PSO | −5.0522 | −5.0522 | 0 | |||
| SSA | 2.9821 | 2.5631 | 1.3330 | SSA | −10.1532 | −10.1532 | 0 | |||
| GNDO | 0.998 | 0.998 | 0 | GNDO | −10.1532 | −10.1532 | 0 | |||
| PPSO | 12.6705 | 12.6705 | 0 | PPSO | −5.0877 | −5.0877 | 0 | |||
| FDA | 0.998 | 1.9920 | 2.3254 | FDA | −10.1532 | −5.0876 | 3.3321 | |||
| AO | 0.998 | 0.998 | 0 | AO | −10.1532 | −10.1527 | 0.2140 | |||
| MIAO | 0.998 | 0.998 | 0 | MIAO | −10.1532 | −10.1532 | 0 | |||
| SOA | 0.0083 | 0.0080 | 0.0053 | SOA | −2.8215 | −2.6531 | 1.1233 | |||
| PSO | 6.782 2×10−4 | 9.159 4×10−4 | 5.735 4×10−4 | PSO | −3.3220 | −3.1123 | 0.023 | |||
| SSA | 3.074 9×10−3 | 7.012 2×10−3 | 4.775 2×10−3 | SSA | −3.3220 | −3.2156 | 0.1543 | |||
| GNDO | 3.074 8×10−4 | 3.074 9×10−4 | 2.324 7×10−4 | GNDO | −3.3219 | −3.3219 | 1.2354×10−5 | |||
| PPSO | 5.325 4×10−4 | 6.327 7×10−4 | 4.325 4×10−4 | PPSO | −3.3220 | −3.3182 | 3.2214×10−4 | |||
| FDA | 0.0004 | 0.0013 | 3.2621×10−3 | FDA | −3.1404 | −3.0749 | 0.6325 | |||
| AO | 5.679 0×10−4 | 8.994 0×10−4 | 3.112 2×10−4 | AO | −3.1037 | −3.0961 | 2.6480 | |||
| MIAO | 3.000 0×10−4 | 3.078 3×10−4 | 9.231 4×10−6 | MIAO | −3.3220 | −3.2834 | 4.6213×10−3 |
表 6
测试函数的结果 (dim=100,
Tab.6
| 函数 | 算法 | 最优值 | 平均值 | 标准差 | 函数 | 算法 | 最优值 | 平均值 | 标准差 | |
| SOA | 86.5542 | 94.1352 | 20.9621 | SOA | 0.0341 | 1.1236 | 2.6557 | |||
| PSO | 0.6220 | 0.6254 | 0.0239 | PSO | 157.3364 | 163.6361 | 25.3142 | |||
| SSA | 3.3646×10−55 | 3.3345×10−31 | 7.223 4×10−30 | SSA | 0 | 0 | 0 | |||
| GNDO | 23.1552 | 33.3120 | 16.3251 | GNDO | 362.36 | 384.21 | 32.6520 | |||
| PPSO | 0.7486 | 0.8998 | 0.3654 | PPSO | 258.24 | 274.65 | 61.0320 | |||
| FDA | 89.7243 | 93.1086 | 9.2320 | FDA | 0 | 0 | 0 | |||
| AO | 9.466 2×10−78 | 8.253×10−75 | 8.223 6×10−76 | AO | 0 | 0 | 0 | |||
| MIAO | 3.371 6×10−158 | 6.223 7×10−129 | 2.678 4×10−129 | MIAO | 0 | 0 | 0 | |||
| SOA | 0.1378 | 1.2355 | 2.6341 | SOA | 1.223 4×10−4 | 4.337 8×10−3 | 3.707 1×10−3 | |||
| PSO | 0.2201 | 0.4436 | 0.6520 | PSO | 1.8752 | 2.0314 | 0.6321 | |||
| SSA | 7.3240×10−3 | 0.0021 | 2.3114×10−3 | SSA | 8.881 8×10−16 | 8.881 8×10−16 | 0 | |||
| GNDO | 5.6488 | 8.0641 | 5.6630 | GNDO | 11.7217 | 13.4094 | 5.3241 | |||
| PPSO | 1.7592 | 2.0900 | 0.4354 | PPSO | 2.3323 | 2.1354 | 0.3542 | |||
| FDA | 4.487 9×10−4 | 5.832 5×10−4 | 2.665 2×10−4 | FDA | 4.440 9×10−15 | 4.440 9×10−15 | 0 | |||
| AO | 9.782 8×10−5 | 3.521 1×10−4 | 4.695 7×10−4 | AO | 8.881 8×10−16 | 8.881 8×10−16 | 0 | |||
| MIAO | 1.704 1×10−5 | 4.122 0×10−4 | 5.314 2×10−4 | MIAO | 8.881 8×10−16 | 8.881 8×10−16 | 0 | |||
| SOA | 0.0021 | 0.9328 | 1.5631 | SOA | 0.0143 | 56.4429 | 83.9514 | |||
| PSO | 1.913 5×10−9 | 3.556 4×10−7 | 2.635 7×10−7 | PSO | 0.0527 | 0.0600 | 1.3255e-3 | |||
| SSA | 0 | 0 | 0 | SSA | 0 | 0 | 0 | |||
| GNDO | 5.551 1×10−17 | 5.551 1×10−17 | 2.392 8×10−19 | GNDO | 61.1138 | 74.3512 | 22.2511 | |||
| PPSO | 0 | 0 | 0 | PPSO | 0.1039 | 0.1173 | 0.0062 | |||
| FDA | 0 | 0 | 0 | FDA | 0 | 0 | 0 | |||
| AO | 0 | 0 | 0 | AO | 0 | 0 | 0 | |||
| MIAO | 0 | 0 | 0 | MIAO | 0 | 0 | 0 | |||
| SOA | 0.0151 | 4.1531 | 8.3361 | SOA | −1 | −0.9889 | 0.1264 | |||
| PSO | 66.3548 | 85.3642 | 51.3260 | PSO | −1 | −1 | 0 | |||
| SSA | 7.572 5×10−80 | 3.214 6×10−65 | 4.012 6×10−65 | SSA | −1 | −1 | 0 | |||
| GNDO | 1141.2 | 1148.7 | 43.2651 | GNDO | −1 | −0.9632 | 0.0023 | |||
| PPSO | 180.23 | 210.24 | 7.3521 | PPSO | −1 | −1 | 0 | |||
| FDA | 3.624 7×10−79 | 5.624 4×10−75 | 9.214 4×10−75 | FDA | −1 | −1 | 0 | |||
| AO | 2.246 3×10−157 | 3.514 4×10−133 | 6.331 4×10−133 | AO | −1 | −1 | 0 | |||
| MIAO | 0 | 0 | 0 | MIAO | −1 | −1 | 0 | |||
| SOA | 2.460 5×10−6 | 0.0553 | 0.3662 | SOA | −957.9990 | −950.6374 | 10.5231 | |||
| PSO | 1.887 8×10−8 | 1.223 6×10−7 | 3.263 1×10−8 | PSO | −66.8437 | −66.8437 | 0 | |||
| SSA | 5.341 9×10−113 | 1.324 9×10−50 | 2.312 6×10−50 | SSA | −894.3315 | −888.1634 | 43.6612 | |||
| GNDO | 1.135 3×10−7 | 4.714 2×10−10 | 3.256 4×10−10 | GNDO | −959.6406 | −959.6406 | 4.125 0×10−4 | |||
| PPSO | 6.154 3×10−9 | 6.734 3×10−7 | 2.663 4×10−9 | PPSO | −66.0970 | −65.4211 | 1.3325 | |||
| FDA | 3.257 8×10−116 | 2.647 6×10−113 | 3.654 2×10−113 | FDA | −959.4607 | −959.4605 | 4.332 1×10−3 | |||
| AO | 1.481 3×10−95 | 2.794 9×10−29 | 3.654 2×10−29 | AO | −959.6407 | −-959.6404 | 3.412 2×10−3 | |||
| MIAO | 4.185×10−178 | 4.893 1×10−152 | 1.233 0×10−152 | MIAO | −959.6407 | −959.6406 | 1.256 1×10−3 |
表 7
测试函数的结果 (dim=100,
Tab.7
| 函数 | 算法 | 最优值 | 平均值 | 标准差 | 函数 | 算法 | 最优值 | 平均值 | 标准差 | |
| SOA | 2300 | 2300 | 4.097 0 | SOA | 2 440.8 | 2 476 | 38.4974 | |||
| PSO | 2300 | 2300 | 13.1361 | PSO | 2450 | 2450 | 8.2315 | |||
| SSA | 2300 | 2300 | 11.8003 | SSA | 2450 | 2450 | 2.286 9×10−4 | |||
| GNDO | 2300 | 2.301 1×103 | 5.5983 | GNDO | 2450 | 2451.8 | 5.8500 | |||
| PPSO | 2300 | 2.300 0×103 | 1.1117 | PPSO | 2450 | 2450.1 | 1.7050 | |||
| FDA | 2300 | 2.300 8×103 | 6.1601 | FDA | 2433.3 | 2435.9 | 12.1862 | |||
| AO | 2300 | 2.300 2×103 | 3.4566 | AO | 2450 | 2450.2 | 4.5863 | |||
| MIAO | 2.293 8×103 | 2.301 6×103 | 11.4552 | MIAO | 2 433.3 | 2 433.7 | 5.2753 |
3.3. 收敛曲线分析
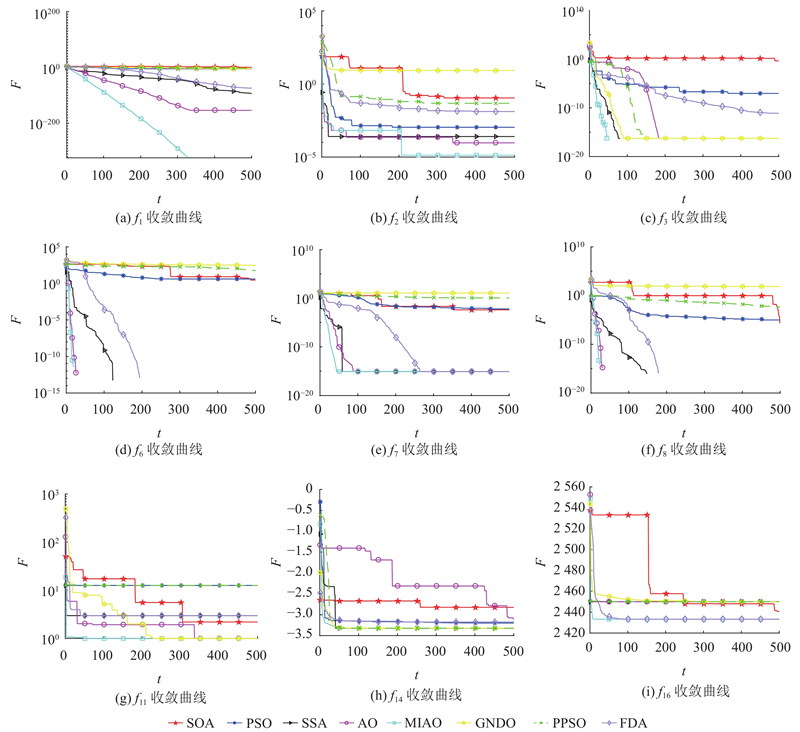
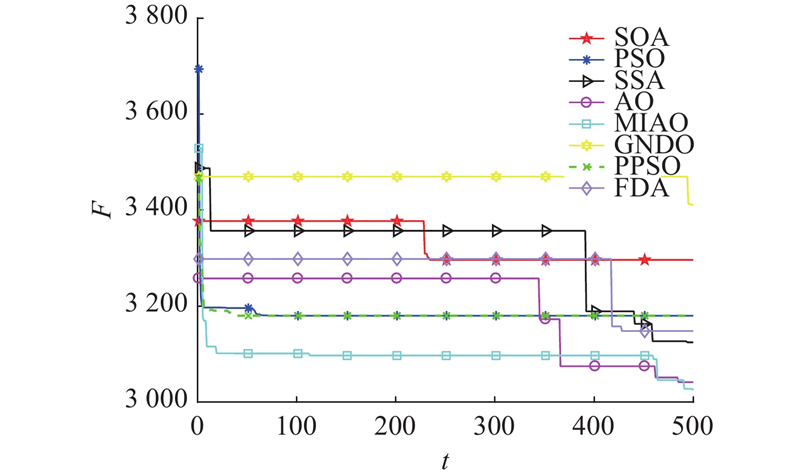
如图3所示为在30维度、500次迭代的条件下部分测试函数的收敛曲线图,分析SOA、PSO、SSA、GNDO、PPSO、FDA、AO、MIAO在优化过程中的收敛性能。图中, F为适应度;
图 3
图 3 MIAO及7种对比算法的收敛曲线
Fig.3 MIAO and convergence curves of seven comparison algorithms
3.4. Wilcoxon秩和检验
表 8 Wilcoxon秩和检验结果
Tab.8
| 函数 | SOA | PSO | SSA | GNDO | PPSO | FDA | AO | |||||||||||||
| p | h | p | h | p | h | p | h | p | h | p | h | p | h | |||||||
| 1.816 5×10−4 | 1 | 1.826 7×10−4 | 1 | 1.826 7×10−4 | 1 | 1.816 5×10−4 | 1 | 1.826 7×10−4 | 1 | 1.826 7×10−4 | 1 | 1.826 7×10−4 | 1 | |||||||
| 1.816 5×10−4 | 1 | 1.826 7×10−4 | 1 | 3.298 4×10−4 | 1 | 1.816 5×10−4 | 1 | 1.826 7×10−4 | 1 | 3.298 4×10−4 | 1 | 4.236 2×10−4 | 1 | |||||||
| 6.386 4×10−5 | 1 | 6.386 4×10−5 | 1 | N/A | 0 | 8.745 0×10−5 | 1 | N/A | 0 | N/A | 0 | N/A | 0 | |||||||
| 8.745 0×10−5 | 1 | 8.745 0×10−5 | 1 | 8.745 0×10−5 | 1 | 8.745 0×10−5 | 1 | 8.745 0×10−5 | 1 | 8.745 0×10−5 | 1 | 8.745 0×10−5 | 1 | |||||||
| 1.826 7×10−4 | 1 | 1.826 7×10−4 | 1 | 0.0257 | 1 | 1.826 7×10−4 | 1 | 1.826 7×10−4 | 1 | 1.826 7×10−4 | 1 | 1.826 7×10−4 | 1 | |||||||
| 2.165 0×10−5 | 1 | 6.340 3×10−5 | 1 | N/A | 0 | 7.235 2×10−5 | 1 | 6.304 3×10−5 | 1 | N/A | 0 | N/A | 0 | |||||||
| 6.386 4×10−5 | 1 | 6.340 3×10−5 | 1 | N/A | 0 | 6.386 4×10−5 | 1 | 6.340 3×10−5 | 1 | N/A | 0 | N/A | 0 | |||||||
| 6.386 4×10−5 | 1 | 6.340 3×10−5 | 1 | N/A | 0 | 6.386 4×10−5 | 1 | 6.340 3×10−5 | 1 | N/A | 0 | N/A | 0 | |||||||
| 6.386 4×10−5 | 1 | 0.368 1 | 0 | N/A | 0 | N/A | 0 | N/A | 0 | N/A | 0 | N/A | 0 | |||||||
| 3.226 4×10−4 | 1 | 6.340 3×10−5 | 1 | 3.221 4×10−4 | 1 | 3.226 4×10−4 | 1 | 6.340 3×10−5 | 1 | 3.221 4×10−4 | 1 | 0.0206 | 1 | |||||||
| 1.333 4×10−8 | 1 | 1.020 3×10−8 | 1 | 1.322 4×10−8 | 1 | 2.355 4×10−10 | 1 | 1.333 4×10−4 | 1 | 1.632 4×10−4 | 1 | 2.355 4×10−10 | 1 | |||||||
| 1.205 9×10−12 | 1 | 1.210 8×10−12 | 1 | 3.469 1×10−8 | 1 | 1.203 4×10−12 | 1 | 1.325 0×10−12 | 1 | 4.358 7×10−8 | 1 | 1.523 4×10−5 | 1 | |||||||
| 1.826 7×10−4 | 1 | 2.092 6×10−7 | 1 | 2.981 6×10−8 | 1 | 2.836 4×10−8 | 1 | 1.532 1×10−7 | 1 | 2.354 1×10−7 | 1 | 2.364 1×10−6 | 1 | |||||||
| 1.333 4×10−8 | 1 | 1.020 3×10−8 | 1 | 1.020 3×10−8 | 1 | 1.032 0×10−8 | 1 | 1.354 2×10−8 | 1 | 6.352 4×10−6 | 1 | 2.330 6×10−4 | 1 | |||||||
| 2.453 2×10−3 | 1 | 2.442 5×10−3 | 1 | 2.442 5×10−3 | 1 | 2.442 5×10−3 | 1 | 2.442 5×10−3 | 1 | 2.442 5×10−3 | 1 | 2.463 0×10−3 | 1 | |||||||
| 2.453 2×10−3 | 1 | 2.442 5×10−3 | 1 | 2.442 5×10−3 | 1 | 2.442 5×10−3 | 1 | 2.442 5×10−3 | 1 | 2.442 5×10−3 | 1 | 2.442 5×10−3 | 1 | |||||||
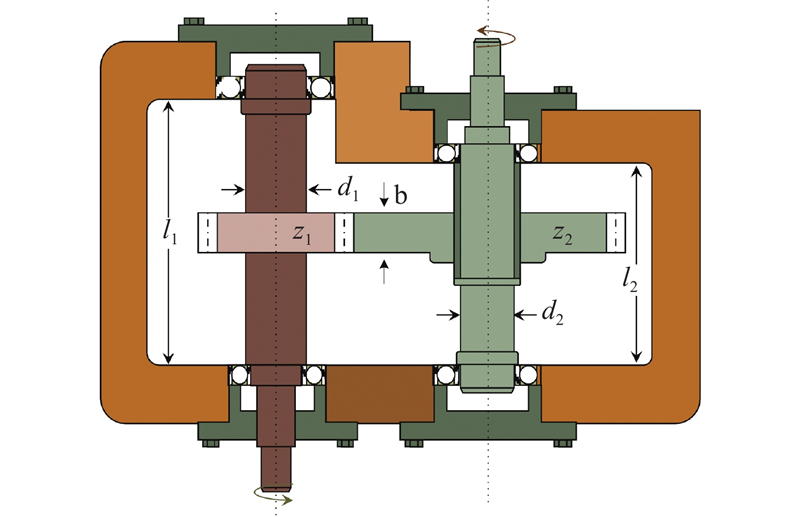
4. 减速器设计问题
减速器优化问题的目的是使减速器的质量最小. 共有11个约束条件和7个变量,这7个变量分别是齿面宽
图 4
表 9 减速器设计问题的结果比较
Tab.9
| 算法 | 变量最优值 | 最小质量/g | ||||||
| SOA[21] | 3.0682 | 0.7175 | 18.1660 | 7.5380 | 7.3182 | 3.4451 | 5.3467 | 3384.0246 |
| PSO[22] | 3.6000 | 0.7000 | 17.0000 | 8.3000 | 7.3000 | 3.3525 | 5.2865 | 3054.5907 |
| SSA[23] | 3.2453 | 0.7166 | 17.5263 | 8.0969 | 7.8539 | 3.6441 | 5.2963 | 3295.7734 |
| GNDO | 3.4909 | 0.7403 | 17.2482 | 8.1480 | 8.0466 | 3.3088 | 5.3688 | 3411.4819 |
| PPSO | 3.6000 | 0.7000 | 17.000 0 | 7.3000 | 7.9500 | 3.3505 | 5.5000 | 3179.9491 |
| FDA | 3.4630 | 0.7200 | 17.0072 | 7.5038 | 7.3158 | 3.3740 | 5.2865 | 3148.1579 |
| AO[17] | 3.4858 | 0.7000 | 17.3920 | 8.1908 | 7.3508 | 3.2767 | 5.3022 | 3150.6512 |
| MIAO | 3.2899 | 0.7000 | 17.0128 | 7.8990 | 7.7708 | 3.3642 | 5.3034 | 3024.8417 |
从图5可知,在减速器工程设计中,提出的MIAO算法的寻优结果(包括收敛速度和收敛精度)都比传统天鹰优化算法及其他对比算法好,这进一步说明了改进策略的巨大作用.
图 5
5. 结 语
为了提高天鹰优化算法的寻优能力,平衡探索和开发阶段,本文提出引入相量算子和流向算子的多策略改进天鹰优化算法. 将广义正态分布优化算法与天鹰优化算法的第1阶段相连接,在扩大搜索空间的同时,提高了解的质量,增强了算法的全局搜索能力. 将相量算子加入天鹰优化算法的第2阶段,减少控制参数对算法寻优能力的影响,利用自适应控制,改善算法的高维搜索能力,平衡算法的探索和开发阶段. 将流向算子融入天鹰优化算法第3阶段的操作加强了天鹰个体间信息的交流,保证了迭代后期解的多样性,增强了算法跳出局部最优点的能力. 这3种策略相互作用,提高了天鹰算法的整体性能,但优化时间略有增加. 下一步考虑将MIAO算法应用到现实问题的参数优化中,进一步检验算法的实用性.
参考文献
Face mask detection using deep convolutional neural network and multi-stage image processing
[J].
Deep learning-based open set multi-source domain adaptation with complementary transferability metric for mechanical fault diagnosis
[J].
A freight inspection volume forecasting approach using an aggregation/disaggregation procedure, machine learning and ensemble models
[J].DOI:10.1016/j.neucom.2019.06.109 [本文引用: 1]
A multi-task memory network with knowledge adaptation for multimodal demand forecasting
[J].DOI:10.1016/j.trc.2021.103352 [本文引用: 2]
Advances in sparrow search algorithm: a comprehensive survey
[J].DOI:10.1007/s11831-022-09804-w [本文引用: 1]
Design of fractional comprehensive learning PSO strategy for optimal power flow problems
[J].
A novel swarm intelligence optimization approach: sparrow search algorithm
[J].DOI:10.1080/21642583.2019.1708830 [本文引用: 2]
The whale optimization algorithm
[J].DOI:10.1016/j.advengsoft.2016.01.008 [本文引用: 1]
A new evolving operator selector by using fitness landscape in differential evolution algorithm
[J].
A multi-external archive-guided Henry gas solubility optimization algorithm for solving multi-objective optimization problems
[J].DOI:10.1016/j.engappai.2021.104588 [本文引用: 1]
Flow direction algorithm (FDA): a novel optimization approach for solving optimization problems
[J].
An advanced teaching-learning-based algorithm to solve unconstrained optimization problems
[J].
Socio evolution and learning optimization algorithm: a socio-inspired optimization methodology
[J].DOI:10.1016/j.future.2017.10.052 [本文引用: 1]
An improved grey wolf optimizer for solving engineering problems
[J].DOI:10.1016/j.eswa.2020.113917 [本文引用: 1]
方波触发勘探与开发的粒子群优化算法
[J].DOI:10.16383/j.aas.c190842 [本文引用: 1]
Particle swarm optimization with square wave triggered exploration and exploitation
[J].DOI:10.16383/j.aas.c190842 [本文引用: 1]
A parallel hybrid PSO-GA algorithm for the flexible flow-shop scheduling with transportation
[J].
Aquila optimizer: a novel meta-heuristic optimization algorithm
[J].
Phasor particle swarm optimization: a simple and efficient variant of PSO
[J].
Aquila optimizer: a novel meta-heuristic optimization algorithm
[J].
基于改进量子粒子群的K-means聚类算法及其应用
[J].
K-means clustering algorithm based on improved quantum particle swarm optimization and its application
[J].
Letter: application of optimization algorithms to engineering design problems and discrepancies in mathematical formulas
[J].
An effective co-evolutionary differential evolution for constrained optimization
[J].
Golden-sine dynamic marine predator algorithm for addressing engineering design optimization
[J].