在实际生活中,存在许多具有多个目标的优化问题,并且这些目标之间是互相冲突的,此类问题被称为多目标优化问题(multi-objective optimization problems, MOPs)[1]. 实际生活中环境是不断发生变化的,如果MOPs的目标函数、约束和参数会随着环境变化而改变,MOPs则转化为动态多目标优化问题(dynamic multi-objective optimization problems, DMOPs). 在处理复杂的DMOPs时,传统的多目标优化算法(multi-objective optimization algorithms, MOAs)[2-7]明显具有局限性. 随着环境的变化,Pareto最优解集 (Pareto-optimal set,PS)[8]和Pareto前沿 (Pareto-optimal front,PF)不断发生变化,传统的MOAs会在环境变化中逐渐丧失种群的多样性,种群在某一时刻陷入局部收敛而不再随环境发生变化. 因此,需要动态多目标优化算法(dynamic multi-object optimization algorithms, DMOAs)[9-14]及时地响应环境变化,从而追踪到变化后的PS和PF.
近年来,DMOAs不断被提出,并应用于各个领域,例如:调度[15]、机械设计[16]、资源管理[17]、路径规划[18]等. 为了解决DMOPs,研究大致可以划分为3大模块:环境变化检测[19-20]、环境变化应答机制[9-14,21-22]、静态多目标优化算法[2-7]. 其中静态多目标优化算法大多是为了提高收敛速度,例如:NSGA-II[5]、RM-MEDA[6]、MOEA/D[7]等. 环境变化检测用于检测环境的变化,为后面设计应答机制提供指导,而变化应答机制是解决DMOPs的重要研究目标. 变化应答机制大多利用多样性引入机制[21]、预测机制[9-14]、记忆机制[22]等方式来响应环境的变化. 其中预测机制对周期性问题和非周期性问题均有不错的效果,该机制通过利用历史信息或者其他方法来预测环境变化后的最优解,如果预测足够准确,那么预测机制对DMOPs非常有效. Zhou等[10]提出种群预测策略(population prediction strategy, PPS),该策略应对DMOPs较有效,但由于在早期阶段缺乏历史信息的积累,前期效果较差. Zou等[11]提出基于中心点和Knee点的预测策略(prediction strategy based on center points and knee points, CKPS),该策略将Knee点引入预测种群,可以更加准确地追踪PF,但后期效果不够理想. Li等[12]提出基于特殊点的预测策略(predictive strategy based on special points, SPPS),利用Knee点、近边缘点、近中心点等特殊点快速地跟踪PF,该策略进一步提高了种群的多样性,但种群中心点的预测缺乏反馈校正,预测的准确性还有待进一步提高. Rong等[13]提出多向预测策略(multidirectional strategy, MDP),该策略利用先前环境中多个代表性解所确定的多个方向来预测PS在决策空间中的位置,从而提高了解决DMOPs的性能. Chen等[14]提出结合混合预测和突变策略的变化响应机制(change response mechanism by combining mixed prediction strategy and mutation strategy, HPPCM),混合预测策略协调基于中心点的预测和基于引导个体的预测,而突变策略可以处理不可预测的环境变化,从而快速适应各种环境变化.
针对上述不足,本研究提出基于个体预测的动态多目标优化算法,其主要贡献如下. 1) 提出参考点联系算法,引入该算法筛选的特殊点,并通过新的特殊点预测策略快速地响应环境变化. 2) 提出针对种群中心点预测的反馈校正机制,对种群中心点预测非支配解集的预测步长进行反馈校正,使预测更加准确. 3) 提出混合多样性维持机制,引入拉丁超立方抽样和精度可控的突变策略分别生成的随机个体,以提高种群的多样性,避免种群陷入局部收敛.
1. 相关工作
1.1. 动态多目标优化相关概念
DMOPs定义[23] 如下:
式中:
式中:
定义1. 如果
则
定义2. 在
定义3. 在
根据PF和PS动态变化的不同组合,确定4种不同类型的DMOPs,如表1所示.
表 1 4种不同类型的DMOPs
Tab.1
| 种类 | PS | PF |
| I | 随时间变化 | 不变 |
| II | 随时间变化 | 随时间变化 |
| III | 不变 | 随时间变化 |
| IV | 不变 | 不变 |
1.2. RM-MEDA
图 1
1.3. 参考点
参考点常常被用来解决多目标优化问题上的收敛性和多样性问题,在Das等[24] 所提方法的基础上,Deb等[25-26]提出基于参考点的多目标优化算法(NSGA-III),利用预定义的参考点对选择个体的方法进行改进,以维持种群之间的多样性,后续将NSGA-III扩展到求解一般约束多目标优化问题. 本研究的参考点采用Das等[24] 的方法设计,所设计的参考点在超平面上均匀分布. 假设
式中:
在Das等[24]的方法中,参考点数量
通常,参考点的数量与种群的大小一致,本研究根据种群中非支配解集的大小设置参考点的数量.
2. 基于个体预测的动态多目标算法
2.1. 特殊点集
追踪PS和PF一直是解决动态多目标优化问题的热点,本研究提出参考点联系算法,利用该算法筛选的特殊点来追踪PF,从而实现更快的收敛.
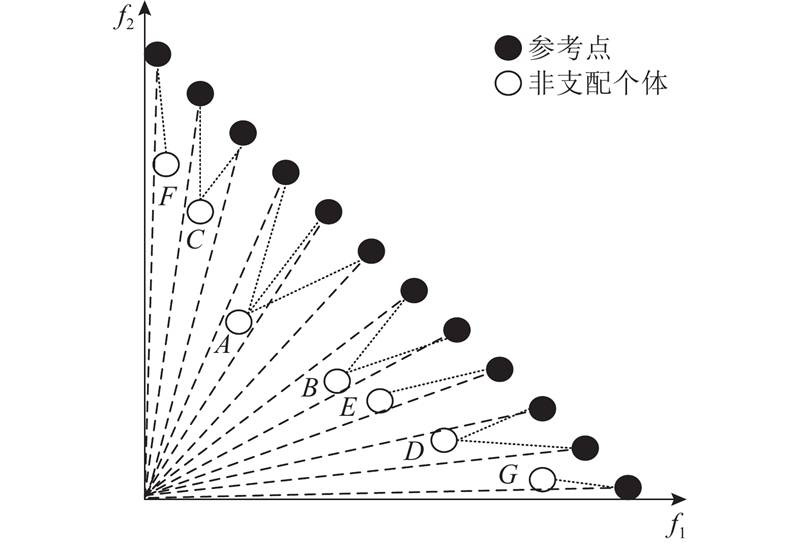
参考点联系算法是将预定义的参考点与非支配个体关联起来. 参考点与原点连接作为该参考点的参考向量,计算每个参考向量与非支配个体的距离,参考点与离其参考向量最近的非支配个体关联. 由于参考点是均匀分布在超平面上的,若有非支配个体关联较少的参考点或没有关联参考点,说明附近有其他非支配个体与其竞争,则这些个体不具备较好的多样性;反之,关联较多参考点的非支配个体具有较好的多样性. 如图2所示,非支配个体
图 2
图 2 非支配个体与参考点关联示意图
Fig.2 Schematic diagram of association between non-dominant individuals and reference points
根据非支配个体关联参考点的数量,从多到少依次选择
算法1 参考点联系算法
1)将种群分层,选择第1层的个体为非支配个体.
2)根据非支配解集的大小,采用式(6)的方法设计参考点集
3)计算每个参考向量与非支配个体的距离,参考点与离其参考向量最近的非支配个体关联.
4)根据非支配个体关联参考点的数量,从多到少依次排列,按照顺序选择
除了以上筛选的点和边界点以外,本研究还采用文献[11]中的方法,选择Knee点加入特殊点集,Knee点是指在PF上具有最大边际效用的点,在Knee点附近,一个目标上有一个较小的改进,将会伴随着至少一个目标的严重退化. 参考点联系算法在筛选过程中会避免出现和Knee点重合的情况,且当实际筛选点的数量少于
图 3
利用式(8)计算
根据
利用特殊点预测出
式中:
算法2 特殊点预测策略
输入:特殊点集
输出:预测的
1)根据式(8)计算
2)根据式(9)计算
3)根据式(10)预测
4)根据式(11)预测
2.2. 种群中心点预测的反馈校正机制
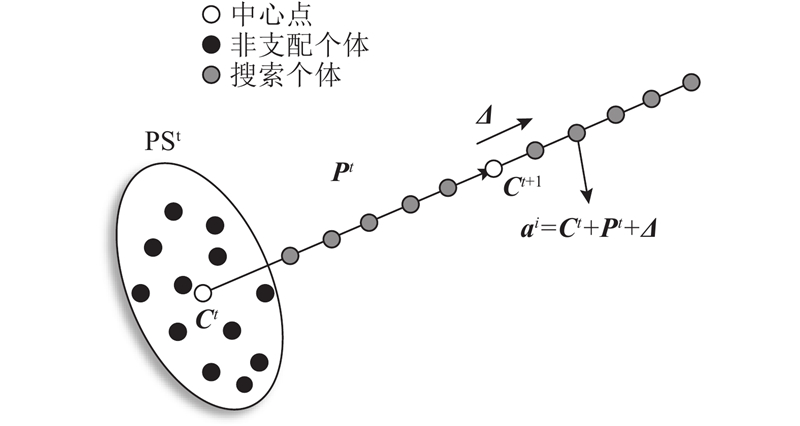
首先须构建一个代表个体,将
式中:
然后对代表个体进行预测:
式中:
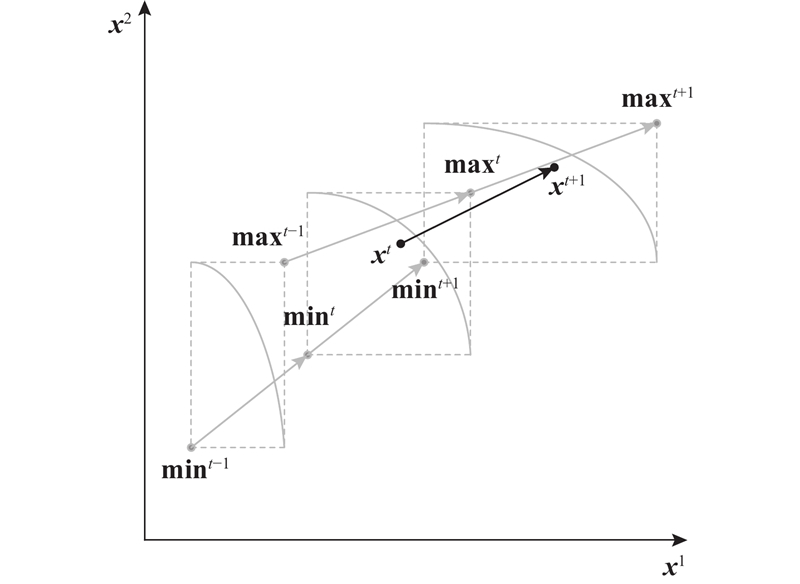
如图4所示,基于
图 4
式中:
最后对这组搜索个体
式中:
算法3 反馈校正机制
输入:非支配解集
输出:校正后的预测步长
1)根据式(12)计算
2)根据式(13)对
3)计算非支配解集中每个维度决策变量的标准差,选择标准差较小的变量为最优变量
4)根据式(14)生成
5)重新评估
6)对于
根据校正后的预测步长对非支配个体进行预测. 为了使预测的非支配个体更接近
式中:
2.3. 混合多样性维持机制
式中:
精度可控的突变策略的具体步骤如算法4所示.
算法4 精度可控的突变策略
输入:非支配解集
输出:随机解
1)计算
2)计算
3)
4)if
if
else
end if
else
if
else
end if
end if
该策略对非支配解集突变生成随机个体,为了保证突变的随机个体仍具有较好的收敛性,只对非最优变量进行突变,变量
2.4. IPS算法详细描述
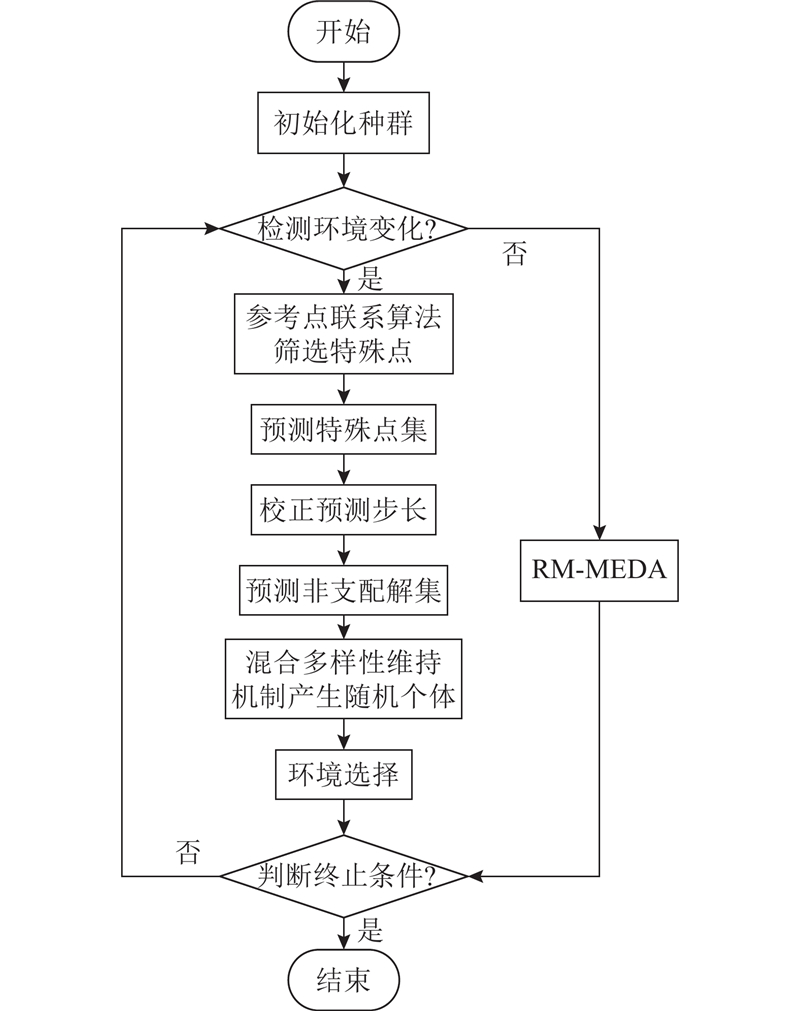
IPS是在动态多目标进化算法的框架下进行的. IPS在环境变化后产生新的初始种群,使新的种群能够对环境变化快速响应并追踪其变化的PF. 算法5是对IPS的详细描述,IPS的流程图如图5所示.
图 5
算法5 IPS算法
初始化:时间变量
1)检测环境变化,如果环境没有发生变化,转步骤10);否则,转步骤2).
2)根据算法1得到参考点联系算法筛选的点,和Knee点、边界点一起作为特殊点.
3)利用式(8)~(10)预测
4)计算非支配解集的中心点
5)利用式(14)~(15)对式(13)的预测步长进行反馈校正,并利用校正的预测步长预测
6)对式(8)~(10)计算的
7)根据算法4对
8)得到新种群
9)对
10)用RM-RMAD对种群进行优化.
11)如果
3. 测试问题及评价指标
3.1. 测试问题
3.2. 性能指标
反向代距离 (inverted generational distance, IGD)[35]被广泛应用到衡量算法的收敛性和多样性,IGD指标的定义如下:
式中:
IGD评价的是标准PF和算法所得PF的接近程度以及算法所得PF中个体的分布性,MIGD是IGD的修改版本,它被定义为运行期间某些时间步长内的IGD平均值:
式中:
MIGD是综合的评价指标,可以评价算法在收敛性和分布性方面的性能,其值越小,说明算法的性能越好.
超体积差 (hypervolume difference, HVD)[36]测量的是标准PF和算法所得PF之间的超体积差,HVD的评价指标如下:
式中:
MHVD是对HVD的修改版本,它被定义为运行期间某些时间步长内的HVD平均值,其表达式如下:
式中:
4. 实验结果与分析
4.1. 参数设置
对每个问题独立实验20次,每次实验都会产生100次环境变化,环境的变化程度
1) CKPS的Knee点个数为9.
2) SPPS在种群中心点预测非支配集的过程中将高斯扰动
3) HPPCM中自主演化的代数
4) IPS中参考点联系算法筛选的特殊点个数
环境变化检测则通过选择种群中5%的个体来检测环境变化,目标值不匹配表明环境发生了改变.
4.2. 性能评价的统计结果对比
表 2 5种策略在FDA和DMOP上的MIGD指标
Tab.2
| 问题 | 阶段 | MIGD | ||||
| PPS | CKPS | SPPS | HPPCM | IPS | ||
| 1)注:‡和†分别表示IPS算法的性能显著优于和等同于相应的算法. | ||||||
| FDA1 | 总阶段 | 0.0592(0.01680)‡1) | 0.0297(0.00636)‡ | 0.0264(0.00630)‡ | 0.0211(0.00518)† | 0.0188(0.00423) |
| 第1阶段 | 0.2743(0.08625)‡ | 0.1168(0.03308)‡ | 0.1032(0.03278)‡ | 0.0813(0.02744)† | 0.0692(0.02245) | |
| 第2阶段 | 0.0100(0.00117)‡ | 0.0090(0.00013)‡ | 0.0082(0.00021)‡ | 0.0068(0.00076)† | 0.0067(0.00029) | |
| 第3阶段 | 0.0063(0.00011) | 0.0089(0.00020)‡ | 0.0081(0.00022)‡ | 0.0067(0.00069) | 0.0070(0.00046) | |
| FDA2 | 总阶段 | 0.0093(0.00120)‡ | 0.0085(0.00056)‡ | 0.0087(0.00044)‡ | 0.0079(0.00087)† | 0.0076(0.00075) |
| 第1阶段 | 0.0219(0.00539)‡ | 0.0183(0.00276)† | 0.0170(0.00248)† | 0.0172(0.00419)† | 0.0160(0.00376) | |
| 第2阶段 | 0.0067(0.00058)‡ | 0.0065(0.00021)‡ | 0.0067(0.00025)‡ | 0.0058(0.00028)† | 0.0057(0.00009) | |
| 第3阶段 | 0.0059(0.00012)‡ | 0.0060(0.00010)‡ | 0.0068(0.00026)‡ | 0.0056(0.00004) | 0.0056(0.00004) | |
| FDA3 | 总阶段 | 0.0843(0.01313)‡ | 0.0383(0.00726)‡ | 0.0363(0.00724)‡ | 0.0216(0.00479) | 0.0258(0.00647) |
| 第1阶段 | 0.2590(0.06128)‡ | 0.1222(0.03371)‡ | 0.1323(0.03870)‡ | 0.0862(0.02561) | 0.1023(0.03297) | |
| 第2阶段 | 0.0436(0.01250)‡ | 0.0189(0.00279)‡ | 0.0137(0.00325)‡ | 0.0064(0.00038) | 0.0074(0.00060) | |
| 第3阶段 | 0.0419(0.00778)‡ | 0.0179(0.00243)‡ | 0.0133(0.00262)‡ | 0.0061(0.00035) | 0.0077(0.00067) | |
| FDA4 | 总阶段 | 0.1314(0.00333)‡ | 0.1184(0.00230)‡ | 0.1095(0.00211)‡ | 0.1020(0.00104)† | 0.1010(0.00148) |
| 第1阶段 | 0.1609(0.00920)‡ | 0.1332(0.00845)‡ | 0.1300(0.00688)‡ | 0.1209(0.00692)† | 0.1161(0.00498) | |
| 第2阶段 | 0.1258(0.00312)‡ | 0.1148(0.00268)‡ | 0.1050(0.00221)‡ | 0.0969(0.00198) | 0.0976(0.00167) | |
| 第3阶段 | 0.1230(0.00312)‡ | 0.1149(0.00232)‡ | 0.1043(0.00234)‡ | 0.0980(0.00245)† | 0.0973(0.00216) | |
| DMOP1 | 总阶段 | 0.1296(0.24085)‡ | 0.0076(0.00174)† | 0.0099(0.00276)‡ | 0.0068(0.00504)† | 0.0064(0.00052) |
| 第1阶段 | 0.5522(1.06835)‡ | 0.0181(0.00901)† | 0.0310(0.01421)‡ | 0.0161(0.00382)† | 0.0118(0.00272) | |
| 第2阶段 | 0.0528(0.09413)‡ | 0.0050(0.00005) | 0.0050(0.00070) | 0.0047(0.00004) | 0.0051(0.00002) | |
| 第3阶段 | 0.0057(0.00002)‡ | 0.0051(0.00006) | 0.0048(0.00054) | 0.0046(0.00006) | 0.0051(0.00005) | |
| DMOP2 | 总阶段 | 0.0659(0.03602)‡ | 0.0267(0.00616)‡ | 0.0316(0.00584)‡ | 0.0252(0.00504)† | 0.0223(0.00254) |
| 第1阶段 | 0.3008(0.16637)‡ | 0.1006(0.03204)‡ | 0.1263(0.03040)‡ | 0.1021(0.02651)† | 0.0848(0.01365) | |
| 第2阶段 | 0.0142(0.01391)‡ | 0.0092(0.00012)‡ | 0.0093(0.00026)‡ | 0.0069(0.00047) | 0.0075(0.00020) | |
| 第3阶段 | 0.0061(0.00003)‡ | 0.0090(0.00020)‡ | 0.0090(0.00030)‡ | 0.0069(0.00042) | 0.0073(0.00030) | |
| DMOP3 | 总阶段 | 0.0482(0.04869)‡ | 0.0277(0.00629) | 0.0279(0.00828) | 0.0242(0.00544) | 0.0288(0.00431) |
| 第1阶段 | 0.2173(0.00125)‡ | 0.1065(0.03292) | 0.1111(0.04314) | 0.0958(0.02797) | 0.1204(0.02258) | |
| 第2阶段 | 0.0099(0.00010)‡ | 0.0091(0.00017)‡ | 0.0082(0.00018)‡ | 0.0078(0.00138)† | 0.0071(0.00047) | |
| 第3阶段 | 0.0062(0.00954) | 0.0089(0.00011)‡ | 0.0081(0.00017)‡ | 0.0066(0.00043) | 0.0069(0.00017) | |
表 3 5种策略在F5~F10上的MHVD指标
Tab.3
| 问题 | 阶段 | MHVD | ||||
| PPS | CKPS | SPPS | HPPCM | IPS | ||
| F5 | 总阶段 | 0.5124(0.07330)‡ | 0.2769(0.01312)† | 0.2782(0.01280)† | 0.2745(0.00810)† | 0.2725(0.01327) |
| 第1阶段 | 1.4519(0.28264)‡ | 0.4064(0.07001) | 0.4155(0.06438)† | 0.3752(0.03314) | 0.4132(0.05877) | |
| 第2阶段 | 0.3309(0.05948)‡ | 0.2466(0.00230)‡ | 0.2455(0.00379)‡ | 0.2508(0.00777)‡ | 0.2379(0.00468) | |
| 第3阶段 | 0.2477(0.00173)‡ | 0.2456(0.00171)‡ | 0.2457(0.00174)‡ | 0.2505(0.00681)‡ | 0.2403(0.00508) | |
| F6 | 总阶段 | 0.3222(0.03755)‡ | 0.2659(0.00655)† | 0.2693(0.01432)† | 0.2652(0.00692) | 0.2655(0.00412) |
| 第1阶段 | 0.6239(0.18580)‡ | 0.3462(0.03272)† | 0.3647(0.07603)† | 0.3470(0.03468)† | 0.3455(0.02249) | |
| 第2阶段 | 0.2545(0.00503)‡ | 0.2467(0.00117)† | 0.2467(0.00093)† | 0.2455(0.00147) | 0.2459(0.00118) | |
| 第3阶段 | 0.2466(0.00144) | 0.2470(0.00104) | 0.2467(0.00095) | 0.2459(0.00084) | 0.2472(0.00165) | |
| F7 | 总阶段 | 0.3596(0.03072)‡ | 0.2690(0.01654)† | 0.2664(0.00844)† | 0.2672(0.01441)† | 0.2614(0.00741) |
| 第1阶段 | 0.8307(0.15396)‡ | 0.3740(0.08647)† | 0.3560(0.04440)† | 0.3633(0.07469)† | 0.3332(0.03972) | |
| 第2阶段 | 0.2492(0.00359)‡ | 0.2443(0.00101) | 0.2454(0.00071)‡ | 0.2444(0.00074)† | 0.2443(0.00105) | |
| 第3阶段 | 0.2463(0.00111)‡ | 0.2439(0.00080) | 0.2447(0.00093)† | 0.2443(0.00075) | 0.2444(0.00094) | |
| F8 | 总阶段 | 0.3954(0.03307)‡ | 0.4108(0.02681)‡ | 0.3852(0.01921)‡ | 0.3223(0.01427) | 0.3277(0.00396) |
| 第1阶段 | 0.6076(0.16045)‡ | 0.5809(0.13203)‡ | 0.5864(0.08519)‡ | 0.4663(0.05926)† | 0.4568(0.02104) | |
| 第2阶段 | 0.3504(0.01283)‡ | 0.3684(0.05066)‡ | 0.3374(0.00970)‡ | 0.2889(0.00725) | 0.2959(0.00706) | |
| 第3阶段 | 0.3397(0.01085)‡ | 0.3725(0.02345)‡ | 0.3373(0.01247)‡ | 0.2872(0.01162) | 0.2983(0.00646) | |
| F9 | 总阶段 | 0.6408(0.07758)‡ | 0.3705(0.03890)‡ | 0.3411(0.01947)‡ | 0.3353(0.04994)† | 0.3113(0.02232) |
| 第1阶段 | 1.6206(0.23861)‡ | 0.7310(0.18668)‡ | 0.6319(0.06566)† | 0.6164(0.12440)† | 0.5565(0.10975) | |
| 第2阶段 | 0.4945(0.09275)‡ | 0.2950(0.01834)‡ | 0.2697(0.01675)† | 0.2695(0.05153)† | 0.2593(0.00953) | |
| 第3阶段 | 0.3216(0.07873)‡ | 0.2746(0.00704)‡ | 0.2744(0.02416)‡ | 0.2674(0.02417)† | 0.2468(0.01399) | |
| F10 | 总阶段 | 0.7720(0.06904)‡ | 0.3612(0.01334) | 0.3361(0.02204) | 0.4034(0.05090)† | 0.3927(0.03353) |
| 第1阶段 | 1.5730(0.10988)‡ | 0.7354(0.05476)‡ | 0.6343(0.10452)† | 0.6220(0.11651)† | 0.5665(0.09724) | |
| 第2阶段 | 0.6341(0.13136)‡ | 0.2782(0.01809) | 0.2652(0.00560) | 0.3423(0.04547) | 0.3631(0.01942) | |
| 第3阶段 | 0.5294(0.08679)‡ | 0.2666(0.01608) | 0.2653(0.00905) | 0.3606(0.06961)† | 0.3398(0.03363) | |
表 4 5种策略在部分测试问题上的MIGD指标
Tab.4
| 问题 | | MIGD | ||||
| PPS | CKPS | SPPS | HPPCM | IPS | ||
| FDA2 | (20,10) | 0.1194(0.00213)‡ | 0.0087(0.00039)† | 0.0097(0.00106)‡ | 0.0087(0.00908)† | 0.0082(0.00034) |
| (25,10) | 0.0093(0.00120)‡ | 0.0085(0.00056)‡ | 0.0087(0.00044)‡ | 0.0079(0.00087)† | 0.0076(0.00075) | |
| (30,10) | 0.0081(0.00046)‡ | 0.0075(0.00024)† | 0.0084(0.00046)‡ | 0.0072(0.00074) | 0.0073(0.00296) | |
| FDA4 | (20,10) | 0.1485(0.00453)‡ | 0.1327(0.00086)‡ | 0.1400(0.04446)‡ | 0.1094(0.00244)† | 0.1082(0.00119) |
| (25,10) | 0.1314(0.00333)‡ | 0.1184(0.00230)‡ | 0.1095(0.00211)‡ | 0.1020(0.00104)† | 0.1010(0.00148) | |
| (30,10) | 0.1221(0.00174)‡ | 0.1132(0.00066)‡ | 0.1067(0.00127)‡ | 0.0962(0.00129) | 0.0964(0.00165) | |
| DMOP1 | (20,10) | 0.1272(0.21435)‡ | 0.0139(0.00559)‡ | 0.0148(0.00274)‡ | 0.0082(0.00175) | 0.0084(0.00118) |
| (25,10) | 0.1296(0.24085)‡ | 0.0076(0.00174)† | 0.0099(0.00276)‡ | 0.0068(0.00504)† | 0.0064(0.00052) | |
| (30,10) | 0.1093(0.19550)‡ | 0.0060(0.00037) | 0.0071(0.00103)† | 0.0062(0.00120)† | 0.0061(0.00044) | |
| DMOP2 | (20,10) | 0.0805(0.01495)‡ | 0.0408(0.00221)† | 0.0353(0.00597) | 0.0374(0.00724) | 0.0384(0.00904) |
| (25,10) | 0.0659(0.03602)‡ | 0.0267(0.00616)‡ | 0.0316(0.00584)‡ | 0.0252(0.00504)† | 0.0223(0.00254) | |
| (30,10) | 0.0391(0.01263)‡ | 0.0224(0.00188)‡ | 0.0196(0.00325)† | 0.0196(0.00645)† | 0.0168(0.00458) | |
| F6 | (20,10) | 0.1212(0.10641)‡ | 0.0284(0.00389)† | 0.0291(0.00198)† | 0.0252(0.00519)† | 0.0248(0.00261) |
| (25,10) | 0.0525(0.02698)‡ | 0.0210(0.00376)† | 0.0219(0.00705)† | 0.0189(0.00492)† | 0.0188(0.00281) | |
| (30,10) | 0.0432(0.02731)‡ | 0.0152(0.00167)† | 0.0155(0.00201)† | 0.0127(0.00207) | 0.0142(0.00106) | |
| F9 | (20,10) | 0.8790(0.27757)‡ | 0.1495(0.03041)‡ | 0.2328(0.10508)‡ | 0.1030(0.01668)† | 0.0864(0.01512) |
| (25,10) | 0.5884(0.20324)‡ | 0.1476(0.06633)‡ | 0.1019(0.02075)‡ | 0.0832(0.03398)† | 0.0677(0.01341) | |
| (30,10) | 0.5169(0.16636)‡ | 0.0872(0.01821)† | 0.1089(0.05834)† | 0.0658(0.01456) | 0.0731(0.02148) | |
表 5 5种策略在部分测试问题上的MHVD指标
Tab.5
| 问题 | | MHVD | ||||
| PPS | CKPS | SPPS | HPPCM | IPS | ||
| FDA2 | (20,10) | 0.0329(0.00083)‡ | 0.0324(0.00033)‡ | 0.0333(0.00155)‡ | 0.0326(0.00105)‡ | 0.0315(0.00044) |
| (25,10) | 0.0320(0.00113)† | 0.0319(0.00074)‡ | 0.0322(0.00061)‡ | 0.0313(0.00068)† | 0.0311(0.00045) | |
| (30,10) | 0.0310(0.00031)† | 0.0310(0.00030)† | 0.0319(0.00046)‡ | 0.0307(0.00040) | 0.0309(0.00036) | |
| FDA4 | (20,10) | 0.4382(0.01399)‡ | 0.3787(0.00302)‡ | 0.4177(0.17410)‡ | 0.2934(0.01041) | 0.2986(0.00405) |
| (25,10) | 0.3799(0.01168)‡ | 0.3294(0.00692)‡ | 0.3024(0.00749)‡ | 0.2876(0.00799)‡ | 0.2728(0.00496) | |
| (30,10) | 0.3459(0.00825)‡ | 0.3116(0.00252)‡ | 0.2909(0.00533)‡ | 0.2473(0.00487) | 0.2544(0.00545) | |
| DMOP1 | (20,10) | 0.2308(0.13815)‡ | 0.1510(0.00239)† | 0.1455(0.00316) | 0.1510(0.00152)† | 0.1503(0.00066) |
| (25,10) | 0.2199(0.12614)‡ | 0.1489(0.00106) | 0.1460(0.00146) | 0.1506(0.00059)† | 0.1502(0.00031) | |
| (30,10) | 0.2193(0.12482)‡ | 0.1492(0.00061) | 0.1473(0.00145) | 0.1508(0.00054)† | 0.1504(0.00044) | |
| DMOP2 | (20,10) | 0.2462(0.01526)‡ | 0.1699(0.00150)‡ | 0.1684(0.00273)‡ | 0.1754(0.00443)‡ | 0.1644(0.00216) |
| (25,10) | 0.2253(0.04903)‡ | 0.1644(0.00351)† | 0.1677(0.00252)‡ | 0.1676(0.00185)‡ | 0.1639(0.00175) | |
| (30,10) | 0.1896(0.02220)‡ | 0.1642(0.00065)† | 0.1619(0.00201)† | 0.1656(0.00429)† | 0.1593(0.00404) | |
| F6 | (20,10) | 0.3912(0.09846)‡ | 0.2744(0.00899)† | 0.2776(0.00544)† | 0.2811(0.01186)† | 0.2729(0.00377) |
| (25,10) | 0.3222(0.03755)‡ | 0.2659(0.00655)† | 0.2693(0.01432)† | 0.2652(0.01061) | 0.2655(0.00412) | |
| (30,10) | 0.3066(0.03760)‡ | 0.2598(0.00432) | 0.2602(0.00464) | 0.2611(0.00575)† | 0.2603(0.00321) | |
| F9 | (20,10) | 0.8048(0.14654)‡ | 0.3967(0.02728)‡ | 0.4101(0.03460)‡ | 0.3551(0.01192)† | 0.3419(0.02853) |
| (25,10) | 0.6408(0.07758)‡ | 0.3705(0.03890)‡ | 0.3411(0.01947)‡ | 0.3353(0.04994)† | 0.3113(0.02232) | |
| (30,10) | 0.6098(0.06508)‡ | 0.3442(0.01784)‡ | 0.3293(0.02125)† | 0.3079(0.01038)† | 0.3014(0.01270) | |
4.2.1. FDA和DMOP问题上的实验结果分析
如表2所示为在FDA和DMOP系列问题上比较5种策略的MIGD指标,总阶段代表所有的环境变化.可以看出,1) 在总阶段和第1阶段,IPS有5个MIGD指标是最优的,HPPCM有2个MIGD指标是最优的. 2) 在第2阶段,IPS有3个MIGD指标是最优的,HPPCM有4个MIGD指标是最优的. 3) 在第3阶段,IPS有2个MIGD指标是最优的,PPS和HPPCM有3个MIGD指标是最优的.
出现这样实验结果的原因如下. IPS不需要经验的积累,其参考点联系算法筛选的特殊点可以加速种群的收敛,因此,在第1阶段IPS表现出了更好的性能. PPS随着经验的积累,在后2个阶段的某些测试问题上的MIGD指标优于IPS的. HPPCM的混合预测机制注重收敛,可以快速地响应环境变化,因此在FDA和DMOP系列问题上也有较好的表现. 对于3个目标的测试问题,IPS整体的性能要好于其他4种策略,说明IPS在高维动态多目标问题上有着更好的表现.
4.2.2. 在F5~F10问题上的实验结果分析
F5~F10是决策空间变量呈非线性相关的测试问题,如表3所示,在F5~F10系列问题上比较了这5种策略的MHVD指标,MHVD和MIGD均为综合的评价指标,可以评价5种策略在收敛性和分布性方面的性能. 可以看出,IPS和HPPCM较其他3种策略表现出了更好的性能. 对于测试问题F5~F8,HPPCM在第2、3阶段的MHVD指标大多优于IPS的,原因如下:HPPCM擅长追踪具有重大变化的PS或PF,而IPS的反馈校正机制和特殊点预测策略可以加速种群的收敛,因此IPS在第1阶段表现更好. 对于复杂测试问题F9, IPS的MHVD指标比其他4种策略的都要好,这是因为IPS在面对较大环境变化时仍能较快地收敛. CKPS和SPPS则在F10测试问题上有着更好的表现,是因为其自适应的种群维持机制可以根据问题困难程度引入不同数量的个体.
4.2.3. 不同环境变化频率下的实验结果分析
为了检验5种策略在不同环境变化频率下的性能,选择6个具有代表性的测试问题,比较5种策略对应3种不同
4.3. 获得的解集分布图对比
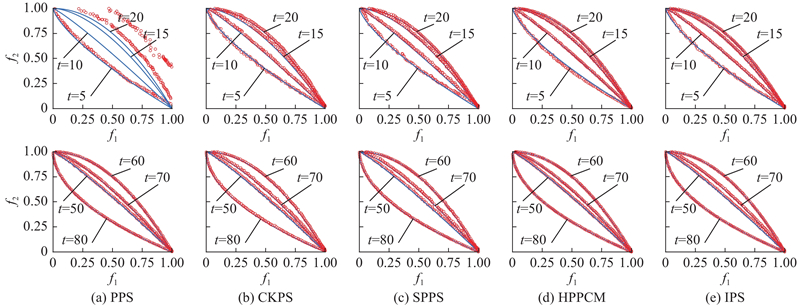
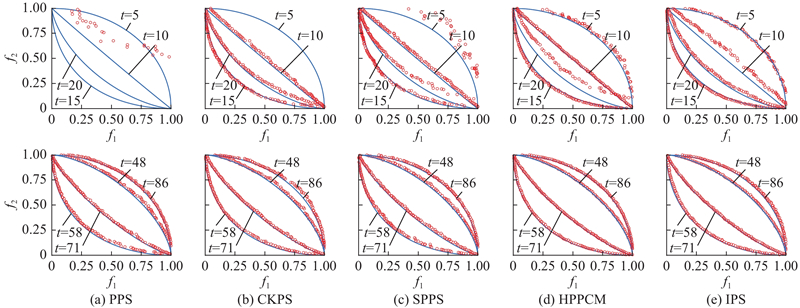
为了进行更加直观的比较,选择DMOP2、F9这2个具有代表性的测试问题来绘制5种策略在不同时刻所获得解集的分布图,如图6、7所示. 图中,横纵坐标表示所获得解集在不同目标上的目标值,圆点表示获得的解集,曲线表示标准PF. 可以看出,对比结果与表2、3的相同,在早期阶段,IPS所获得的解集具有更好的收敛性和分布性,说明IPS可以快速地响应环境变化. 在后期阶段,IPS在环境多次变化后仍能较为准确地追踪到新解,最终得到收敛性和分布性均较好的
图 6
图 6 5种策略在求解DMOP2过程中所获得的解集
Fig.6 Solution set obtained by five strategies in process of solving DMOP2
图 7
图 7 5种策略在求解F9过程中所获得的解集
Fig.7 Solution set obtained by five strategies in process of solving F9
5. 消融实验
5.1. 参考点联系算法筛选的特殊点对IPS的影响
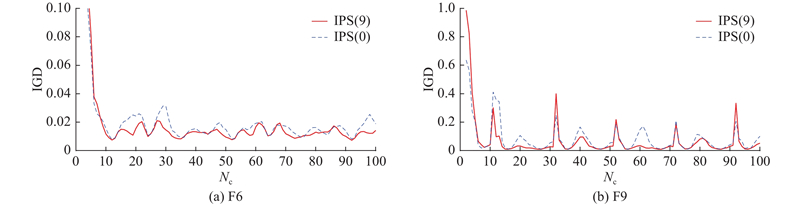
比较参考点联系算法筛选0个特殊点和9个特殊点的IPS,设筛选特殊点的个数为
图 8
图 8 IPS(0)和IPS(9)在F6和F9问题上运行20次时环境变化的IGD趋势
Fig.8 IGD trend comparison of IPS(0) and IPS(9) over number of changes for 20 runs on F6 and F9
5.2. 反馈校正机制对IPS的影响
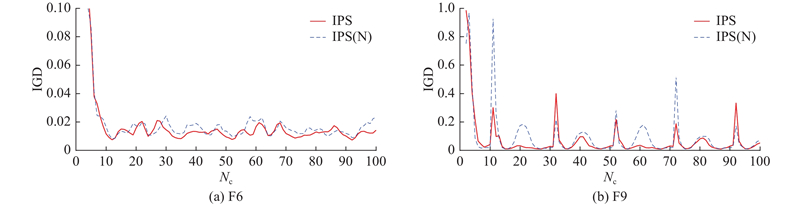
反馈校正机制是为了解决种群中心点预测方法缺乏误差反馈和校正机制,从而预测不够准确的问题. 为了验证反馈校正机制对IPS的影响,比较具有反馈校正机制和不具有反馈校正机制的IPS,设不具有反馈校正机制的IPS为IPS(N). 选择F6和F9测试问题来比较IPS和IPS(N)在20次运行中环境变化的IGD趋势,结果如图9所示. 图中,Nc为环境变化的次数. 可以看出,IPS表现出了比IPS(N)更好的性能. 原因如下:反馈校正机制校正了预测的步长和方向,提高了预测的准确性,使种群更准确地追踪新的最优解,面对复杂测试问题F9,IPS的表现明显优于IPS(N),说明反馈校正机制应对复杂问题也较有效.
图 9
图 9 IPS和IPS(N)在F6和F9问题上运行20次时环境变化的IGD趋势
Fig.9 IGD trend comparison of IPS and IPS(N) over number of changes for 20 runs on F6 and F9
6. 结 语
提出基于个体预测的动态多目标优化算法,种群中心点预测的非支配解集是预测种群的主体,采用反馈校正机制对其预测步长进行校正,从而更准确地追踪PF,同时引入由参考点联系算法筛选的特殊点,继而对特殊点集的预测可以快速响应环境的变化,再由混合多样性维持机制采用拉丁超立方抽样和精度可控的突变策略分别产生一部分随机个体以保持种群的多样性. 选择在FDA系列问题、DMOP系列问题以及F5~F10共13个测试问题上与其他4种算法进行比较,实验结果表明,无论是决策空间变量线性相关的问题,还是线性无关的问题,IPS都能快速响应环境的变化,获得收敛性和多样性均较好的解集.
IPS在应对不连续问题时有待改进,这也给未来的研究指明了一定的方向,如何在后2个阶段延续第1个阶段的表现将是笔者未来研究工作的重点. 此外,特殊点预测策略在种群尚未收敛的时候,可能会存在预测不准确的问题,而记忆策略对PS随时间不发生变化的问题有较好的影响,因此,将预测策略与记忆策略结合也是一项可研究的工作.
参考文献
An evaluation of non-redundant objective sets based on the spatial similarity ratio
[J].
多角色多策略多目标粒子群优化算法
[J].
Multi-objective particle swarm optimization algorithm with multi-role and multi-strategy
[J].
采用多目标蝙蝠算法的电力系统广域协调控制策略
[J].
Wide-area coordination control strategy for power system using multi-objective bat algorithm
[J].
性能感知的核心网控制面资源分配算法
[J].
Performance-aware resource allocation algorithm for core network control plane
[J].
A fast and elitist multiobjective genetic algorithm: NSGA-II
[J].DOI:10.1109/4235.996017 [本文引用: 1]
RM-MEDA: a regularity model-based multiobjective estimation of distribution algorithm
[J].DOI:10.1109/TEVC.2007.894202 [本文引用: 4]
MOEA/D: a multiobjective evolutionary algorithm based on decomposition
[J].DOI:10.1109/TEVC.2007.892759 [本文引用: 3]
To Celigny, in the footprints of vilfredo pareto's "optimum" [Historical Corner]
[J].DOI:10.1109/MAP.2014.6867724 [本文引用: 1]
A population prediction strategy for evolutionary dynamic multiobjective optimization
[J].DOI:10.1109/TCYB.2013.2245892 [本文引用: 2]
A prediction strategy based on center points and knee points for evolutionary dynamic multi-objective optimization
[J].DOI:10.1016/j.asoc.2017.08.004 [本文引用: 5]
A predictive strategy based on special points for evolutionary dynamic multi-objective optimization
[J].DOI:10.1007/s00500-018-3033-0 [本文引用: 3]
Multidirectional prediction approach for dynamic multiobjective optimization problems
[J].
Combining a hybrid prediction strategy and a mutation strategy for dynamic multiobjective optimization
[J].DOI:10.1016/j.swevo.2022.101041 [本文引用: 5]
Ant colony optimization for simulated dynamic multi-objective railway junction rescheduling
[J].DOI:10.1109/TITS.2017.2760981 [本文引用: 1]
Artificial immune system in dynamic environments solving time-varying non-linear constrained multi-objective problems
[J].DOI:10.1007/s00500-010-0674-z [本文引用: 1]
Robust dynamic multi-objective vehicle routing optimization method
[J].DOI:10.1109/TCBB.2017.2685320 [本文引用: 1]
A coevolutionary technique based on multi-swarm particle swarm optimization for dynamic multi-objective optimization
[J].DOI:10.1016/j.ejor.2017.03.048 [本文引用: 2]
Dynamic multiobjective optimization problems: test cases, approximations, and applications
[J].
Normal boundary intersection: a new method for generating the Pareto surface in nonlinear multicriteria optimization problems
[J].DOI:10.1137/S1052623496307510 [本文引用: 3]
An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: solving problems with box constraints
[J].DOI:10.1109/TEVC.2013.2281535 [本文引用: 1]
An evolutionary many-objective optimization algorithm using reference-point based nondominated sorting approach, part II: handling constraints and extending to an adaptive approach
[J].DOI:10.1109/TEVC.2013.2281534 [本文引用: 1]
The effect of diversity maintenance on prediction in dynamic multi-objective optimization
[J].DOI:10.1016/j.asoc.2017.05.008 [本文引用: 1]
A prediction strategy based on decision variable analysis for dynamic multi-objective optimization
[J].DOI:10.1016/j.swevo.2020.100786 [本文引用: 1]
A feedback-based prediction strategy for dynamic multi-objective evolutionary optimization
[J].DOI:10.1016/j.eswa.2021.114594 [本文引用: 2]
A dynamic multiobjective evolutionary algorithm based on decision variable classification
[J].DOI:10.1109/TCYB.2020.2986600 [本文引用: 1]
Novel prediction strategies for dynamic multiobjective optimization
[J].DOI:10.1109/TEVC.2019.2922834 [本文引用: 1]
A comparison of three methods for selecting values of input variables in the analysis of output from a computer code
[J].
Multiobjective evolution strategy for dynamic multiobjective optimization
[J].DOI:10.1109/TEVC.2020.2985323 [本文引用: 1]
A competitive-cooperative coevolutionary paradigm for dynamic multiobjective optimization
[J].DOI:10.1109/TEVC.2008.920671 [本文引用: 1]
Balancing convergence and diversity in decomposition-based many-objective optimizers
[J].