现代高端装备制造业对工件表面加工质量要求越来越高,基于工业机器人打磨已经成为高端制造业中打磨和抛光这类连续接触式作业的有力抓手,是解决人工作业的工作效率低和工作环境危害大问题以及提升工件加工质量的重要工具之一.
针对无先验模型且型面形状复杂多变的曲面工件机器人打磨,通常可以采用离线和在线打磨轨迹规划2种方式. 离线打磨轨迹规划主要通过传感器测量方式,预先获取工件模型相关先验数据,再根据先验数据进行打磨轨迹规划. Yang等[1]利用触发式探头获取工件表面点云数据,采用B样条方法重构曲面工件进行机器人打磨轨迹规划. Li等[2]借助结构光扫描仪,提出一种工件表面形状匹配方法,为离线轨迹规划获取先验数据. Ren等[3]将工件点云数据拟合为曲面,根据曲面的曲率规划机器人打磨轨迹. Princely等[4]通过相机获取工件二维形状数据,自动生成机器人去毛刺轨迹. Zhen等[5] 结合3D点云和机器视觉技术,提出一种机器人自适应打磨轨迹规划方法. 针对多种类、小批量且模型未知的复杂曲面工件,由于标定和安装误差的影响,通过测量获取的先验数据与工件真实模型具有一定误差[6],对此类工件的离线打磨轨迹规划较为耗时,降低了打磨效率.
在线打磨轨迹规划主要通过传感器实时获取打磨工具与工件的接触状态信息,进而预测曲面的几何特性,在线规划或修正打磨轨迹. Kiguchi等[7]提出一种打磨力方向在线调整方法,使接触力方向跟踪工件轮廓曲面法线方向. Jeon等[8]提出一种视觉和力传感器信息相融合的物体轮廓跟踪方法,在线调整机器人轨迹. Li等[9]提出一种工具与工件接触状态实时估计方法,用于跟踪工件曲面法线. Oba等[10]在工件先验数据未知且无力反馈的条件下,提出一种姿态和法向抛光力同步控制方法,使抛光工具的姿态自动适应工件曲面形状. 上述在线轨迹规划方法在针对空间复杂曲面工件打磨时,难以较准确地刻画空间曲面工件的几何特性,且具有较大的力跟踪控制误差.
本研究针对工业机器人柔顺打磨作业需求及法向打磨力需要稳定且准确可控的特点,以无先验模型曲面为打磨对象,开展机器人打磨主动自适应在线轨迹预测研究. 首先,设计一种柔顺浮动打磨力控末端执行器,将导纳控制和比例积分微分(PID)控制应用于末端执行器,以获取稳定准确的法向打磨力. 其次,提出一种无先验模型曲面的机器人打磨主动自适应在线轨迹预测方法. 最后,通过虚拟样机联合仿真分析,以及无先验模型圆台曲面工件自适应在线轨迹预测实验,验证所提出方法的有效性.
1. 机器人打磨力控制系统构建
1.1. 机器人打磨系统设计
机器人打磨系统主要由工业机器人与末端执行器构成,柔顺打磨通过采用主动力控制的末端执行器完成,末端执行器的位置和姿态(简称位姿)由工业机器人控制. 根据 Preston 材料去除理论,材料去除率与工具对工件的法向打磨力正相关[11],为了实现材料去除率可控、保证打磨质量,要求法向打磨力稳定、准确和可控;同时,为了实现此类受限运动,须对工业机器人运动轨迹进行预测或修正[12]. 仅通过机器人与刚性末端执行器的运动控制及被动力控制技术开展打磨作业,难以满足上述需求. 带有主动力控制的柔顺浮动末端执行器,可以将机器人打磨系统对打磨工具的力控制和位姿控制解耦,进而增加机器人打磨系统力控制带宽,提高系统动态响应性能[13].
1.1.1. 柔顺浮动打磨力控末端执行器设计
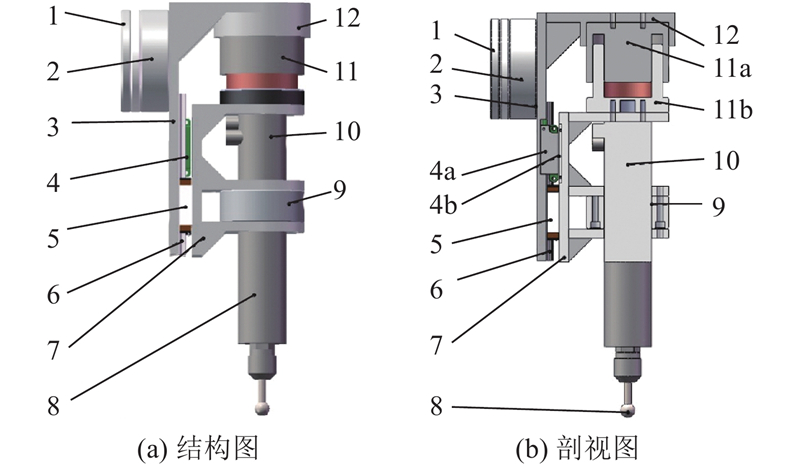
设计柔顺浮动打磨力控末端执行器,如图1所示. 该末端执行器以端面打磨方式进行打磨,采用主动力控制进行打磨力控制,并结合机器人进行位姿控制,实现柔顺打磨,具有机器人打磨系统的力控制和位姿控制解耦的特点.
图 1
图 1 柔顺浮动打磨力控末端执行器
1-连接板;2-力传感器;3-导轨支撑板;4-磁栅编码器(4a-动子;4b-磁栅);5-直线导轨动子;6-直线导轨;7-移动平台;8-打磨工具;9-主轴夹具;10-打磨主轴;11-音圈电机(11a-音圈电机定子;11b-音圈电机动子);12-音圈电机支座 Compliant floating grinding force-controlled end-effector
所设计的柔顺浮动打磨力控末端执行器的关键组件主要由以下3部分构成. 1) 法向打磨力控制组件:采用主动力控制(由力传感器2和磁栅编码器4作为传感元件),通过控制音圈电机11的输出力,实现法向打磨力的稳定、准确控制,减小由刚性接触引起的过切和欠切. 2) 浮动运动组件:由直线导轨模组(直线导轨动子5、直线导轨6)实现移动平台7的往复直线运动,保证打磨主轴10的浮动运动精度. 3) 打磨作业组件:打磨主轴10带动打磨工具8高速旋转打磨作业,可以灵活适配不同打磨工具,适应多场景的打磨作业.
音圈电机选用MOTICONT公司LVCM-051-064-02及810系列驱动器,最大持续输出力为68.2 N,PWM控制频率为50000 Hz;打磨主轴选用NAKANISHI公司BMS-4020电主轴,最高转速为20000 r/min;力传感器选用ATI公司F/T Delta IP65六维力传感器,力采集精度为1/8 N,采样频率为3000 Hz;磁栅编码器选用RLS公司HILIN系列直线式增量磁栅编码器,最高分辨率为0.1 μm;打磨工具采用球形红刚玉磨头.
机器人系统柔顺打磨的关键是依据打磨工况主动自适应进行打磨工具浮动调节. 本设计通过安装在音圈电机支架12下方的音圈电机11,驱动由安装在移动平台7夹板之间的主轴夹具固连的打磨主轴10,在安装于导轨支撑板3内侧的直线导轨6与安装在移动平台外侧的直线导轨动子组成的导轨模组上往复直线运动,带动被打磨主轴前端夹头夹持打磨工具8上下浮动,进而对法向打磨力稳定准确控制,加之打磨主轴10带动打磨工具8高速旋转,实现打磨工具端面打磨的浮动打磨作业;力传感器2用于测量打磨中工件对工具的反作用力,连同磁栅编码器4为主动自适应在线轨迹与姿态预测提供接触和位置状态反馈信息.
1.1.2. 机器人打磨系统虚拟样机构建
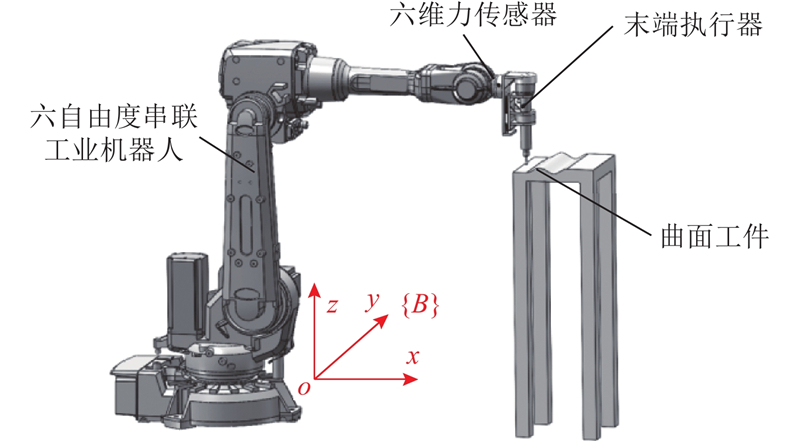
在ADAMS软件中构建机器人打磨系统虚拟样机(由柔顺浮动打磨力控末端执行器、六自由度串联工业机器人和曲面工件组成),如图2所示,将打磨系统虚拟样机导出为Matlab/Simulink仿真控制系统.
图 2
Matlab/Simulink仿真控制系统虚拟样机的输入分别为机器人关节变量q、音圈电机输入力Fi;输出分别为所设计末端执行器打磨主轴的轴向位置变化量dL、工具坐标系{T}的位置P、绕基础坐标系{B}的RPY角(Roll-Pitch-Yaw)以及在机器人工具坐标系{T}表示的工件对工具的反作用力
1.2. 法向打磨力控制
1.2.1. 法向打磨力控制器设计
图 3
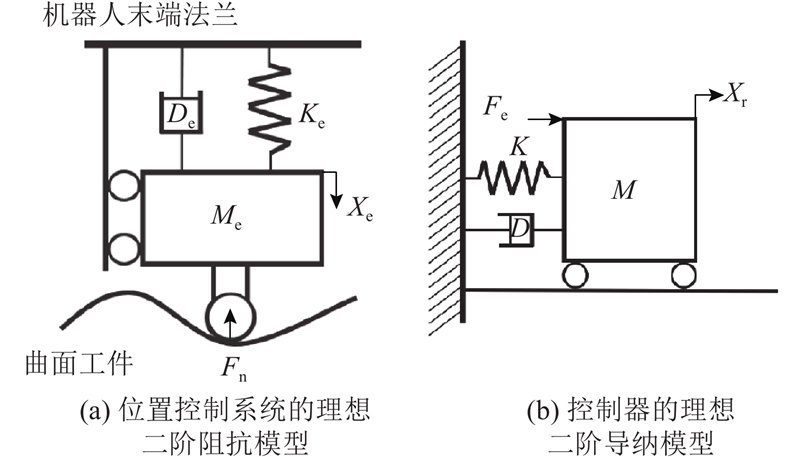
图 3 末端执行器位置控制系统和力控制器简化模型
Fig.3 Simplified model of position control system and force controller for end-effector
将打磨中法向打磨力Fn与期望力Fd之间的偏差Fe作为导纳控制器的输入,通过导纳模型的传递,计算出对位置控制系统输入的补偿量Xr,其数学模型如下:
式中:M、D和K分别为导纳模型的惯性系数、阻尼系数和刚度系数.
对式(3)进行拉普拉斯变换,得到位置补偿量Xr和力偏差Fe的关系为
式中:s为拉普拉斯算子.
将位置补偿Xr与期望位置X0及位置变化量dL叠加,得到位置控制器的输入量Xi:
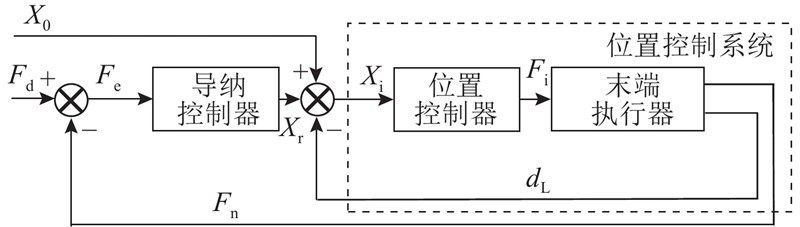
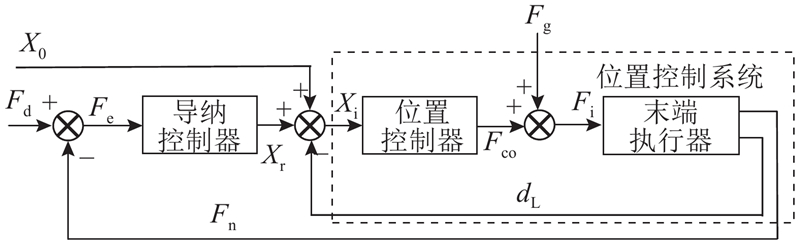
将Xi作用于末端执行器与位置控制器构成的位置控制系统,与导纳控制器一同实现对期望力Fd的跟踪控制,法向打磨力控制框图如图4所示.
图 4
图 4 基于力偏差的法向打磨力控制框图
Fig.4 Block diagram of normal grinding force control based on force error
1.2.2. 重力补偿
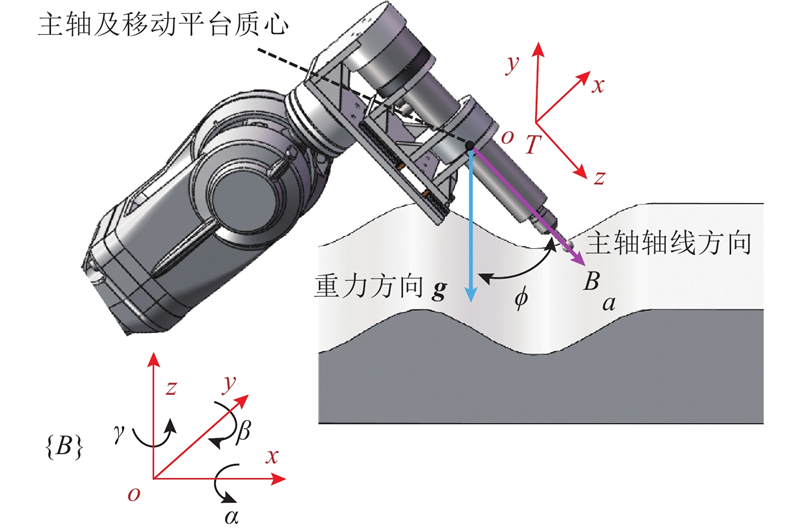
定义打磨主轴的轴线方向从主轴后端沿主轴轴线指向打磨工具. 在对曲面工件打磨时,工业机器人实时调整末端执行器的位姿. 当主轴轴线方向与重力加速度方向不同向时,如图5所示,须计算当前状态下对末端执行器音圈电机的输出力进行重力补偿,用于平衡重力作用,从而实现控制器对法向打磨力的准确控制.
图 5
图 5 主轴轴线方向与重力加速度方向夹角示意图
Fig.5 Schematic diagram of angle between axis of spindle and gravity vector
在虚拟样机中实时获取工具坐标系{T}在基础坐标系{B}中的RPY角,即横滚角α、偏航角β以及俯仰角γ,根据RPY角与姿态矩阵的转换关系,求得工具坐标系{T}的姿态矩阵为
式中:
式中:nx、ny和nz表示坐标系{T}的x轴单位方向向量在坐标系{B}下的方向余弦,ox、oy和oz表示坐标系{T}的y轴单位方向向量在坐标系{B}下的方向余弦,ax、ay和az表示坐标系{T}的z轴单位方向向量在坐标系{B}下的方向余弦.
由打磨主轴的轴线方向与工具坐标系{T}的z轴重合,可知主轴轴线方向单位矢量
式中:
叠加补偿量Fg与位置控制器的输出力Fco,得到音圈电机的输出力Fi:
进而实现法向打磨力控制的重力补偿,以消除主轴和移动平台自身重力对控制器性能的影响. 叠加重力补偿的法向打磨力控制框图如图6所示.
图 6
图 6 基于力偏差的法向打磨力控制框图(叠加重力补偿)
Fig.6 Block diagram of normal grinding force control based on force error (with gravity compensation)
2. 主动自适应在线轨迹预测方法
针对无先验模型的曲面工件,一般通过获取工件曲面的几何信息,求解曲面与基准平面的截交线,将截交线作为机器人打磨的待跟踪曲线,进而进行打磨轨迹规划[21]. 为了提高对无先验模型曲面工件打磨的主动自适应性,本研究提出一种无先验模型曲面的机器人打磨主动自适应在线轨迹预测方法.
进行如下设定.
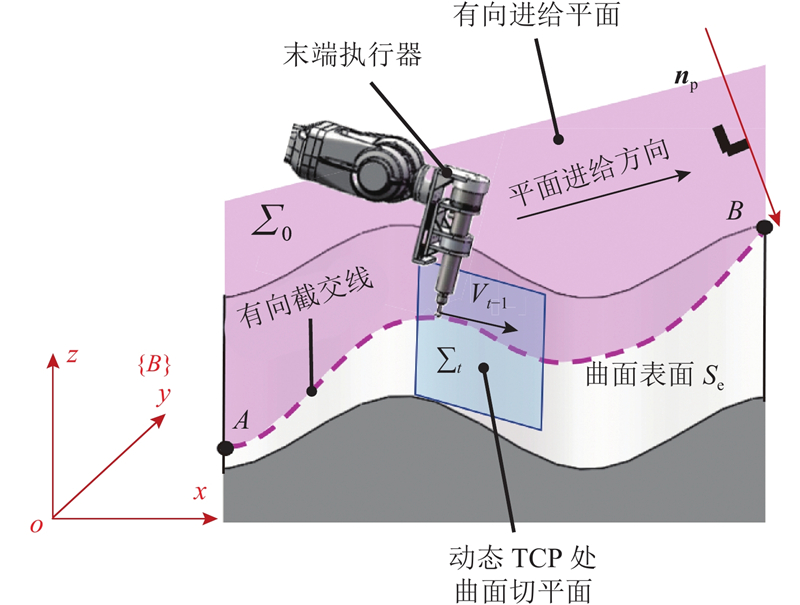
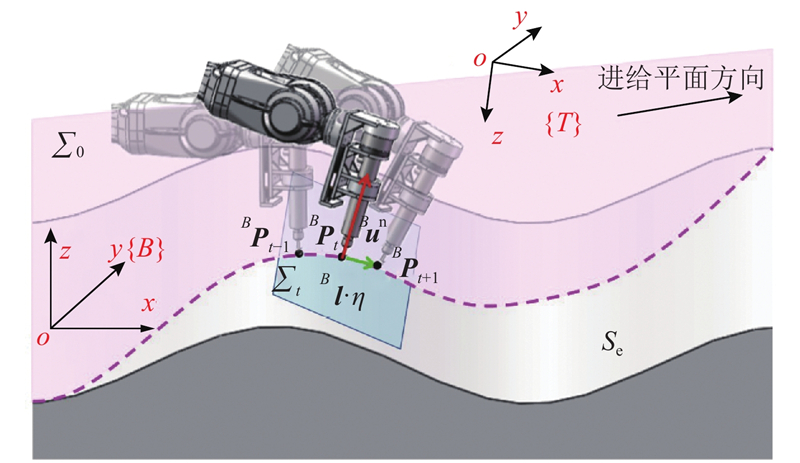
1) 通过在机器人工作空间内设置一个起始点A、一个终止点B和一个法向量np,构建如图7所示的有向进给平面. 图中,点A和点B分别为预规划打磨路径的起始点和终止点,法向量np为过点A和点B平面的法线,一般情况下,法向量np平行于坐标系{B}平面xoy. 平面进给方向可以根据工件待加工曲面的加工条件设定.
图 7
2) 设定TCP(tool central point)为音圈电机处于零位时,固连在打磨工具的末端点,并随工业机器人与打磨主轴浮动改变自身位姿;规定工具坐标系{T}的原点为TCP,工具坐标系{T}的z轴为打磨主轴的轴线方向,z轴正方向为工具接近工件的方向,x轴始终沿机器人末端法兰轴线向内.
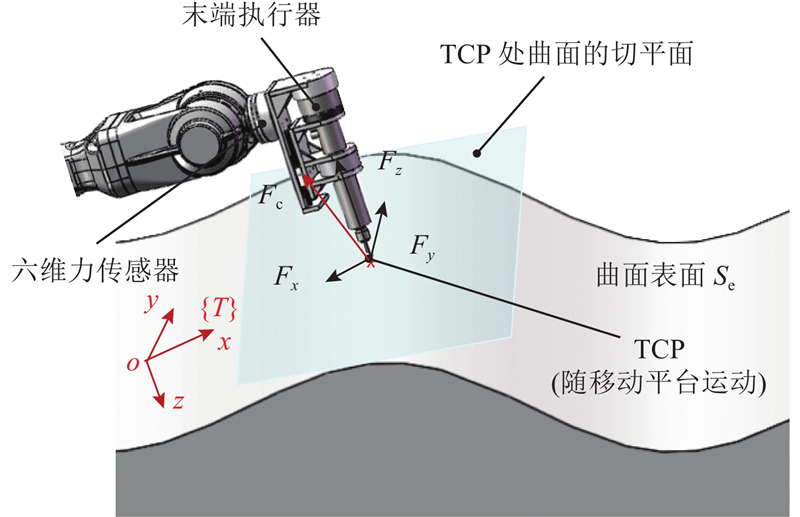
3) 机器人系统打磨时工件对工具的反作用力Fc被分解到工具坐标系{T}的x轴、y轴和z轴上,均由安装在工业机器人法兰上的六维力传感器测得,如图8所示.
图 8
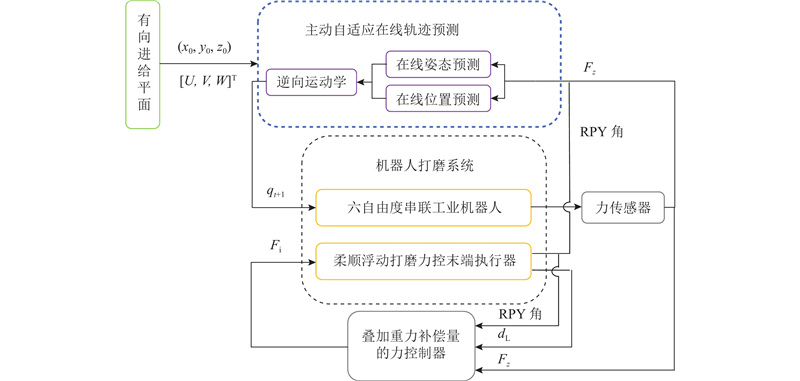
所提出在线轨迹预测方法的控制框图如图9所示. 该方法主要包括两部分:1) 基于反作用力分解的在线姿态预测(曲面法线跟踪预测);2) 基于有向进给平面截交线的在线位置预测. 主要思路如下:通过分解工件对工具的反作用力,对曲面法线进行主动自适应预测,使末端执行器主轴的轴线方向主动跟踪预测的曲面法线,并根据预测的曲面法线求解TCP处曲面切平面与有向进给平面的截交线,进一步预测出下一时刻TCP应达到的目标位姿;根据机器人逆向运动学,解得机器人下一时刻的目标关节变量,将目标关节变量作用于机器人关节驱动,从而使机器人主动自适应调整自身及末端执行器的位姿,实现无先验模型曲面的机器人打磨主动自适应在线轨迹预测. 所提出方法对于无先验模型的复杂多变曲面或平面均具有适用性.
图 9
图 9 无先验模型曲面的机器人打磨主动自适应在线轨迹预测方法控制框图
Fig.9 Block diagram of active adaptive online trajectory prediction method of robotic grinding on surface without prior model
2.1. 在线姿态预测(曲面法线跟踪预测)
再将该力矢量变换到基础坐标系{B}上,坐标变换为
式中:
根据式(12)得到工件对工具的反作用力矢量在基础坐标系{B}下的表示
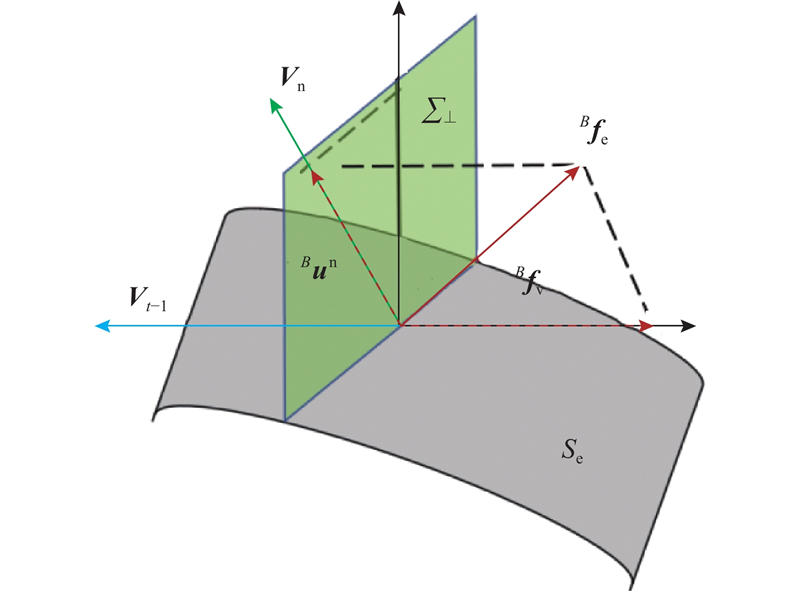
根据打磨工具的进给方向和工具与工件的接触状态,构建进给方向与曲面法线关系,如图10所示. 图中,
图 10
图 10 进给方向与曲面法线关系
Fig.10 Relationship between feed direction and surface normal
在工具旋转作业或进给运动时,若直接利用工件对工具的反作用力方向向量
将下一时刻打磨系统工具坐标系{T}的z轴取为近似曲面法线的负方向
为了实现姿态的稳定连续预测,使基础坐标系{B}下工具坐标系{T}的y轴正方向
进一步可以得到
即有2个解
为了确保姿态稳定连续变化不发生突变,根据式(6)、(7)获取当前时刻工具坐标系{T}的姿态矩阵
通过上述计算,得到下一时刻工具坐标系{T}在基础坐标系{B}下的姿态矩阵为
将式(22)所示的姿态矩阵作为工具坐标系{T}的目标姿态,通过预测的曲面法线向量
2.2. 在线位置预测
设定有向进给平面及方向如图11所示,该平面的一般方程为
图 11
式中:
进一步可以求得有向进给平面与曲面切平面截交线的方向向量为
由于工件轮廓曲线可以通过多个微元直线近似[24],在工具当前位置
将
至此,基于反作用力分解预测的姿态矩阵
3. 仿真性能评估与实验验证
在机器人打磨系统虚拟样机中,分别在导纳控制和PID控制2种力控制器作用下,将正弦曲面作为模型曲面,开展该无先验曲面机器人打磨主动自适应在线轨迹预测仿真分析,验证所提出方法的有效性及法向打磨力控制的稳定性. 同时开展无先验模型圆台曲面工件自适应在线轨迹预测实验,进一步验证所提出方法的有效性.
在Matlab/Simulink与ADAMS的联合仿真分析中,将法向打磨力的期望值设置为30 N,导纳控制器内部导纳模型的惯性系数、阻尼系数和刚度系数分别设置为23、1300和8.25,在ADAMS中设置工具与工件的接触刚度为1.0×104 N/m,穿透深度为1×10−5 m,最大阻尼系数3×104
表 1 自适应在线轨迹预测仿真结果
Tab.1
| 类别 | 位置预测 | 姿态预测(法线跟踪预测) | 法向力跟踪 | ||||||||||
| 误差项 | | | | | | | | | | | | ||
| 导纳控制 | 0.342 | 0.243 | 0.532 | 0.506 | 4.086 | 2.787 | 2.057×10−7 | 4.912 | 0.648 | −0.071 | 0.129 | ||
| PID控制 | 0.128 | 0.248 | 0.422 | 0.677 | 4.058 | 2.767 | 5.136×10−8 | 4.946 | 0.905 | 0.044 | 0.024 | ||
3.1. 位置预测性能评估
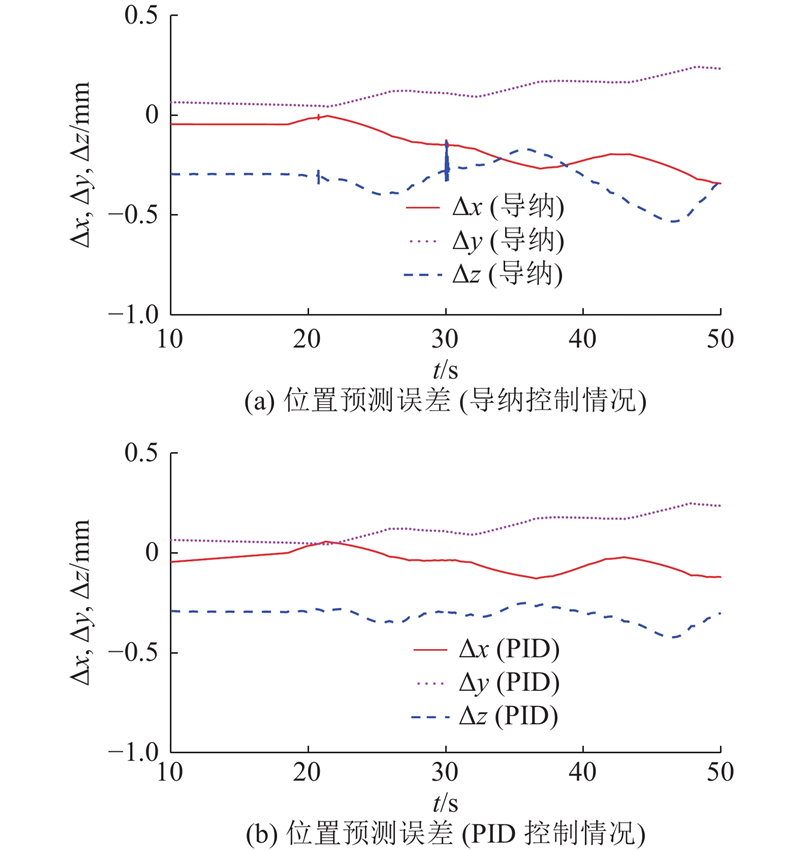
仿真结果表明,所提出方法在稳定法向打磨力控制器下的位置跟踪较准确,利用位置综合误差[25]量化评估位置预测的准确性,表达式为
图 12
图 12 主动自适应在线轨迹预测的位置预测误差
Fig.12 Position prediction error of active adaptive online trajectory prediction
3.2. 姿态预测(曲面法线跟踪)性能评估
图 13
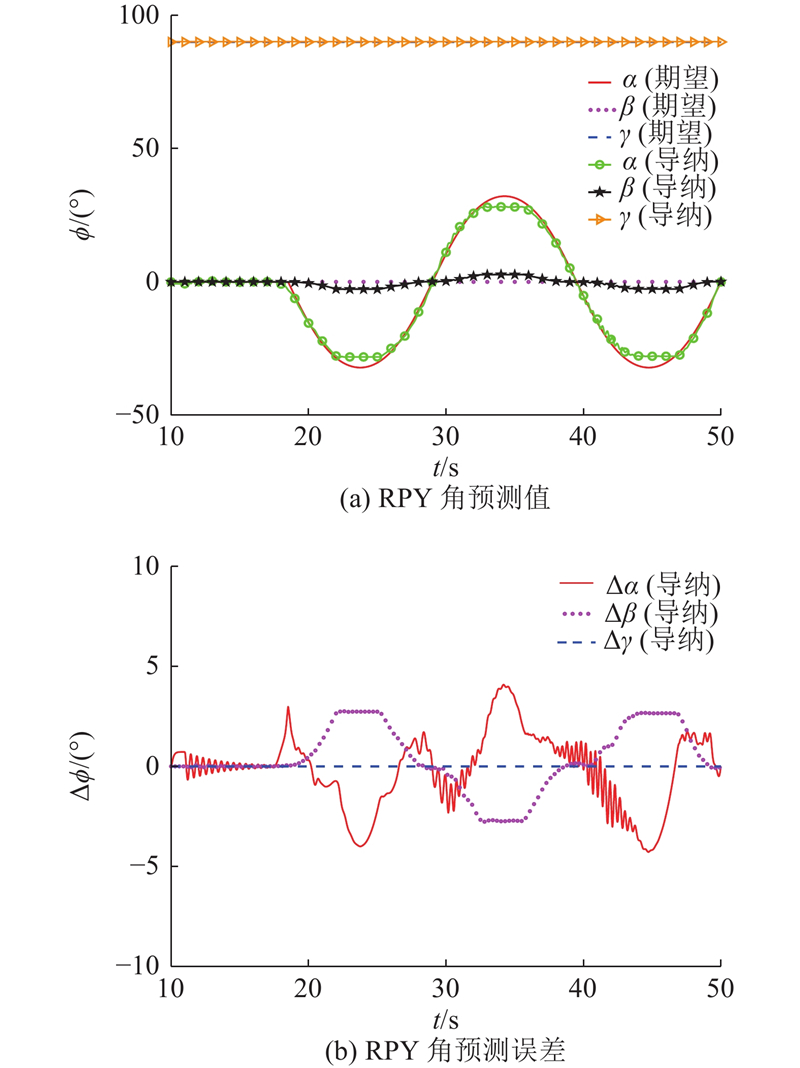
图 13 在导纳控制下RPY角预测值及角度预测误差
Fig.13 RPY angle prediction and angle prediction error with admittance controller
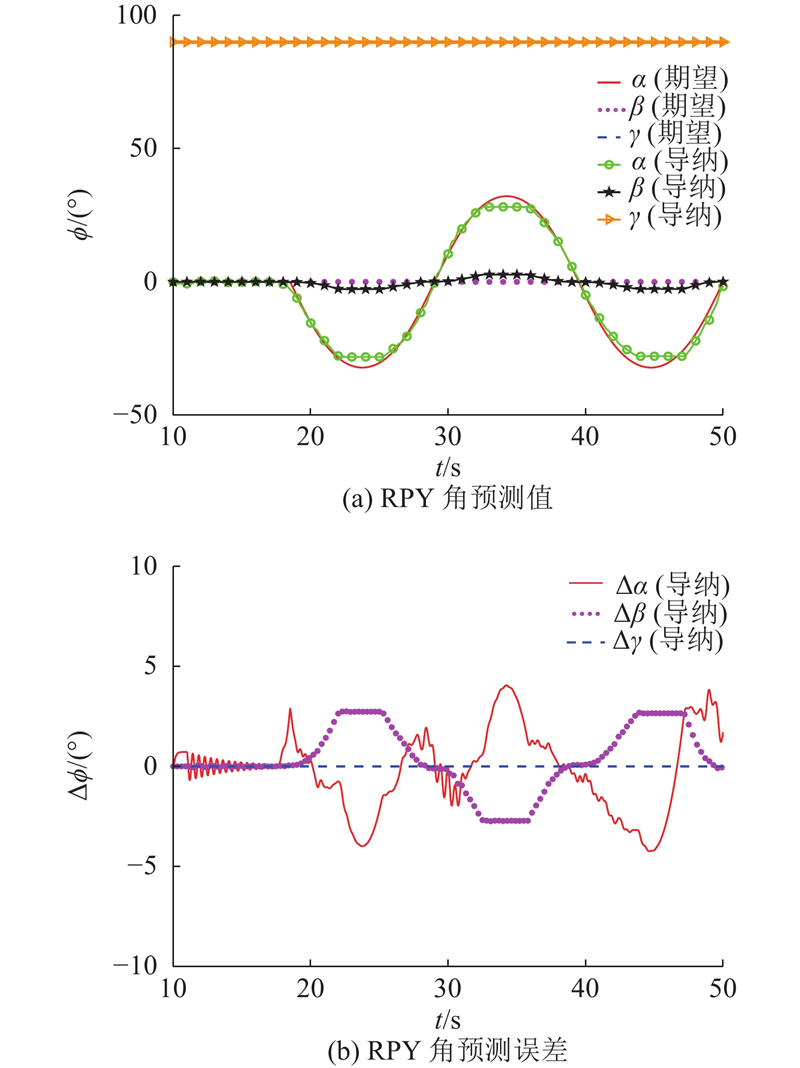
图 14
图 14 在PID控制下RPY角预测值及角度预测误差
Fig.14 RPY angle prediction and angle prediction error with PID controller
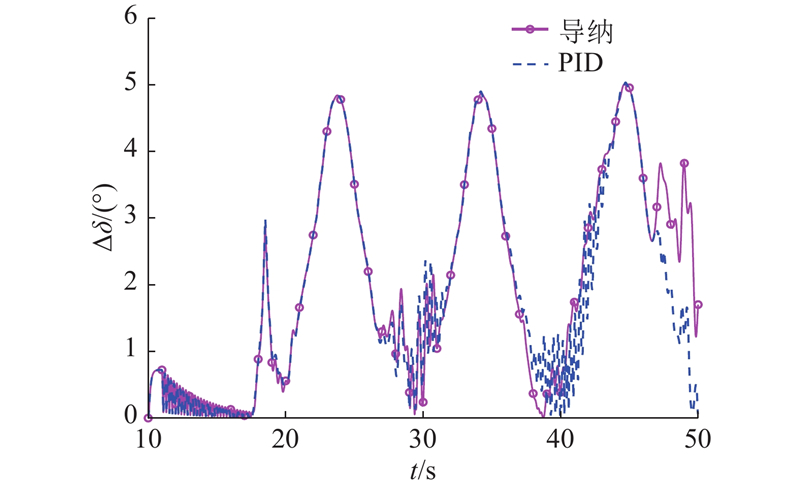
利用姿态综合误差[25]量化评估曲面法线跟踪性能,定义曲面法线跟踪误差为
图 15
3.3. 法向打磨力控制性能评估
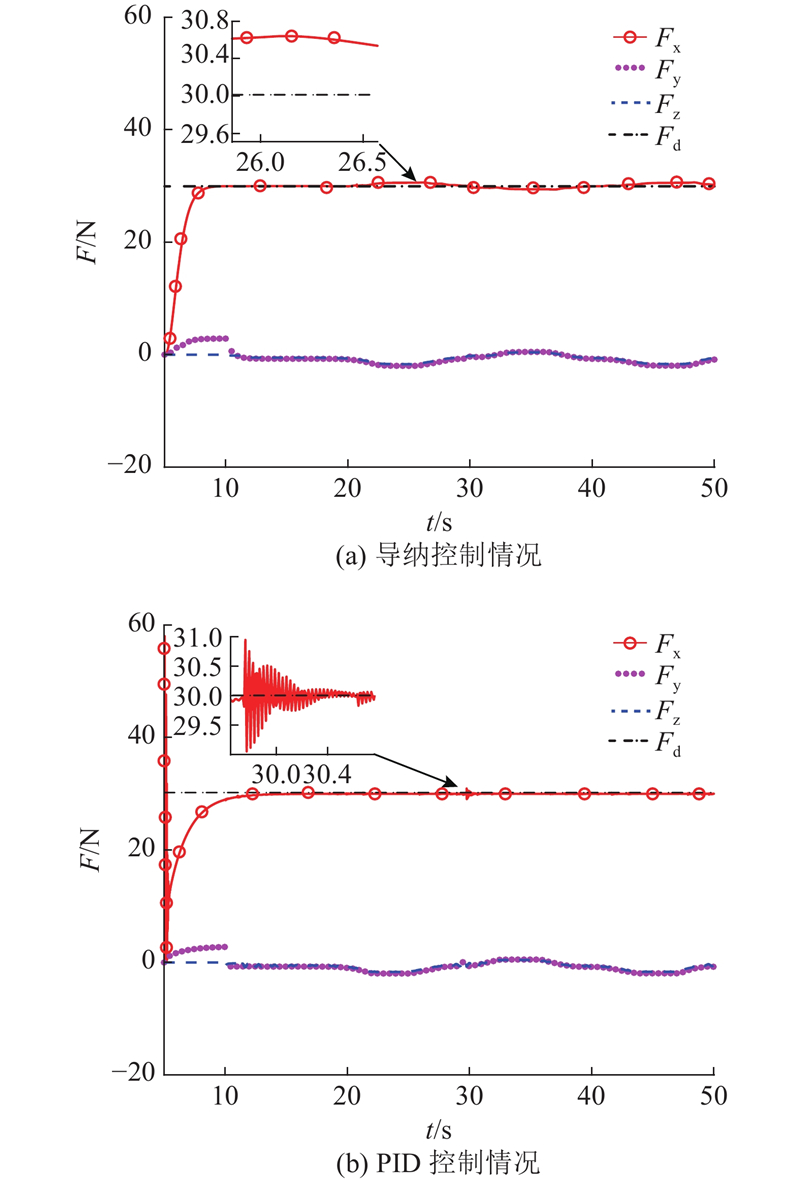
为了提高工件打磨质量,在打磨时不仅要使法向打磨力的方向主动自适应跟踪曲面的法向,同时要求其稳定可控. 导纳控制和PID控制作用下对应的反作用力曲线如图16所示. 图中,Fx、Fy和Fz分别表示反作用力在工具坐标系{T}下的x、y和z轴的分量,Fx与法向打磨力Fn相等,因此可以用Fx量化表征法向打磨力.
图 16
图 16 2种力控制器下跟踪正弦曲面的反作用力曲线
Fig.16 Reaction force tracking curve of a sinusoidal surface with two different force controllers
由上述结果可知,所提出方法在导纳控制下,法向打磨力的跟踪误差方差较大,力跟踪的准确性较差,但颤振抑制能力较好,且最大力跟踪误差较小,法向打磨力响应曲线的上升时间更短,快速性更好;而在PID控制下,力跟踪的准确性较好,但颤振抑制能力较差. 因此,所提出方法在法向打磨力控制器为导纳控制和PID控制下均适用,具有较好的适应性.
3.4. 主动自适应在线轨迹预测实验
为了进一步验证所提出在线轨迹预测方法的有效性,搭建如图17所示的机器人打磨系统实验平台,开展实物平台实验研究.
图 17
ABB IRB-4600/2.05机器人及IRC控制器和示教器作为机器人打磨系统的位姿控制部件;BECKHOFF公司CX-260354嵌入式控制器和力控末端执行器构成打磨力控制部件;工件为无先验几何模型的圆台曲面铸铁工件,如图18所示. CX-260354控制器通过EtherCAT网络协议获取磁栅编码器和力传感器信号,经过计算后,将预测的TCP位姿及力控制信号发送到工业机器人和音圈电机驱动器,开展主动自适应在线轨迹预测.
图 18
有向进给平面如图18所示,法向打磨力采用PID控制,为了防止实验过程中法向打磨力过大引起打磨主轴卡滞,设定期望法向打磨力为15 N. 平台实验如图19所示,工件用夹具固定,在工件表面设定起始点A(1000, 20, 700)和终止点B(1105, −85, 680),单位为mm;法向量设定为
图 19
图 19 主动自适应在线轨迹预测实验
Fig.19 Experiment of active adaptive online trajectory prediction
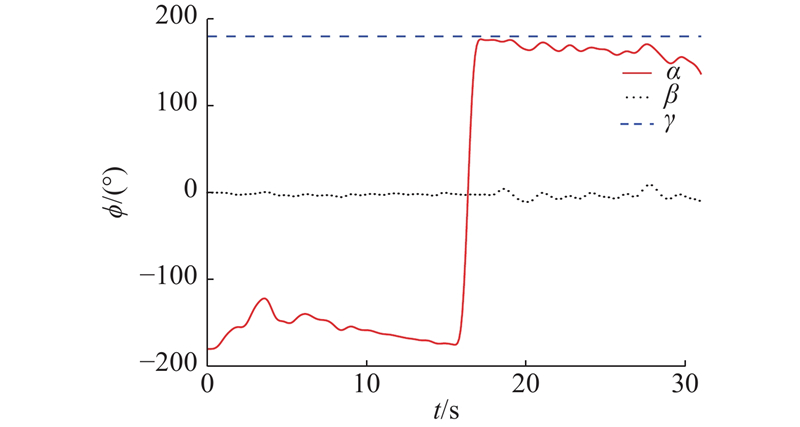
图 20
图 20 平台实验下的圆台曲面RPY角预测轨迹
Fig.20 RPY angle prediction for circular frustum surface on platform experiment
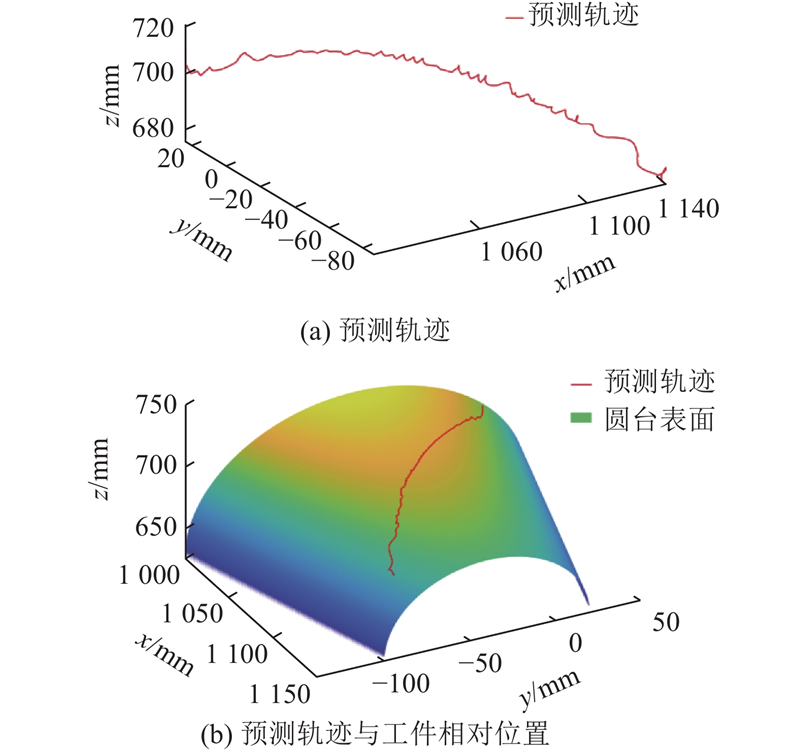
图 21
图 21 平台实验下的圆台曲面位置预测轨迹
Fig.21 Position prediction for circular frustum surface on platform experiment
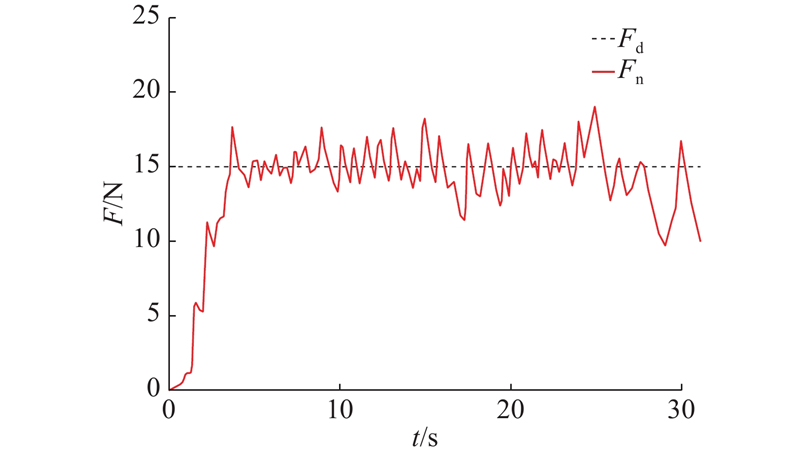
图 22
图 22 平台实验下的法向打磨力跟踪曲线
Fig.22 Normal grinding force tracking curve on platform experiment
由实验结果可知,法向打磨力跟踪误差最大值为4.037 N,平均值为−0.086 N. 实验表明,所提出的在线轨迹预测方法能够沿设定的有向进给平面实现该无先验模型工件的RPY角预测和位置预测以及曲面法线跟踪,验证了所提出方法的有效性.
4. 结 语
为了提高工业机器人打磨的作业柔顺性及无先验模型曲面工件的机器人打磨自适应性,设计了柔顺浮动打磨力控末端执行器,并提出了无先验模型曲面的机器人打磨主动自适应在线轨迹预测方法. 仿真和实验验证了所提出方法对无先验曲面的在线轨迹预测与法线跟踪的有效性,同时其可以实现对法向打磨力的准确跟踪控制,且方法易实现,实时性高. 所提出方法可以为无先验模型曲面工件的机器人打磨提供一种在线轨迹预测方法,具有一定的参考价值. 后续在所提出方法基础上,可以针对机器人打磨过程中复杂时变非线性动力学耦合与不确定性扰动以及机器人打磨作业颤振对在线轨迹预测的影响开展进一步深入研究,提高在强扰动情况下机器人打磨主动自适应在线轨迹预测的鲁棒性.
参考文献
A shape adaptive motion control system with application to robotic polishing
[J].
3-D shape matching of a blade surface in robotic grinding applications
[J].DOI:10.1109/TMECH.2016.2574813 [本文引用: 1]
Vision assisted robotic deburring of edge burrs in cast parts
[J].DOI:10.1016/j.proeng.2014.12.344 [本文引用: 1]
A new aspheric surfaces polishing by parallel orthogonality movement/force servomechanism
[J].
Position/force control of robot manipulators for geometrically unknown objects using fuzzy neural networks
[J].DOI:10.1109/41.847905 [本文引用: 2]
Real-time normal contact force control for robotic surface processing of workpieces without a priori geometric model
[J].
Simultaneous tool posture and polishing force control of unknown curved surface using serial-parallel mechanism polishing machine
[J].DOI:10.1016/j.precisioneng.2017.01.006 [本文引用: 1]
The theory and design of plate glass polishing machines
[J].
基于运动预测和阻抗控制的未知受限机构操作
[J].
Operating unknown constrained mechanisms based on motion prediction and impedance control
[J].
Design and control of an end-effector for industrial finishing applications
[J].DOI:10.1016/j.rcim.2018.04.010 [本文引用: 1]
Polishing pressure investigations of robot automatic polishing on curved surfaces
[J].
机器人磨抛力柔顺控制研究进展
[J].DOI:10.3969/j.issn.1004-132X.2021.18.011 [本文引用: 1]
Research progresses of robot grinding and polishing force compliance controls
[J].DOI:10.3969/j.issn.1004-132X.2021.18.011 [本文引用: 1]
A high-bandwidth end-effector with active force control for robotic polishing
[J].DOI:10.1109/ACCESS.2020.3022930 [本文引用: 1]
Design of a force-controlled end-effector with low-inertia effect for robotic polishing using macro-mini robot approach
[J].DOI:10.1016/j.rcim.2017.05.011 [本文引用: 1]
基于力传感器重力补偿的机器人柔顺控制研究
[J].DOI:10.6041/j.issn.1000-1298.2020.03.045 [本文引用: 1]
Robot compliant control based on force sensor gravity compensation
[J].DOI:10.6041/j.issn.1000-1298.2020.03.045 [本文引用: 1]
基于先验速度修正的工业机器人曲面跟踪柔顺控制
[J].
Compliant control of industrial robot surface tracking based on priori velocity correction
[J].
One hundred years of Hertz contact
[J].DOI:10.1243/PIME_PROC_1982_196_039_02 [本文引用: 1]
Research and application on force control of industrial robot polishing concave curved surfaces
[J].DOI:10.1177/0954405418802309 [本文引用: 1]
Automatic generation of auxiliary cutting paths based on sheet material semantic information
[J].
基于强化学习的机器人曲面恒力跟踪研究
[J].
Research on robot constant force control of surface tracking based on reinforcement learning
[J].
基于自适应迭代的机器人曲面恒力跟踪
[J].DOI:10.13700/j.bh.1001-5965.2018.0441 [本文引用: 2]
Constant-force curved-surface-tracking with robotic manipulator based on adaptive iterative algorithm
[J].DOI:10.13700/j.bh.1001-5965.2018.0441 [本文引用: 2]