(2) $ \begin{split} & P(s'|s,{{\boldsymbol{a}}_1},\cdots ,{{\boldsymbol{a}}_N},{{\boldsymbol{\pi}} _1},\cdots ,{{\boldsymbol{\pi}} _N}) = \\ &\qquad P(s'|s,{{\boldsymbol{a}}_1},\cdots ,{{\boldsymbol{a}}_N},{{{\boldsymbol{\pi}} '_1}},\cdots ,{{{\boldsymbol{\pi}} '_N}}). \end{split} $
(3) $ \left. {\begin{array}{*{20}{l}} {\theta {\text{ = \{ }}{\theta _{\text{1}}}{\text{,}}\cdots {\text{,}}\;{\theta _N}{\text{\} }}}, \\ \begin{gathered} {w_1}{\text{ = \{ }}{w_{{\text{1,1}}}}{\text{,}}\cdots {\text{,}}\;{w_{N,1}}{\text{\} }} , \\ {w_2}{\text{ = \{ }}{w_{{\text{1,2}}}}{\text{,}}\cdots {\text{,}}\;{w_{N,2}}{\text{\} }}, \\ \end{gathered} \\ {\pi {\text{ = \{ }}{{\boldsymbol{\pi}} _{\text{1}}}{\text{,}}\cdots {\text{,}}\;{{\boldsymbol{\pi}} _N}{\text{\} }}}. \end{array}} \right\} $
(4) $ \left. {\begin{array}{*{20}{c}} {{y_1} = {r_i}+\gamma Q_i^{{{w'_{i,2}}}}(s',{{\boldsymbol{a}}_1'},\cdots ,{{\boldsymbol{a}}_N'}){|_{{{\boldsymbol{a}}_{\boldsymbol{j}}'} = {\mu _j}^\prime ({o_j})}}}, \\ {{y_2} = {r_i}+\gamma Q_i^{{{w'_{i,1}}}}(s',{{\boldsymbol{a}}_1'},\cdots ,{{\boldsymbol{a}}_N'}){|_{{{\boldsymbol{a}}_{\boldsymbol{j}}'} = {\mu _j}^\prime ({o_j})}}} . \end{array}} \right\} $
(5) $ \begin{split} y =\;& {r_i}+\gamma \min \; \;(Q_i^{{{w'_{i,1}}}}(s',{{\boldsymbol{a}}_1'},\cdots,{{\boldsymbol{a}}_N'}){|_{{{\boldsymbol{a}}_j'} = {\mu _j}^\prime ({o_j})}}, \\ \;&Q_i^{{{w'_{i,2}}}}(s',{{\boldsymbol{a}}_1'},\cdots,{{\boldsymbol{a}}_N'}){|_{{{\boldsymbol{a}}_j'} = {\mu _j}^\prime ({o_j})}}) . \end{split} $
(6) $ \left. {\begin{array}{*{20}{c}} {{\rm{los}}{{\rm{s}}_1} = {E_{s,{{\boldsymbol{a}}_{{t}}},{R_t},s'}}[{{({Q_i}(s,{{\boldsymbol{a}}_t};{w_{i,1}}) - y)}^2}]}, \\ {{\rm{los}}{{\rm{s}}_2} = {E_{s,{{\boldsymbol{a}}_{{t}}},{R_t},s'}}[{{({Q_i}(s,{{\boldsymbol{a}}_t};{w_{i,2}}) - y)}^2}]}. \end{array}} \right\} $
式中:E 表示数学期望;s 为全局状态, $s = \left\{ {o_1},\cdots , {o_N} \right\}$ ${{\boldsymbol{a}}_t}$ ${{\boldsymbol{a}}_t} = [{{\boldsymbol{a}}_1},\cdots ,{{\boldsymbol{a}}_N}]$ ${R_t}$ ${R_t} = \{ {r_1},\cdots ,{r_N} \}$ ${Q_i}(x,{{\boldsymbol{a}}_t};{w_i})$
(7) $\left. {\begin{array}{*{20}{c}} {{{\boldsymbol{w}}_{i,1}} \leftarrow {{\boldsymbol{w}}_{i,1}} - \rho \times {\rm{los}}{{\rm{s}}_1} \times {\nabla _{w_{i,1}}}{Q_i}(s,{{\boldsymbol{a}}_1},\cdots,{{\boldsymbol{a}}_N},{w_{i,1}})} ,\\ {{{\boldsymbol{w}}_{i,2}} \leftarrow {{\boldsymbol{w}}_{i,2}} - \rho \times {\rm{los}}{{\rm{s}}_2} \times {\nabla _{w_{i,2}}}{Q_i}(s,{{\boldsymbol{a}}_1},\cdots,{{\boldsymbol{a}}_N},{w_{i,2}})} . \end{array}} \right\} $
式中:w i ,1w i ,2w i ,1w i ,2ρ 为学习率, ${\nabla _{w_{i,1}}}、{\nabla _{w_{i,2}}} $ $Q_i $ $w_{i,1} $ $w_{i,2} $ $ {w_{i,1}} $
[2]
李龙跃, 刘付显, 史向峰, 等 导弹攻防对抗中追逃对策模型与配点求解法
[J]. 系统工程与电子技术 , 2016 , 38 (5 ): 1067 - 1073
DOI:10.3969/j.issn.1001-506X.2016.05.15
[本文引用: 1]
LI Long-yue, LIU Fu-xian, SHI Xiang-feng, et al Model of pursuit and escape countermeasures in missile attack and defense countermeasures and collocation solution
[J]. Journal of Systems Engineering and Electronics , 2016 , 38 (5 ): 1067 - 1073
DOI:10.3969/j.issn.1001-506X.2016.05.15
[本文引用: 1]
[3]
刘坤, 郑晓帅, 林业茗, 等. 基于微分博弈的追逃问题最优策略设计[J]. 2021, 47(8): 1840-1854.
[本文引用: 1]
LIU Kun, ZHENG Xiao-shuai, LIN Ye-ming, et al. Optimal strategy design of pursuit and escape problem based on differential game [J]. Journal of Automatica Sinica , 2021, 47(8): 1840-1854.
[本文引用: 1]
[4]
刘肇隆, 宋耀, 徐翊铭, 等 图注意力网络的微分博弈追逃问题最优策略
[J]. 计算机工程与应用 , 2023 , 59 (9 ): 313 - 318
[本文引用: 1]
LIU Zhao-long, SONG Yao, XU Yi-ming, et al Optimal strategy of differential game pursuit problem in graph attention network
[J]. Computer Engineering and Applications , 2023 , 59 (9 ): 313 - 318
[本文引用: 1]
[5]
FANG B, PAN Q, HONG B, et al Research on high speed evader vs. multi lower speed pursuers in multi pursuit-evasion games
[J]. Information Technology Journal , 2012 , 11 (8 ): 989 - 997
DOI:10.3923/itj.2012.989.997
[本文引用: 1]
[6]
张澄安, 邓文, 王李瑞, 等 基于阿波罗尼奥斯圆的无人机追逃问题研究
[J]. 航天电子对抗 , 2021 , 37 (5 ): 40 - 43,48
DOI:10.3969/j.issn.1673-2421.2021.05.008
ZHANG Cheng-an, DENG Wen, WANG Li-rui, et al Research on the pursuit and escape of UAVs based on Apollonius circle
[J]. Aerospace Electronic Warfare , 2021 , 37 (5 ): 40 - 43,48
DOI:10.3969/j.issn.1673-2421.2021.05.008
[7]
苏义鑫, 石兵华, 张华军, 等 水面无人艇的抗追捕-逃跑策略
[J]. 哈尔滨工程大学学报 , 2018 , 39 (6 ): 1019 - 1025
DOI:10.11990/jheu.201705092
[本文引用: 1]
SU Yi-xin, SHI Bing-hua, ZHANG Hua-jun, et al The anti-pursuit and escape strategy of unmanned surface craft
[J]. Journal of Harbin Engineering University , 2018 , 39 (6 ): 1019 - 1025
DOI:10.11990/jheu.201705092
[本文引用: 1]
[8]
LI J, PAN Q, HONG B A new approach of multi-robot cooperative pursuit based on association rule data mining
[J]. International Journal of Advanced Robotic Systems , 2010 , 7 (3 ): 1169 - 1174
[本文引用: 1]
[9]
LIU J, LIU S, WU H, et al. A pursuit-evasion algorithm based on hierarchical reinforcement learning[C]// International Conference on Measuring Technology and Mechatronics Automation . Zhangjiajie: IEEE, 2009: 482-486.
[10]
MOSTAFA D, HOWARD M A decentralized fuzzy learning algorithm for pursuit-evasion differential games with superior evaders
[J]. Journal of Intelligent and Robotic Systems , 2016 , 83 (1 ): 35 - 53
DOI:10.1007/s10846-015-0315-y
[本文引用: 1]
[11]
ALEXANDRE B, MOULAY A. UAV pursuit using reinforcement learning[EB/OL]. [2022-11-01]. https://www.researchgate.net/publication/333122618_UAV_pursuit_using_reinforcement_learning
[本文引用: 1]
[12]
ZHANG B, HU B, CHEN L, et al. Probabilistic reward-based reinforcement learning for multi-agent pursuit and evasion [EB/OL]. (2021-05-22). https://kns.cnki.net/kcms2/article/abstract?v=YhL_Bl4XtC7yyLQqjQmWvQGFaHRks9Y7gEQxMHvbmL7fMP8_n99K976g8Gkzd7ga2CqCUiYClTJD65ep-1s-zhxIW8yOO67CYj63fkZ7BjY%3d&uniplatform=NZKPT.
[本文引用: 1]
[13]
ZHOU X, ZHOU S, MOU X, et al. Multirobot collaborative pursuit target robot by improved MADDPG [EB/OL]. (2022-02-25). https://www.hindawi.com/journals/cin/2022/4757394/.
[本文引用: 1]
[14]
夏家伟, 朱旭芳, 张建强, 等 基于多智能体强化学习的无人艇协同围捕方法
[J]. 控制与决策 , 2023 , 38 (5 ): 1438 - 1447
DOI:10.13195/j.kzyjc.2022.0564
[本文引用: 1]
XIA Jia-wei, ZHU Xu-fang, ZHANG Jian-qiang, et al Research on the method of unmanned boat cooperative encirclement based on multi-agent reinforcement learning
[J]. Control and Decision , 2023 , 38 (5 ): 1438 - 1447
DOI:10.13195/j.kzyjc.2022.0564
[本文引用: 1]
[17]
FUJIMOTO S, HOOF H, MEGER D. Addressing function approximation error in actor-critic methods[EB/OL]. (2018-02-26). https://arxiv.org/abs/1802.09477v1.
[本文引用: 1]
[18]
TOM S, JOHN Q, IOANNIS A, et al. Prioritized experience replay[EB/OL]. (2015-11-18). https://arxiv.org/abs/1511.05952.
[本文引用: 1]
[19]
龚慧雯, 王桐, 陈立伟, 等 基于深度强化学习的多智能体对抗策略算法
[J]. 应用科技 , 2022 , 49 (5 ): 1 - 7
[本文引用: 1]
GONG Hui-wen, WANG Tong, CHEN Li-wei, et al Multi-agent confrontation strategy algorithm based on deep reinforcement learning
[J]. Applied Science and Technology , 2022 , 49 (5 ): 1 - 7
[本文引用: 1]
[20]
SHEIKH H U, BOLONI L. Multi-agent reinforcement learning for problems with combined individual and team reward[C]// 2020 International Joint Conference on Neural Networks (IJCNN) . Glasgow: IEEE, 2020: 1-8,
[本文引用: 1]
[21]
符小卫, 王辉, 徐哲 基于DE-MADDPG的多无人机协同追捕策略
[J]. 航空学报 , 2022 , 43 (5 ): 530 - 543
[本文引用: 1]
FU Xiao-wei, WANG Hui, XU Zhe Multi-UAV cooperative pursuit strategy based on DE-MADDPG
[J]. Acta Aeronautica Et Astronautica Sinica , 2022 , 43 (5 ): 530 - 543
[本文引用: 1]
基于对策论的群机器人追捕-逃跑问题研究
1
2003
... 学术界对追捕-逃逸问题的研究展开了大量探索性工作. 追捕-逃逸问题的解决方法可以分为确定性方法和智能优化算法. 确定性方法的主流方法为微分博弈论. 通过对多智能体追捕-逃跑问题建模并搭建追逃双方的策略选择模型,得出实时策略选择算法[1 ] . 李龙跃等[2 ] 将追逃微分博弈问题转化为单边最优对策问题,提出用改进多项式配点法近似状态变量对时间的微分,降低了问题复杂度. 刘坤等[3 ] 针对追逃双方分散的情形,将多智能体追逃转化为多组双智能体博弈,并求解了追逃双方的最优策略. 刘肇隆等[4 ] 在微分博弈论的基础上通过改进图注意力网络,构建了轨迹预测模型,并用圆环覆盖双方运动的轨迹,建立轨迹连接图,预测指标有明显提升. 除了微分博弈论外,阿波罗尼斯圆也可以用于解决追击-逃逸问题[5 -7 ] . 基于阿波罗尼斯圆构建多智能体追逃模型可以求解逃逸成功条件. 若逃逸者在绝对逃逸区域中,则一定能成功逃脱. 确定性方法用数学公式描述模型,有严格的推导过程,求解难度会因对象数量增加成指数增长,且在设计追击策略时通常须对逃逸者的动作做出假定约束或已知逃逸者的控制策略. 因此,该类方法在多智能体对抗的复杂高动态场景下很难取得较好的应用效果. ...
基于对策论的群机器人追捕-逃跑问题研究
1
2003
... 学术界对追捕-逃逸问题的研究展开了大量探索性工作. 追捕-逃逸问题的解决方法可以分为确定性方法和智能优化算法. 确定性方法的主流方法为微分博弈论. 通过对多智能体追捕-逃跑问题建模并搭建追逃双方的策略选择模型,得出实时策略选择算法[1 ] . 李龙跃等[2 ] 将追逃微分博弈问题转化为单边最优对策问题,提出用改进多项式配点法近似状态变量对时间的微分,降低了问题复杂度. 刘坤等[3 ] 针对追逃双方分散的情形,将多智能体追逃转化为多组双智能体博弈,并求解了追逃双方的最优策略. 刘肇隆等[4 ] 在微分博弈论的基础上通过改进图注意力网络,构建了轨迹预测模型,并用圆环覆盖双方运动的轨迹,建立轨迹连接图,预测指标有明显提升. 除了微分博弈论外,阿波罗尼斯圆也可以用于解决追击-逃逸问题[5 -7 ] . 基于阿波罗尼斯圆构建多智能体追逃模型可以求解逃逸成功条件. 若逃逸者在绝对逃逸区域中,则一定能成功逃脱. 确定性方法用数学公式描述模型,有严格的推导过程,求解难度会因对象数量增加成指数增长,且在设计追击策略时通常须对逃逸者的动作做出假定约束或已知逃逸者的控制策略. 因此,该类方法在多智能体对抗的复杂高动态场景下很难取得较好的应用效果. ...
导弹攻防对抗中追逃对策模型与配点求解法
1
2016
... 学术界对追捕-逃逸问题的研究展开了大量探索性工作. 追捕-逃逸问题的解决方法可以分为确定性方法和智能优化算法. 确定性方法的主流方法为微分博弈论. 通过对多智能体追捕-逃跑问题建模并搭建追逃双方的策略选择模型,得出实时策略选择算法[1 ] . 李龙跃等[2 ] 将追逃微分博弈问题转化为单边最优对策问题,提出用改进多项式配点法近似状态变量对时间的微分,降低了问题复杂度. 刘坤等[3 ] 针对追逃双方分散的情形,将多智能体追逃转化为多组双智能体博弈,并求解了追逃双方的最优策略. 刘肇隆等[4 ] 在微分博弈论的基础上通过改进图注意力网络,构建了轨迹预测模型,并用圆环覆盖双方运动的轨迹,建立轨迹连接图,预测指标有明显提升. 除了微分博弈论外,阿波罗尼斯圆也可以用于解决追击-逃逸问题[5 -7 ] . 基于阿波罗尼斯圆构建多智能体追逃模型可以求解逃逸成功条件. 若逃逸者在绝对逃逸区域中,则一定能成功逃脱. 确定性方法用数学公式描述模型,有严格的推导过程,求解难度会因对象数量增加成指数增长,且在设计追击策略时通常须对逃逸者的动作做出假定约束或已知逃逸者的控制策略. 因此,该类方法在多智能体对抗的复杂高动态场景下很难取得较好的应用效果. ...
导弹攻防对抗中追逃对策模型与配点求解法
1
2016
... 学术界对追捕-逃逸问题的研究展开了大量探索性工作. 追捕-逃逸问题的解决方法可以分为确定性方法和智能优化算法. 确定性方法的主流方法为微分博弈论. 通过对多智能体追捕-逃跑问题建模并搭建追逃双方的策略选择模型,得出实时策略选择算法[1 ] . 李龙跃等[2 ] 将追逃微分博弈问题转化为单边最优对策问题,提出用改进多项式配点法近似状态变量对时间的微分,降低了问题复杂度. 刘坤等[3 ] 针对追逃双方分散的情形,将多智能体追逃转化为多组双智能体博弈,并求解了追逃双方的最优策略. 刘肇隆等[4 ] 在微分博弈论的基础上通过改进图注意力网络,构建了轨迹预测模型,并用圆环覆盖双方运动的轨迹,建立轨迹连接图,预测指标有明显提升. 除了微分博弈论外,阿波罗尼斯圆也可以用于解决追击-逃逸问题[5 -7 ] . 基于阿波罗尼斯圆构建多智能体追逃模型可以求解逃逸成功条件. 若逃逸者在绝对逃逸区域中,则一定能成功逃脱. 确定性方法用数学公式描述模型,有严格的推导过程,求解难度会因对象数量增加成指数增长,且在设计追击策略时通常须对逃逸者的动作做出假定约束或已知逃逸者的控制策略. 因此,该类方法在多智能体对抗的复杂高动态场景下很难取得较好的应用效果. ...
1
... 学术界对追捕-逃逸问题的研究展开了大量探索性工作. 追捕-逃逸问题的解决方法可以分为确定性方法和智能优化算法. 确定性方法的主流方法为微分博弈论. 通过对多智能体追捕-逃跑问题建模并搭建追逃双方的策略选择模型,得出实时策略选择算法[1 ] . 李龙跃等[2 ] 将追逃微分博弈问题转化为单边最优对策问题,提出用改进多项式配点法近似状态变量对时间的微分,降低了问题复杂度. 刘坤等[3 ] 针对追逃双方分散的情形,将多智能体追逃转化为多组双智能体博弈,并求解了追逃双方的最优策略. 刘肇隆等[4 ] 在微分博弈论的基础上通过改进图注意力网络,构建了轨迹预测模型,并用圆环覆盖双方运动的轨迹,建立轨迹连接图,预测指标有明显提升. 除了微分博弈论外,阿波罗尼斯圆也可以用于解决追击-逃逸问题[5 -7 ] . 基于阿波罗尼斯圆构建多智能体追逃模型可以求解逃逸成功条件. 若逃逸者在绝对逃逸区域中,则一定能成功逃脱. 确定性方法用数学公式描述模型,有严格的推导过程,求解难度会因对象数量增加成指数增长,且在设计追击策略时通常须对逃逸者的动作做出假定约束或已知逃逸者的控制策略. 因此,该类方法在多智能体对抗的复杂高动态场景下很难取得较好的应用效果. ...
1
... 学术界对追捕-逃逸问题的研究展开了大量探索性工作. 追捕-逃逸问题的解决方法可以分为确定性方法和智能优化算法. 确定性方法的主流方法为微分博弈论. 通过对多智能体追捕-逃跑问题建模并搭建追逃双方的策略选择模型,得出实时策略选择算法[1 ] . 李龙跃等[2 ] 将追逃微分博弈问题转化为单边最优对策问题,提出用改进多项式配点法近似状态变量对时间的微分,降低了问题复杂度. 刘坤等[3 ] 针对追逃双方分散的情形,将多智能体追逃转化为多组双智能体博弈,并求解了追逃双方的最优策略. 刘肇隆等[4 ] 在微分博弈论的基础上通过改进图注意力网络,构建了轨迹预测模型,并用圆环覆盖双方运动的轨迹,建立轨迹连接图,预测指标有明显提升. 除了微分博弈论外,阿波罗尼斯圆也可以用于解决追击-逃逸问题[5 -7 ] . 基于阿波罗尼斯圆构建多智能体追逃模型可以求解逃逸成功条件. 若逃逸者在绝对逃逸区域中,则一定能成功逃脱. 确定性方法用数学公式描述模型,有严格的推导过程,求解难度会因对象数量增加成指数增长,且在设计追击策略时通常须对逃逸者的动作做出假定约束或已知逃逸者的控制策略. 因此,该类方法在多智能体对抗的复杂高动态场景下很难取得较好的应用效果. ...
图注意力网络的微分博弈追逃问题最优策略
1
2023
... 学术界对追捕-逃逸问题的研究展开了大量探索性工作. 追捕-逃逸问题的解决方法可以分为确定性方法和智能优化算法. 确定性方法的主流方法为微分博弈论. 通过对多智能体追捕-逃跑问题建模并搭建追逃双方的策略选择模型,得出实时策略选择算法[1 ] . 李龙跃等[2 ] 将追逃微分博弈问题转化为单边最优对策问题,提出用改进多项式配点法近似状态变量对时间的微分,降低了问题复杂度. 刘坤等[3 ] 针对追逃双方分散的情形,将多智能体追逃转化为多组双智能体博弈,并求解了追逃双方的最优策略. 刘肇隆等[4 ] 在微分博弈论的基础上通过改进图注意力网络,构建了轨迹预测模型,并用圆环覆盖双方运动的轨迹,建立轨迹连接图,预测指标有明显提升. 除了微分博弈论外,阿波罗尼斯圆也可以用于解决追击-逃逸问题[5 -7 ] . 基于阿波罗尼斯圆构建多智能体追逃模型可以求解逃逸成功条件. 若逃逸者在绝对逃逸区域中,则一定能成功逃脱. 确定性方法用数学公式描述模型,有严格的推导过程,求解难度会因对象数量增加成指数增长,且在设计追击策略时通常须对逃逸者的动作做出假定约束或已知逃逸者的控制策略. 因此,该类方法在多智能体对抗的复杂高动态场景下很难取得较好的应用效果. ...
图注意力网络的微分博弈追逃问题最优策略
1
2023
... 学术界对追捕-逃逸问题的研究展开了大量探索性工作. 追捕-逃逸问题的解决方法可以分为确定性方法和智能优化算法. 确定性方法的主流方法为微分博弈论. 通过对多智能体追捕-逃跑问题建模并搭建追逃双方的策略选择模型,得出实时策略选择算法[1 ] . 李龙跃等[2 ] 将追逃微分博弈问题转化为单边最优对策问题,提出用改进多项式配点法近似状态变量对时间的微分,降低了问题复杂度. 刘坤等[3 ] 针对追逃双方分散的情形,将多智能体追逃转化为多组双智能体博弈,并求解了追逃双方的最优策略. 刘肇隆等[4 ] 在微分博弈论的基础上通过改进图注意力网络,构建了轨迹预测模型,并用圆环覆盖双方运动的轨迹,建立轨迹连接图,预测指标有明显提升. 除了微分博弈论外,阿波罗尼斯圆也可以用于解决追击-逃逸问题[5 -7 ] . 基于阿波罗尼斯圆构建多智能体追逃模型可以求解逃逸成功条件. 若逃逸者在绝对逃逸区域中,则一定能成功逃脱. 确定性方法用数学公式描述模型,有严格的推导过程,求解难度会因对象数量增加成指数增长,且在设计追击策略时通常须对逃逸者的动作做出假定约束或已知逃逸者的控制策略. 因此,该类方法在多智能体对抗的复杂高动态场景下很难取得较好的应用效果. ...
Research on high speed evader vs. multi lower speed pursuers in multi pursuit-evasion games
1
2012
... 学术界对追捕-逃逸问题的研究展开了大量探索性工作. 追捕-逃逸问题的解决方法可以分为确定性方法和智能优化算法. 确定性方法的主流方法为微分博弈论. 通过对多智能体追捕-逃跑问题建模并搭建追逃双方的策略选择模型,得出实时策略选择算法[1 ] . 李龙跃等[2 ] 将追逃微分博弈问题转化为单边最优对策问题,提出用改进多项式配点法近似状态变量对时间的微分,降低了问题复杂度. 刘坤等[3 ] 针对追逃双方分散的情形,将多智能体追逃转化为多组双智能体博弈,并求解了追逃双方的最优策略. 刘肇隆等[4 ] 在微分博弈论的基础上通过改进图注意力网络,构建了轨迹预测模型,并用圆环覆盖双方运动的轨迹,建立轨迹连接图,预测指标有明显提升. 除了微分博弈论外,阿波罗尼斯圆也可以用于解决追击-逃逸问题[5 -7 ] . 基于阿波罗尼斯圆构建多智能体追逃模型可以求解逃逸成功条件. 若逃逸者在绝对逃逸区域中,则一定能成功逃脱. 确定性方法用数学公式描述模型,有严格的推导过程,求解难度会因对象数量增加成指数增长,且在设计追击策略时通常须对逃逸者的动作做出假定约束或已知逃逸者的控制策略. 因此,该类方法在多智能体对抗的复杂高动态场景下很难取得较好的应用效果. ...
基于阿波罗尼奥斯圆的无人机追逃问题研究
0
2021
基于阿波罗尼奥斯圆的无人机追逃问题研究
0
2021
水面无人艇的抗追捕-逃跑策略
1
2018
... 学术界对追捕-逃逸问题的研究展开了大量探索性工作. 追捕-逃逸问题的解决方法可以分为确定性方法和智能优化算法. 确定性方法的主流方法为微分博弈论. 通过对多智能体追捕-逃跑问题建模并搭建追逃双方的策略选择模型,得出实时策略选择算法[1 ] . 李龙跃等[2 ] 将追逃微分博弈问题转化为单边最优对策问题,提出用改进多项式配点法近似状态变量对时间的微分,降低了问题复杂度. 刘坤等[3 ] 针对追逃双方分散的情形,将多智能体追逃转化为多组双智能体博弈,并求解了追逃双方的最优策略. 刘肇隆等[4 ] 在微分博弈论的基础上通过改进图注意力网络,构建了轨迹预测模型,并用圆环覆盖双方运动的轨迹,建立轨迹连接图,预测指标有明显提升. 除了微分博弈论外,阿波罗尼斯圆也可以用于解决追击-逃逸问题[5 -7 ] . 基于阿波罗尼斯圆构建多智能体追逃模型可以求解逃逸成功条件. 若逃逸者在绝对逃逸区域中,则一定能成功逃脱. 确定性方法用数学公式描述模型,有严格的推导过程,求解难度会因对象数量增加成指数增长,且在设计追击策略时通常须对逃逸者的动作做出假定约束或已知逃逸者的控制策略. 因此,该类方法在多智能体对抗的复杂高动态场景下很难取得较好的应用效果. ...
水面无人艇的抗追捕-逃跑策略
1
2018
... 学术界对追捕-逃逸问题的研究展开了大量探索性工作. 追捕-逃逸问题的解决方法可以分为确定性方法和智能优化算法. 确定性方法的主流方法为微分博弈论. 通过对多智能体追捕-逃跑问题建模并搭建追逃双方的策略选择模型,得出实时策略选择算法[1 ] . 李龙跃等[2 ] 将追逃微分博弈问题转化为单边最优对策问题,提出用改进多项式配点法近似状态变量对时间的微分,降低了问题复杂度. 刘坤等[3 ] 针对追逃双方分散的情形,将多智能体追逃转化为多组双智能体博弈,并求解了追逃双方的最优策略. 刘肇隆等[4 ] 在微分博弈论的基础上通过改进图注意力网络,构建了轨迹预测模型,并用圆环覆盖双方运动的轨迹,建立轨迹连接图,预测指标有明显提升. 除了微分博弈论外,阿波罗尼斯圆也可以用于解决追击-逃逸问题[5 -7 ] . 基于阿波罗尼斯圆构建多智能体追逃模型可以求解逃逸成功条件. 若逃逸者在绝对逃逸区域中,则一定能成功逃脱. 确定性方法用数学公式描述模型,有严格的推导过程,求解难度会因对象数量增加成指数增长,且在设计追击策略时通常须对逃逸者的动作做出假定约束或已知逃逸者的控制策略. 因此,该类方法在多智能体对抗的复杂高动态场景下很难取得较好的应用效果. ...
A new approach of multi-robot cooperative pursuit based on association rule data mining
1
2010
... 智能优化算法可以分为仿生学算法、智能群体算法及强化学习算法. 起初,学术界对强化学习算法的研究集中于Q学习算法. 在多智能体追逃问题中,研究者们对其计算难度高、存在维度爆炸的问题做出了各种改进与尝试[8 -10 ] . 随着计算机技术和人工智能技术的快速发展,深度强化学习理论为多智能体追逃问题提供了一条新的发展道路. 相对于单智能体的强化学习理论,多智能体强化学习在智能体的合作对抗任务中更为复杂. 学术界对多智能体强化学习(multi-agent reinforcement learning,MARL)方法的追逃问题开展了大规模的探索性研究. 2019年,Alexandre 等[11 ] 在无人机跟随和追踪任务中使用了深度强化学习框架. 实验结果表明,所提出的算法在室外场景中展现出了较高的性能. Zhang等[12 ] 使用概率分布奖励值来代替Q函数并将其引入到多智能体深度确定性策略梯度算法(multi-agent deep deterministic policy gradient algorithm,MADDPG)中,消除了奖励的延迟,提高了策略的效率,获得了更好的追击结果. Zhou等[13 ] 提出了基于改进的MADDPG的多机器人追捕方法,通过结合内部奖励和外部环境来解决多机器人追逃场景中的稀疏奖励问题. 夏家伟等[14 ] 基于多智能体近端策略优化算法,结合围捕任务需求设计围捕距离、动作空间以及奖励函数,实现了多无人艇对单无人艇的围捕. ...
A decentralized fuzzy learning algorithm for pursuit-evasion differential games with superior evaders
1
2016
... 智能优化算法可以分为仿生学算法、智能群体算法及强化学习算法. 起初,学术界对强化学习算法的研究集中于Q学习算法. 在多智能体追逃问题中,研究者们对其计算难度高、存在维度爆炸的问题做出了各种改进与尝试[8 -10 ] . 随着计算机技术和人工智能技术的快速发展,深度强化学习理论为多智能体追逃问题提供了一条新的发展道路. 相对于单智能体的强化学习理论,多智能体强化学习在智能体的合作对抗任务中更为复杂. 学术界对多智能体强化学习(multi-agent reinforcement learning,MARL)方法的追逃问题开展了大规模的探索性研究. 2019年,Alexandre 等[11 ] 在无人机跟随和追踪任务中使用了深度强化学习框架. 实验结果表明,所提出的算法在室外场景中展现出了较高的性能. Zhang等[12 ] 使用概率分布奖励值来代替Q函数并将其引入到多智能体深度确定性策略梯度算法(multi-agent deep deterministic policy gradient algorithm,MADDPG)中,消除了奖励的延迟,提高了策略的效率,获得了更好的追击结果. Zhou等[13 ] 提出了基于改进的MADDPG的多机器人追捕方法,通过结合内部奖励和外部环境来解决多机器人追逃场景中的稀疏奖励问题. 夏家伟等[14 ] 基于多智能体近端策略优化算法,结合围捕任务需求设计围捕距离、动作空间以及奖励函数,实现了多无人艇对单无人艇的围捕. ...
1
... 智能优化算法可以分为仿生学算法、智能群体算法及强化学习算法. 起初,学术界对强化学习算法的研究集中于Q学习算法. 在多智能体追逃问题中,研究者们对其计算难度高、存在维度爆炸的问题做出了各种改进与尝试[8 -10 ] . 随着计算机技术和人工智能技术的快速发展,深度强化学习理论为多智能体追逃问题提供了一条新的发展道路. 相对于单智能体的强化学习理论,多智能体强化学习在智能体的合作对抗任务中更为复杂. 学术界对多智能体强化学习(multi-agent reinforcement learning,MARL)方法的追逃问题开展了大规模的探索性研究. 2019年,Alexandre 等[11 ] 在无人机跟随和追踪任务中使用了深度强化学习框架. 实验结果表明,所提出的算法在室外场景中展现出了较高的性能. Zhang等[12 ] 使用概率分布奖励值来代替Q函数并将其引入到多智能体深度确定性策略梯度算法(multi-agent deep deterministic policy gradient algorithm,MADDPG)中,消除了奖励的延迟,提高了策略的效率,获得了更好的追击结果. Zhou等[13 ] 提出了基于改进的MADDPG的多机器人追捕方法,通过结合内部奖励和外部环境来解决多机器人追逃场景中的稀疏奖励问题. 夏家伟等[14 ] 基于多智能体近端策略优化算法,结合围捕任务需求设计围捕距离、动作空间以及奖励函数,实现了多无人艇对单无人艇的围捕. ...
1
... 智能优化算法可以分为仿生学算法、智能群体算法及强化学习算法. 起初,学术界对强化学习算法的研究集中于Q学习算法. 在多智能体追逃问题中,研究者们对其计算难度高、存在维度爆炸的问题做出了各种改进与尝试[8 -10 ] . 随着计算机技术和人工智能技术的快速发展,深度强化学习理论为多智能体追逃问题提供了一条新的发展道路. 相对于单智能体的强化学习理论,多智能体强化学习在智能体的合作对抗任务中更为复杂. 学术界对多智能体强化学习(multi-agent reinforcement learning,MARL)方法的追逃问题开展了大规模的探索性研究. 2019年,Alexandre 等[11 ] 在无人机跟随和追踪任务中使用了深度强化学习框架. 实验结果表明,所提出的算法在室外场景中展现出了较高的性能. Zhang等[12 ] 使用概率分布奖励值来代替Q函数并将其引入到多智能体深度确定性策略梯度算法(multi-agent deep deterministic policy gradient algorithm,MADDPG)中,消除了奖励的延迟,提高了策略的效率,获得了更好的追击结果. Zhou等[13 ] 提出了基于改进的MADDPG的多机器人追捕方法,通过结合内部奖励和外部环境来解决多机器人追逃场景中的稀疏奖励问题. 夏家伟等[14 ] 基于多智能体近端策略优化算法,结合围捕任务需求设计围捕距离、动作空间以及奖励函数,实现了多无人艇对单无人艇的围捕. ...
1
... 智能优化算法可以分为仿生学算法、智能群体算法及强化学习算法. 起初,学术界对强化学习算法的研究集中于Q学习算法. 在多智能体追逃问题中,研究者们对其计算难度高、存在维度爆炸的问题做出了各种改进与尝试[8 -10 ] . 随着计算机技术和人工智能技术的快速发展,深度强化学习理论为多智能体追逃问题提供了一条新的发展道路. 相对于单智能体的强化学习理论,多智能体强化学习在智能体的合作对抗任务中更为复杂. 学术界对多智能体强化学习(multi-agent reinforcement learning,MARL)方法的追逃问题开展了大规模的探索性研究. 2019年,Alexandre 等[11 ] 在无人机跟随和追踪任务中使用了深度强化学习框架. 实验结果表明,所提出的算法在室外场景中展现出了较高的性能. Zhang等[12 ] 使用概率分布奖励值来代替Q函数并将其引入到多智能体深度确定性策略梯度算法(multi-agent deep deterministic policy gradient algorithm,MADDPG)中,消除了奖励的延迟,提高了策略的效率,获得了更好的追击结果. Zhou等[13 ] 提出了基于改进的MADDPG的多机器人追捕方法,通过结合内部奖励和外部环境来解决多机器人追逃场景中的稀疏奖励问题. 夏家伟等[14 ] 基于多智能体近端策略优化算法,结合围捕任务需求设计围捕距离、动作空间以及奖励函数,实现了多无人艇对单无人艇的围捕. ...
基于多智能体强化学习的无人艇协同围捕方法
1
2023
... 智能优化算法可以分为仿生学算法、智能群体算法及强化学习算法. 起初,学术界对强化学习算法的研究集中于Q学习算法. 在多智能体追逃问题中,研究者们对其计算难度高、存在维度爆炸的问题做出了各种改进与尝试[8 -10 ] . 随着计算机技术和人工智能技术的快速发展,深度强化学习理论为多智能体追逃问题提供了一条新的发展道路. 相对于单智能体的强化学习理论,多智能体强化学习在智能体的合作对抗任务中更为复杂. 学术界对多智能体强化学习(multi-agent reinforcement learning,MARL)方法的追逃问题开展了大规模的探索性研究. 2019年,Alexandre 等[11 ] 在无人机跟随和追踪任务中使用了深度强化学习框架. 实验结果表明,所提出的算法在室外场景中展现出了较高的性能. Zhang等[12 ] 使用概率分布奖励值来代替Q函数并将其引入到多智能体深度确定性策略梯度算法(multi-agent deep deterministic policy gradient algorithm,MADDPG)中,消除了奖励的延迟,提高了策略的效率,获得了更好的追击结果. Zhou等[13 ] 提出了基于改进的MADDPG的多机器人追捕方法,通过结合内部奖励和外部环境来解决多机器人追逃场景中的稀疏奖励问题. 夏家伟等[14 ] 基于多智能体近端策略优化算法,结合围捕任务需求设计围捕距离、动作空间以及奖励函数,实现了多无人艇对单无人艇的围捕. ...
基于多智能体强化学习的无人艇协同围捕方法
1
2023
... 智能优化算法可以分为仿生学算法、智能群体算法及强化学习算法. 起初,学术界对强化学习算法的研究集中于Q学习算法. 在多智能体追逃问题中,研究者们对其计算难度高、存在维度爆炸的问题做出了各种改进与尝试[8 -10 ] . 随着计算机技术和人工智能技术的快速发展,深度强化学习理论为多智能体追逃问题提供了一条新的发展道路. 相对于单智能体的强化学习理论,多智能体强化学习在智能体的合作对抗任务中更为复杂. 学术界对多智能体强化学习(multi-agent reinforcement learning,MARL)方法的追逃问题开展了大规模的探索性研究. 2019年,Alexandre 等[11 ] 在无人机跟随和追踪任务中使用了深度强化学习框架. 实验结果表明,所提出的算法在室外场景中展现出了较高的性能. Zhang等[12 ] 使用概率分布奖励值来代替Q函数并将其引入到多智能体深度确定性策略梯度算法(multi-agent deep deterministic policy gradient algorithm,MADDPG)中,消除了奖励的延迟,提高了策略的效率,获得了更好的追击结果. Zhou等[13 ] 提出了基于改进的MADDPG的多机器人追捕方法,通过结合内部奖励和外部环境来解决多机器人追逃场景中的稀疏奖励问题. 夏家伟等[14 ] 基于多智能体近端策略优化算法,结合围捕任务需求设计围捕距离、动作空间以及奖励函数,实现了多无人艇对单无人艇的围捕. ...
基于趋近律滑模控制的智能车辆轨迹跟踪研究
1
2018
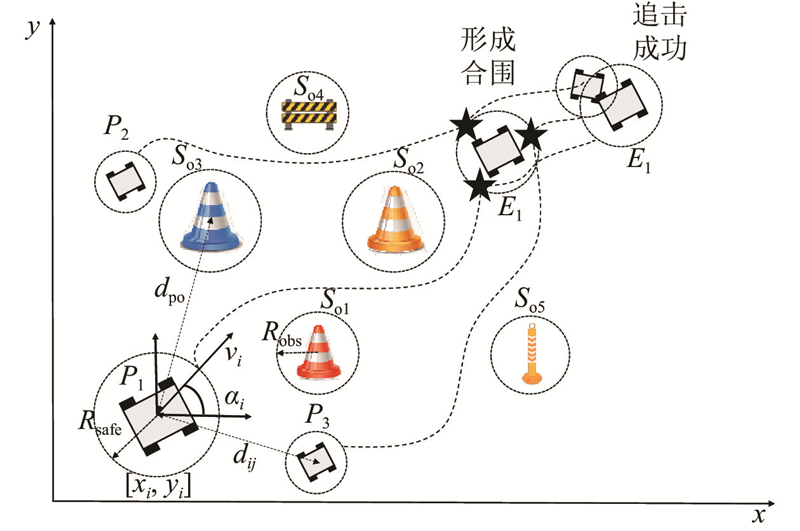
... 设点 $p$ ${\alpha _i}$ x 轴的夹角; ${v_i}$ ${\omega _i}$ x 轴的位移量 ${x_i}$ y 轴的位移量 ${y_i}$ ${\alpha _i}$ [15 ] ,表达式如下: ...
基于趋近律滑模控制的智能车辆轨迹跟踪研究
1
2018
... 设点 $p$ ${\alpha _i}$ x 轴的夹角; ${v_i}$ ${\omega _i}$ x 轴的位移量 ${x_i}$ y 轴的位移量 ${y_i}$ ${\alpha _i}$ [15 ] ,表达式如下: ...
基于MADDPG的边缘网络任务卸载与资源管理
1
2021
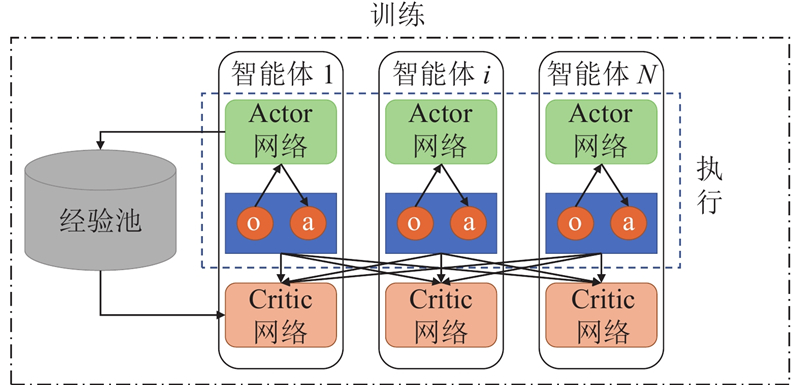
... MATD3算法借鉴MADDPG集中式训练、分布式执行的核心思想,执行框架如图2 所示[16 ] . ...
基于MADDPG的边缘网络任务卸载与资源管理
1
2021
... MATD3算法借鉴MADDPG集中式训练、分布式执行的核心思想,执行框架如图2 所示[16 ] . ...
1
... 在MADDPG算法中,Critic网络的功能与深度Q网络(deep Q network,DQN)中Q网络相似,须通过时序差分(temporal difference,TD)误差更新网络参数. 在使用梯度下降法更新参数时,目标Q值函数根据贪心策略取估计值中的最大值,会导致Q值过估计. 若过估计产生的误差在计算损失函数过程中不断累积,容易造成模型不收敛. TD3算法使用双层Critic网络结构,有效改善了过估计问题[17 ] . MATD3算法借用该思想,将Q值目标值计算2次,表达式如下: ...
1
... TD误差越大,说明当前网络的Q函数与目标网络的Q值相差较大,该样本应该更优先被学习,在此状态处学习效率也更高,价值更高. 然而,采用纯贪心抽取价值最高的经验会造成模型的过拟合. 因此,提出一种贪心和均匀采样相结合的随机采样方法,保证低价值的经验也有可能抽取,每个经验的价值优先级[18 -19 ] 如下: ...
基于深度强化学习的多智能体对抗策略算法
1
2022
... TD误差越大,说明当前网络的Q函数与目标网络的Q值相差较大,该样本应该更优先被学习,在此状态处学习效率也更高,价值更高. 然而,采用纯贪心抽取价值最高的经验会造成模型的过拟合. 因此,提出一种贪心和均匀采样相结合的随机采样方法,保证低价值的经验也有可能抽取,每个经验的价值优先级[18 -19 ] 如下: ...
基于深度强化学习的多智能体对抗策略算法
1
2022
... TD误差越大,说明当前网络的Q函数与目标网络的Q值相差较大,该样本应该更优先被学习,在此状态处学习效率也更高,价值更高. 然而,采用纯贪心抽取价值最高的经验会造成模型的过拟合. 因此,提出一种贪心和均匀采样相结合的随机采样方法,保证低价值的经验也有可能抽取,每个经验的价值优先级[18 -19 ] 如下: ...
1
... 综上所述即为所有奖励函数. 若每个智能体直接使用以上奖励函数进行环境交互和训练,一个追击者的惩罚值会施加至所有追击者造成全局奖励降低多倍,进而影响该交互经验的权重优先级,最终导致追击者的训练效果变差. 为了实现全局奖励和局部奖励最大化,对奖励函数解耦,将奖励函数分为个体奖励和联合奖励[20 -21 ] . 在奖励函数中 ${r_{{\text{cap}}}}$ ${r_{{\text{help}}}}$ $ {r_{{\text{dist}}}} $ $ {r_{{\text{coll}}}} $ $ {r_{{\text{crash}}}} $
基于DE-MADDPG的多无人机协同追捕策略
1
2022
... 综上所述即为所有奖励函数. 若每个智能体直接使用以上奖励函数进行环境交互和训练,一个追击者的惩罚值会施加至所有追击者造成全局奖励降低多倍,进而影响该交互经验的权重优先级,最终导致追击者的训练效果变差. 为了实现全局奖励和局部奖励最大化,对奖励函数解耦,将奖励函数分为个体奖励和联合奖励[20 -21 ] . 在奖励函数中 ${r_{{\text{cap}}}}$ ${r_{{\text{help}}}}$ $ {r_{{\text{dist}}}} $ $ {r_{{\text{coll}}}} $ $ {r_{{\text{crash}}}} $
基于DE-MADDPG的多无人机协同追捕策略
1
2022
... 综上所述即为所有奖励函数. 若每个智能体直接使用以上奖励函数进行环境交互和训练,一个追击者的惩罚值会施加至所有追击者造成全局奖励降低多倍,进而影响该交互经验的权重优先级,最终导致追击者的训练效果变差. 为了实现全局奖励和局部奖励最大化,对奖励函数解耦,将奖励函数分为个体奖励和联合奖励[20 -21 ] . 在奖励函数中 ${r_{{\text{cap}}}}$ ${r_{{\text{help}}}}$ $ {r_{{\text{dist}}}} $ $ {r_{{\text{coll}}}} $ $ {r_{{\text{crash}}}} $