相较于新型路侧感知设备布设方法研究较少的现状,有关地感线圈等断面交通流检测器、高清卡口相机等断面车牌识别设备的道路路段优化布设方法的研究较多. 这些研究的优化目标主要分为3类:提高交通流参数预测精度、缩短突发事件检测时间、提高路段行程时间估计精度. 面向交通流参数预测的路侧感知设备布设方法主要基于断面交通流检测数据构建宏观交通流模型,分析不同设备布设方案下的交通流参数估计精度,优化感知设备布设方案. Liu等[3]基于梯形流量密度曲线的元胞传输模型拟合高速公路实际交通流数据,提出面向交通流瓶颈精确定位的断面检测器布设方法,使用实际数据验证了所提方法的有效性. Contreras等[4]提出基于线性化Lighthill-Whitman-Richards模型的交通流状态能观性分析方法,并通过仿真实验对比不同断面检测器布设方案的交通流状态观测性能. 面向突发事件检测的路侧感知设备布设方法主要通过分析事件发生点上下游断面交通流参数变化获知事件发生,通过宏观交通流模型[5]或者机器学习模型[6]获取交通流参数变化模式. 对于面向行程时间估计的路侧感知设备布设方法,Gentili等[7]发现图论和聚类是2种常用于检测设备布设方法研究的方法论,两者分别将设备布设问题抽象为最短路径搜索问题和最小化组内间距问题.
由上述研究可知,确定交通状态检测需求是设计路侧感知设备布设方案的先决条件,在设备购置及安装预算约束下尽可能提升交通状态检测广度、精度和可靠性是设备布设方法研究的内涵. 道路交通安全是高速公路运营管理的核心关切,以行车安全监测为目标的路侧感知设备布设方法却鲜有研究涉及. 与之相近的面向突发事件检测的设备布设方法,常采用事件平均检测时间、误检率、道路占有率等指标评价设备布设方案优劣. 这种方法只在交通事故发生后造成交通状态变化时才能发挥作用,难以满足道路交通安全状态实时监测的高时效性和精准性需求,无法应用于道路行车风险主动防控中. 本研究提出面向高速公路行车风险路侧感知系统的设备优化布设方法,并基于信息熵理论提出道路行车安全风险综合量化方法,将多种类型交通安全风险评价指标应用于道路行车风险评价中. 在此基础上,以获取行车风险熵最大化为目标,以设备购置预算、设备感知范围为约束,构建路侧感知设备优化布设方案,使用实际公路车辆轨迹数据设计多组算例,验证本研究提出的高速公路行车风险路侧感知系统的设备优化布设方法的适用性.
1. 行车安全风险度量
鉴于交通事故发生频率很低,发生时间和地点随机性较强,且事故致因与个体交通参与者自身属性关系紧密,研究者通常基于仿真或实测数据定义行车风险评价指标,并以行车风险量化评估为切入点,开展重点路段或交叉口事故防控方法的研究. 可用于行车风险评估的数据包括自然驾驶数据[8]、断面交通流参数[9]和车辆行驶轨迹数据[10]. 自然驾驶数据精细度高,可以反映驾驶员生理状态和车辆操控细微动作,但是样本量有限导致驾驶行为多样性匮乏,而且数据难被设计者获得. 断面交通流参数(如车速、密度)可以通过高速公路交通流检测器采集获得,缺点是数据时效性较低,只能借助宏观交通流模型间接推断检测点上下游路段的行车风险. 车辆轨迹数据能够兼顾样本数量和多样性,且新型路侧感知设备具备采集轨迹数据的能力. 本研究使用车辆轨迹数据计算行车安全风险,将量化结果作为计算设备布设位置的输入. 行车安全风险量化流程的具体步骤如下:1)从现有交通安全研究文献中选择合适的替代安全指标(surrogate safety indicator),从不同角度衡量车辆行车风险;2)检测选中的各类替代安全指标的相关性,剔除强相关指标,以降低指标重复使用可能造成的信息冗余;3)基于信息熵理论,设计多指标融合的行车风险量化方法.
1.1. 行车风险指标筛选
表 1 高速公路行车风险替代安全指标分类
Tab.1
| 类型 | 名称 | 含义 | 累积型指标 |
| 时距型 | 碰撞时间(time-to-collision,TTC) | 碰撞车辆以当前速度和相同路径到达碰撞点的时间 | 否 |
| 暴露碰撞时间(time exposed time-to-collision,TET) | 某段时间内TTC值低于阈值(TTC*)的情况下车辆接近前车的时间长度 | 是 | |
| 修正综合碰撞时间(modified time integrated time-to collision,TIT) | 碰撞时间曲线的积分 | 是 | |
| 碰撞时间导数(derivative of TTC,TTCD) | TTC的导数 | 否 | |
| 后侵入时间(post-encroachment time,PET) | 前车车尾与后车车头到达同一位置的时间差 | 否 | |
| 间距型 | 紧急减速下潜在碰撞指数(potential index for collision with urgent deceleration,PICUD) | 前车和后车紧急制动后完全停止时的距离 | 否 |
| 时间暴露追尾碰撞风险指数(time exposed rear-end crash risk index,TERCRI)[16] | 一段时间内前车停止距离小于后车停止距离的时间长度 | 是 | |
| 减速度型 | 避免碰撞减速率(deceleration rate to avoid a crash,DRAC) | 后车及时停车(或与前车的速度相匹配)以避免发生碰撞所需的最小减速度 | 否 |
| 关键指数函数(criticality index function,CIF) | 即将发生冲突的可能性 | 否 | |
| 速度型[17] | DeltaS | 最小碰撞时间时车速(或轨迹)差异 | 否 |
| MaxS | 冲突期间(TTC小于阈值)任一车辆的最高速度 | 否 |
式中:p(u, v)为u、v的联合密度分布函数. 2)计算MIC,
式中:α为u方向上的网格数量,β为v方向上的网格数量,B为最大网格划分数.
1.2. 行车风险指标融合计算
信息熵可以用于度量系统的混乱程度,若系统混乱程度越高,则信息熵越高[20]. 这与道路行车安全环境十分相似:道路上车辆行驶越有秩序,车辆间发生碰撞的概率越低,行车风险越小;反之,在存在车辆间频繁交互的交通流中,出现交通事故的概率较高. 行车风险熵的计算步骤如下.
1)指标值归一化. 各个替代安全指标的有效取值范围不同,为了减少不同指标取值范围差异对多指标合并后的风险熵值的影响,须进行指标归一化处理,使其值在[0, 1.0]分布. 根据行车风险与指标值的对应关系,使用2种指标值归一化方法. i)当指标值与行车风险正相关时,使用越大越优型方法,指标的归一化计算式为
式中: rpq、λpq分别为指标q在统计区间p的原始值、归一化处理后的值,rq为指标q在所有统计区间的可能值. ii)当指标值与行车风险负相关时,使用越小越优型方法,指标的归一化计算式为
2)计算单指标行车风险熵,
式中:hq为指标q的行车风险熵,n为数据统计区间的总数,a为替代安全指标的数量.
3)计算行车风险熵权重ωq. 在合并各个替代安全指标转化的行车风险熵时,采用熵权法[21]确定各指标风险熵的权重ωq. 此方法的原理:对于某个数据统计区间,若某个指标的风险熵值变化大于其他指标的熵值,则说明此指标相对重要,赋予较大的权值;反之,则赋予较小权值.
数据统计区间内的各个替代安全指标的行车风险总熵的计算式为
当λpq=0时,令Sp=0.000 1,以避免出现数据无意义的情况.
2. 路侧感知设备布设方法
2.1. 设备选用与安装
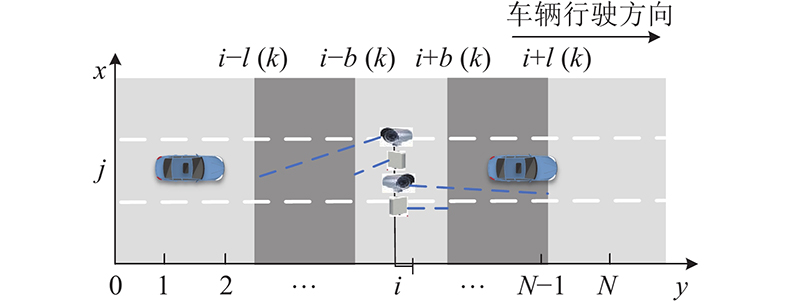
如图1中所示为高速公路路侧感知设备常见的立杆以及门架安装方法示意图,图中深色部分为设备有效感知范围,浅色部分为设备感知盲区. 将研究路段起始点定义为图中的坐标原点,对于第i个设备布设候选点,其坐标满足[l(k), N−l(k)](0≤k≤K),其中l(k)为第k种设备的纵向检测距离,K为路侧感知设备的种类总数. b(k)为第k种设备纵向检测盲区的长度,设为固定值,N为研究路段候选点总数. 为了充分利用基础设施资源,通常在同一立杆上布设感知方向相反的2个设备,同时检测前向与后向车辆. 本研究选用新型毫米波雷达-摄像机一体化集成设备(下文称雷视一体机)作为行车风险感知设备. 此类设备视频图像信息丰富且抗环境干扰能力强,能够精准获取覆盖范围内多条车道上的车辆轨迹信息. 由于雷视一体机的原始数据量较大,须搭配用于数据处理的边缘计算机. 每个设备布设点均设置有1根立杆、1台边缘计算设备和2台路侧感知设备. 经过调研,单个设备布设点位的布设成本主要由设备单价、安装养护成本、计算设备组成,对于不同检测距离的路侧感知设备,安装养护成本与计算设备成本基本不变,此处按照1.48万元与1万元计算. 对于330 m的检测设备,其盲区长度为30 m,设备单价为3.5万元,按照图1所示方式进行布设,成本为9.48万元;对于200 m的检测设备,其盲区长度为30 m,设备单价为1.2万元,按照图1所示方式进行布设,成本为4.88万元.
图 1
图 1 路侧感知设备安装与研究路段
Fig.1 Roadside sensing device installation and studied road section
2.2. 问题描述
研究地点设定为如图1所示的高速公路单向路段,定义车辆运动的方向为雷视一体机的纵向检测方向(y轴),与之垂直的为横向检测方向(x轴). 路侧每隔一段固定距离设置一处设备安装候选点,候选点编号为i(0≤i≤N),N为研究路段候选点总数. 计算替代安全指标需要设定数据统计区间,因此N等于研究路段长度与此统计区间长度的比值.
本文研究的是面向行车安全风险检测的路侧感知设备选址问题. 设备选址问题的属性可以通过设备属性、服务对象、衡量标准和选址目标界定[22]. 数量、空间分布、能力约束等属于设备属性,空间形态、需求特性属于服务对象,距离度量方式如欧氏距离、直角距离属于衡量标准,成本、服务范围属于选址目标. 选址问题的属性可以归纳为以下6个方面. 1)路侧感知设备尺寸相对于路段总长度很小,且每个设备的纵向检测距离有限,可视为有能力约束的点状设备. 2)选择研究路段路侧的N个可行位置中合适的地点安装设备,且设备安装完成后不再移动,属于多设备静态连续选址. 3)任意相邻2个设备的检测范围无重叠,属于非竞争选址.4)服务对象为具有线状特征的时空连续车辆轨迹,由于工程实践中通常采用“先收集数据,再确定选址”的工作流程,本研究使用有限时间内采集的离线数据算出的行车风险总熵作为选址依据,可认为设备感知需求是确定的,不随时间变化. 5)研究路段为平直路段,属于欧氏距离选址. 6)选址的目标是获取最高行车风险熵,其中预算约束控制设备数量,由有限数量的设备获取的行车风险熵决定设备布设位置.
2.3. 模型构建
与Ivanchev等[9]的建模方法类似,为了获取路侧感知设备的最优布设位置,构建0—1的整数规划模型. 引入二进制变量x(i, k),x(i, k)=1表示在第i个候选点布设第k种路侧感知设备,x(i, k)=0表示在i点处不布设第k种设备. 雷视一体机的检测范围可以覆盖多条车道,因此第k种路侧感知设备在候选点i处获取的行车风险熵为
式中:S(i', j)为在候选点i处的第j条车道上采集的行车风险熵,i'为计算i处设备感知范围使用的中间变量;J为路段车道总数. 式(8)的第1项计算的是图1中i处面向道路上游的感知设备获取的行车风险熵,第2项计算的是面向下游的设备获取的行车风险熵.
2.3.1. 目标函数
基于上述设定,将研究问题转化为在特定的约束下,寻找最优的设备布设位置、路侧感知设备种类,使得设备采集到的行车风险熵最高. 设置目标函数为
式中:S为所有感知设备获取的行车风险熵总和.
2.3.2. 主要约束条件
1)预算约束. 所有布设点位的总成本应不高于预算总额C:
式中:c(k)为在某布设点位安装第k种路侧感知设备的总成本.
2)覆盖约束. 为了避免相邻2个布设点位的设备对同个区域重复检测,要求所有设备感知范围无重叠:
式中:i1、i2均为相邻设备布设候选点,i1≤i2;∆d为相邻设备候选点的间隔.
3. 算例分析与讨论
3.1. 数据预处理
图 2
3.2. 行车安全风险熵计算
使用预处理后的轨迹数据计算替代安全指标的值. 在计算时距累积型指标(如 TET、TIT)时,须设定数据统计区间. 考虑到平均车速是路段交通流的基本特征参数之一,采用数据集中车辆在1 s的平均位移9.25 m作为计算替代安全指标的统计区间长度. 此区间定义也用于式(3)、(4)的计算中. 对于等瞬时型指标(如TTC、DRAC),计算其在此区间内的总和,有助于进一步降低数据噪声. 为了确保设备布设候选点位选取的灵活性,以步长1 m依次计算研究区域内的替代安全指标值.
图 3
图 3 替代安全指标的相关性检验结果
Fig.3 Correlation test results of surrogate safety indicators
表 2 替代安全指标的权重
Tab.2
| 指标 | ω | 指标 | ω | |
| TTC | 0.15 | TET | 0.13 | |
| DRAC | 0.14 | PET | 0.12 | |
| CIF | 0.14 | TERCRI | 0.11 | |
| TIT | 0.07 | MaxS | 0.14 |
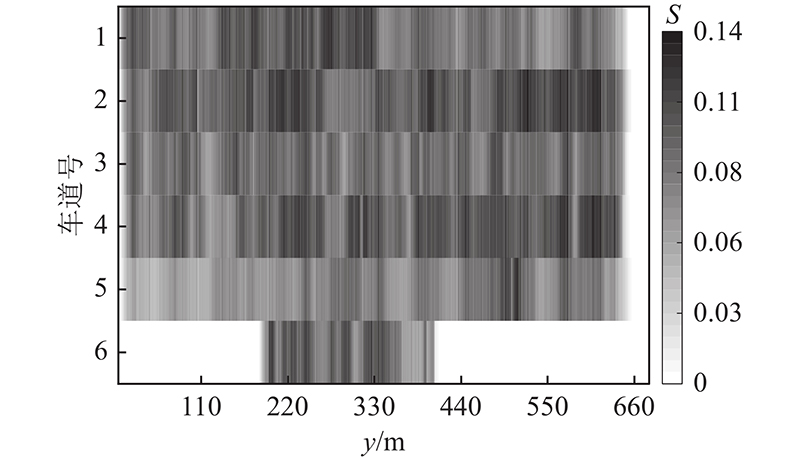
图 4
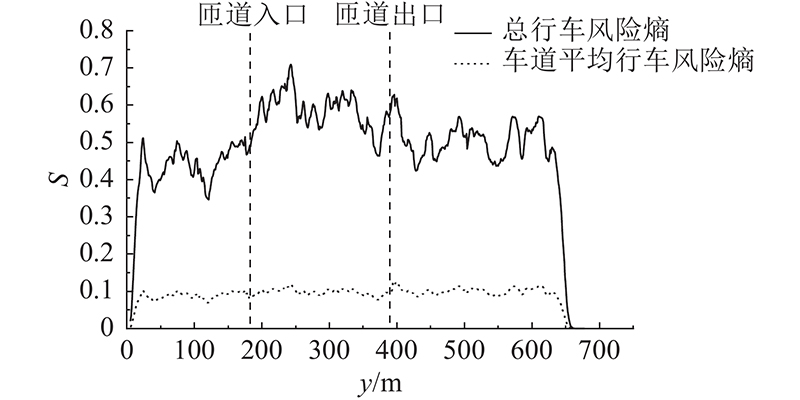
图 5
图 5 研究路段的行车风险总熵以及车道平均熵
Fig.5 Total and lane average driving risk entropy of studied road section
3.3. 设备布设位置计算与分析
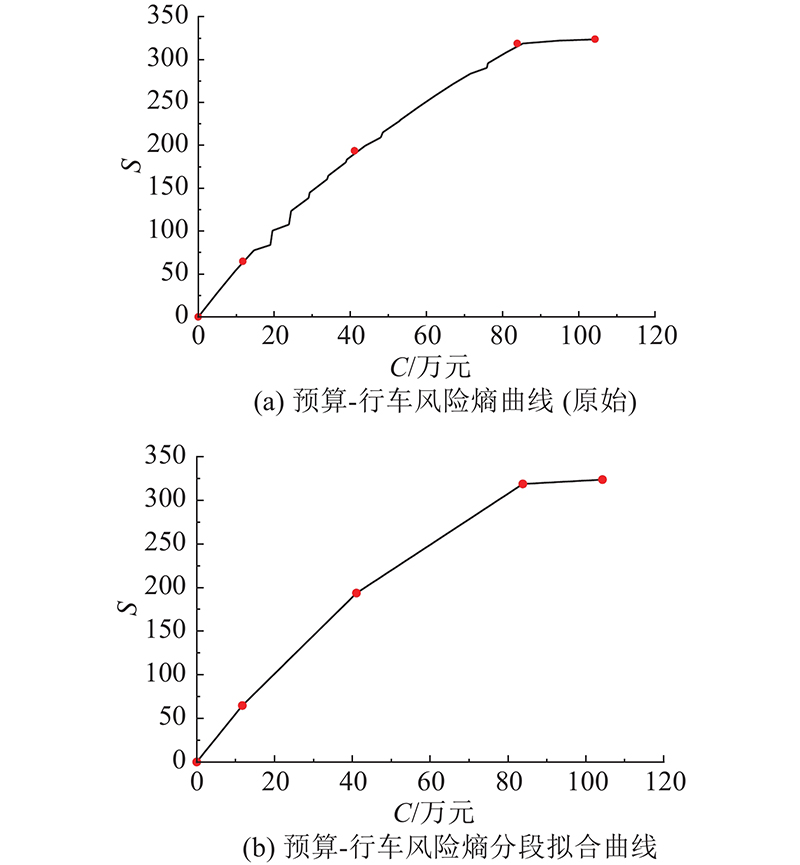
基于路侧感知设备布设模型设置多组算例,在Python环境中使用Gurobi求解器进行建模和求解. 数据集所覆盖道路长度较短,因此在算例中将雷视一体机的纵向检测距离和检测盲区范围均缩小至真实值的10%.
3.3.1. 最优布设方案与费效比分析
图 6
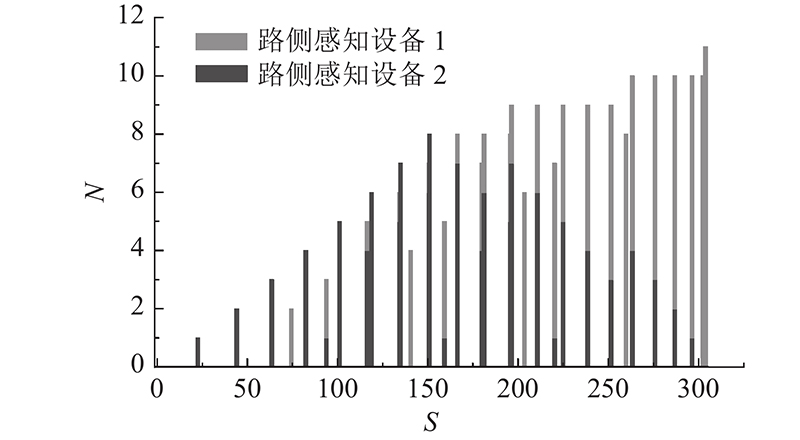
3.3.2. 设备组合方案分析
增加路侧感知数量后,最优设备组合方案下获取的行车风险熵变化趋势如图7所示. 可以发现,增加设备1的数量能够感知更多的行车风险熵,为了获取更多风险熵,设备2的数量呈现先增加后下降的趋势. 与设备1相比,虽然设备2的感知范围与感知盲区的比例高,但是价格便宜,因此在预算不足的情况下,算法会优先选用设备2. 随着预算不断上升,设备1的感知范围更广且盲区占比更小,对于相同长度的感知区域来说,设备1比设备2的费效比高.
图 7
图 7 设备数量-行车风险熵变化叠加柱状图
Fig.7 Bar chart on device number and driving risk entropy
表 3 不同预算约束下的路侧感知设备最优布设方案
Tab.3
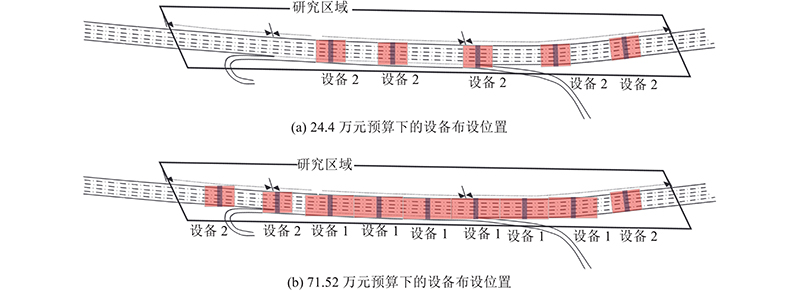
| 方案 | C/万元 | N1,N2 | y1,y2/m | S | |
| 1 | 24.4 | 0,5 | —,{231,315,399,503,587} | 101.99 | |
| 2 | 71.52 | 6,3 | {220,286,352,418,484,550},{83,154,616} | 251.27 | |
| 3 | 90.2 | 9,1 | {89,155,221,287,353,419,485,551,617},{23} | 296.29 | |
| 4 | 104.28 | 11,0 | {30,96,162,228,294,360,426,492,558,624,678 },— | 303.79 | |
图 8
图 8 2种预算约束下的路侧感知设备布设位置
Fig.8 Locations of roadside sensing devices under two budget constraints
3.3.3. 布设方案对比
花费48.8 万元即可使用设备2实现路段全覆盖,为了验证所提布设方案在此预算下的效果,增加方案5如表4所示. 表中优化布设、等间距布设1和等间距布设2分别表示采用优化布设方案、全部使用设备1的等间距布设方案的方案与全部使用设备2的等间距布设方案的方案. 在方案1、5中,与2种等间距布设方案相比,优化布设方案在成本相近的情况下可以采集更高的行车风险熵. 再看方案2、3,与全部使用设备1的等间距布设方案相比,优化布设方案可以在更低的预算下采集更多的行车风险熵. 试验结果说明,所提布设方案相较于等间距布设方案具有更高的费效比. 设备2在预算为48.8 万元时可以实现道路感知全覆盖,因此没有在方案2、3中增加预算. 对比方案4可知,设备1比设备2的盲区占比更小,因此当采用单一类型设备对路段全覆盖时,设备1可以获取更多行车风险熵,说明预算充足时应优先使用设备1.
表 4 优化布设方案与等间距布设方案对比
Tab.4
| 方案 | 优化布设 | 等间距布设1 | 等间距布设2 | |||||
| C/万元 | S | C/万元 | S | C/万元 | S | |||
| 1 | 24.40 | 101.99 | 28.44 | 93.37 | 24.40 | 92.21 | ||
| 2 | 71.52 | 251.27 | 75.84 | 243.77 | 48.80 | 176.71 | ||
| 3 | 90.20 | 296.29 | 94.80 | 294.72 | 48.80 | 176.71 | ||
| 5 | 48.24 | 181.16 | 47.40 | 161.02 | 48.80 | 176.71 | ||
3.3.4. 布设方案敏感性分析
车辆轨迹数据可能由于采集设备性能、车辆遮挡、不良天气等因素产生测量误差. 为了验证所提布设方案对于原始数据测量误差的敏感性,通过对原始车辆轨迹数据分别加入1%、5%、10%的噪声Noise,设置与表3中4个布设方案相同的预算约束,重新计算最优设备布设方案如表5所示. 可以看出,路侧感知设备的数量和类型均未出现明显变化. 在24.4 万元的预算约束下,设备布设位点最大偏移值为8 m,其余点位偏移均不超过5 m;在71.52 万元预算约束下,仅设备2在83 m处出现12 m的偏移,其他点位最多出现1 m的偏移;在90.2、104.28 万元的预算约束下,所有设备点位偏移不超过1 m. 上述结果说明,在预算约束较强时,原始数据测量误差会对设备布设方案产生一定影响,但是总体上本研究所提出设备布设方法对测量误差的敏感性较低,具有一定的工程适用性.
表 5 设备布设方案敏感性分析结果
Tab.5
| C/万元 | y1,y2/m | |||
| 原始 | Noise=1% | Noise=5% | Noise=10% | |
| 24.40 | —,{231,315,399,503,587} | —,{230,323,401,500,586} | —,{228,315,402,500,587} | —,{228,315,399,500,586} |
| 71.52 | {220,286,352,418,484,550},{83,154,616} | {220,286,352,418,484,550},{71,154,616} | {220,286,352,418,484,550},{71,154,616} | {221,287,353,419,485,551},{71,155,617} |
| 90.20 | {89,155,221,287,353,419,485,551,617},{23} | {89,155,221,287,353,419,485,551,617},{23} | {89,155,221,287,353,419,485,551,617},{23} | {89,155,221,287,353,419,485,551,617},{23} |
| 104.28 | {30,96,162,228,294,360,426,492,558,624,678},— | {30,96,162,228,294,360,426,492,558,624,678},— | {31,97,163,229,295,361,427,493,559,625,678},— | {30,96,162,228,294,360,426,492,558,624,678},— |
4. 结 论
(1)本研究提出基于信息熵理论的高速公路行车风险多指标度量与融合方法,构建了以获取行车风险熵最大为目标,考虑建设预算和设备感知范围的路侧感知设备布设优化模型. 分析了感知设备选型、设备采购和安装预算、传统等间距设备布设方案、原始数据测量误差等因素对路侧感知系统获取行车风险能力的影响.
(2)算例分析结果显示,路侧感知设备购置、安装预算投入、路段行车风险感知能力呈现边际效用递减规律. 当预算约束较强时,使用低成本设备具有较高的费效比;当预算相对充足时,采用高成本设备费效比较高. 相较于工程上常用的等间距布设方法,所提路侧感知设备布设方法具有更高的费效比;预算较少情况下获得的路侧设备布设方案比预算充裕情况下的方案对原始数据测量误差更敏感.
(4)虽然本研究在计算原理上避免了车辆轨迹必须具有时空连续性的问题,但数据采集仍需消耗一定的人力物力,下一步准备从如收费站数据、门架数据的现有数据入手,结合历史事故数据优化路侧感知设备布设位置,为智慧高速中设备选址提供依据.
参考文献
延庆至崇礼高速公路雷达路况感知系统
[J].DOI:10.13439/j.cnki.itsc.2021.01.009 [本文引用: 1]
Yanqing-Chongli expressway radar traffic awareness system
[J].DOI:10.13439/j.cnki.itsc.2021.01.009 [本文引用: 1]
Optimal sensor locations for freeway bottleneck identification
[J].DOI:10.1111/j.1467-8667.2009.00614.x [本文引用: 1]
Observability and sensor placement problem on highway segments: a traffic dynamics-based approach
[J].DOI:10.1109/TITS.2015.2491282 [本文引用: 1]
基于流量与占有率模型的交通事件检测器布设研究
[J].
Study of Layout of incident detectors based on traffic flow and occupancy models
[J].
Review of optimal sensor location models for travel time estimation
[J].DOI:10.1016/j.trc.2018.01.021 [本文引用: 1]
High-resolution vehicle trajectory extraction and denoising from aerial videos
[J].DOI:10.1109/TITS.2020.3003782 [本文引用: 2]
Information maximizing optimal sensor placement robust against variations of traffic demand based on importance of nodes
[J].DOI:10.1109/TITS.2015.2481928 [本文引用: 2]
基于自然驾驶数据的跟车场景潜在风险评估
[J].DOI:10.3969/j.issn.1001-7372.2020.04.017 [本文引用: 1]
Assessment of the potential risk in car-following scenario based on naturalistic driving data
[J].DOI:10.3969/j.issn.1001-7372.2020.04.017 [本文引用: 1]
Application of proximal surrogate indicators for safety evaluation: a review of recent developments and research needs
[J].DOI:10.1016/j.iatssr.2017.02.001 [本文引用: 1]
Surrogate safety measure for simulation-based conflict study
[J].
Methodologies for aggregating indicators of traffic conflict
[J].
A review of naturalistic driving study surrogates and surrogate indicator viability within the context of different road geometries
[J].DOI:10.1016/j.aap.2021.106185 [本文引用: 1]
Longitudinal safety evaluation of connected vehicles’ platooning on expressways
[J].DOI:10.1016/j.aap.2017.12.012 [本文引用: 1]
Comprehensive safety assessment in mixed fleets with connected and automated vehicles: a crash severity and rate evaluation of conventional vehicles
[J].DOI:10.1016/j.aap.2020.105567 [本文引用: 1]
Detecting novel associations in large data sets
[J].DOI:10.1126/science.1205438 [本文引用: 1]
基于驾驶行为和信息熵的道路交通安全风险预估
[J].DOI:10.3969/j.issn.1001-7372.2020.06.018 [本文引用: 1]
Road traffic safety risk estimation based on driving behavior and information entropy
[J].DOI:10.3969/j.issn.1001-7372.2020.06.018 [本文引用: 1]
卫星定位数据驱动的营运车辆驾驶人驾驶风险评估模型
[J].DOI:10.19721/j.cnki.1001-7372.2020.06.019 [本文引用: 1]
Driving risk assessment model of commercial drivers based on satellite-positioning data
[J].DOI:10.19721/j.cnki.1001-7372.2020.06.019 [本文引用: 1]
Location analysis: a synthesis and survey
[J].DOI:10.1016/j.ejor.2003.11.032 [本文引用: 1]
Smoothing and differentiation of data by simplified least squares procedures
[J].DOI:10.1021/ac60214a047 [本文引用: 1]
基于 Fisher Score 与最大信息系数的齿轮箱故障特征选择方法
[J].
Fault feature selection method of gearbox based on Fisher Score and maximum information coefficient
[J].